2. 海军航空工程学院科研部, 烟台 264001
2. Department of Scientific Research, Naval Aeronautical Engineering Institute, Yantai 264001, China
随着技术的发展,现代设备结构日趋复杂,逐渐向大型化、自动化等方向发展,各部件之间联系更加紧密,这就为复杂装备的故障诊断带来了新的挑战。在诊断知识获取过程中,由于被测对象结构复杂、诊断系统采集的信息缺失等原因,致使所得到的故障信息存在不完备的情况;同时,在设备实际运行过程中,常常伴随有并发故障的发生。因此,为了保证设备运行安全稳定,对不完备信息条件下的并发故障诊断方法进行研究具有一定的现实意义。
在故障诊断领域,信息不完备是指诊断系统中某一数据或多个数据丢失、不完全或无法确定,即数据信息不完整。Kryszkiewicz[1]提出了不完备信息系统的容差关系模型及其知识约简方法,使得粗糙集理论成为处理不完备信息的有效手段。目前,针对不完备信息条件下的故障诊断方法主要也是围绕粗糙集理论展开,通过构建不完备决策表对故障信息进行表示。在实际诊断应用中,文献[2]提出了基于信息熵的约简算法;文献[3]通过定义最大特征相似集完成约简与规则提取;文献[4]则根据机械故障的特征定义了一种新的相容关系;文献[5]基于约简的不唯一性,提出了一种最优测试信息的选取方法;文献[6]则根据不完备信息的特点设计了新的属性约简方法与基于可信度的诊断方法;文献[7]通过建立中间变量直接将不完备信息系统分解为简单规则的集合,提取诊断规则,同时,将粗糙集理论与其他人工智能方法结合进行不完备信息条件下的故障诊断也取得了较好的效果;文献[8]引入模糊决策系统与神经网络,设计了转台的粗糙神经网络故障诊断系统;文献[9]提出了一种基于粗糙集与灰色理论的不完备信息条件下的变电站故障诊断方法,利用粗糙集进行约简,通过属性的灰色相关梯度进行决策;文献[10]在对锅炉水位控制系统的故障诊断中,面对不完备信息,首先用粗糙集方法构建决策表,然后使用BP神经网络对冗余属性进行约简;文献[11]针对直升机传动系统诊断决策表,在概念上对缺失属性值进行分析,提出粒计算模型的定义,构建算法进行属性约简。
由于多重故障并发时,其表现形式多样,故障和征兆之间并非简单的一一对应关系,造成了对并发故障诊断的困难。针对这一问题,一些新的方法不断地被应用于其中。例如,文献[12]针对核动力装置的并发故障利用复合神经网络实现故障的分离;文献[13]提出了一种基于先验知识和相关向量机的并发故障诊断方法,在新的框架下,只需要使用单发故障模式对相关向量机进行训练,就可以完成对并发故障的判断;文献[14]通过构建2层贝叶斯网络对多源信息进行融合,完成了对地热泵系统的并发故障诊断,有效地提升了诊断准确度。而更为普遍的并发故障诊断研究是在DSmT理论框架中展开的。自DSmT提出以来[15],因其允许辨识框架内元素不互斥,为并发故障模型的建立提供了新的思路。目前,已有学者开展了基于DSmT的并发故障诊断方法的研究。李植良等[16]基于DSmT中的广义辨识框架构建了并发故障诊断模型,通过DSmT组合与决策规则得到最终诊断结果;文献[17]利用随机集方法获得诊断证据,并以此构建了新的适用于单发与并发故障的组合规则;文献[18-20]则给出了DSmT理论在实际并发故障诊断中的应用实例。
目前,针对不完备信息条件下的并发故障诊断还少有研究。为了有效地解决这一问题,本文在已有研究的基础上,将粗糙集与DSmT理论相结合进行并发故障诊断。利用粗糙集构建不完备诊断信息决策表,对存在缺失的测试信息进行表示,鉴于不同的测试属性在决策中的重要程度并不相同,提出不完备边界粗糙熵的概念对测试属性的重要度进行度量;同时给出了不完备情况下属性值频率的计算方法,以构建证据的基本信度赋值函数。在DSmT框架下的并发故障诊断模型中进行证据合成。同时,为了在合成过程中体现出不同测试属性对决策的不同重要度,获得更为精确的诊断结果,在DSmT框架下提出一种基于先验知识的区间信度合成规则。将此方法应用于实际诊断过程中,对效果进行验证。
1 不完备故障信息表示与特征提取 1.1 相容关系下不完备并发故障诊断决策系统定义1 有序数组,*∈V表示不完备并发故障诊断决策系统IDS=(U, C∪{d}, V, f),U为关于测试样本的非空有限集合,C为测试属性的非空有限集合,{d}为故障决策属性,V为测试属性的值域,f为测试信息函数,它为每一次测试样本的每个测试属性赋予一个测试值,同时,系统中至少存在一个c∈C, x∈U, 使得V为缺省值,用符号“*”表示。
定义2 给定一个不完备并发故障诊断决策系统IDS=(U, C∪{d}, V, f),*∈V,对于任意测试属性的子集加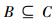
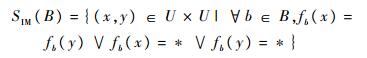
|
令SB(x)表示对象集{y∈U|(x, y)∈SIM(B)},对于集合B而言,SB(x)是与x不可区分的对象的最大集合,fb(x)表示在属性b下与x不可区分的对象的最大集合。
令SIM(B)={SB(x)|x∈U}表示对U的一种分类,则U/SIM(B)中的元素称为相容类。U/SIM(B)中的相容类一般不构成U的划分,其构成U的覆盖,∪U/SIM(B)=U。
定义3 给定一个不完备并发故障诊断决策系统IDS=(U, C∪{d}, V, f),*∈V。对于集合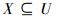

|
在不完备并发故障诊断决策系统中,每一条测试属性相对于决策所起的作用均不相同,为此引进测试属性重要度的概念对其进行度量,该重要度随属性的不确定性大小而变化;并且提出不完备并发故障诊断决策系统中的不完备边界粗糙熵的概念,将属性的不确定性予以量化,并依据量化后的值给出测试属性重要度的计算方法。
定义4 给定IDS=(U, C∪{d}, V, f),*∈V,集合X ⊆ U,对于任意测试属性的子集B ⊆ C,SIM(B)为U上的相容关系,则定义集合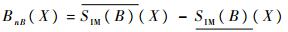
定义5 给定IDS=(U, C∪{d}, V, f),*∈V,集合X ⊆ U,Y⊆U,B⊆C。相容关系SIM(B)对论域U的分类为U/SIM(B)={SB(x1), SB(x2), …, SB(xm)}, 决策{d}对论域U的划分记为U/{d}={Y1, Y2, …, Yn}。如果记Yi=d-1({vd})={k∈U:d(k)=vd},vd为决策属性值,则定义论域U在相容关系SIM(B)下得到的分类对于决策分类Yi的决策边界域为
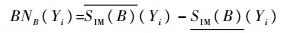
|
定义6 在IDS=(U, C∪{d}, V, f),*∈V中,B⊆C,相容关系SIM(B)对论域U的分类为U/SIM(B)={SB(x1), SB(x2), …, SB(xm)}, 决策{d}对论域U的划分记为U/{d}={Y1, Y2, …, Yn}。定义知识B的不完备边界粗糙熵为
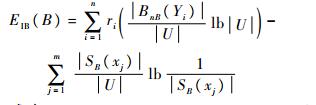
|
(1) |
式中:i=1, 2, …, n;j=1, 2, …, m;ri=Yi / U为等价类Yi的基数与U的基数之比。
IDS中的不完备边界粗糙熵的定义式(1)同时考虑了由相容关系SIM(B)在对U进行分类时,导致不确定的2个方面因素。式(1)等号右端第1项
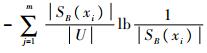
在最优约简结果中,如果去掉某一属性,则随着分类能力的下降,会导致不完备边界粗糙熵的增加,因此,用去掉某一条测试属性后不完备边界粗糙熵的增加量定义该属性的决策重要度。
定义7给定IDS=(U, C∪{d}, V, f),*∈V,B⊆C,对于a∈B,属性a的决策重要度为
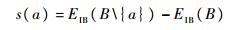
|
(2) |
对式(2)定义的决策重要度经过归一化处理后,就可以得到该测试属性的权重:
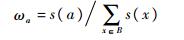
|
(3) |
进行并发故障诊断时,合成的证据群来源于不完备决策表的相对约简,其中每一条测试属性作为证据时的信度赋值函数同样由决策表给出,通过对属性值频率的计算获得。
定义8 在不完备并发故障诊断决策系统IDS=(U, C∪{d}, V, f),*∈V中,对于a∈C,在决策属性dj∈{d}下,在属性a上的属性值fa(Xi)频率区间为

|
式中:|fadj(Xi)|为决策表中某一决策属性dj下与属性a中属性值为fa(Xi)相对应的对象个数;fadj′(Xi)为属性值为fa(Xi)所对应的对象个数与属性值为“*”所对应的对象个数之和;|Va|为决策表中所有决策属性d下与属性a列上属性值为fa(Xi)相对应的对象个数;|Va′|为决策表中所有决策属性下与属性a中属性值为fa(Xi)相对应的对象个数与属性值为“*”所对应的对象个数之和。
如果在决策属性中有n种取值,即系统中存在的故障种类为d1, d2, …,dn。当属性a取值为fa(Xi)时,其作为证据的基本信度赋值为
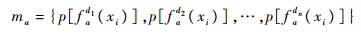
|
DSmT作为信息融合算法中一个新的分支,有效地对D-S证据理论进行了扩展。在DSmT中,Θ={θ1, θ2, …, θn}作为所考虑融合问题的辨识框架,其是包含n个完备命题的有限集合。在DSmT框架下,定义超幂集DΘ,其是由Θ中的命题,以及其通过并、交运算组成的所有符合命题的集合。可表示为:①∅, θ1, θ2,…,θn∈Dθ;②如果A, B∈Dθ,那么A∩B∈Dθ,A∪B∈Dθ;③除了①和②中包含的命题,再无其他命题属于Dθ。
框架Θ中的命题θi(i=1, 2, …, n)组成了表述融合问题所有特征的有限命题集合,其超幂集空间DΘ组成了自由DSm模型,允许表述连续、模糊和相对概念的命题包含其中。在自由DSm模型中,不存在其他约束。但由于框架Θ中的某些子集可能含有相互排斥的命题,或某些命题并不存在,需要将约束条件添加到自由DSm模型中,以便更好地表述真实情况,这样就构造了混合DSm模型。
而DSmT中的DSm模型为并发故障的表述提供了依据。在进行并发故障诊断时,Θ={θ1, θ2, …, θi, …, θn}是一个包含n个单故障模式的有限集合,θi表示其中的一种故障模式。
通过超幂集DΘ组成的自由DSm模型表示整个系统所有可能的故障模式。相比较D-S证据理论框架下必须要求元素间互斥,由于DΘ中包含了∩的运算,所以很好地解决了原有理论无法表示并发故障的问题。例如,当系统有2种单故障模式,Θ={θ1, θ2},则系统所有可能的故障模式,即此时的自由DSm模型可以表示为:{∅, θ1, θ2, θ1∩θ2, θ1∪θ2},∅表示系统无故障,θ1,θ2表示2种单发故障,θ1∩θ2表示2种故障并发,θ1∪θ2表示故障存在,但无法进行判断。
当系统的单故障模式种类为n,即|Θ|=n时,系统所有可能的故障模式,即DΘ的势可达到22n的大多数。这是由于DΘ的产生与列举单调布尔函数集合的Dedekind问题密切相关,当n≥1时,|DΘ|满足Dedekind序列:1,2,5,19,167,7 580,…。
但在实际故障诊断过程中,并非所有可能的故障模式都会发生,在构建诊断模型时应将相应约束条件考虑进来,减少|DΘ|中故障模式的种类,降低计算量。由于约束条件的引入,自由DSm模型此时变为混合DSm模型。例如,当系统存在单故障为3种时,Θ={θ1, θ2, θ3},则自由DSm模型下系统全部可能的故障模式为19种,即∅,θ1,θ2,θ3,θ1∩θ2,θ1∩θ3,θ2∩θ3,θ1∩θ2∩θ3,θ1∪(θ2∩θ3),θ2∪(θ1∩θ3),θ3∪(θ1∩θ2),θ1∩(θ2∪θ3),θ2∩(θ1∪θ3),θ3∩(θ1∪θ2),θ1∪θ2,θ1∪θ3,θ2∪θ3,θ1∪θ2∪θ3,(θ1∩θ2)∪(θ1∩θ3)∪(θ2∩θ3)。由于实际故障中不存在并集情况,故引入非存在性约束条件,此时,模型为混合DSm模型,系统可能故障模式为8种,即∅,θ1,θ2,θ3,θ1∩θ2,θ1∩θ3,θ2∩θ3,θ1∩θ2∩θ3。又知故障θ1,θ3并不会同时发生,再引入排斥性约束条件θ1∩θ3=∅,此时混合DSm模型变为:{∅, θ1, θ2, θ3, θ1∩θ2, θ2∩θ3},表示系统目前可能存在无故障(∅)、3种单发故障(θ1, θ2, θ3)及2种并发故障(θ1∩θ2, θ2∩θ3)。
2.2 基于先验知识的区间信度合成规则测试过程中存在的不确定信息导致得到的信度赋值函数为区间信度赋值函数。并发故障诊断模型作为一种混合DSm模型,目前在DSmT框架下,Smarandache和Dezert[21]通过引入区间值运算方法,将精确信度结构上定义的经典DSm组合规则和混合DSm组合规则推广到区间值信度结构上,给出了DSmT框架下的区间证据合成规则。
用mμ(Θ)I(A)和mμf(Θ)I(A)表示区间的混合DSm组合规则与经典DSm组合规则得到的结果。在进行区间证据合成时,对于所有的A∈DΘ,混合DSm组合规则表示如下:

|
(4) |
式中:
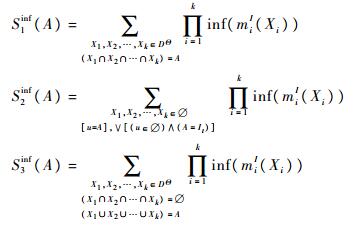
|
以及
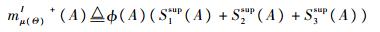
|
(5) |
式中:
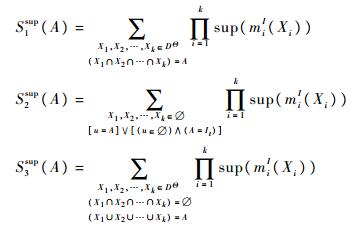
|
根据式(4)和式(5),可以得到最后区间合成结果为: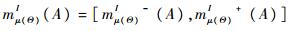
可以看出,整个融合过程等价于将区间基本信度赋值的上界和下界分别应用精确信度结构下的DSm组合规则进行合成。此时得到的结果为次优的,因区间算术在进行区间证据合成时其本身存在的缺陷会导致结果区间过于宽泛。而且当使用混合DSm模型时,可以看出在式(4)中,第1个和式对应信度赋值由合取规则获得;第2个和式将所有对绝对和相对空集的信度赋值,传递到完全或相对未知集上;第3个和式将相对空集的信度赋值传递到非空集合上。这表明如果故障θ1与θ2没有并发故障,即θ1∩θ2=∅时,冲突信度质量m(θ1∩θ2)被传递到焦元θ1∪θ2上,作为未知信息处理。对于故障诊断问题,θ1∪θ2意味着诊断结果为“故障θ1或故障θ2发生”,此时诊断就失去了意义,同时会造成有用信息的丢失。
由于对区间基本信度赋值2个端点进行运算会割裂其内在联系,造成结果误差,故本文使用最优化方法替代区间运算;同时本文认为应将冲突质量重新进行分配,而非如混合DSm规则将冲突质量直接分配到并集上做未知处理,因此,对DSmT下区间证据的组合规则和证据源进行修改,给出新的DSmT下区间信度合成规则,将其称为CDIP规则。
2个区间证据合成时,CDIP方法定义如下。
定义9 m1(·)和m2(·)是广义幂集G下的区间基本信度赋值,满足:m1-(Xi)≤m1(Xi)≤m1+(Xi),1≤i≤g,m2-(Xj)≤m2(Xj)≤m2+(Xj),1≤j≤g,则通过CDIP方法合成后的区间基本信度赋值表示为
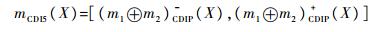
|
式中: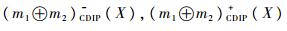
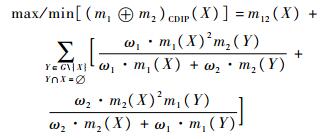
|
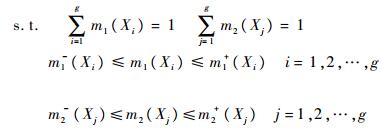
|
(6) |
其中: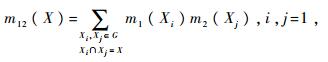
此时,当X∩Y=∅时,总冲突为m(X∩Y)=m1(X)m2(Y)+m2(X)m1(Y)。CDIP方法将其视作2个部分,即由m1(X)和m2(Y)引起的冲突质量m1(X)m2(Y)以及由m2(X)和m1(Y)引起的冲突质量m2(X)m1(Y),分别在焦元X与Y间进行分配。而分配的比例则由先验知识ω1、ω2以及2条证据在其上的信度赋值m1(X)、m2(X)、m1(Y)和m2(Y)给出。
在计算(m1⊕m2)CDIP(X)时,首先通过合取规则获得m12(X),然后计算涉及焦元X的冲突质量分到X上的部分。对于∀Y∈G\{X},Y∩X=∅,冲突质量m1(X)m2(Y)中按照比例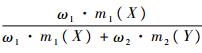
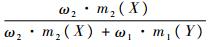
在进行多个区间证据合成时,CDIP方法定义如下。
定义10 m1(·), m2(·), …, mn(·)为n个广义幂集G下的区间基本信度赋值,满足:mi-(Xj)≤mi(Xj)≤mi+(Xj),1≤i≤n,1≤j≤g,则通过CDIP方法合成后的区间基本信度赋值表示为
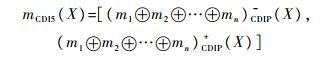
|
式中:(m1∀m2∀…∀mn)-CDIP(X),(m1∀m2∀…∀mn)+CDIP(X)由如下优化模型给出:

|
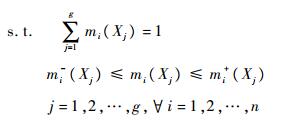
|
其中:

在并发故障诊断过程中,各种传感器采集现场数据,产生测试信息,反映出装备的状态,在此过程中,有些测试信息遗漏或无法获取,造成了测试信息的不完备。此时,进行故障诊断时,需要将这些测试信息进行处理,然后结合当前传感器信息,使用CDIP方法进行信息融合,给出测试结果。
1)选取装备故障信息,构建不完备并发故障诊断决策系统IDS=(U, C∪{d}, V, f),*∈V。
2)对IDS中数据进行预处理。根据测试指标正常区间,按照“高于”、“低于”和“属于”该区间将测试数据进行离散化。
3)使用粗糙集方法对决策表进行约简,获得约简结果B。
4)若得到的约简结果不唯一,计算不完备边界粗糙熵EIB(Bi),选取值最小的约简结果Bi。
5)分别计算每一条测试属性的重要度s(ai),通过计算ωai得到每条证据的权重。
6)计算Bi中每条证据的属性值频率p[fadj(Xi)],构建证据的区间信度赋值函数mi。
7)构建DSm模型,在DSm框架下通过CDIP规则对区间证据进行组合。通过合成后的区间信度赋值对故障进行判断,给出诊断结果。
4 数值实验本节选取模拟放大电路和旋转变压器激励电路的不完备诊断数据,采用本文所提方法对其中存在的并发故障进行诊断;并采用其他DSmT框架下的区间证据合成方法对获得的区间信度赋值函数进行组合,与CDIP方法所得到的结果进行比较,从而对该方法的有效性与适用性进行验证。
本文对比使用的DSmT区间证据合成方法包括区间DSm组合规则、CDI2方法和CDI5方法。区间DSm组合规则通过引入区间运算,将经典DSm规则及混合DSm规则推广到区间值信度结构上;而CDI2方法、CDI5方法与CDIP方法同为基于最优化思想的区间证据合成方法,区别在于冲突证据在各焦元间的分配比例存在差别。以两证据合成为例,CDI2方法给出的优化模型为

|
式中:C(X)为X的特征函数,当焦元X与冲突有关时,C(X)=1,否则,C(X)=0;c12(X)为区间信度质量矩阵M中焦元X所对应的列和,即c12(X)=m1(X)+m2(X);e12为M中与冲突有关的非零焦元所对应的列和;k12为总的冲突质量,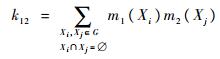
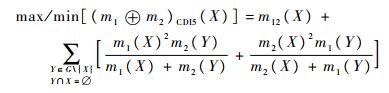
|
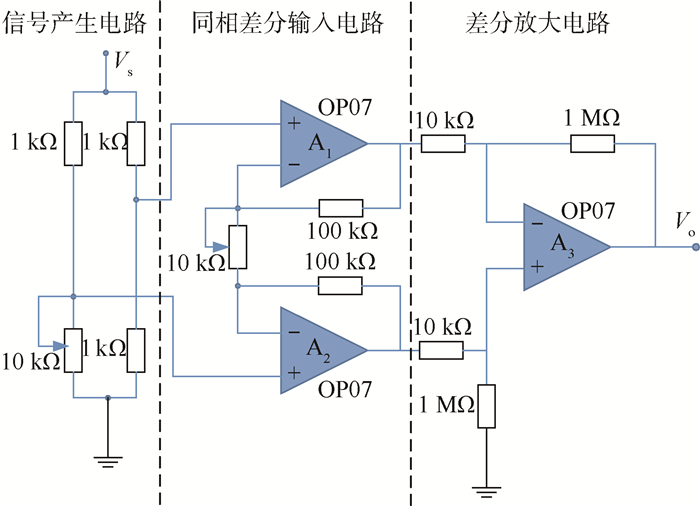
本节选用三运放构成的仪表放大器电路作为并发故障诊断实例。电路主要由运放OP07组成,电路原理图如图 1所示。
|
| 图 1 仪表放大器电路原理 Fig. 1 Principle of instrumentation amplifier circuit |
在过往的故障诊断过程中,发现仪表放大器电路存在3种故障形式,即差分输入电路故障,记为F1;信号产生电路故障,记为F2;差分输入电路与放大电路并发故障,记为F1∩F3。
在3种故障形式下,将对应的信号源Vs的最大、最小输入,电路的最大增益,共模抑制比及电路工作温度进行记录。其中,信号Vs的最大、最小输入是在信号频率f=50 Hz,增益GAIN=72 dB,Rp=5 kΩ时,即电路输出不失真时的信号源的最大、最小输入,在输入端进行采集;最大增益是在信号Vs=100μV,Rp=5 kΩ时,即输出不失真时可实现的电路最大增益值,在输出端进行采集。选取典型的原始测试数据在表 1中给出。
| 编号 | Vs最大 输入/mV |
Vs最小 输入/mV |
共模抑 制比/dB |
电路工 作温度/℃ |
最大增 益/dB |
故障 模式 |
| 1 | 19.5 | 0.61 | 89 | 50.5 | 119 | F1 |
| 2 | 10.1 | 1.03 | 20 | 65.1 | 108 | F1 |
| 3 | 13.9 | * | 102 | 105.9 | 140 | F1 |
| 4 | 17.8 | 0.90 | 117 | 90.4 | 106 | F1 |
| 5 | * | 1.12 | 73 | 93.6 | 117 | F1 |
| 6 | 14.4 | 0.48 | 120 | 77.4 | 103 | F2 |
| 7 | 18.2 | 0.77 | 51 | 81.2 | 84 | F2 |
| 8 | 18.5 | 0.01 | 93 | * | 40 | F2 |
| 9 | 13.3 | 0.53 | 105 | 110.0 | 76 | F2 |
| 10 | * | 0.49 | 81 | 66.3 | 81 | F2 |
| 11 | 17.6 | 1.07 | 68 | 72.1 | 93 | F1∩F3 |
| 12 | 18.0 | 0.96 | * | 58.6 | 101 | F1∩F3 |
| 13 | 12.7 | 1.50 | 44 | 55.9 | 88 | F1∩F3 |
| 14 | 11.9 | 1.91 | 62 | 61.7 | 79 | F1∩F3 |
| 15 | 16.5 | 1.00 | 110 | 88.3 | 96 | F1∩F3 |
| 注:*—缺失的测试数据。 | ||||||
以测试属性C1~C5分别表示与表 1对应的5个项目,通过仿真实验确定各指标的正常区间,以此对原始数据进行离散化。因此,C1表示Vs的最大输入:12.0~18.0 mV;C2表示Vs的最小输入:0.50~1.00 mV;C3表示共模抑制比:≥70 dB;C4表示电路工作温度:≤85.0℃;C5表示最大增益:85~105 dB。其中,测试属性C3、C4赋值过程中,满足正常条件为“1”,不满足为“0”。由此构建诊断决策表如表 2所示。
| 编号 | C1 | C2 | C3 | C4 | C5 | 故障模式 |
| 1 | 2 | 1 | 1 | 1 | 2 | F1 |
| 2 | 0 | 2 | 0 | 1 | 2 | F1 |
| 3 | 1 | * | 1 | 0 | 2 | F1 |
| 4 | 1 | 1 | 1 | 0 | 2 | F1 |
| 5 | * | 2 | 1 | 0 | 2 | F1 |
| 6 | 1 | 0 | 1 | 1 | 1 | F2 |
| 7 | 2 | 1 | 0 | 1 | 0 | F2 |
| 8 | 2 | 0 | 1 | * | 0 | F2 |
| 9 | 1 | 1 | 1 | 0 | 0 | F2 |
| 10 | * | 0 | 1 | 1 | 0 | F2 |
| 11 | 1 | 2 | 0 | 1 | 1 | F1∩F3 |
| 12 | 1 | 1 | * | 1 | 1 | F1∩F3 |
| 13 | 1 | 2 | 0 | 1 | 1 | F1∩F3 |
| 14 | 0 | 2 | 0 | 1 | 0 | F1∩F3 |
| 15 | 1 | 1 | 1 | 0 | 1 | F1∩F3 |
针对不完备并发故障诊断决策表,采用文献[22]的方法进行属性约简,得到的结果为B={ C2, C5}。通过计算属性C2与C5的边界粗糙熵,得到其作为证据的权重为:ω(a2)=0.364,ω(a5)=0.636。然后通过计算属性C2与C5的属性频率区间,得到信度赋值函数(见表 3)。
| i | Ci | mi(F1) | mi(F2) | mi(F1∩F3) |
| 2 | 0 1 2 |
[0,0.250] [0.333,0.429] [0.400,0.500] |
[0.750,1.000] [0.286,0.333] 0 |
0 [0.286,0.333] [0.500,0.600] |
| 5 | 0 1 2 |
0 0 1.000 |
0.800 0.200 0 |
0.200 0.800 0 |
选取实测的4组故障数据,对诊断结果进行验证。对数据离散化后,按照对应约简取得实例为:T1={0, 2},T2={1, 2},T3={1, 1},T4={2, 2}。
在进行区间证据合成前,需要根据系统存在的故障模式构建DSm模型。由于在电路中存在单发故障F1、F2以及并发故障F1∩F3,故电路的诊断框架为Θ={F1, F2, F3},由于不存在其他并发故障,因此需引入排斥性约束F1∩F2=∅,F2∩F3=∅,F1∩F2∩F3=∅。在此框架下,用4种方法分别对区间证据进行组合,得到的结果如表 4所示。
| 方法 | T1={0, 2} | |||
| m(F1) | m(F2) | m(F1∩F3) | m(F1∪F2∪F3) | |
| 区间DSm规则 | [0,0.250] | [0,0] | [0,0] | [0.750,1.000] |
| CDI2方法 | [0.500,0.719] | [0.281,0.500] | [0,0] | |
| CDI5方法 | [0.500,0.679] | [0.321,0.500] | [0,0] | |
| 本文方法 | [0.652,0.786] | [0.214,0.348] | [0,0] | |
| 方法 | T1={1, 2} | |||
| m(F1) | m(F2) | m(F1∩F3) | m(F1∪F2∪F3) | |
| 区间DSm规则 | [0.333,0.429] | [0,0] | [0.286,0.333] | [0.286,0.333] |
| CDI2方法 | [0.556,0.632] | [0.041,0.055] | [0.327,0.388] | |
| CDI5方法 | [0.584,0.650] | [0.064,0.083] | [0.286,0.333] | |
| 本文方法 | [0.617,0.676] | [0.038,0.050] | [0.286,0.333] | |
| 方法 | T1={1, 1} | |||
| m(F1) | m(F2) | m(F1∩F3) | m(F1∪F2∪F3) | |
| 区间DSm规则 | [0,0] | [0.057,0.067] | [0.495,0.610] | [0.352,0.419] |
| CDI2方法 | [0.067,0.080] | [0.147,0.173] | [0.751,0.781] | |
| CDI5方法 | [0.042,0.058] | [0.168,0.195] | [0.755,0.781] | |
| 本文方法 | [0.031,0.046] | [0.166,0.186] | [0.776,0.795] | |
| 方法 | T1={2, 2} | |||
| m(F1) | m(F2) | m(F1∩F3) | m(F1∪F2∪F3) | |
| 区间DSm规则 | [0.400,0.500] | [0,0] | [0.500,0.600] | [0,0] |
| CDI2方法 | [0.400,0.500] | [0,0] | [0.500,0.600] | |
| CDI5方法 | [0.400,0.500] | [0,0] | [0.500,0.600] | |
| 本文方法 | [0.400,0.500] | [0,0] | [0.500,0.600] | |
通过表 4中可以看出,样本T1中2个指标的信息存在严重冲突。在面对高冲突区间证据合成时,区间DSm组合规则会将其冲突部分分配到相应的并集上作为未知信息进行处理。例如,其将m(F1∩F2)的质量转移到了焦元F1∪F2上,而F1∪F2由于包含故障模式F1与F2,因此无法做出诊断。而将冲突在焦元间进行分配的CDI2方法、CDI5方法与CDIP方法都得到了正确的结果。但由于CDIP方法赋予C5更多的权重,使得结果的准确度明显高于CDI2方法与CDI5方法。而在样本T4中,由于决策F1实际包含2种故障模式,单发故障F1和并发故障F1∩F3,即F1=F1∪(F1∩F3),说明证据间完全不存在冲突,在这种不涉及冲突质量分配的情况下,所有4种方法基于合取原则得到了同样的结果。在样本T2中,2条证据相一致,都为焦元F1赋最大值,从合成结果来看,4种方法都得到了正确的结论。由于C5显著支持F1,而CDI2方法、CDI5方法认为2条证据重要度相同,导致结果准确度低于CDIP方法。这点在样本T3上也有所体现。
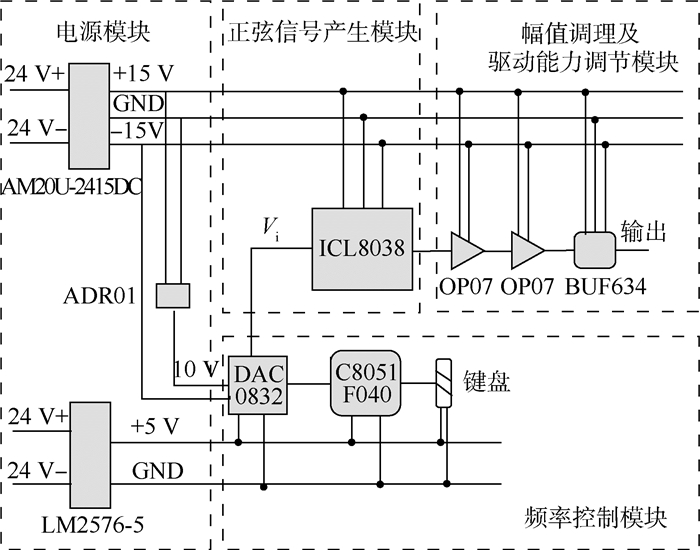
4.2 激励发生电路并发故障诊断实例本节选用某航电系统的旋转变压器激励发生电路作为诊断验证对象,该电路用于产生旋转变压器励磁绕组所需要的正弦信号,为旋转变压器运行提供激励。电路原理图如图 2所示。
|
| 图 2 旋转变压器激励发生电路原理 Fig. 2 Princiople of rotating transformer excitation generating circuit |
由图 2可以看出,该电路主要由电源模块、频率控制模块、正弦信号产生模块以及幅值调理及驱动能力调节模块组成。在之前的测试记录中共有9个测试项目,包括:信号频率、信号幅值、正弦模块输入电压值、信号频率稳定度、+15 V电压值、-15 V电压值、电路工作温度、+5 V电压值和+10 V电压值。其中,信号频率、幅值及频率稳定度数据在整体电路的输出端进行采集;频率控制模块输出电压在ICL8038的输入端进行采集;而各电压值在电源模块相应输出端进行采集。各故障模式下的原始测试数据如表 5所示。
| 编号 | 信号 频率/ Hz |
信号 幅值/ V |
输入 电压/ V |
频率 稳定度/% |
+15 V 电压/ V |
-15 V 电压/ V |
电路 工作 温度 /℃ |
+5 V 电压/ V |
+10 V 电压/ V |
故障 模式 |
| 1 | 1 620 | 13.8 | 3.0 | 5.0 | * | -13.6 | * | 5.8 | 10.1 | F1 |
| 2 | * | 9.0 | 3.3 | 9.3 | 18.9 | -12.7 | 105 | 5.5 | * | F1 |
| 3 | 1 630 | 13.2 | * | 7.9 | 15.1 | -15.9 | 70 | * | 9.0 | F1 |
| 4 | 1 600 | 13.8 | 3.0 | 3.9 | 16.8 | -16.5 | 72 | 6.6 | 11.9 | F1 |
| 5 | 1 640 | 14.0 | 2.1 | * | 14.0 | * | * | 6.0 | * | F1 |
| 6 | 1 630 | * | 4.1 | 7.2 | 13.9 | -16.2 | 80 | 5.0 | 9.3 | F1 |
| 7 | 1 440 | 13.1 | * | 14.0 | 17.2 | -13.1 | 89 | 5.6 | 10.6 | F1 |
| 8 | 1 260 | 13.6 | 2.6 | 2.9 | 15.5 | * | 91 | 6.1 | 10.3 | F2 |
| 9 | 1 020 | 12.9 | 2.6 | 4.4 | 17.0 | -14.5 | 69 | 4.9 | * | F2 |
| 10 | * | 13.0 | 2.8 | * | 13.8 | -13.4 | 88 | 5.0 | 10.0 | F2 |
| 11 | 1 580 | 14.2 | 2.5 | 12.9 | 14.2 | -15.9 | 102 | 6.1 | 10.8 | F2 |
| 12 | 1 530 | 13.8 | * | 8.0 | 16.2 | -16.9 | 85 | 5.0 | 10.1 | F2 |
| 13 | 1 690 | 10.9 | 1.1 | 10.5 | * | -13.6 | 86 | 6.9 | 9.4 | F2 |
| 14 | 1 600 | 14.5 | 2.1 | 4.1 | 15.0 | -19.0 | 72 | * | * | F2 |
| 15 | * | 11.7 | 2.6 | 8.9 | 12.2 | -11.3 | 91 | 5.6 | 8.4 | F3 |
| 16 | 1 610 | 14.6 | 2.8 | 17.2 | * | -10.9 | * | 4.3 | 9.5 | F3 |
| 17 | 1 660 | 9.8 | 2.5 | 11.5 | 10.0 | -17.9 | * | 4.6 | * | F3 |
| 18 | 1 650 | 12.9 | 1.9 | 5.4 | * | -16.7 | 93 | 5.7 | 9.8 | F3 |
| 19 | 1 650 | 13.0 | * | 3.3 | 13.2 | * | 70 | * | 9.1 | F3 |
| 20 | 1 620 | * | 2.2 | 8.3 | 18.4 | -17.7 | 74 | 6.0 | * | F3 |
| 21 | 2 640 | 12.1 | 2.0 | 8.2 | 13.5 | -16.9 | 77 | 6.1 | 9.9 | F3 |
| 22 | 1 730 | 13.9 | 2.1 | 14.4 | * | -15.0 | * | 5.8 | 10.3 | F4 |
| 23 | * | 14.2 | 2.4 | 6.5 | 13.2 | -18.2 | 80 | 4.1 | 10.6 | F4 |
| 24 | 1 690 | 13.1 | 2.8 | 3.1 | * | -17.8 | * | * | * | F4 |
| 25 | 1 810 | * | 3.3 | * | 16.7 | -16.9 | 75 | 5.6 | 11.0 | F4 |
| 26 | 1 670 | 12.5 | 3.0 | 9.4 | 15.5 | -17.3 | * | 3.0 | * | F4 |
| 27 | 1 700 | 14.0 | * | * | 14.3 | * | 70 | 5.1 | 10.1 | F4 |
| 28 | * | 13.1 | 1.8 | 2.5 | 12.0 | -19.0 | 88 | 6.0 | 9.8 | F4 |
| 注:*—缺失的测试数据;F1~F4—频率控制模块故障、幅值调理及驱动能力调节模块故障、电源模块故障及正弦信号产生模块故障。 | ||||||||||
以测试属性C1~C9分别表示9个测试项目,根据对产生的正弦信号的要求以及各芯片的正常范围,对原始测试数据进行离散化。
离散化区间依次为:C1表示输出信号频率:1 610~1 650 Hz;C2表示输出信号幅值:13.1~14.5 V;C3表示正弦模块的输入电压值:2.2~2.8 V;C4表示输出信号频率稳定度:≤10%;C5表示+15 V电压输出:+13.5~+16.5 V;C6表示-15 V电压输出:-16.5~-13.5 V;C7表示电路工作温度:≤85℃;C8表示+5 V电压输出:+4.5~+5.5 V;C9表示+10 V电压输出:+9.5~+10.5 V。按照“高于”、“低于”和“属于”该区间为测试属性赋值“2”、“1”和“0”;在测试属性C4、C7赋值过程中,满足正常条件为“1”,不满足为“0”。以此构建诊断决策表如表 6所示。
| 编号 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | 故障模式 |
| 1 | 1 | 1 | 2 | 1 | * | 1 | * | 2 | 1 | F1 |
| 2 | * | 0 | 2 | 1 | 2 | 2 | 0 | 1 | * | F1 |
| 3 | 1 | 1 | * | 1 | 1 | 1 | 1 | * | 0 | F1 |
| 4 | 0 | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 2 | F1 |
| 5 | 1 | 1 | 0 | * | 1 | * | * | 2 | * | F1 |
| 6 | 1 | * | 2 | 1 | 1 | 1 | 1 | 1 | 0 | F1 |
| 7 | 0 | 1 | * | 0 | 2 | 2 | 0 | 2 | 2 | F1 |
| 8 | 0 | 1 | 1 | 1 | 1 | * | 0 | 2 | 1 | F2 |
| 9 | 0 | 0 | 1 | 1 | 2 | 1 | 1 | 1 | * | F2 |
| 10 | * | 0 | 1 | * | 1 | 2 | 0 | 1 | 1 | F2 |
| 11 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 2 | 2 | F2 |
| 12 | 0 | 1 | * | 1 | 1 | 0 | 1 | 1 | 1 | F2 |
| 13 | 2 | 0 | 0 | 0 | * | 1 | 0 | 2 | 0 | F2 |
| 14 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | * | * | F2 |
| 15 | * | 0 | 1 | 1 | 0 | 2 | 0 | 2 | 0 | F3 |
| 16 | 1 | 2 | 1 | 0 | * | 2 | * | 0 | 1 | F3 |
| 17 | 2 | 0 | 1 | 0 | 0 | 0 | * | 1 | * | F3 |
| 18 | 1 | 0 | 0 | 1 | * | 0 | 0 | 2 | 1 | F3 |
| 19 | 1 | 0 | * | 1 | 0 | * | 1 | * | 0 | F3 |
| 20 | 1 | * | 1 | 1 | 2 | 0 | 1 | 2 | * | F3 |
| 21 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 2 | 1 | F3 |
| 22 | 2 | 1 | 0 | 0 | * | 1 | * | 2 | 1 | F4 |
| 23 | * | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 2 | F4 |
| 24 | 2 | 1 | 1 | 1 | * | 0 | * | * | * | F4 |
| 25 | 2 | * | 2 | * | 2 | 0 | 1 | 2 | 2 | F4 |
| 26 | 2 | 0 | 2 | 1 | 1 | 0 | * | 0 | * | F4 |
| 27 | 2 | 1 | * | * | 1 | * | 1 | 1 | 1 | F4 |
| 28 | * | 1 | 0 | 1 | 0 | 0 | 0 | 2 | 1 | F4 |
对该决策表约简后可得到2个约简结果,B1={C1, C2, C3, C5},B1={C1, C2, C5, C6},通过计算这2个约简的不完备边界粗糙熵可得:EIB (B1)=3.242,EIB (B1)=3.576,故选择约简B1={C1, C2, C3, C5}作为最后的结果。分别对约简中每条属性的重要度进行计算,从而得到权重w(a1)=0.312,w(a2)=0.218,w(a3)=0.220,w(a5)=0.250;计算属性值频率区间获得约简中每条属性的信度赋值(见表 7)。
| i | Ci | mi(F1) | mi(F2) | mi(F3) | mi(F4) |
| 1 | 0 | [0.182,0.375] | [0.455,0.750] | [0,0.125] | [0,0.222] |
| 1 | [0.308,0.500] | [0,0.100] | [0.385,0.600] | [0,0.182] | |
| 2 | [0,0.125] | [0.091,0.250] | [0.091,0.250] | [0.500,0.778] | |
| 2 | 0 | [0.083,0.182] | [0.231,0.300] | [0.417,0.545] | [0.083,0.182] |
| 1 | [0.313,0.400] | [0.235,0.286] | [0,0.067] | [0.313,0.400] | |
| 2 | [0,0.500] | [0,0] | [0.333,1.000] | [0,0.500] | |
| 3 | 0 | [0.100,0.333] | [0.182,0.375] | [0.182,0.375] | [0.182,0.375] |
| 1 | [0,0.167] | [0.286,0.455] | [0.286,0.455] | [0.143,0.273] | |
| 2 | [0.444,0.750] | [0,0.143] | [0,0.143] | [0.200,0.429] | |
| 5 | 0 | [0,0.167] | [0,0.167] | [0.333,0.714] | [0.222,0.571] |
| 1 | [0.176,0.308] | [0.294,0.462] | [0.063,0.214] | [0.188,0.357] | |
| 2 | [0.300,0.666] | [0.100,0.333] | [0.111,0.429] | [0,0.286] |
由于在被诊断电路中共存在6种故障模式,其中4种为单发故障,2种并发故障F1∩F2和F3∩F4。故诊断系统辨识框架为Θ={F1, F2, F3, F4},同时引入排斥性约束F1∩F3,F1∩F4,F2∩F3,F2∩F4,这同时意味着系统存在排斥性约束F1∩F2∩F3=∅,F1∩F2∩F4=∅,F1∩F3∩F4=∅,F2∩F3∩F4=∅,F1∩F2∩F3∩F4=∅。选取实测的4组故障数据作为验证实例,分别为:T1={2, 1, 2, 1},T2={1, 0, 1, 0},T3={2, 1, 0, 0},T4={1, 1, 2, 2}。采用4种方法对区间信度进行合成,得到的结果如表 8所示。
| 方法 | T1={2, 1, 2, 1} | |||||
| m(F1) | m(F2) | m(F3) | m(F4) | m(F1∩F2) | m(F3∩F4) | |
| 区间DSm规则 | [0,0.012] | [0,0.005] | [0,0.001] | [0.006,0.048] | [0.010,0.161] | [0.003,0.109] |
| CDI2方法 | [0.143,0.370] | [0.062,0.180] | [0.002,0.063] | [0.144,0.475] | [0.091,0.483] | [0.019,0.293] |
| CDI5方法 | [0.111,0.463] | [0.028,0.177] | [0,0.028] | [0.152,0.604] | [0.074,0.481] | [0.007,0.268] |
| 本文方法 | [0.105,0.451] | [0.028,0.173] | [0,0.028] | [0.157,0.630] | [0.069,0.474] | [0.008,0.283] |
| 方法 | T1={2, 1, 0, 0} | |||||
| m(F1) | m(F2) | m(F3) | m(F4) | m(F1∩F2) | m(F3∩F4) | |
| 区间DSm规则 | [0,0.003] | [0,0.002] | [0.015,0.106] | [0,0.005] | [0,0.055] | [0.030,0.420] |
| CDI12 | [0.016,0118] | [0.057,0.185] | [0.218,0.553] | [0.029,0.132] | [0.012,0.243] | [0.141,0.590] |
| CDI15 | [0.012,0.141] | [0.079,0.274] | [0.117,0.618] | [0.008,0.134] | [0.021,0.276] | [0.094,0.618] |
| 本文方法 | [0.012,0.150] | [0.074,0.251] | [0.120,0.621] | [0.008,0.132] | [0.023,0.286] | [0.095,0.620] |
| 方法 | T1={1, 0, 1, 0} | |||||
| m(F1) | m(F2) | m(F3) | m(F4) | m(F1∩F2) | m(F3∩F4) | |
| 区间DSm规则 | [0,0.003] | [0,0.004] | [0,0.004] | [0.006,0.067] | [0,0.053] | [0.031,0.391] |
| CDI12 | [0.089,0.235] | [0.074,0.207] | [0.018,0.125] | [0.150,0.442] | [0.012,0.249] | [0.150,0.552] |
| CDI15 | [0.089,0.294] | [0.069,0.243] | [0.001,0.123] | [0.046,0.442] | [0.021,0.260] | [0.132,0.660] |
| 本文方法 | [0.084,0.279] | [0.064,0.235] | [0.001,0.130] | [0.046,0.454] | [0.019,0.254] | [0.143,0.679] |
| 方法 | T1={1, 1, 2, 2} | |||||
| m(F1) | m(F2) | m(F3) | m(F4) | m(F1∩F2) | m(F3∩F4) | |
| 区间DSm规则 | [0.013,0.100] | [0,0.001] | [0,0.002] | [0,0.009] | [0.017,0.265] | [0.003,0.138] |
| CDI12 | [0.213,0.543] | [0.047,0.135] | [0.004,0.109] | [0.067,0.267] | [0.090,0.492] | [0.021,0.379] |
| CDI15 | [0.175,0.610] | [0.017,0.140] | [0.001,0.147] | [0.057,0.358] | [0.062,0.478] | [0.020,0.432] |
| 本文方法 | [0.174,0.613] | [0.018,0.133] | [0.002,0.167] | [0.051,0.343] | [0.060,0.478] | [0.023,0.450] |
在本例中,根据系统存在的并发故障模式可知,决策表中的决策属性实际应为:F1=F1∪(F1∩F2),F2=F2∪(F1∩F2),F3=F3∪(F3∩F4),F4=F4∪(F3∩F4)。由于模型中无非存在性约束,在使用区间DSm规则进行证据合成时,其将冲突部分质量作为未知转移为并集质量m(∪),由于此部分对于诊断无意义,故不在表 8中列出。可以看出,区间DSm规则在验证样本上得到的诊断结果大多无效,这主要因为其结果中焦元过多且质量分布过于松散,而大量的冲突质量作为无意义信息处理,导致在给定焦元上的信度赋值过低,从而无法做出判断。而CDI2方法、CDI5方法和CDIP方法最终都得到了正确的结果,但与第4.1节中的结果相比,得到的结果区间偏大,这是由不完备并发故障诊断决策表中缺失数据过多,使得通过计算属性值频率获得的区间信度范围较大所导致。
5 结论本文在综合分析粗糙集及DSmT理论基础上,提出了可以在诊断信息不完备条件下进行的并发故障诊断的方法。经验证表明:
1)可以有效地对不完备信息,以及在DSmT框架下对并发故障进行表示。
2)通过对测试信息中的特征进行提取,度量其对决策的重要程度。
3)在对区间证据进行合成时,有效地融入了证据特征,可以获得较之前区间合成方法更为精确的合成结果。
随着需要合成的测试属性数量增多,故障模式的增多,方法会出现计算量增大的问题,需要对方法进行进一步的优化。
| [1] | KRYSZKIEWICZ M. Rough set approach to incomplete information systems[J]. Information Sciences, 1998, 12 (1-4) : 39 –49. |
| [2] | 陈利安, 肖明清, 赵鑫. 基于粗糙集与信息熵的不完备测试信息条件下故障诊断[J]. 振动与冲击, 2012, 31 (22) : 24 –28. CHEN L A, XIAO M Q, ZHAO X. Fault diagnosis under condition of incomplete test information based on rough set and information entropy[J]. Journal of Vibration and Shock, 2012, 31 (22) : 24 –28. (in Chinese) |
| [3] | 王珉, 胡茑庆, 秦国军. 基于不完备信息的直升机传动系统故障诊断规则提取方法[J]. 振动与冲击, 2011, 30 (12) : 185 –190. WANG M, HU N Q, QIN G J. Method of rule extraction for fault diagnosis of a helicopter power train based on incomplete information[J]. Journal of Vibration and Shock, 2011, 30 (12) : 185 –190. (in Chinese) |
| [4] | LU X, HUANG W, WANG W, et al.Multi-interpretations valued tolerance relation model of incomplete information in fault diagnosis system[C]//2014 11th World Congress on Intelligent Control and Automation(WCICA).Piscataway, NJ:IEEE Press, 2014:6035-6040. |
| [5] | 杨召, 肖明清, 胡斌, 等. 测试信息不完备条件下航空电子装备故障诊断[J]. 计算机应用, 2013, 33 (A01) : 46 –47. YANG Z, XIAO M Q, HU B, et al. Fault diagnosis under condition of incomplete test information based on rough set and information entropy[J]. Journal of Computer Applications, 2013, 33 (A01) : 46 –47. (in Chinese) |
| [6] | 胡雷刚, 肖明清, 禹航, 等. 不完备信息条件下的航空发动机故障诊断方法[J]. 振动、测试与诊断, 2012, 32 (6) : 903 –908. HU L G, XIAO M Q, YU H, et al. Aero engine fault diagnosis method under incomplete information[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32 (6) : 903 –908. (in Chinese) |
| [7] | RONG Y, ZHAO J, WANG J, et al. Fault diagnosis of transformer based on incomplete information system rule extraction and Petri nets[J]. Power System Protection and Control, 2009, 37 (18) : 1 –4. |
| [8] | 赵佰亭.混合决策系统的粗集模型及在转台故障诊断中的应用[D].哈尔滨:哈尔滨工业大学, 2010:101-110. ZHAO B T.Rough set model of hybrid decision system and application in turntable fault diagnosis[D].Harbin:Harbin Institute of Technology, 2010:101-110(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10613-1013252527.htm |
| [9] | DONG H, LI X, WEI Z. Substation fault diagnosis based on rough sets and grey relational analysis[J]. Telkomnika Indonesian Journal of Electrical Engineering, 2014, 12 (2) : 1162 –1168. |
| [10] | GAO Q, YIN C, DONG G.A novel fault diagnosis method for boiler drum water level based on rough sets and evidence theory[C]//2012 3rd International Conference onIntelligent Control and Information Processing(ICICIP).Piscataway, NJ:IEEE Press, 2012:488-492. |
| [11] | WANG M, HU N, QIN G. A method for rule extraction based on granular computing:Application in the fault diagnosis of a helicopter transmission system[J]. Journal of Intelligent & Robotic Systems, 2013, 71 (3-4) : 445 –455. |
| [12] | 彭俏, 郭立峰, 马杰. 基于混合神经网络的核动力装置并发故障诊断研究[J]. 核动力工程, 2013, 33 (6) : 30 –34. PENG Q, GUO L F, MA J. Intercurrent fault diagnosis of nuclearpower plants based on hybrid artificial neural network[J]. Nuclear Power Engineering, 2013, 33 (6) : 30 –34. (in Chinese) |
| [13] | VONG C M, WONG P K, IP W F, et al. Simultaneous-fault diagnosis of automotive engine ignition systems using prior domain knowledge and relevance vector machine[J]. Mathematical Problems in Engineering, 2013, 2013 : 1 –19. |
| [14] | CAI B, LIU Y, FAN Q, et al. Multi-source information fusion based fault diagnosis of ground-source heat pump using Bayesian network[J]. Applied Energy, 2014, 114 : 1 –9. DOI:10.1016/j.apenergy.2013.09.043 |
| [15] | DEZERT J. Foundations for a new theory of plausible and paradoxical reasoning[J]. Information and Security Journal, 2002, 9 : 13 –57. DOI:10.11610/isij.v09 |
| [16] | 李植良, 徐晓滨, 文成林. 基于扩展证据理论的并发故障诊断方法[J]. 杭州电子科技大学学报, 2009, 28 (6) : 107 –110. LI Z L, XU X B, WEN C L. Simultaneous fault diagnosis method based on extended evidence theory[J]. Journal of Hangzhou Dianzi University, 2009, 28 (6) : 107 –110. (in Chinese) |
| [17] | 徐晓滨, 文成林, 蒋海娜, 等. 基于随机集理论的并发故障诊断信息融合方法[J]. 仪器仪表学报, 2010, 31 (2) : 334 –340. XU X B, WEN C L, JIANG H N, et al. Information fusion method of simultaneous fault diagnosis based on random set theory[J]. Chinese Journal of Scientific Instrument, 2010, 31 (2) : 334 –340. (in Chinese) |
| [18] | 郭清, 夏虹, 韩文伟. DSmT的主冷却剂泵并发故障融合方法分析[J]. 哈尔滨工业大学学报, 2014, 46 (9) : 111 –115. GUO Q, XIA H, HAN W W. Concurrent fault information fusion methods of main cool ant pump based on DSmT[J]. Journal of Harbin Institute of Technology, 2014, 46 (9) : 111 –115. (in Chinese) |
| [19] | WU X, LIU Y, LIU Z, et al.Research on simultaneous faults diagnosis for nuclear power plant based on dezert-smarandache theory[C]//2013 21st International Conference on Nuclear Engineering.New York:ASME, 2013:23-29. |
| [20] | REN J, JIANG B, ZHAO F, et al.Simultaneous fault diagnosis of the reactor coolant system based on the DSM evidence theory[C]//2013 21st International Conference on Nuclear Engineering.New York:ASME, 2013:31-34. |
| [21] | SMARANDACHE F, DEZERT J. An introduction to DSm theory of plausible, paradoxist, uncertain, and imprecise reasoning for information fusion[J]. Octogon Mathematical Magazine, 2007, 15 (2) : 681 –722. |
| [22] | DAI J, WANG W, TIAN H, et al. Attribute selection based on a new conditional entropy for incomplete decision systems[J]. Knowledge-Based Systems, 2013, 39 : 207 –213. DOI:10.1016/j.knosys.2012.10.018 |



