2. 北京航空航天大学 先进航空发动机协同创新中心, 北京 10008;
3. 解放军95809部队, 93分队, 沧州 061736
2. Collaborative Innovation Center of Advanced Aero-Engine, Beijing University of Aeronautics and Astronautics, Beijing 10008 ;
3. Unit 93, Army 95809 of PLA, Cangzhou 061736, China
贝叶斯网络是基于概率分析、图论的一种表达和推理不确定性知识的模型[1],因其在概率推理和故障诊断方面具有的显著优势,被广泛应用于机械、医疗等各个行业。贝叶斯网络的建立通常需要经过结构学习和参数学习2个步骤,其中结构学习难度较大,成为了制约贝叶斯网络建立的关键问题[2]。
贝叶斯网络结构学习的主要方法有基于数据驱动的方法和基于专家知识的方法2大类。数据驱动方法学习效率低,建模过程受到数据样本和算法自身缺陷的制约,难以保证精度[3];基于专家知识的方法完全依赖于咨询专家后的手工构建,对大型复杂系统建模困难,且不利于方法的集成化与自动化。但是专家知识含有的先验信息可以提高建模的效率和准确性。因此,开展数据驱动与专家知识结合的贝叶斯网络结构学习,具有理论研究和实际工程应用价值[4-5]。
多信号流图是一种基于专家知识构建的图模型,其描述信号之间传递关系的能力能够为贝叶斯网络结构的学习提供重要参考。文献[6]提出了一种将多信号流图翻译为诊断贝叶斯网络的手动建模方法,该方法虽然能够充分运用多信号流图中的专家知识,但因其没有引入学习算法,导致建模开发需要大量经验,当面对多层次复杂系统时,手动翻译工作量大、效率低,且无法判断模型是否最优。文献[7]利用多信号流图的故障-测试相关性矩阵(D-矩阵)实现了自动化结构学习,但是该方法并没有考虑故障节点之间的影响关系,因此生成的朴素贝叶斯模型并未充分利用多信号流图蕴含的结构因果关系信息。
本文在上述研究的基础上,充分利用多信号流图的先验知识,同时结合基于数据驱动的K2学习算法,实现了诊断贝叶斯网络结构的自动建模。通过对比实验证明了该建模方法的性能和优势,并通过在某观瞄系统中的应用证明了该算法的工程应用价值。
1 多信号流图模型 1.1 多信号流图概述多信号流图模型采用有向图描述故障传播依赖关系,可用于实现复杂系统诊断建模、算法设计等功能,目前已广泛使用于航空航天、工业控制和医疗设备等高新技术系统的可测性设计、维护管理等领域。多信号流图的主要元件包括模块、子系统、测试、开关、与节点和连接线[8]。其中,模块元件与故障模式对应;子系统模块则用于实现系统的多层次建模;开关元件可用于表示系统的多模式特性;与节点元件则用于表示系统的冗余特性;连接线表示了信号的流向。
1.2 多信号流图与诊断贝叶斯网络对比多信号流图与诊断贝叶斯网络均属于图模型,二者在知识表达方面有诸多相似之处,例如[6]:①2种图模型结构都由节点和有向边2个部分元素组成;②节点代表的均为对象的状态或特征,有向边则表示节点间的关联关系;③节点均可以划分为故障节点和测试节点,前者代表组件或者模块,后者通常是传感器信息;④2种推理模型都支持从原因到结果的正向推理和从结果到原因的反向推理。
但是二者之间也存在显著区别,包括:①多信号流图中的有向连接线反映2个节点之间信号的传递关系,而诊断贝叶斯网络中代表了故障的因果联系,因此二者并不一一对应。②多信号流图模型允许信号流的传递成环形连接,而贝叶斯网络则是严格的有向无环图,这一属性也反映了二者有向边含义的不同;③多信号流图模型节点涵盖信息包括该节点的失效率和虚警率,而贝叶斯网络中节点所具有的信息不仅包含节点本身的故障先验概率,还反映父节点状态对该节点的影响关系;④基于多信号流图的诊断过程是定性分析,推理结果往往是一组可疑组件,而基于贝叶斯网络的诊断是定量分析,不仅可以给出每个怀疑组件的故障概率,还可以处理证据冲突的问题。
以往基于专家知识的建模方法均是人工给出先验知识,因此该知识可能是零散的、片面性的,并且通常只是故障关系存在或发生的可能性。基于系统设计方案的专家知识可以完全满足多信号流图的建模需求,但是对于贝叶斯网络而言,就形成了不确定的先验知识,直接采用该知识进行贝叶斯网络建模而忽略先验知识的不确定性,往往会导致网络结构出现丢失边或冗余边的情况[9]。
多信号流图模型与系统物理模型相契合,可以充分利用系统设计方案所包含的专家知识进行建模,具有建模过程简单、包含系统知识完整等优势,并且由于在诊断系统设计阶段多信号流图模型能够提供可测试性分析和故障模式、影响及危害度分析(FMECA),该模型受到大量复杂系统的青睐,应用广泛。多信号流图模型所包含的专家知识和其模型特点为它与贝叶斯模型间系统知识的共享提供了便利。基于多信号流图模型获取先验知识克服了以往专家知识的不足,并且可以实现知识的自动获取,极大地提高了诊断贝叶斯网络结构学习的效率和准确性。
2 结构学习算法 2.1 数据驱动算法的选取基于数据驱动的贝叶斯网络结构学习算法已存在大量研究,受到使用条件的限制或算法准确度的制约,通过某一种算法单独完成高质量贝叶斯网络的建立仍然十分困难[10]。K2算法作为贝叶斯结构领域的经典算法,具有优异的学习性能,该算法的使用需要满足严格的先验条件[11]:①提供所有节点G的拓扑排序ρ;②指定贝叶斯网络中的最大父节点个数μ。这2项先验知识通常基于对系统的全面认识和分析,在一般情况下很难获取,因此K2算法的应用具有局限性。多信号流图模型含有变量之间信息流的传递关系,依据对该传递关系的分析可以有效实现对变量的排序并提取出变量可能的父节点个数上限,满足K2算法的使用条件。
传统K2算法的初始模型是一个包含所有节点、但是不含边的无边图,在搜索过程中对节点进行逐个考查,确定其父节点,再添加父节点到当前节点的有向边。K2算法需要通过评分函数对每次添加有向边的操作进行打分,最后寻找出整个网络最优评分值所对应的网络结构。由Cooper和Herskovits提出的CH评分函数[12]具有可分解、运算复杂度低等优点,因此以CH评分为例,节点Xi的家族CH评分为
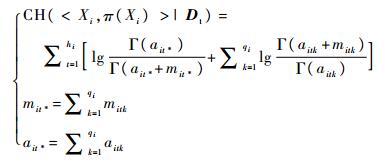
|
(1) |
式中:Xi和π(Xi)分别为第i个故障节点及该节点的父节点组合;Dt为结构学习所使用的数据集;mitk为数据集Dt中满足Xi=k,π(Xi)=t的样本个数;aitk为先验分布的超参数,在实际使用中需要规定一个等价样本量α和先验贝叶斯网络N0,计算过程如式(2)所示。
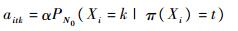
|
(2) |
式中:P为概率函数。
根据CH评分的可分解性,可以通过对各家族评分求和得到完整系统结构G的评分,评分函数如式(3)所示。
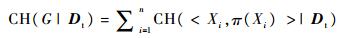
|
(3) |
通过对数据集Dt的分析,找到使得系统评分CH(G|Dt)最高的结构G,该结构与数据集吻合程度最高,被认为是最优贝叶斯结构[13-14]。
2.2 融合算法的原理先验信息在贝叶斯网络学习过程中有着重要的地位。传统数据驱动的学习方法由于缺乏先验信息,存在工作效率低下的问题,而利用多信号流图模型可以自动获取系统先验信息作为专家知识,进而建立先验贝叶斯网络,提前去除大量不合理或无法存在的网络结构,减小结构学习的搜索空间,降低了学习的复杂度。同时,由于数据样本来源的不确定性,在样本数据不足或者可信度不够高的情况下,引入多信号流图知识来对贝叶斯网络的学习结果进行进一步评判,有利于获得更加符合实际的网络结构。
虽然先验知识的引入通常可以提高学习效率,但不准确的先验知识也会对结构学习的准确度产生较大的干扰[15]。多信号流图模型所包含的先验知识真实、准确,以其作为专家知识引入建模过程可以提高算法的准确度和效率。本文实现了多信号流图中先验信息的自动提取,同时结合K2算法构建了专家知识与数据分析相融合的结构学习算法,实现了高性能的诊断贝叶斯网络自动建模过程。算法融合主要表现在3个方面:
1)通过对多信号流图模型进行解析和编号,自动获取模型节点的拓扑排序和最大父节点个数,为使用K2算法进行结构学习提供必要的先验知识。
2)多信号流图模型的D-矩阵知识满足朴素贝叶斯模型建立条件[7],而朴素贝叶斯模型可以作为系统贝叶斯模型建立的基础。
D-矩阵为由故障变量和测试变量所构成的0/1矩阵[16]:

|
(4) |
式中:dij为第i个故障变量在第j个测试变量上的反映,dij=1表示相关,dij=0表示不相关;Fi=[di1 di2…din]为第i个故障对象Fi与各个测试对象上的相关性。
由于多信号流图和诊断贝叶斯网络的节点具有相似的节点含义,前者的故障对象与测试对象可以直接映射到后者,因此通过D-矩阵生成的系统朴素贝叶斯模型包含了所有故障节点到测试节点之间的连接关系。现有的研究仅建立了朴素贝叶斯模型,忽略了故障节点之间的依赖关系。因此,本文在朴素贝叶斯模型基础上进行基于数据驱动的结构学习,使得模型更加符合真实情况。同时相比于采用纯K2算法进行的结构学习,该方法仅学习故障节点之间的连接关系,可以减小学习规模、提升准确性及效率。
3)对复杂系统进行分解可以提升贝叶斯结构的学习效率,而多信号流图知识为系统拆分提供了可能。针对系统规模较大、实现功能复杂的大型贝叶斯网络,可以引入分解的思想,即通过合理的划分,将复杂系统网络结构学习转化为对多个子系统网络的学习,最后对子网络进行合并得到完整贝叶斯网络结构。
考虑到多信号流图连接线对诊断贝叶斯网络连接线所具有的包含关系,在多信号流图模型中,若一组由多个故障节点组成的节点群与另一组节点群之间不存在信号的交联和影响关系,就可以认为它们在贝叶斯网络中也无连接,进而对两组节点群分解,分别进行结构学习。该方法减小了整个贝叶斯网络的结构学习规模,同时也可以降低错误连接的风险。
此外,由于多数结构学习方法都存在迭代计算及样本数据调度等问题,导致并行计算难以实现。但是基于多信号流图知识进行的子系统拆分具有独立性,因此对每个子系统的学习过程可以采用并行计算方法。这一思路为提高学习效率提供了新的途径,使得学习过程可以同时由多个计算资源共同处理, 显著提升学习效率[17]。
值得注意的是,在对多信号流图模型进行解析时,需要考虑环路对拓扑排序造成的干扰。为此,本文算法需要单独对该情况进行拆环处理,具体操作过程可以参见2.3节中的算法步骤。
2.3 算法步骤基于2.2节的原理分析,本文所提出的诊断贝叶斯网络自动建模算法的步骤如下:
步骤1获取多信号流图模型的故障变量、测试变量以及D-矩阵。
步骤2获取多信号流图所有变量的拓扑排序ρ,排序过程依据信号流的传递顺序进行深度优先搜索,保证信号流的输出端变量编号小于输入端变量对象。
步骤3如果多信号流存在环路,对其进行拆环后继续排序,假设拆除Xi指向Xr的连线(Xr为不同于Xi的任意故障节点),将其存入连接线集合l。
步骤4遍历多信号流图模型中故障变量的父节点个数,取最大值作为贝叶斯模型的父节点上限μ。
步骤5以D-矩阵为基础,建立故障变量到测试变量的朴素贝叶斯网络模型,作为诊断贝叶斯网络的初始结构。
步骤6当系统模型复杂,并且由多个局部子系统构成时,依据多信号流图连接关系,对系统进行分割。
步骤7已知故障变量排序ρ及父节点上限μ,读取数据集Dt,假设先验分布为均匀分布,根据式(3),即超参数aitk=1,对故障变量进行K2学习,得到含有故障变量间依赖关系的贝叶斯结构网络。
步骤8检查l中的对象,对于Xi指向Xr的连线,如果Xi与Xr无连接,添加该连接进行评分计算,如果Xi与Xr存在直接或间接连接关系,遍历该环路所有连接关系并打分,最后保留评分较高的连接关系。
2.4 算法效率分析本文的融合算法不仅有效利用了多信号流图提供的先验信息,解决了纯数据驱动算法无法获得有效先验信息的问题,同时还大大降低了网络结构学习算法的运算复杂度。从算法复杂度来看,K2算法的时间复杂度为O(gh2p2q),g为实例样本个数,h为父节点上限个数,p为节点个数,q为每一个节点的取值个数[18]。而本文提出的融合算法由于通过多信号流图生成D-矩阵,能够迅速建立系统的初始朴素贝叶斯模型,因此测试对象的学习过程明显加快,参数p也由此减小。
另外,对于复杂系统,若基于多信号流图对系统进行拆分,同样可以有效减小参数p。假设所有节点拆分成2个集合,每个集合的节点数分别为p1和p2,那么此时的算法复杂度将变为O(gh2p12q)+O(gh2p22q),并且拆分后的部分子系统的父节点上限个数可能小于系统整体取值h,这又将进一步减小计算复杂度。
收敛速度和建模精度是评价算法好坏的两个关键指标。本文中收敛速度通过系统结构学习全过程所用的时间进行衡量,以读取多信号流图模型和数据作为开始,直到输出所有连接关系作为终止。贝叶斯结构学习的精确性能指标通常由以下4个因素衡量:缺失边(Missing Edge, ME)、冗余边(Redundant Edge, RE)、反向边(Inverted Edge, IE)、有效边(Correct Edge, CE),精确度Accuracy为
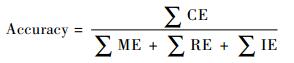
|
(5) |
文献[12]中首次运用K2算法对Alarm网络进行学习,验证了该算法的可行性。本文同样采用Alarm网络进行结构学习,并根据网络信息流向对多信号流图模型进行假设,获得节点编号如图 1所示(编号顺序不唯一),以及父节点上限个数4。

|
| 图 1 Alarm网络结构 Fig. 1 Structure of Alarm network |
采用常用的网络结构学习算法Path Condition(PC)算法、Necessary Path Condition(NPC)算法以及K2算法与本文提出的融合算法进行对比验证,学习所用数据样本根据Alarm网络参数由Monte Carlo法通过逻辑抽样生成[21]。为减小样本数据对学习算法的影响,本文在样本量为500,1 000,3 000,7 000,10 000的情况下分别进行了5次仿真实验,表 1所示为5次仿真结果的平均值。表中最后一列为本文提出的融合算法。
| 数据规模 | 错误类型 | PC算法 | NPC算法 | K2算法 | 融合算法 |
| 500 | 缺失边 | 11.2 | 14.0 | 2.2 | 1.2 |
| 冗余边 | 0 | 0 | 6.4 | 4.0 | |
| 反向边 | 7.2 | 8.2 | 0 | 0 | |
| 有效边 | 27.6 | 23.8 | 37.4 | 40.8 | |
| 1 000 | 缺失边 | 9.0 | 10.8 | 2.0 | 1.0 |
| 冗余边 | 1.2 | 7.8 | 4.4 | 3.2 | |
| 反向边 | 8.8 | 0.8 | 0 | 0 | |
| 有效边 | 27.0 | 26.6 | 39.6 | 41.8 | |
| 3 000 | 缺失边 | 3.4 | 4.4 | 1.0 | 0 |
| 冗余边 | 0 | 0.2 | 2.0 | 0.6 | |
| 反向边 | 4.2 | 5.2 | 0 | 0 | |
| 有效边 | 38.4 | 36.2 | 43.0 | 45.4 | |
| 7 000 | 缺失边 | 1.8 | 2.2 | 1.0 | 0 |
| 冗余边 | 0.4 | 0.4 | 1.4 | 0.4 | |
| 反向边 | 5.2 | 5.6 | 0 | 0 | |
| 有效边 | 38.6 | 37.8 | 43.6 | 45.6 | |
| 10 000 | 缺失边 | 1.4 | 1.6 | 1.0 | 0 |
| 冗余边 | 0.2 | 0 | 1.2 | 0 | |
| 反向边 | 4.8 | 4.6 | 0 | 0 | |
| 有效边 | 39.6 | 39.8 | 43.8 | 46.0 |
假设模型最后一级叶节点是测试组件(即图 1中Alarm网络的节点27~37),它与故障节点的连接关系可以通过D-矩阵获得,因此Alarm模型的规模由37个节点46条边缩小至26个节点27条边。根据式(5)中所提到的汉明距指标进行衡量,在数据规模为10 000时,不正确边数量下降到0,说明数据规模的增加明显降低了建模中出现错误的可能性。
不同数据规模下的4种算法分别计算其精确度,结果如图 2所示。由表 1及图 2可以看出,K2算法的学习精确度要高于PC算法及NPC算法,而融合算法的学习精确度比上述3种学习算法明显更优。

|
| 图 2 不同算法的精确度对比 Fig. 2 Precision comparison among different algorithms |
以往K2算法实现中所运用的节点排序等知识需要通过专家指定,而融合算法首先解决了K2算法中对先验知识的苛刻限制。其次,融合算法利用系统D-矩阵可以减小模型学习范围,显著提高了算法学习的精确度。例如,在数据规模为7 000时,可以计算得融合算法的精确度分别是PC、NPC、K2算法的21.8、24.7、6.3倍,当数据规模增大到10 000时,融合算法达到了100%正确的学习结果,此时根据式(5)求得的精确度指标将趋近于正无穷。最后,融合算法对于训练数据规模较小的情况依然有很好的表现。由图 2可以看出,K2算法在数据规模下降到3 000以下时,有效边的比例将低于总边数的85%,而融合算法在数据规模仅为500的条件下,建模得到有效边的比例仍高于K2算法下数据规模为3 000的学习结果,这将极大地降低结构学习过程对数据规模的要求。
此外,纯数据驱动的算法虽有较好的建模精确度,但是收敛速度过慢,尤其是当系统规模和学习数据增大时,算法时间复杂度迅速上升。在对比实验中,如图 3所示,融合算法相比于K2算法虽然在节点规模上仅减少了不到1/3,但是其收敛时间减小了大约60%。

|
| 图 3 算法收敛时间对比 Fig. 3 Convergence time comparison among different algorithms |
为验证多信号流图对模型的拆分和并行计算具有的潜在贡献,观察图 1所示Alarm系统,根据其信号流的传递关系,可以在节点18和节点19之间对网络系统进行拆分,此时学习对象分别为节点1~18和节点18~26组成的网络。由图 3看出,分割后的融合算法的收敛速度减小为最初的22%~29%。若该计算过程可以实现并行计算,收敛速度将进一步降低。该算法特性弥补了K2算法效率低下的缺点。
3.2 仿真实例本文所使用系统是某型观瞄系统,根据设计人员所提供的产品信号交联关系及故障模式分析结果可搭建多信号流图模型如图 4所示,多信号流图模型完全遵循系统物理连接关系,相比于利用专家知识直接建立贝叶斯模型更加容易实现,并且模型的准确性可以得到保证。图 4中子系统内部由故障组件构成,如观瞄具的内部结构为图中右上角方框内所示。基于2.1节对多信号流图模型可分解性的讨论,本文选取系统主要功能之一的热像观瞄功能进行建模演示,图中控制板与观瞄具间的信号传递产生环路,因此暂不考虑灰色点划线所代表的信号传递关系,以达到拆环的目的。
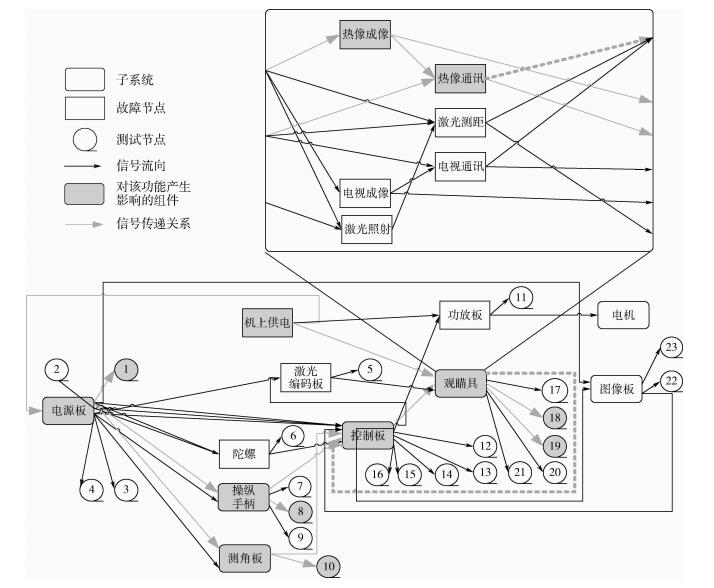
|
| 图 4 某型观瞄系统的多信号流图模型 Fig. 4 Multi-signal flow graphs model of an aiming system |
首先对热像观瞄子系统进行编码,沿灰色实连接线方向由小到大对组件编号,测试组件编码在故障组件全部编码完成后进行,编码结果为:C1~C7依次为故障组件{“机上电源”,“电源板”,“测角板”,“操纵手柄”,“控制板”,“热像成像”,“热像通讯”},C8~C12依次为测试组件{“10”,“19”,“18”,“8”,“1”}。其次,寻找输入端最大的输入量作为父节点上限,图 4中该值出现在控制板输入端及热像通讯输入端,取值为2。D-矩阵可以在多信号流图测试性分析过程中获得,矩阵关系如表 2所示。利用以上信息及系统完整数据,可以进行贝叶斯网络学习。学习步骤如下:
| 测试组件 | 测试组件10 | 测试组件19 | 测试组件18 | 测试组件8 | 测试组件1 |
| 机上电源 | 0 | 1 | 1 | 0 | 1 |
| 电源板 | 0 | 0 | 0 | 0 | 1 |
| 测角板 | 1 | 0 | 0 | 0 | 0 |
| 操纵手柄 | 0 | 0 | 0 | 1 | 0 |
| 控制板 | 0 | 1 | 0 | 0 | 0 |
| 热像成像 | 0 | 1 | 1 | 0 | 0 |
| 热像通讯 | 0 | 1 | 0 | 0 | 0 |
步骤1多信号流图测试组件与诊断贝叶斯网络测点一一对应,因此根据表 2 D-矩阵获得系统朴素贝叶斯模型如图 5(a)所示。
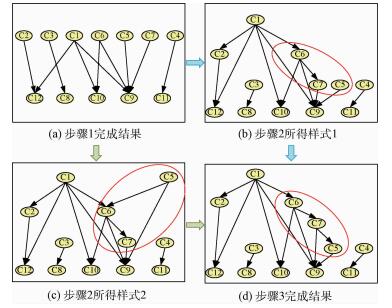
|
| 图 5 子系统贝叶斯模型的建立过程 Fig. 5 Building process of Bayesian model of a subsystem |
步骤2对C1~C7节点通过K2算法进行学习,得到贝叶斯结构如图 5(b)所示。
步骤3考虑图 1中的环形模型,灰色点划线信号流由C7指向C5,此时在贝叶斯网络中添加C7→C5的有向边不会造成环路连接,因此添加该边并对系统进行打分,评分结果显示新的连接关系优于原连接,因此添加该有向边,获得模型如图 5(d)所示。
受到数据和学习精确度的影响,步骤2中贝叶斯网络学习结构可能如图 5(c)所示,此时若添加C7→C5有向边会造成网络环路,因此需对C5、C6和C7这3个节点的每种连接关系进行遍历打分,获得分数最高的连接关系依然如图 5(d)所示,该网络模型唯一。
在实际工程中,多信号流图中故障节点间的信号传递关系仅有少部分具有因果联系,即在贝叶斯网络中存在连接关系,因此,多信号流图中的环路通常不会造成图 5(c)中贝叶斯网络结构矛盾现象,环路越大在贝叶斯网络学习过程中出现矛盾结构的概率就越小。而对于小规模环路而言,遍历该环路的每种连接关系是可以被接受的,同时该遍历过程有机会纠正因编号或数据等问题造成的建模偏差。
通过对系统各个功能区域进行分解,可以得到多个小规模下的贝叶斯网络,由于各个节点编号唯一,因此最终总会得到完整的系统诊断贝叶斯结构。分解建模的过程减小了结构学习的规模和错误率,并且为进一步实现贝叶斯结构的并行学习提供了可能。
4 结论本文提出了多信号流图模型与K2算法融合的诊断贝叶斯网络自动建模方法,经实验验证具有以下特点:
1)对已有多信号流图模型进行知识提取,可以获取K2算法所需要的先验信息。
2)充分利用多信号流图中节点的连接关系对模型进行简化和分解,显著改善了纯数据驱动学习方法存在的搜索空间大、运行效率低、建模精度不够理想等问题。
3)得益于多信号流图在专家知识表述上的准确性、全面性以及K2算法的优异性能,融合算法可以显著提升贝叶斯网络结构学习的精度和效率,同时也为复杂系统的拆分和并行学习提供了有效途径。
| [1] | JENSEN F V. Bayesian networks and decision graphs[M]. New York: Springer, 2001 : 32 -34. |
| [2] | EFRON B. Bayes' theorem in the 21st century[J]. Science, 2013, 340 (6137) : 1177 –1178. DOI:10.1126/science.1236536 |
| [3] | AOUAY S, JAMOUSSI S, BEN AYED Y.Particle swarm optimization based method for Bayesian network structure learning[C]//2013 5th International Conference on Modeling, Simulation and Applied Optimization (ICMSAO).Piscataway, NJ:IEEE Press, 2013:1-6. |
| [4] | 张振海, 王晓明, 党建武, 等. 基于专家知识融合的贝叶斯网络结构学习方法[J]. 计算机工程与应用, 2014, 50 (2) : 1 –4. ZHANG Z H, WANG X M, DANG J W, et al. Bayesian network structure learning method based on expert knowledge fusion[J]. Computer Engineering and Applications, 2014, 50 (2) : 1 –4. (in Chinese) |
| [5] | BALABAN E, SAXENA A, NARASIMHAN S, et al. Prognostic health-management system development for electromechanical actuators[J]. Journal of Aerospace Information Systems, 2015, 12 (3) : 329 –344. DOI:10.2514/1.I010171 |
| [6] | 代京, 于劲松, 张平, 等. 基于多信号流图的诊断贝叶斯网络建模[J]. 北京航空航天大学学报, 2009, 35 (4) : 472 –475. DAI J, YU J S, ZHANG P, et al. Diagnostic Bayesian networks modeling based on multi-signal flow graphs[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35 (4) : 472 –475. (in Chinese) |
| [7] | 陈希祥, 邱静, 刘冠军. 测试不确定条件下基于贝叶斯网络的装备测试优化选择技术[J]. 中国机械工程, 2011, 22 (4) : 379 –384. CHEN X X, QIU J, LIU G J. Test selection of materiel based on Bayesian network under test uncertainty[J]. China Mechanical Engineering, 2011, 22 (4) : 379 –384. (in Chinese) |
| [8] | Qualtech Systems Inc.Testability, engineering and maintenance system(TEAMS)[EB/OL].[2010-07-26]. http://www.teamqsi.com/products/teams-designer/. |
| [9] | 吴红, 王维平, 杨峰. 融合先验信息的贝叶斯网络结构学习方法[J]. 系统工程与电子技术, 2012, 34 (12) : 2585 –2591. WU H, WANG W P, YANG F. Structure learning method of Bayesian network with prior information[J]. Systems Engineering and Electronics, 2012, 34 (12) : 2585 –2591. (in Chinese) |
| [10] | MASEGOSA A R, MORAL S. New skeleton-based approaches for Bayesian structure learning of Bayesian networks[J]. Applied Soft Computing, 2013, 13 (2) : 1110 –1120. DOI:10.1016/j.asoc.2012.09.029 |
| [11] | BOUCHAALA L, MASMOUDI A, GARGOURI F, et al. Improving algorithms for structure learning in Bayesian networks using a new implicit score[J]. Expert Systems with Applications, 2010, 37 (7) : 5470 –5475. DOI:10.1016/j.eswa.2010.02.065 |
| [12] | COOPER G F, HERSKOVITS E. A Bayesian method for the induction of probabilistic networks from data[J]. Machine Learning, 1992, 9 (4) : 309 –347. |
| [13] | CHENG J, GREINER R, KELLY J, et al. Learning Bayesian networks from data: An information-theory based approach[J]. Artificial Intelligence, 2002, 137 (12) : 43 –90. |
| [14] | SILANDER T, ROOS T, MYLLYMÄKI P. Learning locally minimax optimal Bayesian networks[J]. International Journal of Approximate Reasoning, 2010, 51 (5) : 544 –557. DOI:10.1016/j.ijar.2010.01.012 |
| [15] | WELLMAN M P, BREESE J S, GOLDMAN R P. From knowledge bases to decision models[J]. The Knowledge Engineering Review, 1992, 7 (1) : 35 –53. DOI:10.1017/S0269888900006147 |
| [16] | DEB S, PATTIPATI K R, SHRESTHA R.QSI's integrated diagnostics toolset[C]//1997 IEEE Autotestcon Proceedings AUTOTESTCON, 97.Piscataway, NJ:IEEE Press, 1997:408-421. |
| [17] | YU K, WANG H, WU X.A parallel algorithm for learning Bayesian networks[M]//Advances in Knowledge Discovery and Data Mining. Berlin Heidelberg:Springer, 2007:1055-1063. |
| [18] | 曾安, 李晓兵, 杨海东, 等. 基于最小描述长度和K2的贝叶斯网络结构学习算法[J]. 东北师大学报(自然科学版), 2014, 46 (3) : 53 –58. ZENG A, LI X B, YANG H D, et al. Bayesian network structure learning based on minimum description length and K2 algorithm[J]. Journal of Northeast Normal University(Natural Science Edition), 2014, 46 (3) : 53 –58. (in Chinese) |
| [19] | 吴永广, 庞世春. K2 & HC结构学习算法[J]. 计算机与数字工程, 2014, 42 (7) : 1137 –1140. WU Y G, PANG S C. K2 & HC structure learning algorithm[J]. Computer & Digital Engineering, 2014, 42 (7) : 1137 –1140. (in Chinese) |
| [20] | TIAN J, PEARL J.Causal discovery from changes[C]//Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence. San Francisco: Morgan Kaufmann Publishers Inc., 2001:512-521. |
| [21] | TSAMARDINOS I, BROWN L E, ALIFERIS C F. The max-min hill-climbing Bayesian network structure learning algorithm[J]. Machine Learning, 2006, 65 (1) : 31 –78. DOI:10.1007/s10994-006-6889-7 |





