Download PDF  
文章快速检索  
  高级检索
引用本文
颜骥, 李相民, 刘立佳, 张凤霞. 基于Memetic算法的超视距协同空战火力分配[J]. 北京航空航天大学学报, 2014, 40(10): 1424-1429
Yan Ji, Li Xiangmin, Liu Lijia, Zhang Fengxia. Weapon-target assignment based on Memetic optimization algorithm in beyond-visual-rang cooperative air combat[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(10): 1424-1429.
基于Memetic算法的超视距协同空战火力分配
颜骥1, 李相民1, 刘立佳1, 张凤霞2    
1. 海军航空工程学院 兵器科学与技术系, 烟台 264001;
2. 中航工业洛阳电光设备研究所 光电控制技术重点实验室, 洛阳 471009
收稿日期:2013-11-6; 网络出版日期: 2014-03-18
基金项目：航空科学基金资助项目(20135184008);国防预研基金资助项目(40108040402).
作者简介: 颜骥(1984-),男,湖南湘阴人,博士生,53072472@qq.com.
摘要：针对超视距多机协同空战中,火力单元采用一次性完全分配原则容易造成资源浪费的问题,采用一种新的火力分配数学模型.该模型带有毁伤概率门限,能够保证在满足毁伤概率门限的前提下,优先保证威胁度大的目标被分配且选择对各目标杀伤概率相对较大的火力单元,使其对目标的毁伤概率平均值达到最大且尽量少地消耗火力单元,从而节省和充分利用火力资源.在此基础上,提出采用以离散粒子群算法为全局搜索策略,以贪婪算法为局部搜索策略的Memetics算法求解协同空战火力分配问题,有效地提高了算法收敛速度、精度.仿真算例验证了模型的优点及Memetic算法的有效性.
关键词： 超视距     协同空战     火力分配     毁伤概率门限     Memetic算法    
Weapon-target assignment based on Memetic optimization algorithm in beyond-visual-rang cooperative air combat
Yan Ji1, Li Xiangmin1, Liu Lijia1, Zhang Fengxia2     
1. Department of Ordnance Science and Technology, Naval Aeronautical and Astronautical Institute, Yantai 264001, China;
2. Science and Technology on Electro-optic Control Laboratory, Luoyang Institute of Electro-optical Equipment of AVIC Luoyang 471009, China
Abstract:In beyond-visual-rang (BVR) cooperative air-to-air combat, weapon resources could be wasted if all weapon units are fully assigned at a time. To cope with the disadvantage, a new weapon-target assignment mathematical model based on the threshold of damage probability was proposed. The new model guarantees the threshold of damage probability by employing fewer weapon units to save and make full use of weapon resources. The proper fire units were assigned to the targets according to the priority of menace. Meanwhile, the maximum of the target damage probability average value can also be achieved. Based on the new model, a Memetic algorithm, using the discrete particle swarm optimization (DPSO) algorithm as the global search strategy and greedy algorithm as the local search strategy, was proposed to solve the weapon-target assignment problem. Simulation results show the advantage of the proposed new model and the effectiveness of Memetic algorithm.
Key words: beyond-visual-rang (BVR)     cooperative air combat     weapon-target assignment     threshold of damage probability     Memetic algorithm    

多机编队超视距协同作战是现代空战的主要形式,若不涉及作战战术,协同空战决策的核心和热点问题为交战阶段的协同多目标分配,目的是确定多战机在一个决策时间片或一个时间序列中的任务集,使战机间形成协同,以最小的代价达到最优的作战效能[1].对这类具有约束条件的组合优化问题,解决方法一般先构建协同多目标分配模型,然后根据约束条件选择适当的方法对模型进行优化求解,得出目标分配方案用于决策或辅助决策.超视距协同空战中的目标分配一般指导弹目标分配,故本文称其火力分配.

目前大部分火力分配模型都是基于单纯的求毁伤概率越大越好或剩余威胁越小越好的最优准则[1,2,3,4,5,6,7,8,9,10],这种一次性分配的静态模型在火力资源充足、目标数目相对较少的情况下,会导致武器火力资源的浪费,当有后续敌机目标到来时,无法继续为其提供火力.文献[11]提出带毁伤概率门限的火力分配模型,在取得最大的对目标毁伤概率均值的同时,尽量少地消耗火力资源,更符合现代空战多阶段攻防对抗.

求解火力分配的算法有多种,从结构上看可分为集中式算法和分布式算法.诸如粒子群算法、遗传算法等[2,3]仿生算法,差分进化算法等[4,5]启发式算法以及这些算法的改进与混合[1,6,7]的集中式算法,一般应用于数据链组网/退网时间较长且战机计算能力和智能性较差的场景,战机之间信息共享很少,由长机集中负责编队的协同多目标分配;分布式方法源自无人机和无人作战系统的拍卖算法[8,9,10]和完全分布式的群集智能算法[1],涉及目标分配的拍卖算法[8,9,10]一般应用于有指挥中心的分布式协同场景,战机间信息交互频繁,且多针对一次性分配的静态模型;无指挥中心协同模式下的拍卖算法在无人系统间通信拓扑时变及时延时可获得较优的无冲突的任务分配方案,但其属于一对一[12]或一对多[13]的目标分配.文献[8]提出的组合拍卖算法虽解决了战机间不能共享投标而无法协同攻击的问题(弹-目分配的多对一问题),但战机在仅能与部分其他武器平台进行信息共享时分配结果不能保证.文献[14]提出了一种鲁棒的分布式任务分配方法,无人机群在通信网络拓扑变化和态势信息不完全情况下,通过信息一致和计划生成两阶段可得出满意的协同任务分配方案.类似文献[12,13],各无人系统对环境的态势感知并非完全一致,不同之处在于,文献[14]每架无人机都基于自身掌握的不完全态势信息计算编队的协同方案,最后通过冲突消除阶段来获得满意解.

本文基于文献[11]的火力分配模型,采用文献[14]的任务协同分配框架,讨论多战机编队协同火力分配问题.限于篇幅,本文仅对协同火力分配展开研究,采用Memetic算法来解决该问题,以提高算法对全局最优解的搜索效率.信息一致性算法和冲突消除方法可参考文献[12,13,14],本文不再赘述. 1 协同空战火力分配数学模型

假设在某次多机协同攻击多目标的超视距空战中,由r架飞机组成的编队R={R1,R2,…,Rr},挂载了不同类型的导弹,所有导弹的总数量为m,每枚导弹的编号为Mi(i=1,2,…,m),需要攻击的敌机目标有n个,每个目标的编号为Tj(j=1,2,…,n).记Pj为所分配火力对第j个目标的联合毁伤概率,则

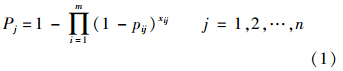
式中,pij为第i枚导弹对第j个目标的毁伤概率;xij为决策变量,若分配第i枚导弹攻击第j个目标,则xij=1,否则xij=0.

一般基于求毁伤概率越大越好的一次性分配模型为

式中Wj为第j个目标的威胁权重.

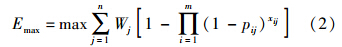
为避免火力资源相对充足、目标数相对较少情况下应用上述模型造成的火力资源浪费,本文采用带毁伤概率门限的火力分配模型[11]为

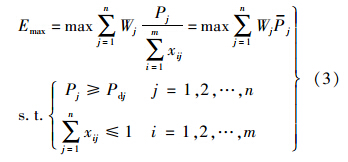
式中,Pdj为第j个目标的预设毁伤概率门限,其值可根据目标战场态势由指挥员确定,或由指挥系统确定;Pj为Pj的均值;约束Pj≥Pdj表示对每个目标的毁伤概率应大于其预设毁伤概率门限,若一个火力分配方案中,对某个目标的毁伤概率低于毁伤概率门限,则该分配方案无效;约束∑xij≤1表示一枚导弹最多只能攻击一个目标.

在符合约束条件下,该模型将毁伤概率和资源消耗问题综合考虑,在选择尽量少的导弹数目前提下,选取对目标毁伤概率最大的导弹组合,达到既节省资源又使毁伤概率尽量大的效果.

上述模型为非线性0-1整数规划问题,目标函数和约束条件均为决策变量的非线性函数.为此,本文先将上述问题化为一个无约束问题,然后采用Memetic算法求解该火力分配问题.

无约束问题的转化采用罚函数法,令

则原问题化为
式中M为罚因子,设M=100.

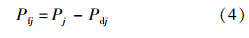
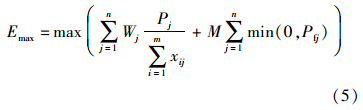
当火力分配方案某目标的毁伤概率低于预设门限时,式(5)的后半部分为负,以式(5)为适应度函数的值劣于符合约束条件方案的值,在种群的进化中容易被淘汰. 2 解火力分配问题的Memetic算法

Memetic算法[15]属于文化进化算法,是一种混合算法框架.其充分吸收全局搜索算法和局部搜索算法的优点,不仅具有很强的全局寻优能力,同时,对每次全局算法产生的新种群(部分或全部)进行局部搜索,通过优化种群分布,及早剔除不良个体,进而减少迭代次数,加快算法的求解速度,这样既保证了较高的收敛性能,又能获得高质量解,从而使Memetic算法的搜索效率在某些问题领域比传统的进化算法要快几个数量级. 2.1 Memetic算法流程

本文解决火力分配问题的Memetic算法是以离散粒子群算法为全局搜索策略,以贪婪算法为局部搜索策略的混合优化算法.在一次迭代中,算法让每个个体(粒子)执行全局进化操作(速度、位置更新)后,再进行局部搜索,直至满足优化准则而终止.具体算法流程如图 1所示,将图中粒子群操作替换为遗传操作则为基于遗传算法框架的Memetic算法. 2.2 全局搜索DPSO算法

针对非线性0-1整数规划的火力分配问题,采用连续空间离散粒子群优化(DPSO,Discrete Particle Swarm Optimization)算法作为Memetic算法的全局搜索策略,这样保留了连续PSO算法的运算模式,从而可以充分利用其矢量计算简单、消耗时间短的优势.

采用一种基于实数的编码方式,用粒子位置代表一种导弹-目标分配的候选方案,粒子位置矢量维数分量(维数m与导弹数相同)代表导弹,维数分量对应的整数代表该导弹分配的目标.设粒子的总数为R,则第r个粒子的位置矢量为Xr=[Xr1,Xr2,…,Xrm],分量Xri(i=1,2,…,m)为0～n之间的整数.粒子速度矢量为Vr=[vr1,vr2,…,vrm],分量vri(i=1,2,…,m)为-(n-1)～(n-1)之间的整数.

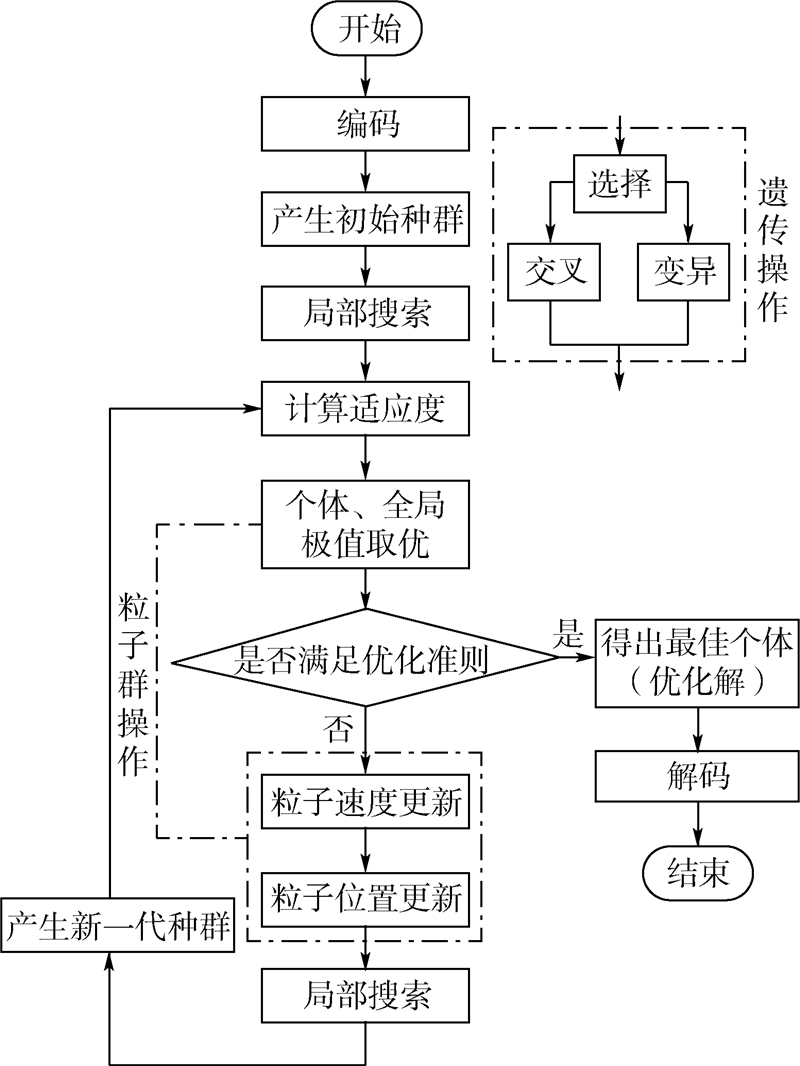图 1 Memetic算法程序流程 Fig. 1 Flow chart of Memetic algorithm
图选项

为将整数编码转化为适合适应值计算的0-1整数规划的决策变量形式x=[xij]m×n(i=1,2，…,m；j=1,2，…,n),采用转化公式:

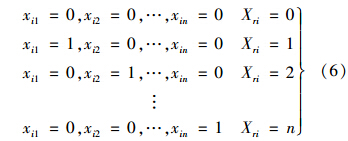
第r个粒子在i维子空间的飞行速度和位置更新公式及参数可以参见文献[11],此处不再赘述. 2.3 局部搜索贪婪算法

针对本文的火力分配问题,为取得个体邻域内目标函数的局部最优解,结合目标函数(5)的结构特点,提出“先删后补”的串行两阶段贪婪策略.

1) 分配冗余删除阶段.

这一阶段对一种导弹-目标分配候选方案Xr,检查所有符合杀伤概率门限约束的目标所分配的导弹数目,若分配给该目标的导弹数大于1,则尝试删除分配给该目标中对该目标单发毁伤概率小的导弹,若删除该导弹分配后,剩余导弹对目标的联合毁伤概率仍大于或等于对目标的毁伤概率门限,则确认删除该导弹分配,否则保留该分配.此阶段通过对冗余导弹分配的删除,提高对目标整个毁伤概率的均值,并选择Pj大的导弹组合,从而使目标函数(5)的前半部分尽可能大.

2) 分配不足补充阶段.

本阶段对上一阶段优化后的分配方案,首先,分别检查方案中未分配目标的导弹集M′i和联合杀伤概率低于预设杀伤概率门限的目标集T′j;然后,对T′j中的目标按其Pfj值大小由低到高排序(若目标j未分配导弹,则Pfj=0－Pdj),并将M′i中对目标j杀伤概率最大的导弹i按序依次分配给目标.此阶段,有未分配目标导弹的前提下,联合毁伤概率小于预设毁伤概率门限的目标可获得一次补充分配的机会,Pfj值越小,其选择剩余导弹的优先级越高.过程中每个目标只能补充分配一枚导弹,分配L次后结束.

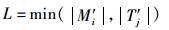
其中|·|表示集合中元素的个数.贪婪算法伪代码如下： 输入:导弹-目标分配候选方案Xr 输出:优化的导弹-目标分配候选方案Xr

1) 分配冗余删除阶段.

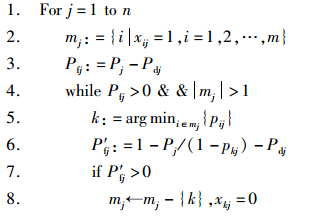
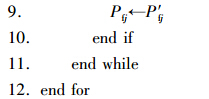
2) 分配不足补充阶段.

3 算例仿真验证及分析

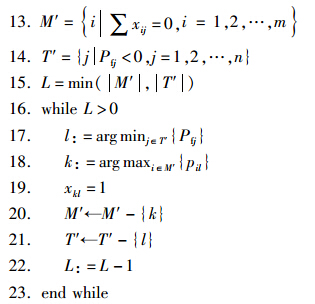
为验证本文提出的Memetic算法求解该火力分配问题的可行性和有效性,进行了仿真实验.

设我方战机编队在超视距条件下与敌机编队进行空战.我方战机架数为4架,每架战机均挂载4枚导弹,协同攻击区内发现10个敌机目标.

仿真中,各目标预设毁伤概率门限Pdj均为0.90.各目标的威胁权重矩阵为

W=[0.60.70.30.50.60.350.650.550.40.75]

各导弹对各目标的毁伤概率矩阵[11]为

采用本文的Memetic算法,包括分别以离散粒子群算法和以遗传算法为全局搜索策略,以本文设计的贪婪策略为局部搜索策略的两种混合优化算法(分别简称为MGA和MPA)、DPSO算法,模拟退火-离散粒子群(SA-DPSO)算法、遗传算法和模拟退火-遗传(SA-GA)算法对该火力分配问题进行优化求解.其中,DPSO算法和SA-DPSO算法的参数设置同文献[11];本文DPSO算法中,设置惯性权重为w=0.8.

本文采用的GA中,使用单点交叉运算和基本位变异运算(文中随机取3个基因位),采用确定性的选择策略,在父代和子代种群中选择目标函数值按从大到小排序的前R个个体进化到下一代.交叉概率pc=0.9,变异概率pm=0.1.SA-GA的参数设置同文献[6].

导弹-目标的最优分配方案见表 1,表中“0”代表未攻击.由表 1可看出,火力分配模型仅用13枚导弹便达到指标要求,大大节省了火力资源,从而为打击后续来袭目标做准备.

表 1 最优攻击分配 Table 1 Optimal attacks allocation
编号战机编队
F1F2F3F4
导弹M1M5M9M13
M2M6M10M14
M3M7M11M15
M4M8M12M16
敌机T7T700
T5T4T9T2
T60T2T10
T3T8T10T1
表选项

文献[15]对Memetic算法的收敛性进行了理论上的证明,本文对上述6种算法分别进行100次仿真实验,以证明Memetic算法解决该火力分配问题的有效性.种群规模均取为60个,迭代次数均为120代.为便于比较,分别将GA,SA-GA和基于GA的Memetic算法分为一组,将DPSO,SA-DPSO和基于DPSO的Memetic算法分为一组分别比较,然后再将这两组做比较,见图 2、图 3.

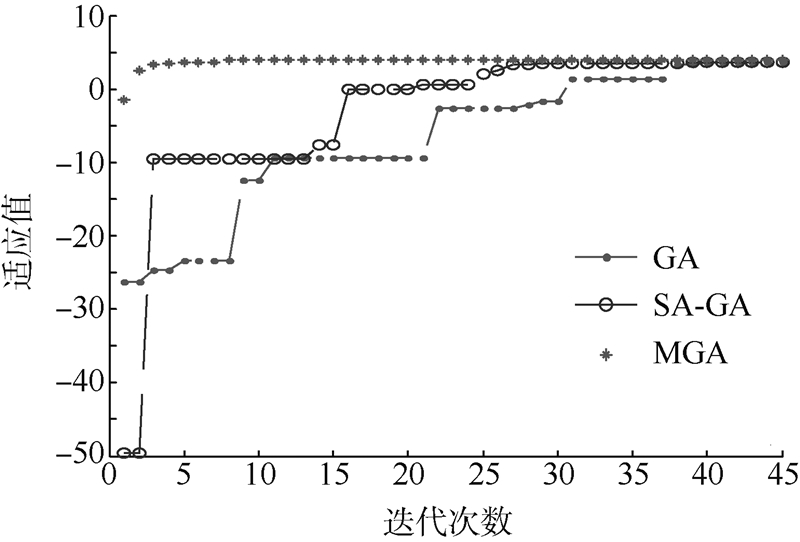图 2 围绕GA的3种算法最优迭代过程比较 Fig. 2 Comparison of iterative process of three algorithms based on GA
图选项
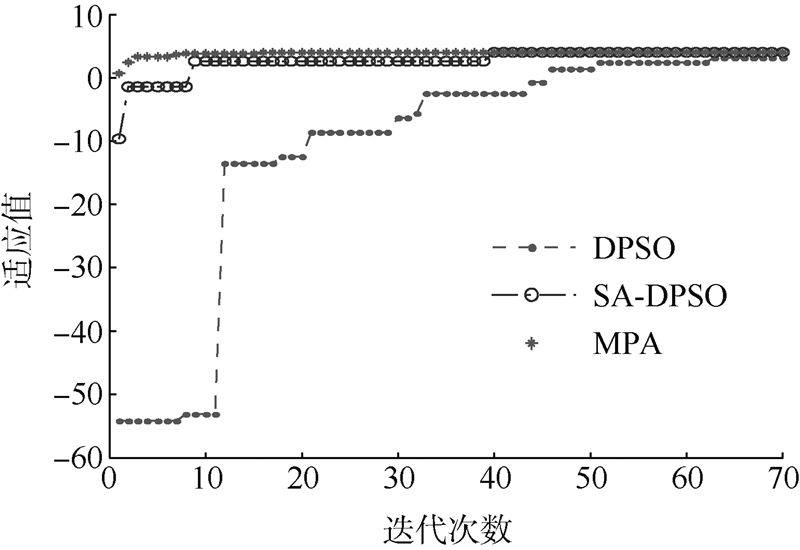图 3 围绕DPSO的3种算法最优迭代过程比较 Fig. 3 Comparison of iterative process of three algorithms based on DPSO
图选项

通过比较可知,Memetic算法能够迅速收敛到全局最优解,100次中,算法每次收敛到最优解的概率MGA为50%,MPA为97%;SA-DPSO算法和SA-GA算法能够收敛到全局最优,但相对Memetic算法较慢,且收敛到最优解的概率都低于20%;基本DPSO算法和GA不仅收敛速度慢,且在迭代过程中常常陷入局部最优.6种算法的综合比较见表 2.可见,本文提出的MPA算法能有效提高对全局最优解的寻优效率.

表 2 6种算法综合比较 Table 2 Comprehensive comparison of six algorithms
算法最优值平均值可靠性/%运行时间/s
GA3.58081.2186100.3232
SA-GA4.00952.2881322.1404
MGA4.02153.8503951.1799
DPSO3.48011.051770.1803
SA-DPSO4.02102.1895231.9715
MPA4.02154.01151000.5633
表选项
4 结 论

本文研究了火力资源相对充足条件下的多机编队超视距协同空战火力分配问题:

1) 研究了一种满足毁伤概率门限的火力分配模型,该模型保证火力分配方案使各目标达到预设毁伤概率门限的前提下,实现对目标的平均毁伤概率最大且所用武器火力单元尽可能少,从而保存火力,便于打击后续目标;

2) 提出求解该火力分配模型的Memetic算法,针对模型特点设计了基于离散粒子群算法的全局搜索策略和先删后补的串行两阶段局部贪婪搜索策略;

3) 仿真结果表明,火力分配模型可有效节约火力资源,本文的Memetic算法在解决该问题时是有效且快速的.

参考文献
[1] 刘波,陈哨东, 贺建良.基于概率群集的多战机协同空战决策算法[J].上海交通大学学报,2011,45(2):257-261 Liu Bo,Chen Shaodong,He Jianliang.Air combat decision-making for multi-fighter coordinated attack based on probability collectives[J].Journal of Shanghai Jiaotong University,2011, 45(2): 257261(in Chinese)
Cited By in Cnki (2)
[2] 肖冰松,方洋旺, 许蕴山,等.编队内协同超视距空战目标分配模型研究[J].系统工程与电子技术,2010,32(7): 14761479 Xiao Bingsong,Fang Yangwang,Xu Yunshan,et al.Research on coordinated formation target assignment model for beyond visual range air combats[J].Systems Engineering and Electronic,2010,32(7):1476-1479(in Chinese)
Cited By in Cnki (9)
[3] Lee Z J, Su S F,Lee C Y.Efficiently solving general weapon-target assignment problem by genetic algorithms with greedy eugenics[J].IEEE Transactions on Systems,Man,and Cybernetics—Part B:Cybernetics,2003,33(1):113-121
[4] Song W D, Zhao C W,Huo J X.Improved differential evolution algorithm for solving WTA problem[J].Energy Procedia, 2011(11): 1348-1353
[5] Madni A M, Andrecut M.Efficient heuristic approach to the weapon-target assignment problem[J].Journal of Aerospace Computing,Information,and Communication,2009,6(6): 405414
[6] 罗德林,王彪, 龚华军,等.基于SAGA的协同多目标攻击决策[J].哈尔滨工业大学学报,2007,39(7):1154-1159 Luo Delin,Wang Biao,Gong Huajun,et al.Air combat decision making for cooperative multiple target attack based on SAGA[J].Journal of Harbin Institute of Technology,2007,39(7):1154-1159(in Chinese)
Cited By in Cnki (7)
[7] 杨飞,王青, 侯砚泽.基于整数域改进粒子群优化算法的多平台武器目标分配[J].兵工学报,2011,32(7):906-912 Yang Fei,Wang Qing,Hou Yanze.Weapon-target assignment in multi-launcher system based on improved integer field particle swarm optimization algorithm[J].Acta Armamentarii,2011, 32(7): 906-912(in Chinese)
Cited By in Cnki (4)
[8] 刘波,张选平, 王瑞,等.基于组合拍卖的协同多目标攻击空战决策算法[J].航空学报,2010,31(7):1433-1444 Liu Bo,Zhang Xuanping,Wang Rui,et al.Air combat decision making for coordinated multiple target attack using combinatorial auction[J].Acta Aeronautica et Astronautica Sinica,2010, 31(7): 1433-1444(in Chinese)
Cited By in Cnki (8)
[9] 张杰勇,姚佩阳, 王欣,等.基于时间约束的多平台协同目标分配方法[J].系统工程与电子技术,2011,33(6): 12871292 Zhang Jieyong,Yao Peiyang,Wang Xin,et al.Multiple platforms coordinated target assignment method based on time restraint[J].Systems Engineering and Electronic,2011,33(6):1287-1292(in Chinese)
Cited By in Cnki (5)
[10] 万路军,姚佩阳, 孙鹏.有人/无人作战智能体分布式任务分配方法[J].系统工程与电子技术,2013,35(2): 310316 Wan Lujun,Yao Peiyang,Sun Peng.Distributed task allocation method of manned/unmanned combat Agents[J].Systems Engineering and Electronics,2013,35(2):310-316(in Chinese)
Cited By in Cnki (1)
[11] 李俨,董玉娜. 基于SA-DPSO混合优化算法的协同空战火力分配[J].航空学报,2010,31(3):626-631 Li Yan,Dong Yuna.Weapon-target assignment based on simulated annealing and discrete particle swarm optimization in cooperative air combat[J].Acta Aeronautica et Astronautica Sinica,2010,31(3):626-631(in Chinese)
Cited By in Cnki (13)
[12] Zavlanos M M, Spesivtsev L,Pappas G J.A distributed auction algorithm for the assignment problem[C]//Proc of the 47th IEEE Conf on Decision and Control.Piscataway,NJ:IEEE,2008:1212-1217
[13] Choi H L, Brunet L,Jonathan P H.Consensus-based decentralized auctions for robust task allocation[J].IEEE Transactions on Robotics,2009,25(4):912-926
Click to display the text
[14] Mehdi A, Jonathan P H.Robust decentralized task assignment for cooperative UAVs[R].AIAA 2006-6454,2006
[15] 段海滨,张祥银, 徐春芳.仿生智能计算[M].北京:科学出版社,2011:130-149 Duan Haibin,Zhang Xiangyin,Xu Chunfang.Bio-inspired computing[M].Beijing:Science Press,2011:130-149(in Chinese)
http://dx.doi.org/10.13700/j.bh.1001-5965.2013.0643 北京航空航天大学主办。
0

文章信息

颜骥, 李相民, 刘立佳, 张凤霞
Yan Ji, Li Xiangmin, Liu Lijia, Zhang Fengxia
基于Memetic算法的超视距协同空战火力分配
Weapon-target assignment based on Memetic optimization algorithm in beyond-visual-rang cooperative air combat
北京航空航天大学学报, 2014, 40(10): 1424-1429
Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(10): 1424-1429.
http://dx.doi.org/10.13700/j.bh.1001-5965.2013.0643

文章历史

收稿日期：2013-11-6
网络出版日期: 2014-03-18

相关文章

工作空间