2. 北京航天长征飞行器研究所 试验物理与计算数学国家级重点实验室, 北京 100076
2. National Key Laboratory of Experimental Physics and Computational Mathematics, Beijing Institute of Space Long March Vehicle, Beijing 100076, China
两轴转台是卫星平台上光学端机等高精度载荷指向控制的关键支撑部件,如空间光通信端机、中继卫星、天线指向等,其末端指向有很高的精度和稳定性要求.
在指向过程中,两自由度(Degree of Freedom,DOF)转台与卫星平台进行角动量交换,使卫星姿态运动发生改变[1, 2, 3, 4].由于指向机构以卫星平台为支撑,转台的转角必然受到平台姿态运动的影响,因此转台与卫星平台间存在耦合关系[5].这一耦合关系将导致指向机构相对于惯性系的转角偏离控制量,从而产生指向偏差.对于大型的指向机构或快速指向要求的平台,转台在指向过程中对平台产生的影响变得不可忽视[6, 7, 8].很多空间应用卫星多搭载扫描镜、CCD相机、天线等转动载荷,由于低轨微小卫星上的转动部件相对质量大,且相对转动范围大,这些载荷的运动会对卫星的本体姿态的稳定性产生干扰,甚至导致卫星失控.因此设计一种同时具有快速性与稳定性的指向控制方法就显得尤为重要[9, 10].
漂浮基转台敏捷跟踪指向控制问题是卫星平台运动机构控制的崭新课题,由于转台与卫星平台间的耦合运动关系,传统的PD控制方法对于漂浮基上大惯量转台的指向跟踪任务无法保证精度,因此针对上述任务条件设计一种控制方法对于提高空间平台上指向机构跟踪指向精度具有重要的实际意义[11, 12].
本文建立了卫星平台与转台的动力学耦合模型,基于反馈线性化设计了状态反馈控制律,并进行了仿真验证,对在轨运行过程中两自由度转台末端指向误差进行了详细研究,验证了控制方法的可行性.
1 动力学模型不考虑柔性附件的卫星平台与两自由度转台基本结构如图 1所示.转台轴系由一个方位轴和一个俯仰轴组成,卫星平台、方位轴、俯仰轴分别定义为1号体、2号体与3号体.1、2、3号体为刚体,2号体与3号体皆视为关于自身转轴对称.1号体为漂浮状态,2号体与3号体各有一个转动自由度,3号体为跟瞄指向装置,其初始时刻指向矢量为P0, t时刻指向矢量为Pt.
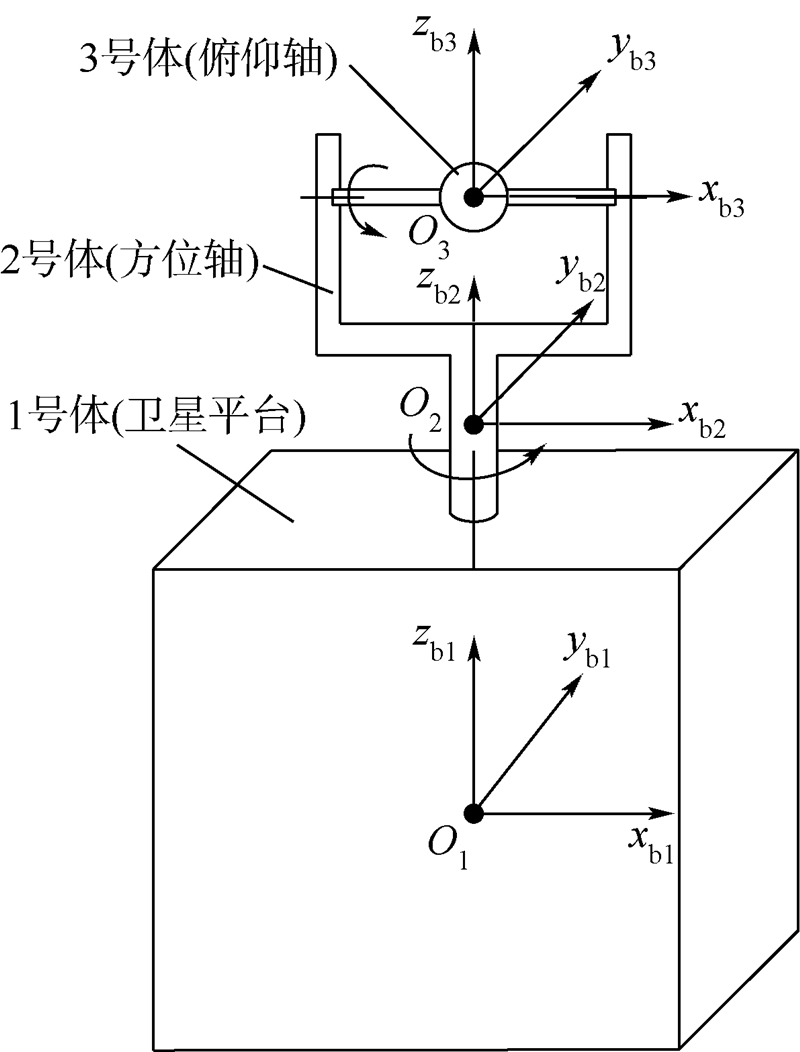 |
| 图 1 卫星平台与两自由度转台结构图 Fig. 1 Structure diagram of satellite platform and 2-DOF gimbal |
1号体本体系Sb1的原点O1与卫星与转台组合体质心重合,坐标系与1号体固连.Sb2为2号体本体坐标系,原点O2与2号体质心重合,Sb2坐标系与2号体固连.Sb3为3号体本体坐标系,原点O3与3号体质心重合,Sb3坐标系与3号体固连.ω2r与ω3r分别为2号体相对卫星本体的转动角速度以及3号体相对2号体的转动角速度.
取2号体为研究对象,矩心取在2号体质心上.应用相对质心的动量矩定理,有
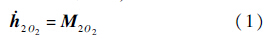
式中:h2O2为2号体的运动对2号体质心O2的动量矩;M2O2为作用在2号体上所有外力对其质心矩的矢量和.设1号体相对惯性坐标系的角速度ω1,在1号体本体坐标系Sb1上的分量列阵为
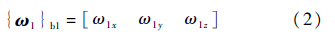
2号体的角速度为

在Sb1上的分量列阵为
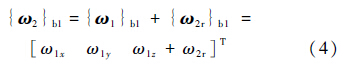
式中:
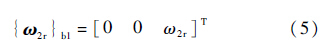
2号体的动量矩在Sb1中的列阵形式为
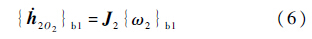
式中:J2为2号体的惯量矩阵:
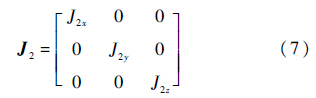
将式(1)投影到Sb1坐标系下,有

式中:ωSb1为坐标系Sb1相对惯性系的角速度,因此有
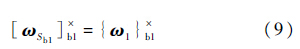
作用在2号体上的外力对质心的矩为
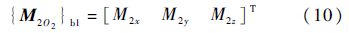
化简可得
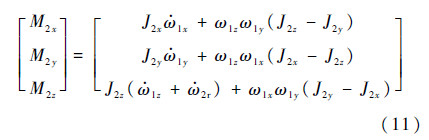
设由Sb1到Sb2的转换矩阵为L21,则坐标系Sb2的角速度在Sb2的分量列阵为
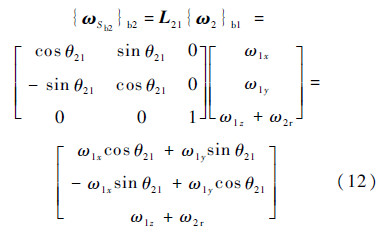
式中:θ21为2号体相对1号体所转过的角度.
3号体的角速度为
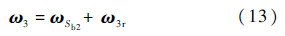
在Sb2上的列阵形式为

式中:
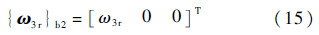
3号体的惯量矩阵为

对3号体有
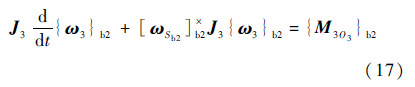
其中作用在3号体上的外力对质心的矩为
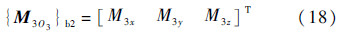
将式(12)、式(14)、式(16)和式(18)代入式(17),可得
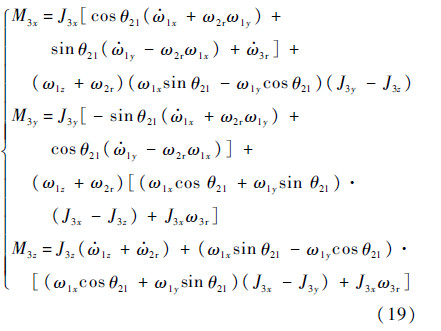
根据2号体与3号体的力矩关系,有
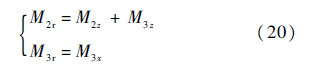
式中:M2r与M3r分别为2号体与3号体转轴方向上的电机驱动力矩.
将式(11)和式(19)代入式(20)得
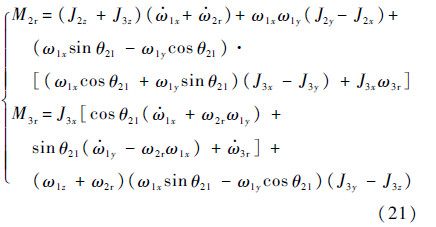
通过式(21)可看出,卫星平台、方位轴与俯仰轴任一个体在运动中会对另外两个体产生扰动力矩,因此给转台的指向控制带来难度.在设计转台跟踪控制方法中应考虑耦合关系的影响,从而提高转台的指向精度.
2 控制律设计轨道间卫星平台与跟踪目标位置关系如图 2所示.P为本体平台质心指向目标平台质心的矢量,为已知的目标位置信息.
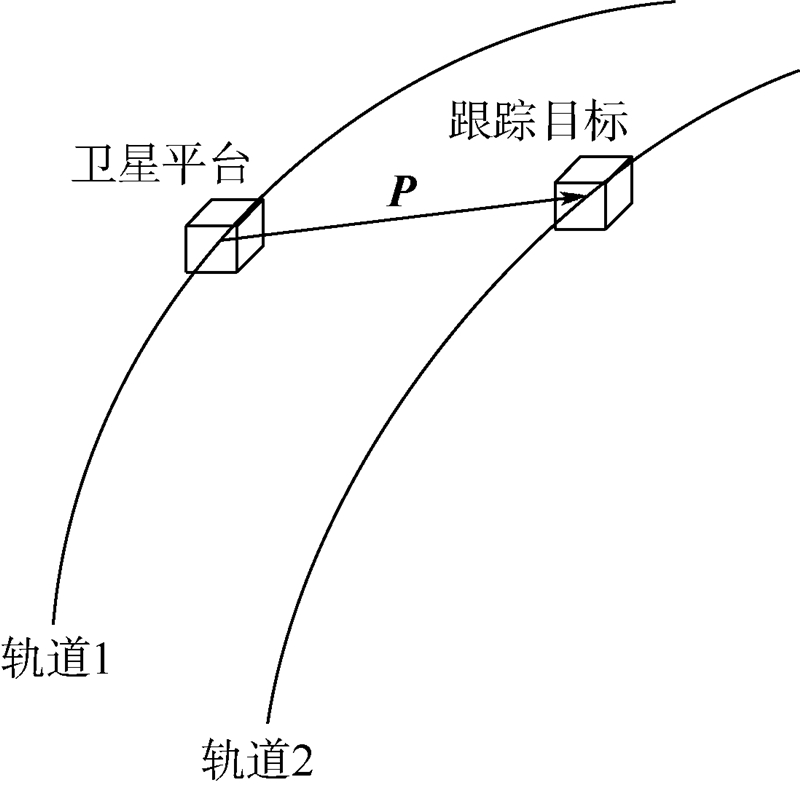 |
| 图 2 跟踪指向关系示意图 Fig. 2 Sketch map of tracking and pointing relation |
转台跟踪控制流程如图 3所示.
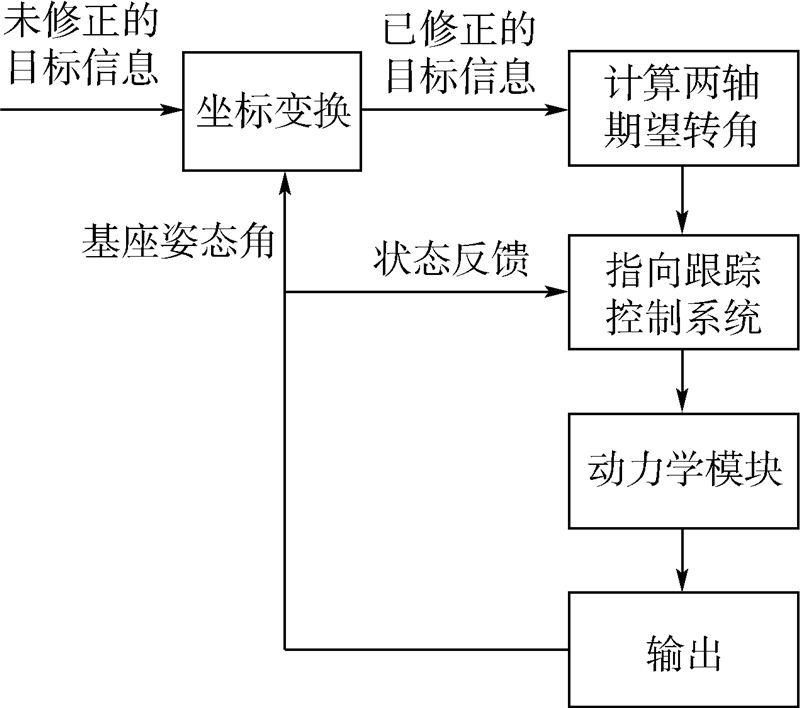 |
| 图 3 转台跟踪控制流程图 Fig. 3 Flow chart of gimbal’s tracking control |
令{P}o为P在卫星平台轨道系下的分量列阵,则P在卫星平台本体系下的分量列阵为
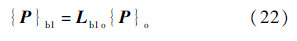
式中:Lb1o为卫星平台轨道系到卫星平台本体系坐标转换矩阵.
则3号体质心到跟踪目标的指向矢量为
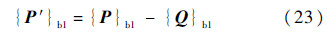
式中:{Q}b1为从1号体质心到3号体质心的矢量在平台本体系Sb1下的分量列阵.
设3号体初始时刻指向矢量在平台本体系下的分量列阵为{P0}b1,则转台两个轴分别的期望转角可以由几何投影关系求出:
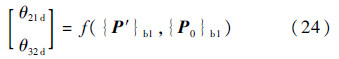
选取系统状态变量为
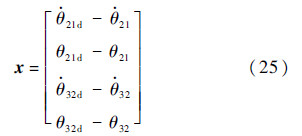
式中:θ32为3号体相对2号体转过的角度;θ21d与θ32d分别为方位轴与俯仰轴的期望角度.
转台两个轴上的电机驱动力矩M2r与M3r为控制量,根据式(21)设计反馈为
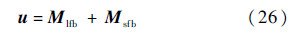
式中:Mlfb为反馈线性化项[13, 14];Msfb为状态反馈项,即
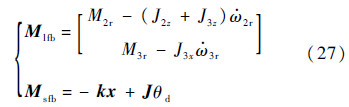
式中:M2r与M3r由式(21)确定;k为状态反馈系数矩阵;J为转动惯量矩阵;θd为期望转角,即
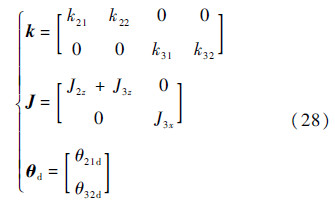
将式(16)、式(21)、式(22)与式(23)代入u=[M2r M3r]T,并令e21=θ21d-θ21,e32=θ32d-θ32,得
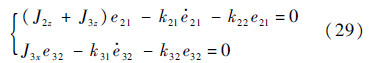
在特征方程分别有两个相异实根λ21、λ22与λ31、λ32的情况下,式(29)的解为
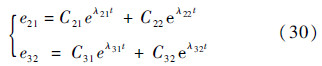
式中:e为自然对数的底;Cij由系统初始条件唯一确定.可看出设计上述的反馈控制律使得转台的关节角误差稳定且渐进趋于0.系统极点λij与反馈系数kij有以下关系:
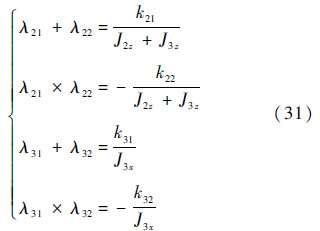
因此可通过调整反馈系数来配置系统极点,从而调整系统的响应性能[15].
式(30)中的e21与e32为期望指向矢量{P}b1与实际指向矢量{Pt}b1投影到方位轴与俯仰轴上的矢量夹角,而在评估系统的跟踪精度时参考的是最终指向角度误差θe,即{P}o与{Pt}o两矢量的夹角:
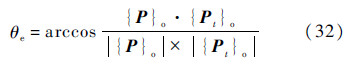
式中:{Pt}o=Lob1{Pt}b1,为t时刻3号体指向矢量在轨道坐标系下的分量列阵,{Pt}b1可由3号体初始指向矢量与转台关节转角确定.
3 仿真验证考虑如图 2所示的跟踪情况,卫星平台与目标分别处在两个倾角相差15°的轨道上,运行相位相差15°,仿真时间为轨道周期的一半,2 750 s.在轨道系下,不考虑平台姿态变化,转台两轴的期望转角如图 4所示.
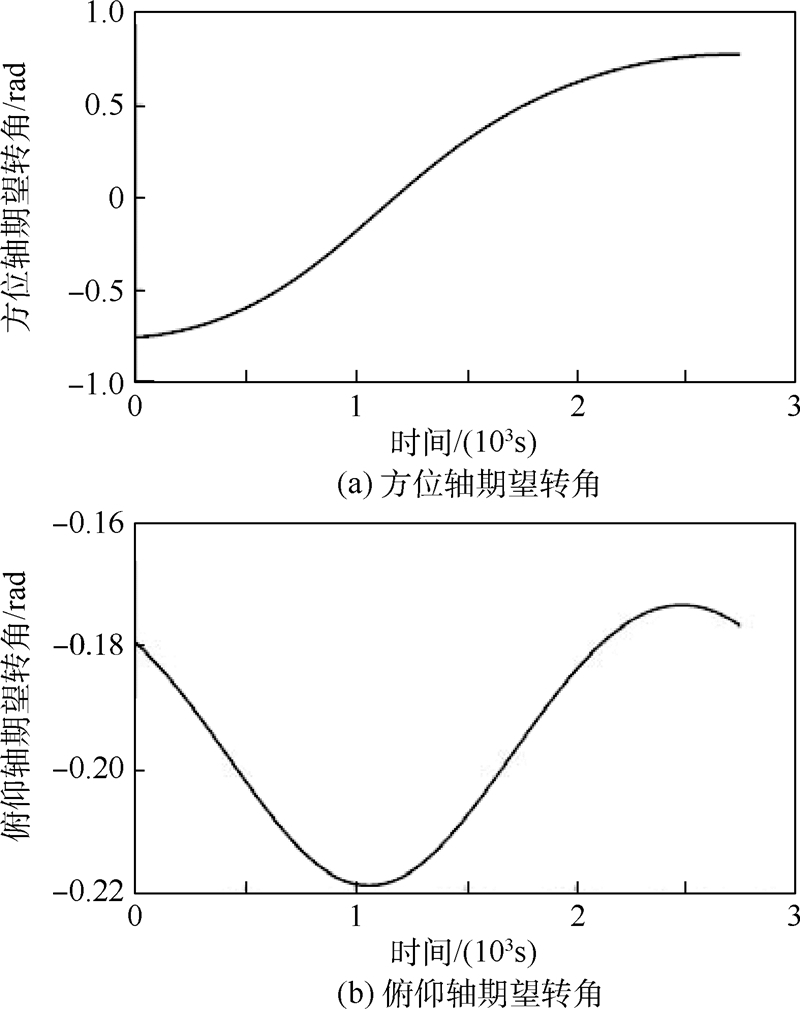 |
| 图 4 轨道系下转台跟踪目标两轴期望转角 Fig. 4 Expected angle of two axes of gimbal to track target under orbit coordinate system |
在不考虑测量误差与执行器件特性的情况下,使用MATLAB建立仿真控制模块,在ADAMS中搭建仿真模型,实现MATLAB与ADAMS的联合仿真.
仿真中,在不加入实时角度修正的情况下,即将卫星平台视为无姿态变化的固定基座,分别使用传统PD控制律与线性化状态反馈控制律,进行仿真并对比转台的关节角度误差e21与e32.然后使用线性化状态反馈控制律,分别仿真加入实时角度修正与不加入实时角度修正情况,对比两种情况的最终指向角度误差θe.
3.1 传统PD控制律使用传统的PD控制方法,忽略转台与卫星平台之间的耦合关系对平台产生的姿态扰动,即在式(22)中令Lb1o为单位阵,未对关节期望转角进行修正.反馈控制律为
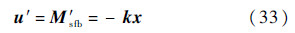
通过选取系统极点来确定反馈参数矩阵k,综合考虑系统响应性能与执行机构能力,方位轴与俯仰轴都选取-0.5±0i作为极点,即令λ21=λ22=λ31=λ32=-0.5,通过式(31)来确定反馈矩阵k.
3.2 线性化状态反馈控制律考虑转台与平台之间耦合运动关系,使用平台姿态实时修正转台的关节期望转角,并使用结合反馈线性化的跟踪状态反馈控制方法,控制律如式(26)所示,针对相同的跟踪任务进行仿真,并且与PD控制使用相同的极点以便进行对比.
3.3 仿真结果 3.3.1 线性化状态反馈与传统PD对比在未使用角度修正且使用相同系统极点的情况下,分别使用传统PD控制律与线性化状态反馈控制律的仿真结果如图 5与图 6所示.
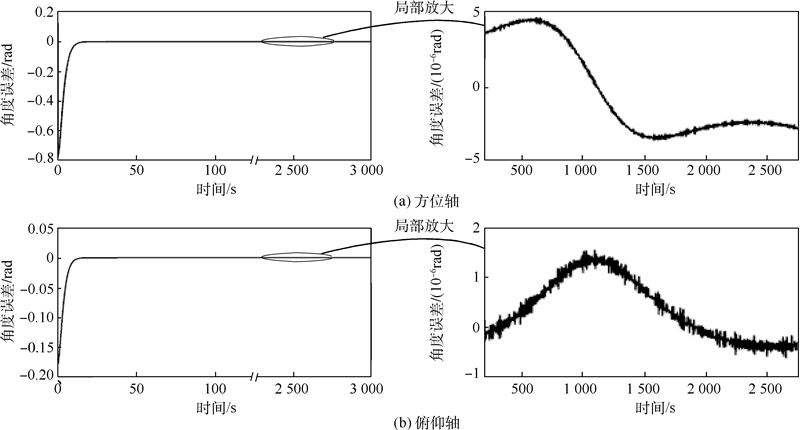 |
| 图 5 PD控制下转台各轴关节角误差 Fig. 5 Joint angle error of each axis of gimbal using PD control |
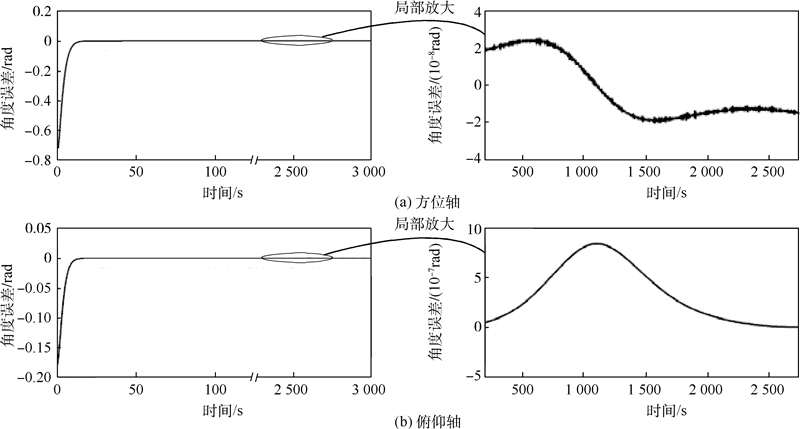 |
| 图 6 线性化状态反馈控制下转台各轴关节角误差 Fig. 6 Joint angle error of each axis of gimbal using linearization state feedback control |
根据上述仿真结果可看出,使用两种控制方法转台跟踪响应速度相近,但使用线性化状态反馈控制律,方位轴与俯仰轴的角度误差相比传统PD控制律有一定降低,波动更加稳定,最大误差值分别降低了约99%与46%,两种控制方法的关节角误差对比如表 1所示.
| 控制方法 | 角度误差/rad | |
| 方位轴 | 俯仰轴 | |
| 传统PD控制律 | -3.61×10-6~4.63×10-6 | -6.04×10-7~1.56×10-6 |
| 线性化状态反馈控制律 | -1.99×10-8~2.54×10-8 | -2.67×10-7~8.42×10-7 |
使用线性化状态反馈控制方法,分别对加入角度修正与不加入角度修正两种情况进行仿真,对比3号体指向角度误差,仿真结果如图 7所示.
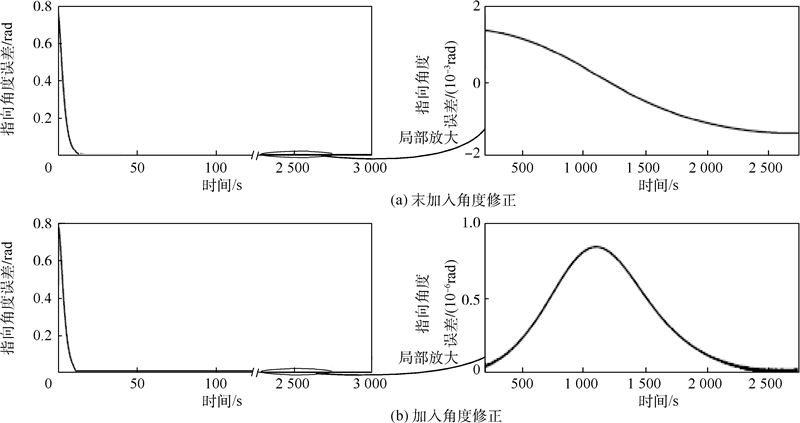 |
| 图 7 线性化状态反馈控制加入角度修正的指向角度对比 Fig. 7 Comparison of pointing angle error between linearization state feedback control with and without angle revision |
根据结果可看出,两种情况的跟踪响应速度相近,但加入角度修正相比未加入角度修正角度误差有一定降低,最大指向角度误差由1.43×10-3rad降低至8.46×10-7rad.两种情况下的关节角误差对比如表 2所示.
| 仿真条件 | 指向角度误差/rad |
| 未加入角度修正 | -1.43×10-3~1.41×10-3 |
| 加入角度修正 | 0~8.46×10-7 |
综合上述仿真结果,在未加入角度修正且使用相同极点的情况下,线性化状态反馈控制在指向精度上优于传统的PD控制,方位轴与俯仰轴的最大关节角误差值分别降低了约99%与46%;在使用线性化状态反馈控制的情况下,使用角度修正比未使用角度修正指向精度高,最大指向角度误差值由1.43×10-3rad降低至8.46×10-7rad.
4 结 论1) 建立了卫星平台与转台的动力学模型,通过模型确定了卫星平台、方位轴与俯仰轴之间的非线性耦合关系,提出的线性化状态反馈控制方法相比传统的PD控制方法具有更高的指向精度.
2) 在使用相同控制方法的情况下,在计算期望转角中利用卫星平台姿态信息实时修正期望转角可以有效地提高转台的指向精度.
| [1] | Sendi C, Ayoubi A M.Robust fuzzy logic-based tracking control of a flexible spacecraft with H∞ performance criteria[C]//AIAA SPACE 2014 Conference and Exposition.Reston:AIAA, 2014:1-17. |
| Click to display the text | |
| [2] | 刘剑峰, 韩琦琦, 于思源, 等.卫星光通信终端二维转台运动参量对天线指向影响研究[J].宇航学报, 2007, 28(4):926-931. Liu J F, Han Q Q, Yu S Y, et al.Research on the influence of the motion parameters of the satellite optical communication terminal’s gimbals on antenna pointing error[J].Journal of Astronautics, 2007, 28(4):926-931(in Chinese). |
| Cited By in Cnki (3) | |
| [3] | 韩琦琦, 于思源, 马晶, 等.耦合运动对星间激光链路瞄准过程影响及补偿方法研究[J].宇航学报, 2006, 27(4):582-587. Han Q Q, Yu S Y, Ma J, et al.Influence analysis of coupled motions on pointing progress of intersatellite optical communication[J].Journal of Astronautics, 2006, 27(4):582-587(in Chinese). |
| Cited By in Cnki (5) | |
| [4] | Sevaston E G, Schier J A, Theodore C I, et al.A precision pointing system for space telescope class optical trackers[C]//Guidance, Navigation and Control Conference.Reston:AIAA, 1988:452-470. |
| Click to display the text | |
| [5] | 韩琦琦, 马晶, 于思源, 等.卫星光通信中耦合运动对光信号跟踪影响分析[J].宇航学报, 2005, 26(4):405-409. Han Q Q, Ma J, Yu S Y, et al.Impact analysis of coupled motions of the optical communication terminal and the satellite platform on optical tracking progress[J].Journal of Astronautics, 2005, 26(4):405-409(in Chinese). |
| Cited By in Cnki (9) | |
| [6] | 谭立英, 吴世臣, 韩琦琦, 等.潜望镜式卫星光通信终端的CCD粗跟踪[J].光学精密工程, 2012, 20(2):270-276. Tan L Y, Wu S C, Han Q Q, et al.Coarse tracking of periscope-type satellite optical communication terminals[J].Optics and Precision Engineering, 2012, 20(2):270-276(in Chinese). |
| Cited By in Cnki (4) | |
| [7] | 刘凌居.空间卫星光通信终端指向误差分析及粗瞄系统控制策略设计[D].哈尔滨:哈尔滨工业大学, 2012. Liu L J.Analysis of satellite optical communication terminal’s pointing error and control design in coarse pointing[D].Harbin:Harbin Institute of Technology, 2012(in Chinese). |
| Cited By in Cnki | |
| [8] | 崔凯.二维跟踪转台与卫星平台的动力学耦合技术研究[D].北京:中国科学院大学, 2013. Cui K.Study of the dynamics coupling between the two-axis gimbal and the satellite bus[D].Beijing:University of Chinese Academy of Sciences, 2013(in Chinese). |
| Cited By in Cnki | |
| [9] | Smith A L, Kunz D L.Dynamic coupling of the KC-135 tanker and boom for modeling and simulation[J].Journal of Aircraft, 2007, 44(3):1034-1039. |
| Click to display the text | |
| [10] | 陈兴林, 郑燕红, 贾琪, 等.星间光通信扫瞄捕获过程分析[J].哈尔滨工业大学学报, 2009, 41(11):34-38. Chen X L, Zheng Y H, Jia Q, et al.Scanning acquisition process of optical communications[J].Journal of Harbin Institute of Technology, 2009, 41(11):34-38(in Chinese). |
| Cited By in Cnki (8) | |
| [11] | 凌志华.卫星光通信中光束粗瞄控制算法设计与仿真[D].哈尔滨:哈尔滨工业大学, 2007. Ling Z H.Design and simulation of control algorithm for laser beam pointing in intersatellite optical communication[D].Harbin:Harbin Institute of Technology, 2007(in Chinese). |
| Cited By in Cnki | |
| [12] | 李铭宽.星上运动部件指向的跟踪控制方法研究[D].哈尔滨:哈尔滨工业大学, 2012. Li M K.Tracking control method for the moving parts on a satellite[D].Harbin:Harbin Institute of Technology, 2012(in Chinese). |
| Cited By in Cnki | |
| [13] | 葛升民, 王磊, 甘克力, 等.星载大型空间天线的一种解耦控制方法[J].宇航学报, 2013, 34(1):46-53. Ge S M, Wang L, Gan K L, et al.A method for decoupling control of satellite-borne large space antenna[J].Journal of Astronautics, 2013, 34(1):46-53(in Chinese). |
| Cited By in Cnki (2) | |
| [14] | Khalil K H.非线性系统[M].北京:电子工业出版社, 2005:373-375. Khalil K H.Nonlinear system[M].Beijing:Publishing House of Electronic Industry, 2005:373-375(in Chinese). |
| [15] | 姚楠.空间激光通信系统中目标跟瞄算法研究[D].长春:长春理工大学, 2007. Yao N.Research on targeting tacking algorithm in space laser communication system[D].Changchun:Changchun University of Science and Technology, 2007(in Chinese). |
| Cited By in Cnki (2) |



