2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100094, China
在卫星上搭载磁力仪开展磁场探测是研究空间环境与空间物理的重要手段,同时也是确定卫星姿态和开展磁自主导航的重要手段[1-3]。在众多开展空间磁场测量的任务中,国际上有代表性的卫星主要有:Cluster、ACE和CHAMP等,国内开展磁场探测的卫星主要有:双星和电磁监测试验卫星。在轨运行期间,卫星本体产生多种不稳定的干扰磁场,开展磁场探测就一定要消除这些干扰磁场,但是这些磁场干扰与卫星各部件的材料、工作状态、所处的背景磁场和自身运动的姿态等都有关系,卫星的磁干扰很难预先消除[4]。因此,开展高精度磁场测量的卫星通常采用将磁力仪安装在伸杆顶端的方式,使磁力仪远离卫星本体以减少平台磁干扰的影响[5],或者结合某些磁场模型进一步去除卫星本体的磁干扰。
根据不同的卫星设计和探测数据精度要求,消除卫星磁干扰的方法大体分为:
1) 多点测量结合模型算法。最常见的方法是双探头梯度测量法,该方法利用伸杆使磁力仪远离卫星本体,利用近似点源磁场随距离3次方衰减的规律消除卫星本体磁干扰[6]。此方法计算简单,使用广泛,但是磁力仪伸杆对卫星提出了一定的要求。
2) 对卫星进行磁测。通过磁测建立卫星整星或者部件的磁源模型,进而在探测数据中逐一减去卫星的磁干扰。这种方法地面磁测过程复杂,对磁测精度要求高[7],而且由于地面磁测无法完全模拟在轨运行状态,最终可能导致在轨数据精度较低。
3) 卫星旋转拟合数据。利用卫星在外磁场中的旋转,获得多姿态下的磁场探测数据,通过测量数据与外部磁场数据的拟合消除磁干扰并获得背景磁场[8-9]。这种方法通常对外部磁场有较高要求,在近地轨道上,通常采用地磁模型计算外部磁场,进行拟合,误差较大。
4) 综合使用多种方法进行数据处理。充分考虑卫星自身特点,采用多种方法(包括在轨滤波、建立局部模型和前述3类方法等方法)结合消除卫星磁干扰。这种方法通常需要较多的人工干预[10]。
磁场梯度张量测量法与最常见的双探头梯度测量法均属于第1类方法。后者通过2点磁场测量消除卫星磁干扰,前者通过多点磁场测量获得磁场梯度张量,再利用一定算法消除卫星磁干扰,在本文中采用欧拉反褶积算法进行计算。该算法诞生于20世纪80年代,源于欧拉齐次方程,是一种磁源定位算法[11],广泛应用于地质测量与深海沉船定位测量[12],也应用于卫星整星的磁源分布分析等领域[13-14]。该方法利用欧拉方程建立磁场衰减模型,拟合磁源的位置并消除干扰磁场,其优点在于模型简单,计算速度较快。
本文创新性地提出了利用磁场梯度张量测量法在轨消除卫星磁干扰并获得背景磁场的方法。本文通过仿真分析,讨论了欧拉反褶积算法中的构造指数、背景磁场反演误差与卫星伸杆长度之间的关系,并对比了该方法与传统的双探头梯度测量法消除磁干扰的优劣。
1 磁场梯度张量的测量在卫星伸杆上布设多点矢量磁力仪,形成测量阵列,就可以得到磁场的梯度张量:
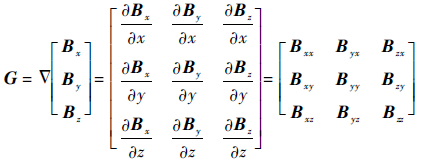 (1)
(1)
式中:B为磁场矢量;G为磁场梯度张量;Bj为磁场矢量在j方向的分量;Bij为磁场分量Bj在i方向的偏导数,i,j=x,y,z。
在通常情况下,空间电流密度在磁力仪阵列的小空间区域内的积分电流非常微弱,对磁场旋度的影响远小于磁场测量误差对磁场旋度的影响,所以不妨忽略空间电流,则由麦克斯韦方程组可知:
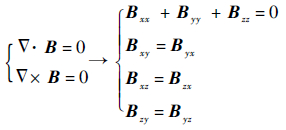 (2)
(2)
此时磁场梯度张量的9个分量中只有5个分量是独立的,因此,通过测量空间磁场3个分量在2个方向上的偏导数可以得到磁场梯度张量中的6个分量,进而得到该空间位置的磁场梯度张量。非共线的3个测点构成了一个测量平面,可以计算磁场3分量在该平面内的2个正交方向上的偏导数,获得它们中心位置的磁场矢量及梯度张量。如在伸杆上布设4个矢量磁力仪,形成正四面体构型,每3个顶点可以获得该三角形中心位置处的磁场矢量和梯度张量,并最终获得4个位置的磁场矢量和梯度张量。
为了获得多个位置的磁场矢量和梯度张量,可以采用不同数目的和不同排列方式的多测点阵列,在本文中仅以4测点构成正四面体为例进行仿真计算。
2 欧拉反褶积算法如果一个实函数f对任何系数t均满足:
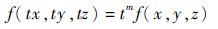 (3)
(3)
则称f为m次欧拉齐次函数。两侧对t求微分后,令t=1,m=-N,可得欧拉方程:
 (4)
(4)
式中:(x0,y0,z0)为磁源的位置;(x,y,z)为探测点的位置;f为探测点的合成磁场;b为背景磁场;系数N为构造指数,N的取值与磁源的形状、强度和分布均有关系,N的实质是磁场在空间的衰减指数。点磁源对应N=3,平面磁棒对应N≈2,无限大薄片磁体对应N=1。形状复杂的磁源,可以看作一系列点线板状磁源的组合。
卫星本体的磁源在其周围产生磁场,该磁场的强度随距离增加而衰减,磁力仪探测得到卫星磁场与背景磁场的合成场。
当磁场f的矢量测量值为Bx、By和Bz,背景磁场b的矢量分量为bx、by和bz时,式(4)变为
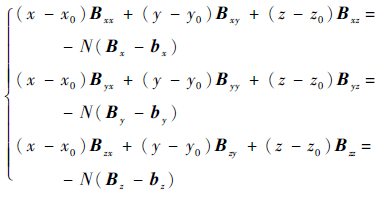 (5)
(5)
将式(5)写成矩阵形式,整理可得
 (6)
(6)
如果把式(6)中的x0、y0、z0、bx、by和bz均视为待定系数,其他项视为自变量和因变量,则可以将式(6)整理为3组式(7)形式的方程:
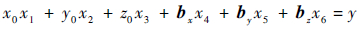 (7)
(7)
式中:自变量x1、x2、x3、x4、x5和x6和因变量y均是磁场矢量、张量、测点位置和N的函数,待定系数是需要反演确定的参数。该线性方程可以简记为
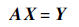 (8)
(8)
当各测量点每获得一组磁场矢量(Bx,By,Bz)和梯度张量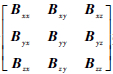
卫星运行在近地轨道,假定其本体外包络为边长1 m的正方体。在卫星本体坐标系中假定外部磁场为(30 000,1 000,35 000)nT。卫星伸杆位于其某个侧面上且垂直该侧面,伸杆的延长线通过卫星的中心。4台矢量磁力仪位于伸杆顶端构成边长0.6 m正四面体,测量并获得各三角形中心的磁场矢量和梯度张量,构成4个间距0.2 m的正四面体数据点(这4个点简称为数据点)。在卫星的本体内预设17个变化的磁源以模仿卫星不断变化的磁干扰:卫星的中心预设一个变化范围为0~10 A·m2的主磁矩磁偶极子,磁矩方向随机;卫星的8个顶点、顶点与卫星中心连线的8个中点分别预设一个磁矩不大于1 A·m2的磁偶极子,磁矩方向和大小随机变化。磁源的位置、磁力仪的位置关系如图 1所示,其中,伸杆长度为其远端点到卫星中心的距离。

|
| 图 1 卫星磁源与磁力仪的位置 Fig. 1 Positions of magnetometers and satellite magnetic sources |
根据预先建立的卫星磁干扰磁源模型与预先设定的背景磁场,正演计算4个数据点受到磁干扰的磁场测量数据,对应的式(6)中磁场矢量测量值Bx、By和Bz。在第3.1节中,将这些受到磁干扰的数据并作为探测数据开展反演计算,消除卫星磁干扰获得背景磁场,在第3.2节中对比几种反演方法,考察反演计算中误差的来源以及对伸杆的要求。
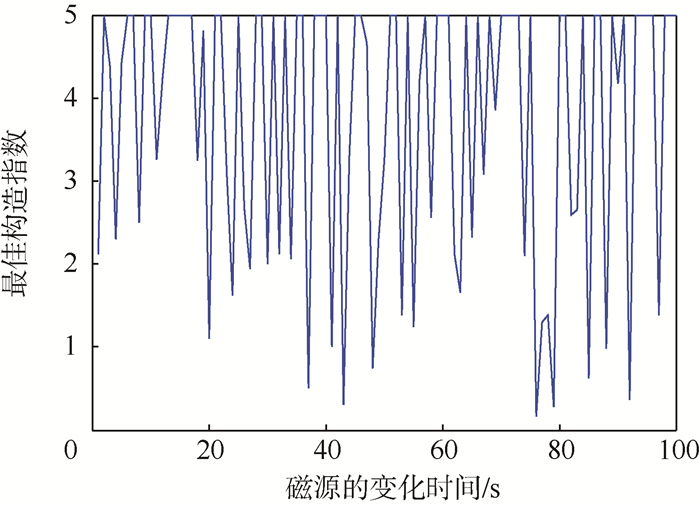
3.1 最佳构造指数N0与卫星伸杆长度构造指数N代表磁场在空间中的衰减指数,当卫星磁源发生变化时,构造指数也随之变化。从0~5扫描N的取值,根据不同的N值反演背景磁场,与预先设定的磁源模型及背景磁场对比,确定反演误差。当反演误差最小时,构造指数N的取值定义为最佳构造指数N0。欧拉反褶积算法在各数据点采用统一的构造指数进行反演计算,而各数据点处的真实构造指数是有差异的,所以最佳构造指数的物理意义是对各数据点整体的磁场衰减指数即构造指数的最佳估计。图 2描述了伸杆长度为1 m时,最佳构造指数与磁源变化的关系。在图 2中,可以看到磁源(包括磁源的方向、强度)发生变化时(变化频率1 Hz),最佳构造指数N0随之变化。
|
| 图 2 最佳构造指数与磁源变化的关系 Fig. 2 Relationship between the best structural index and changing magnetic source |
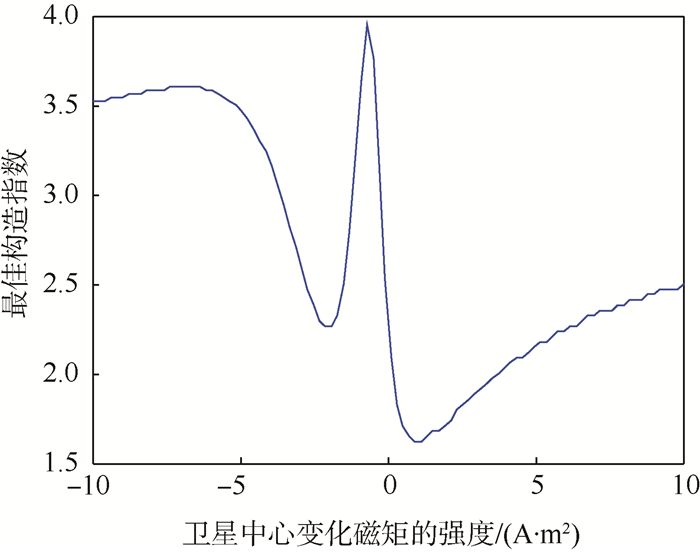
图 3为某组随机磁源分布下,最佳构造指数与中心变化磁矩的关系。在图 3中,卫星中心偶极子的强度发生变化时,N0随之变化,磁矩方向反向时引起了N0的跃变。这是因为磁源分布的变化,改变了各数据点的构造指数,进而改变了它们整体的最佳估计——最佳构造指数。
|
| 图 3 某组随机磁源分布下,最佳构造指数与中心变化磁矩的关系 Fig. 3 Relationship between the best structural index and central changing magnetic moment, under a case of random magnetic sources distribution |
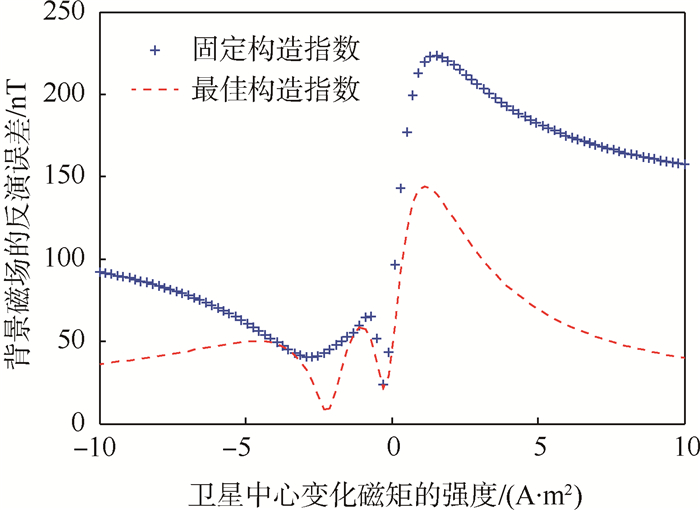
图 4对比了1 m伸杆条件下,采用最佳构造指数N0和固定构造指数N=3的条件下,背景磁场反演误差随卫星中心磁矩变化的曲线。图 4中,构造指数取固定值3,其物理意义为将磁源视为点源。从图 4可以看到,固定构造指数为3时,反演误差非常大,采用最佳构造指数时,误差有所下降,但是反演误差仍然很大。在较短伸杆条件下,磁源并不能近似为点源,采用N=3不能很好地反映数据点位置的磁源磁场的实际衰减率;同时由于伸杆较短,各数据点的构造指数差异较大,即使是最佳构造指数也不能精确地反映数据点间整体的磁场衰减规律,但最佳构造指数是比固定构造指数更贴近实际的整体磁场衰减评估指数。
|
| 图 4 不同构造指数的背景磁场的反演误差 Fig. 4 Changes of error in background magnetic field inversion with different structural indices |
由此可见,构造指数的取值对反演精度有很大的影响,采用最佳构造指数N0进行反演有利于提高背景磁场反演的数据精度。
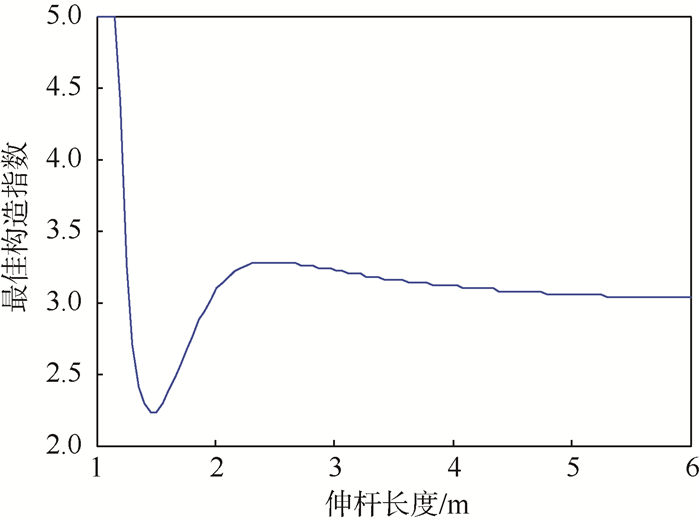
N0的取值不仅与磁源的分布相关,也与数据点的位置相关,也就是与伸杆长度相关。图 5为在一定磁源分布条件下,最佳构造指数与伸杆长度之间的关系。
|
| 图 5 最佳构造指数与伸杆长度的关系 Fig. 5 Relationship between the best structural index and boom length |
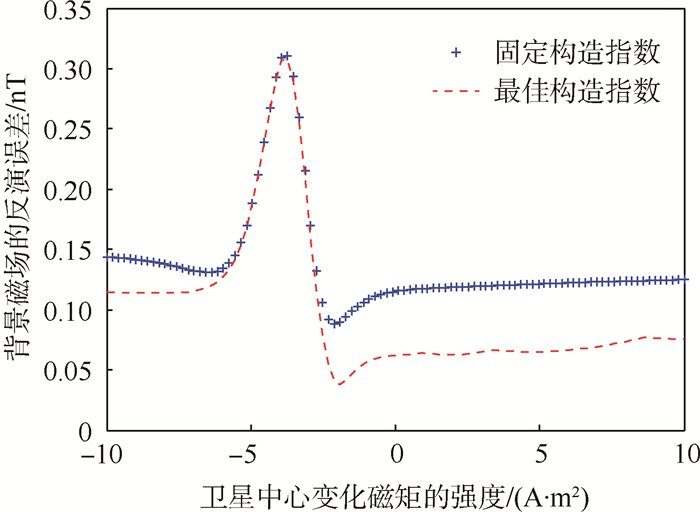
当卫星的伸杆较长时,在伸杆顶端,卫星磁源产生的异常磁场近似于点源产生的磁场,伸杆顶端附近各数据点的构造指数趋于一致,最佳构造指数N0趋近于3。由于数据点构造指数的一致性得到了提高,欧拉反褶积算法反演背景磁场的精度也会有所提高。图 6对比了在卫星伸杆长度为4 m的条件下,采用最佳构造指数N0和固定构造指数N=3时,背景磁场反演误差随卫星中心磁矩变化的曲线。
|
| 图 6 4 m伸杆条件下不同构造指数背景磁场的反演误差 Fig. 6 Background magnetic field inversion error versus different structural indices in case of 4 m boom length |
对比图 6与图 4,采用较长伸杆的磁场探测的反演误差大大下降了。而且在图 6中,2条误差曲线相差很小,说明在较长伸杆条件下,由于最佳构造指数趋近于3,可以采用固定构造指数N=3反演背景磁场。
最佳构造指数N0是数据点位置磁源磁场衰减率的最佳估计,可以通过以下手段获得:①对卫星部件进行磁测,建立磁源的分布模型;②对卫星整星进行磁测,通过磁测数据计算卫星各工况下的N0。2种方法都离不开卫星磁测,依据磁测结果建立磁源模型,确定测点处的N0。在卫星无法进行全面磁测时,则需要采用长伸杆,这样在距离磁源较远的区域内,磁场的衰减率基本上与点源相同,使用一个统一的构造指数N=3,对于各数据点均是适用的。
3.2 磁场梯度张量测量法与双探头梯度测量法的对比在磁场探测中较为常见的双探头梯度测量法,采用较长的卫星伸杆(2.5倍于卫星本体尺寸的距离)[15],假设卫星磁源近似为点源,基于点源磁场强度随距离的3次方衰减的规律,利用双探头矢量磁场数据消除卫星磁干扰。其计算公式为
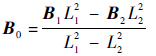 (9)
(9)
式中:B0为背景磁场矢量;B1和B2分别为2个探头的探测磁场矢量;L1和L2分别为2个探头到卫星中心的距离[5]。
利用磁场梯度张量及N=3的欧拉反褶积算法消除磁干扰同样需要采用一定长度的伸杆,使磁力仪远离卫星本体,但是由于拥有更多的数据源和更高阶的磁场信息,并考虑了更多的约束条件,其背景磁场的反演精度较高。
测量系统的误差设置:根据目前磁强计的研制和标定水平,在地磁场条件下高精度矢量磁强计的单轴测量精度可能达到0.01 nT,矢量磁强计正交性标定及刚性平台上两磁强计之间相对安装姿态的标定可能达到0.001°。
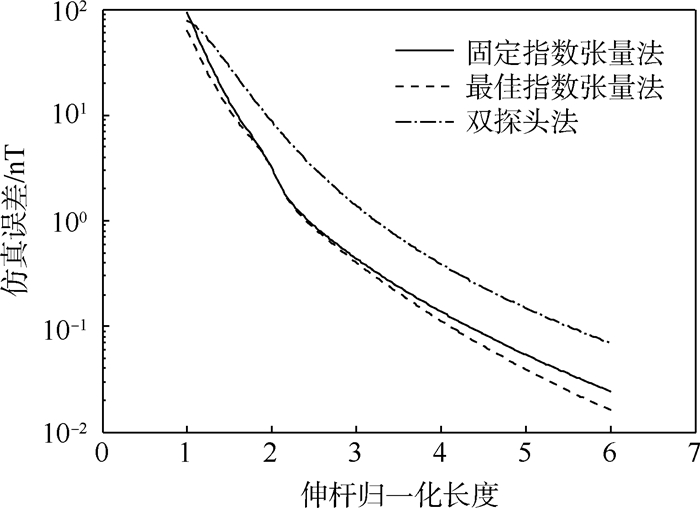
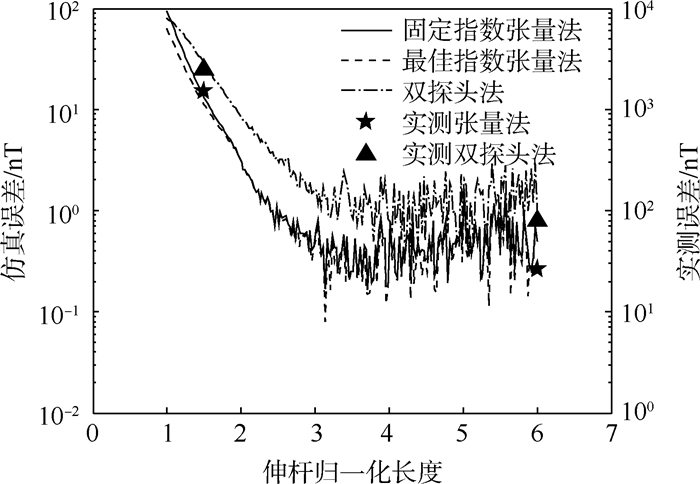
当卫星本体预设的17个磁源的总磁矩为1 A·m2时(各个磁源的等效偶极子磁矩平方和的平方根为1 A·m2),磁场梯度张量测量法与双探头梯度测量法的背景磁场反演误差随伸杆长度的变化关系如图 7与图 8所示。
|
| 图 7 不考虑测量系统误差时的背景磁场的反演误差与伸杆长度的关系 Fig. 7 Relationship between boom length and background magnetic field inversion error without measurement system error |
|
| 图 8 考虑测量系统误差时的背景磁场的反演误差与伸杆长度的关系 Fig. 8 Relationship between boom length and background magnetic field inversion error with measurement system error |
图 7及图 8展示了磁场梯度张量测量法与双探头梯度测量法的3个算例的背景磁场反演误差随伸杆长度的变化。其中误差曲线的纵坐标轴在左侧,横坐标表示伸杆相对于卫星本体尺度的归一化长度,伸杆长度的起点在卫星中心,在本例中卫星本体尺度为1 m。图 7和图 8中:固定指数张量法采用固定构造指数N=3的欧拉反褶积算法;最佳指数张量法采用最佳构造指数N0的欧拉反褶积算法;双探头法采用双探头梯度算法。
在图 7中可以看到:
1) 3条曲线所代表的误差总体而言随距离增加而减少,磁场梯度张量测量法的误差更小。
2) 在伸杆长度较短时(1~2 m),由于卫星磁源不满足点源近似,且各测点构造指数差异较大,所以2种方法反演误差都很大。
3) 在伸杆长度较长时(大于3 m),卫星磁源可近似为点源,各测点构造指数差异较小,2种方法反演误差均明显下降。
4) 伸杆长度较长时,固定构造指数与最佳构造指数对应的反演误差差别不大。
在考虑测量误差的图 8中进一步看到:
5) 伸杆长度在3 m以上时,反演误差不再随着距离的增加而减小,而是基本保持不变。这是由于测量误差相对固定,而其在反演误差中的所占比重逐渐增大。
6) 在4 m伸杆的条件下,磁场梯度张量测量法误差0.5 nT约为双探头梯度测量法的反演误差1.5 nT的1/3;或可以说在相同的精度要求下,采用磁场梯度张量测量法可以减少伸杆长度。
4 实测验证为了验证第3.2节的数值仿真结果,利用实物开展了测试。在试验中,在0.2 m边长的立方体内,预设5个小磁铁,并分别测量了在探测距离为0.3 m和1.2 m(相当于伸杆归一化长度1.5和6)时磁场梯度张量测量法与双探头梯度测量法针对外部磁场的反演误差。误差点的位置如图 8中星号所示,它们的纵坐标轴在右侧。测试结果表明,双探头法的误差大于张量法,误差的分布规律基本符合数值仿真结果。
由于测试设备、实验环境的限制,在测试试验中采用了一定的近似等效处理:①利用5个小磁铁的分布模拟具有一定磁分布的卫星本体;②磁铁分布的尺度和探测距离均调整为仿真值的1/5,但相对比例保持不变;③小磁铁的总磁矩为1.8 A·m2,大于仿真值,这会导致反演误差相应增大;④利用单磁力仪按照一定顺序在多点实施探测模拟多磁力仪的同时探测,忽略测试期间磁环境的改变;⑤假定磁力仪在各测点的姿态一致(在真实的卫星试验中可以进一步标定各磁力仪测量姿态之间的关系,进而修正测量方向)。上述近似等效条件都会在一定程度上影响试验结果,其中放大试验误差的主要因素为条件③和条件⑤,但不会影响误差变化的相对规律。
5 结 论本文在理论推导、仿真分析及实测验证的基础上提出了采用磁场梯度张量测量法消除卫星磁干扰的方法,得到:
1) 磁场梯度张量测量法相比传统双探头梯度测量法可以获得较高的外部磁场反演精度。例如在4 m长伸杆时,张量测量法反演误差约0.5 nT,约为双探头梯度测量法的1/3。
2) 该方法的反演误差随伸杆长度增加而下降。例如在1 m长伸杆时,反演误差可达100 nT。
3) 在一定测量误差条件下,反演误差在伸杆达到一定长度以上时,不再随伸杆长度增加而下降,基本保持一致,这时的误差反映了测量误差水平。
在实际的工程应用中,根据不同的卫星条件及磁场数据精度要求,可以进一步确定伸杆的长度以及磁力仪的数量和阵列布局。
| [1] | 黄琳, 荆武兴. 卫星姿态确定与三轴磁强计校正[J]. 宇航学报,2008, 29 (3) : 854 –859. HUANG L, JING W X. Spacecraft attitude determination and three-axis magnetometer calibration[J]. Journal of Astronautics,2008, 29 (3) : 854 –859. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | 张锐, 朱振才, 张静, 等. 基于磁强计的微小卫星姿态确定[J]. 宇航学报,2006, 27 (4) : 578 –581. ZHANG R, ZHU Z C, ZHANG J, et al. Micro-satellite attitude determination based on magnetometer[J]. Journal of Astronautics,2006, 27 (4) : 578 –581. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | 王淑一, 杨旭, 杨涤, 等. 近地卫星磁测自主导航算法研究[J]. 宇航学报,2003, 24 (6) : 634 –637. WANG S Y, YANG X, YANG D, et al. Algorithm for autonomous navigation of low earth orbit satellite using magnetic measurements[J]. Journal of Astronautics,2003, 24 (6) : 634 –637. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | 陈斯文. 卫星磁洁净的控制和测量[J]. 地球物理学进展,2009, 24 (2) : 797 –800. CHEN S W. Control and measure of satellite magnetic cleanliness[J]. Progress in Geophysics,2009, 24 (2) : 797 –800. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | FAN Y.Mathematic approaches for the calibration of the CHAMP satellite magnetic field measurements[D].Potsdam:University of Potsdam,2010:14. |
| Click to display the text | |
| [6] | 周斌, 王劲东. 卫星磁部件分布对梯度法消除剩磁的影响分析[J]. 中国空间科学技术,2013 (5) : 29 –34. ZHOU B, WANG J D. Influence of magnetic component distribution of satellite on eliminating remanant magnetic field by gradient method[J]. Chinese Space Science and Technology,2013 (5) : 29 –34. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | LOHR D A, ZANETTI L J, ANDERSON B J, et al. NEAR magnetic field investigation, instrumentation,spacecraft magnetics and data access[J]. Johns Hopkins APL Technical Digest,1998, 19 (2) : 136 –141. |
| Click to display the text | |
| [8] | TAKAHASHI F, SHIMIZU H, MATSUSHIMA M, et al. In-orbit calibration of the lunar magnetometer onboard SELENE(KAGUYA)[J]. Earth Planets Space,2009, 61 (11) : 1269 –1274. |
| Click to display the text | |
| [9] | SMITH C W, L'HEUREUX J, NESS N F, et al. The ACE magnetic fields experiment[J]. Space Science Reviews,1998, 86 (1-4) : 613 –632. |
| Click to display the text | |
| [10] | ZHANG T L, BERGHOFER G, MAGNES W, et al. MAG:The fluxgate magnetometer of VENUS express[J]. ESA Special Publication,2007 . |
| Click to display the text | |
| [11] | THOMPSON D T. EULDPH:A new technique for making computer-assisted depth estimates from magnetic data[J]. Geophysics,1982, 47 (1) : 31 –37. |
| Click to display the text | |
| [12] | 王明, 骆遥, 罗锋, 等. 欧拉反褶积在重磁位场中应用与发展[J]. 物探与化探,2012, 36 (5) : 834 –841. WANG M, LUO Y, LUO F, et al. The application and development of Euler deconvolution in gravity and magnetic field[J]. Geophysical and Geochemical Exploration,2012, 36 (5) : 834 –841. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [13] | 陈俊杰, 易忠, 孟立飞, 等. 基于欧拉方法的多磁偶极子分辨技术[J]. 航天器环境工程,2013, 30 (4) : 401 –406. CHEN J J, YI Z, MENG L F, et al. Multi-dipoles discrimination technique based on Euler inverse method[J]. Spacecraft Environment Engineering,2013, 30 (4) : 401 –406. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [14] | 任秀艳, 杜晓娟, 孙瑞雪, 等. 地面磁梯度测量在勘查地下污水管道中的应用[J]. 世界地质,2014, 33 (3) : 659 –665. REN X Y, DU X J, SUN R X, et al. Application of ground magnetic gradient in underground sewage pipe survey[J]. World Geology,2014, 33 (3) : 659 –665. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | 张朝阳, 肖昌汉, 高俊吉, 等. 磁性物体磁偶极子模型适用型的实验研究[J]. 应用基础与工程科学学报,2010, 18 (5) : 862 –867. ZHANG C Y, XIAO C H, GAO J J, et al. Experiment research of magnetic dipole model applicability of a magnetic object[J]. Journal of Basic Science and Engineering,2010, 18 (5) : 862 –867. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |



