卫星导航系统目前已经成为各国军事领域不可或缺的一部分,但是由于导航卫星距离地面较远(2万多公里),且发射功率较小,造成其固有脆弱性。卫星导航信号到达地面时功率只有-160 dBW,利用功率为50 W的GPS干扰机就可以使100 km以内的全球卫星导航系统(GNSS)接收机失效。因此近年来各机构针对卫星导航抗干扰技术的研究越来越多,其中基于自适应天线阵的空域调零抗干扰技术是一种主要的抗干扰手段。
空域调零抗干扰技术的原理是对天线各阵元进行幅度和相位的加权,使得天线阵方向图在干扰方向形成零陷。早在1979年Compton等[1]就提出了著名的功率倒置自适应抗干扰天线阵列,该阵列能够对接收信号的能量进行倒置,从而抑制强的干扰信号,保留较弱的期望信号。最小方差无失真响应(Minimum Variance Distortionless Response,MVDR)[2]、采样矩阵求逆(Sample Matrix Inverse,SMI)[3]和线性约束最小方差(Linearly Constraint Minimum Variance,LCMV)[4]等准则在空域调零领域得到了广泛应用。
多重信号分类(MUSIC)算法[5]能够对多个空间进行识别,故称为MUSIC算法。MUSIC算法由于测向精度高、不需要先验信息等优点而被广泛应用在测向和空间谱估计领域,特别是利用MUSIC算法进行信号来向(Direction of Arrival,DOA)估计方面。由于导航信号很弱,无法利用MUSIC算法直接进行信号来向的估计,卢燕娥[6]和Mohamed[7]等利用MUSIC算法中噪声子空间和信号子空间的正交性提出了基于正交权值算法的阵列天线抗干扰技术。Amin和Sun[8]通过将输入信号向噪声子空间进行投影,消除干扰信号,实现空域调零。
对于阵列天线而言,通道间的不一致性是不可避免的。根据变化的特点,通道不一致性分为以下两类:
1) 慢变化
包括阵元位置误差、阵元间的互耦[9]和阵元通道误差等。其中,阵列在排布时阵元位置的微小偏差、阵元之间的互耦效应或者是各阵元馈线不同等因素造成的不一致性不随时间变化,属于非时变的。这种变化是慢变化,慢变化可以认为在一次权值更新时间内通道的幅相不一致性基本保持不变。
2) 快变化
各阵列通道射频部分放大器幅相特性不一致、混频器和滤波器的特性不一致、以及数字部分AD采样的不一致、正交解调器I/Q不平衡等因素造成的阵列各通道不一致性随时间变化,属于时变的。这种变化是快变化,快变化是指一次权值更新的时间内通道的幅相不一致性随机变化。对于快变化,只能尽量减小通道滤波器的群延时抖动和带内纹波。
阵列各通道的不一致性会影响空域抗干扰效果,因此不一致性的影响分析也是至关重要的。Steinberg[10]在1976年分析了幅相不一致性矩阵对自适应阵列主波束增益的影响,提出幅相不一致性等因素导致的通道失配会使得主波束增益下降。Quazi[11]研究了相位和幅度波动对波束形成的影响,得出幅相误差会使得天线旁瓣电平高于设计值的结论。国内方面也做了许多关于通道不一致性的研究,苏卫民等[12]研究了利用FIR滤波器模型来描述通道不一致性,分析通道幅相不一致性对MUSIC算法估计信号来向的影响,指出通道失配会影响来向估计精度。张建军和项建弘[13]分析了通道不一致性对PI算法的影响,指出通道不一致性在一定范围内波动时并不影响PI算法的抗干扰效果。王玲等[14]通过仿真分析了通道不一致性对基于LCMV准则的抗干扰算法的影响,分析表明通道失配和天线间的互耦会影响LCMV准则的鲁棒性。
虽然分析通道失配对抗干扰算法影响的文献[10-16]较多,目前还未见通道不一致性对空域MUSIC算法效果的影响分析。本文从空域MUSIC算法基本原理着手,建立通道不一致性模型,通过理论分析和仿真实验两个方面验证通道不一致性对MUSIC算法的影响。
1 阵列信号模型在本文中主要研究N个阵元均匀分布在圆环上的均匀圆环阵列。以圆环中心为参考点,假设有D个入射信号,则第k个阵元接收到的信号为
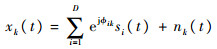
|
(1) |
式中:φik为第i个信号si(t)入射到第k个阵元时相对于参考点的相位差;nk(t)为第k个阵元的热噪声。
则N个阵元的接收信号向量为
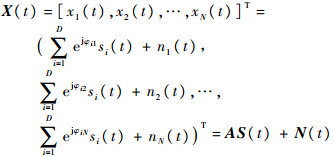
|
(2) |
式中:A=[a(θ1,φ1),a(θ2,φ2),…,a(θD,φD)]=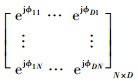
本文主要讨论慢变化对于MUSIC算法性能的影响。假设通道不一致性变化是慢变化,则可以通过在方向矢量中引入误差矩阵T来建立信号的模型。
假设误差与信源的方位无关,设阵元1为阵列的参考阵元,第k个阵列通道相对于参考阵元的幅度偏差为ρk,相位偏差为γk(ρ1=1,γ1=0),则存在幅度和相位不一致性时,天线阵的方向矢量矩阵为

|
(3) |
式中:
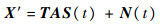
|
(4) |
理想情况下,不存在一致性时,阵列信号的协方差矩阵为
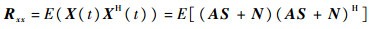
|
(5) |
假设各入射信号互不相关,各阵元热噪声是均值为0、方差为σ2的互不相关高斯白噪声,则式(5)可化为
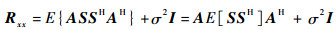
|
(6) |
式中:I为单位矩阵。令E[SSH]=PS,PS为入射信号的功率,则
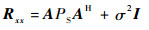
|
(7) |
由式(7)易知,Rxx是一个Hermite矩阵,根据Hermite矩阵性质,必有

|
(8) |
式中:λi为Rxx的按照大小排序的第i个特征值;ei为其对应的特征向量。
由于干扰信号比噪声功率大很多,理想情况下经过排序的特征值有如下关系式:
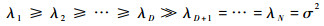
|
(9) |
式中:>>表示远大于。前D个较大的特征值与干扰信号相关,后N-D个相等的小特征值与噪声相关。因此相应的称由前D个大特征值所对应的特征向量构成的线性子空间span{e1,e2,…,eD}为干扰子空间,后N-D个较小的特征值所对应的特征向量构成的线性子空间span{eD+1,eD+2,…,eN}为噪声子空间。
由Hermite矩阵性质可知:
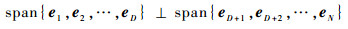
|
(10) |
由欧氏空间性质可知二者互为正交补空间。
设ei∈span{eD+1,eD+2,…,eN},λmin为Rxx的最小特征值。则有
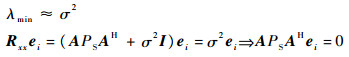
|
(11) |
式中:A为满秩矩阵,PS=E[SSH] 为一个正定Hermite矩阵,因此使得式(11)恒成立必须有
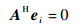
|
(12) |
由于ei是噪声子空间中任意一个方向矢量,因此可以得出干扰信号的方向矢量垂直于噪声子空间。
由于干扰子空间和噪声子空间互为正交补空间,根据正交补空间的唯一性可知,A的列向量必属于span{ej},j=1,2,…,D,即每个干扰对应的方向矢量都属于干扰子空间。
卫星导航系统中,由于导航信号淹没在噪声中,因此导航信号和噪声构成噪声子空间,干扰信号构成干扰子空间,空域MUSIC算法中,如果取最优权值:
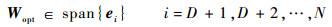
|
(13) |
则输出信号
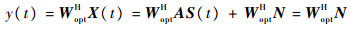
|
(14) |
从式(14)可以看出输出信号中较大的干扰信号被去除,而淹没在噪声中的导航信号得到保留。
3 不一致性对MUSIC算法影响分析 3.1 幅度不一致性对MUSIC算法的影响 3.1.1 理论分析假设有D个干扰源,干扰源互不相干,入射方向为(θi,φi)(i=1,2,…,D),则干扰子空间的维度为D。假设阵列通道只存在幅度不一致性,幅度偏差矩阵T=diag[1,ρ2,…,ρN]T,则阵列协方差矩阵为
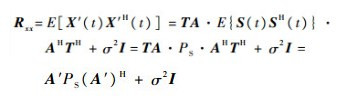
|
(15) |
式中:干扰信号方向矢量矩阵为
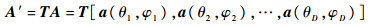
|
对其中任意一个方向矢量进行归一化可得
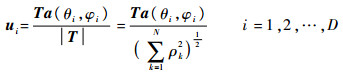
|
(16) |
A′为列满秩矩阵,因此ui(i=1,2,…,D)为干扰空间的一组基。
设US为干扰子空间的任意一个单位向量,则

|
(17) |
式中:ki(i=1,2,…,D)为不全为0的一组实数,其中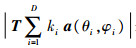
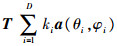
设ej(j=1,2,…,M)为噪声子空间的一组基,M为噪声子空间的维数,UN为噪声子空间的任意一个单位向量,则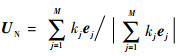
根据正交互补空间的性质,UN和US有如下关系式:
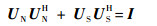
|
(18) |
将式(17)代入式(18)可得
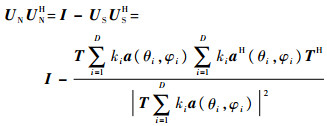
|
(19) |
抗干扰阵列天线方向图函数为
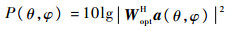
|
(20) |
在MUSIC算法中,最优权值Wopt是噪声子空间单位向量,因此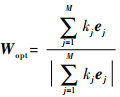

|
(21) |
将式(21)代入式(20)得

|
(22) |
式中:a(θ,φ)=[ejφ1(θ,φ),ejφ2(θ,φ),…,ejφN(θ,φ)]T。
1) 单干扰情况
当D=1时,由式(22)可以看出:
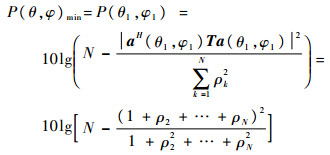
|
(23) |
式(23)表明天线阵方向图函数的最小值在干扰来向(θ1,φ1)处取得,因此幅度不一致性矩阵对方向图函数取得最小值点的位置没有影响,即单干扰时,幅度不一致性并不会影响抗干扰天线的零陷位置。
当不存在幅度不一致性时,即T=I时,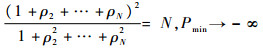
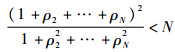
2) 多干扰情况
当D>1时,在不存在不一致性即矩阵T=I时,能在各干扰来向上产生零陷,式(22)在(θ,φ)=(θi,φi)(i=1,2,…,D)处取得极小值,也就是说此时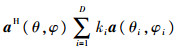
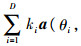
当存在幅度不一致性时,即T≠I时,同理等效于向量a(θ,φ)平行于Ta(θi,φi),i=1,2,…,D中的某个向量时,向量a(θ,φ)和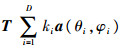
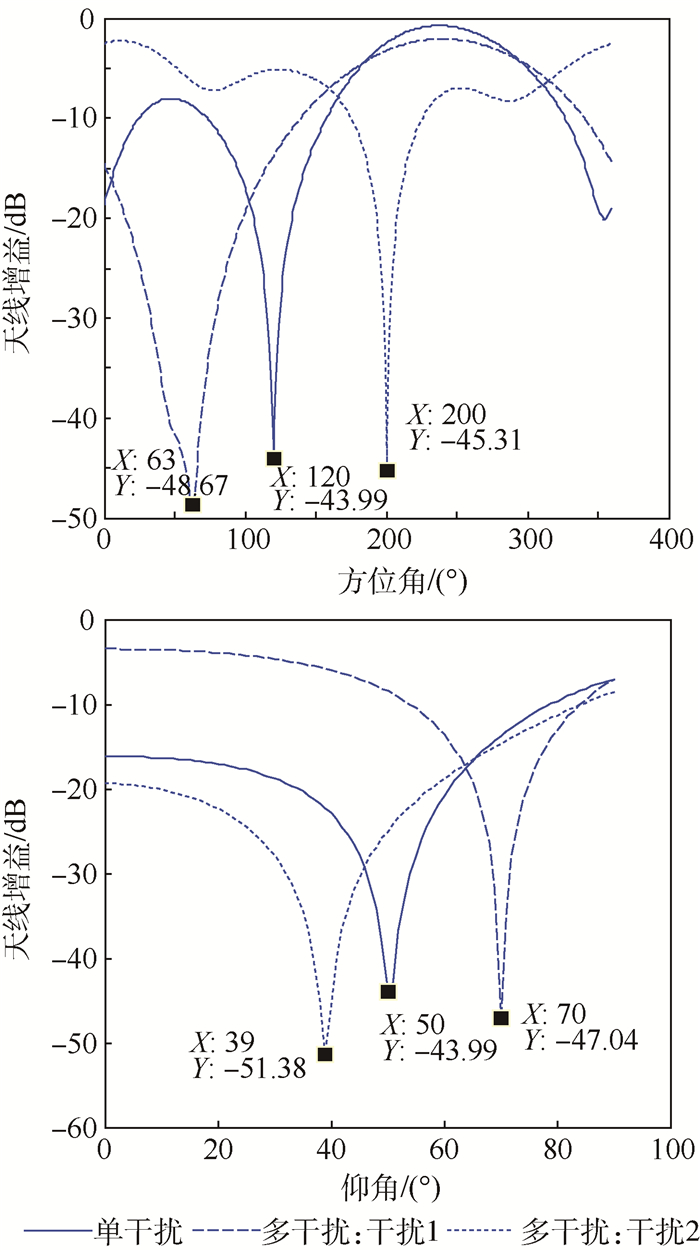
阵元个数:4个;天线布阵:均匀圆环阵列;干扰个数分别为:1个,2个;干扰来向:单干扰来向为(120°,50°),两个干扰来向为(200°,40°),(60°,70°);干扰类型:单干扰为单频干扰,两个干扰为单频干扰和窄带干扰。信号功率:-130 dBm;干扰功率:-70 dBm;快拍数:1 024个。幅度不一致性:相对于第一通道分别为:0,0.2,0.5,0 dB。图 1为通道幅相一致时形成零陷的位置和大小,图 2为幅度不一致时形成零陷的位置和大小。

|
| 图 1 通道幅相一致时形成的零陷位置和深度 Fig. 1 Nulling direction and depth when amplitude and phase of channels are consistent |
由图 1和图 2对比发现,单干扰时在通道幅度不一致性存在的情况下,其零陷形成的位置没有变化,但是零陷深度由68.16 dB降低到43.99 dB,说明单干扰情况下通道幅度不一致性对零陷位置没有影响,但对零陷深度有影响,使得零陷变浅;多干扰存在时,图 2中的干扰1在方位角上形成零陷最深的位置在63°而不是60°,干扰2在仰角上形成的零陷最深的位置在39°而不是40°,这说明多干扰情况下通道幅度不一致性使得零陷的位置发生了变化;上面两种现象和理论分析是一致的。
|
| 图 2 通道幅度不一致时形成的零陷位置和深度 Fig. 2 Nulling direction and depth when amplitude of channels are inconsistent |
假设阵列通道只存在相位不一致性,则相位偏差矩阵:
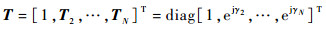
|
(24) |
阵列协方差矩阵为
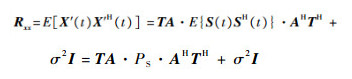
|
(25) |
假设有D个干扰源,干扰源互不相干,入射方向为(θi,φi),i=1,2,…,D,则干扰子空间的维度为D。
同3.1.1节中分析可得

|
(26) |
式中:a(θ,φ)=[ejφ1(θ,φ),ejφ2(θ,φ),…,ejφN(θ,φ)]T。
1) 单干扰情况
当D=1时,有
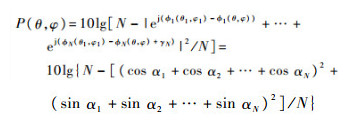
|
(27) |
式中:
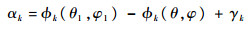
|
(28) |
由式(27)可以看出,P(θ,φ)min≠P(θ1,φ1),它和相位不一致性1,γ2,…,γN有关,因此可以得出结论是在单干扰情况下相位不一致性会影响到形成零陷的位置。另外,由柯西不等式可以证明:(cosα1+cosα2+…+cosαN)2<N(cos2α1+cos2α2+…+cos2αN),(sinα1+sinα2+…+sinαN)2<N(sin2α1+sin2α2+…+sin2αN),因此[(cosα1+cosα2+…+cosαN)2+(sinα1+sinα2+…+sinαN)2]/N<N,当不存在相位不一致性时,这一项等于N,从而使得零陷深度趋于负无穷;存在相位不一致时,零陷深度不再趋于负无穷,而是一个有限的数,故单干扰情况下相位不一致性对零陷深度也存在影响。
2) 多干扰情况
当D>1时,同幅度不一致性分析中D>1的情况,相位不一致性矩阵T的存在也会使向量a(θ,φ)和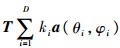
所以无论是单个干扰还是多个干扰,相位不一致性的存在都会导致方向图零陷位置和深度发生变化,在单干扰情况下会使得零陷变浅。
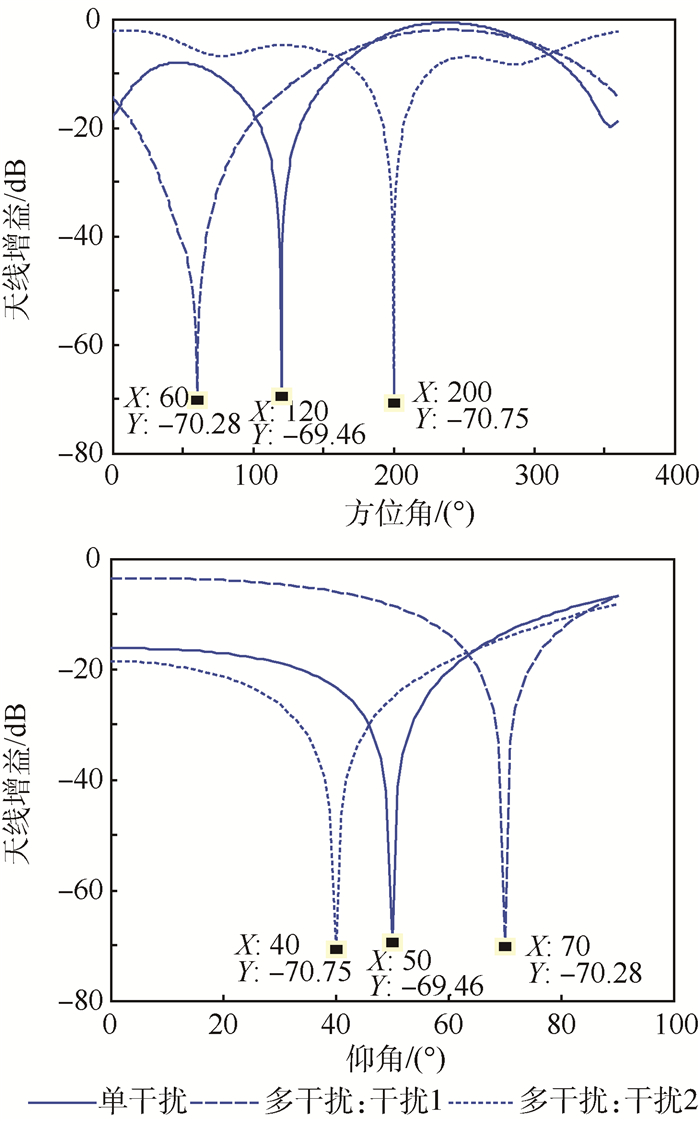
3.2.2 实验分析阵元个数:4个;天线布阵:均匀圆环阵列;干扰个数分别为:1个,2个;干扰来向:单干扰来向为(120°,50°),两个干扰来向为(200°,40°),(60°,70°);干扰类型:单干扰为单频干扰,两个干扰为单频干扰和窄带干扰。信号功率:-130 dBm;干扰功率:-70 dBm;快拍数:1 024个。相位不一致性:相对于第一通道分别为0°,10°,20°,10°。图 3为相位不一致时形成零陷的位置和大小。
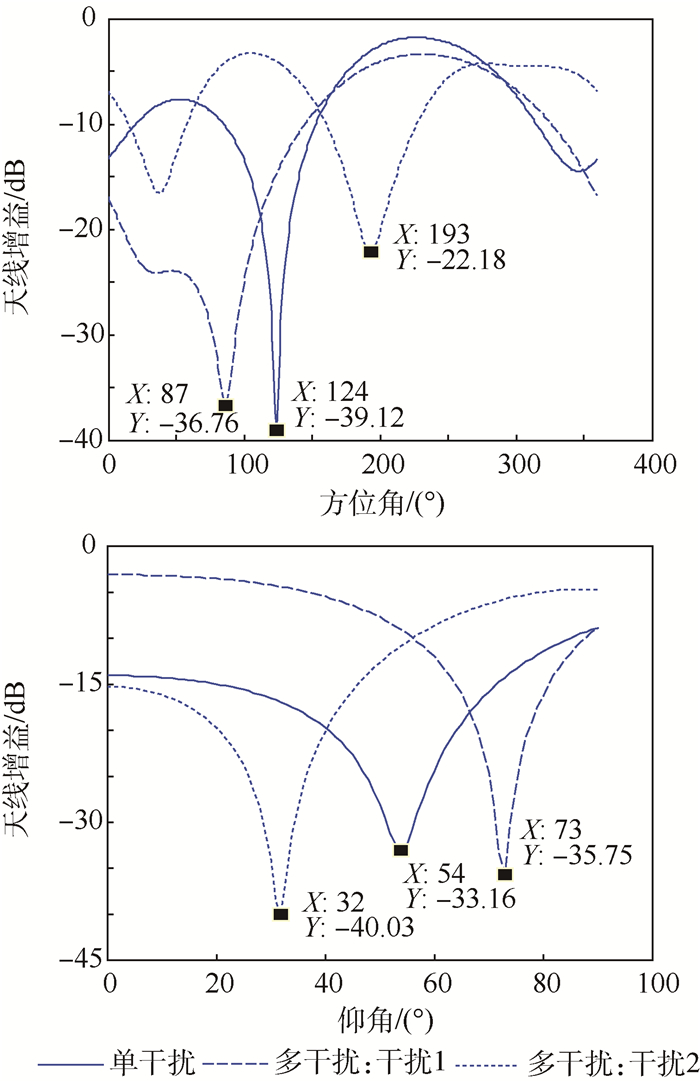
|
| 图 3 通道相位不一致时形成的零陷位置和深度 Fig. 3 Nulling direction and depth when phase of channels are inconsistent |
由图 3和图 1对比发现,在单干扰情况下,存在相位不一致性的方向图方位角零陷最深处为124°,在120°方位角的零陷深度更是由68.16 dB降低到小于40 dB,说明单干扰情况下,相位不一致性对方向图的零陷位置产生了影响,且零陷深度变浅了。多干扰情况下,图 3中干扰1和干扰2的方位角零陷最深位置分别为87°和193°,仰角零陷最深位置分别为73°和32°,都不是实验设置的干扰来向。因此无论单干扰还是多干扰,相位不一致性都会对方向图零陷位置产生影响,单干扰情况下还会使得零陷深度变浅。这个现象和理论分析也是一致的。
3.3 方向图纠正实际中,MUSIC算法在数字端实现,存在通道不一致性的信号经过模数转换器(ADC)采样之后进入数字端口,则根据式(3)和式(4),数字端接收到的信号为:X′=TAS(t)+N(t)=A′S(t)+N(t),这表明存在通道不一致性后,相当于天线阵的方向矢量发生变化,变化为a′(θ,φ)=Ta(θ,φ),也等效于天线的布阵发生变化。这时如果能确定误差矩阵T则可以对方向图函数进行纠正,纠正后的方向图函数为
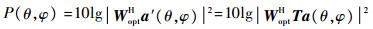
|
(29) |
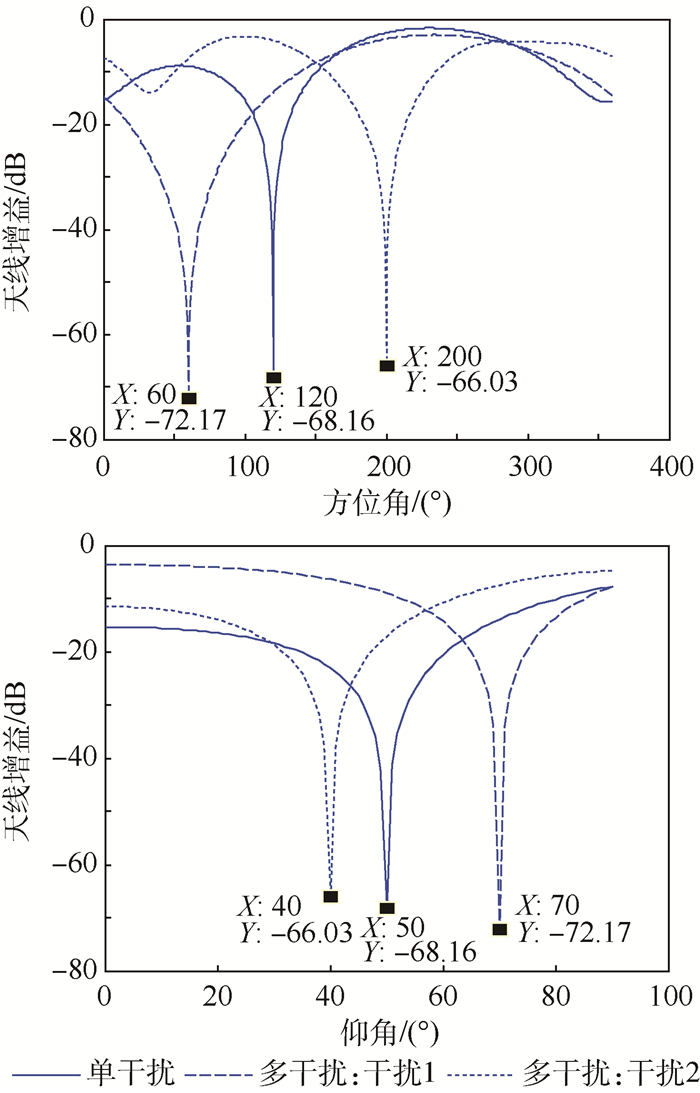
根据式(29)对图 2和图 3中的方向图进行纠正,纠正后的方向图如图 4和图 5所示。
|
| 图 4 幅度不一致纠正后的方向图 Fig. 4 Antenna array pattern with amplitude calibration |
由图 4和图 5可以看出,对方向图函数进行纠正后,方向图在干扰位置能够正确地产生零陷,且零陷深度和通道一致时没有降低。实际的应用中,对于慢变化的通道可以近似测出通道幅相偏差矩阵进行方向图纠正,对于快变化的通道来说,其对抗干扰的影响更加复杂,因此实际中用方向图来评价抗干扰的指标往往不能得到理想的效果。
|
| 图 5 相位不一致纠正后的方向图 Fig. 5 Antenna array pattern with phase calibration |
本文从幅度和相位两方面分析了通道不一致性对空域MUSIC算法抗干扰效果的影响。根据理论证明和实验验证,结果表明:
1) 单干扰情况下通道幅度不一致性会降低MUSIC算法方向图的零陷深度,但不影响零陷位置;多干扰情况下通道幅度不一致性对MUSIC算法方向图零陷位置和深度都有影响。
2) 通道相位不一致性对MUSIC算法方向图零陷位置和零陷深度均有影响。
3) 在通道不一致性慢变化的条件下,MUSIC算法利用方向图进行性能评估时需要测出通道幅相偏差矩阵进行方向图纠正。
实际工程中对于慢变化的通道不一致性,可以通过在数字端进行简单的补偿以消除其影响,对于快变化的通道不一致性,则可以采用通道均衡[17-19]的方法进行补偿,但该方法实现比较复杂。
| [1] | COMPTON R, HUFF R, SWARNER W, et al. The power-inversion adaptive array:Concept and performance[J]. IEEE Transactions on Aerospace and Electronic Systems, 1979, AES-15 (6) : 803 –814. DOI:10.1109/TAES.1979.308765 |
| [2] | BEHAR V,KABAKCHIEV C,ROHLING H.MVDR radar signal processing approach for jamming suppression in satellite navigation receivers[C]//11th International Radar Symposium (IRS).Piscataway,NJ:IEEE Press,2010:1-4. |
| [3] | JOHNSON J R, FENN A J, AUMANN H M, et al. An experimental adaptive nulling receiver utilizing the sample matrix inversion algorithm with channel equalization[J]. IEEE Transactions on Microwave Theory and Techniques, 1991, 39 (5) : 798 –808. DOI:10.1109/22.79107 |
| [4] | FINN A M,GRIFFIN M F.Radar adaptive beamforming algorithms and architectures[C]//Proceedings of IEEE 9th Digital Avionics Systems Conference.Piscataway,NJ:IEEE Press,1990:194-199. |
| [5] | SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34 (3) : 276 –280. DOI:10.1109/TAP.1986.1143830 |
| [6] | LU Y E,YANG J,DING Z M,et al.The orthogonal weighted algorithm for GPS receiver anti-jamming[C]//Proceedings of 2001 CIE International Conference on Radar.Piscataway,NJ:IEEE Press,2001:1190-1194. |
| [7] | MOHAMED E A, WANG Y F, TAN Z Z. Comparison between adaptive algorithms using in GPS receiver[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32 (5) : 561 –565. |
| [8] | AMIN M G, SUN W. A novel interference suppression scheme for global navigation satellite systems using antenna array[J]. IEEE Journal on Selected Areas in Communications, 2005, 23 (5) : 999 –1012. DOI:10.1109/JSAC.2005.845404 |
| [9] | 李苗, 吕善伟, 薛明华, 等. 考虑互耦和激励误差时智能天线波束形成[J]. 北京航空航天大学学报, 2004, 30 (8) : 732 –734. LI M, LÜ S W, XUE M H, et al. Performance of smart antenna when coupling and excitation error are considered[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30 (8) : 732 –734. (in Chinese) |
| [10] | STEINBERG B D. Principles of aperture and array system design[M]. New York: John Wiley & Sons, 1976 : 139 -168. |
| [11] | QUAZI A H. Array beam response in the presence of amplitude and phase fluctuations[J]. The Journal of the Acoustical Society of America, 1982, 72 (1) : 171 –180. DOI:10.1121/1.388001 |
| [12] | SU W M,NI J L,LIU G S,et al.A performance analysis of the MUSIC algorithm in the presence of channel mismatch[C]//3rd International Conference on Signal Processing.Piscataway,NJ:IEEE Press,1996:221-224. |
| [13] | 张建军, 项建弘. 通道不一致性对GPS天线自适应算法的影响[J]. 无线电工程, 2010 (2) : 35 –38. ZHANG J J, XIANG J H. Influences of channel mismatch on GPS adaptive algorithm[J]. Radio Engineering, 2010 (2) : 35 –38. (in Chinese) |
| [14] | WANG L,LI Y L,XU S B,et al.Robustness analysis of adaptive anti-jamming algorithms with channel mismatch and mutual coupling for GNSS systems[C]//IEEE International Conference on Signal Processing,Communication and Computing.Piscataway,NJ:IEEE Press,2012:705-710. |
| [15] | GAO F,WANG Y L,CHEN H,et al.Effect of channel mismatch on STAP performance[C]//CISP'08 Congress on Image and Signal Processing.Piscataway,NJ:IEEE Press,2008:85-89. |
| [16] | AALFS D D,HOLDER E J.Impact of wideband channel-to-channel mismatch on adaptive arrays[C]//Sensor Array and Multichannel Signal Processing Workshop.Piscataway,NJ:IEEE Press,2000:459-463. |
| [17] | 饶蓉.基于圆形天线阵的阵列校准方法与实现[D].武汉:华中科技大学,2013:45-56. RAO R.The method and implementation of array calibration on circular-antenna array[D].Wuhan:Huazhong University of Science and Technology,2013:45-56(in Chinese). |
| [18] | 申秋明.数字阵列雷达接收通道均衡技术研究与实现[D].成都:电子科技大学,2005:12-20. SHEN Q M.Research and implementation of channel equalization technology on digital array radar receiver[D].Chengdu:University of Electronic Science and Technology of China,2013:12-20(in Chinese). |
| [19] | 陈静静.阵列幅相误差校正及实现研究[D].南京:南京理工大学,2014:23-29. CHEN J J.Research on antenna array amplitude and phase error calibration[D].Nanjing:Nanjing University of Science and Technology,2014:23-29(in Chinese). |





