北京航空航天大学学报（社会科学版）  2014, Vol. 27 Issue (5): 85-92   PDF (1221KB)    
引用本文
郝书池. 多配送中心二级库存系统的库存策略比较研究——基于中心化安全库存和横向转运思想[J]. 北京航空航天大学学报（社会科学版）, 2014, 27(5): 85-92.  
Hao Shuchi. Comparative study on inventory strategies of multiple distribution centers two-level inventory system：based on centre safety inventory and lateral transport. JOURNAL OF BEIJING UNIVERSITY OF AERONAUTICS AND ASTRONAUTICS SOCIAL SCIENCES EDITION, 2014, 27(5): 85-92.  
多配送中心二级库存系统的库存策略比较研究——基于中心化安全库存和横向转运思想
郝书池    
暨南大学 管理学院, 广东 广州 510632
收稿日期：2013-9-23
基金项目：国家自然科学基金面上项目（41271175）
作者简介：郝书池（1975- ），男，湖南常德人，副教授，博士研究生，研究方向为物流与供应链系统优化.
摘要：基于中心化安全库存和横向转运思想，采用数学建模和算例研究的方法，对多配送中心二级库存系统的库存策略进行了研究，探讨了各种库存策略的优劣性及其参数的影响。结果表明，中心化存储优于分散存储策略，多级中心化存储优于单级中心化存储；当服务水平要求较高和标准差系数较大时，多级中心化存储和横向转运相结合策略的优势更明显；当提前期较长时，将安全库存靠近需求点存放有利于应对提前期内的不确定性。
关键词： 中心化安全库存     横向转运     多配送中心     库存策略     二级库存系统    
Comparative Study on Inventory Strategies of Multiple Distribution Centers Two-level Inventory System：Based on Centre Safety Inventory and Lateral Transport
Hao Shuchi    
Management School, Jinan University, Guangzhou 510632, China
Abstract: Based on the ideas of centre safety inventory and lateral transport, the methods of mathematical modeling and case study have been used to discuss the inventory strategies of two-level inventory system with multiple distribution centers, the advantages and disadvantages of different inventory strategies and the effects of different parameters. The results show that the centre storage strategy is better than distributed storage strategy. Multi'stage centre storage strategy is superior to single'stage centre storage strategy. Higher service level is and greater coefficient of standard deviation is, more obvious the superiority of combination multi'stage centre storage and lateral transport strategy is. If the lead time is longer, the safety inventory should be closer to the demand point to avoid the uncertainty in lead time.
Key words: centre safety inventory     lateral transport     multiple distribution centers     inventory strategy     two-level inventory system    
一、供应链库存优化的基本理论 (一)中心化库存理论

传统的库存管理采用分散式库存管理方法，各存储点独立运作，负责各自对应的需求点，其决策目标是达到各存储点库存策略最优，是一种系统局部优化。中心化库存是通过风险分担(risk pooling)实现库存的集中管理，其理论基础是多个地点需求总和的变动性小于各个地点需求变动性的总和。中心化库存风险分担效应受需求相关性的影响，一般来说，需求相关性越小，效应越好。Eppen研究了各点需求为正态分布，且具有相同的线性持有成本和惩罚成本的多地区报童模型，根据需求的相关系数，得到了集中模型的库存期望成本比分散模型的低。[1]498—501邓佩等用数值分析的方法探讨了空间聚集效应下，需求的相关系数变化对安全库存的影响，建立了不同情况的关系式，通过实例证明了聚集存储的安全库存量更低。[2]程晓华采用聚集效应理论，利用随机函数验证了库存的平方根法则，并得出利用平方根法则计算出来的结果应该是安全库存聚集值的上限，聚集的效应取决于不同需求相关性的大小。[3]宋殿辉和苗壮通过1个算例得出随着需求相关性系数ρij的增大，分散模式与集中模式下总安全库存之间的差距在缩小。由于需求的不确定性，当把不同地点的需求集合起来处理时，一个零售商(顾客) 高于平均值的需求很可能被另一个零售商(顾客) 低于平均值的需求所抵消，需求变动性的减小可以降低平均库存水平，从而降低库存成本。[4]逄兆勇不仅考虑了需求相关性的影响，还考虑了变异系数对风险分担效应的影响，发现需求的变异系数越大，从集中库存中的获益越大，风险吸收的程度就越高。[5]Berman等对比了中心化系统和非中心化系统，发现在需求变异系数水平较高时，风险分担效益更明显，供应和提前期的不确定性会影响中心化库存的效果。[6]解琨和刘凯探讨了安全库存存在的必要性，研究了提前期和需求不确定对安全库存的影响，并通过实例对比了集中库存系统和分散库存系统的差异性，得出集中库存可以在不影响服务水平的同时降低安全库存。[7]Schmitt等对比了中心化和非中心化库存策略，认为需求不确定、供应确定时应考虑风险共担，中心化策略是最优的；供应和需求都不确定时应选择非中心化策略。从系统优化的角度，还应考虑中心化库存对其他成本的影响，在满足一定服务水平的基础上，以系统总成本最低为目标。①Stulman则采用先到先服务的原则，确定了服务水平约束下中心化库存系统最小的初始库存，也证明了集中使系统库存降低。[8]Mehrez和Stulman考虑了缺货成本，用最大缺货概率作为约束来代替缺货惩罚成本，证明了集中式库存相对于分散式库存的优势。[9]Chang和Lin在Eppen模型的基础上考虑运输成本，探讨了3个成本方程为凹和线性情况下中心化和非中心化库存策略的成本关系，但未考虑运输距离对运输成本的影响。[10]

(二)横向转运理论

横向转运的主要目的是在非正常补货时间，通过将库存系统中其他节点的冗余库存调运到已经发生或者可能发生缺货的同级节点，实现安全库存水平降低或者在同样库存水平下提高客户服务水平。横向转运的基本思路是通过风险共担来实现库存集中化管理和客户集中化服务。因此，当库存点之间的运输时间(或成本)小于零售商从外部订货所需的时间(或成本)时，横向转运是调整需求和库存差异的有效机制，可以在不增加库存水平的前提下，减少缺货成本，提高顾客服务水平。此外，转运允许库存点共享库存，因此，各库存点可以通过协调订货策略减小订货成本。

1.单级多点间的横向转运

制定转运决策一是要考虑转运成本或转运价格的高低。Arnold等开发了仿真和平行进化算法相结合的方法来求解非线性转运成本问题，从而确定最佳转运策略，并对策略参数进行了敏感性分析。[11]Kukreja 和Schmidt考虑需求和提前期的变化，研究了完全转运策略、不计转运时间、每次转运成本固定与转运数量无关的转运模型。[12]Archibald等针对2个储存点的情况，不考虑转运时间，采用能减少马尔科夫决策过程的分解方法来研究转运策略，并估算了转运价格对采用紧急运输还是转运策略的影响。[13]禹爱民和刘丽文研究了互联网环境下网络零售商与实体零售商之间的转运问题，得出它们的最优库存水平随转运价格的升高而升高，当转运价格适中时，网络零售商的库存水平低于无转运的库存水平，而实体零售商的库存水平相反，能够实现双赢。[14]二是要考虑转运对其它成本的影响，需要从系统总成本的角度进行决策，Hu等构造了动态规划算法，分析当系统采用(s，S)存贮策略时的最小化库存成本和转运成本，并研究了转运成本、库存持有成本和缺货成本对转运决策的影响。[15]霍佳震和李虎建立了零备件单级多点转运的批量订货模型，分析并确定了稳定状态下库存水平的概率及其状态转移，并运用库存水平、提前期需求量和净库存三者的关系计算库存点需求能够满足、需要转运及发生缺货的概率，最后构建了以服务水平为约束，以库存成本和转运成本最小为目标的规划模型。[16]此外，还有学者对转运对库存水平、缺货水平及需求满足率带来的影响进行了研究。Minner等利用信息了解库存水平和未完成订单的到达时间，探讨转运对库存水平和未来再订货点的影响。[17]Xu等研究了具有固定订货费用的转运问题，仓库采用独立的(Q，R)订货策略，并考虑转运出货物的仓库可以保留的库存量，分析了转运对需求满足率的影响。[18]

2.两级或多级供应链中同级间的横向转运

首先，转运价格是转运决策的重要影响因素。Hu等假设产量和需求量随机分布，求解使得销售商分散决策和一体化决策相同的协同转运价格，并分析了需求量和产量的变化对转运价格的影响。[19]其次，对于转运量的问题，可以选择需要多少转运多少，但可能导致转出点在随后的时间出现缺货；也可以选择自己预留一定的量，多余的按转运需求转出；还可以选择转移量超过实际缺货量。Needham 和 Evers分析了完全共享转运或不完全共享转运，探讨了影响转运的各项成本因素，发现缺货成本是考虑是否转运的主要因素。[20]王继亮研究了一个供货能力有限的供应商向2个不同的零售商供货，零售商间可以采用预防性或者应急性转运策略进行调货的情形，比较了预防性转运、应急性完全库存共享转运和控制库存转运3种不同策略对于系统平均期望总成本的影响。[21]汪传旭等研究了不确定环境下多需求点应急转运库存策略，形成了由1个中央物资供应点、1个共享仓库和多个需求点组成的二级应急物资供应系统，探讨了需求依靠自己、转运和直运满足的比例，建立了以需求点的服务水平为约束条件、以各个需求点的库存水平和转运点为决策变量、以总费用最小为目标的模型，并针对主要参数的变化分析了完全转运策略、部分转运策略和不转运策略的优劣条件。[22]Van Wijk 等研究了需求泊松分布、存在有限转运和紧急运输、(S-1，S)库存检查策略的情况，发现有限转运比不转运和完全转运更能节省成本。[23]Paterson等改变了传统不转移或者缺多少就转移多少的假设，考虑到转移成本及未来的缺货风险，认为转移量可以超过实际缺货量。[24]第三，对于转运方向问题，一般学者假设多个库存点间相互可以转运，但是在某种情况下会出现安全库存倒流的问题，近来有学者对转运方向进行了研究。Zhang等在保证自己不缺货的情况下进行转移，改变了过去研究基于所有库存点间都可以转移库存的假设，给定一定的转移方向，在各地缺货成本不同的情况下非常有意义。[25]张光宇等突破了传统的双向转运假设，建立了基于库存稳态概率的可维修备件、适用于具有不同缺货费用的横向供应策略下的多点库存单向转运模型，并探讨了不同库存水平和订购量对单向转运模型的影响。[26]

(三)研究述评

中心化库存理论的研究成果丰富，但以下问题值得进一步研究：首先，已有的研究成果假设运输成本仅是运输量的函数，没有考虑到运输距离的影响，但如果假设运输成本随着运输距离的增加而增加，那么中心化库存并不一定总是带来效益的提高，反而呈现出先增加后减少的趋势，可以预测中心化程度(即最佳中心化策略)应该有1个最优值；其次，考虑单位库存持有成本的影响，在单位库存持有成本很低的情况下，安全库存分散存储模式下的总成本可能更低，即非中心化决策也许最优。

关于横向转运成本方面，仅考虑其与转运量有关，未考虑转运距离的影响。已有研究成果均假设库存分散存储、所有库存点之间满足一定条件都可以转运，存在转运的无序化问题，而中心化存储模式下的横向转运问题缺乏研究。一般仅研究需求点间或者零售商间的横向转运，而供应链多个层级都可以进行同级横向转运的问题有待研究。

中心化存储可以降低安全库存量，却增加了服务时间和运输成本；横向转运可以做到零安全库存，但缺货成本和转运成本大大增加。它们之间存在一定的优势互补关系，但已有研究成果均是单方面对中心化存储或横向转运问题进行研究，所以，笔者的第1个研究目的是将这2种优化方法结合起来运用。此外，已有研究成果仅探讨单级供应链间(几个存储点或几个需求点间)中心化库存或横向转运问题，而缺乏对在二级或多级供应链中考虑系统安全库存存放位置不同、每个层级内部都在中心化存储的模式下进行横向转运的情况的 研究，这是笔者的第2个研究目的。笔者的第3个研究目的是在已有文献的基础上进一步探讨需求分布、提前期、服务水平等因素对横向转运与中心化存储联合决策的影响。

二、系统需求均值、方差和缺货量计算 (一)系统需求均值、方差模型 1.1个需求点，考虑提前期的情形

(1)提前期固定

假设需求点的需求服从均值为u、标准差为σ的正态分布，提前期为L不变。则有总需求均值为

总标准差为

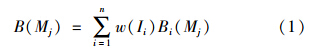
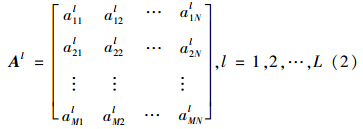
(2)提前期服从均值为L、标准差s的正态分布，UT同式(1)

2.多个需求点，需求变化、不考虑提前期、分散存储的情形

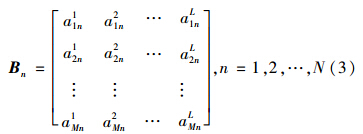
假设有N个需求点，需求点i的需求服从均值为ui、标准差为σi的正态分布，不考虑提前期。则有

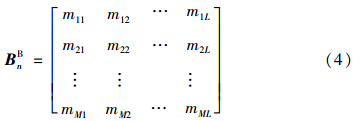
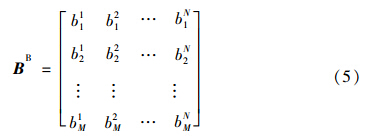
若假设各需求点的分布相同，则有

3.多个需求点，需求变化、不考虑提前期、集中存储的情形

在集中存储条件下，UT同式(4)，

其中：ρij为各需求点的需求相关性系数。

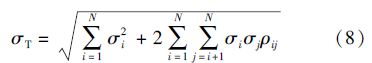
若假设各需求点服从相同的正态分布σ，且需求相关性系数相等，则有

当ρ=1时，完全正相关，σT同式(7)，集中存放与分散存放的标准差一致，则没有聚集效应；当ρ=－1时，完全负相关

当ρ=0时，完全不相关，即

集中存放小于分散存放的标准差，存在聚集效应，可以降低安全库存。[1]498—501

4.多个需求点，需求变化、考虑提前期、分散存储的情形

(1)假设各需求点的提前期都服从均值L、标准差s的正态分布，则有

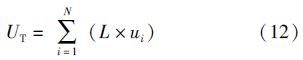
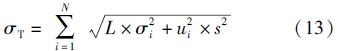
(2)假设提前期固定为L，则UT同式(12)

5.多个需求点，需求变化、考虑提前期、集中存储的情形

假设各地需求完全不相关，即ρij=0，则有

(1)假设各需求点的提前期都服从均值L、标准差s的正态分布，则UT同式(12)

(2)假设提前期固定为L，则UT同式(12)

(二)缺货量的计算

假设需求服从均值为u、标准差为σ的正态分布。k为安全系数，用来衡量库存可得性指标，与服务水平有关。若服务水平为A，则

其中：NORMSINV(A)为求A的反标准正态累积分布。 例如：提前期内的缺货可能性为0.1，货物的可得性为0.9，即服务水平为0.9，则k=1.28。

1.若不考虑提前期，订货点R=SS=kσ，则缺货量的期望值ε为

由于

则有

其中：p(k)=kφ(k)+φ(k)－k，且φ(x)=·,

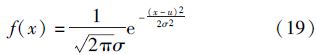
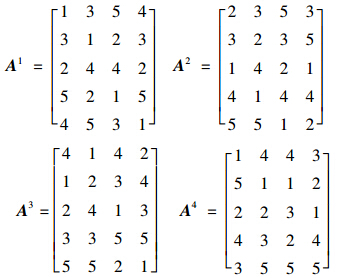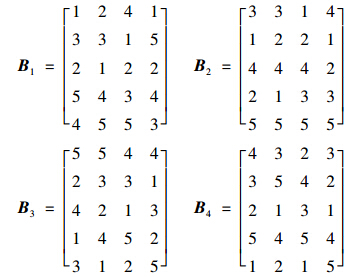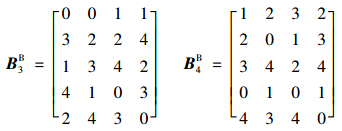
2.假设提前期固定为L，订货点R=Lu+SS，SS=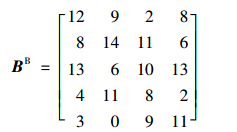，则缺货量的期望值ε依然为式(18)，由于

则有

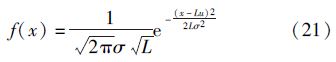
3.假设提前期服从均值为L，标准差为s的正态分布，订货点R=Lu+SS，SS=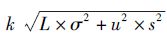，则缺货量的期望值ε仍然为式(18)，由于

则

三、多配送中心二级库存系统的库存策略分析 (一)分析内容

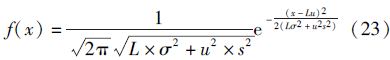
考虑由1个供应商、多个配送中心、多个需求点构成的二级库存系统，综合运用中心化安全库存和横向转运来控制系统库存。只有配送中心间或同一群组内的需求点允许横向转运，且不考虑转运时间，各需求点的需求独立。根据系统安全库存存放位置和是否中心化存储2个要素对上述库存系统进行分析，仅考虑安全库存成本、横向转运成本和紧急调运成本，可以分为8种情况，如表 1所示。

表 1 各种策略的库存设置与运输要求
(二)各种库存策略的基本模型 1.参数假设

K为安全系数；i为配送中心，i=1，2…N；ai为配送中心i所服务的需求点个数，ai为整数；ui为配送中心i所服务需求点的需求量的均值(假设同一个群组的均值相同)；σi为配送中心i所服务需求点的需求量的标准差(假设同一个群组的标准差相同)；Ti为配送中心i所服务需求点的提前期均值(假设同一个群组的均值相同)；Si为配送中心i所服务需求点的提前期标准差(假设同一个群组的标准差相同)；Mi为配送中心i的需求均值；Qi为配送中心i的需求标准差；P为从供应商到配送中心的提前期(取从供应商到各个配送中心的平均时间)；b为从供应商到配送中心的提前期标准差；εij为配送中心i所服务需求点j可能产生的缺货量；εi为配送中心i可能产生的缺货量；为配送中心i服务各需求点间的平均距离，di为各需求点所在群内的分布密度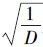；为各配送中心间平均距离，D为所在区域内配送中心的分布密度；Wi为配送中心i到所服务需求点的平均距离，用1个相对于配送中心平均距离的无量纲数据表示。

2.各种库存策略的模型构建

结合表 1中的各种库存策略和式(1)~式(24)，可以得出8种策略的基本模型，如表 2所示。

表 2 各种策略的基本模型
四、算例研究 (一)算例计算 算例以表 1中的库存策略为思路，结合某公司的实际数据，为该公司探讨最优库存决策。由于行业或企业的差异性，参数的取值也有较大的不同，因此，算例的计算结果并不能代表在任何企业某个决策都是最优，只是为其他企业的库存决策提供思路和方法。 假设某公司有5个配送中心(N=5)，每个配送中心负责8个需求点(ai=8)。C2为配送中心级单位转运成本；C3为单位调运成本；C4为单位安全库存成本；CLT1为需求点级横向转运成本；CLT2为配送中心级横向转运成本；CET为紧急调运成本；CSS1为需求点级安全库存成本；CSS2为配送中心级安全库存成本；CTC为总成本。算例的基本参数如表 3所示，各配送中心i的值如表 4所示，算例的计算结果如表 5所示。
表 3 算例的基本参数

表 4 各配送中心i的值

表 5 算例的计算结果

从表 5可以看出，策略7，即系统安全库存全部集中存储在需求点级且横向转运最优；策略3，即配送中心级和需求级都有安全库存，但是配送中心是中心化存储、需求点是分散存储次之；策略6，即仅在配送中心存放安全库存，且分散存储成本最高。

(二)参数影响分析

在模型中，各项价格按行业平均水平取值，波动性较小，此外，当客户确定后，距离参数可以认为是已知。服务水平要求、需求点的分布、提前期有较大的随机性，对库存决策有着重要影响。

1.安全系数(K)的影响

假定其他参数已知，并用算例数据代入，各种策略的总成本分别为

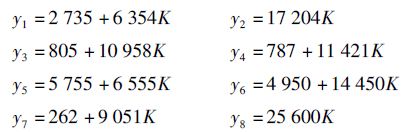
由于K>0，所以必存在y7＜y6，y7＜y4，y7＜y3，y2＜y8，y1＜y5，所以决策在1，2，7之间进行，如图 1所示。

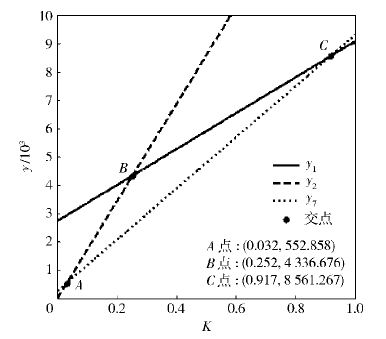图 1 安全系数K影响图
图 1

从图 1可知K<0.032时策略2最优，一般不允许这么低的服务水平；0.032<K<0.917时，策略7最优，即仅在需求点中心化存储，但由于在配送中心级没有集中存储安全库存，一旦缺货，需要从供应商紧急调运，服务水平不会达到很高；0.917<K时，策略1最优，需要在配送中心级和需求级都集中存储安全库存且允许横向转运才能满足较高的服务水平要求。

2.标准差系数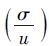的影响

这是反映标志变动程度的相对指标，假设θ=σu，则有σ=θu。假设σi用θui替代，其他参数用算例数据代入，各项策略的总成本分别为

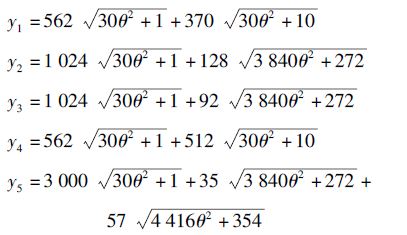
标准差系数影响如图 2所示。

图 2 标准差系数影响图

由图 2可知标准差系数的变化对最优结果的排序影响不大，尤其当θ较大时，策略1优势明显；在需求点不中心化存储安全库存的成本较高(策略8，策略6，策略5，策略2和策略3)，尤其当标准差系数较大时(如θ>0.245)，若在需求点不存放安全库存，总成本会更高(策略5和策略6)。

3.需求点提前期(Ti)的影响

由图 3可知提前期在需求点存放安全库存的情况下对结果影响不大(策略7和策略8)；一般情况下提前期的变化并没有改变最优策略的排序，仅当提前期很小(0.1)时，可以把部分安全库存存放于配送中心处，即出现了决策4最优。

图 3 需求点提前期敏感性分析
五、结论与展望

文章以多级供应链、多配送中心为研究对象，对供应链多个层级内部都有横向转运和中心化安全库存的问题进行了研究。根据安全库存集中存储的位置不同，针对每个库存策略建立了包含安全库存成本、横向转运成本和紧急调运成本的总成本最低库存模型，最后通过算例对各种库存策略进行比较。可以发现：第一，通过中心化存储安全库存和横向转运相结合更能降低总成本；第二，当服务水平要求较高和标准差系数较大时，配送中心级和需求级都中心化存储，安全库存和横向转运成本更低；第三，尽量将安全库存存放靠近需求点，可以有效应对提前期内的不确定性。

注释： ① 参见：Schmitt A J，Snyder L V和Shen Z J M所写的Centralization versus Decentralization: Risk Pooling,Risk Diversification,and Supply Uncertainty in a One-Warehouse Multiple-Retailer System. Working paper，Rossin P C,College of Engineering and Applied Sciences，Lehigh University，Bethlehem，PA，2007年。
参考文献
[1] Eppen G D.Effects ofcentralization on expected costs in a multi-location newsboy problem[J].Management Science,1979,25(5):498-501.
[2] 邓佩,张俊婧,苏翔,等.空间需求聚集下安全库存模型及其实证[J].工业工程与管理,2006(4):21-23.
[3] 程晓华. 利用随机函数验证库存的平方根法则[J].物流技术与应用,2007,12(1):96-97.
[4] 宋殿辉,苗壮. 集中存储对安全库存影响机理研究[J].物流技术,2008,27(8):72-73.
[5] 逄兆勇.基于风险分担的供应链库存最优控制策略研究.青岛:中国海洋大学,2009.
[6] Berman O,Krass D,Mahdi T M.On the benefits of risk pooling in inventory management[J].Production and Operations Management,2011,20(1):57-71.
[7] 解琨,刘凯.供应链库存管理中的风险问题研究[J].中国安全科学学报,2003,13(5):26-29.
[8] Stulman A.Benefits of centralized stocking for the multi-centre newsboy problem with first come, first served allocation[J].Journal of the Operational Research Society,1987,38(9):827-832.
[9] Mehrez A,Stulman A.Priority centralization of the one period multi-location inventory system [J].ZOR-Z Oper Res.,1984,28:B298-B304.
[10] Chang P L,Lin C T.On the effect of centralization on expected costs in a multi-location newsboy problem[J].Journal of the Operational Research Society,1991,42(11): 1025-1030.
[11] Arnold J,Kchel P,Uhlig H.With parallel evolution towards the optimal order policy of a multi-location inventory with lateral transshipments[J].Research Papers of the 3rd ISIR Summer School,1997,31(10):1-14.
[12] Kukreja A,Schmidt C P.A model for lumpy demand parts in a multi-location inventory system with transshipments[J].Computers & Operations Research,2005,32(8):2059-2075.
[13] Archibald T W,Black D,Glazebrook K D.An index heuristic for transshipment decisions in multi-location inventory systems based on a pairwise decomposition[J].European Journal of Operational Research,2009,192(1):69-78.
[14] 禹爱民,刘丽文.供应链下游零售商的转运库存策略[J].系统管理学报,2013,22(1):1-9.
[15] Hu J,Watson E,Schneider H.Approximate solutions for multi-location inventory systems with transshipments[J].International Journal of Production Economics,2005,97(1):31-43.
[16] 霍佳震,李虎.零备件库存多点转运的批量订货模型与算法[J].系统工程理论与实践,2007,12(12):62-67.
[17] Minner S,Silver E A,Robb D J.An improved heuristic for deciding on emergency transshipments[J].European Journal of Operational Research,2003,148(2):384-400.
[18] Xu K,Evers P T,Fu M C.Estimating customer service in a two-location continuous review inventory model with emergency transshipments[J].European Journal of Operational Research,2003,145(3): 569-584.
[19] Hu X,Duenyas I,Kapuscinski R.Existence of coordinating transshipment prices in a two-location inventory model[J].Management Science,2007,53(8):1289-1302.
[20] Needham P M,Evers P T.The influence of individual cost factors on the use of emergency transshipments[J].Transportation Research Part E: Logistics and Transportation Review,1998,34(2):149-160.
[21] 王继亮.物流系统转运和库存策略研究.北京:清华大学, 2007.
[22] 汪传旭,许长延,刘学恒.不确定环境下多需求点应急转运库存策略[J].计算机集成制造系统,2011,17(9): 2022-2028.
[23] Van Wijk A C C,Adan I,Van Houtum G J.Approximate evaluation of multi-location inventory models with lateral transshipments and hold back levels[J].European Journal of Operational Research,2012,218(3):624-635.
[24] Paterson C,Teunter R,Glazebrook K.Enhanced lateral transshipments in a multi-location inventory system[J].European Journal of Operational Research,2012,221(2):317-327.
[25] Zhang G,Li Q,Wang S.Batch ordering policy of spare parts in multi-location inventory system with unidirectional lateral transshipments[C]//Computational and Information Sciences. Chongqing:2012 Fourth International Conference on IEEE,2012:317-320.
[26] 张光宇,李庆民,李华.零备件的多点库存单向转运模型与算法[J].航空学报,2012,33(1):1-8.