电液负载模拟器常用于飞行器(如飞机、火箭等)伺服机构性能测试,其性能的好坏,直接影响伺服机构的出厂质量.通过分析现有技术资料以及目前已完成和正在开展的负载模拟器项目,可以发现,飞行器性能的不断提高,对电液负载模拟器也提出了越来越高的要求:加载力矩从6N·m超小力矩到70000N·m超大力矩;多余力补偿从原来消除80%提升到95%以上;频率响应也从低频0.02Hz到高频60Hz[1,2].为实现所要求的极限性能,摩擦补偿是必须面对的问题.
针对电液负载模拟器中的摩擦干扰,广大学者和工程技术人员从多个方面进行了有益探索.文献[3]提出了较为精确的电液负载模拟器数学模型,为负载模拟器的分析奠定了理论基础.文献[1]在文献[3]的基础上,通过引入舵机安装刚度、负载刚度、力矩传感器刚度等,建立了更精确的模型,拓展了负载模拟器极限性能提升的思路.文献[4,5]从摩擦补偿的角度分别论述了一点补偿和多点补偿的策略,对系统极限性能改进具有一定的指导意义.文献[6]综述了多余力补偿的各种方法,文献[7,8,9,10,11]探讨了摩擦补偿的种类和具体补偿实现方式.现有的摩擦补偿文献,过多的聚焦于系统的力矩补偿及补偿结论,而欠缺对摩擦补偿的全面分析和论述.本文充分借鉴前人的工作,讨论了包含摩擦力的负载模拟器数学模型;摩擦模型的参数辨识以及位移伺服、力矩伺服、多余力控制等多方面的摩擦补偿细节,较全面论述了摩擦补偿在电液负载模拟器中的应用. 1 含有摩擦效应的负载模拟器模型
针对不同设备的负载特性要求,如火箭喷管以惯量负载、弹性负载、摩擦力负载、常值力矩为主[12];普通飞行器舵机以惯量负载、弹性负载、可变力矩负载为主[1,3];无人机舵机则以可变力矩负载为主[13,14].可以建立典型的电液负载模拟器工作结构如图 1所示.整个负载模拟器可模拟飞行器伺服机构(下面称为被试件)的弹性负载、惯量负载、可变力矩负载等.其中弹性负载采用图 1中可调负载刚度G进行调节,惯量负载通过中间的可调惯量盘J来实现,可变力矩负载经左侧的液压摆动马达进行.被试件安装于可调惯量盘J与弹性支撑K中间,带动惯量盘J、马达、可调负载刚度G工作,考虑到传动轴采用滚动轴承进行支撑,系统的摩擦主要集中于马达转子[1].
 |
| Ki—电流放大器增益;Mf—马达转子摩擦力;θm—马达轴角位移;Kf—马达侧力矩传感器扭转刚度; θi—惯量盘转动角度;R—被试件连接处距传动主轴中心的距离;Kd—弹性负载和阻尼负载侧力矩传感器的扭转刚度; Kt—角度传感器扭转刚度;Bm—负载等效阻尼系数;Yx—试件相对长度变化量;θd—弹性负载侧的角位移. 图 1 电液负载模拟器结构图 Fig. 1 Structure of electro-hydraulic load simulator |
在图 1所示的负载模拟器结构中,考虑到被试件是甲方产品,无法获取准确的数学模型,其对外仅表现为长度的变化.同时相对于可调惯量盘来说,被试件质量很小,可将被试件简化为长度变化的刚性杆.其相对长度变化量为Yx.
被试件上的受力全部通过弹性支撑K传递到台体上,弹性支撑对被试件的力为

可调惯量盘上的受力为
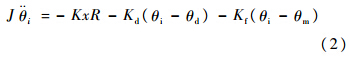
弹性负载及阻尼负载侧力矩传感器的受力为
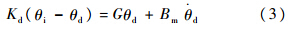
放大器用于将输入的电压信号转变为伺服阀所用的电流信号.其关系表达式为

伺服阀的线性化流量方程:
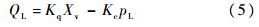
伺服马达为液压摆动马达,其流量连续性方程为
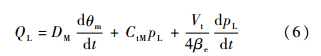
摆动马达在考虑摩擦干扰情况下的受力为
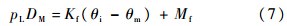
考虑到惯量盘在很小的角度范围内运行(±5°),因此其运动角度θi可用下式近似代替:

对式(1)~式(8)进行拉氏变换,并以伺服阀电压为输入量,传递到被试件的力矩为输出量,所得到的系统结构如图 2实线部分所示.
 |
| 图 2 系统结构图 Fig. 2 System structure |
由图 2可知,系统中的摩擦力Mf通过马达转轴传递到整个系统中,为消除该干扰,摩擦力的获取是首先要解决的问题.
经摩擦模型获取摩擦力的众多模型中,LuGre模型能精确描述摩擦的各种现象,应用较广.LuGre模型用下面3个公式描述:
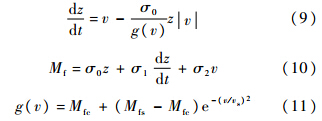
在式(9)~式(11)所示的LuGre模型中,参数σ0,σ1,σ2,Mfc,Mfs,vs是表征LuGre模型的6个参数,其中参数σ0和σ1用于描述鬃毛的变形及变形速度对摩擦力的影响,属于动力摩擦系数;σ2,Mfc,Mfs,vs是Stribeck摩擦中的4个系数,属静力摩擦系数[7].
为获得准确的摩擦模型,需辨识模型中的6个系数.具体辨识分两步进行,首先辨识系统的静力系数,随后辨识系统的动力系数.在以上思想的指导下,将负载模拟器与舵机相连,放弃对加载系统的控制,连通要辨识摆动马达进出油口,消除油液背压的影响,被试件做位置闭环控制,拖动电液负载模拟器运动,此时经力矩传感器Kf测得的力矩,可以认为是摆动马达的摩擦力矩[5].
2.1 静力摩擦系数辨识
假设系统处于稳定状态(静止或匀速),此时

从而可得
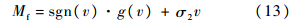
文献[4,5]在辨识摩擦系数时,采用一定幅值和频率的正弦波位移信号进行激励,该方式在静力摩擦系数辨识时容易引起鬃毛变形,使摩擦模型中耦合动力摩擦系数无法直接用于静力摩擦系数辨识.考虑到负载模拟器运行范围较小(±5°内),为方便获取均匀速度下的摩擦力,可使被试件以不同频率的三角波进行工作,从而获取不同速度下的摩擦力.在此基础上,通过一定的识别算法(如遗传算法等)识别出系统的静力摩擦系数如下:
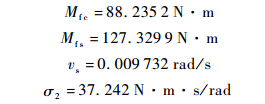
辨识结果和实测曲线对比如图 3所示.
 |
| 图 3 LuGre静力参数辨识 Fig. 3 Identification of LuGre static parameter |
摩擦模型的两个动力参数分别为:σ0是鬃毛的刚度,σ1是微观阻尼系数.由于鬃毛的平均变形z不容易测量,给参数辨识带来了较大难度.
为简化参数辨识过程,可将式(9)在z=0和v=0附近进行线性化处理[10],得

此时式(10)变为
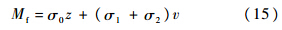
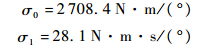
对辨识后的参数分别在微位移和微速度条件下进行了验证,验证实验曲线如图 4所示.
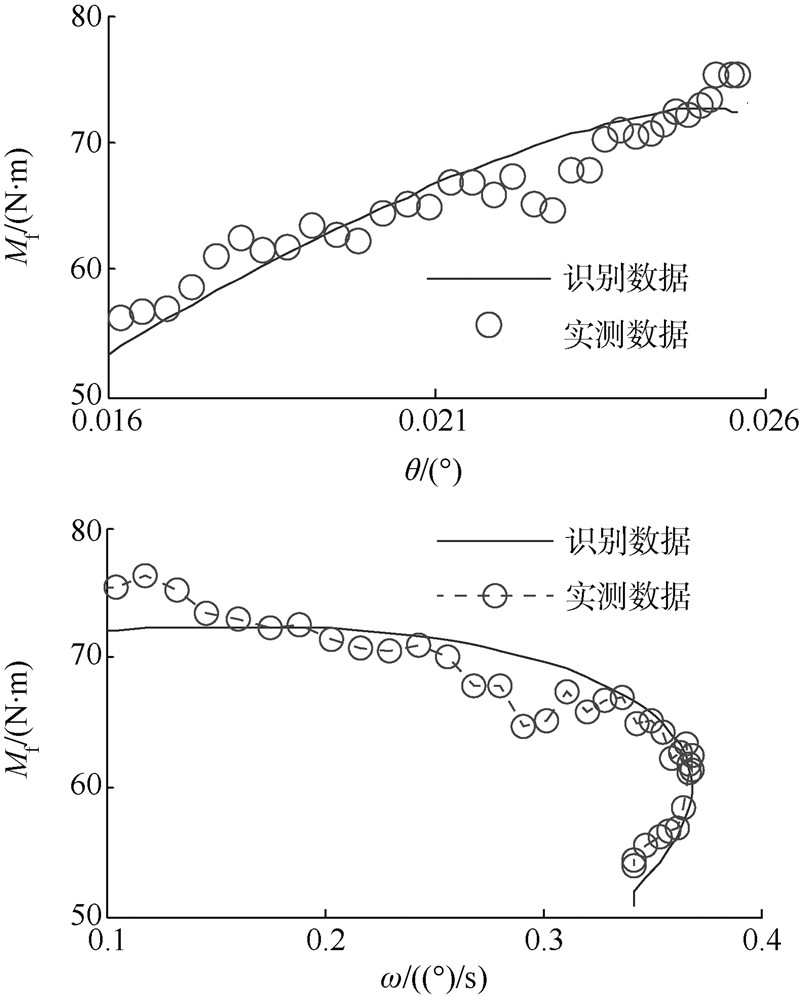 |
| 图 4 LuGre动力参数识别 Fig. 4 Identification of LuGre dynamic parameter |
由图 4可知,所辨识的参数可以在一定精度范围内模拟系统在小位移时的摩擦力,误差基本在5N·m范围内,满足系统精度要求.
至此,LuGre模型的所有参数均已获得,实际使用时只需将所测到的位移和速度实时代入摩擦公式,即可估计出当前的摩擦力. 3 摩擦补偿的具体实施
获得较精确的摩擦力Mf是实施摩擦补偿的第1步,为有效消除摩擦力的影响,还需采用一定的控制策略.
由图 2可知,摩擦力Mf经一定的反馈通道,反馈到比较点B处,对比较点B处的影响为
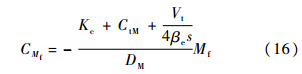
为消除摩擦力的影响,需在伺服阀的输入端叠加相应的信号,使摩擦力在B点的影响为0.根据结构不变性原理[15],可将摩擦力通过一定的控制器Gc引入到伺服阀的前端,如图 2所示虚线部分.
依据图 2,摩擦补偿控制器Gc应使摩擦力在B点的输出为-CMf,才能达到消除摩擦力的效果.由此可推导出摩擦补偿控制器:
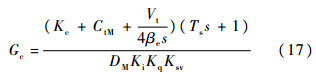
通过式(9)~式(11)以及式(17)即可实施摩擦的补偿,补偿实现前,式(17)中的部分参数可通过查看马达及伺服阀的技术手册获取,部分参数则通过系统开环运行方式进行识别.本系统中的相应控制参数如表 1所示.
| 参数 | 单位 | 值 |
| DM | m3/rad | 2.5×10-4 |
| βe | N/m2 | 6.9×108 |
| Ki | A/V | 0.004 |
| Kc+CtM | m5/(N·s) | 2.5×10-9 |
| Kq | m2/s | 0.04444 |
| Vt | m2 | 9.0×10-5 |
| Ksv | m/A | 3.75 |
| Ts | s | 0.0075 |
负载模拟器工作过程中,摩擦对系统的影响体现在多个方面.本节从位移伺服、力矩伺服、多余力控制等方面讨论摩擦补偿细节.具体实验时,所用到的关键实验设备如表 2所示.
| 设备名称 | 型号 | 作用 |
| 采集控制板卡 | 研华PCI 1716L | 力矩信号采集、伺服阀控制 |
| 计数卡 | 研华PCI 1784 | 角度传感器读数 |
| 角度传感器 | 雷尼绍RESM圆光栅 | 角度测量 |
| 扭矩传感器 | 长城计量TS3500 | 力矩测量 |
| 伺服阀 | 303所3Q-40 | 驱动摆动马达 |
| 伺服阀驱动器 | 609厂MKZ801F.14 | 伺服阀驱动电路 |
依摩擦模型可知,摩擦在高速时基本稳定,可用相对简单的线性化方法对其补偿,在低速时则表现为较强的非线性,补偿较复杂.为此,摩擦补偿验证时需寻找一种高速、低速都能兼顾,且对低速有局部描述能力的信号.在典型的输入信号中,正弦信号具备相应的性质.实际实施时,位移伺服采用幅值1°、频率0.5Hz的正弦信号对系统进行考核,图 5、图 6分别给出了摩擦补偿前、摩擦补偿后的位移伺服控制曲线.图 7则对摩擦补偿前后的位移伺服误差进行对比.
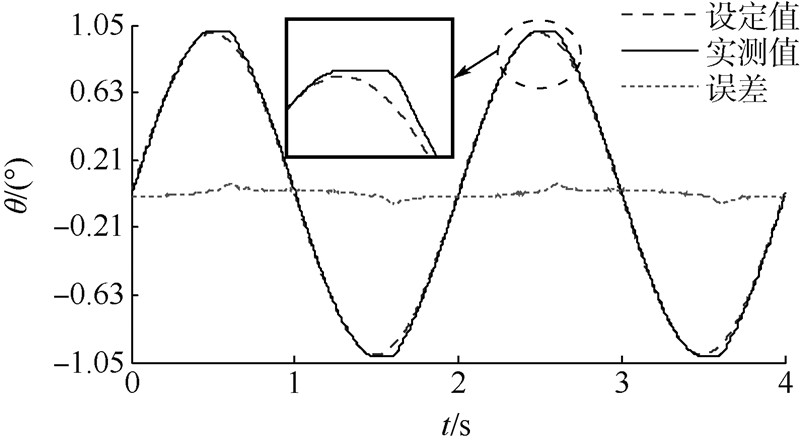 |
| 图 5 位移伺服摩擦补偿前控制曲线 Fig. 5 Displacement servo without friction compensation |
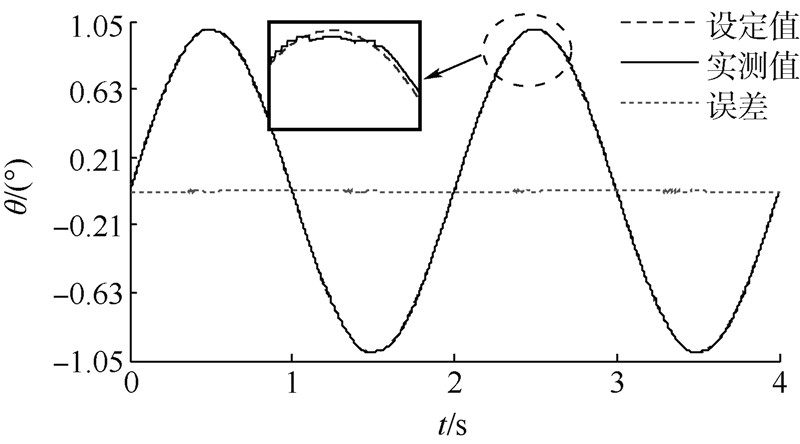 |
| 图 6 位移伺服摩擦补偿后控制曲线 Fig. 6 Displacement servo with friction compensation |
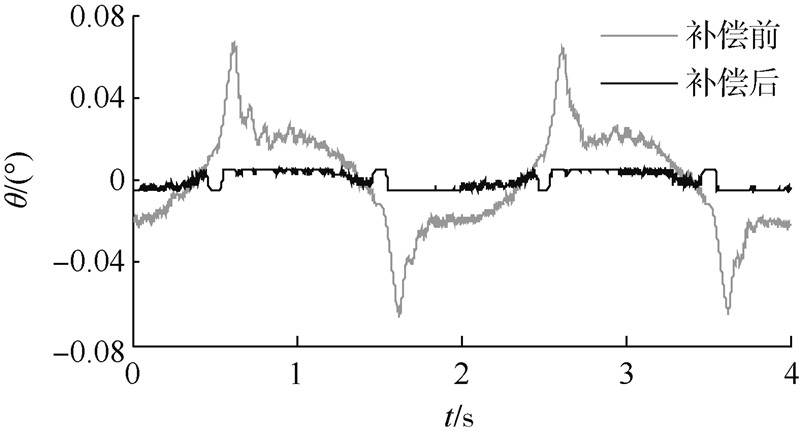 |
| 图 7 摩擦补偿前后位移伺服误差对比 Fig. 7 Servo displacement error comparison of the system without and with friction compensation |
由图 5可知,位移伺服过程中,跟踪误差最大点发生在位移的峰值部分,此时位移运行到幅值最大点,执行元件处于位移换向时刻,运行速度实现正负转换.对摩擦力而言,经历了动摩擦到静摩擦再到动摩擦的过程,摩擦幅值也在正负最大值内快速变化,相当于对整个系统控制产生阶跃干扰.此时,未考虑摩擦补偿时的控制信号在摩擦非线性变化时,无法快速适应,导致位移峰值处无法快速换向,从而产生平峰现象.图 6显示了摩擦力补偿后的效果,经摩擦前馈补偿后,控制信号可以依据当前摩擦力的大小实时变化,相当于在原控制信号上,又额外增加了一定的力来消除摩擦,从而加速位移信号的跟踪,大幅消除幅值平峰现象.图 7给出了补偿前后位移伺服误差,摩擦力补偿后,位移跟踪最大误差从补偿前的0.07°下降到0.01°,下降到原来的14.3%,下降幅度超过80%,误差的波动也大幅减小,验证了摩擦前馈对位移伺服控制有较好的补偿效果.
力矩伺服与位移伺服有所不同,力矩加载时,摩擦力始终反抗加载力矩,摩擦力的方向与加载力矩方向相反.因此,力矩的过零点即为摩擦力的过零点.在力矩的过零点位置,摩擦力在正负最大值内快速变化,对系统产生较强干扰.实际实验时,采用0.5Hz,1000N·m的正弦信号进行考核,摩擦补偿前和补偿后力矩伺服如图 8、图 9所示,补偿前后的力矩跟踪误差如图 10所示.
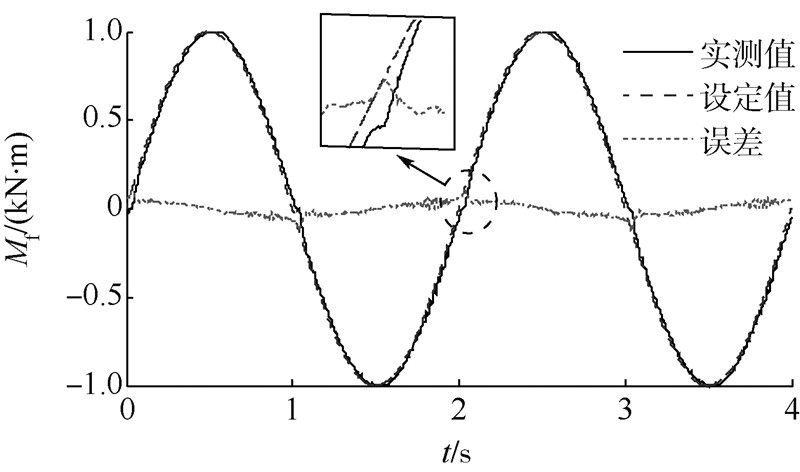 |
| 图 8 力矩伺服摩擦补偿前控制曲线 Fig. 8 Torque servo without friction compensation |
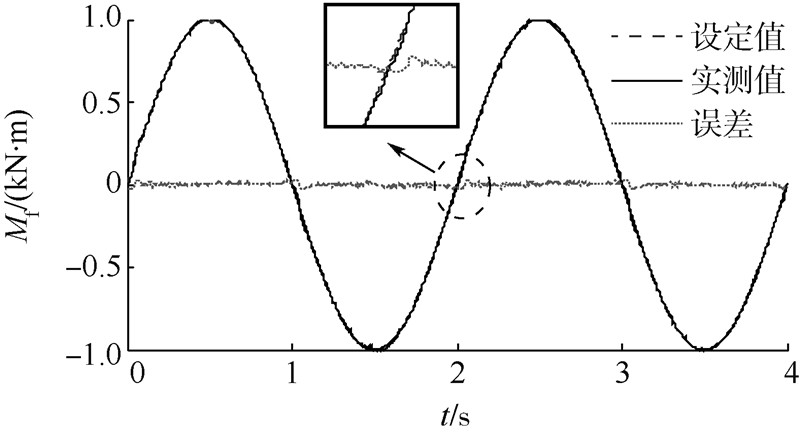 |
| 图 9 力矩伺服摩擦补偿后控制曲线 Fig. 9 Torque servo with friction compensation |
由图 8可知,在力矩过零点处,由于摩擦力的作用,力矩跟踪误差达到了最大值,其原因是原力矩控制算法,在力矩过零点时,无法有效适应摩擦力的非线性造成的.采用摩擦力补偿算法,可有效改善力矩控制性能,补偿后的力矩伺服如图 9所示,对比图 8和图 9可知,采用摩擦力矩补偿后,力矩伺服加载可以达到较好效果.图 10给出了力矩补偿前后的跟踪误差曲线,最大误差从补偿前的115N·m下降到补偿后的34N·m,下降幅度超过70%.
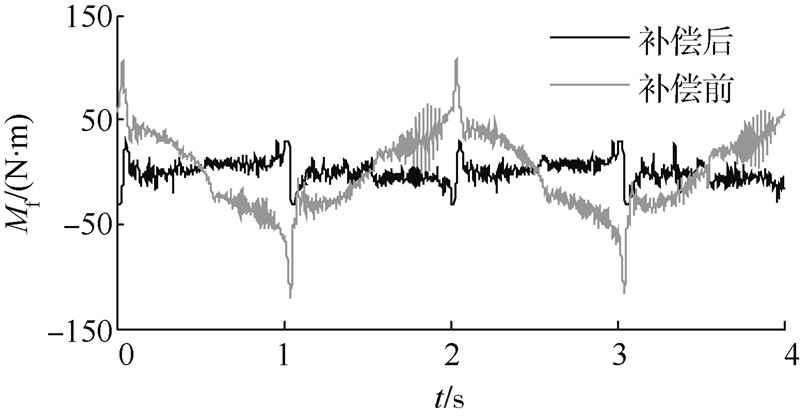 |
| 图 10 力矩伺服摩擦补偿前后误差对比 Fig. 10 Servo torque error comparison of the system without and with friction compensation |
在负载模拟器工作中,多余力[16]一直是用户关心的指标,常见的结构不变性原理虽然可以消除大部分的多余力,但由于结构不变性原理需要依据速度信号进行工作,被试件在换向瞬间速度信号达到最小,而摩擦力却达到最大,此时只采用结构不变原理,无法很好地消除因摩擦而造成的多余力.如果辅以摩擦力补偿,则能达到较好的消除效果.经被试件扫频测试,结构不变原理单独补偿和附加摩擦力补偿的多余力消除效果如图 11所示.图 11的补偿曲线反映了摩擦补偿在多余力消除中也具有一定的效果.
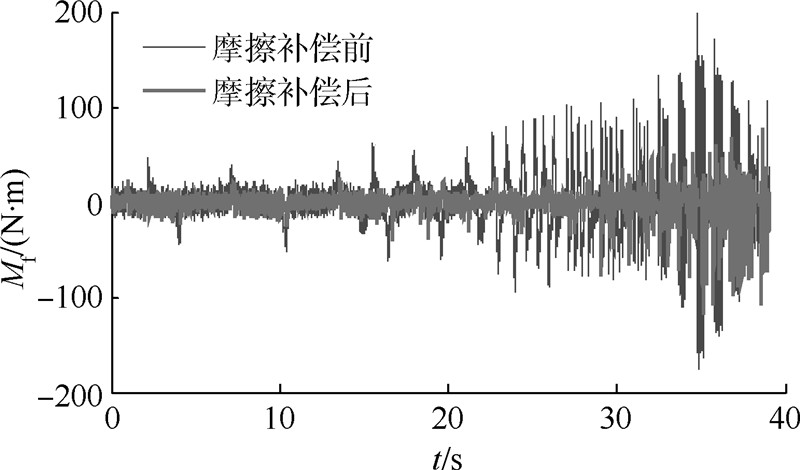 |
| 图 11 摩擦补偿在多余力消除时的效果 Fig. 11 Effect of surplus force elimination by friction compensation |
为提高电液负载模拟器的加载精度,重点讨论了摩擦补偿在电液负载模拟器加载中的应用.通过摩擦补偿过程和补偿实验的详细阐述可得如下结论:
1) 依据LuGre模型的特点,对模型进行简化处理,可分别辨识出模型的静力参数和动力参数.有效解决了LuGre模型参数不容易辨识的问题.通过辨识曲线可以看出所得出的辨识参数具有较高的准确性;
2) 通过分析和建立包含摩擦的系统模型,可为设计摩擦补偿控制器提供清晰的思路.在此基础上,利用结构不变性原理,可获得摩擦补偿具体控制模型和补偿流程;
3) 依据负载模拟器的任务,较全面地对摩擦补偿进行了实验验证,通过实验曲线,证明了摩擦补偿的有效性,可为类似应用提供一定的参考.
| [1] | 尚耀星,吴帅,焦宗夏,等.基于极限性能要求的电液负载模拟器多刚度与非线性复合数学模型[J].航空学报,2009,30(7):1331-1340 Shang Yaoxing,Wu Shuai,Jiao Zongxia,et al.Complex mathematical model of electro-hydraulic load simulator including multi-stiffness and nonlinear factors in ultimate performance research[J].Acta Aeronautica et Astronautica Sinica,2009,30(7):1331-1340(in Chinese) |
| Cited By in Cnki (12) | |
| [2] | 张彪.电液负载模拟器多余力矩抑制及其反步自适应控制研究[D].哈尔滨:哈尔滨工业大学,2009 Zhang Biao.Extra torque rejection and adaptive backstepping control of electro hydraulic load simulator[D].Harbin:Harbin Institute of Technology,2009(in Chinese) |
| Cited By in Cnki (23) | |
| [3] | 华清,焦宗夏,王晓东,等.电液负载模拟器的精确数学模型[J].机械工程学报,2002,38(11):31-35 Hua Qing,Jiao Zongxia,Wang Xiaodong,et al.Complex mathematical model of electro-hydraulic torque load simulator[J].Chinese Journal of Mechanical Engineering,2002,38(11):31-35(in Chinese) |
| Cited By in Cnki (38) | |
| [4] | 王晓东,焦宗夏,谢劭辰.基于LuGre模型的电液加载系统摩擦补偿[J].北京航空航天大学学报,2008,34(11):1254-1257 Wang Xiaodong,Jiao Zongxia,Xie Shaochen.LuGre-based compensation for friction in electro-hydraulic loading[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(11):1254- 1257( in Chinese) |
| Cited By in Cnki (12) | |
| [5] | 姚建勇,焦宗夏.改进型LuGre模型的负载模拟器摩擦补偿[J].北京航空航天大学学报,2010,36(7):812-820 Yao Jianyong,Jiao Zongxia.Friction compensation for hydraulic load simulator based on improved LuGre friction model[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(7):812-815(in Chinese) |
| Cited By in Cnki (20) | |
| [6] | 高俊霞,华清,焦宗夏.电液加载系统中的多余力及各种补偿方法的比较[J].液压气动与密封,2003(5):1-6 Gao Junxia,Hua Qing,Jiao Zongxia.Comparison of various compensation methods about surplus torque in electro-hydraulic loading system[J].Hycl Pneum & Seals,2003(5):1-6 (in Chinese) |
| Cited By in Cnki (22) | |
| [7] | 刘丽兰,刘宏昭,吴子英,等.机械系统中摩擦模型的研究进展[J].力学进展,2008,38(2):201-213 Liu Lilan,Liu Hongzhao,Wu Ziying,et al.An overview of friction models in mechanical[J].Advances in Mechanics,2008,38(2):201-213(in Chinese) |
| Cited By in Cnki (108) | |
| [8] | 向红标,裘祖荣,李型飞,等.精密实验平台的非线性摩擦建模与补偿[J].光学精密工程,2010,18(5):1119-1127 Xiang Hongbiao,Qiu Zurong,Li Xingfei,et al.Nonlinear friction modeling and compensation of high-precision experimental platforms[J].Opt Precision Eng,2010,18(5):1119-1127(in Chinese) |
| Cited By in Cnki (26) | |
| [9] | 孙洪鑫,王修勇,陈政清.基于改进遗传算法的LuGre模型参数辨识[J].武汉理工大学学报,2009,31(23):113-117 Sun Hongxin,Wang Xiuyong,Chen Zhengqing.Parameter identification of LuGre model with improved genetic algorithms[J].Journal of Wuhan University of Technology,2009,31(23):113-117(in Chinese) |
| Cited By in Cnki (9) | |
| [10] | 刘柏希.基于改进链码法的LuGre摩擦模型动态参数辨识[J].计算力学学报,2012,29(2):278-282 Liu Baixi.Parameters identification for LuGre friction model based on modified chain code recognition method[J].Chinese Journal of Computational Mechanics,2012,29(2):278-282(in Chinese) |
| Cited By in Cnki (2) | |
| [11] | Shang Y X,Jao Z X,Wang X D,et al.Study on friction torque loading with an electro-hydraulic load simulator[J].Chinese Journal of Aeronautics,2009,22(6):691-699 |
| Click to display the text | |
| [12] | 孙萌,李长春,延皓,等.多自由度伺服机构负载模拟系统动态特性研究[J].兵工学报,2013,34(3):378-384 Sun Meng,Li Changchun,Yan Hao,et al.Study on dynamic performance of multiple-DOF servo mechanism’s load simulator system[J].Journal of China Ordnance,2013,34(3):378-384(in Chinese) |
| Cited By in Cnki (3) | |
| [13] | 杨波,王俊奎.无人机舵面负载模拟系统的小脑模型控制[J].北京航空航天大学学报,2009,35(11):1361-1365 Yang Bo,Wang Junkui.CMAC neural network for the rudder dynam ic load smiulator of unmanned aerial vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(11):1361-1365(in Chinese) |
| Cited By in Cnki (4) | |
| [14] | 杨波,程龙.提高电动加载系统输出平滑的CMAC复合控制[J].北京航空航天大学学报,2013,39(6):723-727 Yang Bo,Cheng Long.Improving the output smoothing of the electric loading system based on the CMAC+PD compound control strategy[J].Beijing University of Aeronautics and Astronautics,2013,39(6):723-727(in Chinese) |
| Cited By in Cnki (2) | |
| [15] | 牛国臣,王巍,魏志强,等.基于力矩前馈和舵机角度补偿的力矩控制[J].北京航空航天大学学报,2013,39(3):300-304 Niu Guochen,Wang Wei,Wei Zhiqiang,et al.Torque control based on torque feedforward and rudder angle compensation[J].Beijing University of Aeronautics and Astronautics,2013,39(3):300-304(in Chinese) |
| Cited By in Cnki (3) | |
| [16] | 汪成文,焦宗夏,罗才瑾.基于改进的速度同步控制的电液负载模拟器[J].航空学报,2012,33(9):1717-1725 Wang Chengwen,Jiao Zongxia,Luo Caijin.An improved velocity synchronization control on electro-hydraulic load simulator[J].Acta Aeronautica et Astronautica Sinica,2012,33(9):1717-1725(in Chinese) |
| Cited By in Cnki (6) |


