表1(Table 1)
成形极限是板材成形中十分重要的性能指标和工艺参数,反映了变形过程中板材在塑性失稳状态前的最大变形程度,对于航空航天飞行器上的薄壁零件成形具有重要的指导意义,也是进行模具设计和工艺设计的主要依据.在板材成形性能评价方法中,成形极限曲线(FLC)应用最广泛且直观有效.
对成形极限进行的理论研究,概括起来分成以下两类:第1类是经典的分叉理论,如Swift分散性失稳理论[1]、Hill集中性失稳理论[2]和Stren和Rice的方法[3, 4];第2类是基于材料局部初始不均匀性是导致颈缩的假设,如M-K理论[5]等.其中,M-K理论应用最普遍,目前关于成形极限的理论研究绝大多数是建立在M-K理论的基础之上[6, 7, 8].它是以试验观察为基础而提出的,但是初始厚度不均度究竟如何确定并无准确的方法.因此,由于初始厚度不均值的不同,M-K理论与试验结果的符合程度难免具有一定的主观随意性.同时,M-K模型中关于集中颈缩时刻判定的准则也需要进一步讨论.
与FLC相比,利用韧性断裂准则预测板料成形极限的优点是可以更加方便地考虑应变路径的变化[9].到目前为止,多种不同的韧性断裂准则[10]被提出.近年来,韧性断裂准则被应用到双向拉伸[11]、液压成形[12]、拉深[13]等成形过程的成形极限预测.一般而言,金属板料的韧性越好,其断裂成形极限曲线FLCF(Forming Limit Curves at Fracture)越趋近于直线;韧性越差,则其FLCF形状越复杂[14].因此,目前所用的几种韧性断裂准则具有一定的局限性[15].
在本文中,为准确预测AA7075-O铝合金板材的成形极限图,将韧性断裂准则和传统M-K模型相结合,提出一种基于韧性断裂准则的修正M-K模型.利用单向拉伸模拟和试验相结合的方法,提取危险单元的应力应变历史并代入C-L韧性断裂准则中,得到材料常数.通过MATLAB编程得到修正M-K模型的初始厚度不均度.在常温下,以单向拉伸、宽板弯曲、液压胀形获得AA7075-O铝合金板材的成形极限试验点,与修正M-K模型和传统M-K模型计算得到的理论成形极限曲线进行对比,验证了修正M-K模型的可行性和准确性.
1 修正M-K模型建立 1.1 传统M-K假设传统M-K模型以凹槽假设为理论核心,认为板材具有不可避免的厚度不均性,这种不均性用凹槽表示,如图 1所示.根据假设,板材的集中性失稳是由板材表面初始存在的缺陷引起的.该模型广泛用于预测平面应力条件下的板材成形极限,理论假设包括以下几点[5].
 |
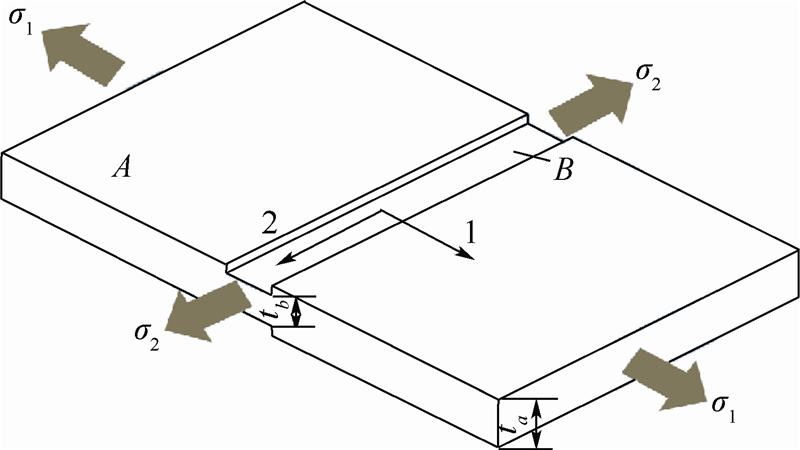| 图 1 M-K模型理论框架图 Fig. 1 Theoretical frame diagram of M-K model |
1) 简单加载条件:A区主应力及主应变均成比例增加且在整个变形过程中比值为常数;
2) 变形协调条件:B区第二主应变增量dε2b与A区第二主应变增量dε2a相等,即dε2a=dε2b=dε2;
3) 力平衡条件:A区与B区第一主方向力始终平衡,即F1a=F1b.
为考虑板材的厚向异性,在模型推导中采用Hill′48塑性屈服准则[16]:
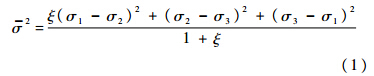
A区—变形安全区;B区—不均匀变形区;
ta,tb—变形过程中A,B区板材的厚度 1.2 韧性断裂准则根据应变能理论,材料的塑性变形程度可以用总塑性功来体现,其表达式[17]为
Cockcroft和Latham(C-L)等[17]考虑最大拉伸主应力在材料变形至断裂过程中的作用,提出如下公式:
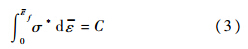
假设图 1中平面内应力主轴方向的主应力比值为α=σ2/σ1(0≤α≤1),G1=2ξ/(1+ξ),在平面应力状态下,则式(1)可表示为
等效应力与最大主应力方向的比值为
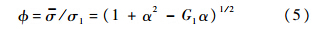
由Levy-Mises增量理论关系式,有
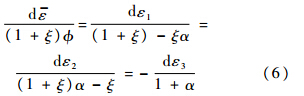
记ρ为面内应变比值,β为等效应变与第一主应变比值.分别表示如下:
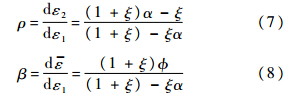
根据力平衡条件的理论假设,可得:
板材厚度法向方向的应变,即
可表示为
已知f0=tb0/ta0,可得变形过程中板材厚度不均度为
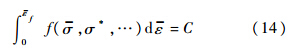
对B区进行判断,当
时,得到对应时刻的A区面内主应变ε1a,ε2a,作为相应α=σ2/σ1值下的成形极限点.对α=σ2/σ1在0≤α≤1范围内进行遍历,得到板材的成形极限曲线.
本文所用材料为1 mm厚的AA7075-O铝合金板材,对其进行单向拉伸试验以确定应力应变曲线,试件的几何尺寸如图 2所示.试验在北京航空航天大学的WDW-100电子万能试验机上进行(如图 3所示).
 |
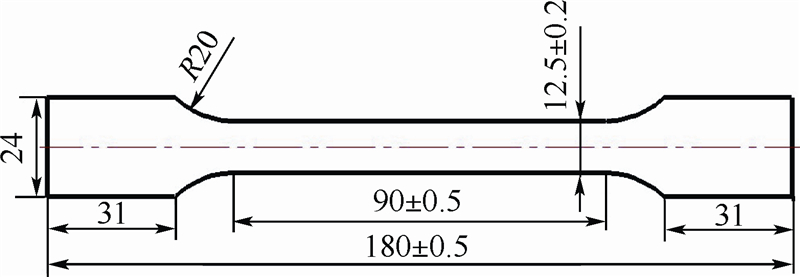| 图 2 AA7075-O铝合金单拉试样的几何形状及尺寸Fig. 2 Uniaxial tensile specimen geometry and dimension of AA7075-O aluminum alloy sheet |
 |
| 图 3 单向拉伸试验设备Fig. 3 Uniaxial tensile experimental equipment |
针对单拉试验数据,考虑各参数对AA7075-O铝合金板材力学性能的影响,对Swift模型进行修正,得到本构方程:
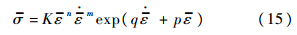
本构方程中的材料参数K,n,m,q,p通过拟合确定,同时计算得到板材厚向异性指数和弹性模量E,如表 1所示.在拉伸速率v=15 mm/min情况下,拟合得到应力应变曲线与试验结果对比如图 4所示,结果符合较好.
| 参数 | E/GPa | n | m | K/MPa | ξ | q | p |
| 数值 | 71 | 0.458 | 0.023 | 804 | 0.713 | 35.48 | 2.19 |
 |
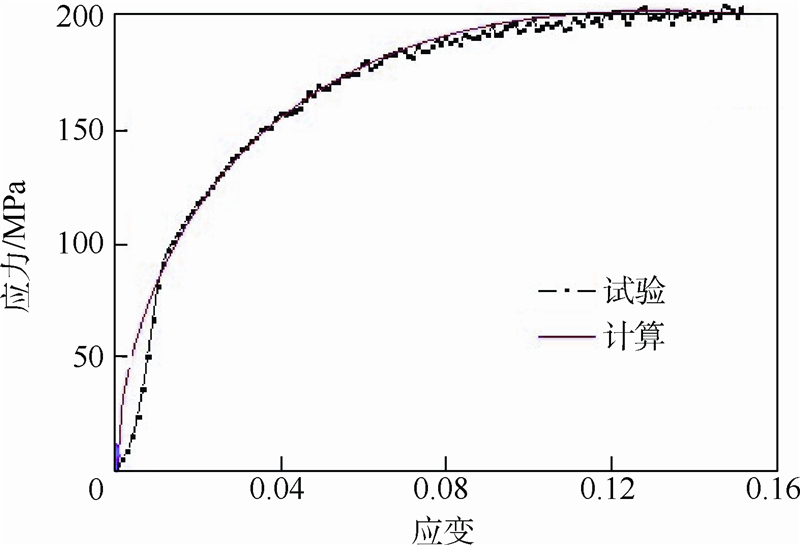| 图 4 拟合应力应变曲线与试验数据比较Fig. 4 Comparison of stress-strain curve between fitting and experimental data |
为确定韧性断裂准则中的材料常数,本文采用单向拉伸数值模拟和试验对比的方法.利用Abaqus/Explicit进行有限元分析,材料参数采用表 1中的数据.数值模拟得到试件的载荷-位移曲线,与试验得到的曲线对比结果如图 5所示,二者符合较好,该条件下的模拟参数可信.图 6为试件拉断时等效应变分布云图,将危险单元在变形过程中的应力应变历史代入C-L准则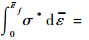
C, 可以得到材料常数C=192.43.
 |
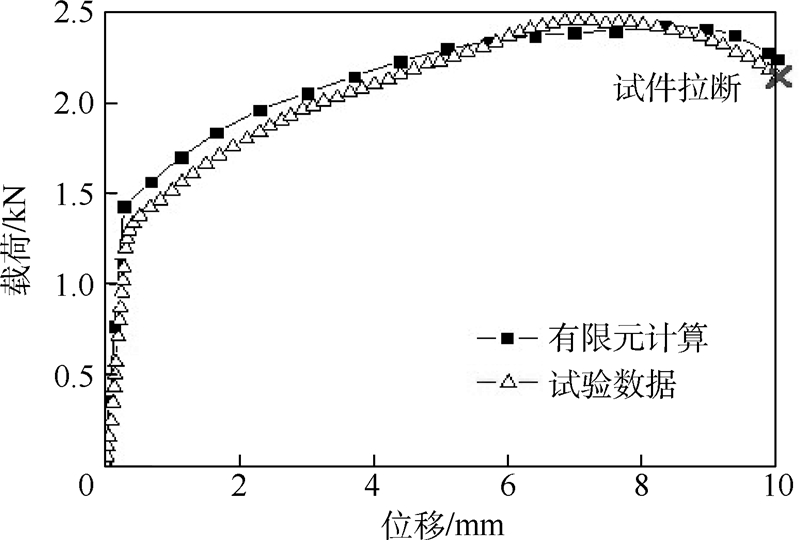| 图 5 有限元计算与试验得到的载荷-位移曲线对比Fig. 5 Comparison of loading-displacement curve between FEM and experimental data |
 |
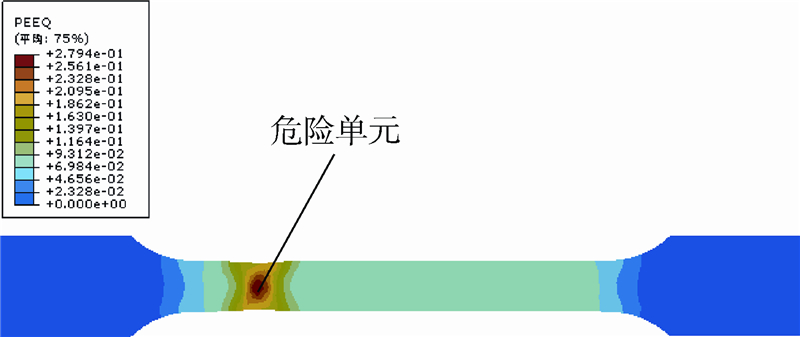| 图 6 临近拉断时刻等效塑性应变分布云图Fig. 6 Equivalent plastic strain distribution close to failure |
在修正M-K模型中,为确定初始厚度不均度值,利用MATLAB编程获得.流程如下:
1) 设定f0初值,遍历α=σ2/σ1(0≤α≤1),得到板材的理论成形极限曲线;
2) 比较单向拉伸试验所得成形极限点与理论成形极限曲线差值,差值为正,则增大f0值;差值为负,减小f0值;直至差值小于0.005为止;
利用该方法确定f0=0.955,并得到理论成形极限曲线.同时,利用单向拉伸、宽板弯曲、液压胀形试验得到AA7075-O铝合金板材在常温下的成形极限,试验件如图 7所示.
 |
| 图 7 单向拉伸、宽板弯曲、胀形试验件Fig. 7 Test pieces for uniaxial tensile,wide plate bending and hydrobulging |
图 8为利用修正的M-K模型及传统M-K模型分别得到的理论成形极限曲线与成形极限试验点的对比图.由图可知,与传统M-K模型相比,修正的M-K模型能更好地预测AA7075-O铝合金板材的成形极限曲线,与成形极限试验点贴合度更高.
 |
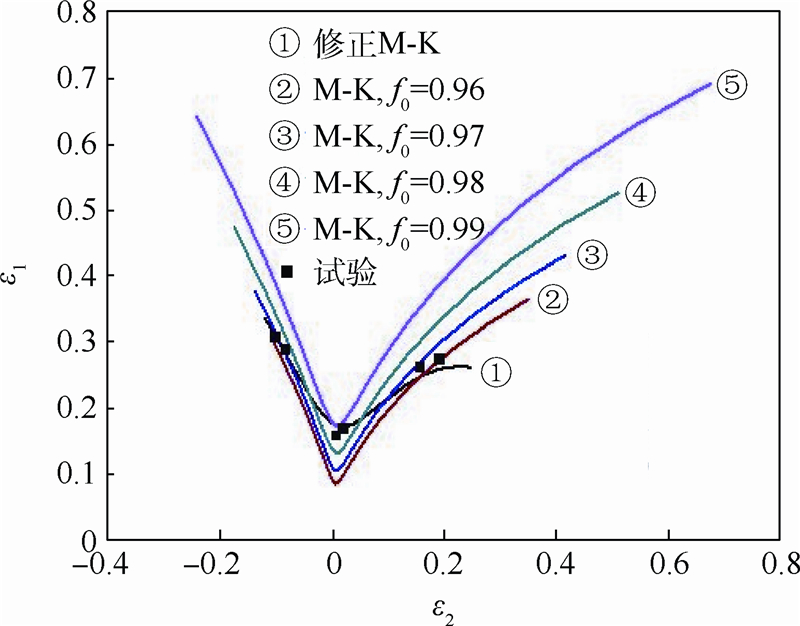| 图 8 成形极限对比图Fig. 8 Comparison of forming limit |
在传统M-K模型中,板材破裂失效时的判断准则为B区第一主应变增量Δε1b与A区第一主应变增量Δε1a的比值是常数,即,Δε1b/Δε1a=10.该判断准则表明Δε1b/Δε1a值与加载路径无关.同时,由修正M-K模型所得到的Δε1b/Δε1a值如图 9所示.从中可以看出,随着α从0到1遍历,Δε1b/Δε1a值先增大后减小.在α=0.5附近,该值达到极值.Δε1b/Δε1a值的变化趋势同样可以在成形极限图中得到反映.如图 8所示,f0=0.96时的传统M-K模型预测的成形极限曲线,在单向拉伸和双向拉伸点处与试验点接近;在平面应变处,远低于试验值.由此可知,只有通过提高平面应变加载路径下的Δε1b/Δε1a值作为判断准则,才能提高该处的成形极限值.修正M-K模型中Δε1b/Δε1a值的变化趋势与实际相符,表明以C-L韧性断裂准则能更加准确地反应A区凹槽的破坏,用于预测板材的成形极限曲线.
 |
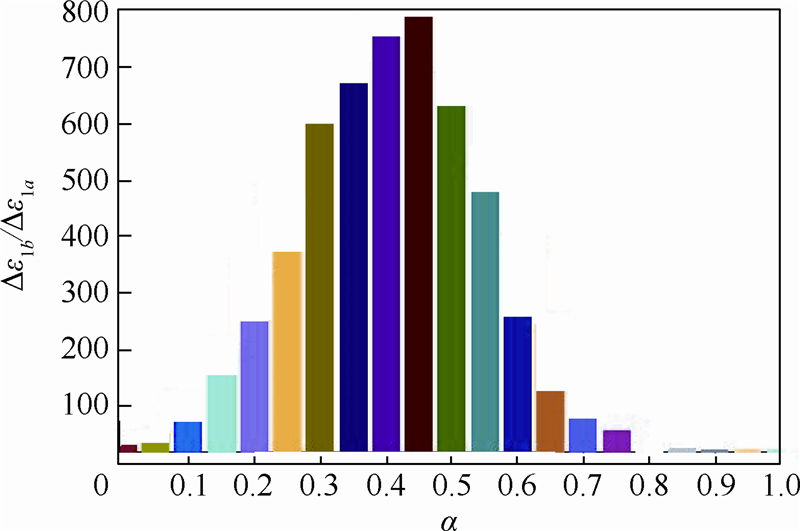| 图 9 α从0到1遍历下Δε1b/Δε1a值分布图Fig. 9 Distribution of Δε1b/Δε1a when α ranges from 0 to 1 |
本文将传统M-K模型框架和基于应变能的韧性断裂准则相结合,提出一种修正的M-K模型预测板材的成形极限曲线,并进行了数值计算和试验对比验证.
1) 利用单向拉伸数值模拟和试验相结合的方法,得到C-L韧性断裂准则中的材料常数.基于单向拉伸试验所得成形极限点,通过MATLAB编程得到修正M-K模型的初始厚度不均度.结果表明,针对同种规格板材及试验条件,材料常数及初始厚度不均度为定值.
2) 试验得到AA7075-O铝合金板材的成形极限,对比表明,M-K模型中A区凹槽破裂失效时的判断准则应修正为C-L韧性断裂准则,与试验符合程度更高,验证了本文提出的修正M-K模型的正确性.
| [1] | Swift H W. Plastic instability under plane stress[J].Journal of the Mechanics and Physics of Solid,1952,1(1):1-18. |
| Click to display the text | |
| [2] | Hill R. On discontinuous plastic states with special reference to localized necking in thin sheets[J].Journal of Mechanics and Physics of Solids,1952,1(1):19-31. |
| Click to display the text | |
| [3] | Stören S, Rice J.Localized necking in thin sheets[J].Journal of the Mechanics and Physics of Solid,1975,23(6):421-441. |
| Click to display the text | |
| [4] | Zhu X H, Weinmann K,Chandra A.A unified bifurcation analysis of sheet metal forming limits[J].Journal of Engineering Materials and Technology,2001,123(3):329-333. |
| Click to display the text | |
| [5] | Marciniak Z, Kuczynski K.Limit strains in the processes of stretch-forming sheet metal[J].International Journal of Mechanical Science,1967,9(3):609-620. |
| Click to display the text | |
| [6] | 杜平梅,郎利辉, 刘宝胜,等.基于M-K模型的成形极限预测及参数影响[J].塑性工程学报,2011,18(5):84-89. Du P M,Lang L H,Liu B S,et al.Theoretical prediction and parameter influence of FLDs based on M-K model[J].Journal of Plasticity Engineering,2011,18(5):84-89(in Chinese). |
| Cited By in Cnki (354) | |
| [7] | 马高山,万敏, 吴向东.基于M-K模型的铝锂合金热态下成形极限预测[J].中国有色金属学报,2008,18(6):980-984. Ma G S,Wan M,Wu X D.Theoretical prediction of FLDs for Al-Li alloy at elevated temperature based on M-K model[J].The Chinese Journal of Nonferrous Metals,2008,18(6):980-984(in Chinese). |
| Cited By in Cnki (288) | |
| [8] | Assempour A, Nejadkhaki H K,Hashemi R.Forming limit diagrams with the existence of through-thickness normal stress[J].Computational Materials Science,2010,48(3):504-508. |
| Click to display the text | |
| [9] | 陈劼实,周贤宾. 成形极限预测韧性断裂准则及屈服准则的影响[J].北京航空航天大学学报,2006,32(8):969-973. Chen J S,Zhou X B.Suitability of some ductile fracture criteria and yield criteria in forming limit prediction[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(8):969-973(in Chinese). |
| Cited By in Cnki (608) | |
| [10] | 谢延敏,于沪平, 陈军,等.板料成形中韧性断裂准则应用研究进展[J].工程设计学报,2007,14(1):6-10. Xie Y M,Yu H P,Chen J,et al.Recent advances of research on application of ductile fracture criteria in sheet metal forming process[J].Journal of Engineering Design,2007,14(1):6-10(in Chinese). |
| Cited By in Cnki (594) | |
| [11] | Takuda H, Mori K.Finite element analysis of limit strains in biaxial stretching of sheet metals allowing for ductile fracture[J].International Journal of Machine Tools and Manufacturing,2000,42(4):785-798. |
| Click to display the text | |
| [12] | Lei L P, Kim J.Bursting failure prediction in tube hydroforming process by using rigid-plastic FEM combined with ductile fracture criterion[J].International Journal of Mechanical Sciences,2002,44(7):1411-1428. |
| Click to display the text | |
| [13] | 高付海,桂良进, 范子杰.基于韧性准则的金属板料冲压成形断裂模拟[J].工程力学,2010,27(2):204-208. Gao F H,Gui L J,Fan Z J.Numerical simulation of the fracture in sheet metal stamping based on ductile criterion[J].Engineering Mechanics,2010,27(2):204-208(in Chinese). |
| Cited By in Cnki (395) | |
| [14] | Vallellano C, Morales D,Garcia-Lomas F J.A study to predict failure in biaxially stretched sheets of aluminum alloy 2024-T3[J].Materials and Manufacturing Processes,2008,23(3):303-310. |
| Click to display the text | |
| [15] | Jain M,Allin J, Lloyd D J.Fracture limit prediction using ductile fracture criteria for forming of an automotive aluminum sheet[J].International Journal of Mechanical Sciences,1999,41(10) :273-288. |
| Click to display the text | |
| [16] | Hill R. A theory of the yielding and plastic flow of anisotropic metals[C]//Proceedings of the Royal Society of London Series A.London:The Royal Society,1948:281-297. |
| Click to display the text | |
| [17] | Takuda H, Mori K,Hatta N.The application of some criteria for ductile fracture to the prediction of the forming limit of sheet metals[J].Journal of Materials Processing Technology,1999,95(1-3):116-121. |
| Click to display the text |
