与传统金属材料相比，碳纤维增强复合材料(Carbon Fiber Reinforced Polymer, CFRP)不仅具有优越的物理化学性能，如高比模量、高比强度、耐腐蚀、抗疲劳、易隐形、优良的化学稳定性，而且结构尺寸稳定和设计性好可以大面积整体成型^[1-2]。因其独特、卓越的性能，CFRP已广泛地应用于航天航空、国防军工和民用工业等各个领域，但是CFRP在制造和使用过程中可能造成结构损伤。损伤可能位于聚合物基体中或纤维本身，它们可能有黏结或螺纹连接的损伤^[3]。

针对常见的材料结构损伤对应有多种结构健康监测的无损检测方法，现代方法主要有超声、X线、红外成像和电涡流检测^[4-7]。然而这些方法均具有一定局限性。目前，利用碳纤维自传感特点及结构损伤电学敏感特性，电学阻抗检测方法以其非侵入、无辐射、响应快等优点在CFRP无损检测领域已逐步受到国内外学者的广泛关注^[8-9]。Baltopoulos等^[10]首先进行该领域的探究，能够通过电阻抗层析成像(Electrical Impedance Tomography, EIT)定位的缺陷的大小和位置，证明这种无损检测技术的可用性。范文茹等^[11]通过研究稀疏正则化算法进一步提高被测物体成像质量和边缘分辨率，仿真实验结果表明了该方法在不同噪声强度和电导率对比度下提高图像质量和实时性的有效性。Cagan^[12]用环形电极排布对真实CFRP损伤进行基本图像重建，对关键硬件部件进行可用性验证。

本文采用一种导电能力更强更均匀的嵌入式铜钉作为电极，结合改进的SpaRSA算法对碳纤维层合板常见结构损伤进行仿真研究。其次建立一套基于数字万用表的嵌入式16电极的电阻抗层析成像硬件系统。该系统主要包括传感器单元、数据采集与处理单元以及上位机图像重建单元。利用EIT系统检测平台对CFRP层合板单孔、双孔损伤的位置、大小进行检测，结果显示损伤材料图像重建效果良好，证明EIT方法在碳纤维增强复合材料结构损伤检测中的可行性。

1.   电阻抗层析成像原理

1.1   线性逼近与正问题

EIT图像重建的目的是利用边界电压V和注入电流I得到电导率σ。通过物理建模和有限元离散化，可以得到EIT的确定性观测模型为

式中：U(σ; I)为σ和I到V映射的正演模型；R(σ)为σ到电阻的映射模型。V=R(σ)I模型与电导率σ呈非线性关系，与电流I呈线性关系。在电导率变化较小的情况下，考虑线性化方程组，可以求解精度足够高的逆问题。

其中：δσ∈R^n×1为电导率变化量，n为重建图像中的像素数；σ₀为材料初始电导率；δU∈R^m×1为材料电导率改变导致的边界电压改变量，m为测量值数量；J∈R^m×n为Jacobian矩阵。

基于四端口网络的Geselowitz灵敏度定理^[13]，灵敏度图的快速计算方法为

式中：u(I^d)和u(I^e)分别为d次和e次驱动模式的电势分布；Ω_k为边界条件；σ_k为对应边界条件Ω_k的电导率变化。

1.2   反向重建算法及改进

EIT的逆问题是利用边界测量来估计未知介质分布。对复合材料结构进行损伤识别时，被测区域的介质往往存在不连续性，为了反映问题的稀疏性和改善图像重建质量，采用基于L1范数的稀疏正则化进行图像重建。

式中：δσ_reg为反向问题计算得到的电导率变化量；λ为正则化系数。

SpaRSA^[14]算法解决式(4)所示的最优化问题, 根据式(5)进行迭代获得一个估计值序列{δσ^t，t=0, 1, …, M}，其中M为算法设置的最大迭代次数。

式中：

然而，稀疏正则化的局限性在于解决问题的时间消耗。为了进一步提高稀疏正则化算法的计算速度，利用自适应步长和预处理技术，提出了一种基于可分逼近算法的改进方法。

式(5)中步长α_t是迭代全局收敛的关键，这里采用了一种ABB(Adaptive Barzilai-Borwein)方法^[15]，该方法使用类似信任区域的策略，从原始BB(Barzilai-Borwein)^[16]方法的2个备选方案中选择其步长，不需要对一般函数进行直线搜索，因此可以节省大量的计算工作量。当系统要求高精度或系数矩阵条件非常差时，ABB方法是一个很好的选择，α_t表达式为

式中：

其中:g_t=Jδσ^t－δU，r_t－1=δσ^t－δσ^t－1=－α_t－1·g_t－1，y_t－1=g_t－g_t－1，每次迭代只计算2个内积g_t^Tg_t和g_t－1^Tg_t－1。

另外，由于式(6)基于梯度法，灵敏度映射J的病态性导致SpaRSA算法收敛速度慢，利用右平滑预条件^[17]可以提高梯度法的性能，从而线性问题(2)可以写为

式中：W^-1为预处理器。那么，问题(4)的优化形式为

本文所研究的EIT稀疏正则化预处理的重点不仅在于提高图像的收敛速度，还在于提高图像的分辨率。因此本文提出了一种新的基于灵敏度映射的预处理器。

假设矩阵W是非奇异的，这意味着其有一个唯一且表现良好的W^-1，而保证W的非奇异性的最简单的方法是使其对角W=diag(ω_j)满足ω_j≠0。ω_j的一个有效选择是将每个像素中的总灵敏度标准化，即

问题(4)的优化可描述为J=J×W，δσ=W^-1×δσ。根据SpaRSA算法框架解决问题(10)，然后，用δσ=W×δσ给出原问题(4)的解。

2.   仿真实验

CFRP是一种多相材料，由导电的碳纤维和绝缘的树脂聚合物复合而成。其纤维方向具有较高的电导率，而垂直纤维方向和厚度方向由于纤维间的相互接触形成的导电率相对较低。因此，CFRP层合板有较强的各向异性，为简化EIT分析，将CFRP简化为单层均质连续各向异性材料。本文使用COMSOL软件以单层碳纤维(10 cm×10 cm×0.04 cm)为基础构建8层结构类型CFRP层合板正交([0°/90°]₄)模型，0°纤维电导率{1 000   0  0，0  10   0, 0   0   10}，90°纤维电导率为{10   0   0，0   1 000   0, 0   0   10}，如图 1所示。

图  1  正交型CFRP层合板模型

Figure  1.  Orthogonal CFRP laminate model

下载: 全尺寸图片 幻灯片

Todoroki等^[18]在自感CFRP表面镀铜电极，但由于CFRP材料有很强各向异性的电特性，因此当表面铜电极受到激励信号时，材料内部的电信号很微弱，这对材料内部损伤检测有较大影响。采用嵌入式电极不仅可以有效地克服材料各向异性，而且保持接触稳定，材料电极模型如图 2所示。

图  2  嵌入式电极的CFRP层合板模型

Figure  2.  CFRP laminate model of embedded electrode

下载: 全尺寸图片 幻灯片

结合碳纤维层合板常见结构损伤，构建3种材料损伤模型：

1) 冲击损伤模型，材料表面中心区域设置一个半径0.5 cm，高0.12 cm的圆锥体为冲击损伤，电导率改变量分别为50%(model 1)和20%(model 2)。

2) 分层损伤模型，在材料内部设置一个半径为0.5 cm，高为0.04 cm的圆柱体，电导率改变量为50%。

3) 裂纹损伤模型，设置横向裂缝尺寸为4 cm×0.2 cm×0.04 cm，电导率改变量为50%。图 3给出了3种损伤模型的截面图，获取相邻激励相邻测量模式下空场和满场电压差，选取被测材料厚度方向中心层XY截面计算灵敏度矩阵，利用Tikhonov、CG、SpaRSA和改进的算法MSpaRSA进行图像重建。

图  3  损伤模型图像重建

Figure  3.  Image reconstruction of damage model

下载: 全尺寸图片 幻灯片

引入相关系数r对重建图像质量进行评价：

式中：σ^*为电导率的真实分布矩阵；σ为计算值；σ^*为电导率真实分布的平均值；σ为平均计算值。

图 3给出了损伤模型不同算法的重建图像，对于表面不同程度的冲击损伤和内部损伤都有较好的重建图像；对于裂纹损伤，稀疏重构方法可探测出损伤的存在和大概位置，但形状和尺寸的失真较为严重。表 1给出了图 3中使用的不同算法重建图像的耗时。可以看出，MSpaRSA算法比SpaRSA算法的速度更快，这意味着稀疏重构的实时性得到了提高。表 2给出了图 3中使用不同算法重建图像的相关系数，对于材料的冲击损伤、分层损伤，稀疏重构方法能保持边缘分辨率，证明MSpaRSA算法可以进一步提高图像的质量。

表  1  不同算法的重建图像消耗时间

Table  1.  Reconstructed image consumption time of different algorithm  s

损伤类型	Tikhonov	CG	SpaRSA	MSpaRSA
冲击损伤model 1	0.712	0.492	0.051	0.047
冲击损伤model 2	0.665	0.451	0.065	0.047
分层损伤	0.688	0.438	0.062	0.056
裂纹损伤	0.685	0.460	0.085	0.052

下载: 导出CSV 

| 显示表格

表  2  不同算法的重建图像相关系数

Table  2.  Reconstructed image correlation coefficients of different algorithms

损伤类型	Tikhonov	CG	SpaRSA	MSpaRSA
冲击损伤model 1	0.405 9	0.352 0	0.829 0	0.952 3
冲击损伤model 2	0.418 1	0.353 9	0.700 3	0.929 8
分层损伤	0.403 2	0.332 8	0.825 2	0.926 8
裂纹损伤	0.069 6	0.119 4	0.200 0	0.462 5

下载: 导出CSV 

| 显示表格

3.   实验验证

3.1   测试对象

CFRP中的碳纤维具有良好的导电性，当材料有损伤时将引起层合板对应位置发生电导率变化，因此利用碳纤维自传感特点及结构损伤电学敏感特性对材料进行检测。

实验选用正交型CFRP层合板进行常见损伤检测，材料尺寸为10 cm×10 cm，厚度为0.3 cm。如图 4所示，在CFRP四周边缘等间距布置16个电极，电极用铜钉代替嵌入式穿过层合板，并使用导电银胶(conduction凯特森，广州楷翔电子产品有限公司)将铜钉与层合板孔的间隙黏结，改善了铜钉与复合材料的连接，即使铜钉出现小的松动，电连接仍保持稳定。这些电极被连接到多路电流注入和电压测量的多路复用器上。

图  4  分布16个嵌入式电极的CFRP层合板

Figure  4.  CFRP laminated plates with sixteen embedded electrodes

下载: 全尺寸图片 幻灯片

3.2   测试系统结构

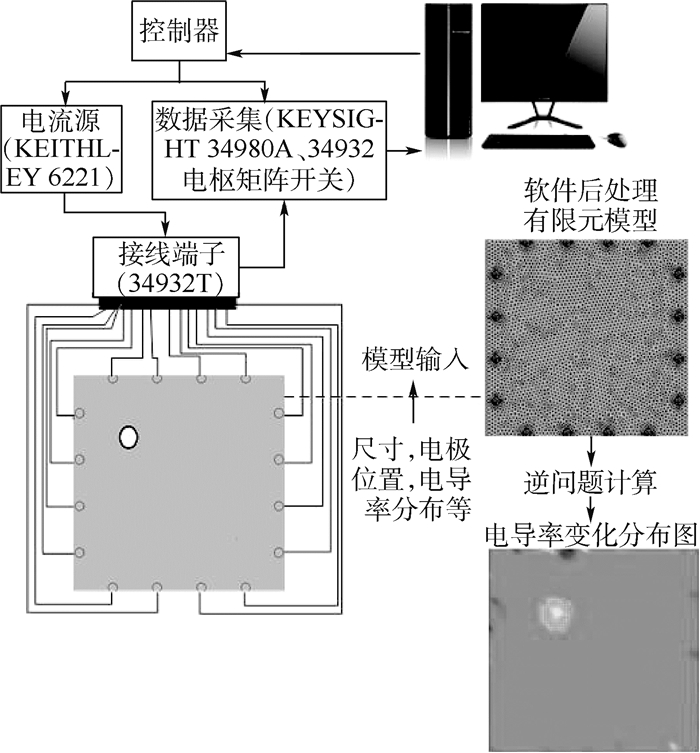
为检测CFRP材料损伤，开发了一套基于数字万用表的嵌入式16电极的EIT硬件系统。图 5显示了EIT系统结构。工作站基于LabVIEW开发的系统软件根据一定的测量协议进行开关量的切换驱动和测量通道的导通断开，实现对外部电流源激励输入和万用表数据采集的控制，其次用接线端子连接被测材料与测量设备。该实验测试中，选用相邻电极激励和相邻电极测量模式，共有16组相邻电极对，当电流激励一组电极时，依次测量与电流激励无关的余下的13组电极对间的电压值，循环激励循环测量最终共测得13×16=208个边界电压值。实验分别测量2组电压值(损伤发生前后)。根据电学成像重建原理，通过COMSOL软件建立有限元模型，计算灵敏度矩阵，利用重建算法反演得到电导率变化分布图。

图  5  EIT系统结构及处理部分

Figure  5.  Structure and processing part of EIT system

下载: 全尺寸图片 幻灯片

本文使用的实验设备如图 6所示，控制器为HP工作站Z238。驱动电流由吉时利KEITHLEY6221电流源产生，为直流100 mA的电流信号。输入输出信号控制由KEYSIGHT 34932电枢矩阵开关模块组成，驱动测量通道开关选通时序由上位机LabVIEW编程实现。数据测量是由KEYSIGHT 34980A多功能开关/测量单元内置数字万用表来完成，该仪器可通过以太网实现远程访问和控制。

图  6  搭建的EIT硬件系统和测试材料

Figure  6.  Established EIT hardware system and testing materials

下载: 全尺寸图片 幻灯片

3.3   损伤材料检测

在评估EIT检测实际损伤的初始研究阶段，最好从简单的CFRP层合板损伤开始。本实验通过钻孔来代替CFRP层合板的损伤形式，钻孔会导致导电碳纤维的断裂，材料对应位置电导率分布发生变化，通激励电流该区域电势分布也会随之发生改变。如图 7所示，在CFRP上钻取一个6 mm的圆孔作为损伤，占材料板总面积的0.44%，通过电阻抗成像数据采集试验件损伤前后的各相邻电极间的边界电压值，利用MATLAB (R2014b，MathWorks^®)对EIT逆问题计算，获得电导率变化分布图像。

图  7  CFRP单孔损伤形式重建结果

Figure  7.  Reconstruction results of CFRP single hole damage form

下载: 全尺寸图片 幻灯片

为了验证改进的基于L1稀疏正则化MSpaRSA算法对CFRP层合板损伤图像重建的稀疏性优势，将其与Tikhonov正则化、CG算法和SpaRSA算法作对比。图 7显示出4种不同算法的材料损伤图像重构图，其中小圆圈标记为真实损伤在CFRP层合板的位置。可以清楚地看出，4种算法均可有效地重构出损伤图像，且与真实损伤定位一致，但MSpaRSA算法损伤重建图像的边缘稀疏性较好，伪影较少，有效改进了重构图像质量，提高了物体边缘的空间分辨率，而Tikhonov正则化和CG算法重建的图像较为模糊。

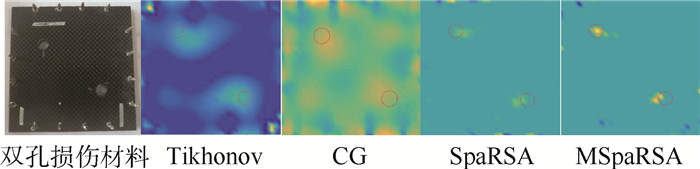
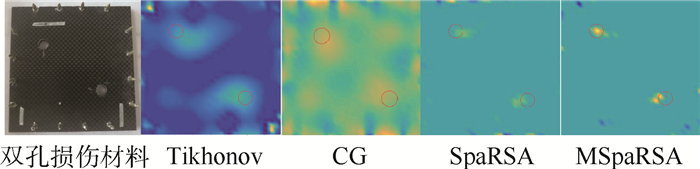
此外，为进一步研究EIT方法对CFRP层合板损伤检测能力，利用相同的原理及方法，对双孔损伤形式进行图像重建。如图 8所示，在方形CFRP层合板对角钻取2个8 mm通孔时，占材料板总面积的1.6%，通过EIT系统采集试验件损伤前后的2组边界电压值，4种不同算法依旧能够重建得到CFRP层合板双孔损伤的图像重构图，与其他算法相比，MSpaRSA算法重建图像中的边界稀疏性较好，干扰信息明显较少，但显示出的图像重建损伤区域与真实的CFRP层合板损伤位置有一定的偏移。这种现象在CFRP单孔损伤的图像重构图中是不存在的，说明当有多个损伤存在时，它们相互影响使重构的损伤位置发生偏移。

图  8  CFRP双孔损伤形式重建结果

Figure  8.  Reconstruction results of CFRP double hole damage form

下载: 全尺寸图片 幻灯片

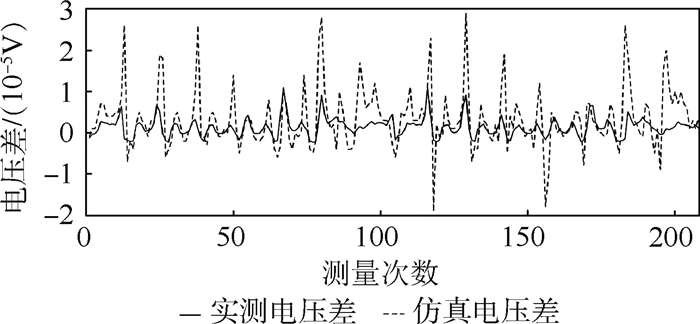
重复测量边界电压，图 9显示了仿真和实测的差分电压(损伤状态和非损伤状态之间的边界电压差)的差别，其中为了清晰起见，描述了208次的测量数据。其中最高的边界电压差幅值对应于损伤附近的测量值，峰值大小受不均匀导电性(损伤)的位置和尺寸以及电极阻抗的影响。实测和仿真的差分电压变化基本一致，验证了简化CFRP层合板为连续均质各向异性材料模型的适用性。

图  9  双孔损伤测量与仿真电压差值的对比

Figure  9.  Comparison of double hole damage measurement and simulation voltage difference

下载: 全尺寸图片 幻灯片

4.   结论

本文结合CERP的常见损伤、阻抗分布等先验知识，进一步研究稀疏正则化的图像重建算法，提高成像速度和图像分辨率，结合硬件系统对复合材料结构损伤检测的可行性进行验证。实验结果表明：

1) 采用改进的基于L1范数稀疏正则化MSpaRSA算法进行电导率变化图像重建，能够有效地增强边缘分辨率减少伪影，帮助提高损伤检测的精度。

2) EIT系统对实际单孔、双孔损伤的CFRP层合板能获得较好的图像重建效果，证明该系统用于CFRP层合板损伤检测的可行性。