Solution method of fractional moments involved in probability density estimation of structural output response
-
摘要:
鉴于概率不确定性背景下基于分数矩极大熵准则的结构可靠性分析方法具有较大的效率与精度优势,综合研究并给出了可以用于极大熵准则中约束条件输出响应分数矩求解的3种分数矩求解方法,包括降维积分(DRI)方法、稀疏网格积分(SGI)方法和无迹变换(UT)方法。阐述了分数矩求解原理及过程,给出了方法的计算效率,并分析了方法的适用性。3种分数矩求解方法在确保计算精度的同时可以很大程度减少结构输入-输出模型的调用次数,大幅提高统计分析效率。通过与Monte Carlo仿真分析法对比,验证了3种分数矩求解方法的正确性与高效性。
-
关键词:
- 极大熵准则 /
- 分数矩 /
- 降维积分(DRI) /
- 稀疏网格积分(SGI) /
- 无迹变换(UT)
Abstract:For the fact that the fractional moment based principle of maximum entropy for structural reliability analysis has some advantages in computational efficiency and precision, in this paper, three computational methods for accurately estimating the fractional moments of constraint condition output response involved in the principle of maximum entropy, are studied and presented, including the dimension reduction integration (DRI) method, the sparse gird integration (SGI) method and the unscented transformation (UT) method. The computational theory and process are expounded, the calculation efficiency of each method is given, and the applicability of each method is analyzed in the paper. The presented three methods can greatly reduce the number of structural input-output model estimates and ensure the accuracy of calculation at the same time, so the efficiency of statistical analysis can be greatly improved. Besides, compared with the Monte Carlo simulation method, the accuracy and efficiency of the presented methods are verified according to the applied examples.
-
表 1 一元函数分数矩计算的高斯积分表达式[19]
Table 1. Gauss integral expression of one-variable function fractional moment computation[19]
分布类型 积分区域 高斯积分准则 数值积分表达式 均匀 [a, b] 高斯-
勒让德
正态 (-∞, +∞) 高斯-
埃尔米特
对数正态 (0, +∞) 高斯-
埃尔米特
指数 (0, +∞) 高斯-
拉盖尔
威布尔 (0, +∞) 高斯-
拉盖尔
积分准则 积分权重与点 j=1 j=2 j=3 j=4 j=5 高斯-埃尔米特 wj 1.13×10-2 0.222 1 0.533 3 0.222 1 1.13×10-2 zj -2.857 0 -1.355 6 0 1.355 6 2.857 0 高斯-勒让德 wj 0.236 9 0.478 6 0.568 9 0.478 6 0.236 9 zj -0.906 2 -0.538 5 0 0.538 5 0.906 2 高斯-拉盖尔 wj 0.521 8 0.398 7 7.59×10-2 3.61×10-3 2.34×10-5 zj 0.263 6 1.413 4 3.596 4 7.085 8 12.641 输入变量 均值 误差因子 X1 2 2.0 X2 3 2.0 X3 1×10-3 2.0 X4 2×10-3 2.0 X5 4×10-3 2.0 X6 5×10-3 2.0 X7 3×10-3 2.0 注:误差因子表征对数正态分布的分散程度。 表 4 数值算例分数矩计算结果
Table 4. Calculation results of fractional moments of numerical example
α DRI SGI(k=2) UT SGI(k=3) Monte Carlo -0.3 13.228 13.228 13.825 13.243 13.208 -0.05 1.535 1.535 1.543 1.535 1.535 0.62 5.217×10-3 5.171×10-3 5.146×10-3 5.204×10-3 5.209×10-3 1.3 1.856×10-5 1.743×10-5 1.859×10-5 1.838×10-5 1.849×10-5 1 2.197×10-4 2.131×10-4 2.190×10-4 2.186×10-4 2.190×10-4 2 6.407×10-8 5.202×10-8 6.265×10-8 6.142×10-8 6.445×10-8 3 2.449×10-11 1.313×10-11 1.386×10-11 2.008×10-11 2.640×10-11 Ncall 36 15 15 113 104 表 5 十杆桁架结构输入变量信息
Table 5. Input variable information of ten-bar truss structure
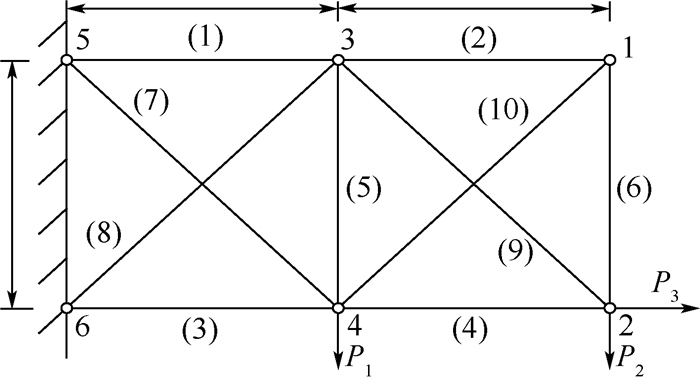
输入变量 均值 变异系数 Ai/m2 0.001 0.15 E/GPa 100 0.05 L/m 1 0.05 P1/kN 80 0.05 P2/kN 10 0.05 P3/kN 10 0.05 表 6 十杆桁架结构分数矩计算结果
Table 6. Calculation results of fractional moments of ten-bar truss structure
方法 分数矩 Ncall d=-1.5 d=-0.47 d=0.08 d=1.8 d=2.5 DRI 0.787 4 0.925 0 1.013 7 1.382 8 1.585 6 61 SGI(k=2) 0.786 1 0.924 8 1.013 7 1.383 0 1.585 6 31 UT 0.792 9 0.926 3 1.013 5 1.382 1 1.586 9 31 Monte Carlo 0.786 3 0.924 6 1.013 7 1.384 0 1.587 2 104 -
[1] 王晓军, 杨海峰, 邱志平, 等.基于测量数据的不确定性结构分析的模糊理论[J].北京航空航天大学学报, 2010, 36(8):887-891. http://bhxb.buaa.edu.cn/CN/abstract/abstract8404.shtmlWANG X J, YANG H F, QIU Z P, et al.Fuzzy theory for uncertain structural analysis based on measurement data[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(8):887-891(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract8404.shtml [2] WANG X J, WANG L, ELISHAKOFF I, et al.Probability and convexity concepts are not antagonistic[J].Acta Mechanica, 2011, 219(1-2):45-64. doi: 10.1007/s00707-010-0440-4 [3] QIU Z P, WANG L.The need for introduction of non-probabilistic interval conceptions into structural analysis and design[J].Science China-Physics, Mechanics & Astronomy, 2016, 59(11):114632. doi: 10.1007%2Fs11433-016-0329-3 [4] ZHAO Y G, ONO T.A general procedure for first/second-order reliability method (FORM/SORM)[J].Structural Safety, 1999, 21(2):95-112. doi: 10.1016/S0167-4730(99)00008-9 [5] KIUREGHIAN A D.The geometry of random vibrations and solutions by FORM and SORM[J].Probabilistic Engineering Mechanics, 2000, 15(1):81-90. https://www.sciencedirect.com/science/article/pii/S0266892099000119 [6] 吕震宙, 宋述芳, 李洪双, 等.结构机构可靠性及可靠性灵敏度分析[M].北京:科学出版社, 2009.LU Z Z, SONG S F, LI H S, et al.Reliability and reliability sensitivity analysis of structural and mechanism[M].Beijing:Science Press, 2009(in Chinese). [7] MELCHERS R E.Importance sampling in structural system[J].Structural Safety, 1989, 6(1):3-10. doi: 10.1016/0167-4730(89)90003-9 [8] ZHANG L G, LU Z Z, WANG P.Efficient structural reliability analysis method based on advanced Kriging model[J].Applied Mathematical Modelling, 2015, 39(2):781-793. doi: 10.1016/j.apm.2014.07.008 [9] ROCCO C, MORENO J.Fast Monte Carlo reliability evaluation using support vector machine[J].Reliability Engineering and System Safety, 2002, 76(3):237-243. doi: 10.1016/S0951-8320(02)00015-7 [10] JAYNES E.Information theory and statistical mechanics[J].Physical Review, 1957, 108(2):171-190. doi: 10.1103/PhysRev.108.171 [11] INVERARDI P, TAGLIANI A.Maximum entropy density estimation from fractional moments[J].Communications in Statistics-Theory and Methods, 2003, 32(2):327-345. doi: 10.1081/STA-120018189 [12] ZHANG X F, PANDEY M D.Structural reliability analysis based on the concepts of entropy, fractional moment and dimensional reduction method[J].Structural Safety, 2013, 43:28-40. doi: 10.1016/j.strusafe.2013.03.001 [13] ZHANG L G, LU Z Z, CHENG L, et al.A new method for eva-luating Borgonovo moment-independent importance measure with its application in an aircraft structure[J].Reliability Engineering and System Safety, 2014, 132:163-175. doi: 10.1016/j.ress.2014.07.011 [14] 张磊刚, 吕震宙, 陈军.基于失效概率的矩独立重要性测度的高效算法[J].航空学报, 2014, 35(8):2199-2206. http://www.cnki.com.cn/Article/CJFDTotal-HKXB201408013.htmZHANG L G, LU Z Z, CHEN J.An efficient method for failure probability-based moment-independent importance measure[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(8):2199-2206(in Chinese). http://www.cnki.com.cn/Article/CJFDTotal-HKXB201408013.htm [15] LI B Y, ZHANG L G, ZHU X J, et al.Reliability analysis based on a novel density estimation method for structures with correlations[J].Chinese Journal of Aeronautics, 2017, 30(3):1021-1030. doi: 10.1016/j.cja.2017.04.005 [16] 郭健彬, 曾声奎, 陈云霞.稳健协同优化方法的改进和应用[J].火力与指挥控制, 2010, 35(4):32-35. http://www.cnki.com.cn/Article/CJFDTOTAL-TRYS200404000.htmGUO J B, ZENG S K, CHEN Y X.Improvement and application of multidisciplinary robust design optimization method[J].Fire Control and Command Control, 2010, 35(4):32-35(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-TRYS200404000.htm [17] GUO J B, ZHAO Z T, ZHAO J Y, et al.Integral robust design method based on maximum tolerance region[J].Journal of Donghua University, 2014, 31(6):737-740. doi: 10.1007/s00170-012-4550-0?view=classic [18] LI G, ROSENTHAL C, RABITZ H.High dimensional model representations[J].Journal of Physical Chemistry, 2001, 105(33):7756-7777. doi: 10.1021/jp010450t [19] 张旭方, PANDEY M D, 张义民.结构随机响应计算的一种数值方法[J].中国科学:技术科学, 2012, 42(1):103-114. http://mall.cnki.net/magazine/article/JSJG201005014.htmZHANG X F, PANDEY M D, ZHANG Y M.A numerical method for calculating the random response of structures[J].Scientia Sinica Technologica, 2012, 42(1):103-114(in Chinese). http://mall.cnki.net/magazine/article/JSJG201005014.htm [20] 张磊刚. 不确定性结构的局部和矩独立灵敏度方法研究[D]. 西安: 西北工业大学, 2015.ZHANG L G. Study of local and moment-independent sensitivity analysis method for structures with uncertainty[D]. Xi'an: Northwestern Polytechnical University, 2015(in Chinese). [21] SMOLYAK S A.Quadrature and interpolation formulas for tensor products of certain classes of functions[J].Soviet Mathematics Doklady, 1963, 4:240-243. http://citeseerx.ist.psu.edu/showciting?cid=1618151&start=10 [22] GERSTNER T, GRIEBEL M.Numerical integration using sparse grids[J].Number Algorithms, 1998, 18(3-4):209-232. doi: 10.1023%2FA%3A1019129717644.pdf [23] ZHANG L G, LU Z Z, CHENG L, et al.Moment-independent regional sensitivity analysis of the complicated models with great efficiency[J].International Journal for Numerical Methods in Engineering, 2015, 103(13):996-1014. doi: 10.1002/nme.v103.13 [24] JULIER S J, UHLMANN J K.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE, 2004, 92(3):401-422. doi: 10.1109/JPROC.2003.823141 [25] 张勇刚, 费玉龙, 武哲民, 等.一种高阶无迹卡尔曼滤波方法[J].自动化学报, 2014, 40(5):838-848. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zdhxb201405006ZHANG Y G, FEI Y L, WU Z M, et al.A high order unscented Kalman filtering method[J].Acta Automatica Sinica, 2014, 40(5):838-848(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zdhxb201405006 [26] IMAN R L.A matrix-based approach to uncertainty and sensitivity analysis for fault tree[J].Risk Analysis, 1987, 7(1):21-33. doi: 10.1111/risk.1987.7.issue-1 -







 下载:
下载: