-
摘要:
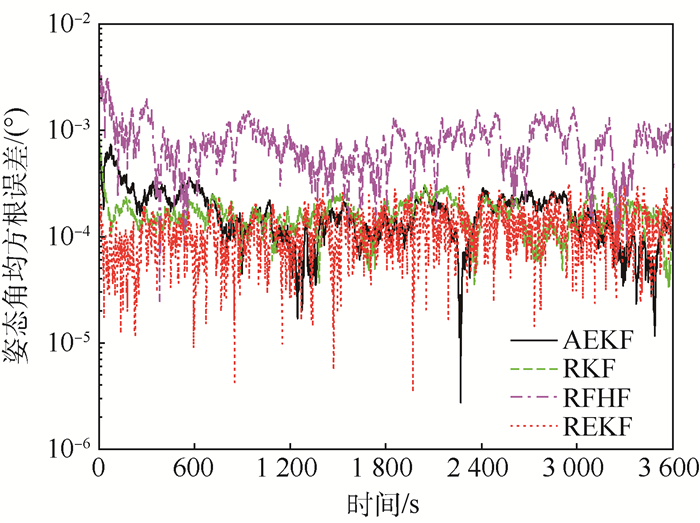
针对小视场（NFOV）星敏感器用于姿态估计时存在的量测延时情况，提出了一种用于解决量测延时的鲁棒扩展卡尔曼滤波（REKF）算法。根据最小方差准则的思想求解各方差的最小上界，通过最小上界确定滤波增益，设计的REKF算法可以有效解决量测延时问题，提高了姿态估计的精度。对REKF算法进行了仿真验证，结果表明：该算法优于常规加性扩展卡尔曼滤波（AEKF）算法、鲁棒有界时域滤波（RFHF）算法及鲁棒卡尔曼滤波（RKF）算法，能较好解决非线性系统存在的量测延时问题，验证了该算法的有效性。
-
关键词:
- 小视场(NFOV)星敏感器 /
- 姿态估计 /
- 扩展卡尔曼滤波(EKF) /
- 鲁棒滤波 /
- 量测延时
Abstract:Aimed at measurement delay in the narrow field of view (NFOV) star sensor used for attitude estimation, a robust extended Kalman filter (REKF) algorithm is proposed to solve the measurement delay. According to the minimum mean square error criterion, the minimum upper bound of the variance is solved and the filter gain is determined by the minimum upper bound. The designed REKF algorithm can effectively solve the problem of measurement delay and improve the accuracy of attitude estimation. Finally, the simulation results show that the algorithm is superior to the conventional additive robust extended Kalman filter (AEKF), robust finite-horizon filter (RFHF) and robust Kalman filter (RKF) algorithm, which can better solve the problem of measurement delay in nonlinear systems, and the effectiveness of the algorithm is verified.
-
图 1 情况1时姿态角均方根误差对比
Figure 1. Comparison of root mean square error of attitude angle in Case 1
-
[1] XIONG K, WEI C L, LIU L D.Robust extended Kalman filtering for nonlinear systems with stochastic uncertainties[J].IEEE Transactions on Systems, Man, and Cybernetics-Part A:Systems and Humans, 2010, 40(2):399-405. doi: 10.1109/TSMCA.2009.2034836 [2] XIONG K, WEI C L, LIU L D.Robust Kalman filtering for discrete-time nonlinear systems with parameter uncertainties[J].Aerospace Science & Technology, 2012, 18(1):15-24. http://www.sciencedirect.com/science/article/pii/S1270963811000708 [3] XIONG K, LIU L D, LIU Y.Robust extended Kalman filtering for nonlinear systems with multiplicative noises[J].Optimal Control Applications & Methods, 2011, 32(1):47-63. doi: 10.1002/oca.928/citedby [4] REZAEI H, ESFANJANI R M, FARSI M.Robust filtering for uncertain networked systems with randomly delayed and lost measurements[J].IET Signal Processing, 2015, 9(4):320-327. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=fa9a615038aae276e7866cef497e25e3 [5] INOUE R S, TERRA M H, CERRI J P.Extended robust Kalman filter for attitude estimation[J].IET Control Theory & Applications, 2016, 10(2):162-172. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0220708619/ [6] DONG Z, YOU Z.Finite-horizon robust Kalman filtering for uncertain discrete time-varying systems with uncertain-covariance white noises[J].IEEE Signal Processing Letters, 2006, 13(8):493-496. doi: 10.1109/LSP.2006.873148 [7] ZHENG J H, LIU J F.A robust finite-horizon Kalman filter for uncertain discrete time-varying systems with state-delay and missing measurements[J].International Journal of Grid and Distributed Computing, 2016, 9(3):229-242. [8] WANG F, WANG Z D, LIANG J L, et al.Robust finite-horzion filtering for 2-D systems with randomly varying sensor delays[J].IEEE Transactions on Systems, Man, and Cybernetics:Ssytems, 2018:1-13. http://ieeexplore.ieee.org/document/8260972/ [9] QIN W T, WANG X G, BAI Y L, et al.Arbitrary-step randomly delayed robust filter with application to boost phase tracking[J].Acta Astronautica, 2018, 145:304-318. doi: 10.1016/j.actaastro.2018.01.056 [10] FAN Z, YANG J.A research of gyro/star-sensor integrated attitude determination based on particle filter[C]//Third International Conference on Instrumentation, Measurement, Computer, Communication and Control.Piscataway, NJ: IEEE Press, 2013: 256-261. [11] REIF K, GVNTHER S, YAZ E, et al.Stochastic stability of the discrete-time extended Kalman filter[J].IEEE Transactions on Automatic Control, 1999, 44(4):714-728. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=07093f2f97280d5338d49a76c357574d [12] XIONG K, LIU L D, ZHANG H Y.Modified unscented Kalman filtering and its application in autonomous satellite navigation[J].Aerospace Science & Technology, 2009, 13(4):238-246. doi: 10.1016-j.ast.2009.04.001/ [13] WANG S, FANG H, TIAN X.Recursive estimation for nonlinear stochastic systems with multi-step transmission delays, multiple packet dropouts and correlated noises[J].Signal Processing, 2015, 115:164-175. doi: 10.1016/j.sigpro.2015.03.022 [14] 黄蔚.CKF及鲁棒滤波在飞行器姿态估计中的应用研究[D].哈尔滨: 哈尔滨工程大学, 2015.HUANG W.Application of CKF and robust filter in aircraft attitude estimation[D].Harbin: Harbin Engineering University, 2015(in Chinese). [15] XIE L, SOH Y C, DE SOUZA C E.Robust Kalman filtering for uncertain discrete-time systems[J].IEEE Transactions on Automatic Control, 1994, 39(6):1310-1314. doi: 10.1109/9.293203 -
下载:
点击查看大图
计量
- 文章访问数: 631
- HTML全文浏览量: 56
- PDF下载量: 262
- 被引次数: 0
