Three-dimensional integrated guidance and control design with fixed-time convergence
-
摘要:
针对终端角度约束、状态约束和控制受限问题,在三维空间内,提出一种固定时间收敛的导弹制导控制一体化设计方法。构建了带终端角度约束的制导控制系统三通道全耦合设计模型,采用固定时间收敛的滑模干扰观测器对一体化设计模型中的未知干扰进行估计和补偿。基于固定时间稳定性理论、终端滑模控制和反演控制方法等对制导控制系统进行一体化设计,并采用二阶指令滤波器对系统状态及控制指令进行约束。对所提方法的固定时间收敛特性进行证明,并给出具体的收敛时间表达式。通过导弹六自由度仿真,验证了所提方法的有效性和优越性。
Abstract:This paper proposes a three-dimensional integrated design method for missile guidance and control with fixed-time convergence to address the issues of impact angle constraints, state constraints, and control constraints. A three-channel fully coupled design model of guidance and control system with impact angle constraints is constructed, and the unknown disturbances in the integrated design model are estimated and compensated by a fixed-time convergent sliding mode disturbance observer. Based on the fixed-time stability theory, terminal sliding mode control and backstepping control method, the integrated design of the guidance and control system is carried out, and the second-order instruction filter is used to restrict the system states and control instructions. The fixed-time convergence property of the integrated algorithm is proved, and the specific convergence time expression is given. The effectiveness and superiority of the integrated guidance and control law are verified by six degrees of freedom simulation of the missile.
-
表 1 导弹动力学参数
Table 1. Missile dynamics parameters
参数 数值 参数 数值 参数 数值 $m$/kg 1200 $m_{x1}^{\beta}$ −0.38 $C_y^{\beta}$ −0.081 $S$/m2 0.42 $m_{x1}^{\delta_x}$ 2.13 $C_y^{\delta_{\textit{z}}}$ 5.75 $ L $/m2 0.69 $m_{y1}^{\beta}$ −27.30 $C_{\textit{z}}^{\alpha}$ 0.09 $J_{x1} $/(kg·m2) 100 $m_{y1}^{\delta_y}$ −26.60 $C_{\textit{z}}^{\beta}$ −56.32 $J_{y1} $/(kg·m2) 5800 $m_{{\textit{z}}1}^{\alpha}$ −28.15 $C_{\textit{z}}^{\delta_y}$ −5.6 $J_{{\textit{z}}1}$/(kg·m2) 5700 $m_{{\textit{z}}1}^{\delta_{\textit{z}}}$ −27.90 g/(m·s−2) 9.8 $m^\alpha_{x1} $ 0.45 $C_y^{\alpha}$ 57.15 $V_{\rm{m}}$/(m·s−1) 600 表 2 不同一体化控制律的仿真结果
Table 2. Simulation results of different integrated control laws
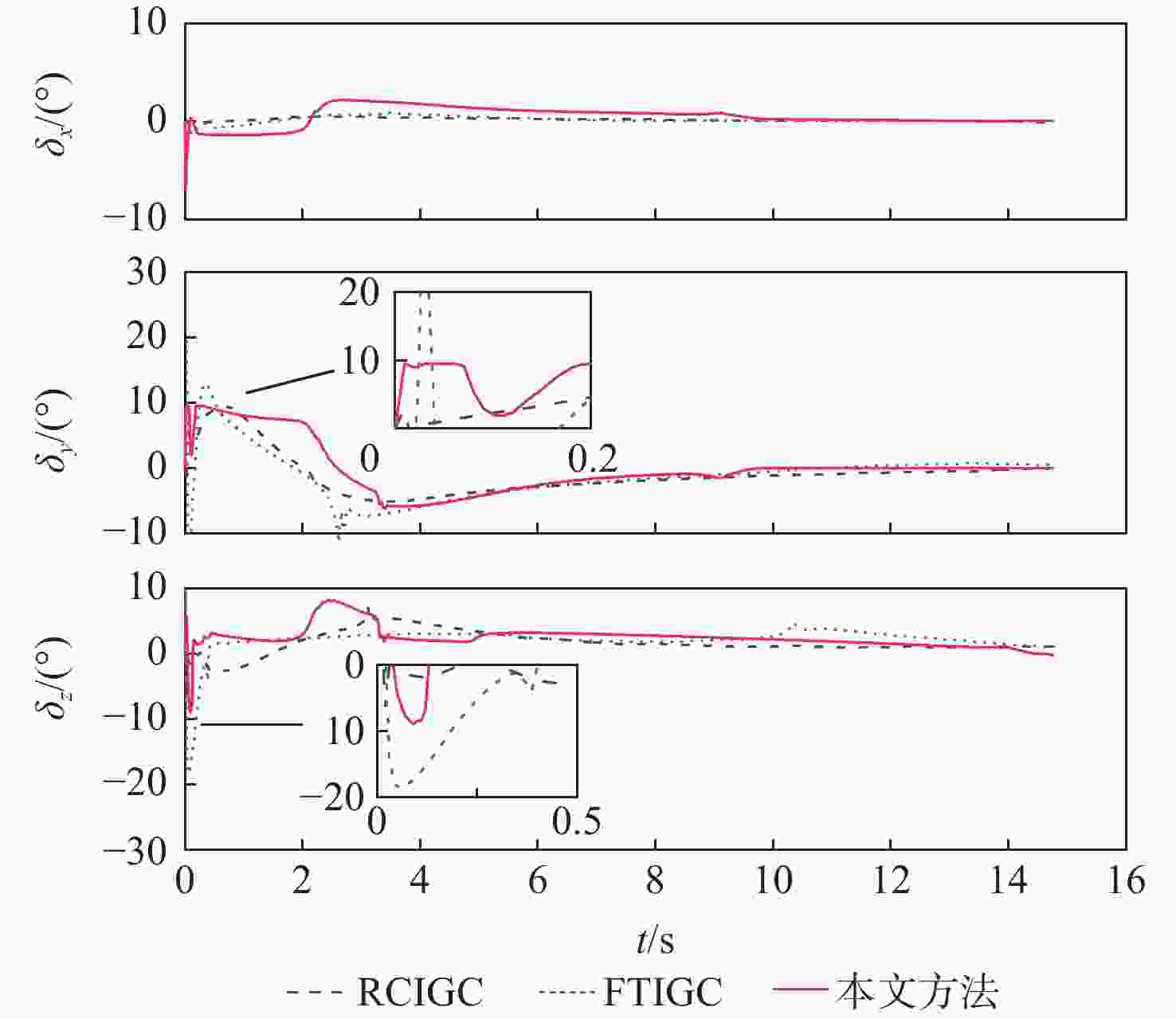
控制律 攻击
时间/s脱靶量/m 视线倾角
误差/(°)视线偏角
误差/(°)RCIGC 14.69 2.33 0.63 0.51 FTIGC 14.82 1.71 0.22 0.43 本文方法 14.77 0.71 0.05 0.04 -
[1] WILLIAMS D E, RICHMAN J, FRIEDLAND B. Design of an integrated strapdown guidance and control system for a tactical missile[C]//Proceedings of AIAA Guidance and Control Conference. Reston: AIAA, 1983: 57-66. [2] TAKESHI Y, BALAKRISHNAN S N. Integrated guidance and autopilot design for a chasing UAV via high-order sliding modes[J]. Journal of the Franklin Institute, 2012, 349(2): 531-558. doi: 10.1016/j.jfranklin.2011.08.004 [3] YAN H, TAN S P, HE Y Z. A small-gain method for integrated guidance and control in terminal phase of reentry[J]. Acta Astronautica, 2017, 132: 282-292. doi: 10.1016/j.actaastro.2016.12.027 [4] XIN M, BALAKRISHNAN S N, OHLMEYER E J. Integrated guidance and control of missiles with θ-D method[J]. IEEE Transactions on Control Systems Technology, 2006, 14(6): 981-992. doi: 10.1109/TCST.2006.876903 [5] WANG Z K, MA J W, FU J T. Research on sliding mode method about three-dimensional integrated guidance and control for air-to-ground missile[J]. Journal of Aerospace Technology and Management, 2019, 11(1): 1-15. [6] SONG H T, ZHANG T, ZHANG G L. L1 adaptive state feedback controller for three-dimensional integrated guidance and control of interceptor[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2014, 228(10): 1693-1701. [7] RAN M P, WANG Q, HOU D L, et al. Backstepping design of missile guidance and control based on adaptive fuzzy sliding mode control[J]. Chinese Journal of Aeronautics, 2014, 27(3): 634-642. doi: 10.1016/j.cja.2014.04.007 [8] 张宽桥, 刘连照, 马晖, 等. 考虑攻击角约束和输入饱和的制导控制一体化设计[J]. 弹道学报, 2021, 33(3): 9-18. doi: 10.12115/j.issn.1004-499X(2021)03-002ZHANG K Q, LIU L Z, MA H, et al. Design on integrated guidance and control considering the constraint of impact angle and input saturation[J]. Journal of Ballistics, 2021, 33(3): 9-18(in Chinese). doi: 10.12115/j.issn.1004-499X(2021)03-002 [9] SEYEDIPOUR S H, JEGARKANDI M F, SHAMAGHDARI S. Nonlinear integrated guidance and control based on adaptive backstepping scheme[J]. Aircraft Engineering and Aerospace Technology, 2017, 89(3): 415-424. doi: 10.1108/AEAT-12-2014-0209 [10] TIAN J Y, XIONG N, ZHANG S F, et al. Integrated guidance and control for missile with narrow field-of-view strapdown seeker[J]. ISA Transactions, 2020, 106: 124-137. doi: 10.1016/j.isatra.2020.06.012 [11] ZHAO B, XU S Y, GUO J G, et al. Integrated strapdown missile guidance and control based on neural network disturbance observer[J]. Aerospace Science and Technology, 2019, 84: 170-181. doi: 10.1016/j.ast.2018.10.025 [12] ZHANG L, WEI C Z, WU R, et al. Fixed-time extended state observer based non-singular fast terminal sliding mode control for a VTVL reusable launch vehicle[J]. Aerospace Science and Technology, 2018, 82-83: 70-79. doi: 10.1016/j.ast.2018.08.028 [13] SONG H T, ZHANG T. Fast robust integrated guidance and control design of interceptors[J]. IEEE Transactions on Control Systems Technology, 2016, 24(1): 349-356. doi: 10.1109/TCST.2015.2431641 [14] LAI C, WANG W H, LIU Z H, et al. Three-dimensional integrated guidance and control for terminal angle constrained attack against ground maneuvering target[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2019, 233(7): 2393-2412. doi: 10.1177/0954410018778988 [15] 梁晓玲. 控制受限的导引与控制一体化设计[D]. 哈尔滨: 哈尔滨工业大学, 2015: 7-10.LIANG X L. The integrated design method of guidance and control with control constraints[D]. Harbin: Harbin Institute of Technology, 2015: 7-10(in Chinese). [16] SAEED K, FARID S. Robust extended state observer-based three dimensional integrated guidance and control design for interceptors with impact angle and input saturation constraints[J]. ISA transactions, 2020, 104: 299-309. doi: 10.1016/j.isatra.2020.05.019 [17] ZHANG D H, MA P, WANG S Y, et al. Multi-constraints adaptive finite-time integrated guidance and control design[J]. Aerospace Science and Technology, 2020, 107: 106334. doi: 10.1016/j.ast.2020.106334 [18] CHONG Z Y, GUO J G, ZHAO B, et al. Finite-time integrated guidance and control system for hypersonic vehicles[J]. Transactions of the Institute of Measurement and Control, 2021, 43(4): 842-853. doi: 10.1177/0142331220941934 [19] HE S M, WANG W, WANG J. Three-dimensional multivariable integrated guidance and control design for maneuvering targets interception[J]. Journal of the Franklin Institute, 2016, 353(16): 4330-4350. doi: 10.1016/j.jfranklin.2016.08.008 [20] SHU Y J, TANG S. Integrated guidance and control backstepping design for blended control missile based on NDO[J]. Journal of Astronautics, 2013, 34(1): 79-85. [21] LIU X D, HUANG W W, DU L F. An integrated guidance and control approach in three-dimensional space for hypersonic missile constrained by impact angles[J]. ISA Transactions, 2017, 66: 164-175. doi: 10.1016/j.isatra.2016.10.008 [22] HE S M, LIN D F, WANG J. Continuous second-order sliding mode based impact angle guidance law[J]. Aerospace Science and Technology, 2015, 41: 199-208. doi: 10.1016/j.ast.2014.11.020 [23] NI J K, LIU L, LIU C X, et al. Fixed-time dynamic surface high-order sliding mode control for chaotic oscillation in power system[J]. Nonlinear Dynamics, 2016, 86(1): 401-420. doi: 10.1007/s11071-016-2897-8 [24] WANG X, GUO J, TANG S J, et al. Fixed-time disturbance observer based fixed-time back-stepping control for an air-breathing hypersonic vehicle[J]. ISA Transactions, 2019, 88: 233-245. doi: 10.1016/j.isatra.2018.12.013 [25] JIANG B Y, HU Q L, FRISWELL M I. Fixed-time attitude control for rigid spacecraft with actuator saturation and faults[J]. IEEE Transactions on Control Systems Technology, 2016, 24(5): 1892-1898. doi: 10.1109/TCST.2016.2519838 [26] BASIN M, PANATHULA C B, SHTESSEL Y. Multivariable continuous fixed-time second-order sliding mode control: Design and convergence time estimation[J]. IET Control Theory & Applications, 2017, 11(8): 1104-1111. [27] HALL C E, SHTESSEL Y B. Sliding mode disturbance observer-based control for a reusable launch vehicle[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(6): 1315-1328. doi: 10.2514/1.20151 [28] 张宽桥, 杨锁昌, 李宝晨, 等. 考虑驾驶仪动态特性的固定时间收敛制导律[J]. 航空学报, 2019, 40(11): 323227. doi: 10.7527/S1000-6893.2019.23227ZHANG K Q, YANG S C, LI B C, et al. Fixed-time convergent guidance law considering autopilot dynamics[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(11): 323227(in Chinese). doi: 10.7527/S1000-6893.2019.23227 -







 下载:
下载: