基于AE-BN的发电机滚动轴承故障诊断

王进花; 高媛; 曹洁; 马佳林

doi:10.13700/j.bh.1001-5965.2021.0581

基于AE-BN的发电机滚动轴承故障诊断

doi: 10.13700/j.bh.1001-5965.2021.0581

王进花^{1, 2, 3, ,},
高媛¹,
曹洁^{1, 4},
马佳林⁵

1.
兰州理工大学电气工程与信息工程学院，兰州 730050
2.
兰州理工大学甘肃工业过程先进控制重点实验室，兰州 730050
3.
兰州理工大学电气与控制工程国家实验教学中心，兰州 730050
4.
甘肃省制造信息工程研究中心，兰州 730050
5.
兰州理工大学计算机与通信学院，兰州 730050

基金项目: 国家自然科学基金(62063020,61763028)；甘肃省自然科学基金(20JR5RA463)

详细信息

通讯作者:
E-mail：wjh0615@lut.edu.cn

中图分类号: TP277
计量
- 文章访问数: 293
- HTML全文浏览量: 63
- PDF下载量: 58
- 被引次数: 0
出版历程
- 收稿日期: 2021-09-30
- 录用日期: 2021-12-27
- 网络出版日期: 2022-01-26
- 整期出版日期: 2023-08-31

Fault diagnosis of generator rolling bearing based on AE-BN

WANG Jinhua^{1, 2, 3
, ,},
GAO Yuan¹,
CAO Jie^{1, 4},
MA Jialin⁵

1.
College of Electrical & Information Engineering，Lanzhou University of Technology，Lanzhou 730050，China
2.
Key Laboratory of Gansu Advanced Control for Industrial Processes，Lanzhou University of Technology，Lanzhou 730050，China
3.
National Experimental Teaching Center of Electrical and Control Engineering，Lanzhou University of Technology，Lanzhou 730050，China
4.
Engineering Research Center of Manufacturing Information of Gansu Province，Lanzhou 730050，China
5.
College of Computer and Communication，Lanzhou University of Technology，Lanzhou 730050，China

Funds: National Natural Science Foundation of China (62063020,61763028); Natural Science Foundation of Gansu Province, China (20JR5RA463)

More Information

Corresponding author: E-mail：wjh0615@lut.edu.cn

摘要

摘要:
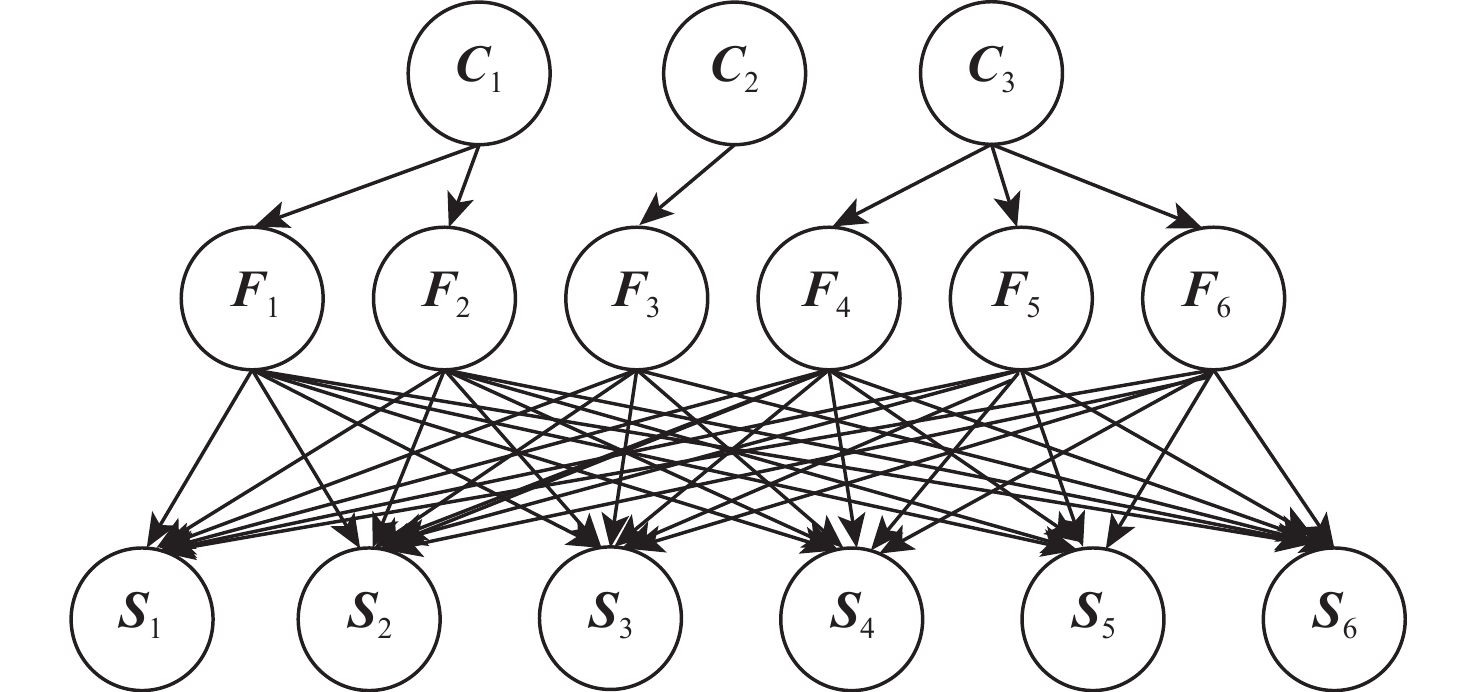
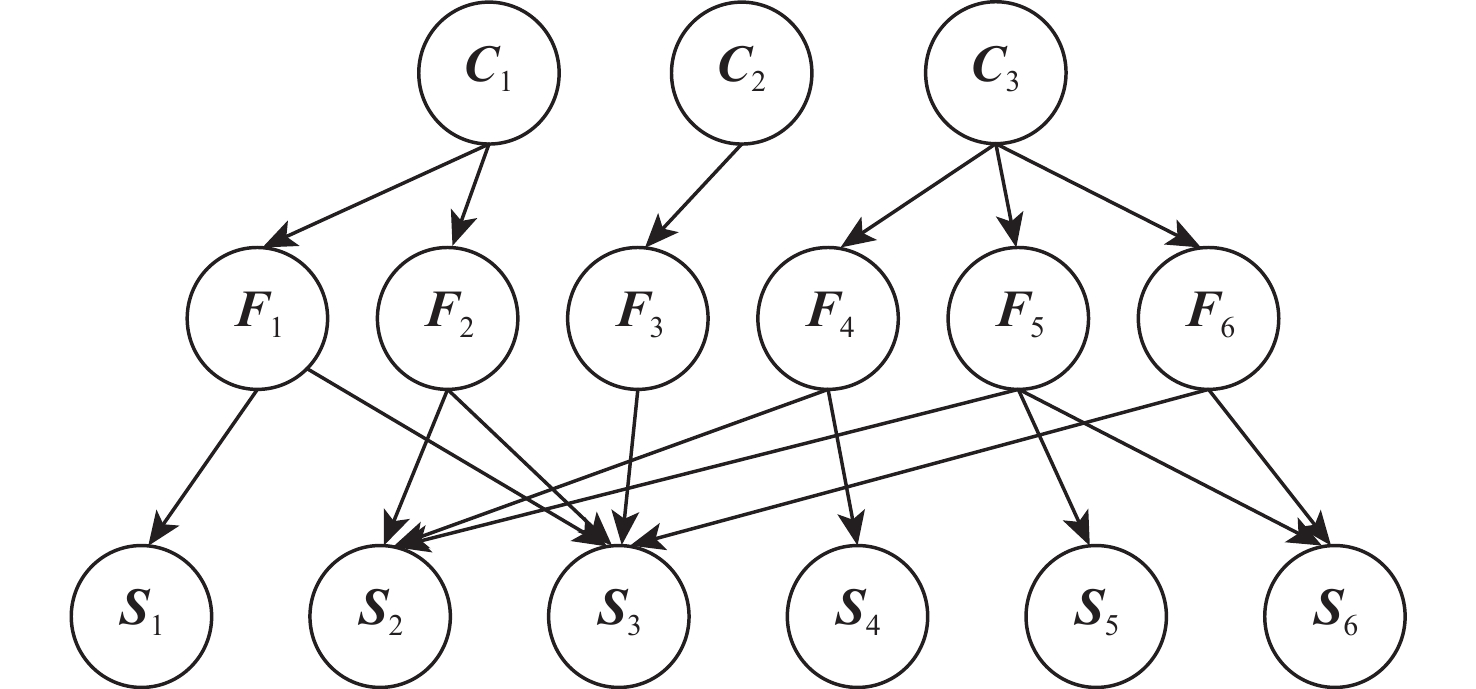
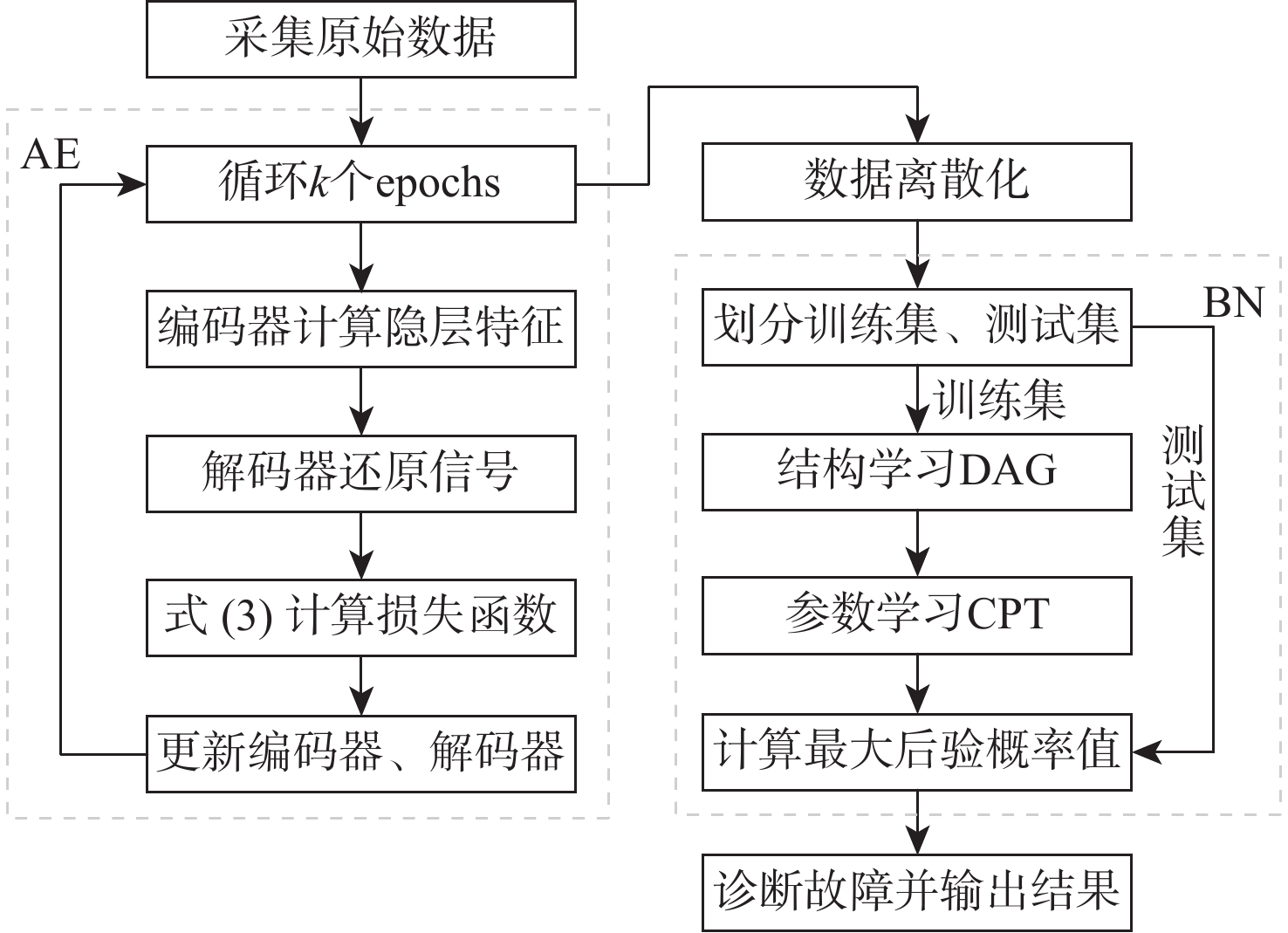
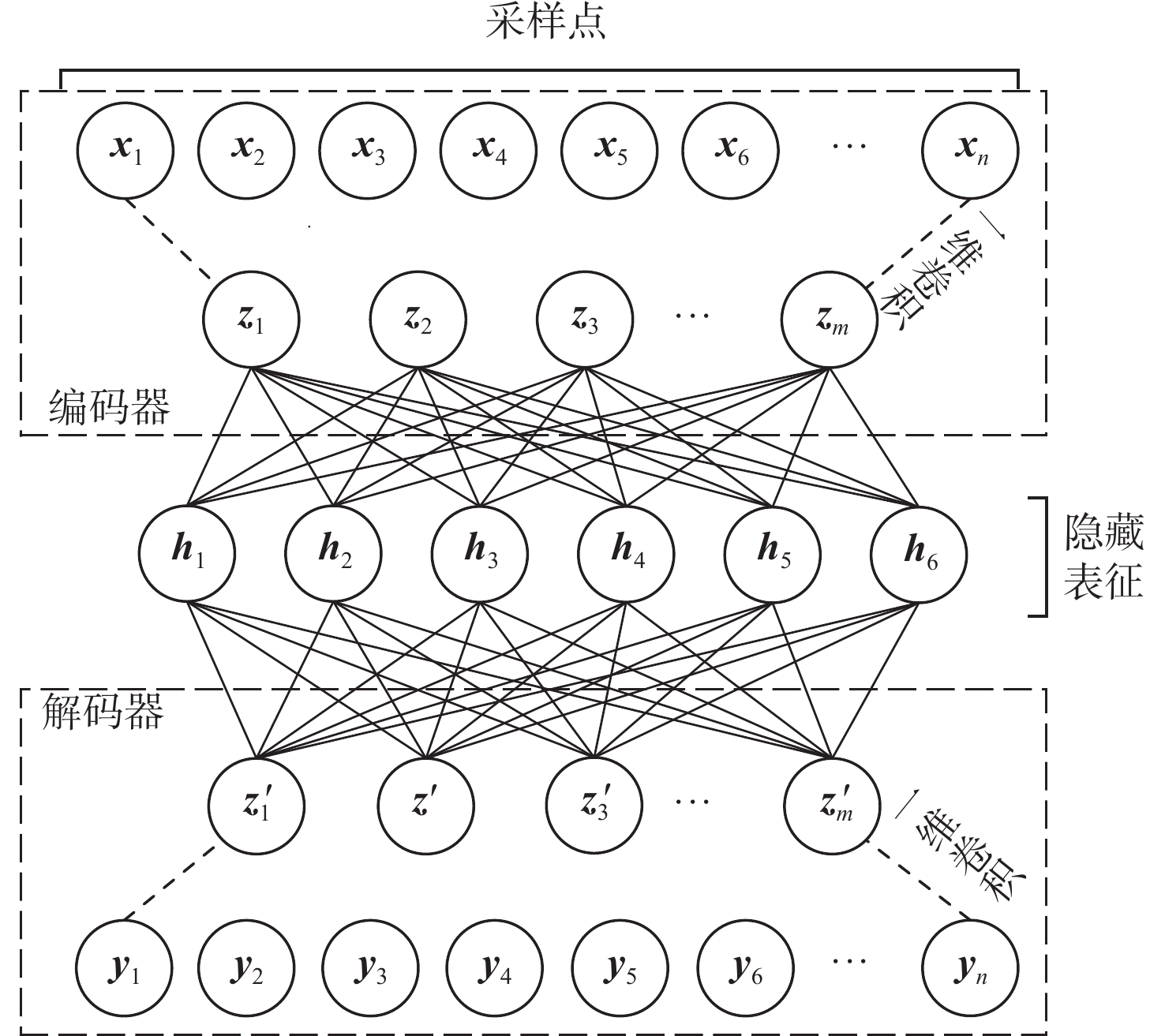
为解决风力发电机在复杂工况及耦合性、不确定性条件下故障识别的准确性问题，提出了一种基于自动编码器(AE)与贝叶斯网络(BN)的AE-BN故障诊断方法。采用AE对电流信号进行特征提取，得到能够高度表征信号的特征分量；基于故障与特征之间的因果关系，建立由故障位置、故障状态和故障特征搭建的三层BN；将AE的特征分量与BN的拓扑结构相结合建立风力发电机故障诊断模型，解决故障诊断中的不确定性问题，提高多故障诊断的准确性。实验结果表明：所提方法能够对故障特征信号进行分析及诊断，精确辨识不同故障类型，相比K近邻算法等具有明显优势。
- 故障诊断 /
- 自动编码器 /
- 贝叶斯网络 /
- 结构学习 /
- 特征提取
Abstract:
To solve the accuracy of fault identification of wind turbines under complex working conditions, coupling, and uncertainty, an AE-BN fault diagnosis method based on a auto-encoder (AE) and Bayesian network (BN) is proposed. AE is used to extract the characteristics of the current signal, and the characteristic component that can highly characterize the signal is obtained; based on the causal relationship between fault and feature, a three-layer BN composed of fault location, fault state, and fault feature is established; The wind turbine fault diagnostic model is then established, the uncertainty problem in fault diagnosis is solved, and the precision of multi fault diagnosis is enhanced by combining the characteristic component of AE with the topology of BN. Experimental results show that the proposed method can analyze and diagnose fault characteristic signals and accurately identify different fault types, which has obvious advantages over other algorithms.
- fault diagnosis /
- auto-encoder /
- Bayesian network /
- structure learning /
- feature extraction

HTML全文

图 1 自动编码器结构

Figure 1. Structure of AE

下载: 全尺寸图片幻灯片

图 2 贝叶斯网络结构

Figure 2. Structure of BN

下载: 全尺寸图片幻灯片

图 3 滚动轴承故障诊断的贝叶斯网络模型

Figure 3. Bayesian network model for fault diagnosis of rolling bearings

下载: 全尺寸图片幻灯片

图 4 故障诊断方法流程

Figure 4. Fault diagnosis algorithm flow chart

下载: 全尺寸图片幻灯片

图 5 滚动轴承状况监测实验台

Figure 5. Rolling bearing condition monitoring test bench

下载: 全尺寸图片幻灯片

图 6 6种故障电流信号时域波形

Figure 6. Time domain waveform of six types of fault current signals

下载: 全尺寸图片幻灯片

图 7 特征提取散点图

Figure 7. Feature extraction scatter plot

下载: 全尺寸图片幻灯片

图 8 RadViz雷达图

Figure 8. RadViz radar map

下载: 全尺寸图片幻灯片

图 9 轴承故障分类混淆矩阵

Figure 9. Confusion matrix of bearing fault classification

下载: 全尺寸图片幻灯片

表 1 结构评分对比

Table 1. Comparison of structure scores

结构搭建方法	BDeu/10⁴	K2/10⁴	BIC/10⁴
贝叶斯搜索方法	−3.2329	−3.2417	−3.2384
贪婪厚细化方法	−3.0882	−3.0993	−3.1018
爬山搜索算法	−2.2358	−2.2754	−2.7692

下载: 导出CSV

表 2 不同的运行条件

Table 2. Different operating conditions

运行工况	转速/(r·min⁻¹)	径向力/N	负载转矩/(N·m)
K0	1500	1000	0.7
K1	1500	1000	0.1
K2	900	1000	0.7
K3	1500	400	0.7

下载: 导出CSV

表 3 故障类型与状态标签

Table 3. Fault types and status labels

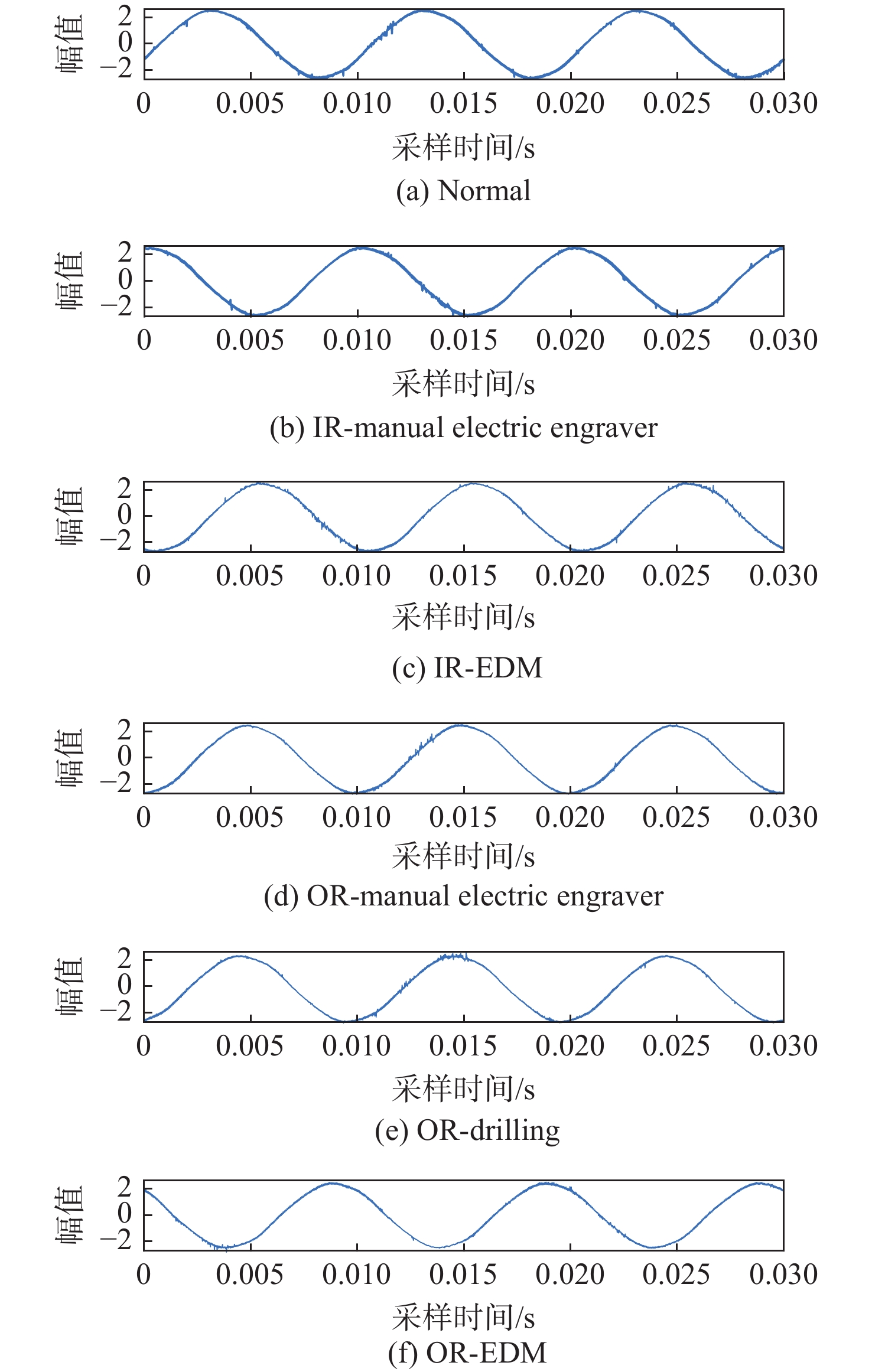
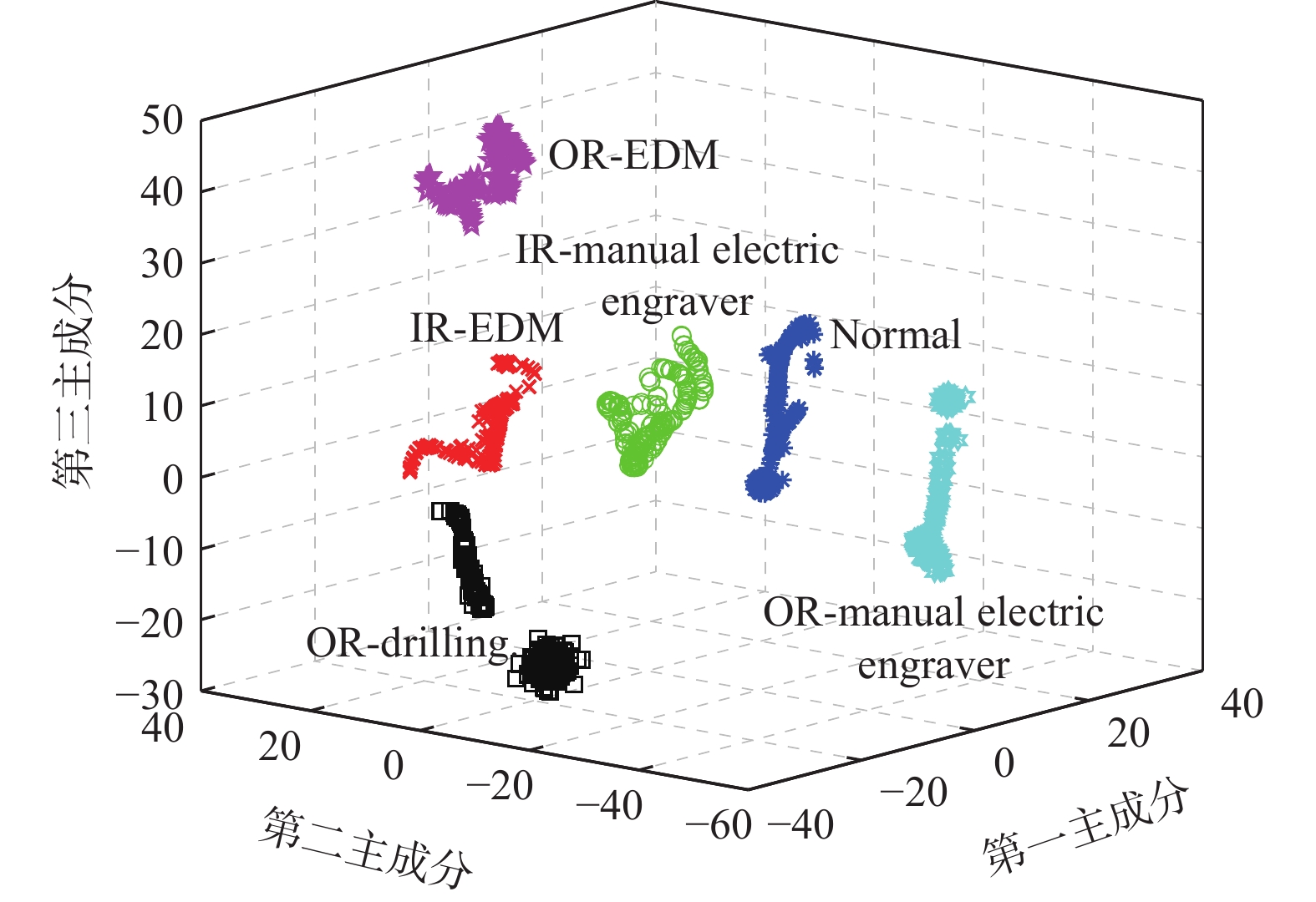
故障位置	故障类型	轴承代码	标签
$ C_{1} $	IR-EDM	KI01	1
$ C_{1} $	IR-manual electric engraver	KI05	2
$ C_{2} $	Normal	K002	3
$ C_{3} $	OR-drilling	KA07	4
$ C_{3} $	OR-EDM	KA01	5
$ C_{3} $	OR-manual electric engraver	KA05	6
注：Normal表示正常数据，将其作为一种特殊的故障与其余5种故障一起进行故障分类的研究。

下载: 导出CSV

表 4 贝叶斯网络子节点条件概率

Table 4. Conditional probability of subnodes of Bayesian network

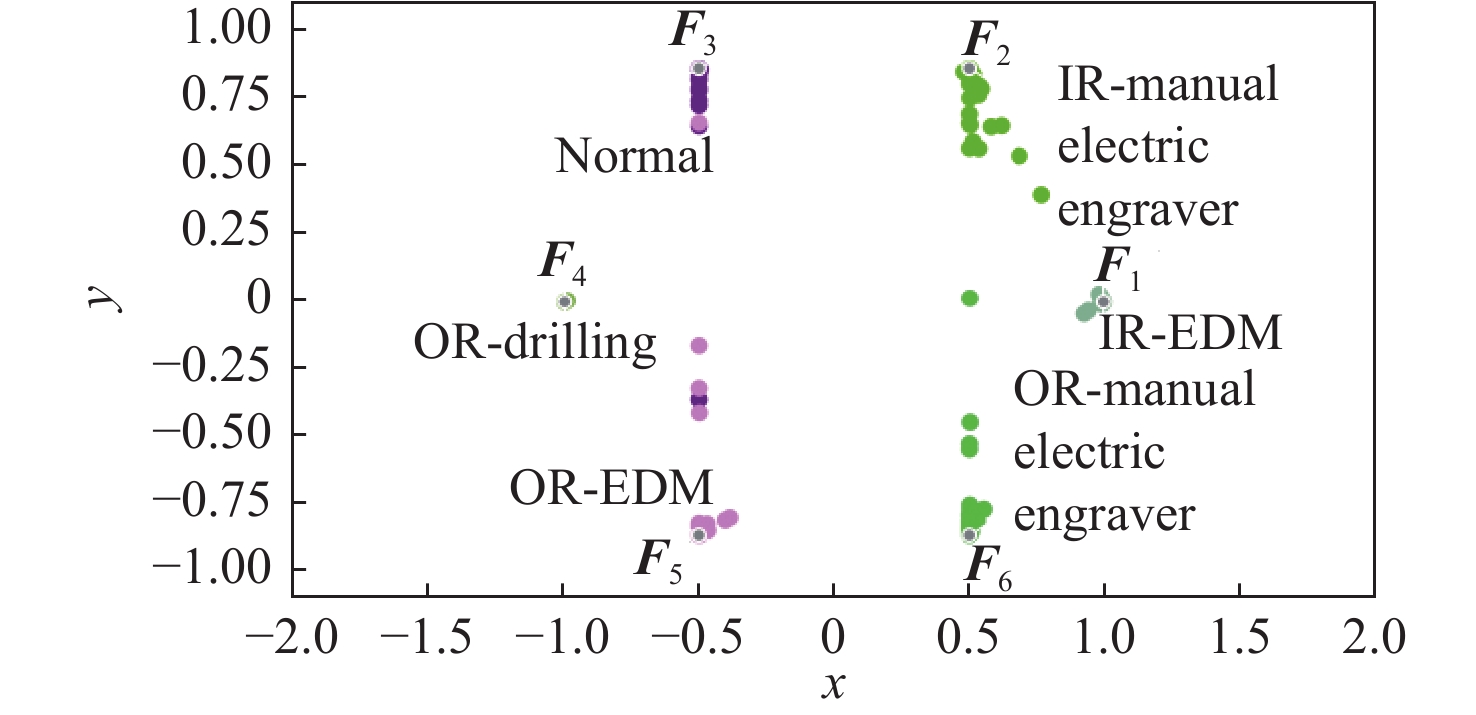
节点	节点取值	父节点取值	条件概率
${{\boldsymbol{F}}_1}$	0	0	0.4807
${{\boldsymbol{F}}_2}$	0	0,1	0.5111
${{\boldsymbol{F}}_2}$	0	1,0	0.4962
${{\boldsymbol{F}}_2}$	0	1,1	0.5128
${{\boldsymbol{F}}_3}$	0	0,0	0.3068
${{\boldsymbol{F}}_3}$	0	0,1	0.6031
${{\boldsymbol{F}}_3}$	0	1,0	0.5204
${{\boldsymbol{F}}_3}$	0	1,1	0.3753
${{\boldsymbol{F}}_4}$	0		0.3050
$ {{\boldsymbol{F}}_5} $	0		0.4033
${{\boldsymbol{F}}_6}$	0	0,1	0.4929
${{\boldsymbol{F}}_6}$	0	1,0	0.4872

下载: 导出CSV

表 5 4种工况下不同故障诊断模型的分类精度对比

Table 5. Comparison of classification accuracy of different fault diagnosis models under four types of working conditions

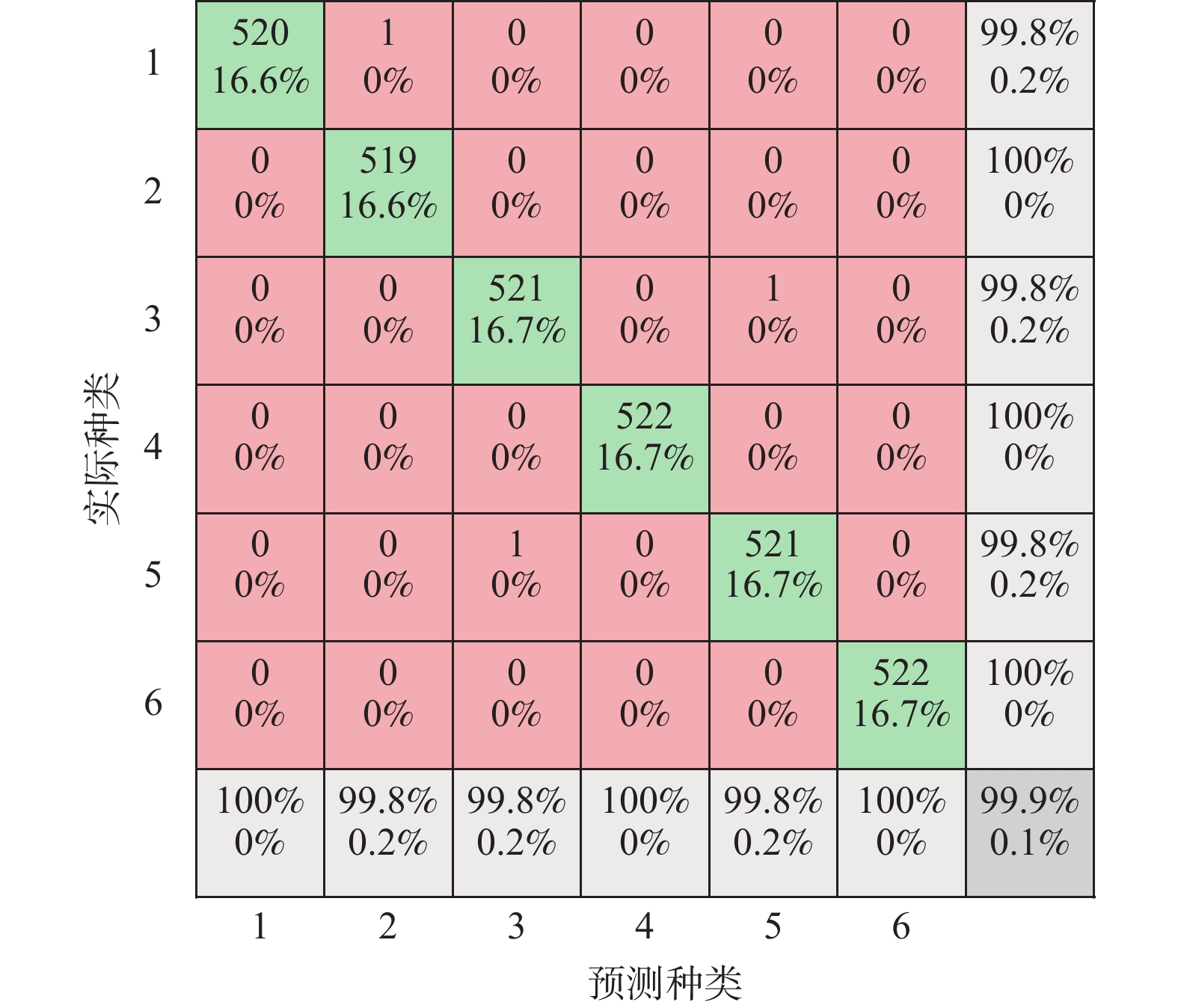
运行工况	VMD-KNN	AE-KNN	AE-BN
K0	0.7124	0.8733	0.9983
K1	0.6324	0.8914	0.9772
K2	0.7231	0.8932	0.9955
K3	0.7377	0.8715	0.9981

下载: 导出CSV

参考文献(23)

[1]	曾军, 陈艳峰, 杨苹, 等. 大型风力发电机组故障诊断综述[J]. 电网技术, 2018, 42(3): 849-860. doi: 10.13335/j.1000-3673.pst.2017.2311 ZENG J, CHEN Y F, YANG P, et al. Review of fault diagnosis methods of large-scale wind turbines[J]. Power System Technology, 2018, 42(3): 849-860(in Chinese). doi: 10.13335/j.1000-3673.pst.2017.2311
[2]	陈是扦, 彭志科, 周鹏. 信号分解及其在机械故障诊断中的应用研究综述[J]. 机械工程学报, 2020, 56(17): 91-107. doi: 10.3901/JME.2020.17.091 CHEN S Q, PENG Z K, ZHOU P. Review of signal decomposition theory and its applications in machine fault diagnosis[J]. Journal of Mechanical Engineering, 2020, 56(17): 91-107(in Chinese). doi: 10.3901/JME.2020.17.091
[3]	唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5): 73-81. doi: 10.7652/xjtuxb201505012 TANG G J, WANG X L. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J]. Journal of Xi’an Jiaotong University, 2015, 49(5): 73-81(in Chinese). doi: 10.7652/xjtuxb201505012
[4]	ZHONG J, YANG K. Failure prediction for linear ball bearings based on wavelet transformation and self-organizing map[C]//2018 IEEE 4th Information Technology and Mechatronics Engineering Conference (ITOEC). Piscataway: IEEE Press, 2018: 34-38.
[5]	张超, 陈建军, 郭迅. 基于EMD能量熵和支持向量机的齿轮故障诊断方法[J]. 振动与冲击, 2010, 29(10): 216-220. doi: 10.3969/j.issn.1000-3835.2010.10.004 ZHANG C, CHEN J J, GUO X. A gear fault diagnosis method based on EMD energy entropy and SVM[J]. Journal of Vibration and Shock, 2010, 29(10): 216-220(in Chinese). doi: 10.3969/j.issn.1000-3835.2010.10.004
[6]	CHIANG L H, KOTANCHEK M E, KORDON A K, et al. Fault diagnosis based on Fisher discriminant analysis and support vector machines[J]. Computers & Chemical Engineering, 2004, 28(8): 1389-1401.
[7]	SHAO S, MCALEER S, YAN R, et al. Highly accurate machine fault diagnosis using deep transfer learning[J]. IEEE Transactions on Industrial Informatics, 2019, 15(4): 2446-2455. doi: 10.1109/TII.2018.2864759
[8]	SHAO H, JIANG H, ZHAO H, et al. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis[J]. Mechanical Systems and Signal Processing, 2017, 95: 187-204. doi: 10.1016/j.ymssp.2017.03.034
[9]	陈东超. 基于贝叶斯网络的汽轮发电机组故障诊断方法及应用研究[D]. 北京: 华北电力大学(北京), 2018. CHEN D C. Research on methods and application of fault diagnosis for turbo-generator unit based on bayesian network[D]. Beijing: North China Electric Power University (Beijing), 2018(in Chinese).
[10]	王双成, 张立, 郑飞. 异步动态贝叶斯网络分类器研究[J]. 计算机学报, 2020, 43(9): 1737-1754. doi: 10.11897/SP.J.1016.2020.01737 WANG S C, ZHANG L, ZHENG F. Asynchronous dynamic Bayesian network classifiers[J]. Chinese Journal of Computers, 2020, 43(9): 1737-1754(in Chinese). doi: 10.11897/SP.J.1016.2020.01737
[11]	仝兆景, 芦彤, 秦紫霓. 基于PSO-VMD与贝叶斯网络的滚动轴承故障诊断[J]. 河南理工大学学报(自然科学版), 2021, 40(1): 95-104. doi: 10.16186/j.cnki.1673-9787.2019060034 TONG Z J, LU T, QIN Z N. Fault diagnosis of rolling bearing based on PSO-VMD and Bayesian network[J]. Journal of Henan Polytechnic University (Natural Science), 2021, 40(1): 95-104(in Chinese). doi: 10.16186/j.cnki.1673-9787.2019060034
[12]	王金鑫, 王忠巍, 马修真, 等. 基于贝叶斯网络的柴油机润滑系统多故障诊断[J]. 控制与决策, 2019, 34(6): 1187-1194. doi: 10.13195/j.kzyjc.2017.1399 WANG J X, WANG Z W, MA X Z, et al. Diagnosis of multiple faults of diesel engine lubrication system based on Bayesian networks[J]. Control and Decision, 2019, 34(6): 1187-1194(in Chinese). doi: 10.13195/j.kzyjc.2017.1399
[13]	尹爱军, 王昱, 戴宗贤, 等. 基于变分自编码器的轴承健康状态评估[J]. 振动、测试与诊断, 2020, 40(5): 1011-1016. YIN A J, WANG Y, DAI Z X, et al. Evaluation method of bearing health state based on variational auto-encoder[J]. Journal of Vibration, Measurement & Diagnosis, 2020, 40(5): 1011-1016(in Chinese).
[14]	孙叶, 王钢, 魏东. 贝叶斯网络在智能电网研究中的应用[J]. 自动化应用, 2020(7): 108-109. doi: 10.19769/j.zdhy.2020.07.039 SUN Y, WANG G, WEI D. The application of Bayesian network in the research of smart grid[J]. Automation Application, 2020(7): 108-109(in Chinese). doi: 10.19769/j.zdhy.2020.07.039
[15]	CAI B, HUANG L, XIE M. Bayesian networks in fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2017, 13(5): 2227-2240. doi: 10.1109/TII.2017.2695583
[16]	李硕豪, 张军. 贝叶斯网络结构学习综述[J]. 计算机应用研究, 2015, 32(3): 641-646. doi: 10.3969/j.issn.1001-3695.2015.03.001 LI S H, ZHANG J. Review of Bayesian networks structure learning[J]. Application Research of Computers, 2015, 32(3): 641-646(in Chinese). doi: 10.3969/j.issn.1001-3695.2015.03.001
[17]	WEN Z, KVETON B, ERIKSSON B, et al. Sequential Bayesian search[C]//Proceedings of the 30th International Conference on Machine Learning. New York: ACM, 2013: 226-234.
[18]	CHENG J, BELL D A, LIU W. An algorithm for Bayesian belief network construction from data[C]//Proceedings of the 6th International Workshop on Artificial Intelligence and Statistics. Amsterdam: Elesvier, 1997: 83-90.
[19]	CONSTANTINOU A C, LIU Y, CHOBTHAM K, et al. Large-scale empirical validation of Bayesian network structure learning algorithms with noisy data[J]. International Journal of Approximate Reasoning, 2021, 131: 151-188. doi: 10.1016/j.ijar.2021.01.001
[20]	BEHJATI S, BEIGY H. Improved K2 algorithm for Bayesian network structure learning[J]. Engineering Applications of Artificial Intelligence, 2020, 91: 103617. doi: 10.1016/j.engappai.2020.103617
[21]	刘浩然, 王念太, 王毅, 等. 基于V-结构&对数似然函数定向与禁忌爬山的贝叶斯网络结构算法[J]. 电子与信息学报, 2021, 43(11): 3272-3281. doi: 10.11999/JEIT210032 LIU H R, WANG N T, WANG Y, et al. Bayesian network structure algorithm based on V-structure & Log-likelihood orientation and tabu hill climbing[J]. Journal of Electronics & Information Technology, 2021, 43(11): 3272-3281(in Chinese). doi: 10.11999/JEIT210032
[22]	LESSMEIER C, KIMOTHO J K, ZIMMER D, et al. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification[C]//European Conference of the Prognostics and Health Management Society, 2016: 1-17.
[23]	VAN DER MAATEN L, HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9: 2579-2605.