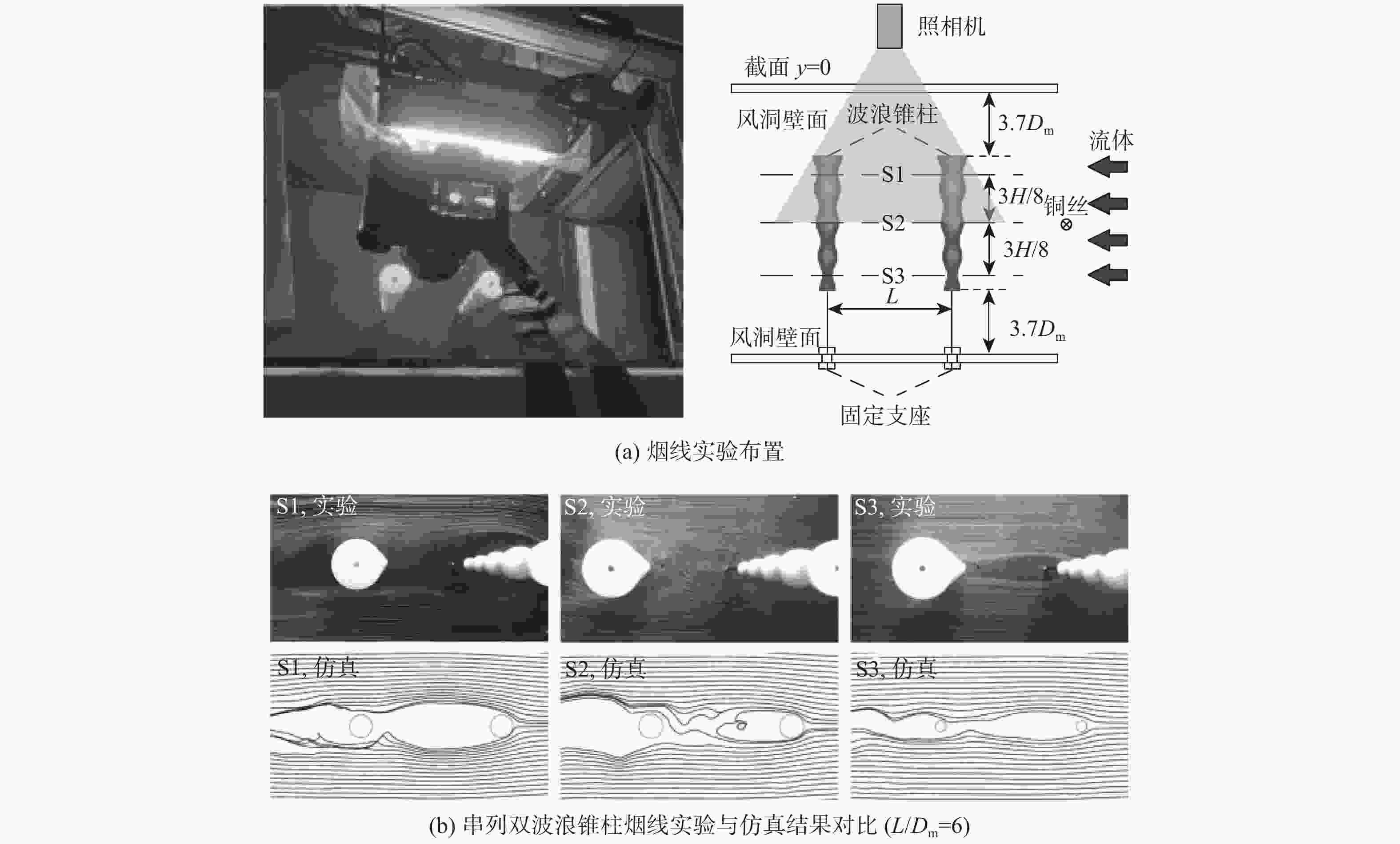
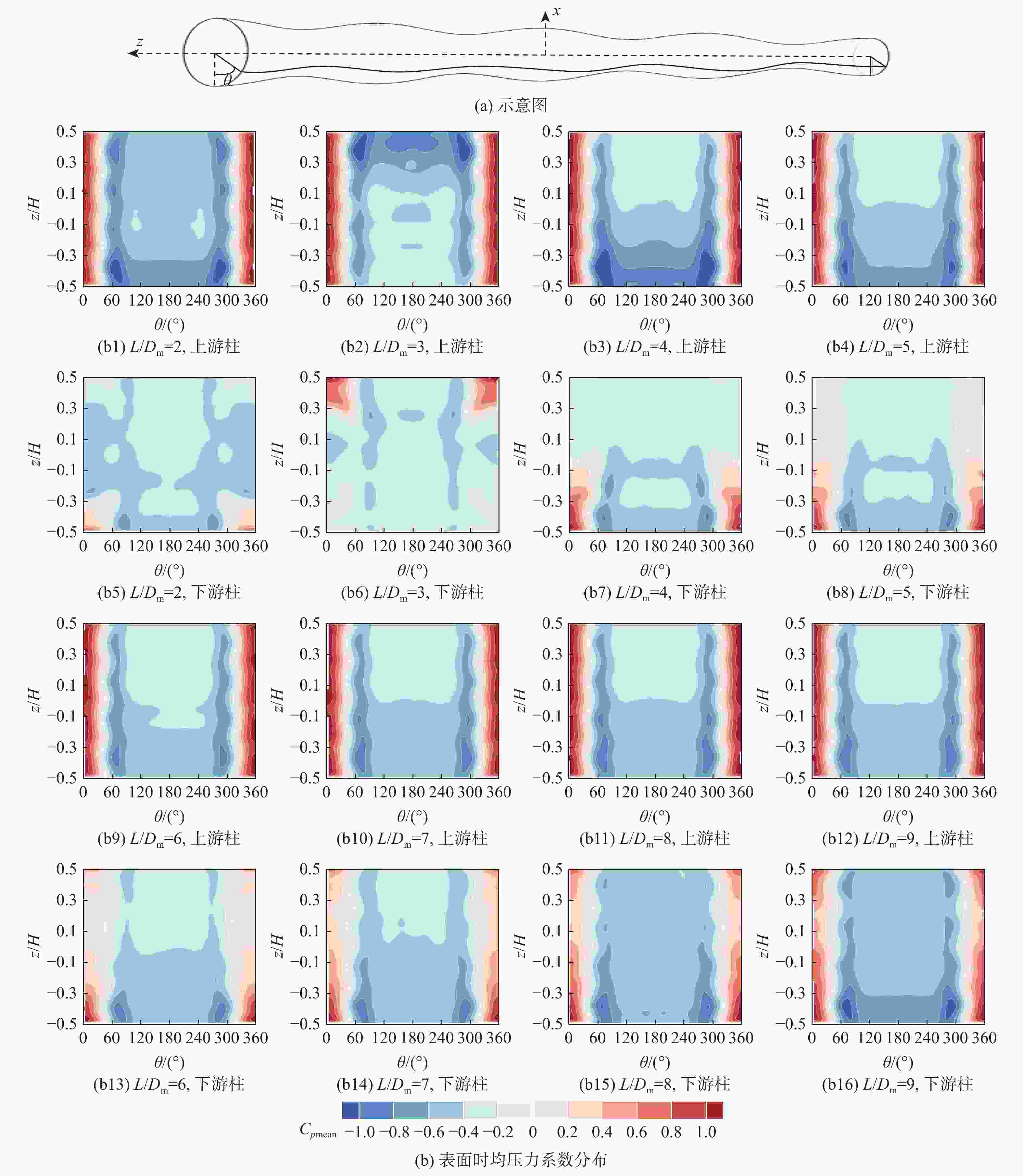
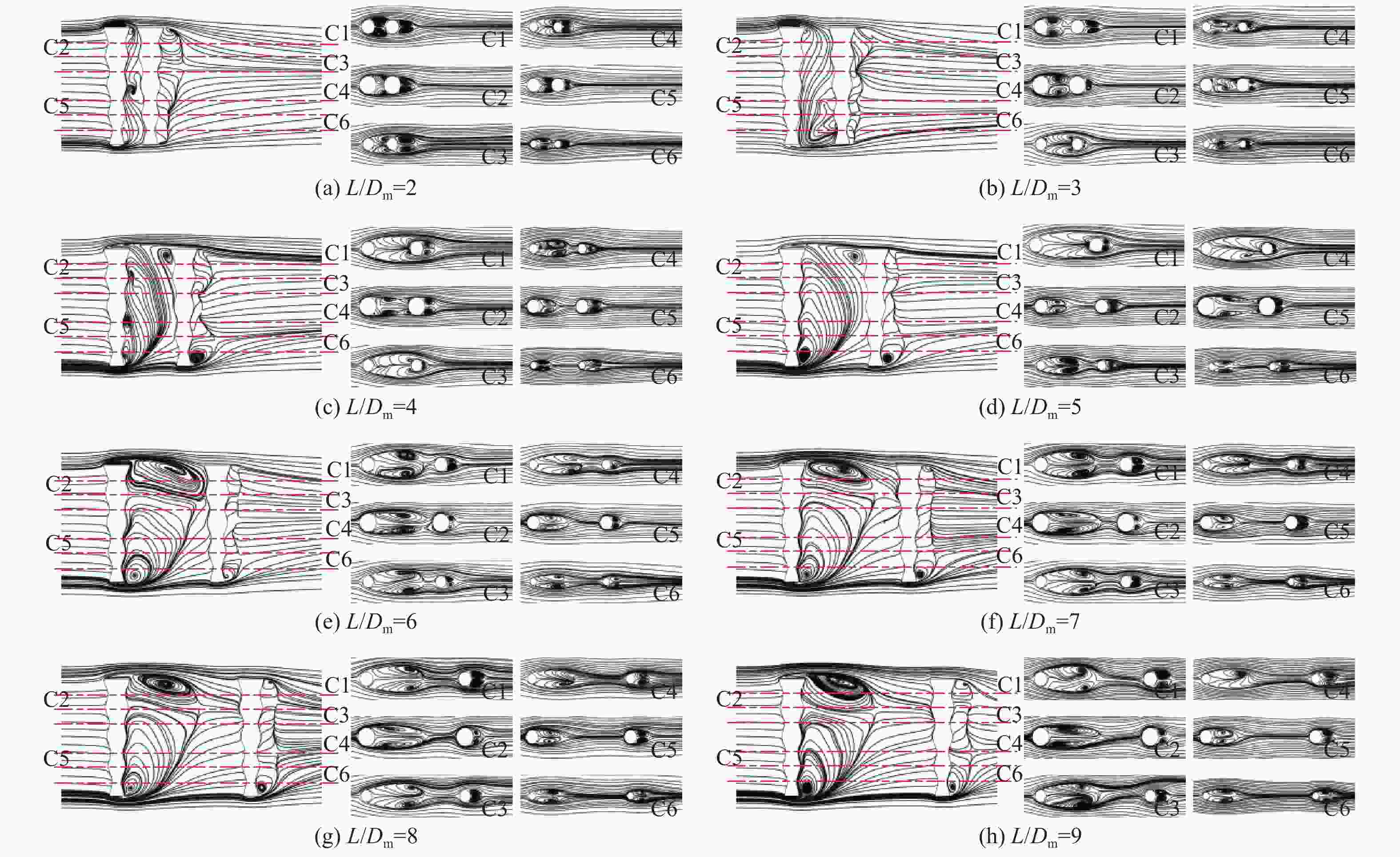
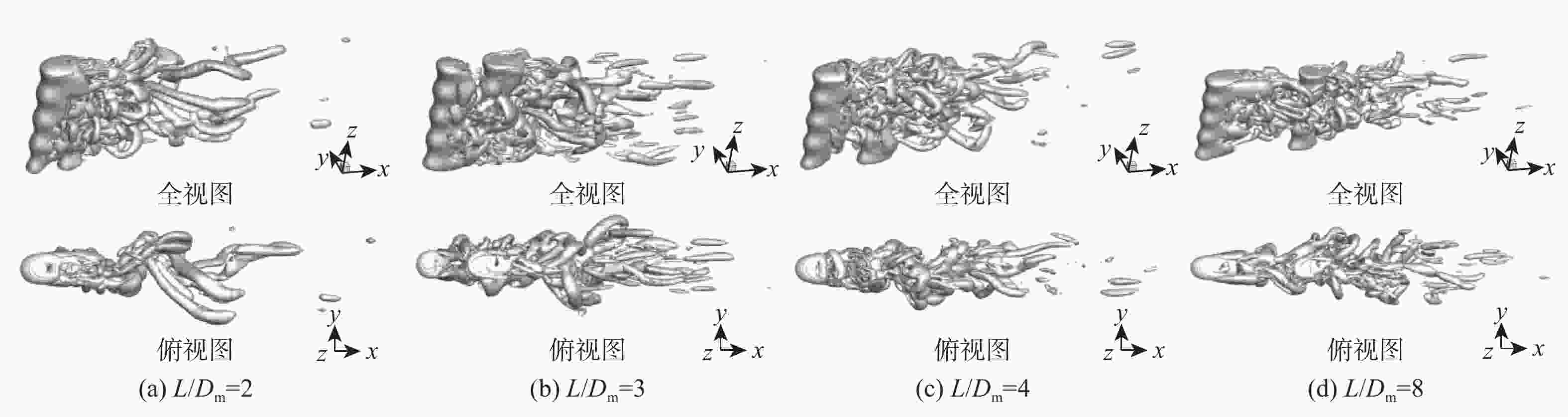
Numerical simulation of flow around two tandem wavy conical cylinders at subcritical Reynolds number
-
摘要:
针对风力俘能结构布局问题,基于大涡模拟(LES)方法,在亚临界雷诺数下(
Re = 3900)研究有限长串列双波浪锥柱的升阻力特性及其流动结构随间距比的变化规律。结果表明:由于上游波浪锥柱的影响,下游波浪锥柱的脉动升力系数大幅增大,当间距比为 3时,表面时均压力系数分布形式呈反向分布;随间距比增加,上游波浪锥柱尾流充分发展,并产生大量肋状涡撞击在下游波浪锥柱表面,下游波浪锥柱产生大的脉动升力,相较于单直圆柱提升约15.3倍,阻力系数降低约0.172。所得结果可为风力俘能结构布局提供有益参考。Abstract:Regarding the arrangement of wind energy harvesting structures, based on the large eddy simulation (LES) method, the lift-drag characteristics and flow structures of two tandem wavy conical cylinders are studied with a subcritical Reynolds number (
Re = 3900) and the spacing ratio. Results show that due to the influence of the upstream wavy conical cylinder, the fluctuating lift coefficients of the downstream wavy conical cylinder increase substantially. When the spacing ratio is 3, the distribution form of the time-averaged pressure coefficient is different from that of other spacing ratios, showing a reverse distribution. With the increasing spacing ratio, a large number of rib vortices are generated after the wake of the upstream wavy conical cylinder is fully developed, causing impact on the surface of the downstream wavy conical cylinder and generating a large fluctuating lift. Compared with the single straight cylinder, the two tandem wavy conical cylinders increase the fluctuating lift coefficient by about 15.3 times, and reduce the drag coefficient by about 0.172. These results can provide a useful reference for the arrangement of wind energy harvesting structures. -
表 1 有限长直圆柱计算验证
Table 1. Calculation verification of finite-length straight cylinder
数据来源 网格数量 圆周节点数 亚格子尺度模型 Δy/Dm Δt* Nfe Re H/Dm Cdmean Clrms Case1 1 177 434 120 Smagorinsky-Lilly 0.001 0.001 2 3 900 7.0 0.749 0.0150 Case2 2 998 158 160 Smagorinsky-Lilly 0.001 0.001 2 3 900 7.0 0.757 0.0122 Case3 5 517 295 200 Smagorinsky-Lilly 0.001 0.001 2 3 900 7.0 0.757 0.0123 Case4 2 859 560 160 Smagorinsky-Lilly 0.002 0.001 2 3 900 7.0 0.743 0.0112 Case5 3 126 920 160 Smagorinsky-Lilly 0.0005 0.001 2 3 900 7.0 0.756 0.0122 Case6 2 998 158 160 Smagorinsky-Lilly 0.001 0.0005 2 3 900 7.0 0.756 0.0124 Case7 2 998 158 160 Smagorinsky-Lilly 0.001 0.002 2 3 900 7.0 0.741 0.0115 Case8 2 998 158 160 WALE 0.001 0.001 2 3 900 7.0 0.762 0.0120 Case9 2 998 158 160 WMLES 0.001 0.001 2 3 900 7.0 0.741 0.0115 Case10 2 998 158 160 WMLES S-Omega 0.001 0.001 2 3 900 7.0 0.765 0.0128 Case11 2 998 158 160 Kinetic-Energy Transport 0.001 0.001 2 3 900 7.0 0.770 0.0116 文献[15] 2 464 056 Smagorinsky-Lilly 0.0005 1 3 900 1.5 0.755 0.050 文献[16] 2 88 000 5.0 0.742 注:Cdmean为时均阻力系数,Clrms为脉动升力系数。 -
[1] NAUDASCHER E, ROCKWELL D. Flow-induced vibrations: An engineering guide[M]. Boca Raton: CPC Press, 1994. [2] WANG J, ZHAO W, SU Z, et al. Enhancing vortex-induced vibrations of a cylinder with rod attachments for hydrokinetic power generation[J]. Mechanical Systems and Signal Processing, 2020, 145: 106912. doi: 10.1016/j.ymssp.2020.106912 [3] MEI Y F, ZHENG C, AUBRY N, et al. Active control for enhancing vortex induced vibration of a circular cylinder based on deep reinforcement learning[J]. Physics of Fluids, 2021, 33(10): 103604. doi: 10.1063/5.0063988 [4] 李椿萱, 彭少波, 吴子牛. 附属小圆柱对主圆柱绕流影响的数值模拟[J]. 北京航空航天大学学报, 2003, 29(11): 951-958.LI C X, PENG S B, WU Z N. Numerical study of flow around a main cylinder by controlled satellite cylinders[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(11): 951-958(in Chinese). [5] 周潇, 胡烨, 王晋军. 前置隔板对圆柱绕流影响的实验分析[J]. 北京航空航天大学学报, 2016, 42(1): 172-179.ZHOU X, HU Y, WANG J J. Experimental analysis on flow past circular cylinder attached to frontal splitter plate[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 172-179(in Chinese). [6] LAM K, LIN Y F. Large eddy simulation of flow around wavy cylinders at a subcritical Reynolds number[J]. International Journal of Heat and Fluid Flow, 2008, 29(4): 1071-1088. doi: 10.1016/j.ijheatfluidflow.2008.01.006 [7] 邹琳, 秦傲, 杨耀宗, 等. 波浪锥型圆柱流固耦合振动机理研究[J]. 振动与冲击, 2022, 41(3): 18-26.ZOU L, QIN A, YANG Y Z, et al. Fluid-structure coupled vibration mechanism of wave conical cylinder[J]. Journal of Vibration and Shock, 2022, 41(3): 18-26(in Chinese). [8] HARIMI I, SAGHAFIAN M. Numerical simulation of fluid flow and forced convection heat transfer from tandem circular cylinders using overset grid method[J]. Journal of Fluids and Structures, 2012, 28: 309-327. doi: 10.1016/j.jfluidstructs.2011.12.006 [9] HU X F, ZHANG X S, YOU Y X. On the flow around two circular cylinders in tandem arrangement at high Reynolds numbers[J]. Ocean Engineering, 2019, 189: 106301. doi: 10.1016/j.oceaneng.2019.106301 [10] PAPAIOANNOU G V, YUE D K P, TRIANTAFYLLOU M S, et al. Three-dimensionality effects in flow around two tandem cylinders[J]. Journal of Fluid Mechanics, 2006, 558: 387-413. doi: 10.1017/S0022112006000139 [11] 涂佳黄, 曹波, 谭潇玲, 等. 串列双圆柱体绕流特性与互扰效应研究[J]. 应用力学学报, 2019, 36(4): 869-875.TU J H, CAO B, TAN X L, et al. Study on flow characteristics and mutual interference effect around tandem double cylinders[J]. Chinese Journal of Applied Mechanics, 2019, 36(4): 869-875(in Chinese). [12] KUMAR D, SOURAV K, SEN S. Steady separated flow around a pair of identical square cylinders in tandem array at low Reynolds numbers[J]. Computers & Fluids, 2019, 191: 104244. [13] DERAKHSHANDEH J F, GHARBIA Y, JI C. Numerical investigations on flow over tandem grooved cylinders[J]. Ocean Engineering, 2022, 251: 111160. doi: 10.1016/j.oceaneng.2022.111160 [14] 王裕夫, 陶国权, 刘东旭, 等. 基于大涡模拟的平流层浮空器气动特性分析[J]. 北京航空航天大学学报, 2015, 41(4): 616-623.WANG Y F, TAO G Q, LIU D X, et al. Analysis of stratospheric lighter-than-air vehicle’s aerodynamic characteristics based on large eddy simulation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(4): 616-623(in Chinese). [15] ZHANG H, YANG J, XIAO L, et al. Large-eddy simulation of the flow past both finite and infinite circular cylinders at Re = 3900 [J]. Journal of Hydrodynamics, 2015, 27(2): 195-203. doi: 10.1016/S1001-6058(15)60472-3 [16] ZDRAVKOVICH M M, BRAND V P, MATHEW G, et al. Flow past short circular cylinders with two free ends[J]. Journal of Fluid Mechanics, 1989, 203: 557-575. doi: 10.1017/S002211208900159X [17] BREUER M. Large eddy simulation of the subcritical flow past a circular cylinder: Numerical and modeling aspects[J]. International Journal for Numerical Methods in Fluids, 1998, 28(9): 1281-1302. doi: 10.1002/(SICI)1097-0363(19981215)28:9<1281::AID-FLD759>3.0.CO;2-# [18] 刘小兵, 姜会民, 王世博, 等. 串列三圆柱的脉动气动力特性试验研究[J]. 振动与冲击, 2021, 40(13): 96-103. doi: 10.13465/j.cnki.jvs.2021.13.013LIU X B, JIANG H M, WANG S B, et al. Tests for fluctuating aerodynamic force characteristics of three cylinders in series[J]. Journal of Vibration and Shock, 2021, 40(13): 96-103(in Chinese). doi: 10.13465/j.cnki.jvs.2021.13.013 [19] 赵桂欣, 桂洪斌, 王晓聪. 有限长波浪形圆柱绕流数值模拟[J]. 哈尔滨工业大学学报, 2021, 53(6): 163-170.ZHAO G X, GUI H B, WANG X C. Numerical simulation of flow around finite-length wavy cylinders[J]. Journal of Harbin Institude of Technology, 2021, 53(6): 163-170(in Chinese). [20] 赵斌娟, 谢昀彤, 廖文言, 等. 第二代涡识别方法在混流泵内部流场中的适用性分析[J]. 机械工程学报, 2020, 56(14): 216-223. doi: 10.3901/JME.2020.14.216ZHAO B J, XIE Y T, LIAO W Y, et al. Adaptability analysis of second generation vortex recognition method in internal flow field of mixed-flow pumps[J]. Journal of Mechanical Engineering, 2020, 56(14): 216-223(in Chinese). doi: 10.3901/JME.2020.14.216 -






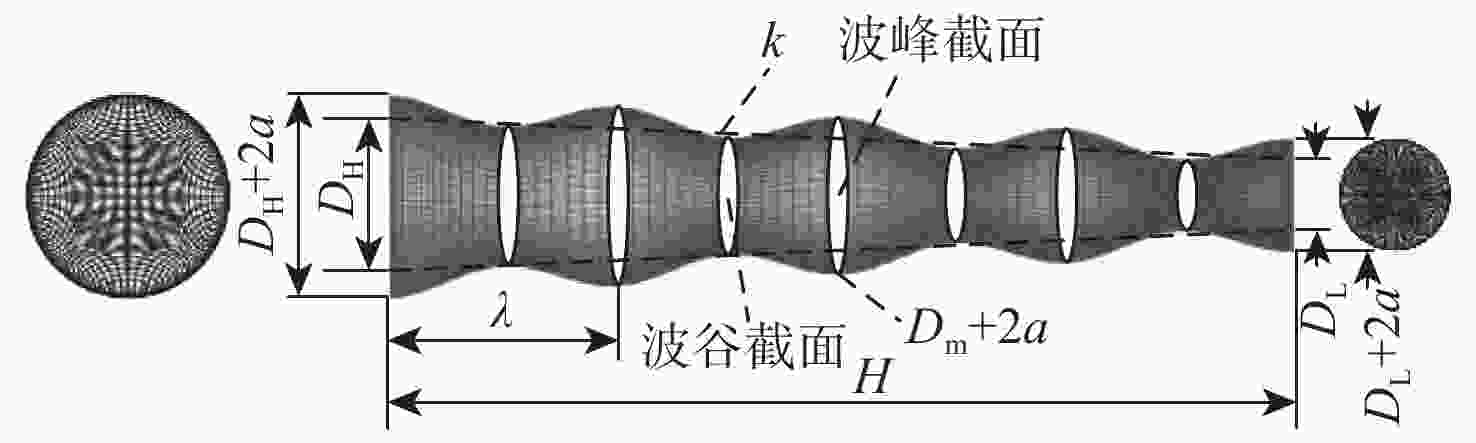
 下载:
下载: