Efficient surrogate-based aerodynamic optimization with parameter-free adaptive penalty function
-
摘要:
在飞行器气动外形优化设计中,复杂约束条件导致设计空间可行域呈现不连续的特征,且理想解大多靠近约束边界,传统高效代理模型方法难以适用。研究了参考点对优化设计的影响,提出了一种考虑约束的参考点选择机制;对于最优解靠近边界的问题,罚函数法更加有效,但惩罚因子的设置对于罚函数方法影响很大,不合适的惩罚因子反而会损害优化效率,分析了优化过程中罚函数方法对惩罚因子的要求,提出了一种无参数自适应罚函数的代理模优化设计方法,引入基于样本分析的惩罚项,结合归一化目标值和约束值,在优化过程中动态调整惩罚因子,使优化能够尽可能地聚焦于可行域内,迅速收敛到最优解,实现样本的高效配置。通过带约束的函数算例和翼型优化算例证实,所提方法可以大幅提高飞行器气动外形优化设计效率。
Abstract:Complex constraints must be addressed in the aerodynamic optimizations. Distinct constraints not only influence the optimization outcomes but also significantly influence the optimization method's efficacy. This paper investigates the impact of reference points on optimization design results using the constrained efficient global optimization method (EGO) and suggests a mechanism for selecting reference points that takes constraints into account. Afterwards, for the problem of constraint processing, the constrained expected improvement (EI) method and the penalty function method are compared and found that the penalty function method can find a feasible solution that satisfies the constraints more quickly. However, in this process, the penalty factor has a great influence on the optimization efficiency, and inappropriate penalty factors will damage the optimization efficiency. Drawing on the aforementioned evaluation, this study suggests a constrained EGO technique utilizing an adaptive penalty function that is free of parameters. By normalizing the target value and the constraint value, the feasible solution with the smallest target value or the infeasible solution closest to the feasible region is selected as the reference point. The penalty factor is adaptively adjusted, so that the algorithm can search for the ideal solution sufficiently. This approach can significantly increase the optimization efficiency, as shown by the constrained test functions and airfoil design challenges.
-
Key words:
- optimization design /
- surrogate model /
- reference point /
- aerodynamic design /
- adaptive penalty function
-
表 1 全局优化函数问题
Table 1. Benchmark problems for global optimization
函数 维度 约束数量 设计范围 最优解 G1 13 9 ${[0,1]^9} \times {[0,100]^3} \times [0,1]$ −15 G3 10 1 ${[0,10]^{10}}$ −1.0005 G5 4 5 ${[0,1200]^2} \times {[ - 0.55,0.55]^2}$ 5126.49 G6 2 2 ${[0,10]^2}$ −6961.8 G24 2 2 $[0,3] \times [0,4]$ −5.508 表 2 函数测试结果
Table 2. Results of benchmark problem
函数 CEI PCEI APCEI G1 200(30) >124.9(2) 115.1(17.48) G3 200(30) >191.7(9) 175.3(9.6) G5 200(30) 53.6(1.75) 44.8(2.71) G6 74.6(3.55) 32.6(1.21) 14.3(0.99) G24 22.4(3.08) 13.5(1.11) 8.6(1.35) 表 3 RAE2822翼型计算网格参数
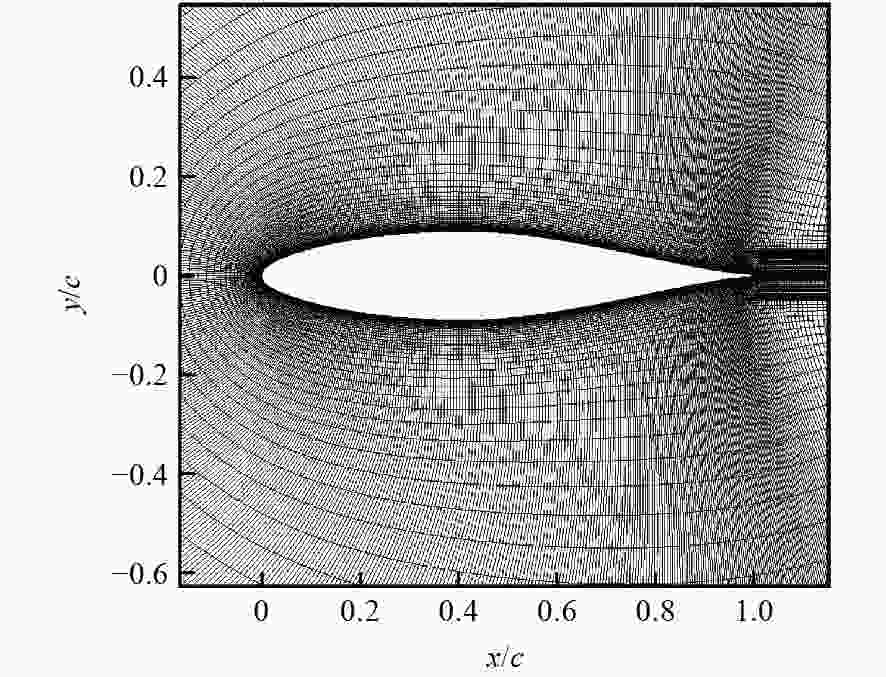
Table 3. Parameter settings of computational grid of RAE2822
参数 数值 远场大小 50 网格规模 601×213 物面第一层网格距离 5×10−6 物面法向网格增长率 1.13 翼型前缘网格距离 0.001 翼型后缘网格距离 0.001 表 4 不同方法设计结果对比
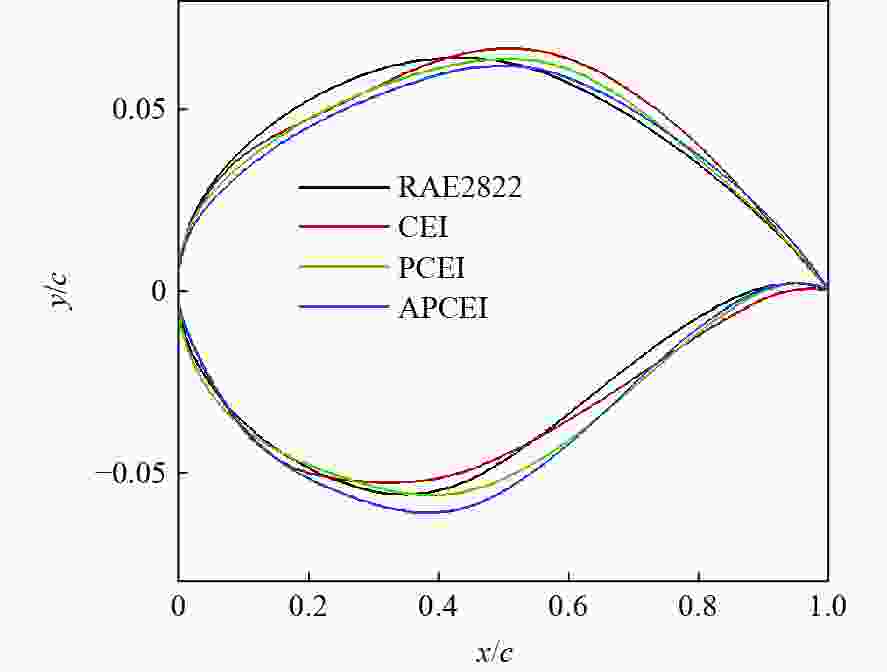
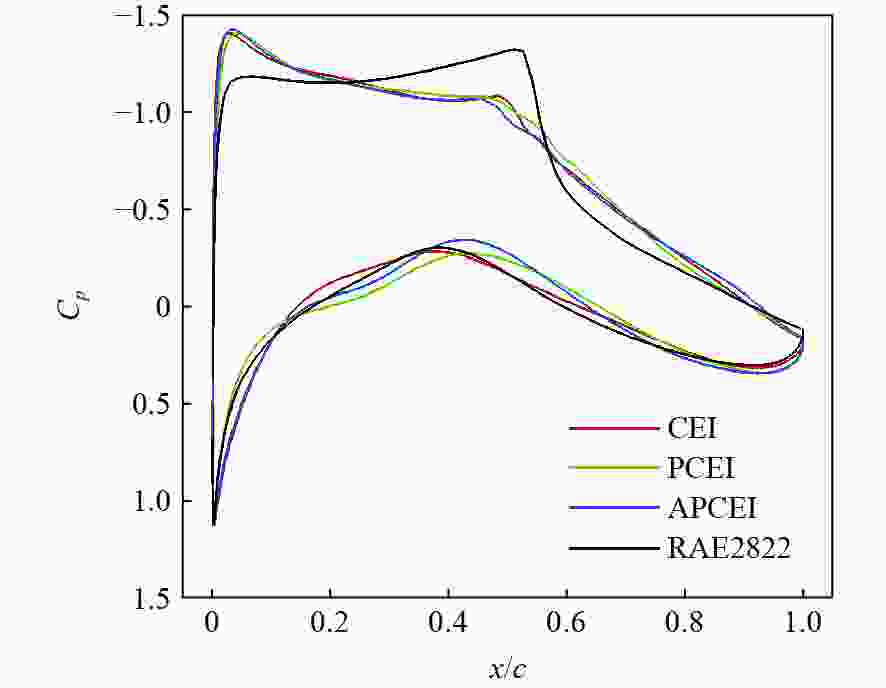
Table 4. Comparison of design results for different methods
方法 Cd /counts Cm A RAE2822 203.1 −0.0927 0.07787 CEI 113.5 −0.0892 0.07787 PCEI 112.1 −0.0916 0.07787 APCEI 111.6 −0.0919 0.07787 表 5 NACA 65,3-018翼型计算网格参数
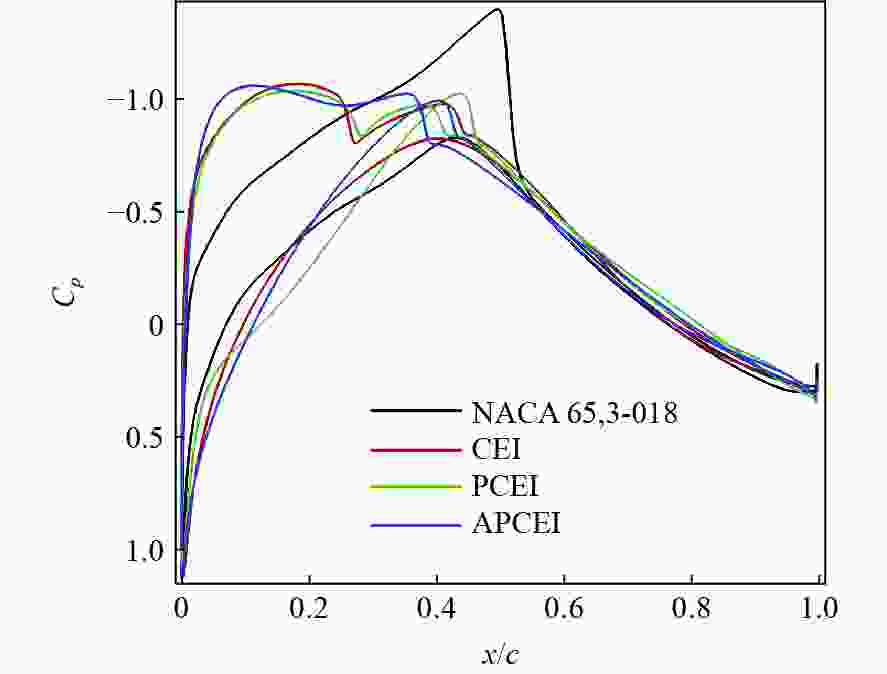
Table 5. Parameter settings of computational grid of NACA 65,3-018
参数 数值 远场大小 50 网格规模 401×201 物面第一层网格距离 5×10−6 物面法向网格增长率 1.12 翼型前缘网格距离 0.001 翼型后缘网格距离 0.0005 表 6 不同约束EGO方法设计结果对比
Table 6. Comparison of design results for different EGO methods
方法 Cd /counts Cm 相对厚度 RAE2822 114.1 −0.0098 0.18 CEI 87.9 0.0307 0.18 PCEI 87.2 0.0303 0.18 APCEI 86.5 0.0300 0.18 -
[1] QUEIPO N V, HAFTKA R T, SHYY W, et al. Surrogate-based analysis and optimization[J]. Progress in Aerospace Sciences, 2005, 41(1): 1-28. doi: 10.1016/j.paerosci.2005.02.001 [2] JONES D R. A taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization, 2001, 21(4): 345-383. doi: 10.1023/A:1012771025575 [3] LOCATELLI M. Bayesian algorithms for one-dimensional global optimization[J]. Journal of Global Optimization, 1997, 10(1): 57-76. doi: 10.1023/A:1008294716304 [4] WANG G G, SHAN S. Review of metamodeling techniques in support of engineering design optimization[J]. Journal of Mechanical Design, 2007, 129(4): 370-380. doi: 10.1115/1.2429697 [5] XING J, LUO Y J, GAO Z H. A global optimization strategy based on the Kriging surrogate model and parallel computing[J]. Structural and Multidisciplinary Optimization, 2020, 62(1): 405-417. [6] LI Y H, SHI J J, CEN H, et al. A Kriging-based adaptive global optimization method with generalized expected improvement and its application in numerical simulation and crop evapotranspiration[J]. Agricultural Water Management, 2021, 245: 106623. doi: 10.1016/j.agwat.2020.106623 [7] 夏露, 王丹. 基于Kriging自适应代理模型的气动优化方法[J]. 航空计算技术, 2013, 43(1): 13-17. doi: 10.3969/j.issn.1671-654X.2013.01.004XIA L, WANG D. Aerodynamic optimization method based on Kriging adaptive surrogate model[J]. Aeronautical Computing Technique, 2013, 43(1): 13-17(in Chinese). doi: 10.3969/j.issn.1671-654X.2013.01.004 [8] 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225.HAN Z H. Kriging surrogate model and its application to design optimization: A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225(in Chinese). [9] BHOSEKAR A, IERAPERTRITOU M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review[J]. Computers & Chemical Engineering, 2018, 108(4): 250-267. [10] BONS N P, HE X L, MADER C A, et al. Multimodality in aerodynamic wing design optimization[J]. AIAA Journal, 2019, 57(3): 1004-1018. doi: 10.2514/1.J057294 [11] LEIFSSON L, KO A, MASON W H, et al. Multidisciplinary design optimization of blended-wing-body transport aircraft with distributed propulsion[J]. Aerospace Science and Technology, 2013, 25(1): 16-28. [12] VISWANATH A, FORRESTER A I J, KEANE A J. Constrained design optimization using generative topographic mapping[J]. AIAA Journal, 2014, 52(5): 1010-1023. doi: 10.2514/1.J052414 [13] ZHOU L, HUANG J T, GAO Z H, et al. Three-dimensional aerodynamic/stealth optimization based on adjoint sensitivity analysis for scattering problem[J]. AIAA Journal, 2020, 58(6): 2702-2715. doi: 10.2514/1.J059136 [14] 黄江涛, 高正红, 余婧, 等. 大型民用飞机气动外形典型综合设计方法[J]. 航空学报, 2019, 40(2): 522369.HUANG J T, GAO Z H, YU J, et al. A typical integrated design method for aerodynamic shape optimization of large civil aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(2): 522369(in Chinese). [15] SASENA M J, PAPALAMBROS P, GOOVAERTS P. Exploration of metamodeling sampling criteria for constrained global optimization[J]. Engineering Optimization, 2002, 34(3): 263-278. doi: 10.1080/03052150211751 [16] PARR J M, KEANE A J, FORRESTER A I J, et al. Infill sampling criteria for surrogate-based optimization with constraint handling[J]. Engineering Optimization, 2012, 44(10): 1147-1166. doi: 10.1080/0305215X.2011.637556 [17] BASUDHAR A, DRIBUSCH C, LACAZE S, et al. Constrained efficient global optimization with support vector machines[J]. Structural and Multidisciplinary Optimization, 2012, 46(2): 201-221. [18] BRERETON R G, LLOYD G R. Support vector machines for classification and regression[J]. Analyst, 2010, 135(2): 230-267. doi: 10.1039/B918972F [19] BAGHERI S, KONEN W, ALLMENDINGER R, et al. Constraint handling in efficient global optimization[C]// Proceedings of the Genetic and Evolutionary Computation Conference. New York: ACM, 2017, 1: 673-680. [20] KRAMER O. A review of constraint-handling techniques for evolution strategies[J]. Applied Computational Intelligence and Soft Computing, 2010, 2010: 3. [21] MEZURA-MONTES E, COELLO C A C. Constraint-handling in nature-inspired numerical optimization: past, present and future[J]. Swarm and Evolutionary Computation, 2011, 1(4): 173-194. doi: 10.1016/j.swevo.2011.10.001 [22] LIU B, GROUT V, NIKOLAEVA A. Efficient global optimization of actuator based on a surrogate model assisted hybrid algorithm[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5712-5721. [23] ZAEFFERER M, STORK J, FRIESE M, et al. Efficient global optimization for combinatorial problems[C]// Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation. New York: ACM, 2014, 1: 871-878. [24] 王红涛, 竺晓程, 杜朝辉. 改进EGO算法在跨声速翼型气动优化设计中的应用[J]. 上海交通大学学报, 2009, 43(11): 1832-1836. doi: 10.3321/j.issn:1006-2467.2009.11.033WANG H T, ZHU X C, DU Z H. Application of the improved EGO algorithm in transonic airfoil aerodynamic optimization design[J]. Journal of Shanghai Jiao Tong University, 2009, 43(11): 1832-1836(in Chinese). doi: 10.3321/j.issn:1006-2467.2009.11.033 [25] 龙腾, 刘建, 陈余军, 等. 基于约束EGO的对地观测卫星多学科设计优化[J]. 机械工程学报, 2018, 54(10): 133-142. doi: 10.3901/JME.2018.10.133LONG T, LIU J, CHEN Y J, et al. Multi-disciplinary design optimization of earth observation satellite based on constrained EGO[J]. Journal of Mechanical Engineering, 2018, 54(10): 133-142(in Chinese). doi: 10.3901/JME.2018.10.133 [26] DONG H C, SONG B W, DONG Z M, et al. SCGOSR: Surrogate-based constrained global optimization using space reduction[J]. Applied Soft Computing, 2018, 65(c): 462-477. [27] NADARAJSH S. Aerodynamic design optimization: Drag minimization of the NACA 0012 in transonic inviscid flow[EB/OL]. (2017-09-15)[2022-05-31]. https://info.aiaa.org/tac/ASG/APATC/AeroDesignOpt-DG/Tes. [28] KEANE A, FORRESTER A, SOBESTER A. Engineering design via surrogate modelling: A practical guide[M]. Reston: AIAA, 2008. [29] CASTILLO O, MELIN P. Genetic algorithms and simulated annealing[M]// Soft Computing and Fractal Theory for Intelligent Manufacturing. Heidelberg: Physica, 2003, 1: 93-125. [30] AKBARI H, KAZEROONI A. KASRA: A Kriging-based adaptive space reduction algorithm for global optimization of computationally expensive black-box constrained problems[J]. Applied Soft Computing, 2020, 90: 106154. doi: 10.1016/j.asoc.2020.106154 [31] KULFAN B, BUSSOLETTI J. Fundamental parameteric geometry representations for aircraft component shapes[C]// 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Reston: AIAA, 2006: 6948. [32] 王超, 高正红, 张伟, 等. 自适应设计空间扩展的高效代理模型气动优化设计方法[J]. 航空学报, 2018, 39(7): 121745.WANG C, GAO Z H, ZHANG W, et al. Efficient surrogate-based aerodynamic design optimization method with adaptive design space expansion[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 121745(in Chinese). [33] SEARS W. Flying-wing airplanes-The XB-35/YB-49 program[C]// The evolution of aircraft wing design; Proceedings of the Symposium. Reston: AIAA, 1980: 3036. [34] LIEBECK R H. Design of the blended-wing-body subsonic transport[J]. Journal of Aircraft, 2004, 41(1): 10-25. doi: 10.2514/1.9084 -






 下载:
下载: