Incremental guidance method for kinetic kill vehicles with target maneuver compensation
-
摘要:
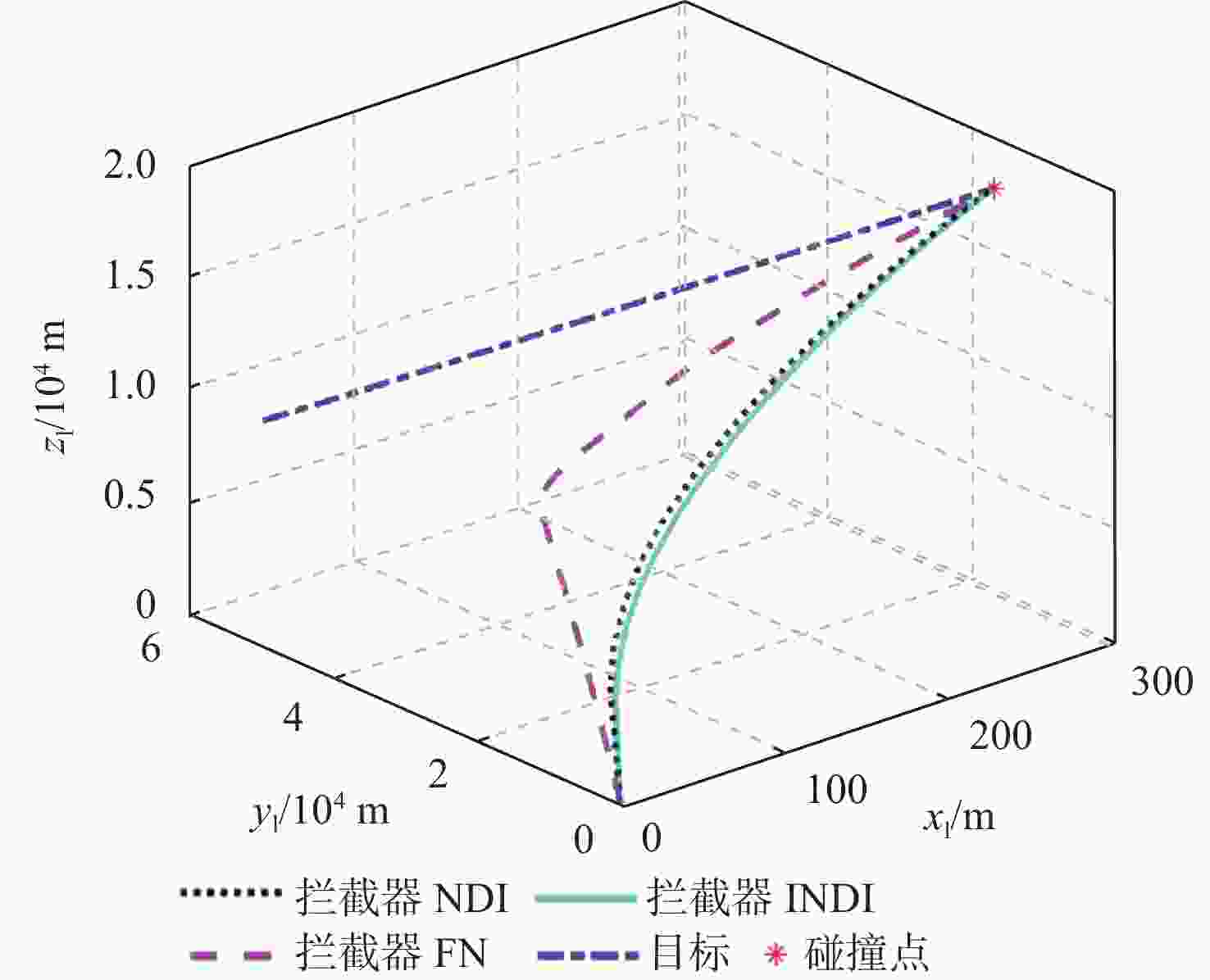
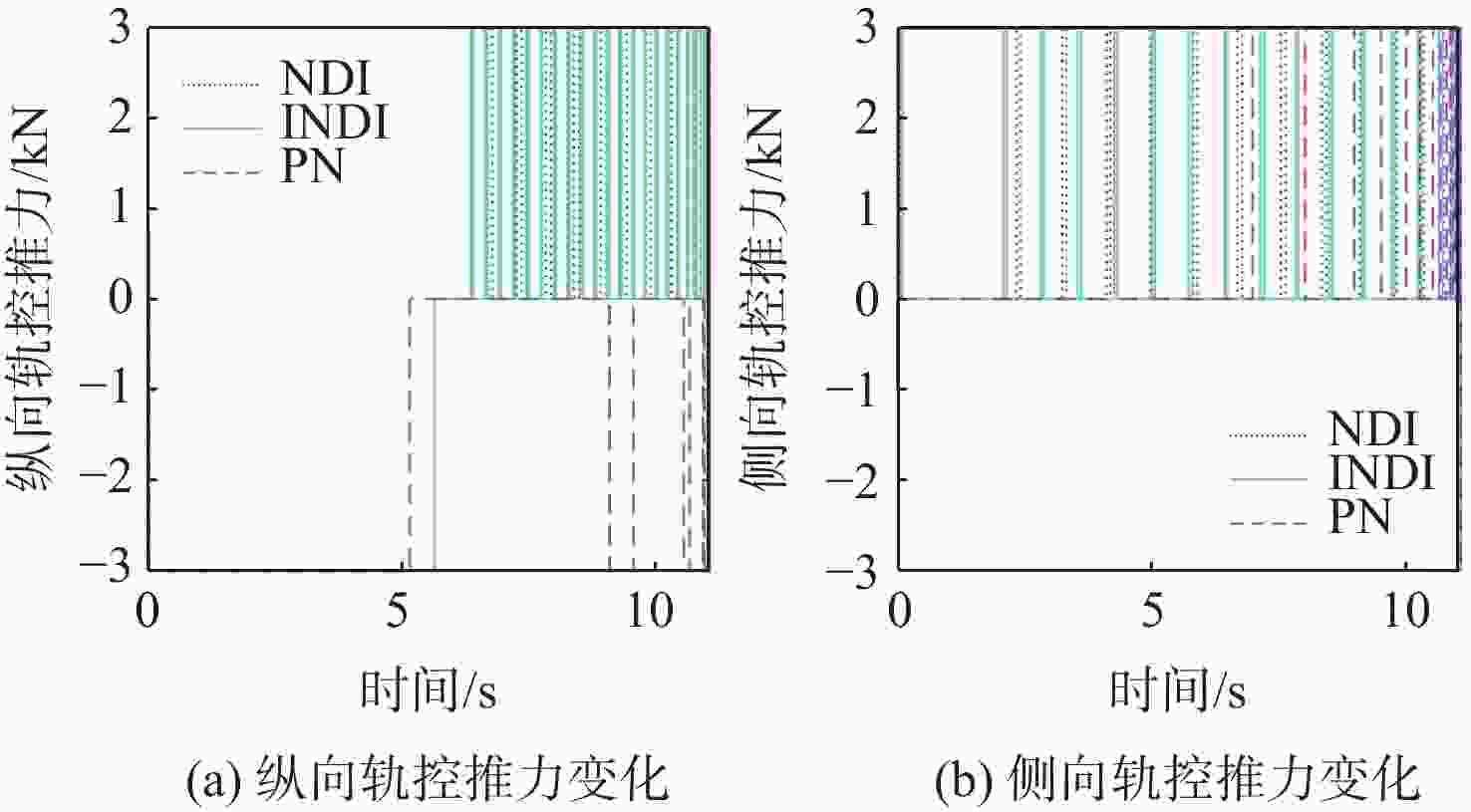
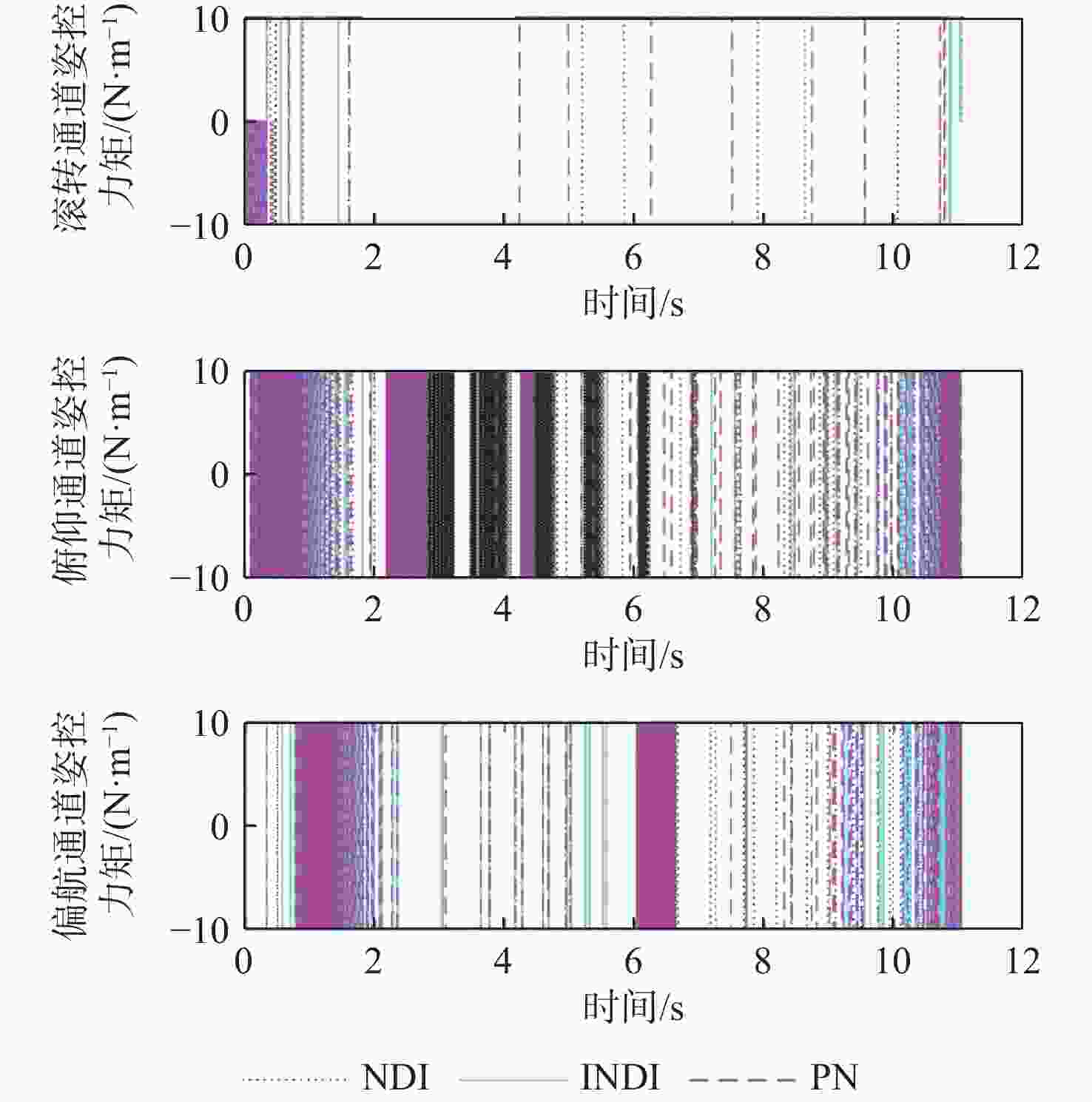
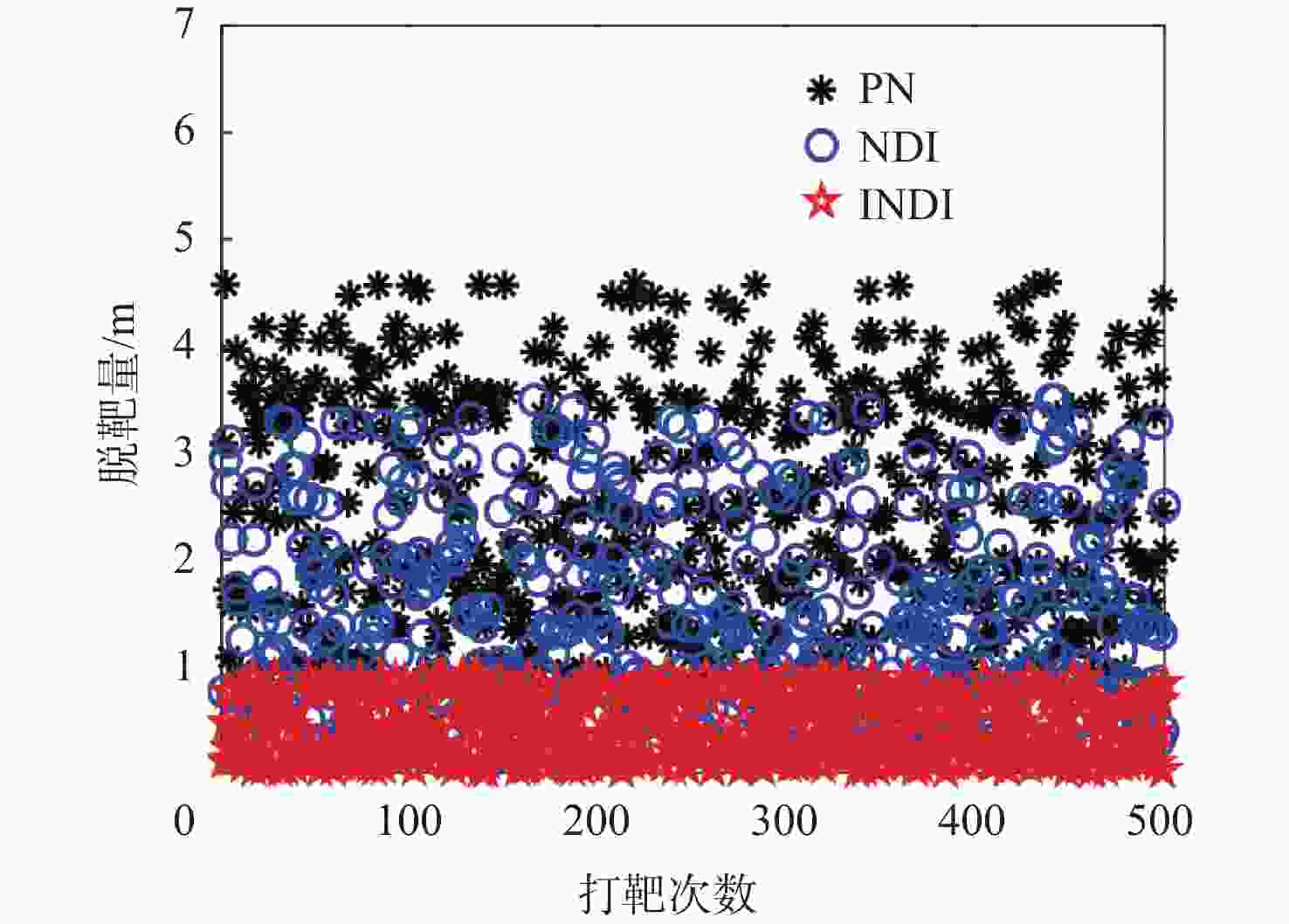
面向目标强机动、推力干扰、测量偏差的动能拦截器强抗扰末制导方法设计问题,提出一种目标机动补偿的大气层外动能拦截器增量式强抗扰末制导方法。通过回采推力传感信息、视线转率辅助微分信息,同时联合增量式制导方法与惯性时延的扰动估计方法,对目标机动等不确定性和内外部不确定性等带来的扰动进行实时补偿并融合至制导算法,从而实现复杂工况下拦截器对抗机动目标的制导系统扰动降级与鲁棒增强等目的。复杂工况下仿真结果表明:所提方法对强机动目标、测量偏差、推力干扰等多源扰动具有强抗扰能力,并且能够实现精确碰撞式拦截任务。
Abstract:In view of the design problem of a strong anti-disturbance terminal guidance method for kinetic kill vehicles against highly maneuvering targets, thrust disturbance, and measurement deviation, an incremental strong anti-disturbance terminal guidance method for extra-atmospheric kinetic kill vehicles with target maneuver compensation is proposed. By exploiting the thrust sensing information and the auxiliary differential information of the line-of-sight rate and combining the incremental guidance law and the inertial time delay-based disturbance estimation method, the disturbance caused by the uncertainties brought by target maneuvers and the internal and external uncertainties was compensated in real time and integrated into the guidance algorithm, so as to degrade the disturbance and enhance the robustness of the kinetic kill vehicle’s guidance system against maneuvering targets under complex working conditions. The simulation results under complex working conditions show that the proposed method has strong anti-disturbance capability against multi-source disturbances such as highly maneuvering targets, measurement deviations, and thrust disturbance and thus can fulfill interception tasks by precise collision.
-
表 1 抗扰能力对比
Table 1. Comparison of anti-disturbance capability
制导律 增益条件 系统扰动 收敛域 $ {A_{{\textit{z}}{\rm{M}}}} = \dfrac{{{f_{\textit{z}}} + {k_{\textit{z}}}\alpha }}{{{b_{\textit{z}}}}} $ $ {k_{\textit{z}}} > \dfrac{{\left| {{d_{\textit{z}}}} \right|}}{{\left| \alpha \right|}} $ $ \left| {{d_{\textit{z}}}} \right| $ $ \left| \alpha \right| \leqslant \dfrac{{\left| {{d_{\textit{z}}}} \right|}}{{{k_{\textit{z}}}}} $ $ \Delta {A_{{\textit{z}}{\rm{Mc}}}} = \dfrac{{{{\dot \alpha }_0} + {k_{{\textit{z}}{\rm{i}}}}\alpha + \Delta {{\hat d}_{\textit{z}}}}}{{{b_{{\textit{z}}0}}}} $ $ {k_{{\textit{z}}{\rm{i}}}} > \dfrac{{\left| {\Delta {{\tilde d}_{\textit{z}}}} \right|}}{{\left| \alpha \right|}} $ $ \left| {\Delta {{\tilde d}_{\textit{z}}}} \right| $ $ \left| \alpha \right| \leqslant \dfrac{{\left| {\Delta {{\tilde d}_{\textit{z}}}} \right|}}{{{k_{{\textit{z}}{\rm{i}}}}}} $ 表 2 不同制导方法结果对比
Table 2. Comparison results of different guidance methods
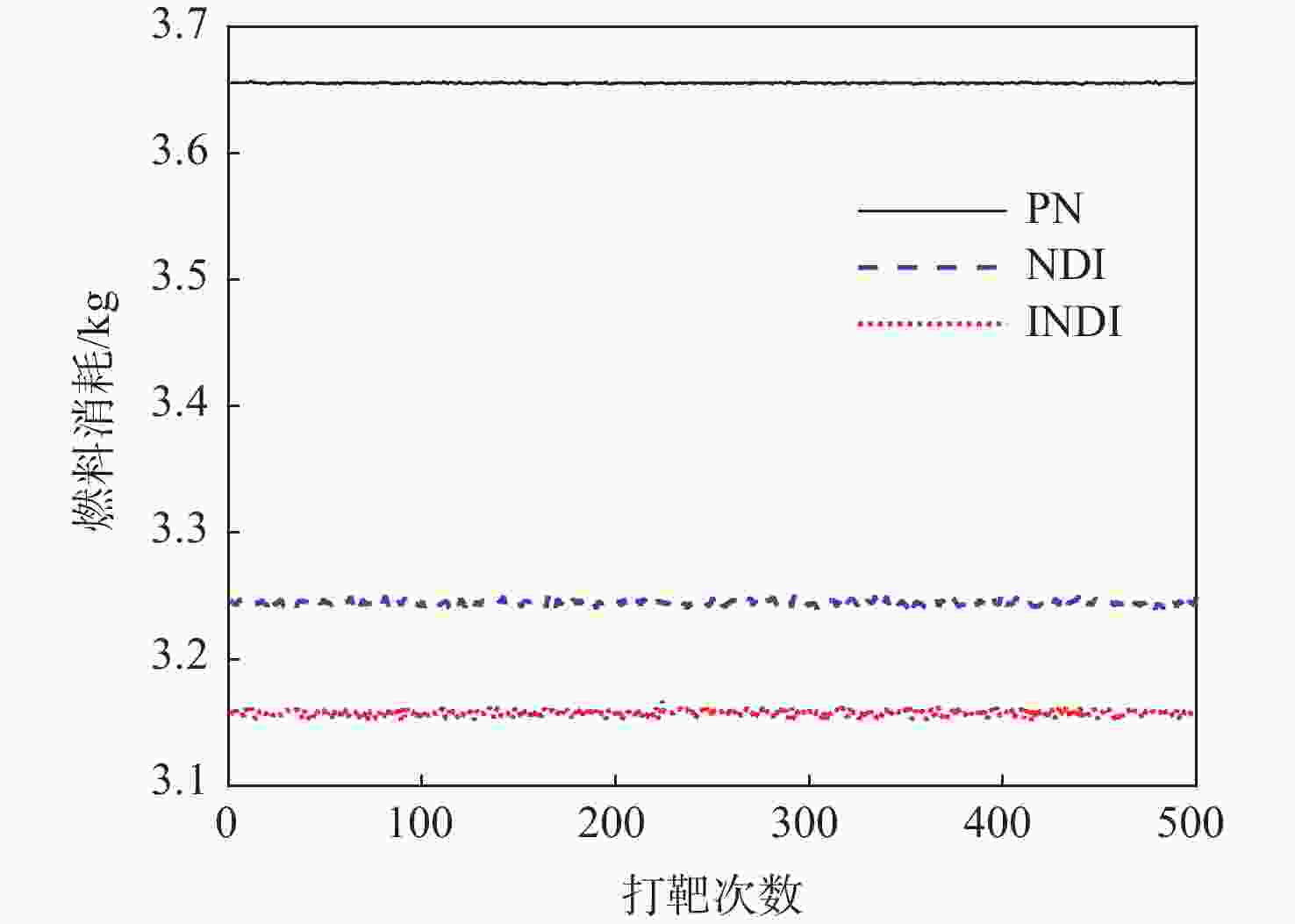
制导方法 仿真情形 脱靶量/m 燃料消耗/kg NDI 标称低机动 0.920 1.995 偏差高机动 2.015 3.245 INDI 标称低机动 0.394 1.930 偏差高机动 0.405 3.157 PN 标称低机动 0.870 1.971 偏差高机动 2.553 3.655 -
[1] 谢愈, 刘鲁华, 汤国建, 等. 多拦截器总体拦截方案设计与分析[J]. 北京航空航天大学学报, 2012, 38(3): 303-308.XIE Y, LIU L H, TANG G J, et al. Design and analysis of interception project for multiple kill vehicle interceptor[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(3): 303-308(in Chinese). [2] 姚郁, 郑天宇, 贺风华, 等. 飞行器末制导中的几个热点问题与挑战[J]. 航空学报, 2015, 36(8): 2696-2716.YAO Y, ZHENG T Y, HE F H, et al. Several hot issues and challenges in terminal guidance of flight vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2696-2716(in Chinese). [3] ADLER F P. Missile guidance by three-dimensional proportional navigation[J]. Journal of Applied Physics, 1956, 27(5): 500-507. doi: 10.1063/1.1722411 [4] JEON I S, KARPENKO M, LEE J I. Connections between proportional navigation and terminal velocity maximization guidance[J]. Journal of Guidance Control Dynamics, 2020, 43(2): 383-388. doi: 10.2514/1.G004672 [5] 刘刚. 阻力和升力加速度指令快速解析与跟踪制导[J]. 北京航空航天大学学报, 2022, 48(3): 401-411.LIU G. Drag and lift acceleration commands rapid calculation and tracking guidance[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(3): 401-411(in Chinese). [6] 汤一华, 陈士橹, 徐敏, 等. 基于Terminal滑模的动能拦截器末制导律研究[J]. 空军工程大学学报(自然科学版), 2007, 8(2): 22-25.TANG Y H, CHEN S L, XU M, et al. Terminal guidance law of kinetic interceptor based on terminal sliding mode[J]. Journal of Air Force Engineering University (Natural Science Edition), 2007, 8(2): 22-25(in Chinese). [7] 朱波, 全权, 蔡开元. 动能拦截器末制导启控点的BP网络方法[J]. 北京航空航天大学学报, 2007, 33(3): 332-335. doi: 10.3969/j.issn.1001-5965.2007.03.020ZHU B, QUAN Q, CAI K Y. BP networks method of handing-over point of KKV[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(3): 332-335(in Chinese). doi: 10.3969/j.issn.1001-5965.2007.03.020 [8] 田源, 王俊波, 任章. 拦截大气层外机动目标的模糊导引规律[J]. 北京航空航天大学学报, 2010, 36(7): 816-820.TIAN Y, WANG J B, REN Z. Fuzzy guidance law for interception of exoatmospheric maneuvering targets[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(7): 816-820(in Chinese). [9] 高乾, 周林, 王云鹏, 等. 大气层外动能拦截器顺轨拦截制导律设计[J]. 导弹与航天运载技术, 2011(6): 1-5.GAO Q, ZHOU L, WANG Y P, et al. A guidance law design for exoatmospheric kinetic interceptor[J]. Missiles and Space Vehicles, 2011(6): 1-5(in Chinese). [10] REISNER D, SHIMA T. Optimal guidance-to-collision law for an accelerating exoatmospheric interceptor missile[J]. Journal of Guidance Control Dynamics, 2013, 36(6): 1695-1708. doi: 10.2514/1.61258 [11] 邹昕光, 周荻, 杜润乐, 等. 大气层外主动防御三维自适应滑模制导律[J]. 系统工程与电子技术, 2015, 37(2): 365-371. doi: 10.3969/j.issn.1001-506X.2015.02.22ZOU X G, ZHOU D, DU R L, et al. Active defense exo-atmospheric adaptive sliding mode guidance law in three dimensions[J]. Systems Engineering and Electronics, 2015, 37(2): 365-371(in Chinese). doi: 10.3969/j.issn.1001-506X.2015.02.22 [12] 杨旭, 张皎, 刘源翔. 基于碰撞航线的动能拦截器滑模制导律设计[J]. 北京航空航天大学学报, 2015, 41(11): 2095-2102.YANG X, ZHANG J, LIU Y X. Sliding mode guidance law for KKV based on collision course[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 2095-2102(in Chinese). [13] GUTMAN S, RUBINSKY S. 3D-nonlinear vector guidance and exo-atmospheric interception[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 3014-3022. doi: 10.1109/TAES.2015.140204 [14] 郭建国, 韩拓, 周军, 等. 大气层外动能拦截器末制导律与能量优化方法[J]. 系统工程与电子技术, 2017, 39(2): 376-382. doi: 10.3969/j.issn.1001-506X.2017.02.22GUO J G, HAN T, ZHOU J, et al. Terminal guidance law for exoatmospheric kill vehicle with energy optimization method[J]. Systems Engineering and Electronics, 2017, 39(2): 376-382(in Chinese). doi: 10.3969/j.issn.1001-506X.2017.02.22 [15] JUNG Y S, LEE J I, LEE C H, et al. A new collision control guidance law based on speed control for kill vehicles[J]. International Journal of Aeronautical and Space Sciences, 2019, 20(3): 792-805. doi: 10.1007/s42405-019-00147-8 [16] 李炯, 张涛, 王华吉, 等. 侧窗探测动能拦截器轨控有限时间收敛制导律[J]. 控制与决策, 2019, 34(5): 973-980.LI J, ZHANG T, WANG H J, et al. Finite-time convergence guidance law of side windows detection kinetic kill vehicle with orbit control in terminal[J]. Control and Decision, 2019, 34(5): 973-980(in Chinese). [17] 杨彪, 荆武兴, 李涧青, 等. 动能拦截器运动伪装末制导律设计[J]. 宇航学报, 2020, 41(1): 91-100.YANG B, JING W X, LI J Q, et al. Motion camouflage terminal guidance law of kinetic energy interceptor[J]. Journal of Astronautics, 2020, 41(1): 91-100(in Chinese). [18] KIM Y W, SEO M G, LEE C H. Investigation on energy-effective guidance-to-collision strategies for exo-atmospheric interceptors[J]. Aerospace Science and Technology, 2022, 124: 107563. doi: 10.1016/j.ast.2022.107563 [19] WANG X R, VAN KAMPEN E J, CHU Q P, et al. Incremental sliding-mode fault-tolerant flight control[J]. Journal of Guidance Control Dynamics, 2019, 42(2): 244-259. doi: 10.2514/1.G003497 [20] WANG X R, SUN S H, VAN KAMPEN E J, et al. Quadrotor fault tolerant incremental sliding mode control driven by sliding mode disturbance observers[J]. Aerospace Science and Technology, 2019, 87: 417-430. doi: 10.1016/j.ast.2019.03.001 [21] HAN T, HU Q L, SHIN H S, et al. Sensor-based robust incremental three-dimensional guidance law with terminal angle constraint[J]. Journal of Guidance Control Dynamics, 2021, 44(11): 2016-2030. doi: 10.2514/1.G006038 [22] HAN T, SHIN H S, HU Q L, et al. Differentiator-based incremental three-dimensional terminal angle guidance with enhanced robustness[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(5): 4020-4032. doi: 10.1109/TAES.2022.3158639 [23] 方艺忠, 韩拓, 胡庆雷. 导引头量测故障下的增量式三维制导律设计[J]. 宇航学报, 2022, 43(4): 508-517. doi: 10.3873/j.issn.1000-1328.2022.04.012FANG Y Z, HAN T, HU Q L. Incremental three dimensional guidance law design under seeker’s measuring faults[J]. Journal of Astronautics, 2022, 43(4): 508-517(in Chinese). doi: 10.3873/j.issn.1000-1328.2022.04.012 [24] PHADKE S B, TALOLE S E. Sliding mode and inertial delay control based missile guidance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3331-3346. doi: 10.1109/TAES.2012.6324711 -






 下载:
下载: