多策略融合改进的飞蛾火焰优化算法

何加文; 许贤泽; 高波

doi:10.13700/j.bh.1001-5965.2022.0707

多策略融合改进的飞蛾火焰优化算法

doi: 10.13700/j.bh.1001-5965.2022.0707

武汉大学电子信息学院，武汉 430072

基金项目: 国家自然科学基金(51975422)

详细信息

通讯作者:
E-mail：xxz@whu.edu.cn

中图分类号: TP301
计量
- 文章访问数: 215
- HTML全文浏览量: 102
- PDF下载量: 21
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-11
- 录用日期: 2022-09-02
- 网络出版日期: 2022-11-08
- 整期出版日期: 2024-09-27

Improved moth-flame optimization algorithm with multi-strategy integration

Electronic Information School，Wuhan University，Wuhan 430072，China

Funds: National Natural Science Foundation of China (51975422)

More Information

Corresponding author: E-mail：xxz@whu.edu.cn

摘要

摘要:
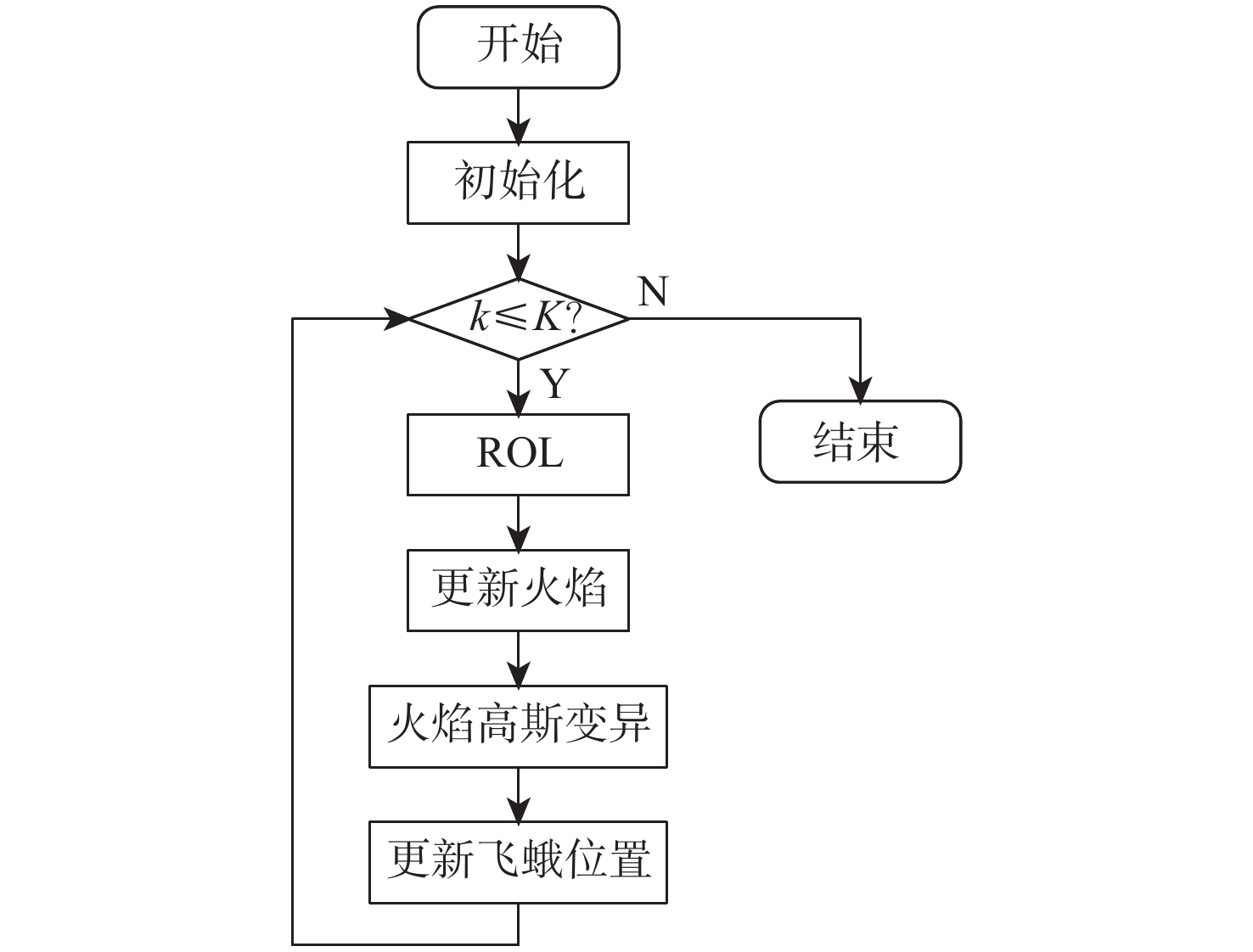
针对飞蛾火焰优化算法容易出现局部最优解、接近全局最优时开发能力不足等问题，提出一种多策略融合改进的飞蛾火焰优化 (RGMFO) 算法。在每次迭代开始时，使用随机反向学习策略获得高质量飞蛾种群；利用高斯变异将较差的火焰个体替换为优秀个体；使用阿基米德螺线、权重因子和围绕最优火焰飞行3种方式改进飞蛾更新机制。为验证所提算法的有效性，与11个不同类型的基准函数进行寻优测试，基准函数实验结果与秩和检验表明：相较于其他优化算法及其他MFO改进算法，所提算法具有更好的全局搜索能力与更高的寻优精度。将所提算法应用于减速器设计和槽形舱壁设计的实际工程场景中，以进一步验证算法的实用性与可行性。
- 飞蛾火焰优化算法 /
- 多策略融合 /
- 随机反向学习 /
- 高斯变异 /
- 智能优化
Abstract:
An enhanced moth-flame optimization algorithm with multi-strategy integration (RGMFO) was proposed in order to address the issues that the moth-flame optimization algorithm was prone to falling into the local optimum and that its exploitation ability was insufficient while it was approaching the global optimum. To generate high-quality moth populations, a random opposition-based learning strategy was applied at the start of each iteration. To generate high-quality moth populations, a random opposition-based learning strategy was applied at the start of each iteration. Gaussian mutation was then used to swap out subpar flame individuals with superior ones. Archimedes spirals, weighting factors, and the surrounding of a small number of optimal flames were employed to enhance the moth update mechanism. The proposed algorithm was tested on 11 benchmark functions of different types. The test results and rank sum test show that RGMFO has better global search ability and higher search accuracy. Lastly, RGMFO is applied to the engineering scenarios of reducer design and trough bulkhead design, which further verifies the practicability and feasibility of the algorithm.
- moth-flame optimization algorithm /
- multi-strategy integration /
- random opposition-based learning /
- Gaussian mutation /
- intelligent optimization

HTML全文

图 1 E值折线图及散点图（500次迭代）

Figure 1. E-value line chart and scatter chart (500 iterations)

下载: 全尺寸图片幻灯片

图 2 RGMFO算法流程

Figure 2. RGMFO algorithm flow

下载: 全尺寸图片幻灯片

图 3 RGMFO算法与对比算法迭代收敛曲线

Figure 3. Iterative convergence curves of RGMFO algorithm and comparative algorithms

下载: 全尺寸图片幻灯片

表 1 各算法参数设置

Table 1. Parameter setting of each algorithms

算法	参数
RGMFO	b=1，e₁=0.5，e₂=1，β=10
IMFO	b=1，A=0.5，B=0.6，c_rmin=0.55，c_rmax=0.65 σ_min=0.1，σ_max=0.15
CGMFO	b=2，β=8
ODSFMFO	m=6，γ=5，P_c=0.5，a_alpha=1， b_beta=1.5，l=10，b=1
MFO	b=1
GWO	a从2线性递减至0，r₁、r₂∈[0,1]
SCA	a=2，r₁从a线性递减至0
PSO	V_max=8，V_min=−8，w=0.2，c₁=3，c₂=3
DE	p_c=0.5
GA	p_c=0.7，p_m=0.1

下载: 导出CSV

表 2 基准测试函数

Table 2. Benchmark functions

函数类型	基准测试函数	维度	搜索区间	最优值
高维单峰	$ {F_1}(x) = \displaystyle\sum\limits_{i = 1}^d {x_i^2} $	30	[−100,100]^d	0
	$ {F_2}(x) = \displaystyle\sum\limits_{i = 1}^d {\left\| {{x_i}} \right\|} + \displaystyle\prod\limits_{i = 1}^d {\left\| {{x_i}} \right\|} $	30	[−10,10]^d	0
	$ {F_3}(x) = \displaystyle\sum\limits_{i = 1}^d {{{\left(\displaystyle\sum\limits_{j = 1}^i {{x_j}} \right)}^2}} $	30	[−100,100]^d	0
	$ {F_4}(x) = {\max _i}\{ \left\| {{x_i}} \right\|,1 \leqslant i \leqslant d\} $	30	[−100,100]^d	0
	$ {F_5}(x) = \displaystyle\sum\limits_{i = 1}^{d{{ - }}1} {[100{{({x_{i + 1}} - {x_i})}^2} + {{({x_i} - 1)}^2}]} $	30	[−30,30]^d	0
	$ {F_6}(x) = \displaystyle\sum\limits_{i = 1}^d {i \cdot x_i^4} + {\text{random[}}0,1{\text{)}} $	30	[−1.28,1.28]^d	0
高维多峰	$ {F_7}(x) = \displaystyle\sum\limits_{i = 1}^d {[x_i^2 - 10\cos (2{\text{π}}{x_i} + 10)]} $	30	[−5.12,5.12]^d	0
	$ {F_8}(x) = - 20\exp \left( - 0.2\sqrt {\dfrac{1}{d}\displaystyle\sum\limits_{i = 1}^d {x_i^2} } \right) - \exp \left(\dfrac{1}{d}\displaystyle\sum\limits_{i = 1}^d {\cos (2{\text{π}}{x_i})} \right) + 20 + {\text{e}} $	30	[−32,32]^d	0
	$ {F_9}(x) = \dfrac{1}{{4\;000}}\displaystyle\sum\limits_{i = 1}^d {x_i^2} - \displaystyle\prod\limits_{i = 1}^d {\cos \left(\dfrac{{{x_i}}}{{\sqrt i }}\right)} + 1 $	30	[−600,600]^d	0
	$ {F_{10}}(x) = 0.1 \left\{ {\sin ^2}(3{\text{π}}{x_1}) + \displaystyle\sum\limits_{i = 1}^d {{{({x_i} - 1)}^2}[1 + {{\sin }^2}(3{\text{π}}{x_1} + 1)]} + {({x_d} - 1)^2}[1 + {\sin ^2}(2{\text{π}}{x_d})]\right\} + \displaystyle\sum\limits_{i = 1}^d {u({x_i},5,100,4)} $	30	[−50,50]^d	0
低维多峰	$ {F_{11}}(x) = - \displaystyle\sum\limits_{i = 1}^{10} {{{[(X - {{\boldsymbol{a}}_{{\mathrm{SHi}}}}){{(X - {{\boldsymbol{a}}_{{\mathrm{SHi}}}})}^{\text{T}}} + {{\boldsymbol{c}}_{{\mathrm{SHi}}}}]}^{ - 1}}} $	4	[0,10]⁴	−10.536

下载: 导出CSV

表 3 RGMFO算法及其他算法高维单峰函数寻优结果

Table 3. High-dimensional single-peak function optimization results of RGMFO algorithm and other algorithms

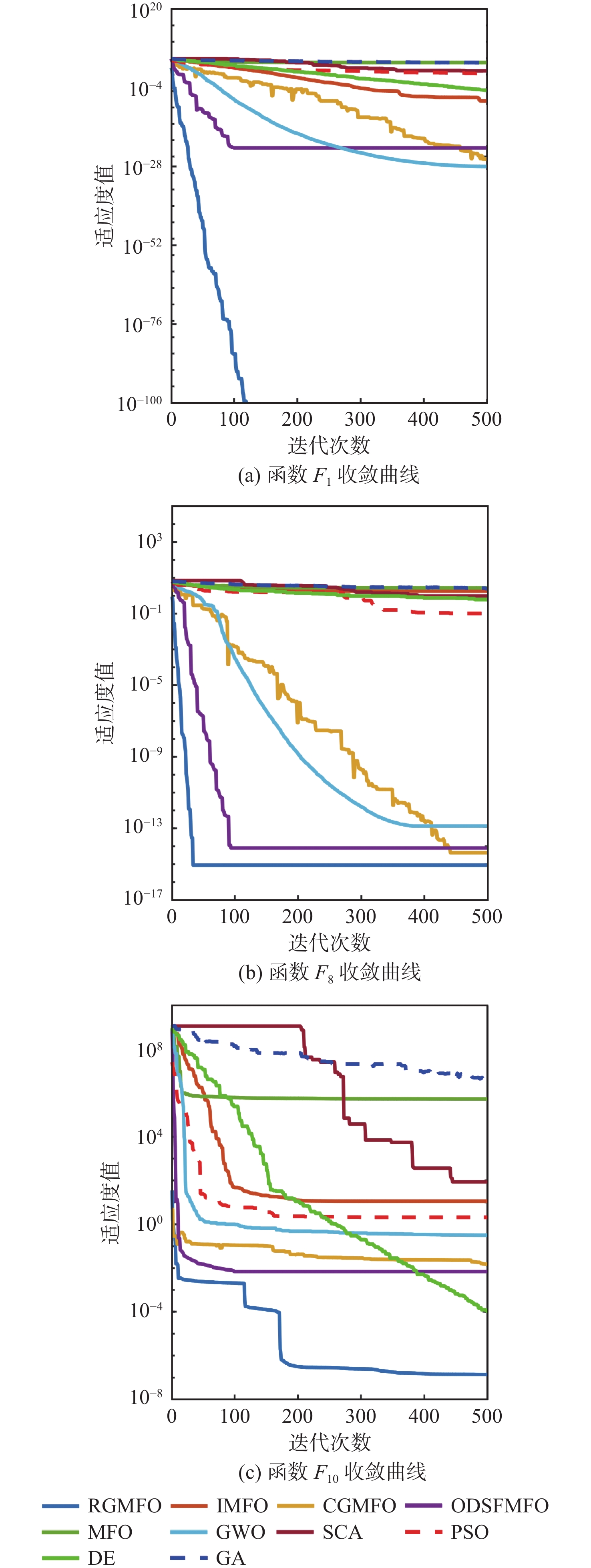
算法	平均值						标准差
算法	F₁	F₂	F₃	F₄	F₅	F₆	F₁	F₂	F₃	F₄	F₅	F₆
RGMFO	0	1.68×10⁻²⁰⁸	0	4.19×10⁻²⁰⁸	1.98×10⁻⁵	1.07×10⁻⁴	0	0	0	0	3.07×10⁻⁵	1.2×10⁻⁴
IMFO	2.68×10⁻⁷	5.13×10⁻⁴	5850	17.6	15700	0.117	5.15×10⁻⁷	6.74×10⁻⁴	3440	4.85	11000	0.0447
CGMFO	1.66×10⁻²³	7.32×10⁻¹⁴	1.81×10⁻¹⁷	7.50×10⁻¹⁵	1.46×10⁻³	0.0268	7.45×10⁻²³	2.92×10⁻¹³	9.93×10⁻¹⁷	1.66×10⁻¹⁴	2.92×10⁻³	0.0218
ODSFMFO	1.96×10⁻²⁴	4.98×10⁻¹³	1.40×10⁻¹⁴	8.87×10⁻¹⁴	0.017	0.0563	8.54×10⁻²⁴	1.55×10⁻¹²	6.08×10⁻¹⁴	2.12×10⁻¹³	0.0459	0.0403
MFO	4970	20.3	59600	22.6	494	0.824	2350	4.54	58600	6.94	2690	0.439
GWO	9.68×10⁻²⁸	1.01×10⁻¹⁶	2.09×10⁻⁵	5.60×10⁻⁷	27.9	2.18×10⁻³	1.65×10⁻²⁷	1.19×10⁻¹⁶	4.99×10⁻⁵	4.36×10⁻⁷	0.851	1.48×10⁻³
PSO	12.2	0.0269	10500	37.2	7480	0.1	17.8	0.041	8450	9.88	26100	0.0839
DE	0.399	0.402	1120	0.179	36.2	7.43×10⁻³	0.344	0.312	2940	0.124	7.33	3.91×10⁻³
GA	2.12×10⁻⁵	2.61×10⁻⁴	18500	14.1	752	0.314	1.31×10⁻⁵	6.69×10⁻⁵	3530	4.79	460	0.0679

下载: 导出CSV

表 4 RGMFO算法及其他算法高维多峰函数寻优结果

Table 4. High-dimensional multi-peak function optimization results of RGMFO algorithm and other algorithms

算法	平均值				标准差
算法	F₇	F₈	F₉	F₁₀	F₇	F₈	F₉	F₁₀
RGMFO	0	8.88×10⁻¹⁶	0	7.58×10⁻⁶	0	0	0	1.10×10⁻⁵
IMFO	69.9	1.16	8.86×10⁻³	7.16	19.5	0.246	9.33×10⁻³	5.34
CGMFO	0	1.60×10⁻¹⁴	0	0.0226	0	4.58×10⁻¹⁴	0	0.0309
ODSFMFO	0	1.92×10⁻¹⁴	0	0.0231	0	4.16×10⁻¹⁴	0	0.0214
MFO	113	2.58	36.2	3.87×10⁶	25	0.321	13.8	3.51×10⁶
GWO	4.09	0.0215	3.73×10⁻³	0.653	6.06	0.0562	8.01×10⁻³	0.26
PSO	39.9	1.07	0.876	1.90×10⁵	30.6	0.529	0.357	8.09×10⁵
DE	33.2	0.395	0.591	2.78	35.6	0.387	0.296	0.639
GA	27.4	0.631	1.33×10⁻⁴	0.358	6.85	0.0874	3.17×10⁻⁴	0.965

下载: 导出CSV

表 5 RGMFO算法及其他算法低维多峰函数寻优结果

Table 5. Low-dimensional multi-peak function optimization results of RGMFO algorithm and other algorithms

算法	平均值	标准差
RGMFO	−10.5	4.47×10⁻⁹
IMFO	−8.2	3.43
CGMFO	−10.5	4.34×10⁻⁴
ODSFMFO	−8.19	2.72
MFO	−8.72	2.88
GWO	−9.99	2.06
PSO	−3.89	1.65
DE	−10.5	6.09×10⁻³
GA	−10.4	0.987

下载: 导出CSV

表 6 Wilcoxon秩和检验p值

Table 6. P-value for Wilcoxon rank sum test

函数	RGMFO-IMFO	RGMFO-CGMFO	RGMFO-ODSFMFO	RGMFO-MFO	RGMFO-GWO	RGMFO-SCA	RGMFO-PSO	RGMFO-DE	RGMFO-GA
F₁	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²
F₂	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹
F₃	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²
F₄	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹
F₅	3.02×10⁻¹¹	2.44×10⁻⁹	3.69×10⁻¹¹	5.57×10⁻¹⁰	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹
F₆	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹
F₇	1.21×10⁻¹²			1.21×10⁻¹²	1.94×10⁻⁹	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²
F₈	1.21×10⁻¹²	2.82×10⁻⁵	2.16×10⁻⁶	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²
F₉	1.21×10⁻¹²			1.21×10⁻¹²	0.011	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²
F₁₀	3.02×10⁻¹¹	3.34×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.01×10⁻⁷	3.02×10⁻¹¹
F₁₁	0.0254	3.47×10⁻¹⁰	2.30×10⁻⁷	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	2.20×10⁻¹⁰	3.02×10⁻¹¹

下载: 导出CSV

表 7 RGMFO算法及其他算法寻优运算时间

Table 7. Optimization operation time of RGMFO algorithm and other algorithms s

函数	RGMFO	IMFO	CGMFO	ODSFMFO	MFO	GWO	SCA	PSO	DE	GA
F₁	0.257 9	0.163 1	0.084 2	0.785 5	0.0675	0.2406	0.1729	0.0579	0.1858	0.0850
F₂	0.469 5	0.363 9	0.193 7	1.020 6	0.0716	0.2331	0.1767	0.0606	0.1223	0.0750
F₃	0.503 8	0.389 3	0.222 8	1.036 6	0.0905	0.2476	0.1948	0.0761	0.1404	0.0839
F₄	0.535 0	0.373 7	0.198 1	1.023 0	0.0702	0.2257	0.1815	0.1136	0.1206	0.0729
F₅	0.567 6	0.357 8	0.183 3	1.012 7	0.0648	0.2369	0.1685	0.0569	0.1455	0.0656
F₆	0.980 2	0.747 9	0.366 2	1.608 0	0.2153	0.3963	0.3933	0.2093	0.2361	0.1320
F₇	0.718 6	0.426 6	0.200 4	1.324 6	0.0961	0.2395	0.1878	0.0901	0.1378	0.0779
F₈	0.732 1	0.466 9	0.230 5	1.494 8	0.1001	0.2531	0.2131	0.0924	0.1401	0.0800
F₉	0.727 0	0.605 8	0.320 0	1.995 9	0.1672	0.3148	0.2644	0.1271	0.2096	0.1371
F₁₀	1.172 2	0.740 3	0.415 1	1.930 5	0.3277	0.4571	0.4770	0.3205	0.6867	0.4184
F₁₁	0.809 2	0.473 8	0.346 4	1.463 1	0.1527	0.1711	0.1607	0.1379	0.3427	0.2041

下载: 导出CSV

表 8 高维单峰函数消融实验结果

Table 8. High-dimensional single-peak function experimental results of model ablation

算法	平均值						标准差
算法	F₁	F₂	F₃	F₄	F₅	F₆	F₁	F₂	F₃	F₄	F₅	F₆
RGMFO	0	1.68×10⁻²⁰⁸	0	4.19×10⁻²⁰⁸	1.98×10⁻⁵	1.07×10⁻⁴	0	0	0	0	3.07×10⁻⁵	1.20×10⁻⁴
GMFO	2.00×10⁻²¹⁰	6.63×10⁻¹¹⁵	2.59×10⁻¹⁶⁵	3.66×10⁻¹¹⁰	2.66	0.0225	0	3.16×10⁻¹¹⁴	0	1.86×10⁻¹⁰⁹	3.23	0.0164
RMFO	0.263	1.66	7.38	0.178	5.72×10⁻⁵	0.62	0.144	0.823	5.47	0.0888	2.15×10⁻⁴	1.02
MFO	4970	20.3	59600	22.6	494	0.824	2350	4.54	58600	6.94	2690	0.439

下载: 导出CSV

表 9 高维多峰函数消融实验结果

Table 9. High-dimensional multi-peak function experimental results of model ablation

算法	平均值				标准差
算法	F₇	F₈	F₉	F₁₀	F₇	F₈	F₉	F₁₀
RGMFO	0	8.88×10⁻¹⁶	0	7.58×10⁻⁶	0	0	0	1.10×10⁻⁵
GMFO	0	8.88×10⁻¹⁶	0	0.145	0	0	0	0.0615
RMFO	0.477	0.0147	0.0103	2.37×10⁻⁵	0.947	0.016	6.74×10⁻³	4.97×10⁻⁵
MFO	113	2.58	36.2	3.87×10⁶	25	0.321	13.8	3.51×10⁶

下载: 导出CSV

表 10 低维多峰函数消融实验结果

Table 10. Low-dimensional multi-peak function experimental results of model ablation

算法	平均值	标准差
RGMFO	−10.5	4.47×10⁻⁹
GMFO	−7.72	2.66
RMFO	−5.13	1.83×10⁻¹²
MFO	−8.72	2.88

下载: 导出CSV

表 11 减速器设计变量边界约束

Table 11. Reducer design variable boundary constraints

变量	下界	上界
x₁	2.6	3.6
x₂	0.7	0.8
x₃	17	28
x₄	7.3	8.3
x₅	7.8	8.3
x₆	2.9	3.9
x₇	5.0	5.5

下载: 导出CSV

表 12 减速器设计结果

Table 12. Reducer design results

算法	x₁	x₂	x₃	x₄	x₅	x₆	x₇	适应度值
RGMFO	3.50	0.70	17.00	7.30	7.80	3.35	5.29	2996.41
IMFO	3.50	0.70	17.00	7.30	7.80	3.35	5.29	2996.41
CGMFO	3.50	0.70	17.00	7.60	7.80	3.80	5.29	3130.09
ODSFMFO	3.50	0.70	17.00	7.30	7.80	3.35	5.29	2996.41
MFO	3.50	0.70	17.00	7.30	7.80	3.35	5.37	3047.56
GWO	3.50	0.70	17.00	7.39	7.85	3.36	5.29	3003.19
SCA	3.60	0.70	17.00	8.30	8.30	3.45	5.37	3133.94
PSO	3.60	0.70	17.00	7.30	8.28	3.35	5.29	3046.37
DE	3.50	0.70	17.00	7.30	7.80	3.35	5.29	2996.41
GA	3.57	0.70	17.16	7.67	7.82	3.43	5.30	3096.49

下载: 导出CSV

表 13 槽形舱壁设计结果

Table 13. Trough bulkhead design results

算法	x₁	x₂	x₃	x₄	适应度值
RGMFO	37.51	33.11	37.51	0.74	5.89
IMFO	37.83	33.19	37.83	0.74	5.89
CGMFO	31.34	32.48	37.88	0.78	6.23
ODSFMFO	38.89	33.46	38.89	0.76	5.90
MFO	37.28	33.23	38.13	0.74	5.90
GWO	37.69	33.20	37.85	0.74	5.90
SCA	32.71	35.53	46.11	0.90	6.70
PSO	40.91	33.30	39.36	0.79	6.02
DE	37.49	33.11	37.49	0.73	5.89
GA	90.70	33.53	75.91	1.67	10.29

下载: 导出CSV

参考文献(15)

[1]	MIRJALILI S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm[J]. Knowledge-Based Systems, 2015, 89: 228-249. doi: 10.1016/j.knosys.2015.07.006
[2]	张淑清, 段晓宁, 张立国, 等. Tsne降维可视化分析及飞蛾火焰优化ELM算法在电力负荷预测中应用[J]. 中国电机工程学报, 2021, 41(9): 3120-3130. ZHANG S Q, DUAN X N, ZHANG L G, et al. Tsne dimension reduction visualization analysis and moth flame optimized ELM algorithm applied in power load forecasting[J]. Proceedings of the CSEE, 2021, 41(9): 3120-3130(in Chinese).
[3]	安许锋, 田洲, 钱锋. 基于多策略扰动机制的飞蛾火焰算法及在乙烯聚合过程动力学参数估计中的应用[J]. 高校化学工程学报, 2018, 32(4): 918-925. doi: 10.3969/j.issn.1003-9015.2018.04.023 AN X F, TIAN Z, QIAN F. Moth-flame optimization algorithm based on multi-strategy disturbance and its application in kinetic parameter estimation of ethylene polymerization[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(4): 918-925(in Chinese). doi: 10.3969/j.issn.1003-9015.2018.04.023
[4]	田鸿, 陈国彬, 刘超. 新型飞蛾火焰优化算法的研究[J]. 计算机工程与应用, 2019, 55(16): 138-143. doi: 10.3778/j.issn.1002-8331.1805-0027 TIAN H, CHEN G B, LIU C. Research on new moth-flame optimization algorithm[J]. Computer Engineering and Applications, 2019, 55(16): 138-143(in Chinese). doi: 10.3778/j.issn.1002-8331.1805-0027
[5]	黄鹤, 吴琨, 王会峰, 等. 基于改进飞蛾扑火算法的无人机低空突防路径规划[J]. 中国惯性技术学报, 2021, 29(2): 256-263. HUANG H, WU K, WANG H F, et al. Path planning of UAV low altitude penetration based on improved moth-flame optimization[J]. Journal of Chinese Inertial Technology, 2021, 29(2): 256-263(in Chinese).
[6]	刘倩, 冯艳红, 陈嶷瑛. 基于混沌初始化和高斯变异的飞蛾火焰优化算法[J]. 郑州大学学报(工学版), 2021, 42(3): 53-58. LIU Q, FENG Y H, CHEN Y Y. Moth-flame optimization algorithm based on chaotic initialization and Gaussian mutation[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(3): 53-58(in Chinese).
[7]	PELUSI D, MASCELLA R, TALLINI L, et al. An improved moth-flame optimization algorithm with hybrid search phase[J]. Knowledge-Based Systems, 2020, 191: 105277. doi: 10.1016/j.knosys.2019.105277
[8]	LI Z F, ZENG J H, CHEN Y Q, et al. Death mechanism-based moth-flame optimization with improved flame generation mechanism for global optimization tasks[J]. Expert Systems with Applications, 2021, 183: 115436. doi: 10.1016/j.eswa.2021.115436
[9]	刘宝宁, 章卫国, 李广文, 等. 一种改进的多目标粒子群优化算法[J]. 北京航空航天大学学报, 2013, 39(4): 458-462. LIU B N, ZHANG W G, LI G W, et al. Improved multi-objective particle swarm optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(4): 458-462(in Chinese).
[10]	MIRJALILI S. SCA: A sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120-133. doi: 10.1016/j.knosys.2015.12.022
[11]	MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007
[12]	TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence[C]//Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce. Piscataway: IEEE Press, 2006, 1: 695-701.
[13]	LONG W, JIAO J J, LIANG X M, et al. A random opposition-based learning grey wolf optimizer[J]. IEEE Access, 2019, 7: 113810-113825. doi: 10.1109/ACCESS.2019.2934994
[14]	XU Y T, CHEN H L, LUO J, et al. Enhanced moth-flame optimizer with mutation strategy for global optimization[J]. Information Sciences, 2019, 492: 181-203. doi: 10.1016/j.ins.2019.04.022
[15]	HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris Hawks optimization: algorithm and applications[J]. Future Generation Computer Systems, 2019, 97: 849-872. doi: 10.1016/j.future.2019.02.028