Analysis and improvement of lateral instability of quasi-biconical lifting reentry spacecraft
-
摘要:
类双锥型升力式返回器的横航向稳定性对其理想再入策略的实施构成严苛的约束，且在设计阶段需要进行专门分析。针对类双锥型升力式返回器的标称再入过程，使用数值仿真方法计算该飞行器在全速域、宽迎角范围内的横航向稳定性，结合流场特征分析亚/跨/超声速速域内的横航向稳定性突变规律；重点分析涡流发生器、航向增强型面、重心偏置对横航向稳定性的影响及其作用机理，最终确定了航向舵偏转与重心偏置相结合的方案就是最佳横航向增稳方案。
Abstract:The lateral stability of the quasi-biconical lifting reentry spacecraft is a strict constraint on the implementation of its ideal reentry strategy, which requires specialized analysis in the design stage. In this paper, for the nominal reentry process of the quasi-biconical lifting reentry spacecraft, the lateral stability of the spacecraft in the range of full speed and wide angle of attack was calculated by using the numerical simulation method. According to the flow field characteristics, the mutation regularity of the lateral stability in the sub-/trans-/supersonic domain was analyzed. Then, the effect of the eddy current generator, lateral stability enhancement surface, and center-of-gravity offset on the lateral stability was analyzed, as well as the corresponding mechanism. The results reveal that the combination of rudder deflection and center-of-gravity offset is the optimal solution to enhance lateral stability.
-
类双锥型升力式返回器结合了传统返回舱和航天飞机的特点，能够进行大范围的机动滑翔，并可有效降低过载和热载峰值，是天地往返运输系统的一个重要发展方向[1]。由于升力式返回器再入过程中飞行高度和速度变化巨大，气动特性变化复杂，因此为保障飞行安全，在设计过程中必须保证返回器本体的稳定性。
早在20世纪60年代，研究人员就注意到返回舱的稳定性问题。1968年Moseley等 [2]针对阿波罗返回舱的飞行稳定性问题进行了研究, 指出返回器表面流动不稳定，之后国内外大量的研究人员对此进行数值模拟。Abe等[3]通过分析返回器的动态俯仰力矩，指出飞船纵向不稳定是返回器后部的涡流造成的；张涵信等[4-5]从非线性动力学理论出发对飞船返回舱的俯仰运动进行了定性理论分析；Teramoto 等[6-7]则针对钝头返回舱跨声速产生失稳现象的流动机理进行了研究。然而受限于计算流体动力学（computational fluid dynamics，CFD）当时的发展水平，计算误差较大且对不稳定性产生机理的研究较为粗略。朱德华等[8]采用大涡模拟法分析了钝头返回舱再入过程的分离和转捩现象，并分析了其稳定性特征。部分研究者则采用风洞试验的方法来研究返回器表面的流动。Mitcheltree等[9]基于风洞试验研究了钝头返回器外形半锥角在亚声速飞行时对稳定性的影响；何开锋与和争春[10]在全局稳定性分析和数值模拟的基础上，使用风洞试验验证了返回舱在亚、跨声速飞行时的动稳定性。宋玉辉等[11-12]采用风洞自由振动试验方法研究了钝头返回器的动稳定特性，结果表明在亚、跨声速，甚至超声速范围均出现了动不稳定现象。宋威等[13]也采用风洞自由飞试验技术，研究了钝头类联盟号返回舱在跨声速时的气动特性与运动特性。同时，他们还指出，由于风洞试验中的支撑干扰、动壁干扰等，不可避免会的产生误差。这种误差和数值计算中存在的模型误差、网格误差、离散误差一样，会对试验或计算结果产生影响，因此，需采取撑杆优化、模型尺度控制等措施进行误差控制及修正。
随着高超声速飞行器的发展，研究人员发现此类横航向与纵向特性制约、横航向气动耦合严重等问题也普遍存在于高超声速飞行器中，并对飞行器稳定性的影响因素、失稳后的运动形态和增稳措施开展了大量的研究，而这些研究主要集中在纵向稳定性方面。鲍文和姚照辉[14]针对吸气式升力体高超声速飞行器建立了面向巡航控制的纵向运动模型。贾子安等[15-16]结合牛顿理论和流线简化模型，推导了高超飞行器外形流线特征对纵向静稳定性的影响；在此基础上，王柯穆[17]研究了乘波体流线特征对纵向压心的影响。Mangin等[18]则将飞行器上表面尾部设计为膨胀面，使得纵向压心后移以改善纵向静稳定性。针对横航向稳定性的研究则相对较少，高清等[19-20]基于风洞试验和模态分析对类高超声速技术验证飞行器（hypersonic technology test vehicle, HTV-2 ）外形的横侧向稳定性进行了研究；祝立国等[21]基于横航向小扰动方程推导了开环动态偏航稳定判据，并对高速飞行器的横航向稳定性进行了探讨；闵昌万[22]则针对副翼控制下的高超声速飞行器横侧向稳定性判据开展了研究。
当前，针对类双锥型升力式返回器横航向稳定性变化机理的分析及增稳控制措施方面鲜有研究。为弥补现有研究的不足，本文使用数值仿真方法对类双锥型升力式返回器在全速域、宽迎角范围内的横航向稳定性进行分析，结合流场特征分析了亚/跨/超声速速域内的横航向稳定性突变规律。重点针对该类返回器的横航向稳定性问题研究了涡流发生器、航向增强型面、重心偏置3种增稳方案，从流场特征角度分析了3种方案的作用机理和效果，最终确定了最佳横航向增强方案。
1. 返回器外形及标称再入过程
类双锥型升力式返回飞行器是一种新构型返回器，与传统构型返回器相比，该类返回器具有升阻比高、过载小、落点精度高等特点。典型的类双锥型升力式返回器外形如图1所示，该返回器主要包含本体和升降舵2个部分。在总体设计过程中，本体外形可基于多约束条件优化设计生成，升降舵几何参数则根据典型状态下的配平要求确定。
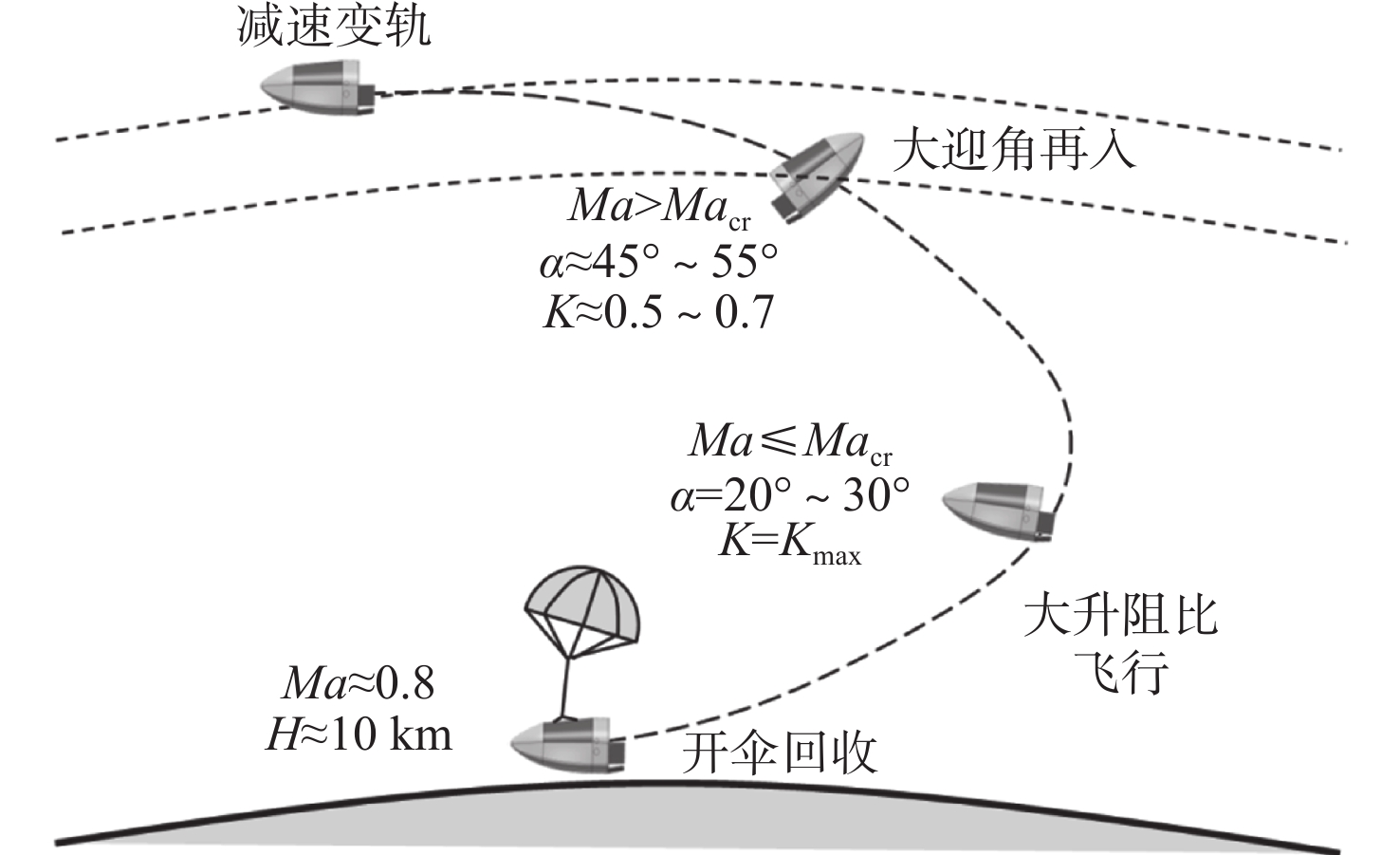
再入返回过程中，由返回器纵向特性所决定的理想再入策略如图2所示，其中，α为迎角，Ma为马赫数，Macr为临界马赫数，H为飞行高度，K和Kmax分别为升阻比和最大升阻比。其中：在高马赫数区间（Ma>Macr），返回器以45°以上大迎角执行再入，以降低热流峰值；在低马赫数区间（Ma<Macr），返回器以20°～30°的小迎角接续飞行，以发挥升力体构型的大升阻比优势，直至速度降至0.8马赫附近时执行开伞程序。大小迎角切换的临界马赫数Macr取10～12，由热流、动压共同决定。
这种标称再入策略以返回器纵向特性为基础，理论上可发挥返回器在大迎角和小迎角范围内的不同性能优势，但在实施过程中需进一步考虑横航向特性与纵向特性之间的匹配关系，即在再入过程中的每一个状态点均需保证返回器具有良好的横航向稳定性，这种横纵向匹配是保证飞行安全可控的关键，在设计阶段需要对其开展专门分析。
2. 返回器横航向稳定性分析
2.1 数值计算方法
针对图1所示的类双锥型升力式返回器外形，使用数值计算方法来获取其在再入过程中的横航向稳定性。计算过程采用如图3所示的全模结构化网格逼近返回器外形，同时对头锥、肩部、迎风面进行网格加密以提高流动细节捕捉精度。计算所采用的主控方程为守恒形式的非定常可压缩Navier-Stokes方程，无黏通量采用二阶迎风Roe通量差分分裂格式离散，网格界面上采用MUSCL格式插值以获得高阶精度，黏性项则采用中心差分格式离散[23]。湍流模型采用SST两方程湍流模型，湍流控制方程空间离散采用二阶迎风格式。时间推进基于隐式LU-SGS格式完成。为验证该数值方法的准确性，将该方法用于文献[23]中类神舟返回舱的典型工况（Ma=6，α=20°）气动特性模拟，并将试验结果进行比较，结果如表1所示，气动力系数预测值与实验值间的误差在3%左右（表中CA、CN、CL、CD、Cm依次为轴向力系数、法向力系数、升力系数、阻力系数、俯仰力矩系数），由此表明数值仿真模型具有较高的可信度。
表 1 类神舟返回器计算值与实验值对比Table 1. Comparison of calculated and experimental values of Shenzhou-like reentry spacecraft参数项 CA CN CL CD Cm 预测值 1.315 0.1587 − 0.3006 1.290 0.0999 实验值 1.335 0.1590 − 0.3072 1.309 0.1025 2.2 横航向计算及结果讨论
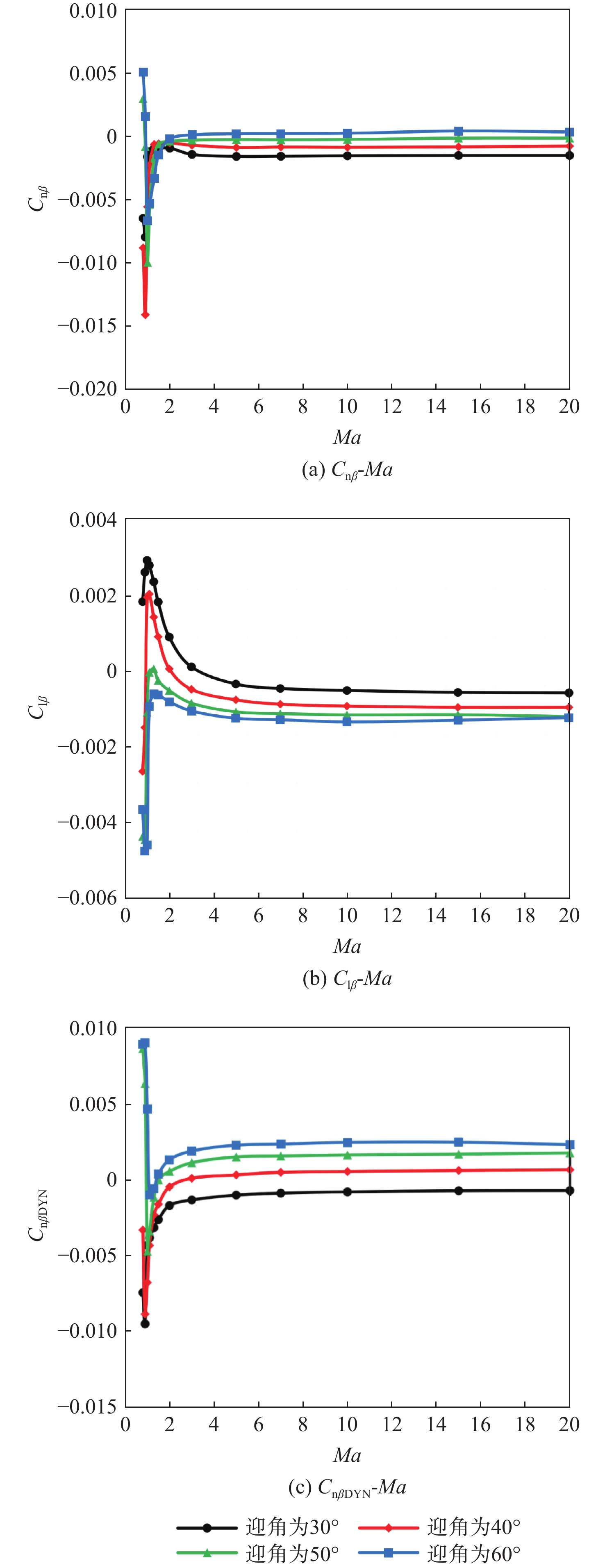
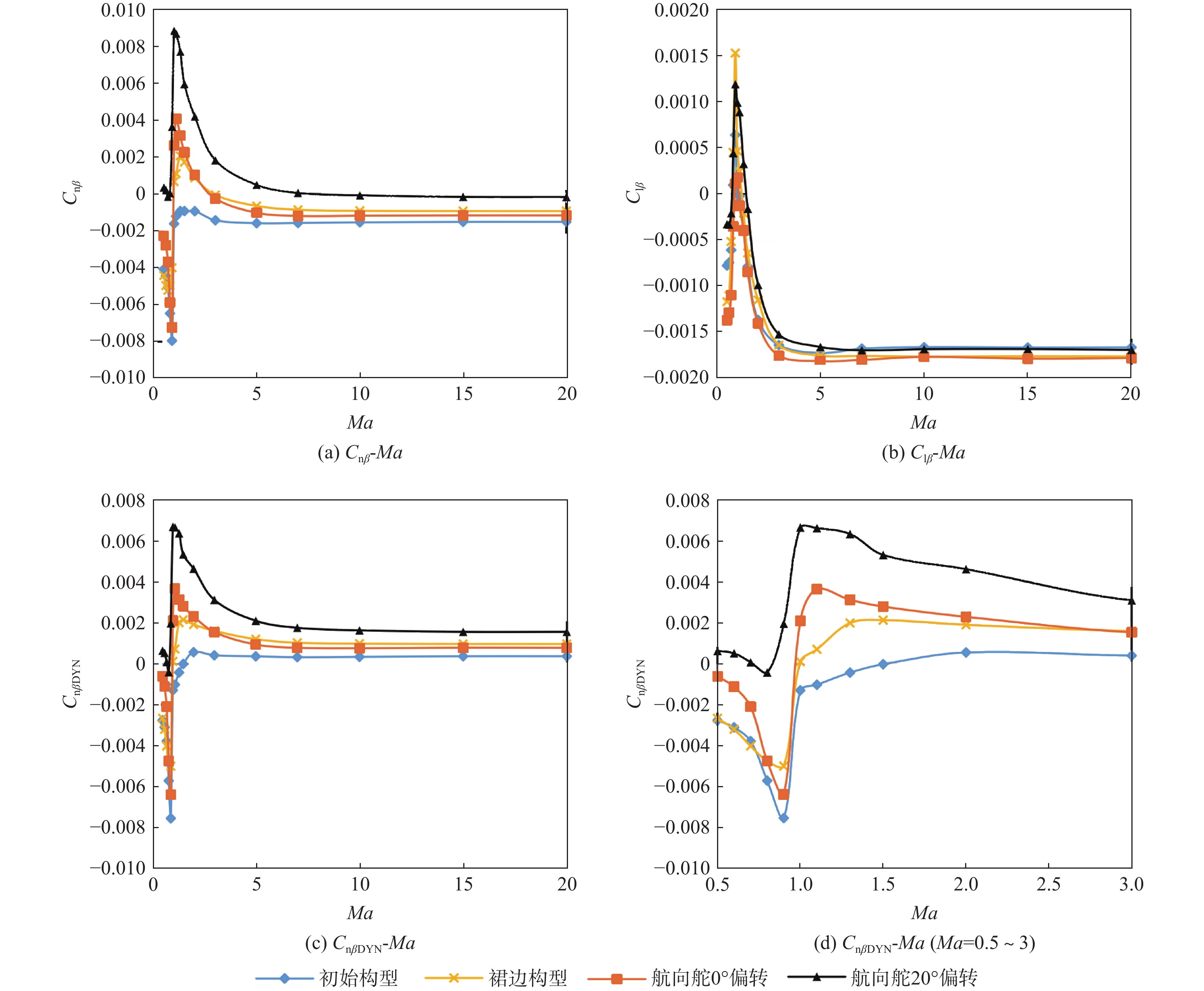
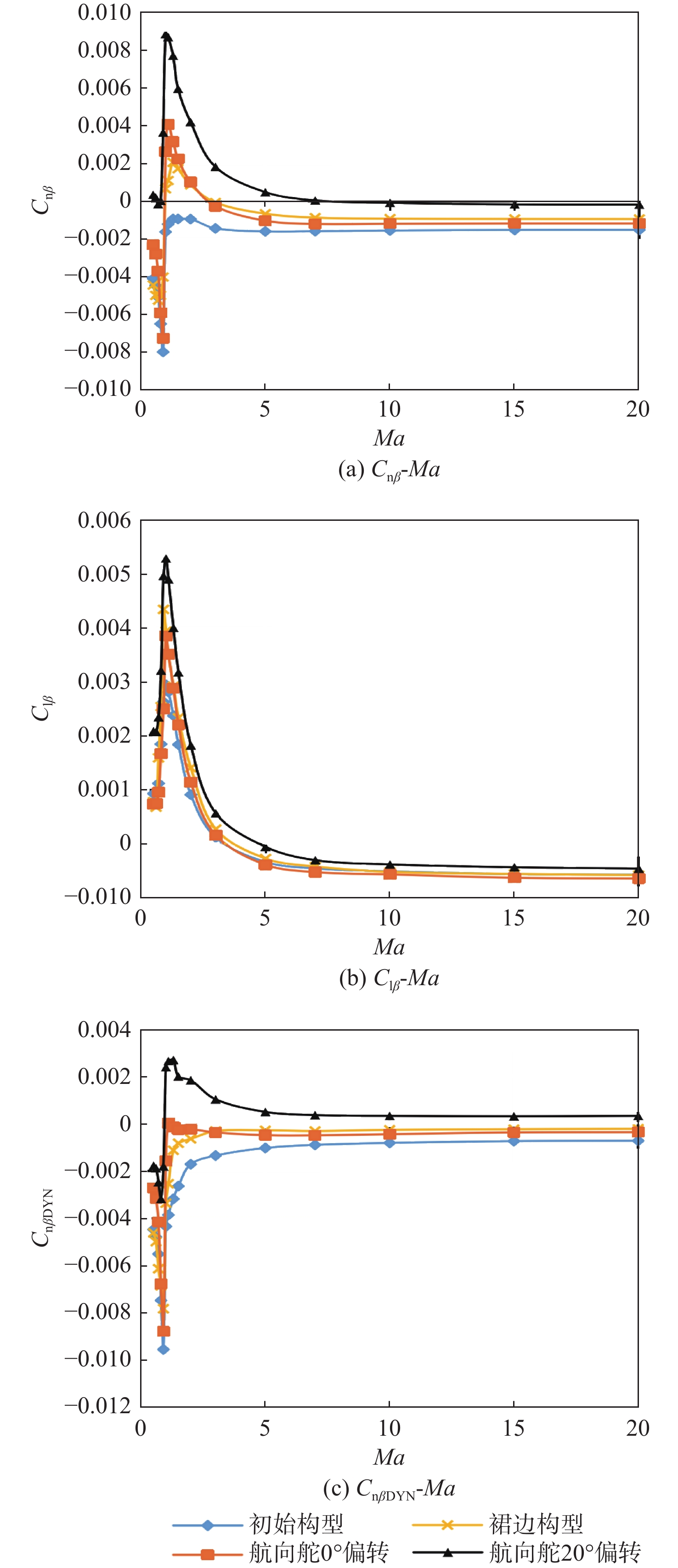
横航向稳定性分析计算工况的设置覆盖了再入返回的整个过程，其中，马赫数为0.5～20，迎角为30°～60°（10°间隔），侧滑角为2°～4°。使用2.1节所述方法开展数值计算，可得到返回器横航向特性随马赫数的变化，如图4所示，其中，力矩参考点距离头部顶点间距Xcg/L = 60%（L为本体长度），Ycg = Zcg = 0。由于小侧滑角范围内偏航力矩系数Cn和滚转力矩系数Cl随侧滑角变化呈近似线性，因此，在图4（a）和图4（b）中直接将Cn和Cl表示为侧滑角β的偏导数形式，即将Cnβ、Clβ，作为传统横航向静稳定性的主要判据。
图 4 返回器横航向特性随马赫数变化Figure 4. Changes in the lateral features of reentry spacecraft with Mach number在Cnβ和Clβ的基础上可进一步导出开环动态偏航稳定性判据CnβDYN，如图4（c）所示。CnβDYN= Cnβcos α−Iz/IxClβsin α，其中，Iz/Ix为惯量系数，图1中的返回器取
0.4985 。开环动态偏航稳定性判据在传统静稳定性判据的基础上考虑了横航向的相互耦合效应，能够更全面地反映飞行器的真实横航向稳定性能。传统静稳定性判据要求Cnβ>0, Clβ<0，开环动态偏航稳定要求CnβDYN>0。分析图4中的Cnβ、Clβ及CnβDYN，可得到以下结论。
1） 迎角越小，横航向稳定性越差：再入初期迎角处于30°～50°时返回器呈航向不稳定状态（见图4（a）），在该迎角范围内实施再入无法保障飞行安全；再入迎角达60°时可保证再入初期的横航向稳定性，但在马赫数降至3以下时，亦会进入航向不稳定状态。
2） 横航向耦合对横航向稳定性有改善作用：开环动态偏航稳定性（CnβDYN>0）计算结果表明，考虑横航向耦合的实际横航向静稳定性略优于传统静稳定性判据下的分析结果。以CnβDYN>0来看，返回器以40°、50°、60°迎角执行再入时均可维持开环动态偏航稳定，直至马赫数降低至与各迎角相对应的稳定速域下限。迎角越大，稳定速域下限马赫数越小（α=40°、50°、60°时下限马赫数分别为2、1.75、1.5），迎角为30°以下时在全速域内均无法维持开环动态偏航稳定。
3） 跨声速区间内横航向稳定性发生剧烈变化，导致横纵向不匹配：速度降至跨声速区间时，Cnβ、Clβ、CnβDYN均出现剧烈变化，导致返回器横航向特性恶化。随着马赫数的降低，迎角40°、50°、60°依次进入开环动态偏航不稳定状态，如图4（c）所示，各马赫数对应的满足开环动态偏航稳定的最小迎角值也开始出现大幅波动。
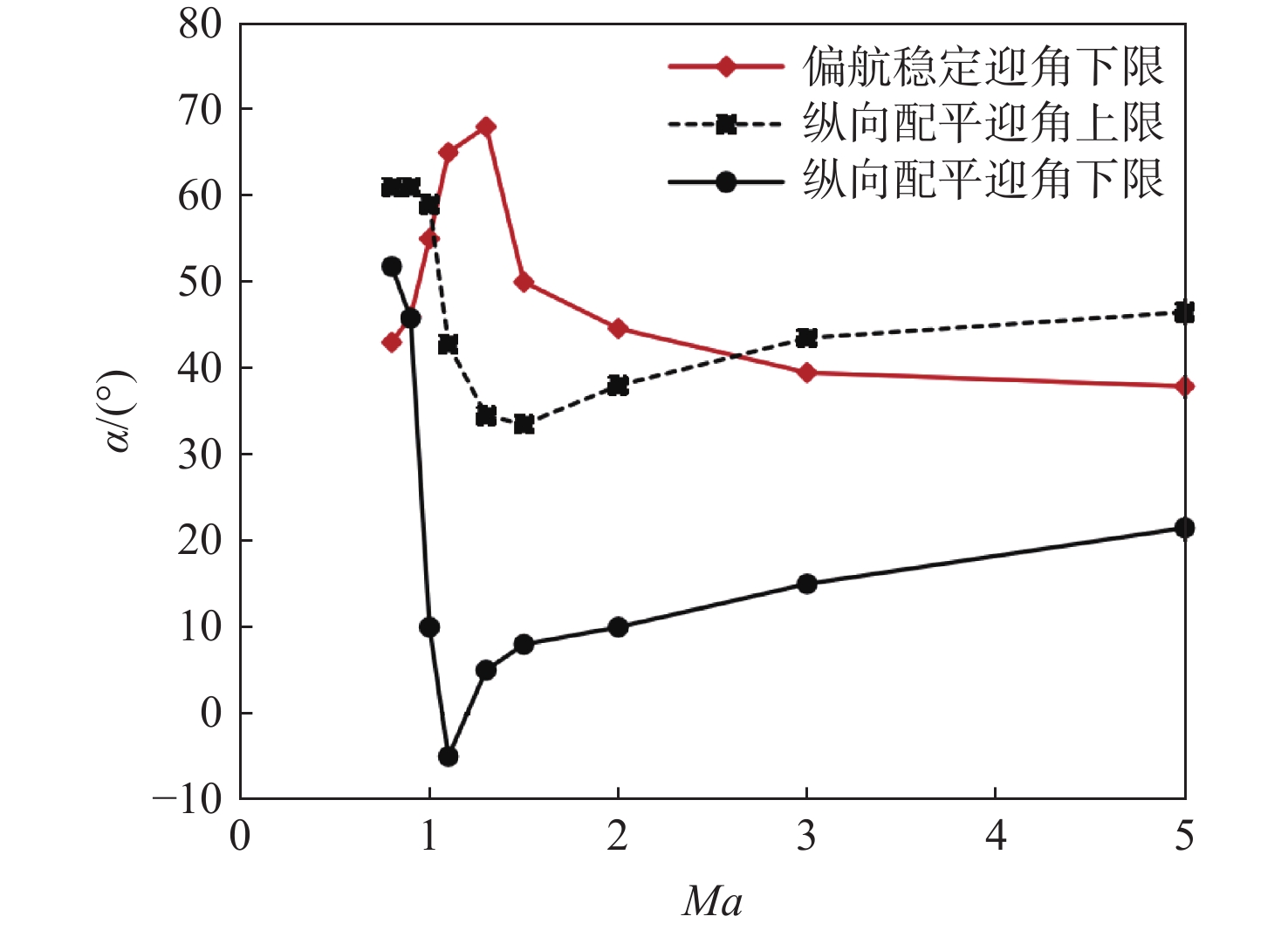
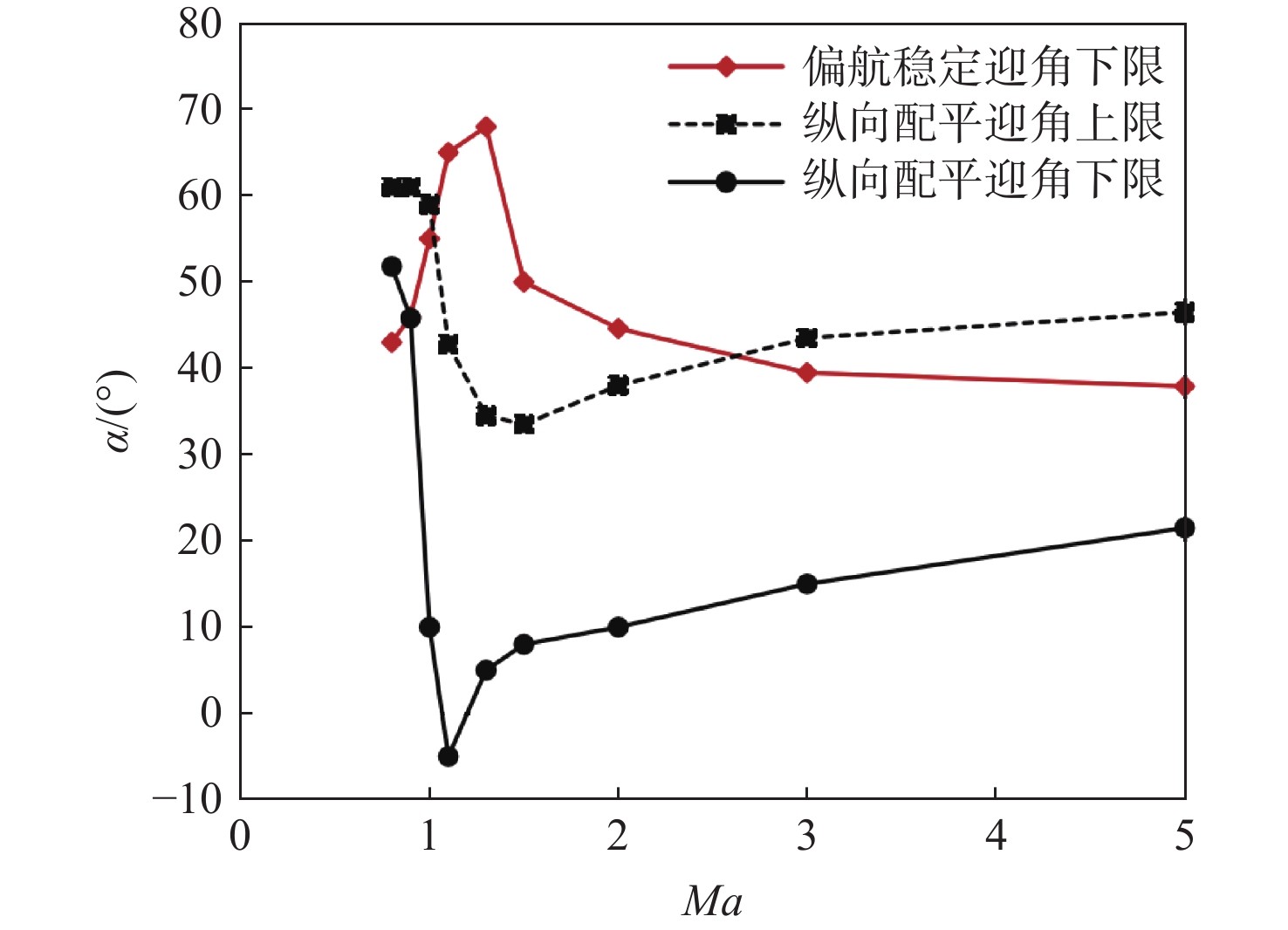
图5为再入迎角走廊，图中展示了跨声速附近的开环动态偏航稳定迎角下限，以及升降舵极限偏转（+20°/−10°）所能提供的配平迎角范围。由图可知，当前横航向稳定最小迎角在部分马赫数下已经超出了升降舵面的配平极限，造成了横纵向不匹配。由此引发的再入迎角走廊闭塞，会导致该返回器在任意迎角策略下，均无法稳定执行再入并减速至0.8Ma附近的开伞点。
3. 横航向稳定性变化机理分析
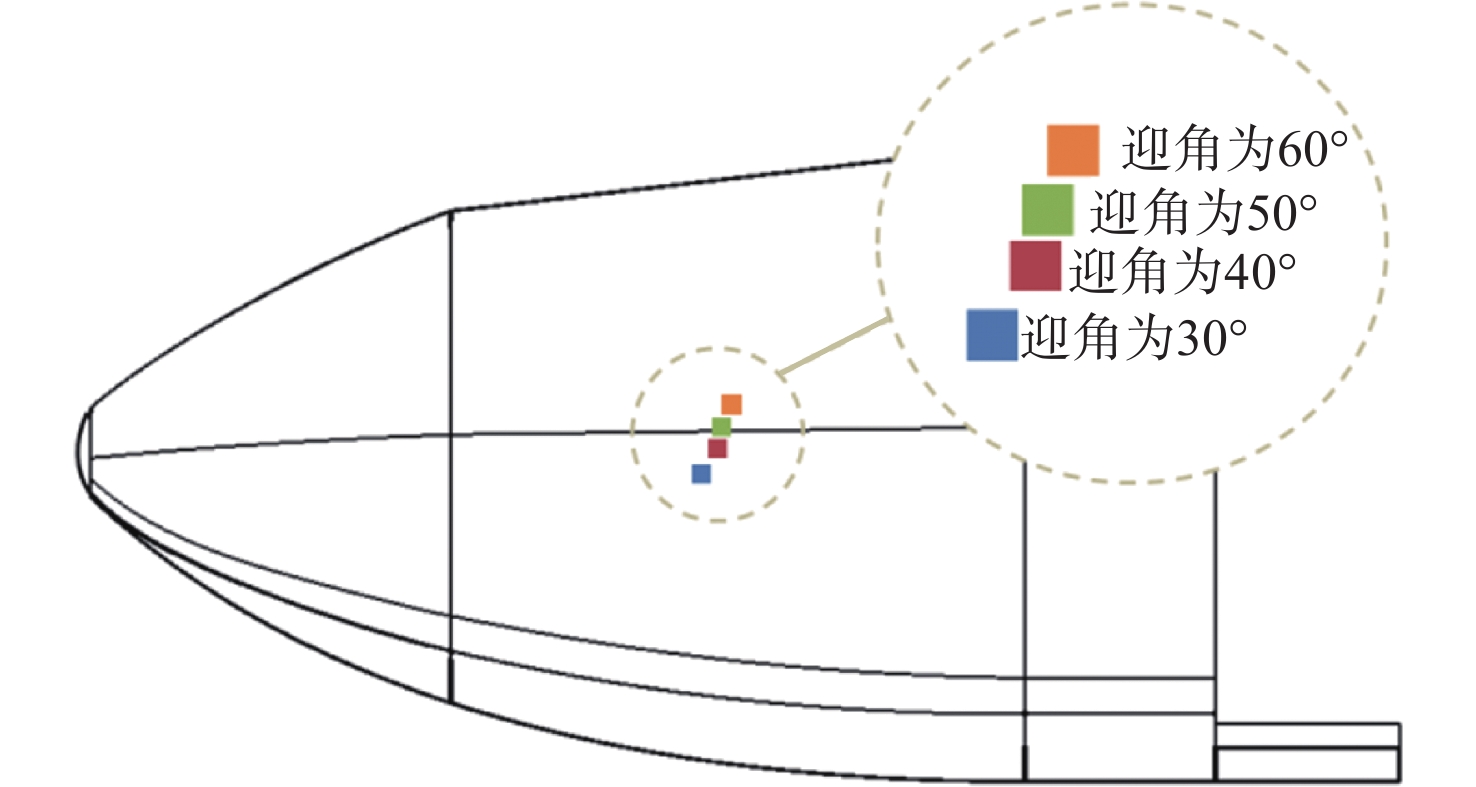
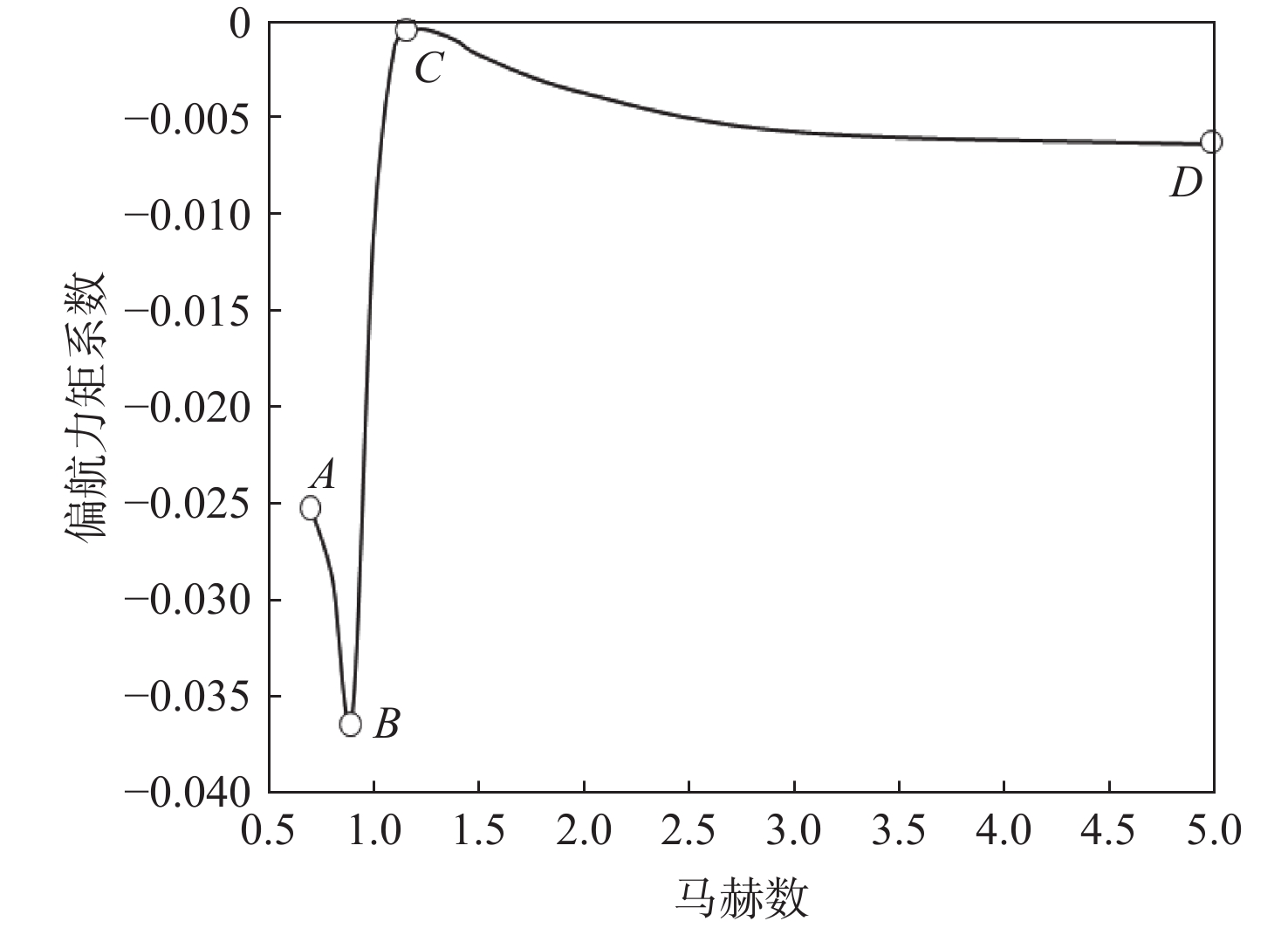
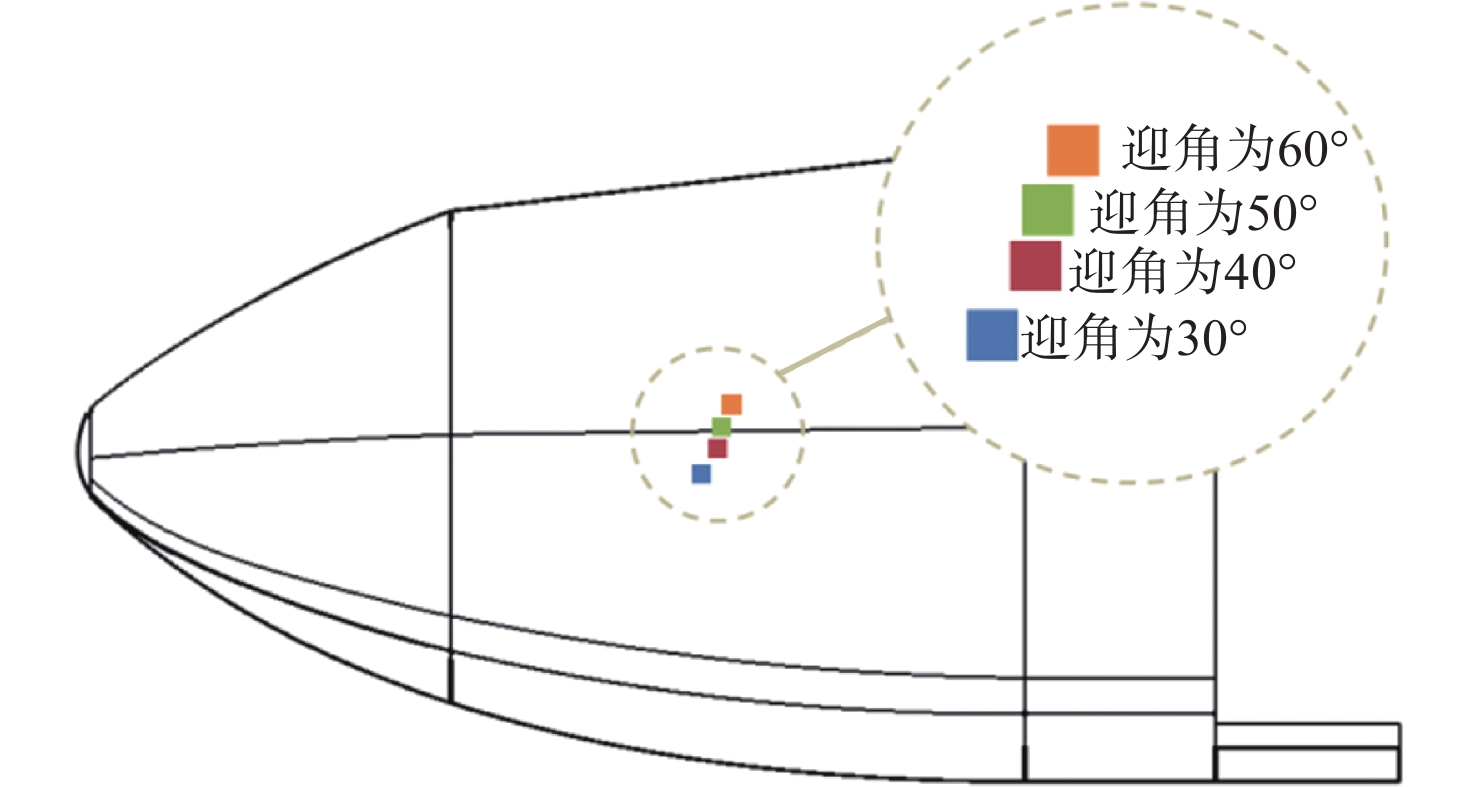
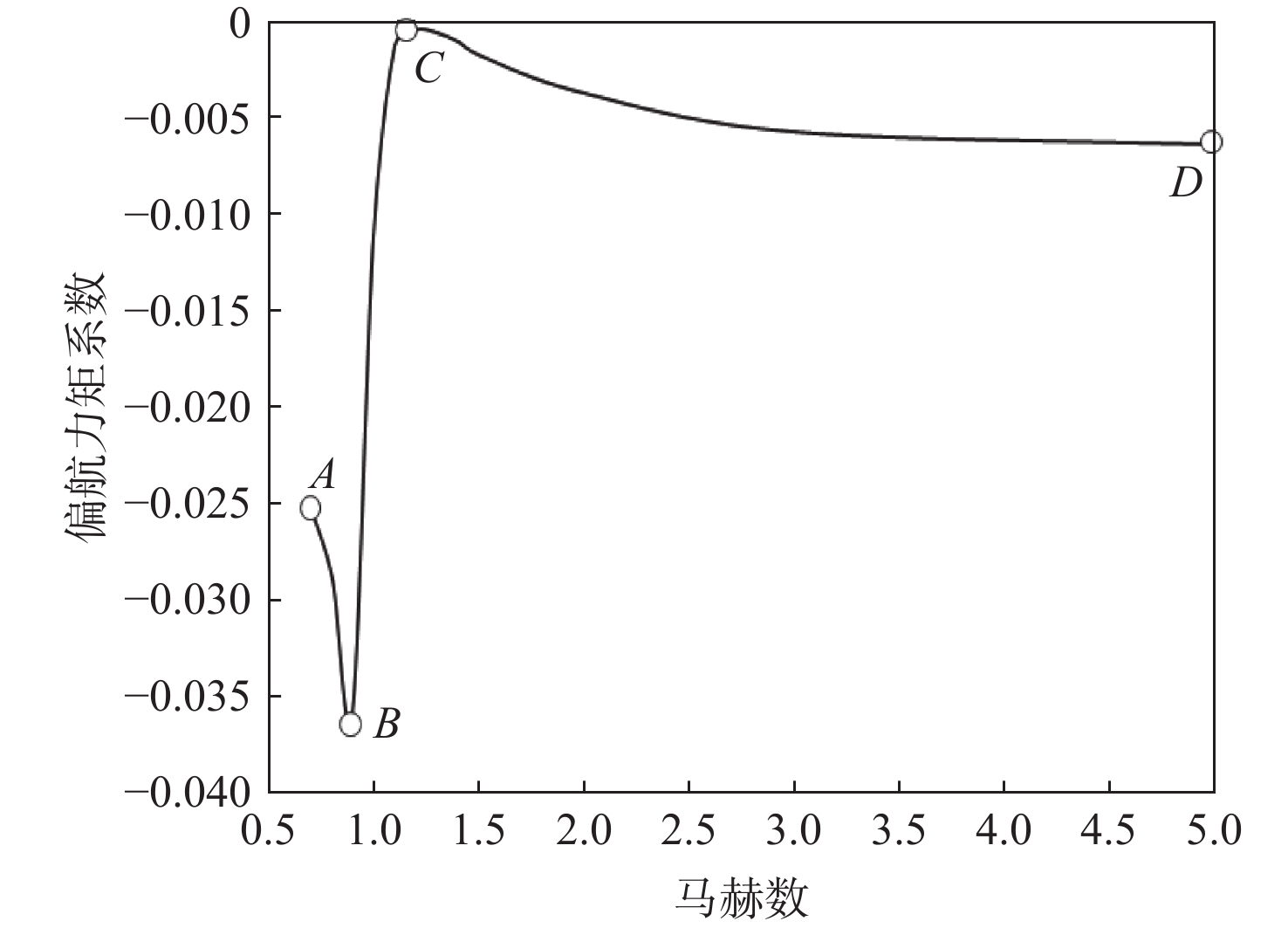
根据数值仿真结果可对返回器产生如第2节所述的横航向特性变化的机理进行分析。其中，返回器在马赫数为5以上的高超声速流域内的横航向稳定性主要受迎角影响，且具有良好的规律性：迎角增加，返回器压心向后上方移动，横航向稳定性改善，如图6所示。马赫数为5以下的亚跨超声速速域内的横航向稳定性变化则具有更高的复杂性，其中以跨声速区域的表现最为明显。以30°迎角为例，马赫数在0.7～5的偏航力矩系数变化如图7所示，该曲线可分为AB、BC、CD这3个阶段， AB段压心前移，偏航稳定性恶化；BC段压心迅速后移，偏航稳定性改善；CD段压心缓慢前移，压心位置随马赫数的增加而逐渐收敛。
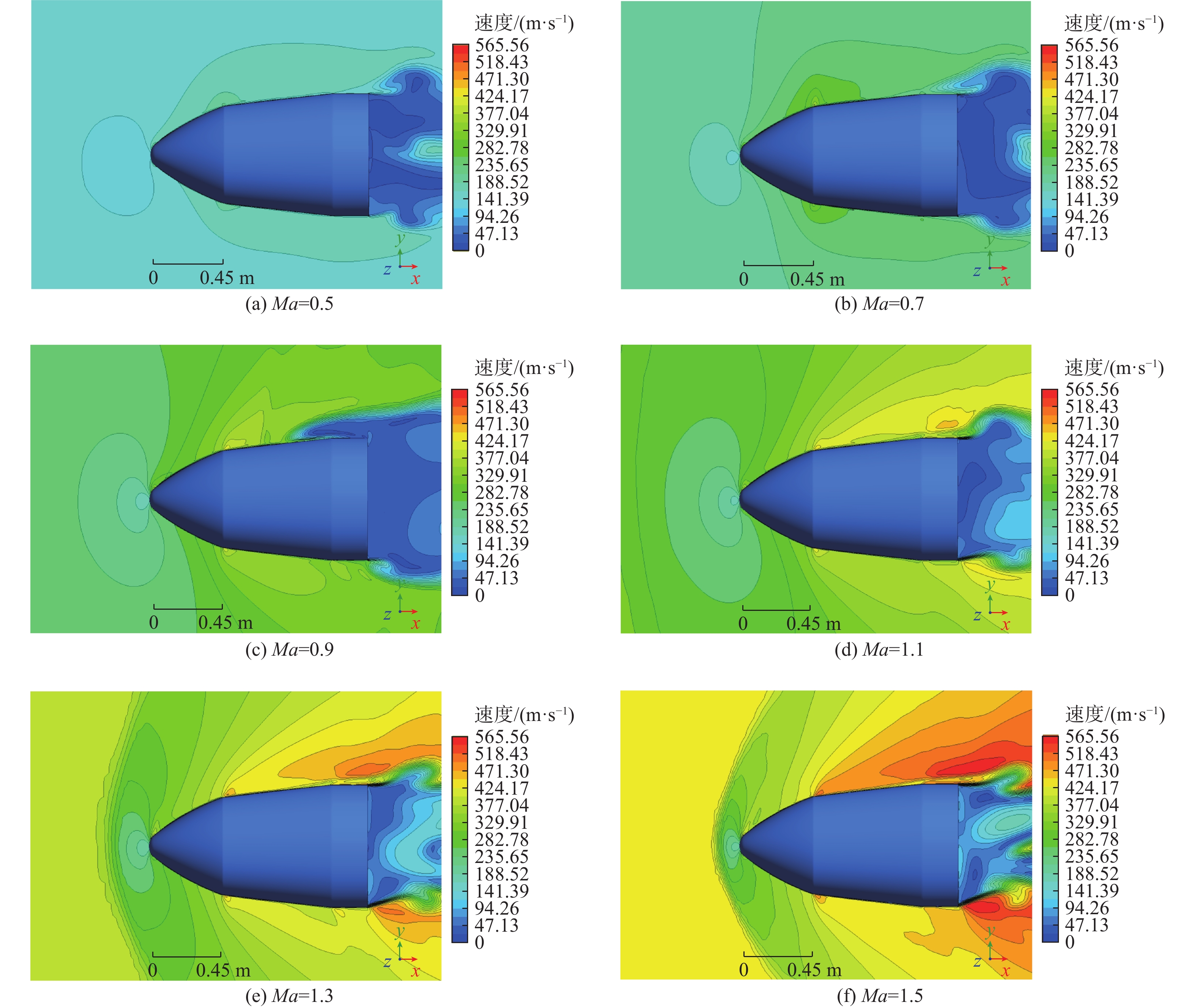
图 6 横航向压心位置随迎角变化（Ma = 5）Figure 6. Variation of lateral pressure center with angle of attack (Ma = 5)通过流场分析可以获知马赫数在0.5～5的压心位置移动机理。图8为30°迎角、4°侧滑角下马赫数分别为0.5、0.7、0.9、1.1、1.3、1.5时的流场速度分布。在该迎角下，当马赫数从亚声速（见图8（a））增加至高亚声速（见图8（c））的过程中，返回器表面逐渐出现局部激波，激波后流速降低，在背风一侧诱导出边界层分离（见图8（c）），分离区内压强增大、吸力降低，导致压心前移，在图7中表现为AB段偏航力矩系数的快速下降；随着马赫数的继续增加，背风侧激波位置逐渐后移，并在Ma=1.1时到达返回器后缘位置（见图8（d）），背风侧分离区在该过程中逐渐消除，使得压心快速后移，在图7中表现为BC段偏航力矩系数的明显恢复。该现象与翼型跨声速流动俯仰稳定性变化规律[24]具有一致性。
马赫数增加至1.1以上时，返回器前方开始出现弓形激波（见图8（d）和图8（e）），且激波距离物面的距离随马赫数的增加而不断缩减，返回器头部吸力峰逐步增强，压心向前侧移动，在图7中表现为CD段偏航力矩系数的缓慢降低。
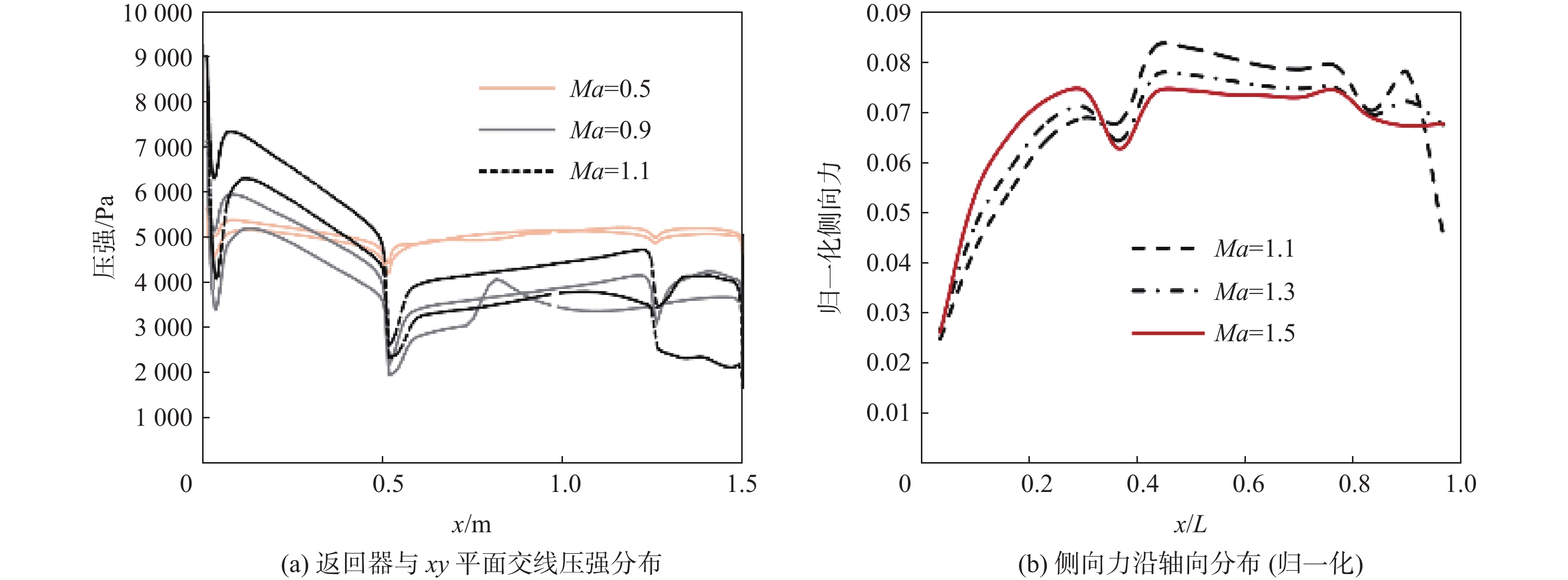
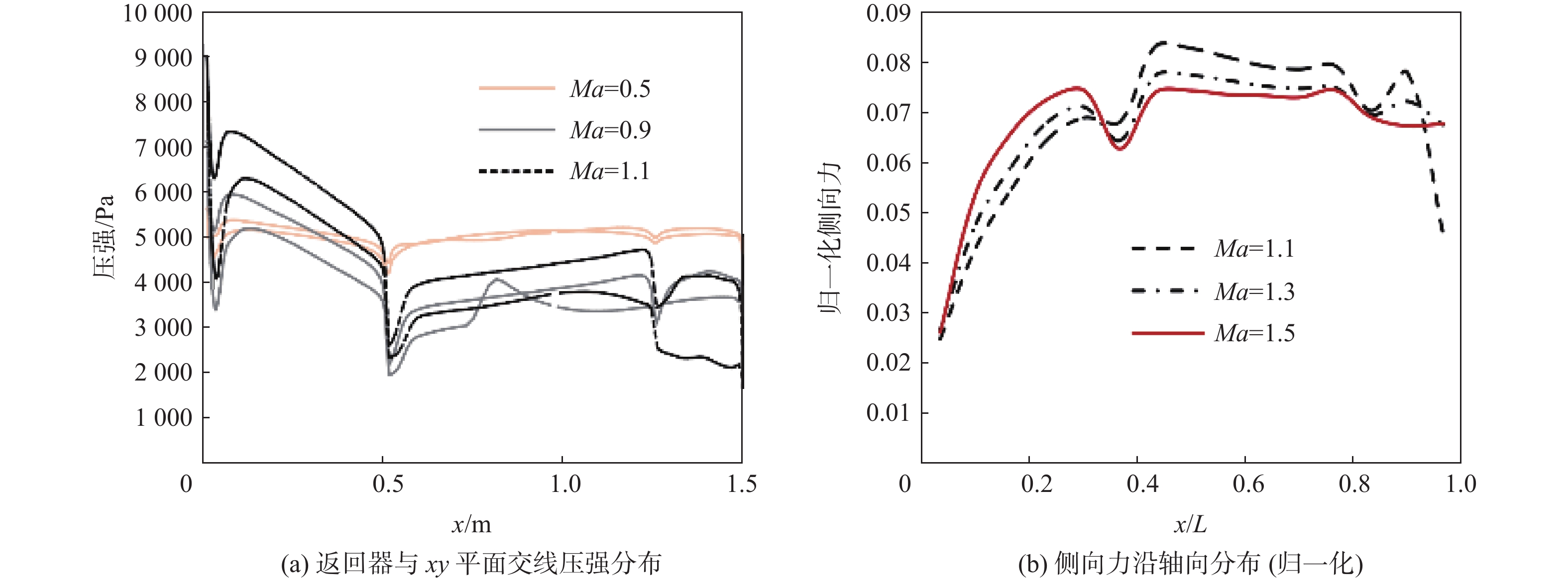
图9为马赫数为0.5、0.9、1.1时，返回器与xy平面交线上的压力系数分布及马赫数为1.1、1.3、1.5时对应的侧向力沿轴向分布（为便于对比进行归一化处理），从图中可观察到局部激波诱发分离区的产生和消除，以及超声速区压心随马赫数增加的前移规律。
综合来看，由于局部激波、激波诱导边界层分离和激波推移的共同作用，跨声速区域内的横航向稳定性对飞行安全带来了最严峻的挑战，这也是导致返回器无法以第1节所述的理想再入策略实施再入的主要原因，因此，需采取增稳措施对该区域内的横航向稳定性进行改善。
4. 横航向稳定性控制措施
改善跨声速区间内的横航向稳定性可考虑以下3种方法：①利用涡流发生器消除因局部激波诱导产生的边界层分离；②使用航向增强型面来提供额外的偏航恢复力矩；③调整重心位置。
4.1 涡流发生器
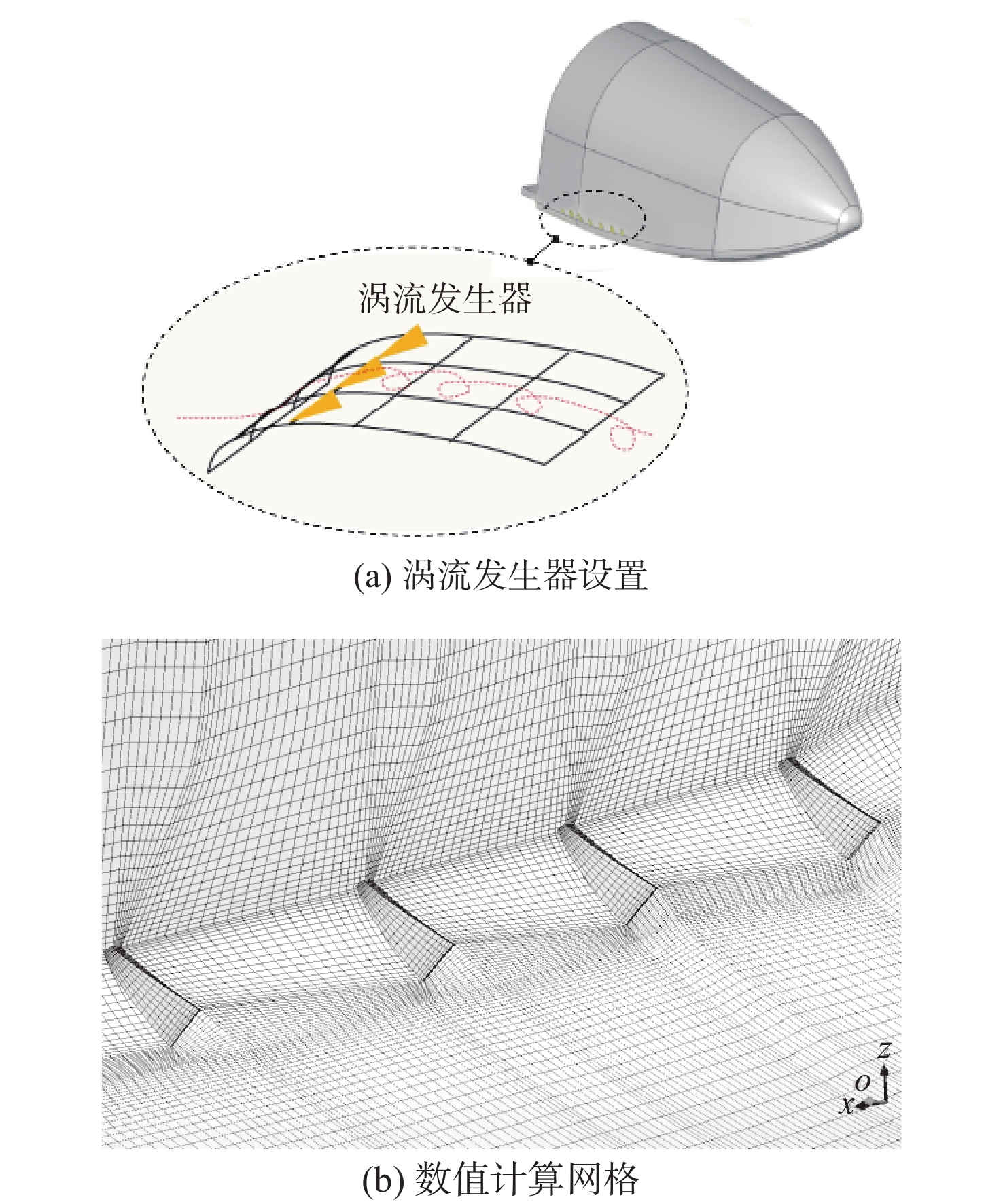
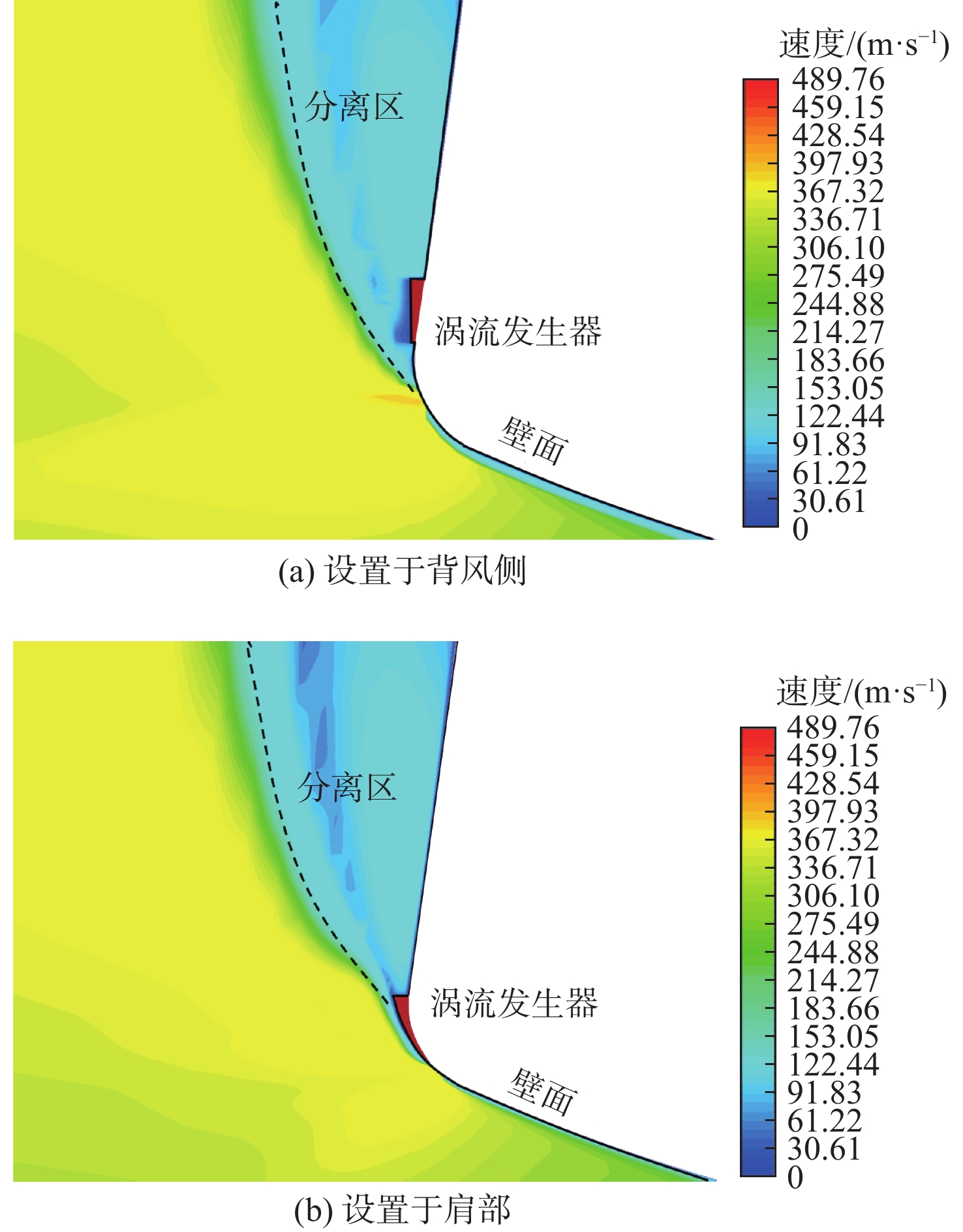
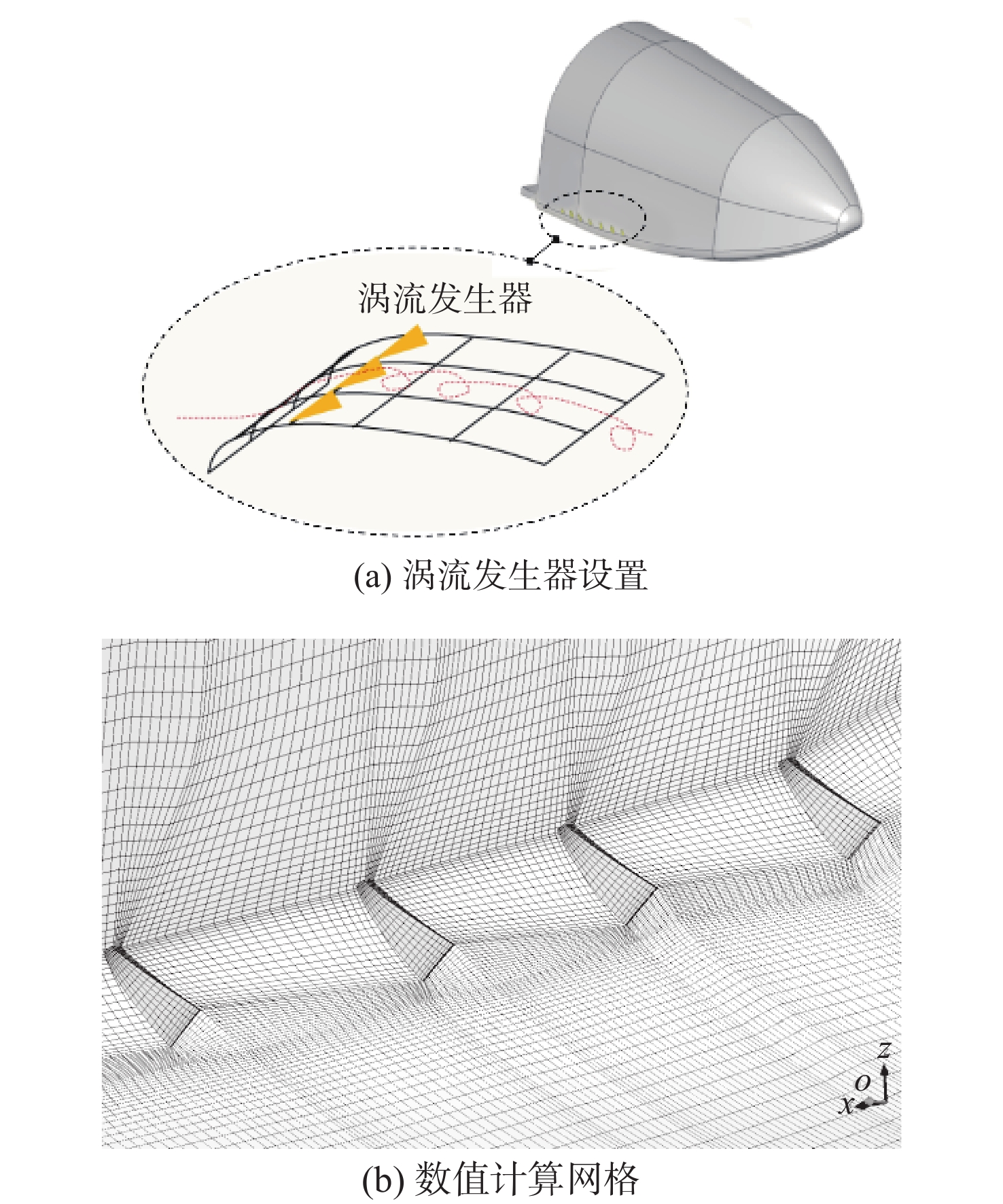
在分离区域前端加装微型涡流发生器来增加边界层动能是消除或抑制机翼边界层分离的常用方法。本文中的返回器流动分离位置型面与传统机翼存在显著差异，表现为较大的几何扩张角，这种大几何扩张角所产生的逆压梯度可能对涡流发生器的应用效果产生影响，因此，需使用数值计算方法进行详细分析。所使用的涡流发生器为一种常用的楔形结构，以串列形式安装在返回器侧部（方式1）或肩部（方式2），如图10（a）所示，计算所采用的数值分析方法与2.1节相同，计算网格如图10（b）所示。
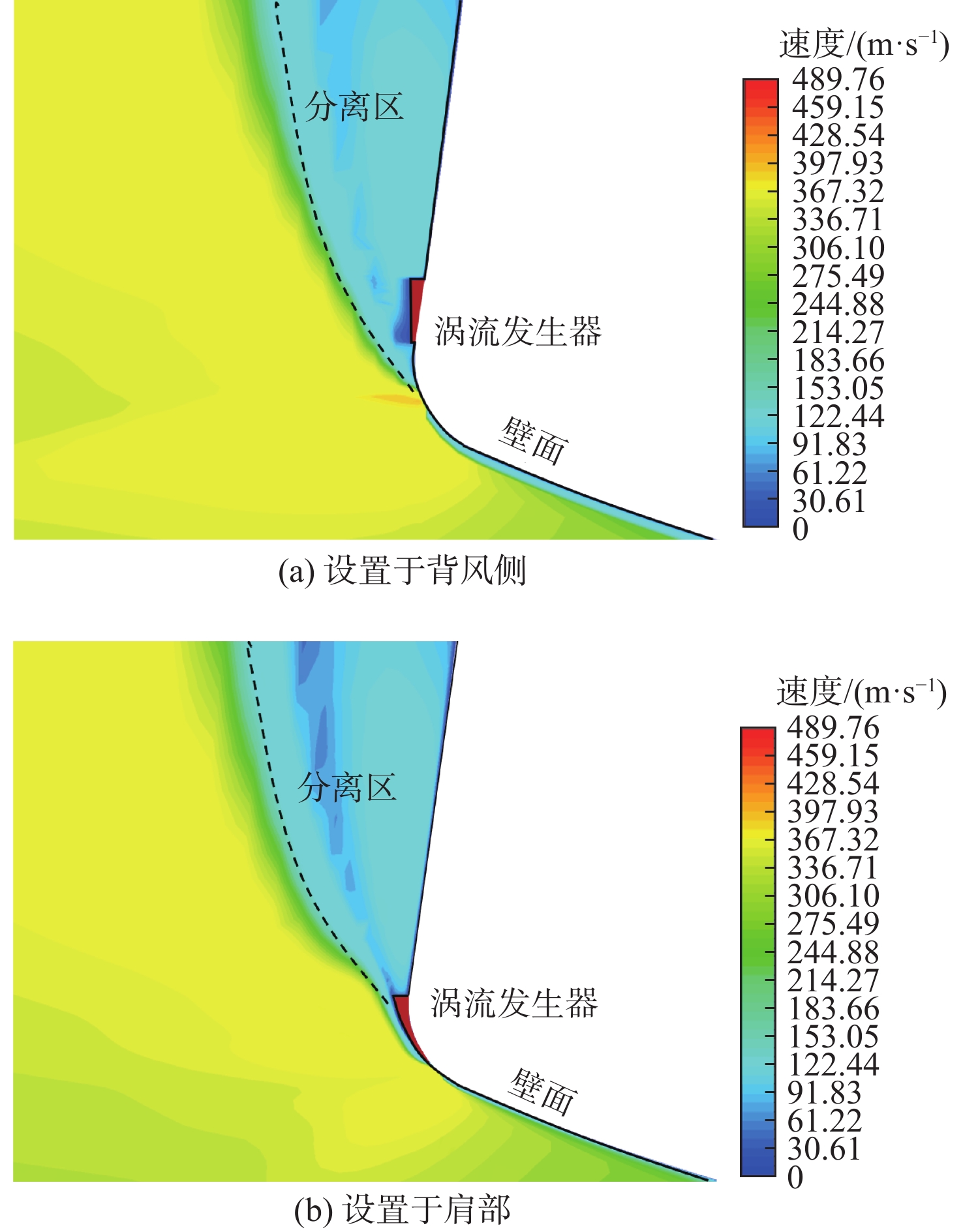
图11为数值计算得到的2种不同涡流发生器配置下的yz平面流场速度分布（对应迎角为30°、侧滑角为4°、马赫数为0.9）。结果显示，背风侧较大的几何扩张角抑制了涡流向分离区域的有效注入，使得背风侧边界层分离未受到有效控制或消除。增大涡流发生器的尺寸来改善涡流强度可提升涡流发生器的实际作用，但也降低了该结构在再入严苛热环境下的生存能力。据此可判定，利用涡流发生器来消除或抑制边界层分离进而改善跨声速速域内的横航向稳定性，对当前返回器而言并不具有良好的适应性。
图 11 涡流发生器不同安装位置及对应流场速度分布Figure 11. Vortex generator locations and corresponding field velocity distribution4.2 航向增强型面
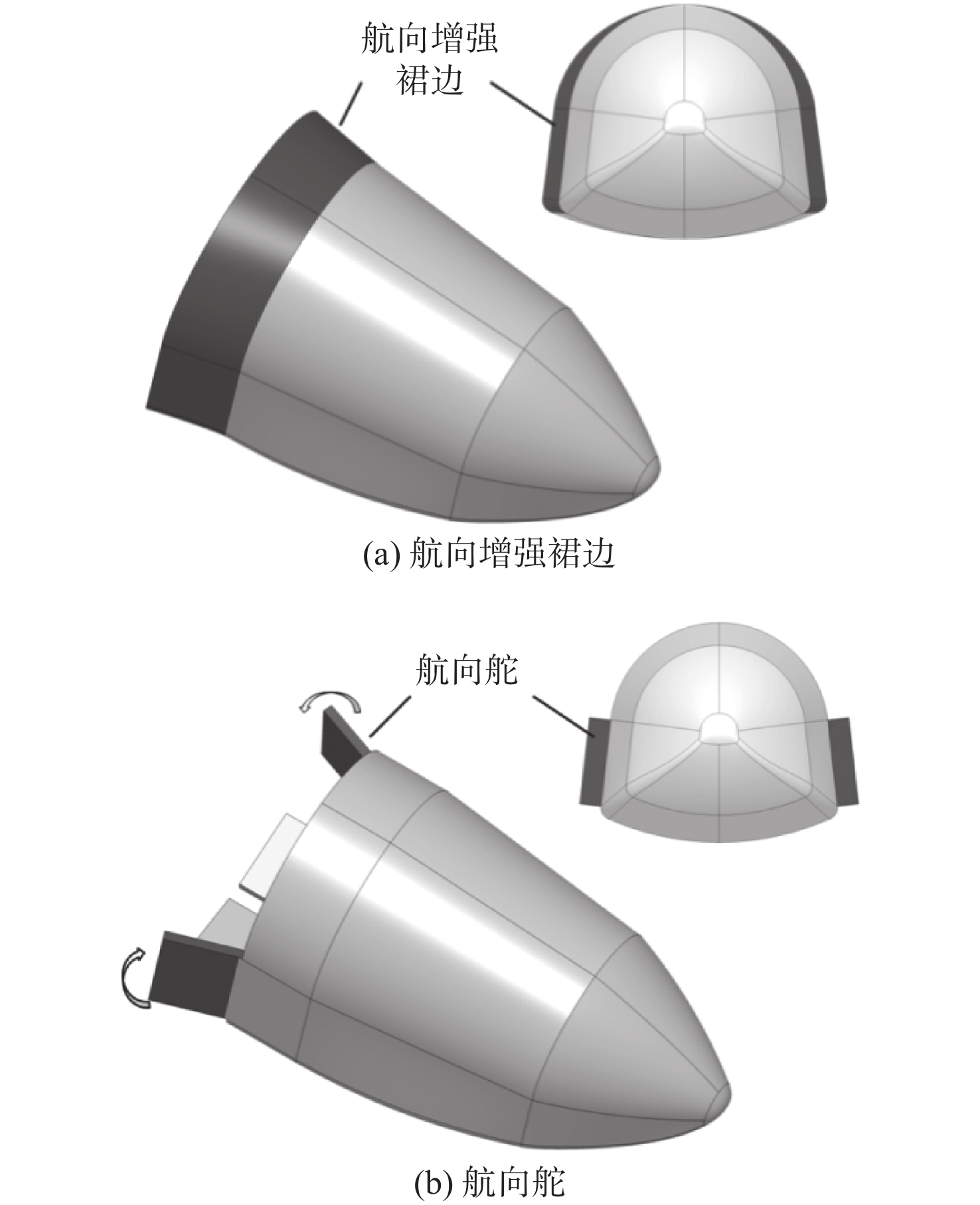
在返回器尾部加装航向增强型面形成附加偏航恢复力矩，是改善跨声速横航向稳定性更直接的方法。可使用的航向增强型面包括航向增强裙边（见图12（a））、航向舵（见图12（b））等。其中，裙边构型在原构型基础上增加了侧边几何倾角；航向舵构型则是将航向舵安装于返回器尾部侧面，其角度偏转为0°～20°（外偏为正）。
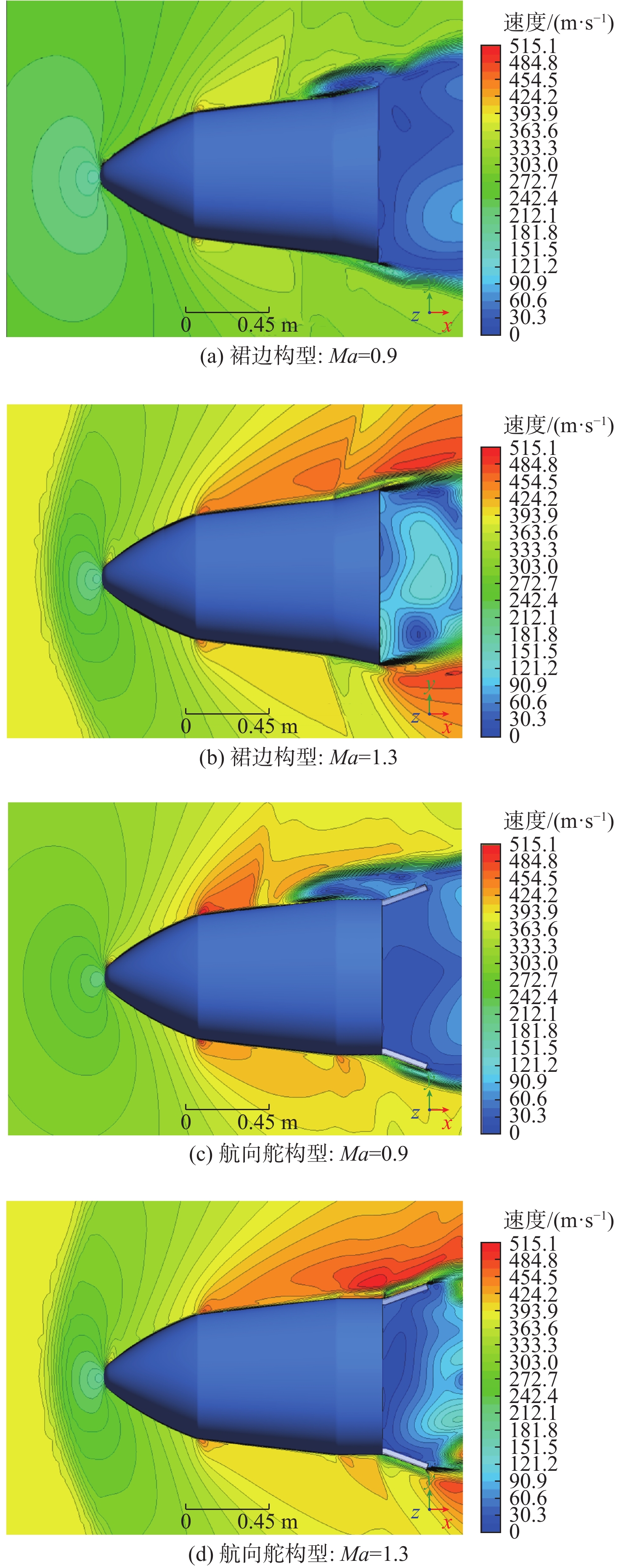
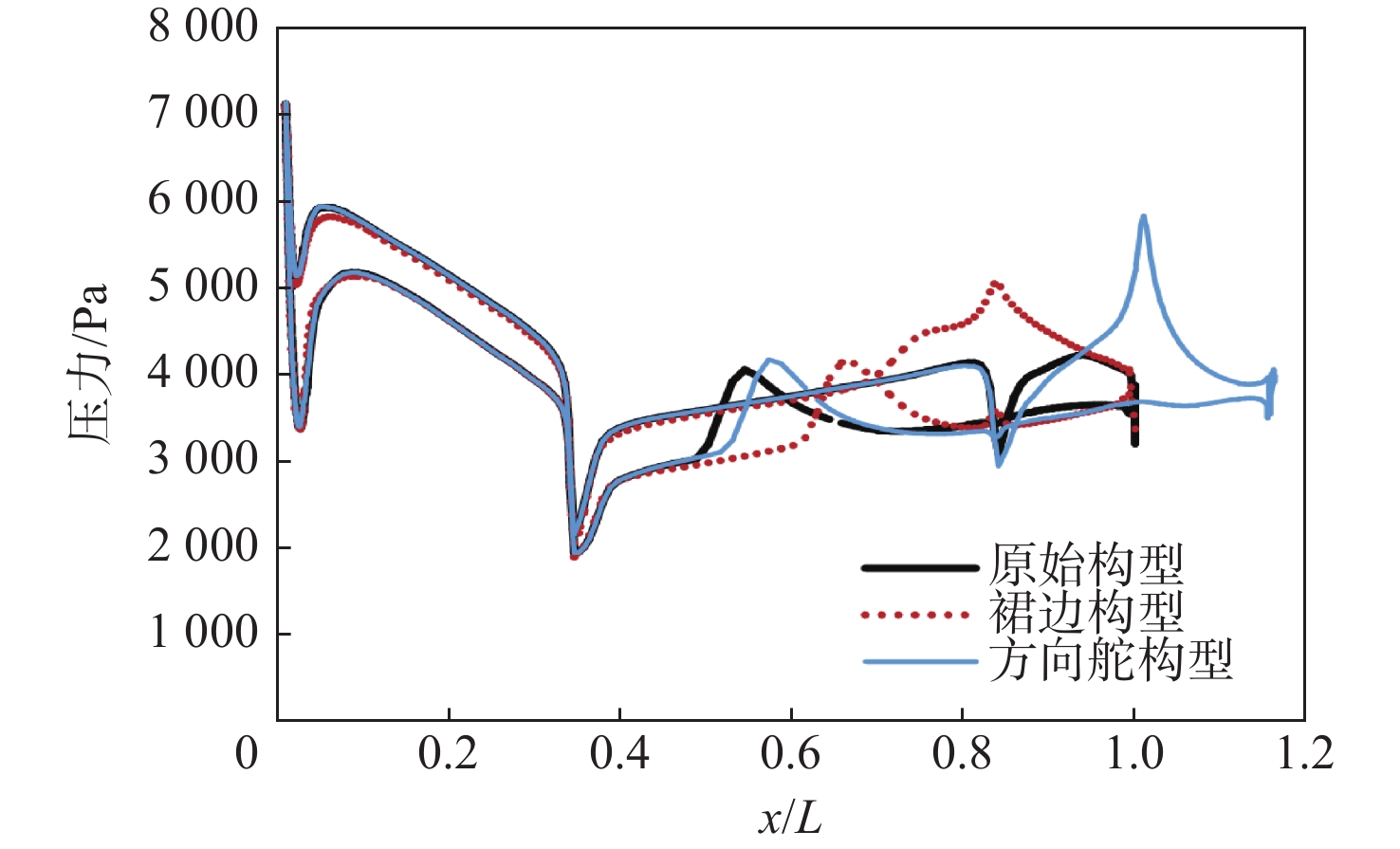
使用第3节所述数值仿真方法，对2种新构型在跨声速区间内的流动特性进行模拟，可得到流场速度分布如图13所示。将图13与图8（c）和图8（e）所示的原始构型流场分布进行对比可知，新构型中航向增强型面的使用对激波边界层分离现象的抑制效果不明显，然而图14所示的压力分布显示，2种航向增强型面均不同程度地增加了返回器尾部的吸力峰，产生了额外的偏航恢复力矩，因而对返回器的横航向稳定性产生了改善作用。
图 13 使用航向增强型面流场速度分布Figure 13. Flow field velocity distribution with lateral stability enhancement surfaces
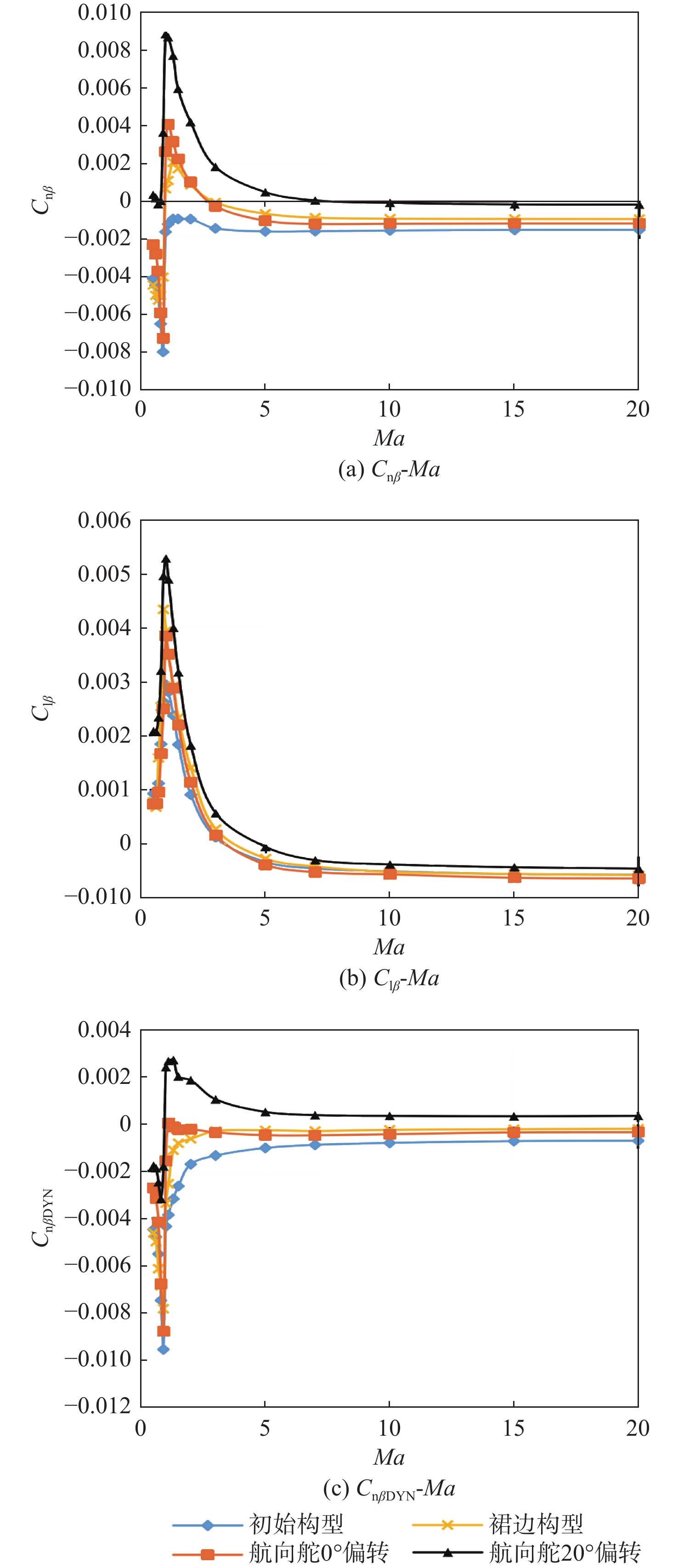
图 14 不同构型返回器与xy平面交线压力分布对比Figure 14. Pressure distribution on intersection lines of xy plane and reentry spacecraft with different configurations图15为裙边构型、航向舵0°及20°偏转构型在全速域、30°迎角下的的横航向特性计算结果，且与原始构型进行了比较。数据显示，裙边方案的横航向增稳效果与0°航向舵接近，而航向舵20°偏转对横航向稳定性的改善效果最为明显。
图 15 航向增强返回器横航向特性计算结果分析Figure 15. Calculated lateral feature of reentry spacecraft lateral stability enhancement analysis在航向舵20°偏转状态下，返回器在30° 迎角下的偏航稳定性从全速域不稳定变为在马赫数0.8以上稳定（Cnβ>0）或临界稳定（Cnβ≈0），但由于航向舵位置靠下，因此其横向稳定性出现小幅恶化（横向稳定的最小临界马赫数由3提升到5）。从开环动态偏航稳定性的综合判据（CnβDYN>0）分析，添加航向舵并偏转20°可将返回器开环动态偏航稳定的最低速度降至0.95Ma，此时返回器稳定性和初始外形相比已明显提升，但依然无法保证返回器稳定降速至开伞点的状态（约0.8Ma）。
4.3 调整重心位置
改变横航向特性的第3种方法是调整重心位置。对返回器来说，重心前后偏移主要影响偏航特性和俯仰特性，上下偏移主要改变滚转特性。在给定的迎角下，将重心向前配置既增加了偏航恢复力矩，又增加了俯仰低头力矩，偏航恢复力矩的增加有利于改善航向稳定性，但俯仰低头力矩的增加会降低纵向配平迎角，这会对偏航恢复力矩产生不利影响（见第2.2节）。两者的共同作用限制了重心前后移动对横航向稳定性的改善作用，因此，在利用重心偏移来改善横航向稳定性时，主要考虑重心的上下移动。
图16以30°迎角为例，给出了重心下偏6%（Zcg/L=6%）时，各构型状态返回器横航向特性随马赫数的变化情况。结果显示，重心向下偏移6%，可在不影响航向稳定性（见图16（a））的前提下明显改善横向稳定性（见图16（b）），从而将返回器的开环动态偏航的稳定性（见图16（c）和图16（d））显著改善：在30°迎角下，初始构型、裙边构型、航向舵0°偏转、航向舵20°偏转构型所对应的横航向稳定速域下限马赫数分别为1.5、1.0、0.99、0.82。其中，航向舵外偏20°对应的不稳定临界马赫数已达到亚声速开伞点附近，这意味着在该构型状态下，返回器可以第2节理想再入策略执行再入飞行。
图 16 重心下偏6%返回器横航向特性计算结果Figure 16. Calculated lateral features of reentry spacecraft center-of-gravity offset 6%尽管航向舵20°偏转方案为跨声速区间内的横航向稳定性改善提供了最有效的途径，但该方案同时也会对返回器气动特性、防热性能产生不利影响（不同迎角下的升阻比降低3%～5%）。与此同时，通过进一步分析图16可知，在相同重心偏置下，航向舵0°偏转偏在超声速、高超声速阶段亦可保持足够的横航向稳定性，因此，在制定再入策略时，可考虑从航向舵0°（超声速、高超声速阶段）向航向舵外偏20°（跨声速阶段）的切换过程，以实现系统整体效能的最大化。
5. 结 论
1） 类双锥型升力式返回器的横航向稳定性在跨声速阶段存在显著恶化，其许用迎角下限超出了升降舵面的配平极限，如无增稳措施将无法实现安全开伞。
2） 该类返回器横航向稳定性波动机理在不同速域内存在显著差异，其中，亚声速阶段为背风侧局部激波的生成和边界层的诱导分离；跨声速阶段为激波推移和分离区的消除；超声速阶段为头部弓形激波的生成和移动。
3） 可加装航向增强型面（裙边、航向舵等）或实行重心偏置来改善该类返回器的横航向稳定性，其中，舵向舵20°偏转、重心下偏6%为将不稳定临界马赫数降至亚声速开伞点附近。
4） 航向舵偏转对返回器气动特性、防热性能存在不利影响，在制定再入策略时可考虑从0°偏转（超声速/高超声速）向20°偏转（亚/跨声速）的控制阶段切换，以优化系统整体效能。
-
图 4 返回器横航向特性随马赫数变化
Figure 4. Changes in the lateral features of reentry spacecraft with Mach number
图 6 横航向压心位置随迎角变化（Ma = 5）
Figure 6. Variation of lateral pressure center with angle of attack (Ma = 5)
图 11 涡流发生器不同安装位置及对应流场速度分布
Figure 11. Vortex generator locations and corresponding field velocity distribution
图 13 使用航向增强型面流场速度分布
Figure 13. Flow field velocity distribution with lateral stability enhancement surfaces
图 14 不同构型返回器与xy平面交线压力分布对比
Figure 14. Pressure distribution on intersection lines of xy plane and reentry spacecraft with different configurations
图 15 航向增强返回器横航向特性计算结果分析
Figure 15. Calculated lateral feature of reentry spacecraft lateral stability enhancement analysis
图 16 重心下偏6%返回器横航向特性计算结果
Figure 16. Calculated lateral features of reentry spacecraft center-of-gravity offset 6%
表 1 类神舟返回器计算值与实验值对比
Table 1. Comparison of calculated and experimental values of Shenzhou-like reentry spacecraft
参数项 CA CN CL CD Cm 预测值 1.315 0.1587 − 0.3006 1.290 0.0999 实验值 1.335 0.1590 − 0.3072 1.309 0.1025 
下载: 导出CSV
-
[1] VASHCHENKOV P, KASHKOVSKY A, DYADKIN A, et al. Numerical study of high-altitude aerodynamics of the clipper reentry vehicle[C]//Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2008: 1188. [2] MOSELEY W C, GRAHAM R E, HUGHES J E. Aerodynamic stability characteristics of the apollo command module: NASA TN D-4688[R]. Houston: Manned Spacecraft Center, 1968: 171-175. [3] ABE T, SATO S I, MATSUKAWA Y, et al. Study for dynamically unstable motion of reentry capsule[C]//Proceedings of the 34th Thermophysics Conference. Reston: AIAA, 2000: 2589. [4] 张涵信, 袁先旭, 叶友达, 等. 飞船返回舱俯仰振荡的动态稳定性研究[J]. 空气动力学学报, 2002, 20(3): 247-259. doi: 10.3969/j.issn.0258-1825.2002.03.001ZHANG H X, YUAN X X, YE Y D, et al. Research on the dynamic stability of an orbital reentry vehicle in pitching[J]. Acta Aerodynamica Sinica, 2002, 20(3): 247-259(in Chinese). doi: 10.3969/j.issn.0258-1825.2002.03.001 [5] 袁先旭, 张涵信, 谢昱飞. 飞船返回舱再入俯仰动稳定吸引子数值仿真[J]. 空气动力学学报, 2007, 25(4): 431-436. doi: 10.3969/j.issn.0258-1825.2007.04.004YUAN X X, ZHANG H X, XIE Y F. Numerical simulation for dynamic stability in pitching of unfinned reentry capsule and bifurcation with Mach number prediction[J]. Acta Aerodynamica Sinica, 2007, 25(4): 431-436(in Chinese). doi: 10.3969/j.issn.0258-1825.2007.04.004 [6] TERAMOTO S, FUJII K. Study on the mechanism of the instability of a re-entry capsule at transonic speeds[C]//Proceedings of the Fluids Conference and Exhibit. Reston: AIAA, 2000: 2603. [7] TERAMOTO S, HIRAKI K, FUJII K. Numerical analysis of dynamic stability of a reentry capsule at transonic speeds[J]. AIAA Journal, 2001, 39(4): 646-653. doi: 10.2514/2.1357 [8] 朱德华, 沈清, 杨武兵. 返回舱高雷诺数再入过程底部流动稳定性[J]. 力学学报, 2021, 53(3): 752-760. doi: 10.6052/0459-1879-20-318ZHU D H, SHEN Q, YANG W B. Base flow stability of return capsule during reentry process with high Reynolds number[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(3): 752-760(in Chinese). doi: 10.6052/0459-1879-20-318 [9] MITCHELTREE R, FREMAUX C, YATES L. Subsonic static and dynamic aerodynamics of blunt entry vehicles[C]//Proceedings of the 37th Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 1999: 1020. [10] 何开锋, 和争春. 飞船返回舱跨声速全局稳定性研究[J]. 飞行力学, 1999, 17(3): 34-38. doi: 10.3969/j.issn.1002-0853.1999.03.007HE K F, HE Z C. The global stability analysis of reentry capsule transonic flight[J]. Flight Dynamics, 1999, 17(3): 34-38(in Chinese). doi: 10.3969/j.issn.1002-0853.1999.03.007 [11] 宋玉辉, 陈农, 秦永明. 亚跨超声速返回舱动稳定特性[J]. 航天返回与遥感, 2014, 35(2): 31-38. doi: 10.3969/j.issn.1009-8518.2014.02.005SONG Y H, CHEN N, QIN Y M. Sub-, trans- and super-sonic dynamic stability characteristics for reentry capsule[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(2): 31-38(in Chinese). doi: 10.3969/j.issn.1009-8518.2014.02.005 [12] 胡静, 宋玉辉, 陈农, 等. 返回舱动稳定特性风洞试验的影响参数[J]. 航天返回与遥感, 2013, 34(5): 14-19. doi: 10.3969/j.issn.1009-8518.2013.05.003HU J, SONG Y H, CHEN N, et al. Study of key parameters for dynamic stability of reentry capsule[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(5): 14-19(in Chinese). doi: 10.3969/j.issn.1009-8518.2013.05.003 [13] 宋威, 艾邦成, 蒋增辉, 等. 返回舱跨声速自由飞行的静动稳定性[J]. 实验流体力学, 2019, 33(4): 89-94. doi: 10.11729/syltlx20180083SONG W, AI B C, JIANG Z H, et al. Free flight static and dynamic aerodynamic characteristics for re-entry capsule at transonic speed[J]. Journal of Experiments in Fluid Mechanics, 2019, 33(4): 89-94(in Chinese). doi: 10.11729/syltlx20180083 [14] 鲍文, 姚照辉. 综合离心力/气动力的升力体高超声速飞行器纵向运动建模研究[J]. 宇航学报, 2009, 30(1): 128-133. doi: 10.3873/j.issn.1000-1328.2009.00.023BAO W, YAO Z H. Study on longitudinal modeling for integrated centrifugal/aero force lifting-body hypersonic vehicles[J]. Journal of Astronautics, 2009, 30(1): 128-133(in Chinese). doi: 10.3873/j.issn.1000-1328.2009.00.023 [15] 贾子安, 张陈安, 王柯穆, 等. 乘波布局高超声速飞行器纵向静稳定特性分析[J]. 中国科学: 技术科学, 2014, 44(10): 1114-1122. doi: 10.1360/N092014-00058JIA Z A, ZHANG C A, WANG K M, et al. Longitudinal static stability analysis of hypersonic waveriders[J]. Scientia Sinica (Technologica), 2014, 44(10): 1114-1122(in Chinese). doi: 10.1360/N092014-00058 [16] 贾子安. 乘波飞行器气动布局初步设计研究[D]. 北京: 中国科学院大学, 2014: 56-75.JIA Z A. Preliminary design of aerodynamic layout of waverider vehicle[D]. Beijing: University of Chinese Academy of Sciences, 2014: 56-75(in Chinese). [17] 王柯穆. 幂次体乘波飞行器纵向静稳定及升阻比优化设计[D]. 北京: 中国科学院大学, 2013.WANG K M. Longitudinal static stability and optimal design of lift-drag ratio of power-law waverider[D]. Beijing: University of Chinese Academy of Sciences, 2013(in Chinese). [18] MANGIN B, BENAY R, CHANETZ B, et al. Optimization of viscous waveriders derived from axisymmetric power-law blunt body flows[J]. Journal of Spacecraft and Rockets, 2006, 43(5): 990-998. doi: 10.2514/1.20079 [19] 高清, 赵俊波, 李潜. 类HTV-2横侧向稳定性研究[J]. 宇航学报, 2014, 35(6): 657-662.GAO Q, ZHAO J B, LI Q. Study on lateral-directional stability of HTV-2 like configuration[J]. Journal of Astronautics, 2014, 35(6): 657-662(in Chinese). [20] 高清, 李潜. 美国高超声速飞行器横侧向稳定性研究[J]. 飞航导弹, 2012(12): 14-18.GAO Q, LI Q. Study on lateral stability of American hypersonic vehicle[J]. Aerodynamic Missile Journal, 2012(12): 14-18(in Chinese). [21] 祝立国, 王永丰, 庄逢甘, 等. 高速高机动飞行器的横航向偏离预测判据分析[J]. 宇航学报, 2007, 28(6): 1550-1553. doi: 10.3321/j.issn:1000-1328.2007.06.022ZHU L G, WANG Y F, ZHUANG F G, et al. The lateral-directional departure criteria analysis of high-speed and high maneuverability aircraft[J]. Journal of Astronautics, 2007, 28(6): 1550-1553(in Chinese). doi: 10.3321/j.issn:1000-1328.2007.06.022 [22] 闵昌万. 高超声速飞行器横侧向气动布局准则研究[J]. 宇航总体技术, 2018, 2(3): 1-10.MIN C W. The aerodynamic configuration criteria for the lateral-directional stability of hypersonic vehicle[J]. Astronautical Systems Engineering Technology, 2018, 2(3): 1-10(in Chinese). [23] 王亮, 周玲. 基于改进的k-ω-γ转捩模式预测高超声速飞行器气动特性[J]. 空气动力学学报, 2021, 39(3): 51-61. doi: 10.7638/kqdlxxb-2019.0146WANG L, ZHOU L. Prediction of aerodynamic characteristics of hypersonic vehicle by improved k-ω-γ transition model[J]. Acta Aerodynamica Sinica, 2021, 39(3): 51-61(in Chinese). doi: 10.7638/kqdlxxb-2019.0146 [24] 钱翼稷. 空气动力学[M]. 北京: 北京航空航天大学出版社, 2004: 287-289.QIAN Y J. Aerodynamics[M]. Beijing: Beihang University Press, 2004: 287-289(in Chinese). -
下载:
下载:
点击查看大图
计量
- 文章访问数: 334
- HTML全文浏览量: 125
- PDF下载量: 24
- 被引次数: 0
