基于联合仿真的曲面共形多孔结构拓扑优化方法

付君健; 徐勇; 周祥曼; 舒正涛; 田启华

doi:10.13700/j.bh.1001-5965.2022.0751

基于联合仿真的曲面共形多孔结构拓扑优化方法

doi: 10.13700/j.bh.1001-5965.2022.0751

付君健^{1, 2, 3},
徐勇²,
周祥曼^{1, 2, ,},
舒正涛²,
田启华^{1, 2}

1.
水电机械设备设计与维护湖北省重点实验室，宜昌 443002
2.
三峡大学机械与动力学院，宜昌 443002
3.
智能制造装备与技术全国重点实验室，武汉 430074

基金项目: 国家自然科学基金(51775308)；湖北省自然科学基金(2021CFB236)；智能制造装备与技术全国重点实验室开放基金(IMETKF2023016)

详细信息

通讯作者:
E-mail：zhouxman@ctgu.edu.cn

中图分类号: TH112
计量
- 文章访问数: 103
- HTML全文浏览量: 42
- PDF下载量: 18
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-31
- 录用日期: 2023-01-14
- 网络出版日期: 2023-02-28
- 整期出版日期: 2024-09-27

Topological optimization method for conformal cellular structures on surfaces based on co-simulation

FU Junjian^{1, 2, 3},
XU Yong²,
ZHOU Xiangman^{1, 2
, ,},
SHU Zhengtao²,
TIAN Qihua^{1, 2}

1.
Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance，Yichang 443002，China
2.
College of Mechanical & Power Engineering，China Three Gorges University，Yichang 443002，China
3.
Stale Key Laboratory of Intelligent Manufacturing Equipment and Technology, Wuhan 430074, China

Funds: National Natural Science Foundation of China (51775308); Natural Science Foundation of Hubei Province (2021CFB236); Open Fund of Stale Key Laboratory of Intelligent Manufacturing Equipment and Technology (IMETKF2023016)

More Information

Corresponding author: E-mail：zhouxman@ctgu.edu.cn

摘要

摘要:
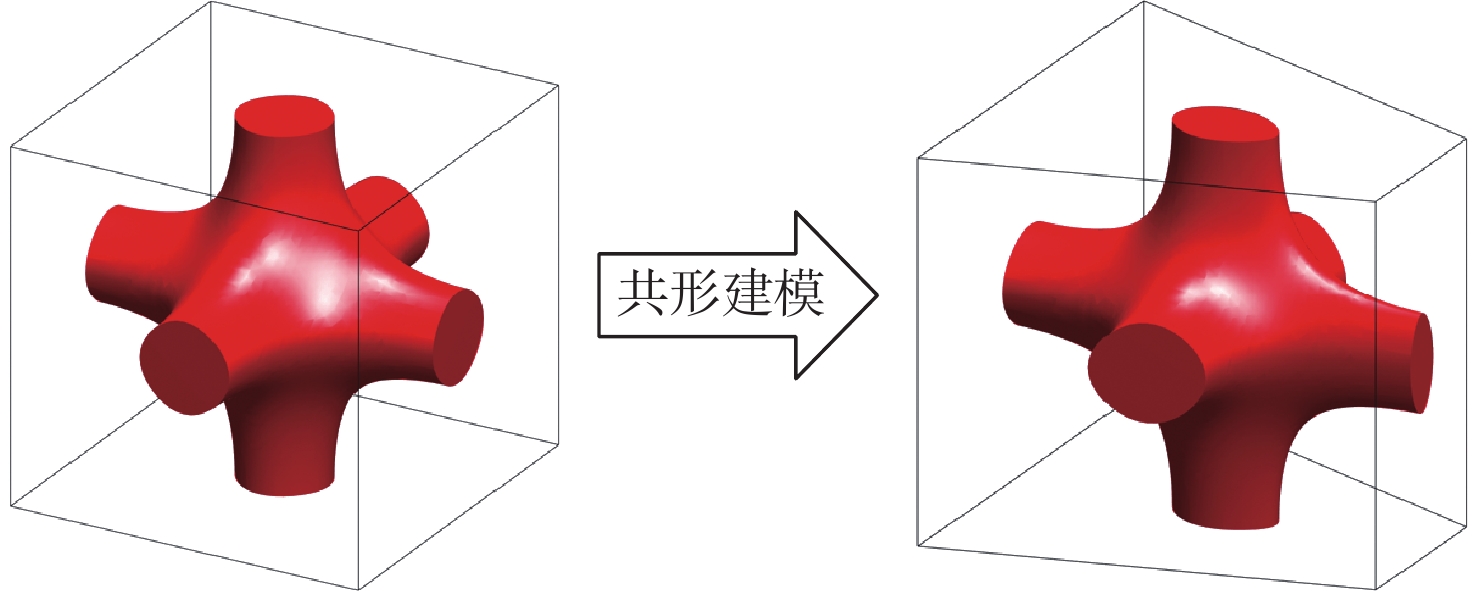
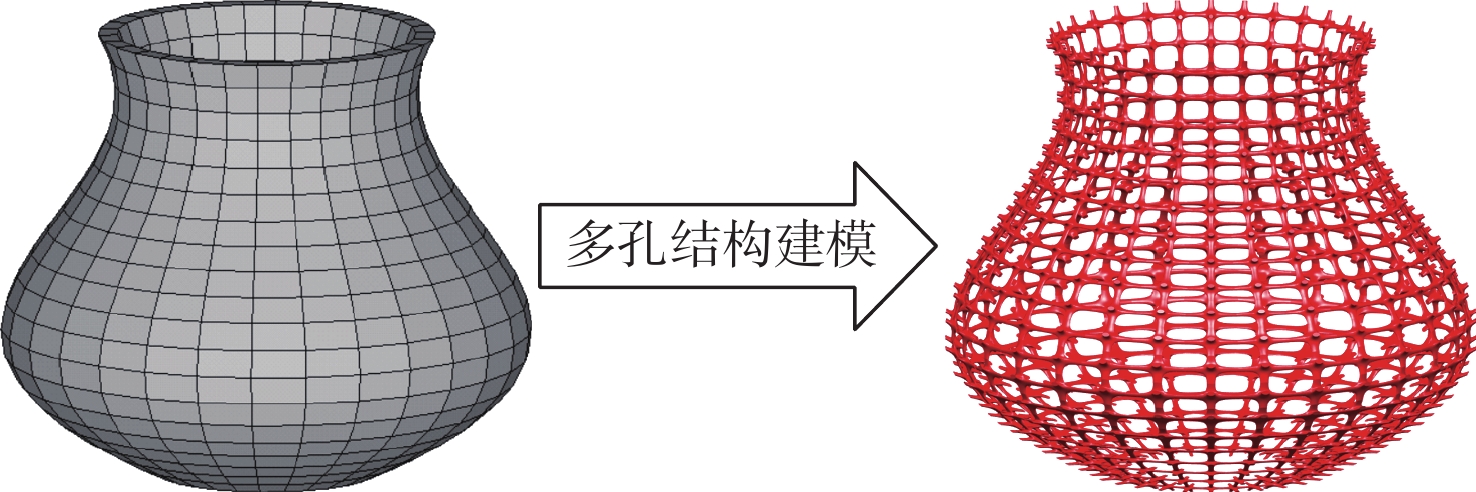
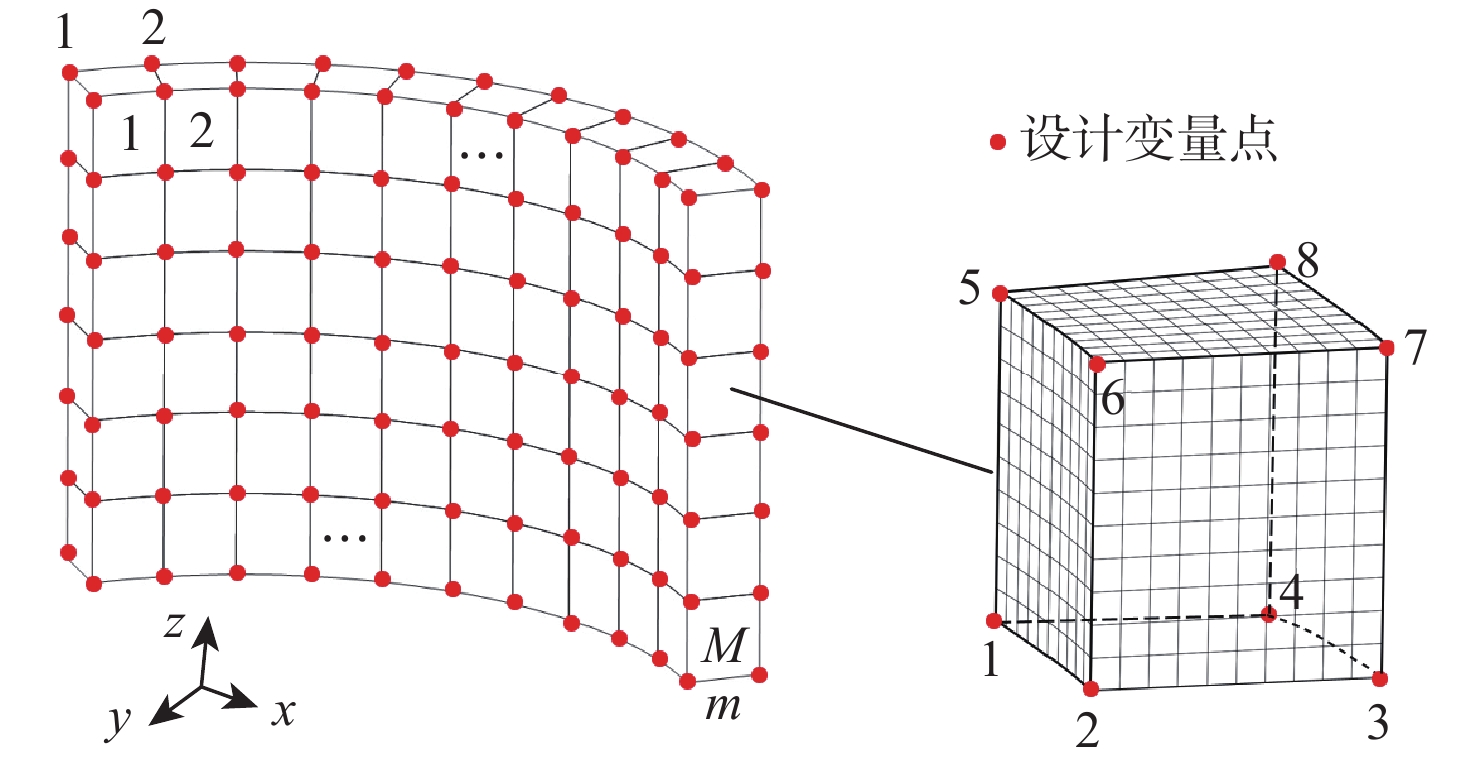
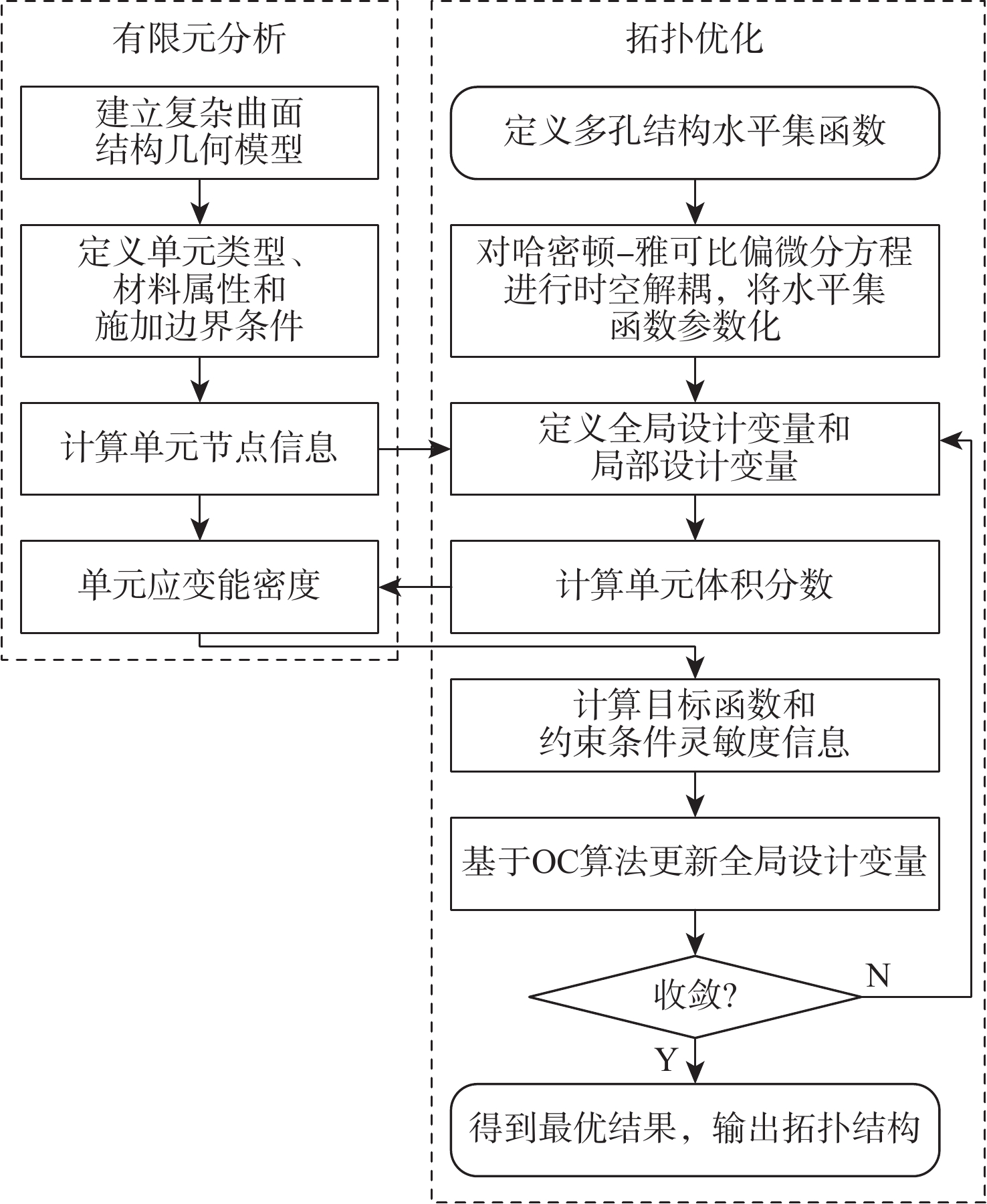
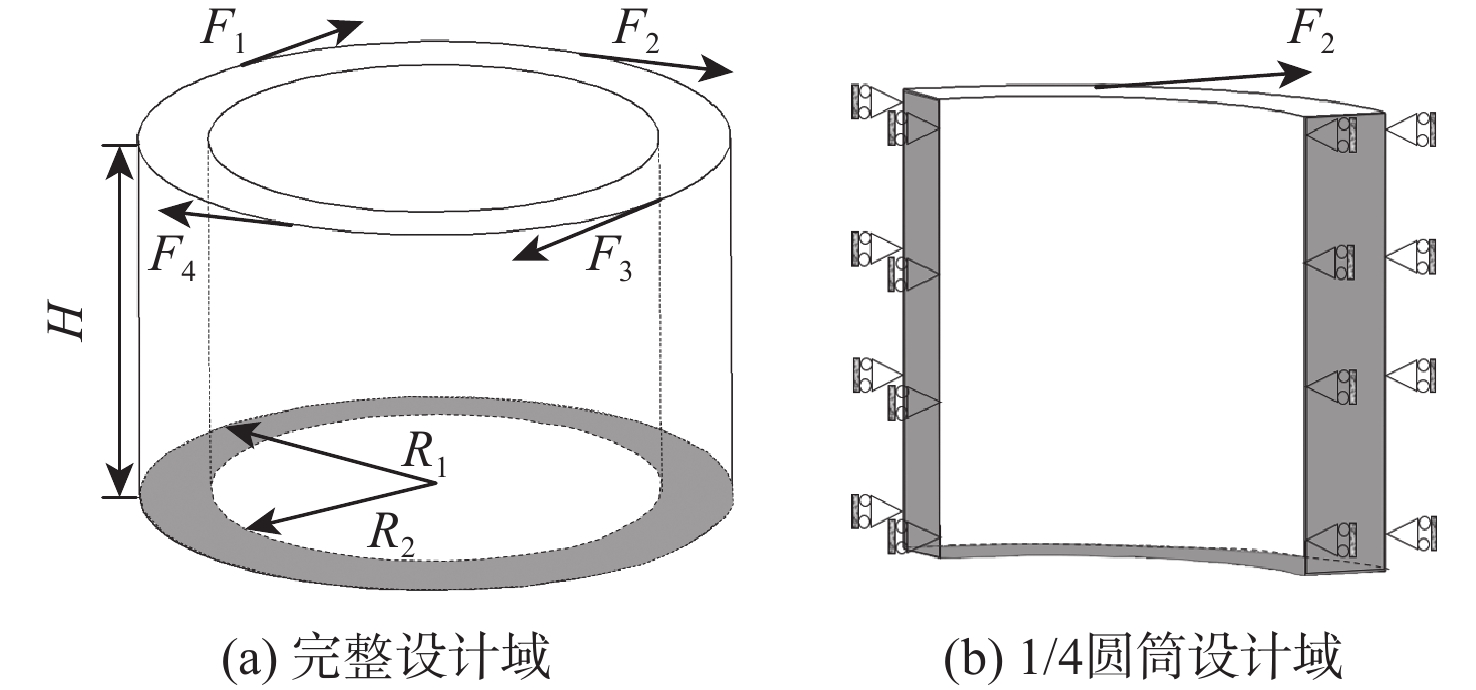
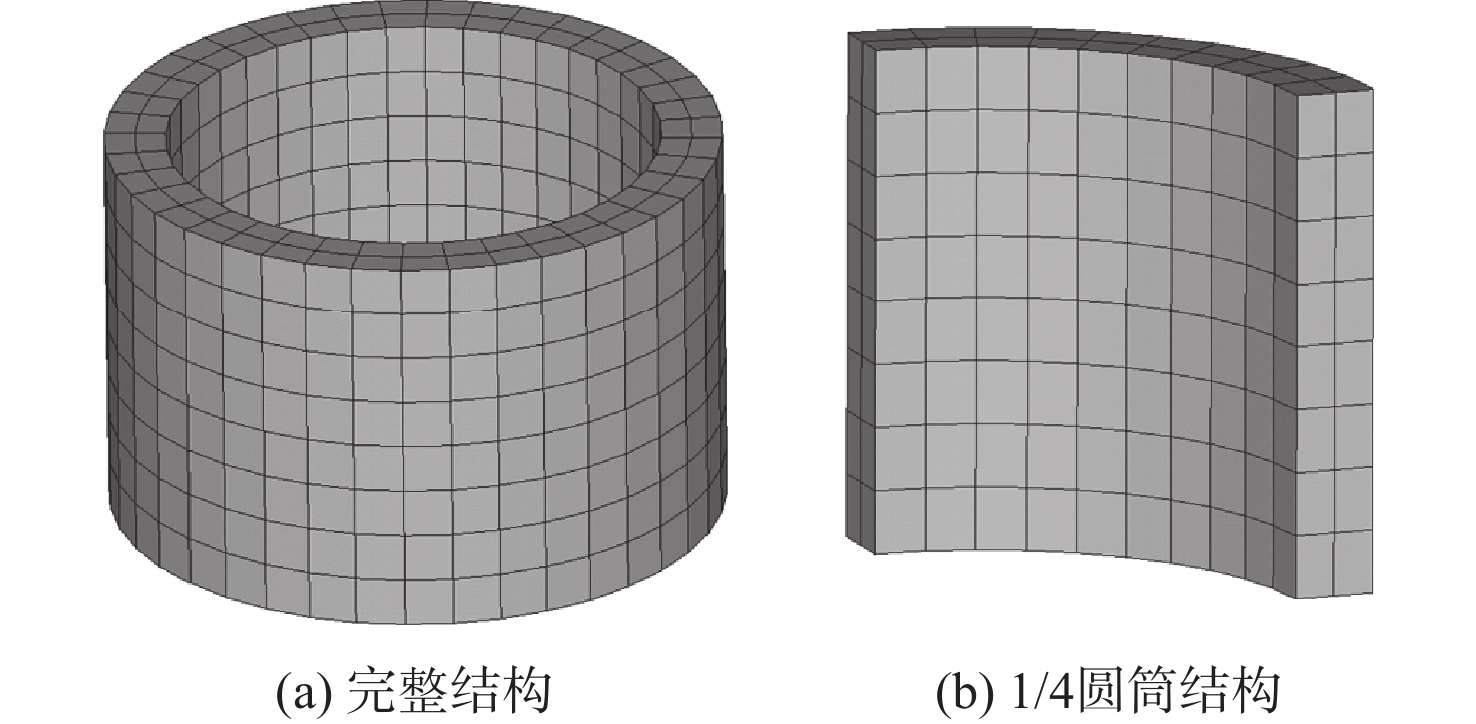
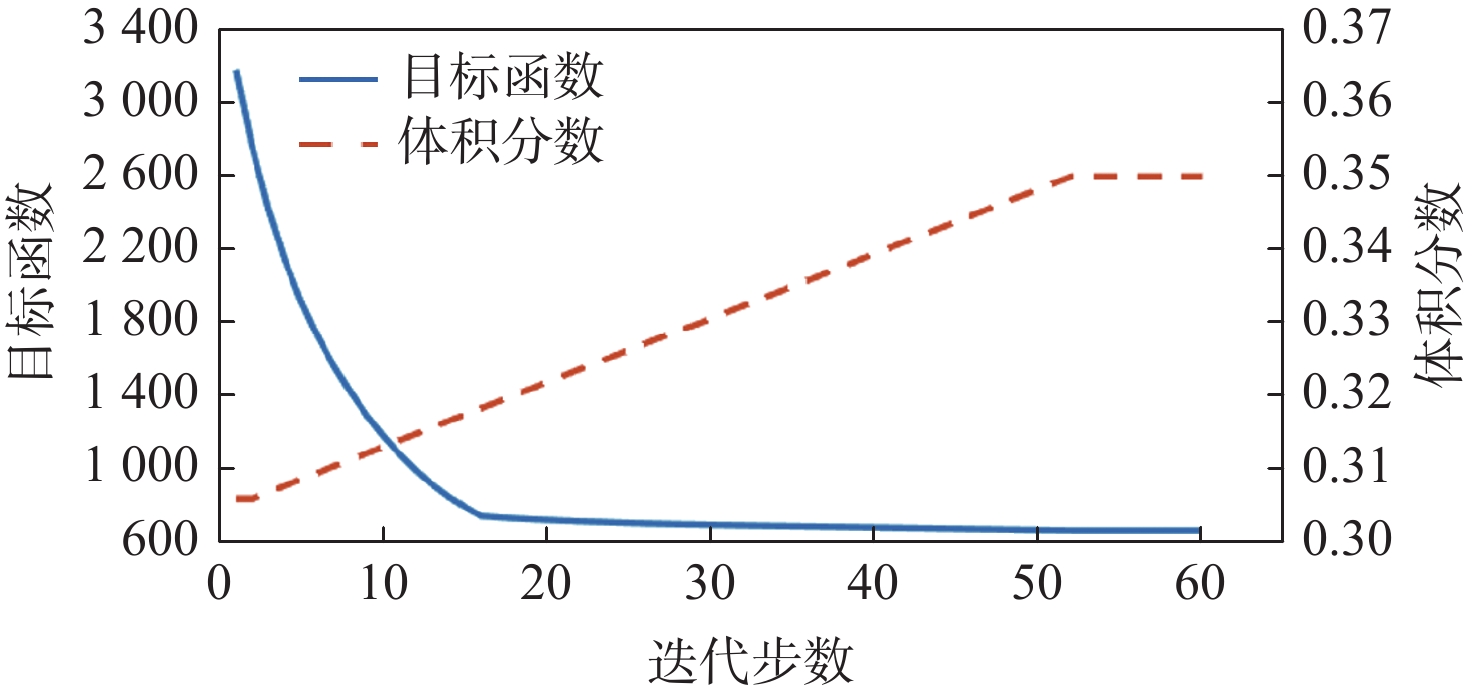
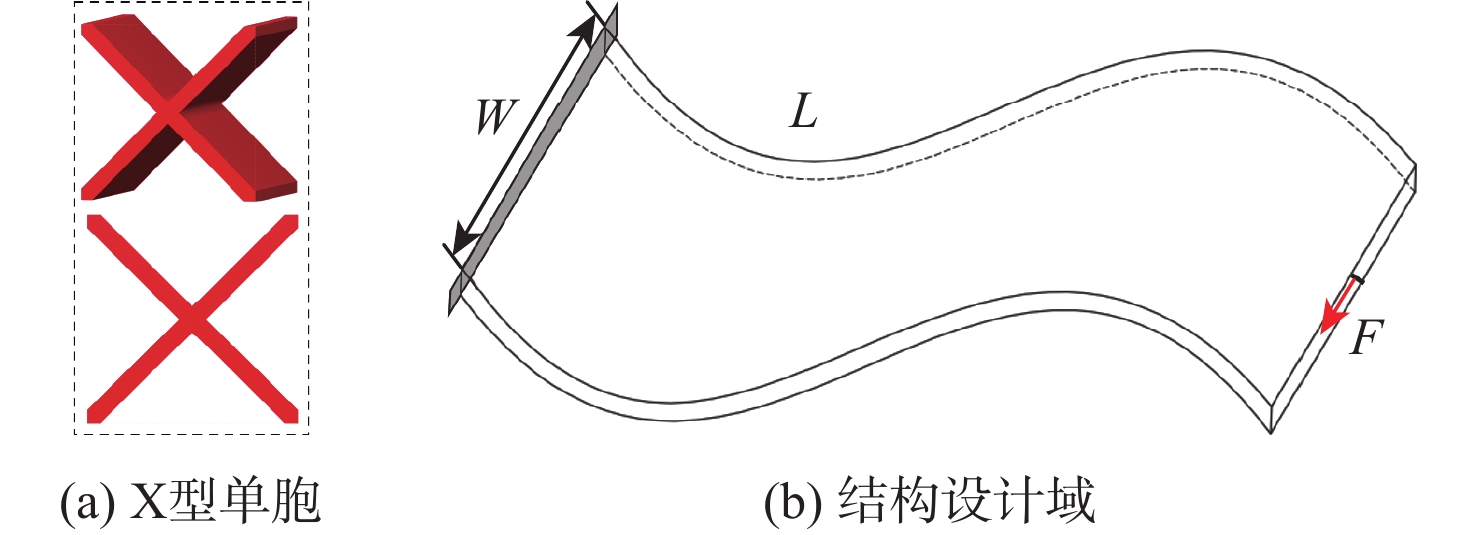
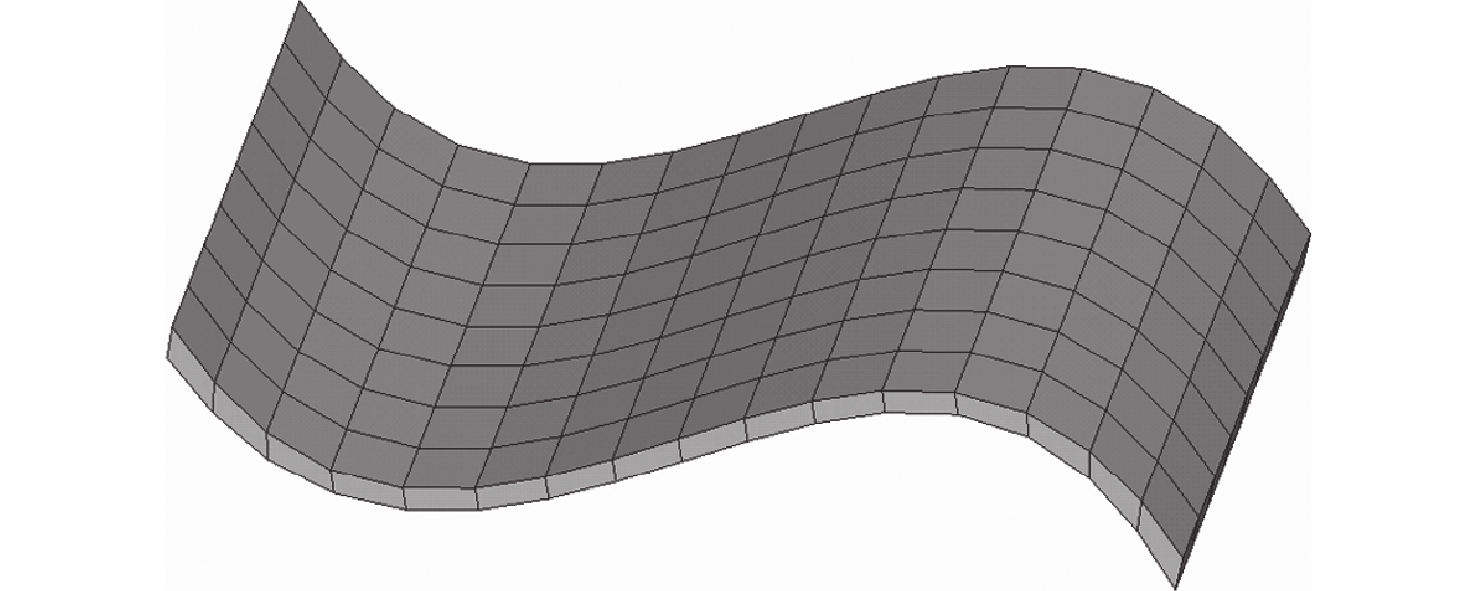
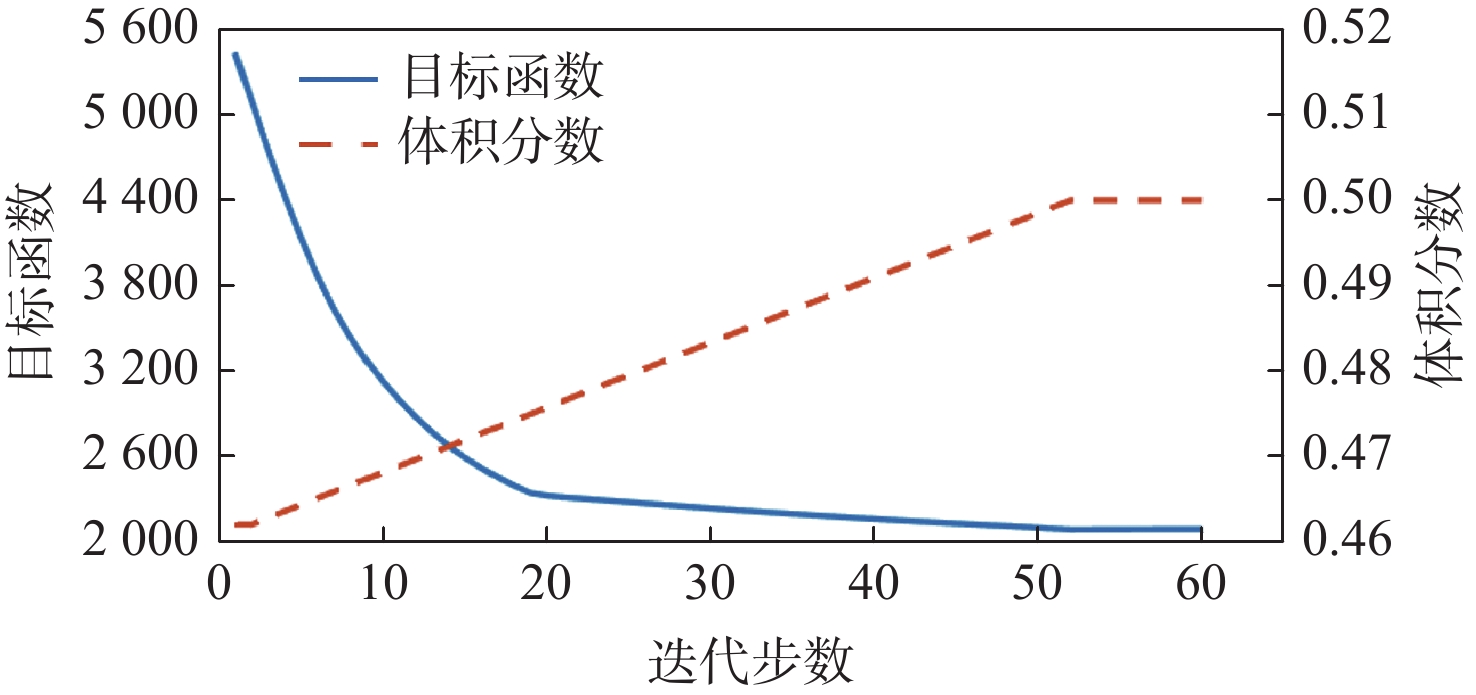
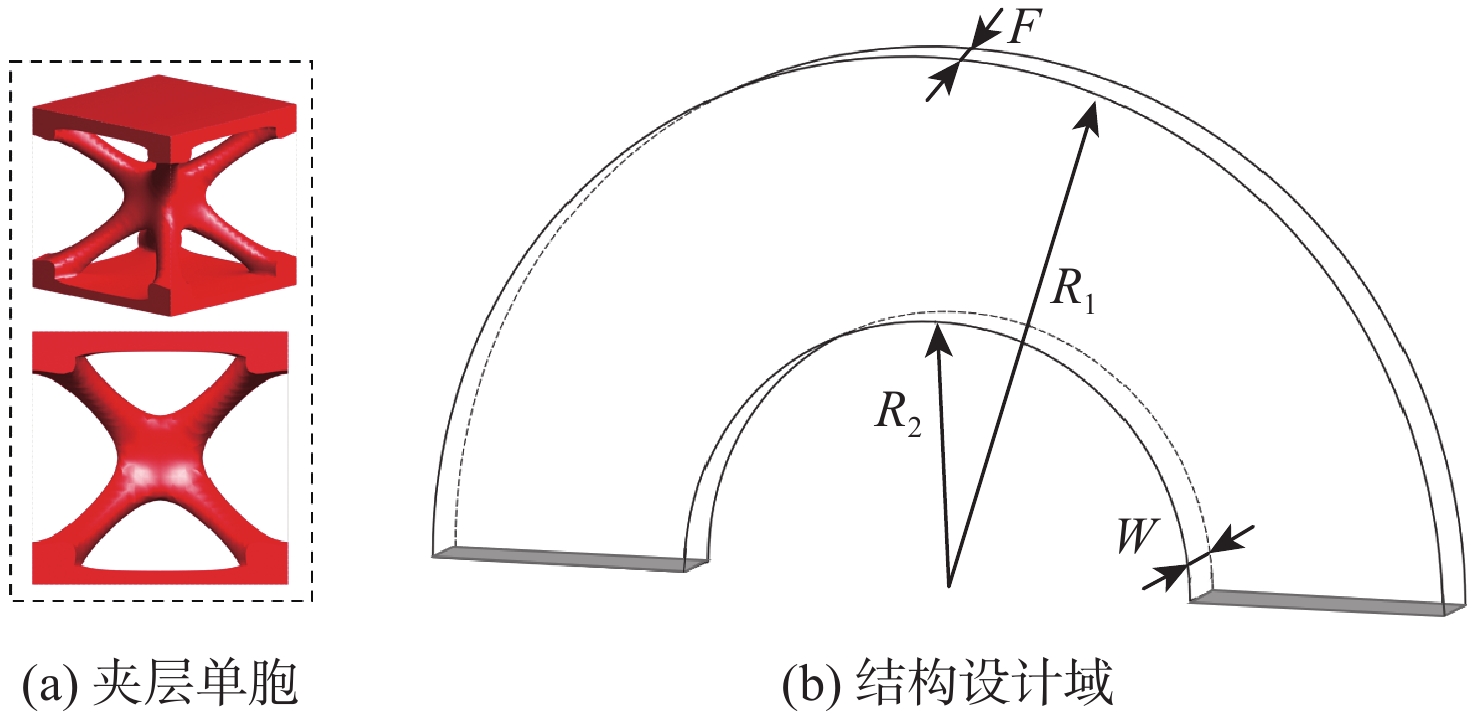
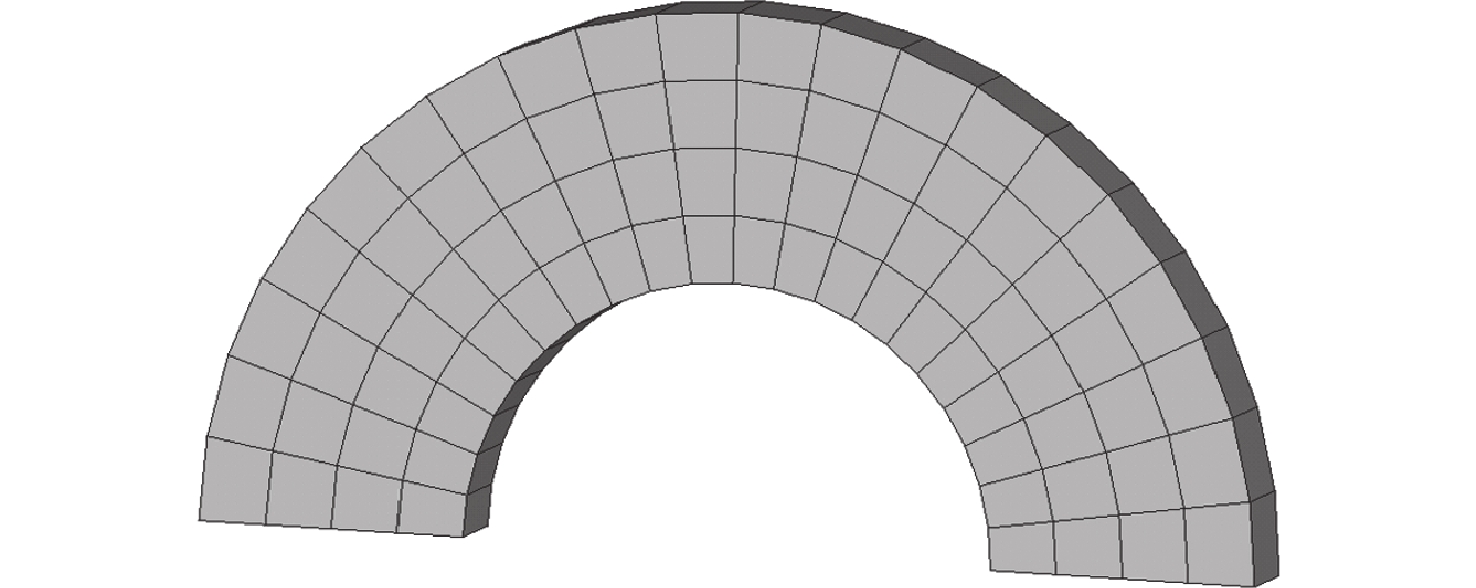
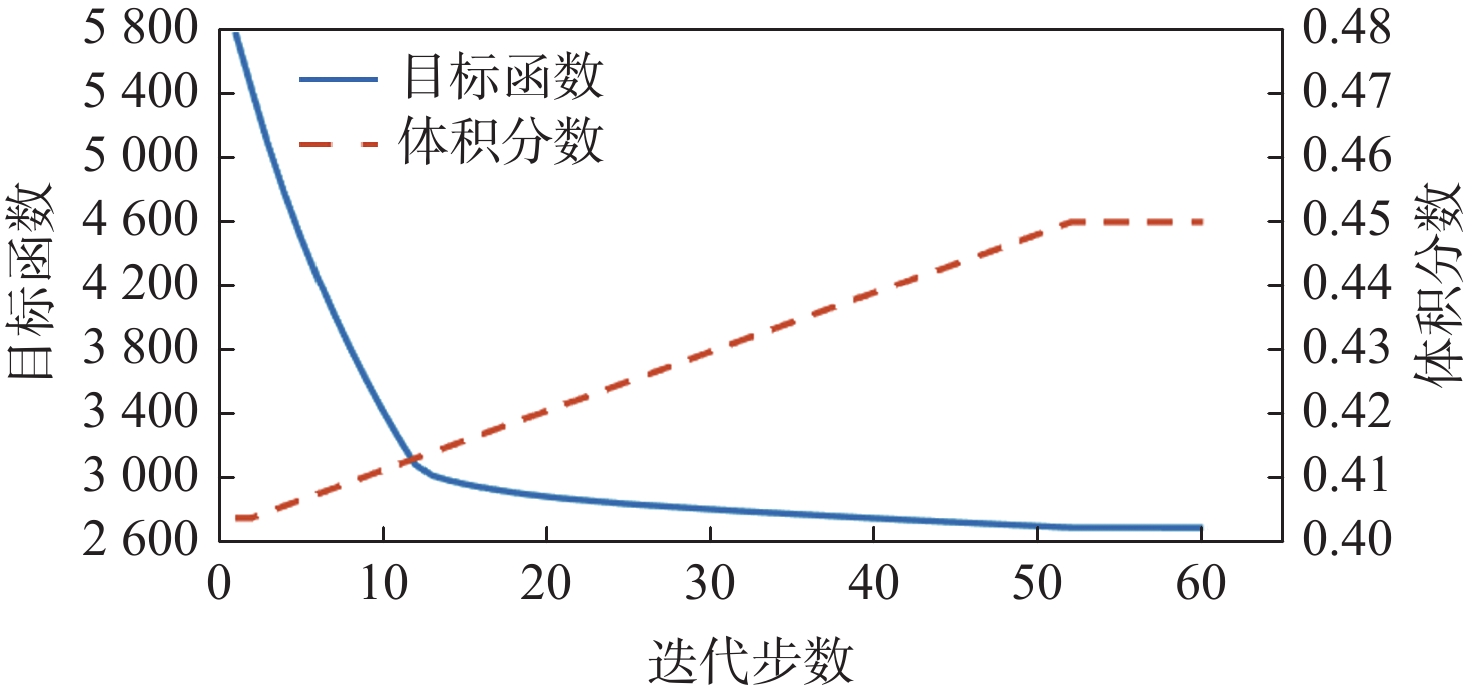
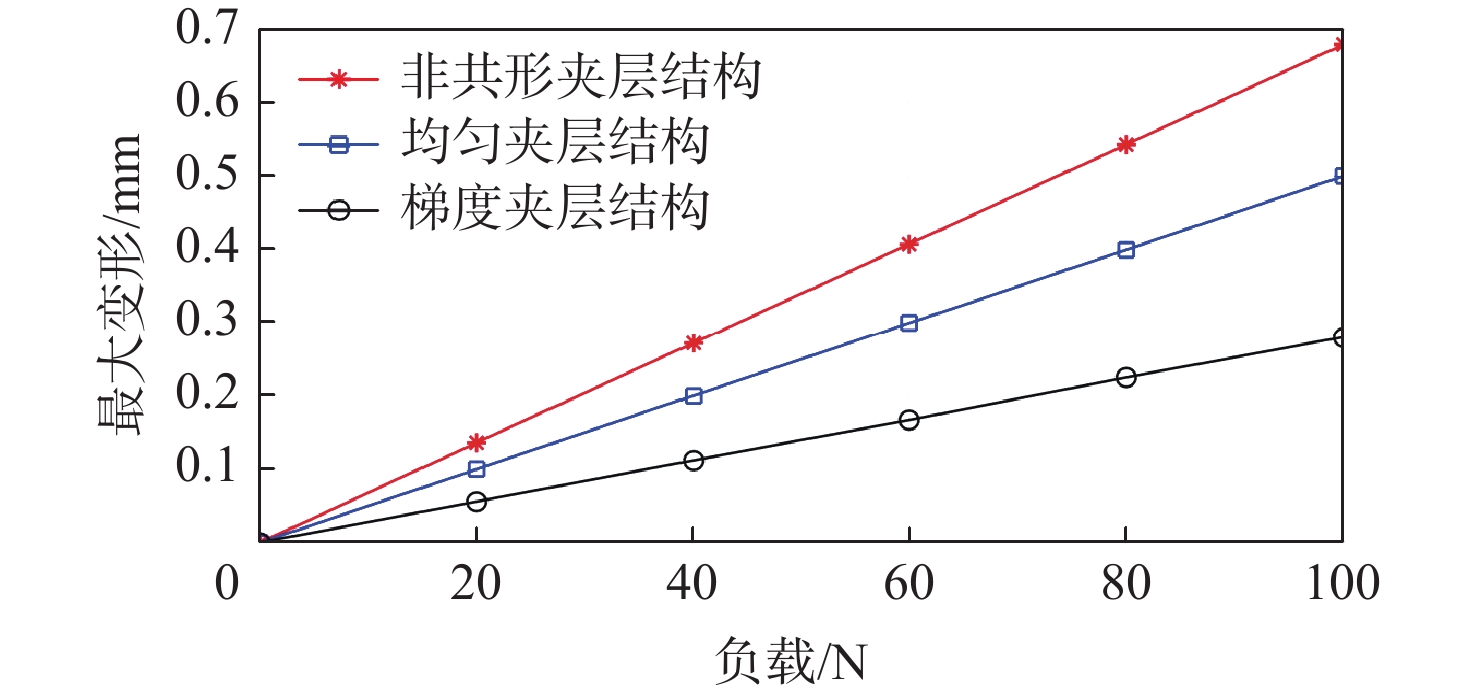
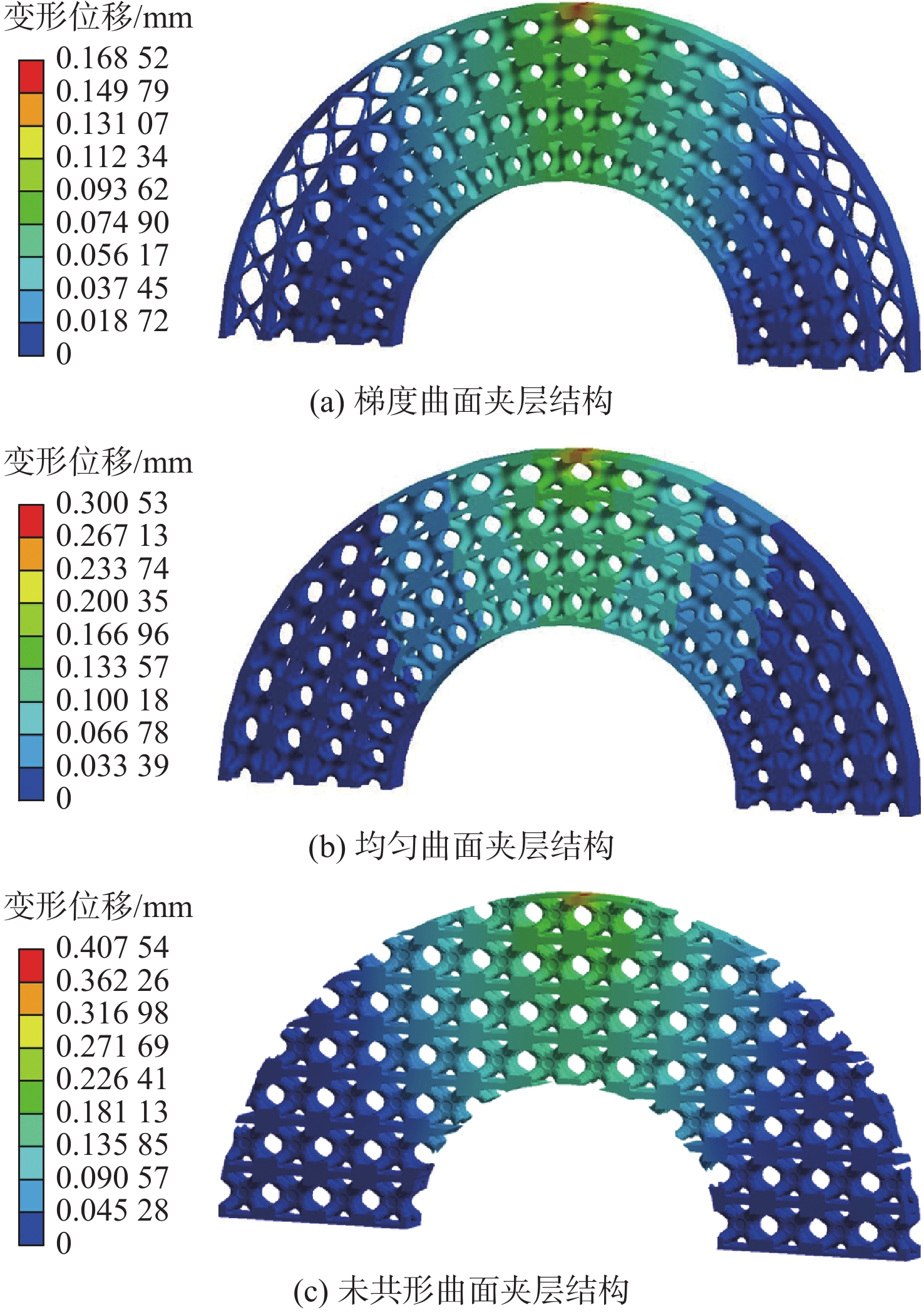
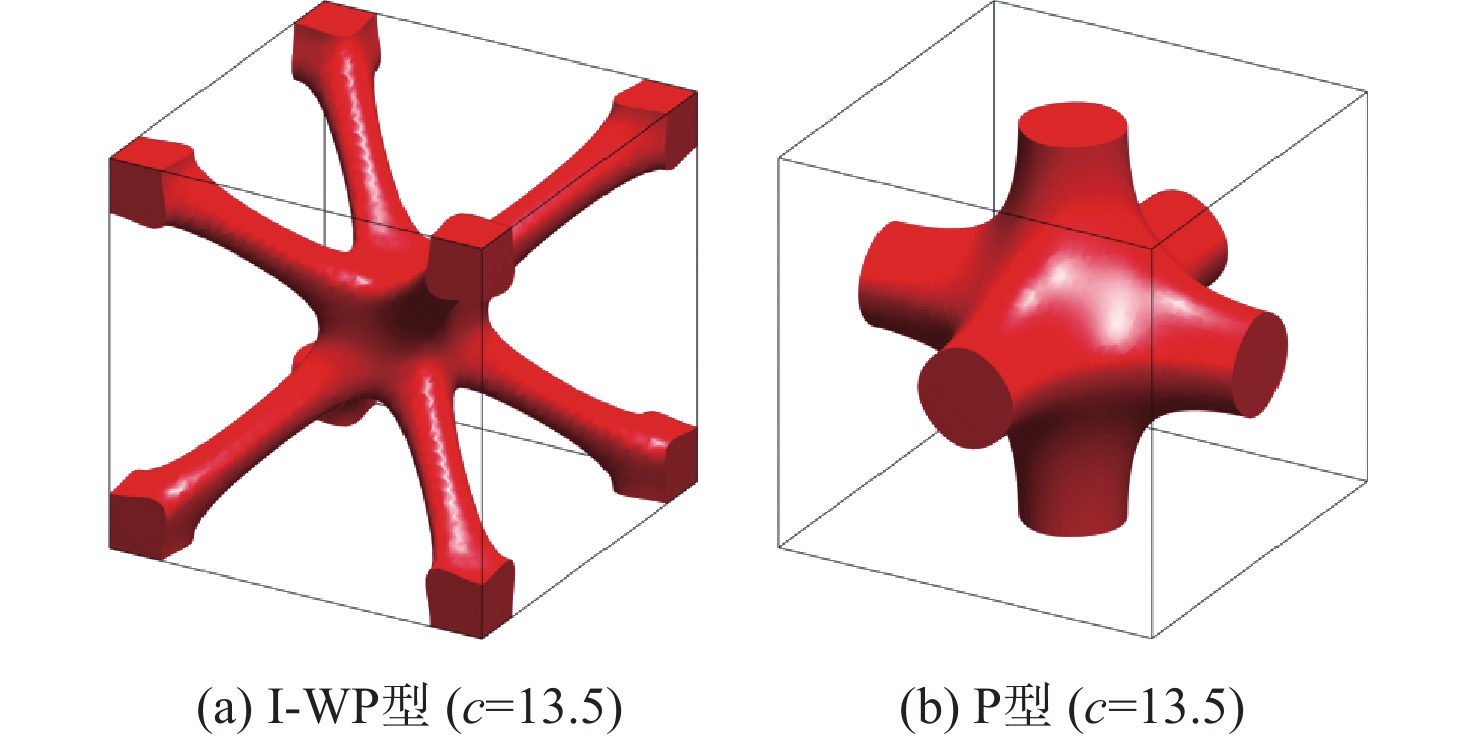
针对宏观曲面结构上多孔结构单胞构型与设计域外形不匹配，导致曲面结构优化困难的问题，提出一种基于联合仿真的曲面共形多孔结构拓扑优化方法。基于三周期极小曲面隐式水平集函数，实现多孔结构的参数化建模。采用等参单元法理论，建立自然坐标系到笛卡儿坐标系的映射关系，实现曲面多孔结构的共形建模。构造线性插值函数，保证多孔结构单胞之间的C⁰连续。引入可变切割水平集函数，建立MATLAB与ANSYS联合仿真的多孔结构拓扑优化框架。数值算例表明：所提方法可有效实现曲面多孔结构的拓扑优化设计，确保多孔结构单胞与设计域外形的匹配，提升多孔结构的力学性能。
- 拓扑优化 /
- 多孔结构 /
- 共形建模 /
- 可变切割水平集函数 /
- 联合仿真
Abstract:
The optimization design for structures with surface is challenging due to the mismatch between cellular unit cell configuration and the design domain shape. Thus, a topological optimization design method for conformal cellular structures on surfaces based on co-simulation is proposed. The parametric modelling of cellular structures is achieved by utilising the implicit level set functions derived from triply periodic minimal surfaces. By using the isoparametric element method, the mapping relationship between the natural coordinate system and the cartesian coordinate is established to realize the conformal modeling of the cellular structures on surfaces. A linear interpolation function is constructed to ensure the C⁰ continuity of the cellular unit cell. An optimization framework for cellular structures is built by combining MATLAB and ANSYS with the use of variable cutting level set functions.Numerical examples show that this method can effectively realize the topological optimization design of cellular structures on surfaces. The method also ensures the matching of the cellular structures unit cell with the shape of the design domain, and improves the mechanical properties of the cellular structures.
- topology optimization /
- cellular structures /
- conformal modeling /
- variable cutting level set function /
- co-simulation

HTML全文

图 1 三周期极小曲面多孔结构

Figure 1. Triply periodic minimal surfaces based cellular structures

下载: 全尺寸图片幻灯片

图 2 P型单胞共形建模

Figure 2. Conformal modeling of P unit cell

下载: 全尺寸图片幻灯片

图 3 多孔结构建模过程

Figure 3. Modeling of cellular structures

下载: 全尺寸图片幻灯片

图 4 局部插值模型

Figure 4. Local interpolation model

下载: 全尺寸图片幻灯片

图 5 几何突变的梯度多孔结构

Figure 5. Graded cellular structures with abrupt geometric features

下载: 全尺寸图片幻灯片

图 6 几何连续的梯度多孔结构

Figure 6. Graded cellular structures with geometric continuity

下载: 全尺寸图片幻灯片

图 7 联合仿真程序流程

Figure 7. Flow of co-simulation program

下载: 全尺寸图片幻灯片

图 8 圆筒结构设计域

Figure 8. Design domain of cylinder structure

下载: 全尺寸图片幻灯片

图 9 圆筒结构有限元网格划分

Figure 9. Finite element meshing of cylinder structure

下载: 全尺寸图片幻灯片

图 10 圆筒结构优化迭代曲线

Figure 10. Optimize iterative curve of cylinder structure

下载: 全尺寸图片幻灯片

图 11 圆筒结构最优拓扑构型

Figure 11. The optimal configuration of cylinder structure

下载: 全尺寸图片幻灯片

图 12 预定义单胞及结构设计域

Figure 12. Predefined unit cell and structural design domains

下载: 全尺寸图片幻灯片

图 13 自由曲面结构有限元网格划分

Figure 13. Finite element meshing of free-form surface structure

下载: 全尺寸图片幻灯片

图 14 自由曲面结构优化迭代曲线

Figure 14. Optimize iterative curve of free-form surface structure

下载: 全尺寸图片幻灯片

图 15 自由曲面结构最优拓扑构型

Figure 15. Optimal configuration of free-form surface structure

下载: 全尺寸图片幻灯片

图 16 预定义单胞及结构设计域

Figure 16. Predefined unit cell and structural design domains

下载: 全尺寸图片幻灯片

图 17 曲面夹层结构有限元网格划分

Figure 17. Finite element meshing of curving sandwich structure

下载: 全尺寸图片幻灯片

图 18 曲面夹层结构优化迭代曲线

Figure 18. Optimize iterative curve of curving sandwich structure

下载: 全尺寸图片幻灯片

图 19 曲面夹层结构最优拓扑构型

Figure 19. Optimal configuration of curving sandwich structure

下载: 全尺寸图片幻灯片

图 20 未共形的曲面夹层结构

Figure 20. Non-conformal curving sandwich structure

下载: 全尺寸图片幻灯片

图 21 载荷-最大变形曲线

Figure 21. Load-maximum deformation curve

下载: 全尺寸图片幻灯片

图 22 3种结构最大变形位移云图

Figure 22. Maximum deformation nephogram of three structures

下载: 全尺寸图片幻灯片

参考文献(32)

[1]	王向明, 苏亚东, 吴斌, 等. 微桁架点阵结构在飞机结构/功能一体化中的应用[J]. 航空制造技术, 2018, 61(10): 16-25. WANG X M, SU Y D, WU B, et al. Application for additive manufacturing of lattice materials on integrated aircraft structures and functions[J]. Aeronautical Manufacturing Technology, 2018, 61(10): 16-25(in Chinese).
[2]	邓昊宇, 王春洁. 三维点阵结构等效热分析与优化方法[J]. 北京航空航天大学学报, 2019, 45(6): 1122-1128. DENG H Y, WANG C J. Equivalent thermal analysis and optimization method for three-dimensional lattice structure[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(6): 1122-1128(in Chinese).
[3]	WANG B, YANG M S, ZHANG D Y, et al. Alternative approach for imperfection-tolerant design optimization of stiffened cylindrical shells via energy barrier method[J]. Thin-Walled Structures, 2022, 172: 108838. doi: 10.1016/j.tws.2021.108838
[4]	张壮雅, 赵珂, 杨晓峰, 等. 基于三周期极小曲面和等参单元法的骨支架建模方法研究[J]. 机械设计与制造, 2017(11): 234-237. doi: 10.3969/j.issn.1001-3997.2017.11.060 ZHANG Z Y, ZHAO K, YANG X F, et al. Reseachon bone scaffold modeling method basedon triply periodic minimaland isoperimetric element method[J]. Machinery Design & Manufacture, 2017(11): 234-237(in Chinese). doi: 10.3969/j.issn.1001-3997.2017.11.060
[5]	王清辉, 夏刚, 徐志佳, 等. 面向组织工程的松质骨微观结构TPMS建模方法[J]. 计算机辅助设计与图形学学报, 2016, 28(11): 1949-1956. doi: 10.3969/j.issn.1003-9775.2016.11.017 WANG Q H, XIA G, XU Z J, et al. Modelling the microstructures of cancellous bone based on triply periodic minimal surface for tissue engineering[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(11): 1949-1956(in Chinese). doi: 10.3969/j.issn.1003-9775.2016.11.017
[6]	YOO D J. Porous scaffold design using the distance field and triply periodic minimal surface models[J]. Biomaterials, 2011, 32(31): 7741-7754. doi: 10.1016/j.biomaterials.2011.07.019
[7]	余学伟, 李琳慧, 张涛, 等. 基于三周期极小曲面和体素距离场的复杂轮廓点阵结构建模[J]. 重庆大学学报, 2022, 45(6): 75-84. doi: 10.11835/j.issn.1000-582X.2021.115 YU X W, LI L H, ZHANG T, et al. Modeling of complex contour lattice structure based on triply periodic minimal surface and voxel distance field[J]. Journal of Chongqing University, 2022, 45(6): 75-84(in Chinese). doi: 10.11835/j.issn.1000-582X.2021.115
[8]	任毅如, 向剑辉, 何杰, 等. 基于导重法的自重载荷下悬臂梁结构拓扑优化[J]. 北京航空航天大学学报, 2021, 47(7): 1338-1344. REN Y R, XIANG J H, HE J, et al. Topology optimization of cantilever structure with self-weight load based on guide-weight method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(7): 1338-1344(in Chinese).
[9]	付君健, 舒正涛, 田启华, 等. 功能梯度多孔结构拓扑优化的混合水平集方法[J]. 机械工程学报, 2022, 58(17): 249-260. doi: 10.3901/JME.2022.17.249 FU J J, SHU Z T, TIAN Q H, et al. A hybrid level set method for topology optimization of functionally graded cellular structures[J]. Journal of Mechanical Engineering, 2022, 58(17): 249-260(in Chinese). doi: 10.3901/JME.2022.17.249
[10]	孙鹏飞, 张跃, 尹鹏, 等. 隐式曲面梯度多孔结构拓扑优化设计方法[J]. 西安交通大学学报, 2022, 56(1): 85-95. doi: 10.7652/xjtuxb202201010 SUN P F, ZHANG Y, YIN P, et al. A topology optimization design method of graded cellular structures with implicit surfaces[J]. Journal of Xi’an Jiaotong University, 2022, 56(1): 85-95(in Chinese). doi: 10.7652/xjtuxb202201010
[11]	NIKNAM H, AKBARZADEH A H, RODRIGUE D, et al. Architected multi-directional functionally graded cellular plates[J]. Materials & Design, 2018, 148: 188-202.
[12]	QI D X, LU Q Y, HE C W, et al. Impact energy absorption of functionally graded chiral honeycomb structures[J]. Extreme Mechanics Letters, 2019, 32: 100568. doi: 10.1016/j.eml.2019.100568
[13]	赵芳垒, 敬石开, 刘晨燕. 基于局部相对密度映射的变密度多孔结构设计方法[J]. 机械工程学报, 2018, 54(19): 121-128. doi: 10.3901/JME.2018.19.121 ZHAO F L, JING S K, LIU C Y. Variable density cellular structure design method base on local relative density mapping[J]. Journal of Mechanical Engineering, 2018, 54(19): 121-128(in Chinese). doi: 10.3901/JME.2018.19.121
[14]	蔡金虎, 王春洁. 基于映射的梯度点阵结构设计方法[J]. 振动与冲击, 2020, 39(20): 74-81. CAI J H, WANG C J. A graded lattice structure design method based on mapping process[J]. Journal of Vibration and Shock, 2020, 39(20): 74-81(in Chinese).
[15]	TOWNSEND S, KIM H A. A level set topology optimization method for the buckling of shell structures[J]. Structural and Multidisciplinary Optimization, 2019, 60(5): 1783-1800. doi: 10.1007/s00158-019-02374-9
[16]	VOGIATZIS P, MA M, CHEN S K, et al. Computational design and additive manufacturing of periodic conformal metasurfaces by synthesizing topology optimization with conformal mapping[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 328: 477-497. doi: 10.1016/j.cma.2017.09.012
[17]	YE Q, GUO Y, CHEN S K, et al. Topology optimization of conformal structures on manifolds using extended level set methods (X-LSM) and conformal geometry theory[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 344: 164-185. doi: 10.1016/j.cma.2018.08.045
[18]	ZHOU Y, GAO L, LI H. Graded infill design within free-form surfaces by conformal mapping[J]. International Journal of Mechanical Sciences, 2022, 224: 107307. doi: 10.1016/j.ijmecsci.2022.107307
[19]	HUO W D, LIU C, DU Z L, et al. Topology optimization on complex surfaces based on the moving morphable component method and computational conformal mapping[J]. Journal of Applied Mechanics, 2022, 89(5): 051008. doi: 10.1115/1.4053727
[20]	ZONG H M, LIU H, MA Q P, et al. VCUT level set method for topology optimization of functionally graded cellular structures[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 354: 487-505. doi: 10.1016/j.cma.2019.05.029
[21]	WANG L, LI Z S, NI B W, et al. A robust topology optimization method considering bounded field parameters with uncertainties based on the variable time step parametric level-set method[J]. Applied Mathematical Modelling, 2022, 107: 441-463. doi: 10.1016/j.apm.2022.03.008
[22]	LI D W, DAI N, TANG Y L, et al. Design and optimization of graded cellular structures with triply periodic level surface-based topological shapes[J]. Journal of Mechanical Design, 2019, 141(7): 071402. doi: 10.1115/1.4042617
[23]	蔡升勇, 习俊通. 基于形函数控制的组织工程骨架孔隙结构实体建模方法[J]. 机械工程学报, 2009, 45(7): 297-304. doi: 10.3901/JME.2009.07.297 CAI S Y, XI J T. Computer modeling approach for a porous scaffold structure in tissue engineering based on the shape function control[J]. Journal of Mechanical Engineering, 2009, 45(7): 297-304(in Chinese). doi: 10.3901/JME.2009.07.297
[24]	WANG Y Q, CHEN F F, WANG M Y. Concurrent design with connectable graded microstructures[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 317: 84-101. doi: 10.1016/j.cma.2016.12.007
[25]	CRAMER A D, CHALLIS V J, ROBERTS A P. Microstructure interpolation for macroscopic design[J]. Structural and Multidisciplinary Optimization, 2016, 53(3): 489-500. doi: 10.1007/s00158-015-1344-7
[26]	杜义贤, 张跃, 付君健, 等. 承载散热一体化的功能梯度多孔结构拓扑优化设计[J]. 计算机辅助设计与图形学学报, 2021, 33(7): 1141-1150. DU Y X, ZHANG Y, FU J J, et al. Topology optimization design of functionally graded cellular structure with integrated load bearing and heat dissipation[J]. Journal of Computer-Aided Design & Computer Graphics, 2021, 33(7): 1141-1150(in Chinese).
[27]	LIU H, ZONG H M, SHI T L, et al. M-VCUT level set method for optimizing cellular structures[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 367: 113154. doi: 10.1016/j.cma.2020.113154
[28]	ALLAIRE G, JOUVE F, TOADER A M. Structural optimization using sensitivity analysis and a level-set method[J]. Journal of Computational Physics, 2004, 194(1): 363-393. doi: 10.1016/j.jcp.2003.09.032
[29]	龙凯, 左正兴. 基于拓扑优化和形状优化方法的主轴承盖结构设计[J]. 农业机械学报, 2008, 39(4): 152-156. LONG K, ZUO Z X. Structural design of main bearing cap based on topological optimization and shape optimization[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(4): 152-156(in Chinese).
[30]	范文杰, 徐进永, 张子达. 基于双向渐进结构优化法的装载机动臂拓扑优化[J]. 农业机械学报, 2006, 37(11): 24-27. doi: 10.3969/j.issn.1000-1298.2006.11.007 FAN W J, XU J Y, ZHANG Z D. Topology optimization on arm of loader based on BESO[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(11): 24-27(in Chinese). doi: 10.3969/j.issn.1000-1298.2006.11.007
[31]	ZHOU M, ROZVANY G. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization[J]. Computer Methods in Applied Mechanics and Engineering, 1991, 89(1-3): 309-336. doi: 10.1016/0045-7825(91)90046-9
[32]	XIE Y M, ZUO Z H, HUANG X D, et al. Convergence of topological patterns of optimal periodic structures under multiple scales[J]. Structural and Multidisciplinary Optimization, 2012, 46(1): 41-50. doi: 10.1007/s00158-011-0750-8