基于MDk-DPC的空中目标自动分群方法

马钰棠; 孙鹏; 张杰勇; 闫云飞; 赵亮

doi:10.13700/j.bh.1001-5965.2022.0797

基于MDk-DPC的空中目标自动分群方法

doi: 10.13700/j.bh.1001-5965.2022.0797

空军工程大学信息与导航学院，西安 710077

详细信息

通讯作者:
E-mail：281126096@qq.com

中图分类号: V247.5
计量
- 文章访问数: 172
- HTML全文浏览量: 83
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2022-09-19
- 录用日期: 2022-11-30
- 网络出版日期: 2022-12-16
- 整期出版日期: 2024-10-31

Aerial target automatic grouping method based on MDk-DPC

Information and Navigation College，Air Force Engineering University，Xi’an 710077，China

More Information

Corresponding author: E-mail：281126096@qq.com

摘要

摘要:
空中目标分群本质上是一个类数未知的聚类问题，也是战场态势估计领域中的研究热点。针对未知的空战场环境，从聚类角度提出一种基于流形距离和k近邻采样密度的MDk-DPC算法。引入流形距离代替欧氏距离，以增加同一流形中目标的相似性；利用k近邻计算目标的局部密度，使其能更真实地反映目标周围分布；通过自适应选取聚类中心方法确定聚类中心，并运用密度峰值算法指定剩余点类别完成分群。仿真实验表明，所提方法在人工合成数据集和UCI真实数据集上均有更好的聚类性能，同时通过对空战场仿真数据进行分群验证了所提方法的可行性和有效性。
- 态势估计 /
- 目标分群 /
- 流形距离 /
- k近邻 /
- 密度峰值聚类
Abstract:
Air target grouping is a popular topic for research in the area of combat scenario assessment and can be thought of as essentially an uncountable class clustering issue. Aiming at the unknown air battlefield environment, a MDk-DPC algorithm based on manifold distance and k-nearest neighbor sampling density is proposed from the perspective of clustering. First, manifold distance is introduced to replace Euclidean distance to increase the similarity of objects in the same manifold. Secondly, the target's local density is determined using the k-nearest neighbors method, allowing the local density to more accurately represent the distribution surrounding the targets. Finally, an adaptive cluster center selection method is proposed to automatically determine cluster centers, and the DPC algorithm is used to specify the remaining point categories to complete the clustering. Simulation experiments show that the proposed method has better clustering performance on both artificial synthetic datasets and UCI real datasets. At the same time, the feasibility and effectiveness of the method are verified by clustering the simulated air battlefield data.
- situation assessment /
- target grouping /
- manifold distance /
- k-nearest neighbors /
- density peak clustering

HTML全文

图 1 数据集中各点二维分布

Figure 1. Two-dimensional distribution of points in the dataset

下载: 全尺寸图片幻灯片

图 2 ρ=e²时，ab与bc间的欧氏距离和流形距离

Figure 2. When ρ=e² the Euclidean distance and manifold distance between ab and bc

下载: 全尺寸图片幻灯片

图 3 不同k值下的密度热分布图

Figure 3. Density heat distribution diagram at different k values

下载: 全尺寸图片幻灯片

图 4 自适应选取聚类中心方法流程

Figure 4. Flow of adaptive selection of cluster centers

下载: 全尺寸图片幻灯片

图 5 5种算法在Jain数据集上的结果比较

Figure 5. Comparison of the results of five algorithms on the Jain dataset

下载: 全尺寸图片幻灯片

图 6 5种算法在Threecircles数据集上的结果比较

Figure 6. Comparison of the results of five algorithms on the Threecircles dataset

下载: 全尺寸图片幻灯片

图 7 5种算法在R15数据集上的结果比较

Figure 7. Comparison of the results of five algorithms on the R15 dataset

下载: 全尺寸图片幻灯片

图 8 初始时刻空中目标分布

Figure 8. Air targets distribution at the initial moment

下载: 全尺寸图片幻灯片

图 9 t时刻空中目标分布

Figure 9. Air targets distribution at time t

下载: 全尺寸图片幻灯片

图 10 空中目标分群结果

Figure 10. Aerial targets grouping results

下载: 全尺寸图片幻灯片

表 1 不同伸缩因子下的Jain数据集聚类结果对比

Table 1. Comparison of clustering results of Jain dataset with different scaling factors

ρ	纯度
e^0.5	0.9249
e³	1
e¹⁰	1

下载: 导出CSV

表 2 人工数据集基本信息

Table 2. Basic information of artificial dataset

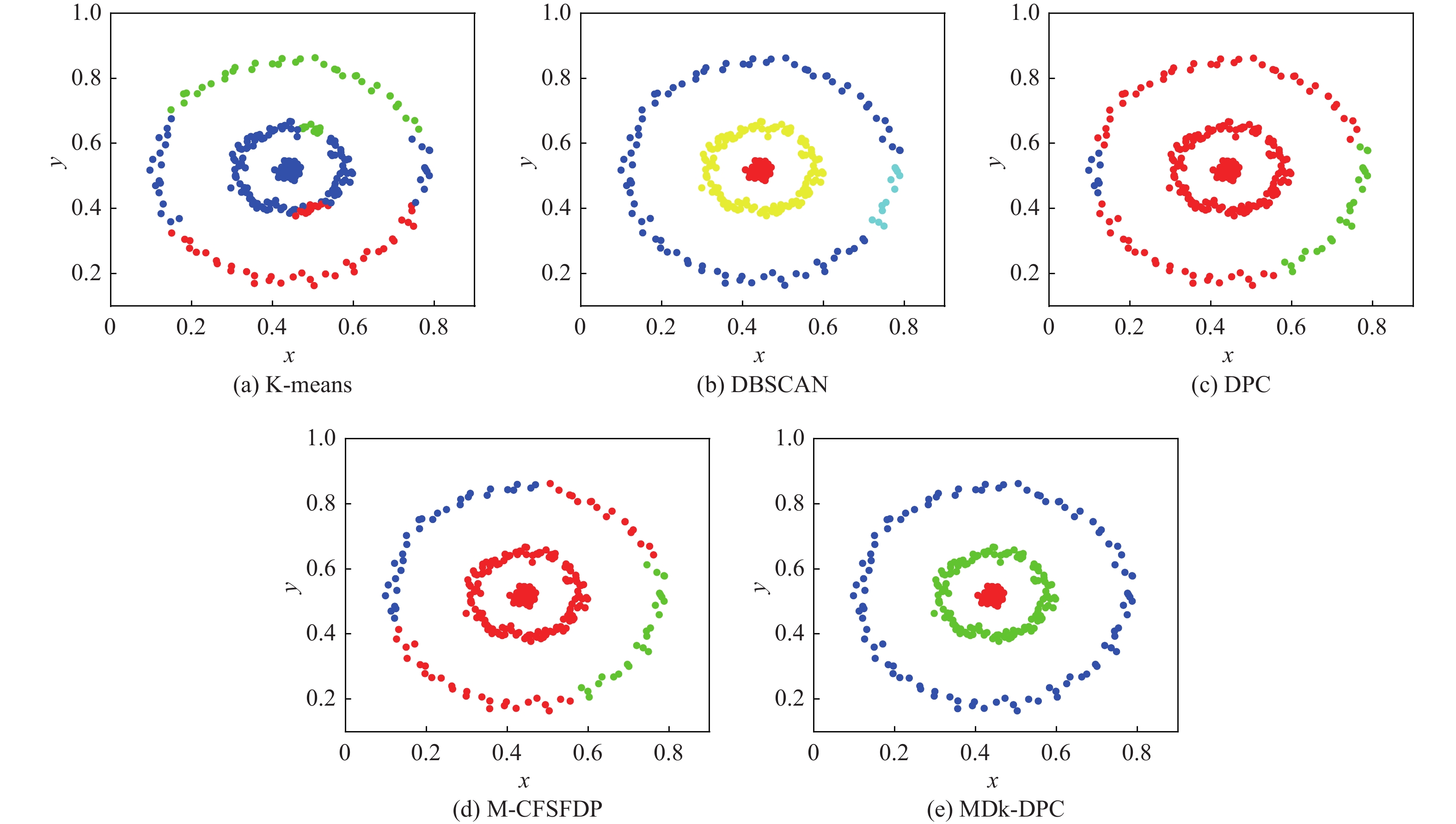
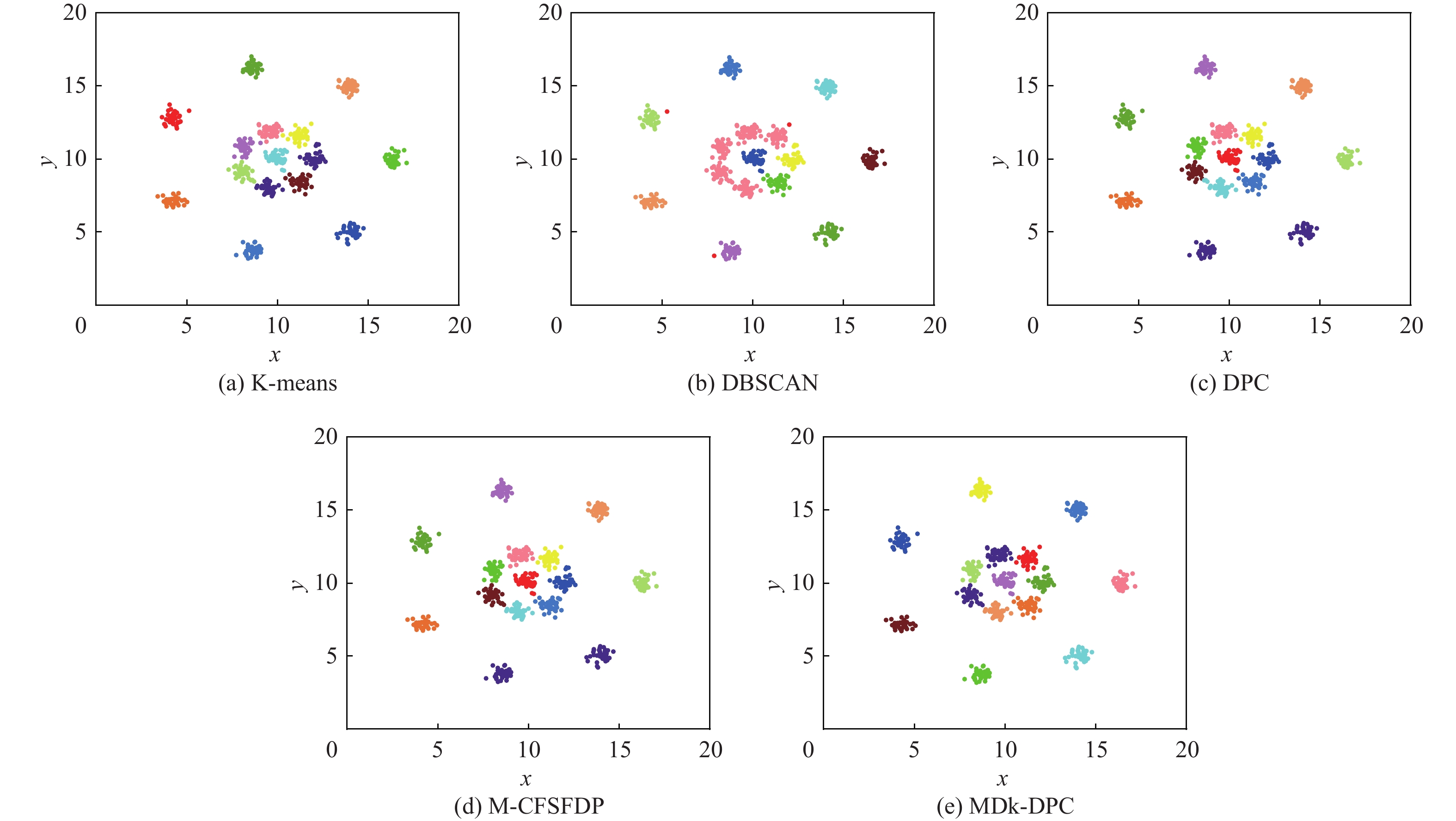
数据集	数据数量	类数	维数
Spiral	312	3	2
Flame	240	2	2
Jain	373	2	2
Lineblobs	266	3	2
Threecircles	299	3	2
R15	600	15	2

下载: 导出CSV

表 3 人工数据集上的分群结果比较

Table 3. Comparison of clustering results on artificial datasets

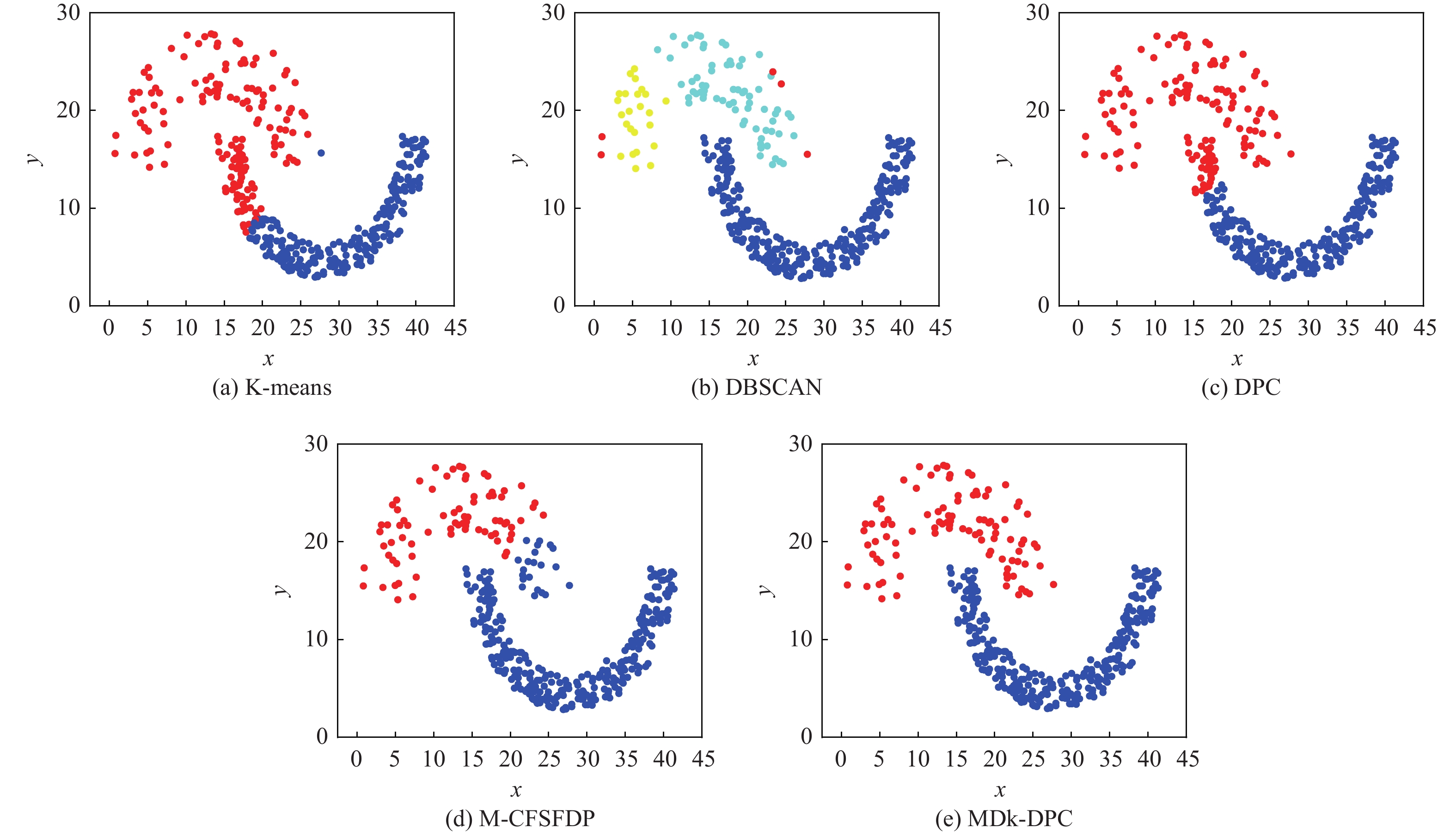
数据集	算法	纯度	RI	ARI	NMI
Spiral	K-means	0.3686	0.5553	−0.0030	0.0031
	DBSCAN	1	1	1	1
	DPC	1	1	1	1
	M-CFSFDP	1	1	1	1
	MDk-DPC	1	1	1	1
Flame	K-means	0.8375	0.7267	0.4535	0.4193
	DBSCAN	0.9667	0.9200	0.8408	0.7566
	DPC	1	1	1	1
	M-CFSFDP	1	1	1	1
	MDk-DPC	1	1	1	1
Jain	K-means	0.8365	0.7257	0.4483	0.4428
	DBSCAN	1	0.9698	0.9373	0.8550
	DPC	0.9035	0.8251	0.6438	0.5960
	M-CFSFDP	0.9437	0.8935	0.7684	0.6855
	MDk-DPC	1	1	1	1
Lineblobs	K-means	0.7444	0.7284	0.4077	0.5358
	DBSCAN	1	1	1	1
	DPC	0.7519	0.7345	0.4201	0.5450
	M-CFSFDP	0.8534	0.8318	0.6283	0.7430
	MDk-DPC	1	1	1	1
Threecircles	K-means	0.6254	0.5758	0.1598	0.2298
	DBSCAN	1	0.9766	0.9488	0.9448
	DPC	0.5719	0.4565	0.0659	0.1823
	M-CFSFDP	0.6522	0.5452	0.1697	0.3085
	MDk-DPC	1	1	1	1
R15	K-means	0.9933	0.9983	0.9857	0.9893
	DBSCAN	0.7317	0.9112	0.5511	0.8852
	DPC	0.9950	0.9987	0.9893	0.9922
	M-CFSFDP	0.9967	0.9991	0.9928	0.9942
	MDk-DPC	0.9967	0.9991	0.9928	0.9942

下载: 导出CSV

表 4 UCI真实数据集基本信息

Table 4. Basic information of UCI real dataset

数据集	数据数量	类数	维数	各类数量
WDBC	569	2	30	357,212
Iris	150	3	4	50,50,50
Wine	178	3	13	59,71,48
Seeds	210	3	7	70,70,70
Vowel	871	6	3	72,89,172,151,207,180
Ecoli	336	8	8	143,77,2,2,259,20,5,52

下载: 导出CSV

表 5 UCI真实数据集上的分群结果比较

Table 5. Comparison of clustering results on UCI real datasets

数据集	算法	纯度	RI	ARI	NMI
WDBC	K-means	0.8506	0.7454	0.4811	0.4567
	DBSCAN	0.7996	0.6558	0.3191	0.2851
	DPC	0.7891	0.6666	0.3133	0.3400
	M-CFSFDP	0.8664	0.7681	0.5282	0.5070
	MDk-DPC	0.8822	0.7919	0.5773	0.5459
Iris	K-means	0.8800	0.8679	0.7028	0.7277
	DBSCAN	0.9333	0.8786	0.7063	0.7130
	DPC	0.8333	0.8322	0.6334	0.7174
	M-CFSFDP	0.9067	0.8923	0.7592	0.8057
	MDk-DPC	0.9600	0.9495	0.8858	0.8705
Wine	K-means	0.7022	0.7187	0.3711	0.4288
	DBSCAN	0.6461	0.6258	0.2897	0.4029
	DPC	0.7191	0.7350	0.4070	0.3913
	M-CFSFDP	0.7921	0.7739	0.5054	0.5646
	MDk-DPC	0.8933	0.8654	0.6990	0.7262
Seeds	K-means	0.8762	0.8573	0.6793	0.7023
	DBSCAN	0.7476	0.6861	0.2146	0.4083
	DPC	0.8905	0.8715	0.7227	0.7126
	M-CFSFDP	0.8952	0.8748	0.7170	0.6744
	MDk-DPC	0.8952	0.8766	0.7108	0.7245
Vowel	K-means	0.5511	0.8013	0.3360	0.4692
	DBSCAN	0.6958	0.8165	0.2885	0.4864
	DPC	0.5982	0.7852	0.3214	0.4839
	M-CFSFDP	0.6705	0.8103	0.3936	0.5475
	MDk-DPC	0.7405	0.8328	0.4072	0.5360
Ecoli	K-means	0.8006	0.8340	0.5386	0.5771
	DBSCAN	0.6637	0.7601	0.3937	0.4518
	DPC	0.8065	0.8197	0.5000	0.6039
	M-CFSFDP	0.7679	0.8659	0.6913	0.6710
	MDk-DPC	0.7887	0.8852	0.7316	0.6971

下载: 导出CSV

表 6 空中目标状态信息

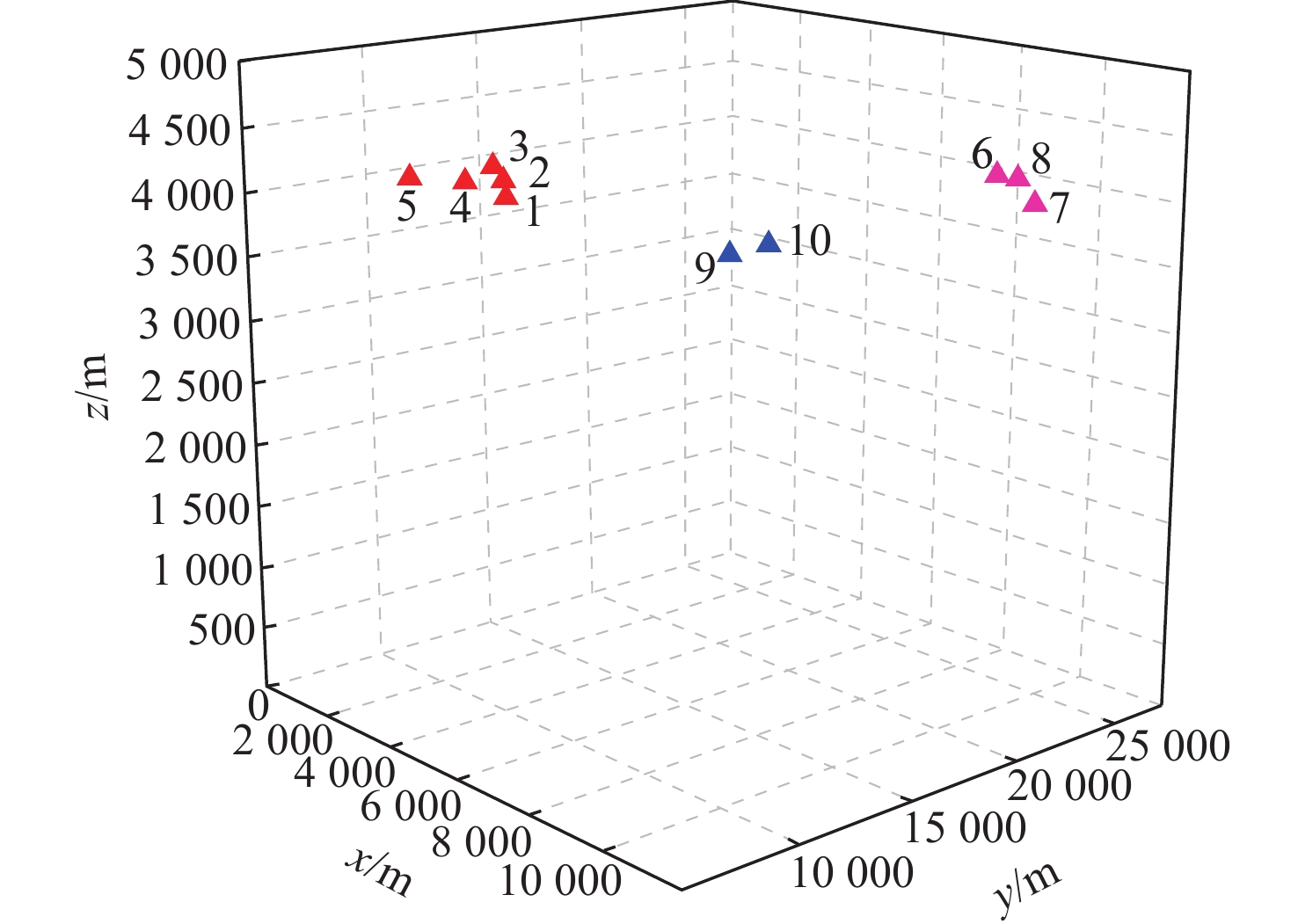
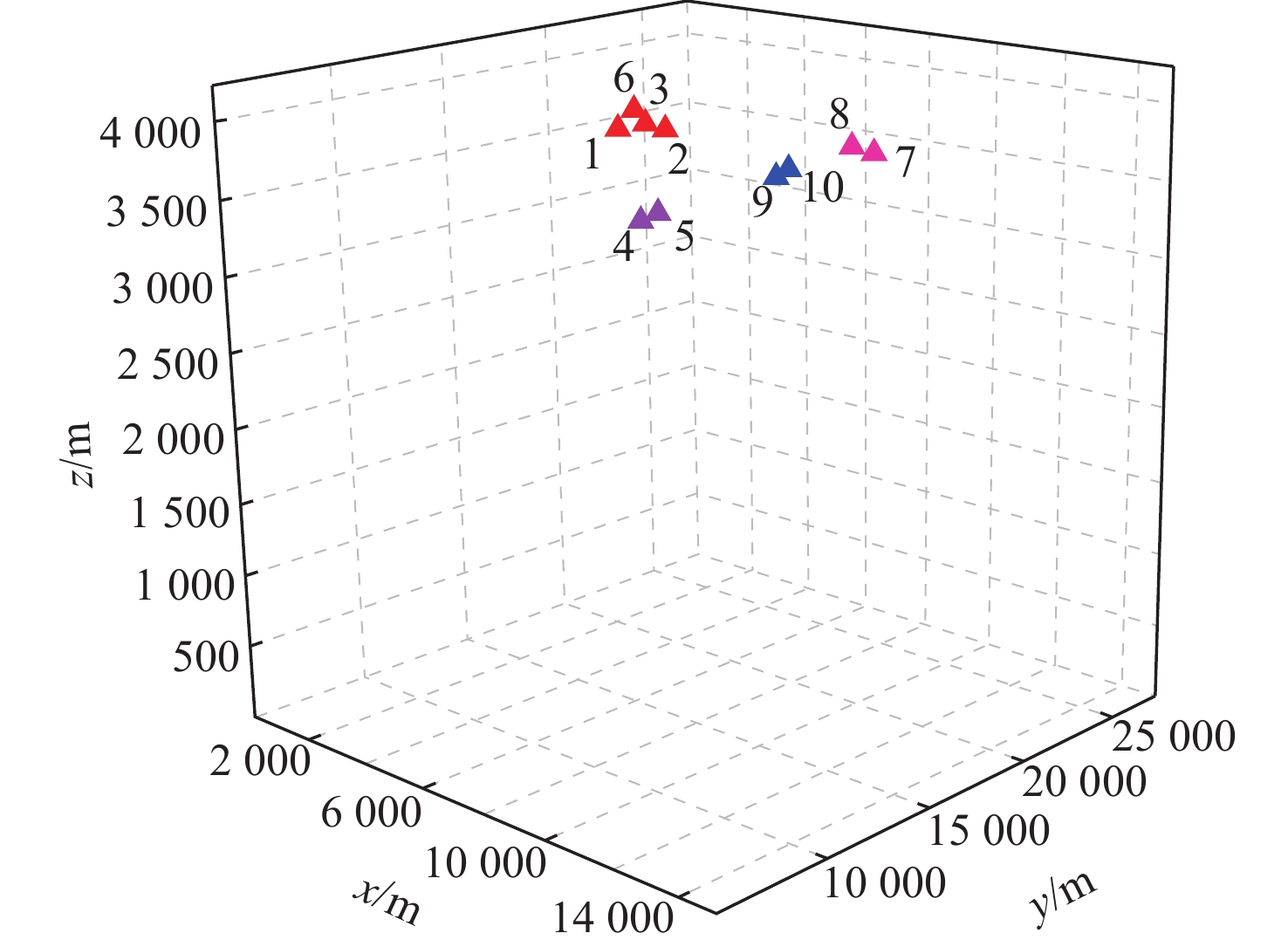
Table 6. Air targets status information

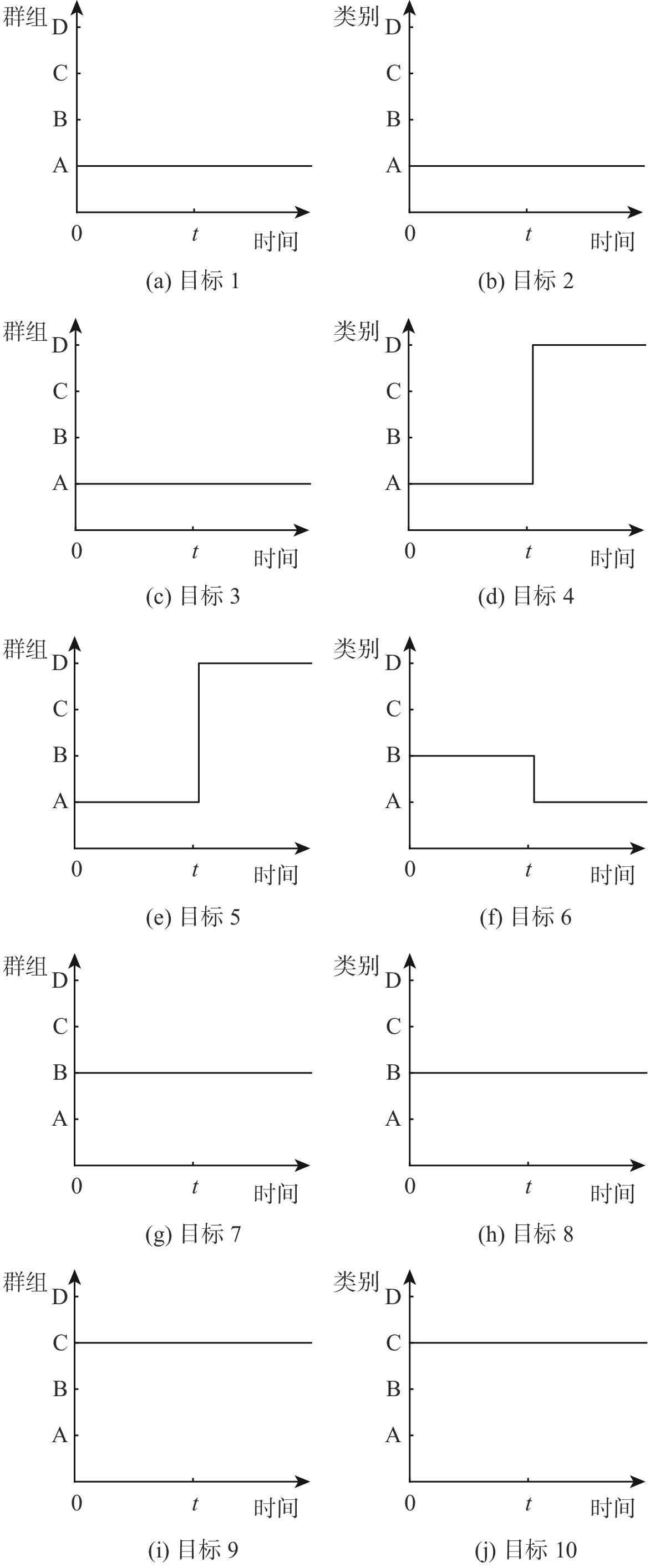
序号	x/m	y/m	z/m	速度/(km·h⁻¹)	航向角/(°)	群组
1	4597	9856	4221	959	90	A
2	4098	10182	4197	934	90	A
3	3092	11210	4213	967	90	A
4	3785	9045	4203	980	90	A
5	2890	8002	4208	942	90	A
6	9013	24345	4127	931	150	B
7	9854	24521	3951	964	150	B
8	9470	23698	4055	954	150	B
9	11013	10132	4195	980	120	C
10	10311	9780	4089	979	120	C

下载: 导出CSV

参考文献(21)

[1]	郭明. 关于智能化战争的基本认知[J]. 人民论坛·学术前沿, 2021(10): 14-21. GUO M. Basic understandings of the intelligent wars[J]. Frontiers, 2021(10): 14-21(in Chinese).
[2]	张绪亮, 张宏军, 綦秀利, 等. 基于改进K-means算法的陆战场机动目标分群方法[J]. 信息技术, 2016, 40(3): 128-131. ZHANG X L, ZHANG H J, QI X L, et al. A clustering method of land battlefield maneuvering targets based on improved K-means algorithm[J]. Information Technology, 2016, 40(3): 128-131(in Chinese).
[3]	詹环, 宋爱斌, 罗俊芝, 等. 基于混合属性无监督聚类的作战目标分群[J]. 火力与指挥控制, 2021, 46(12): 166-170. doi: 10.3969/j.issn.1002-0640.2021.12.026 ZHAN H, SONG A B, LUO J Z, et al. Operational system target grouping method based on mixed attribute unsupervised clustering[J]. Fire Control & Command Control, 2021, 46(12): 166-170(in Chinese). doi: 10.3969/j.issn.1002-0640.2021.12.026
[4]	DUAN Y X, LIU C Y, LI S. Battlefield target grouping by a hybridization of an improved whale optimization algorithm and affinity propagation[J]. IEEE Access, 2021, 9: 46448-46461. doi: 10.1109/ACCESS.2021.3067729
[5]	袁德平, 郑娟毅, 史浩山, 等. 一种多作战编队下的目标编群算法[J]. 计算机科学, 2016, 43(2): 235-238. doi: 10.11896/j.issn.1002-137X.2016.02.049 YUAN D P, ZHENG J Y, SHI H S, et al. Target grouping algorithm based on multiple combat formations[J]. Computer Science, 2016, 43(2): 235-238(in Chinese). doi: 10.11896/j.issn.1002-137X.2016.02.049
[6]	ESTER M, KRIEGEL H, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]// Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, 1996: 226–231.
[7]	RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. doi: 10.1126/science.1242072
[8]	闫孟达, 杨任农, 王新, 等. 改进cell密度聚类算法在空战目标分群中的应用[J]. 国防科技大学学报, 2021, 43(4): 108-117. doi: 10.11887/j.cn.202104014 YAN M D, YANG R N, WANG X, et al. Air combat target grouping based on improved CBSCAN algorithm[J]. Journal of National University of Defense Technology, 2021, 43(4): 108-117(in Chinese). doi: 10.11887/j.cn.202104014
[9]	李伟楠, 章卫国, 史静平, 等. 基于M-CFSFDP算法的战场目标分群方法[J]. 西北工业大学学报, 2018, 36(6): 1121-1128. doi: 10.3969/j.issn.1000-2758.2018.06.013 LI W N, ZHANG W G, SHI J P, et al. A battlefield target grouping method based on M-CFSFDP algorithm[J]. Journal of Northwestern Polytechnical University, 2018, 36(6): 1121-1128(in Chinese). doi: 10.3969/j.issn.1000-2758.2018.06.013
[10]	段同乐, 张冬宁. 二叉树多分类SVM在目标分群中的应用[J]. 无线电工程, 2015, 45(6): 88-91. DUAN T L, ZHANG D N. Application of multiclass SVM based on binary tree in target grouping[J]. Radio Engineering, 2015, 45(6): 88-91(in Chinese).
[11]	樊振华, 师本慧, 陈金勇, 等. 基于模糊ART划分的目标分群算法[J]. 无线电工程, 2017, 47(9): 27-31. doi: 10.3969/j.issn.1003-3106.2017.09.06 FAN Z H, SHI B H, CHEN J Y, et al. A fuzzy ART based target clustering algorithm[J]. Radio Engineering, 2017, 47(9): 27-31(in Chinese). doi: 10.3969/j.issn.1003-3106.2017.09.06
[12]	陶宇, 蒋序平. 基于深度自编码网络的智能目标分群算法[J]. 指挥控制与仿真, 2020, 42(6): 52-58. doi: 10.3969/j.issn.1673-3819.2020.06.009 TAO Y, JIANG X P. Intelligent target clustering algorithm based on deep auto-encoder network[J]. Command Control & Simulation, 2020, 42(6): 52-58(in Chinese). doi: 10.3969/j.issn.1673-3819.2020.06.009
[13]	WU Z H, LI C, ZHOU F, et al. A new weighted fuzzy C-means clustering approach considering between-cluster separability[J]. Journal of Intelligent & Fuzzy Systems, 2021, 40(1): 1017-1024.
[14]	REHMAN A U, BELHAOUARI S B. Divide well to merge better: A novel clustering algorithm[J]. Pattern Recognition, 2022, 122: 108305. doi: 10.1016/j.patcog.2021.108305
[15]	马萌. 基于流形距离的聚类算法研究及其应用[D]. 西安: 西安电子科技大学, 2010: 9-21. MA M. The study and the application of clustering algorithm based on manifold distance[D]. Xi’an: Xidian University, 2010: 9-21(in Chinese).
[16]	CAO X F, QIU B Z, LI X L, et al. Multidimensional balance-based cluster boundary detection for high-dimensional data[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(6): 1867-1880. doi: 10.1109/TNNLS.2018.2874458
[17]	SAMET H. K-nearest neighbor finding using MaxNearestDist[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(2): 243-252. doi: 10.1109/TPAMI.2007.1182
[18]	DAI Q Z, XIONG Z Y, XIE J, et al. A novel clustering algorithm based on the natural reverse nearest neighbor structure[J]. Information Systems, 2019, 84: 1-16. doi: 10.1016/j.is.2019.04.001
[19]	XIE J, XIONG Z Y, ZHANG Y F, et al. Density core-based clustering algorithm with dynamic scanning radius[J]. Knowledge-Based Systems, 2018, 142: 58-70. doi: 10.1016/j.knosys.2017.11.025
[20]	TONG W N, LIU S, GAO X Z. A density-peak-based clustering algorithm of automatically determining the number of clusters[J]. Neurocomputing, 2021, 458: 655-666. doi: 10.1016/j.neucom.2020.03.125
[21]	ZHANG R L, SONG X H, YING S R, et al. CA-CSM: A novel clustering algorithm based on cluster center selection model[J]. Soft Computing, 2021, 25(13): 8015-8033. doi: 10.1007/s00500-021-05835-w