面向突防的滑翔制导炮弹弹道规划方法

尹秋霖; 陈琦; 王中原; 王庆海

doi:10.13700/j.bh.1001-5965.2023.0049

面向突防的滑翔制导炮弹弹道规划方法

doi: 10.13700/j.bh.1001-5965.2023.0049

南京理工大学能源与动力工程学院，南京 210094

基金项目: 国家自然科学基金(52202475)；江苏省自然科学基金(BK20200498)

详细信息

通讯作者:
E-mail：qichen@njust.edu.cn

中图分类号: TJ413⁺.6
计量
- 文章访问数: 263
- HTML全文浏览量: 101
- PDF下载量: 17
- 被引次数: 0
出版历程
- 收稿日期: 2023-02-14
- 录用日期: 2023-06-02
- 网络出版日期: 2023-06-26
- 整期出版日期: 2024-10-31

Trajectory programming method of gliding-guided projectiles for penetration

School of Energy and Power Engineering，Nanjing University of Science and Technology，Nanjing 210094，China

Funds: National Natural Science Foundation of China (52202475); Natural Science Foundation of Jiangsu Province (BK20200498)

More Information

Corresponding author: E-mail：qichen@njust.edu.cn

摘要

摘要:
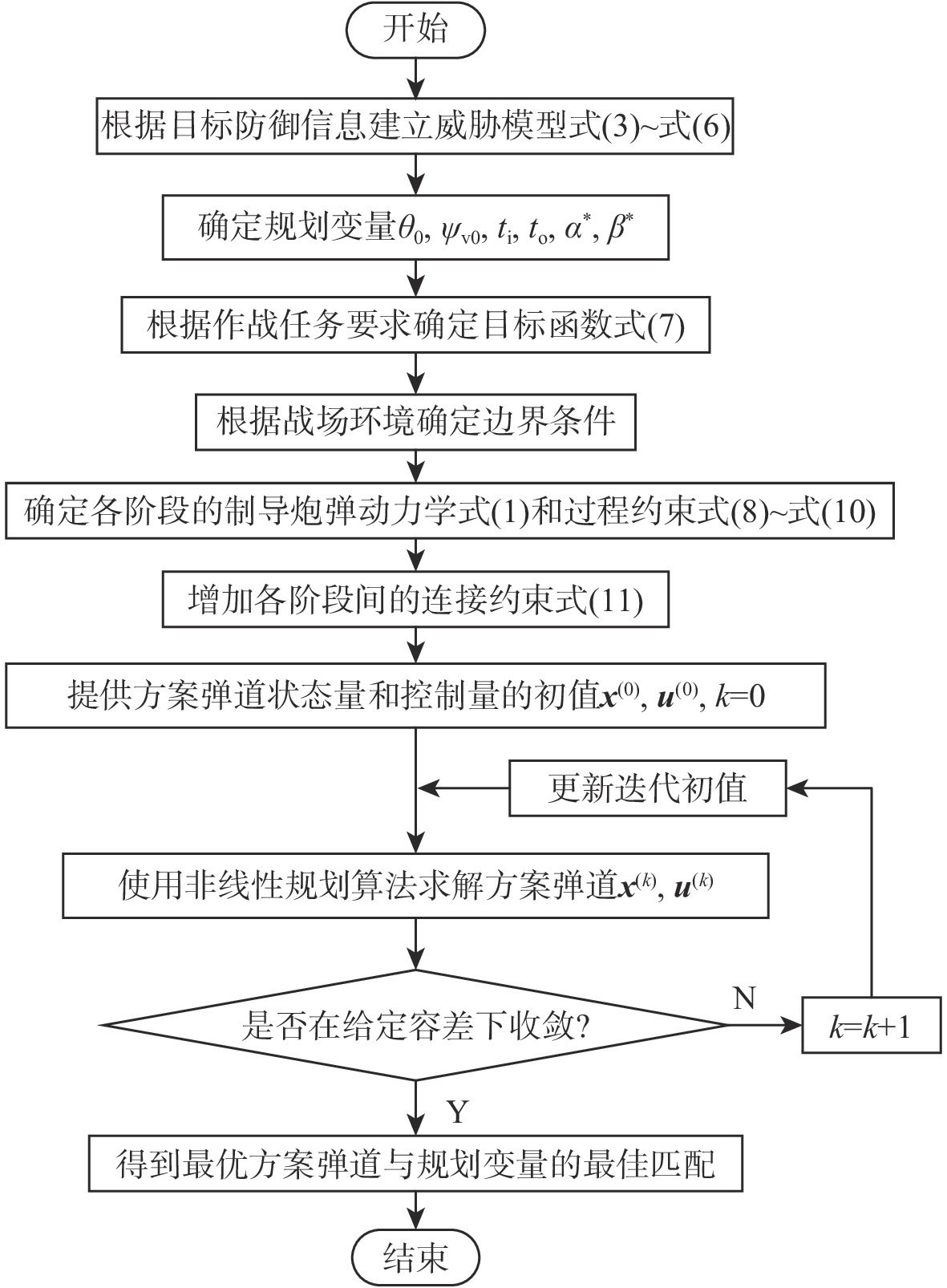
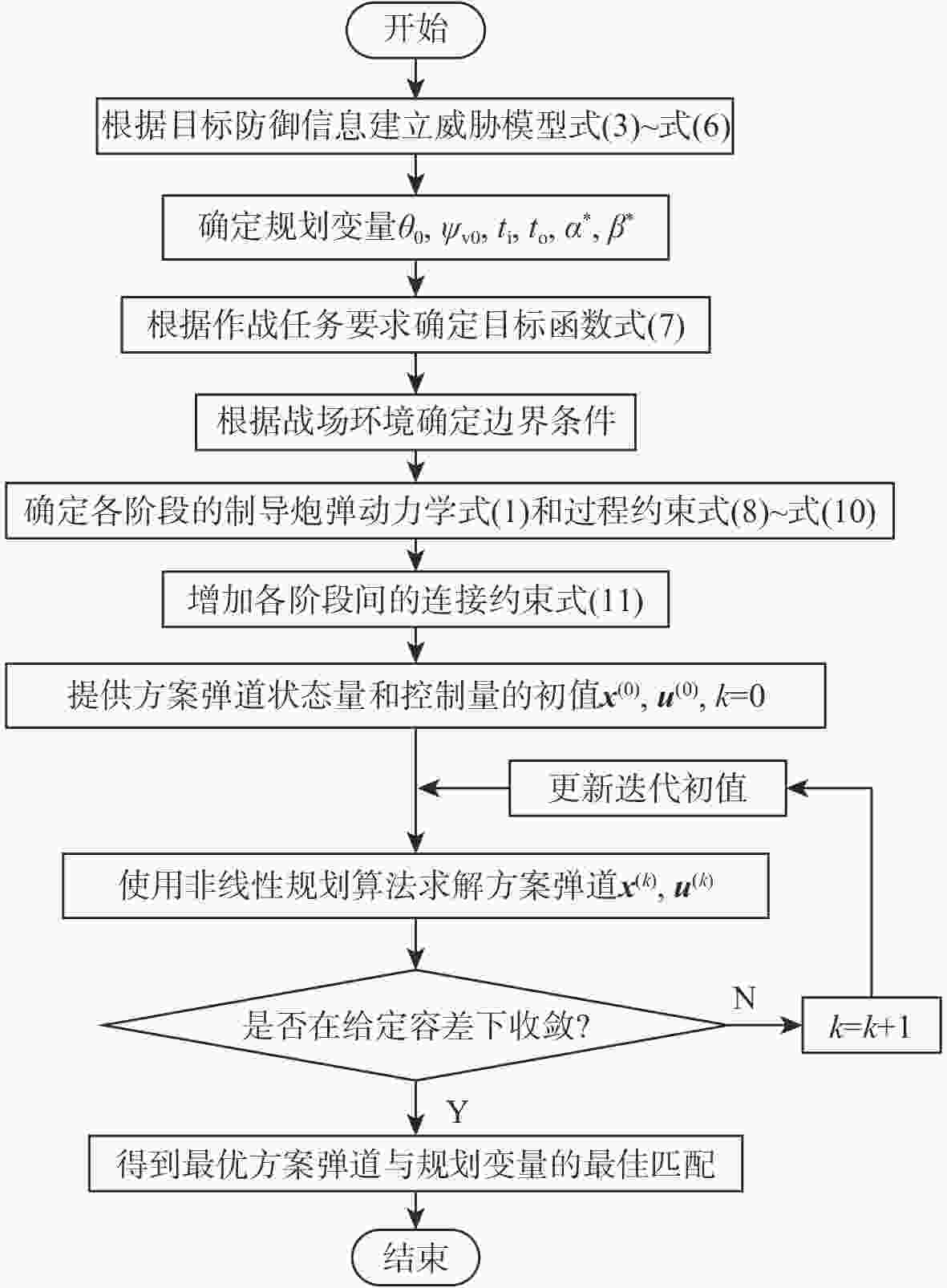
针对滑翔制导炮弹在不可避免的威胁区域内选择突防方案的问题，从量化威胁值的角度建立了敌方防御手段的数学模型，基于模型设计了全程综合威胁值最低的规划指标，提出考虑目标防御威胁的弹道规划方法。为实现滑翔制导炮弹全程飞行过程中初始弹道倾角、偏角、火箭点火时刻、滑翔启控时刻等各参数的最佳匹配，建立了多阶段全弹道规划模型，并采用hp自适应伪谱法将最优控制问题转换为非线性规划问题求解。通过仿真验证了在该指标下滑翔制导炮弹对目标防御的规避效果，分析了影响有效性的因素。与传统弹道规划方法进行对比，证明了所提方法的优越性。
- 滑翔制导炮弹 /
- 突防 /
- 威胁建模 /
- 全弹道规划 /
- hp自适应伪谱法
Abstract:
Aiming at the problem of gliding-guided projectile penetration schemes in inevitable threat areas, mathematical models of the enemy’s defense are established from the perspective of quantifying the threat value. Based on the model, a cost function with the lowest comprehensive threat value in the whole process is designed. To accomplish the best possible matching of the initial trajectory inclination, deflection angle, rocket ignition time, gliding start time, and other parameters over the course of the flight, a multi-stage full trajectory planning model is created. Then, the hp adaptive pseudo-spectral method is used to transform the optimal control problem into a nonlinear programming problem. The evading effect of the projectile on target defense is verified by simulation, and the factors affecting the effectiveness are analyzed. The proposed method’s advantages over conventional trajectory programming techniques are also examined.
- gliding-guided projectile /
- penetration /
- threat modeling /
- full trajectory programming /
- hp adaptive pseudo-spectral method

HTML全文

图 1 全弹道规划流程

Figure 1. Flow of full trajectory planning

下载: 全尺寸图片幻灯片

图 2 场景1仿真结果

Figure 2. Simulation results of Scene 1

下载: 全尺寸图片幻灯片

图 3 场景2仿真结果

Figure 3. Simulation results of Scene 2

下载: 全尺寸图片幻灯片

图 4 场景3仿真结果

Figure 4. Simulation results of Scene 3

下载: 全尺寸图片幻灯片

图 5 与传统方法对比结果（算例3）

Figure 5. Results compared with traditional methods (Example 3)

下载: 全尺寸图片幻灯片

表 1 滑翔弹参数

Table 1. Gliding-guided projectile parameter

参数	数值
$m/{\text{kg}}$	44.5
${m_{\rm{p}}}/{\text{kg}}$	7.23
$S/{{\text{m}}^2}$	0.013 3
${T_{\rm{p}}}/{\text{N}}$	1 219.2
${t_{\mathrm{b}}}/{\text{s}}$	14.068
${k_{\rm{c}}}$	35

下载: 导出CSV

表 2 目标防御参数

Table 2. Target defense parameter

参数	数值
${R_{{\mathrm{r}}\max }}/{\text{km}}$	50
${R_{{\mathrm{g}}\min }}/{\text{km}}$	2
${R_{{\mathrm{g}}\max }}/{\text{km}}$	7
${R_{{\mathrm{p}}\min }}/{\text{km}}$	1
${R_{{\mathrm{p}}\max }}/{\text{km}}$	3

下载: 导出CSV

表 3 仿真参数

Table 3. Simulation parameter

参数	数值	参数	数值
${x_0}/{\text{km}}$	0	${\psi _{{\mathrm{v}}0\max }}/({\text{°}})$	90
${y_0}/{\text{km}}$	0	${T_{\max }}/{\text{s}}$	300
${{\textit{z}}_0}/{\text{km}}$	0	$ {V}_{{\mathrm{f}}\mathrm{min}}/(\text{m}\cdot {\text{s}}^{-1})$	250
${x_{\mathrm{T}}}/{\text{km}}$	60	$\alpha _{\max }^*/({\text{°}})$	15
${y_{\mathrm{T}}}/{\text{km}}$	0	$\beta _{\max }^*/({\text{°}})$	10
${{\textit{z}}_{\mathrm{T}}}/{\text{km}}$	1	$\alpha $	0.1
$ {V}_{0}/(\text{m}\cdot {\text{s}}^{-1}) $	800	$\beta $	0.5
${\theta _{0\min }}/({\text{°}}) $	0	$\gamma $	0.2
${\theta _{0\max }}/({\text{°}})$	90	$\eta $	0.3
${\psi _{{\mathrm{v}}0\min }}/({\text{°}})$	−90

下载: 导出CSV

表 4 场景1雷达位置

Table 4. Radar position of Scene 1

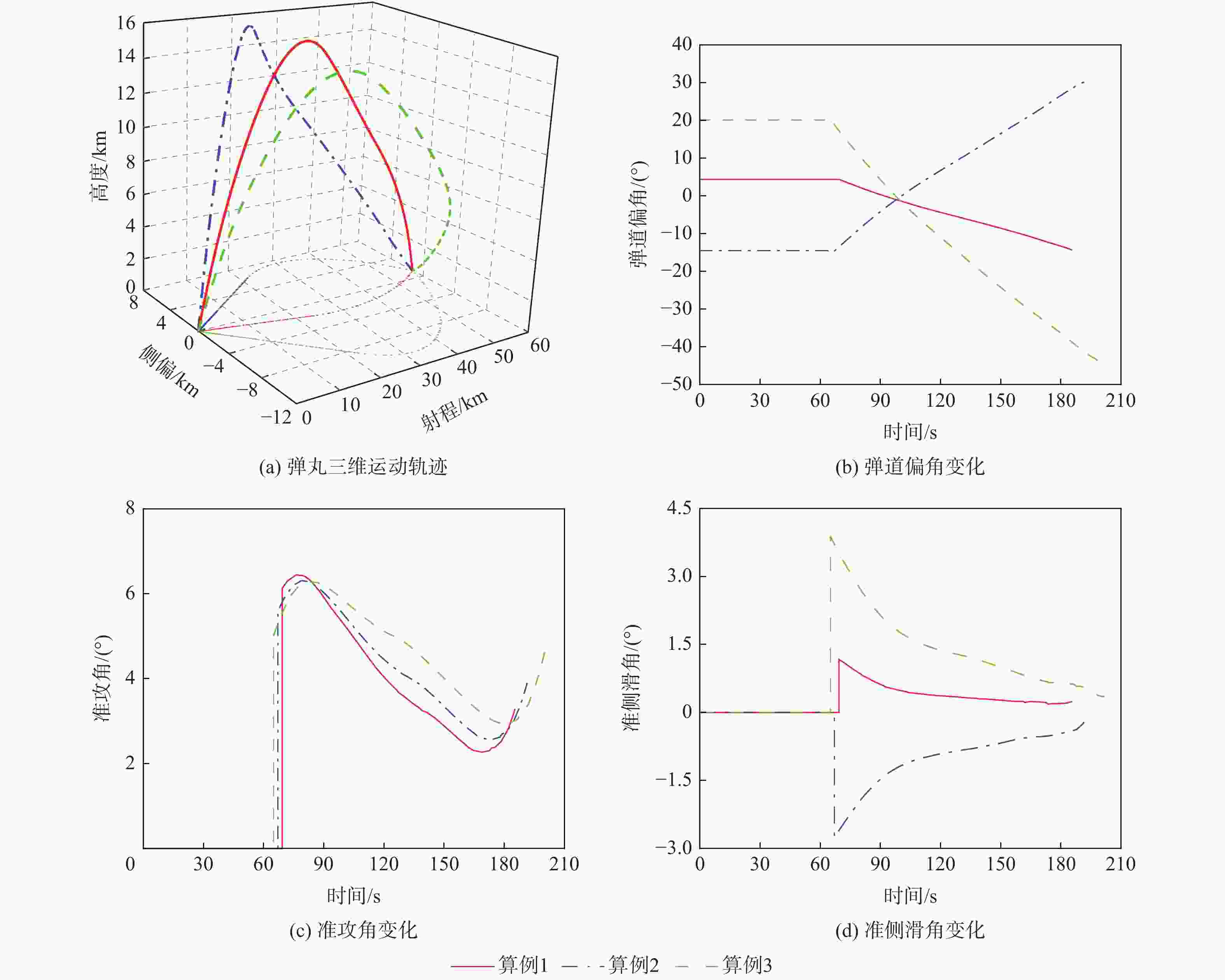
算例	雷达位置坐标/km
1	(10,0,2)
2	(10,0,−5)
3	(10,0,10)

下载: 导出CSV

表 5 场景1全弹道规划结果

Table 5. Full trajectory programming results of Scene 1

算例	$ {\theta _0}/({\text{°}}) $	$ {\psi _{{\mathrm{v}}0}}/({\text{°}}) $	$ {t_{\mathrm{i}}}/{\mathrm{s}} $	$ {t_{\rm{o}}}/{\mathrm{s}} $	$ {t_{\mathrm{f}}}/{\mathrm{s}} $	威胁值
1	56.72	4.38	9.55	69.31	185.29	19.61
2	56.26	−14.53	9.80	67.10	191.34	16.13
3	56.02	20.09	10.51	65.09	201.38	12.25

下载: 导出CSV

表 6 场景2雷达位置

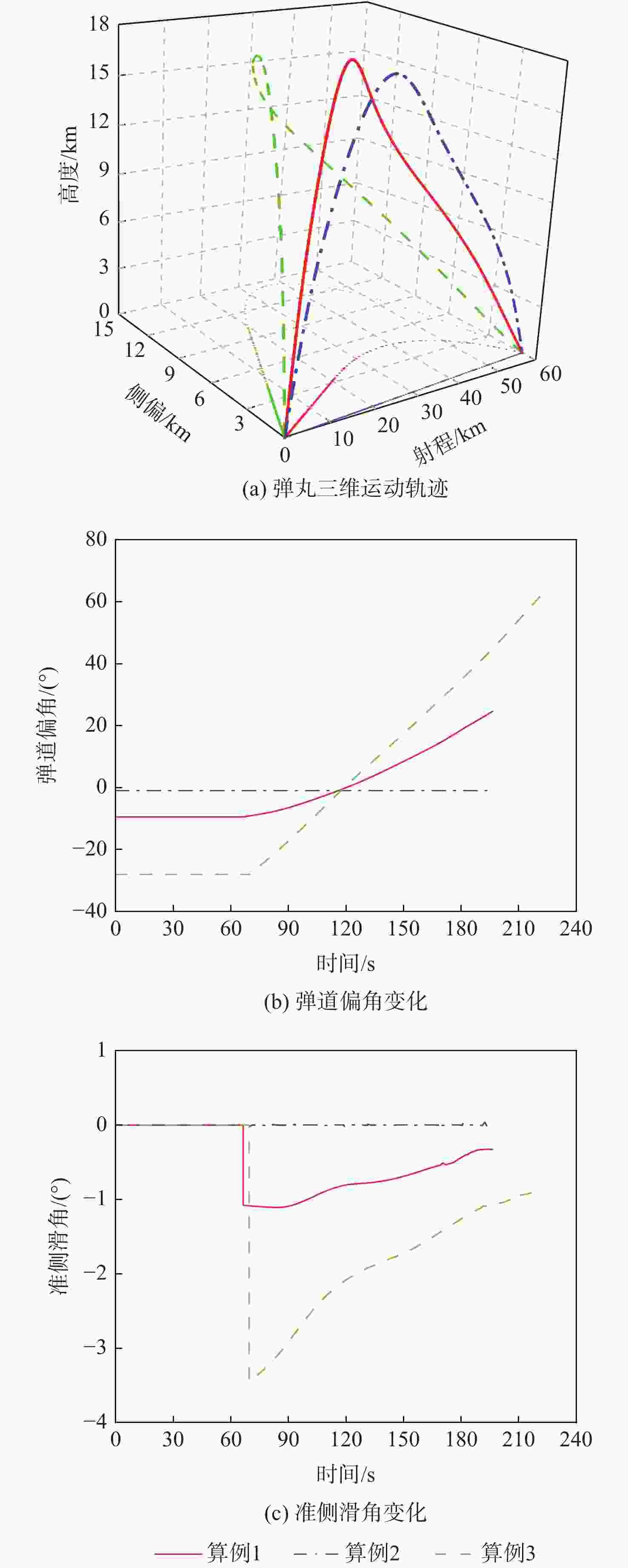
Table 6. Radar position of Scene 2

算例	雷达位置坐标/km
1	(40,0,−1)
2	(40,0,2/3)
3	(40,0,−15)

下载: 导出CSV

表 7 场景2全弹道规划结果

Table 7. Full trajectory programming results of Scene 2

算例	$ {\theta _0}/({\text{°}}) $	$ {\psi _{{\mathrm{v}}0}}/({\text{°}}) $	$ {t_{\mathrm{i}}}/{\mathrm{s}} $	$ {t_{\rm{o}}}/{\mathrm{s}} $	$ {t_{\mathrm{f}}}/{\mathrm{s}} $	威胁值
1	64.12	−9.44	16.34	66.42	196.29	29.40
2	64.13	−0.96	16.08	69.54	193.20	30.25
3	65.11	−27.99	22.71	69.60	221.87	8.85

下载: 导出CSV

表 8 场景3雷达位置

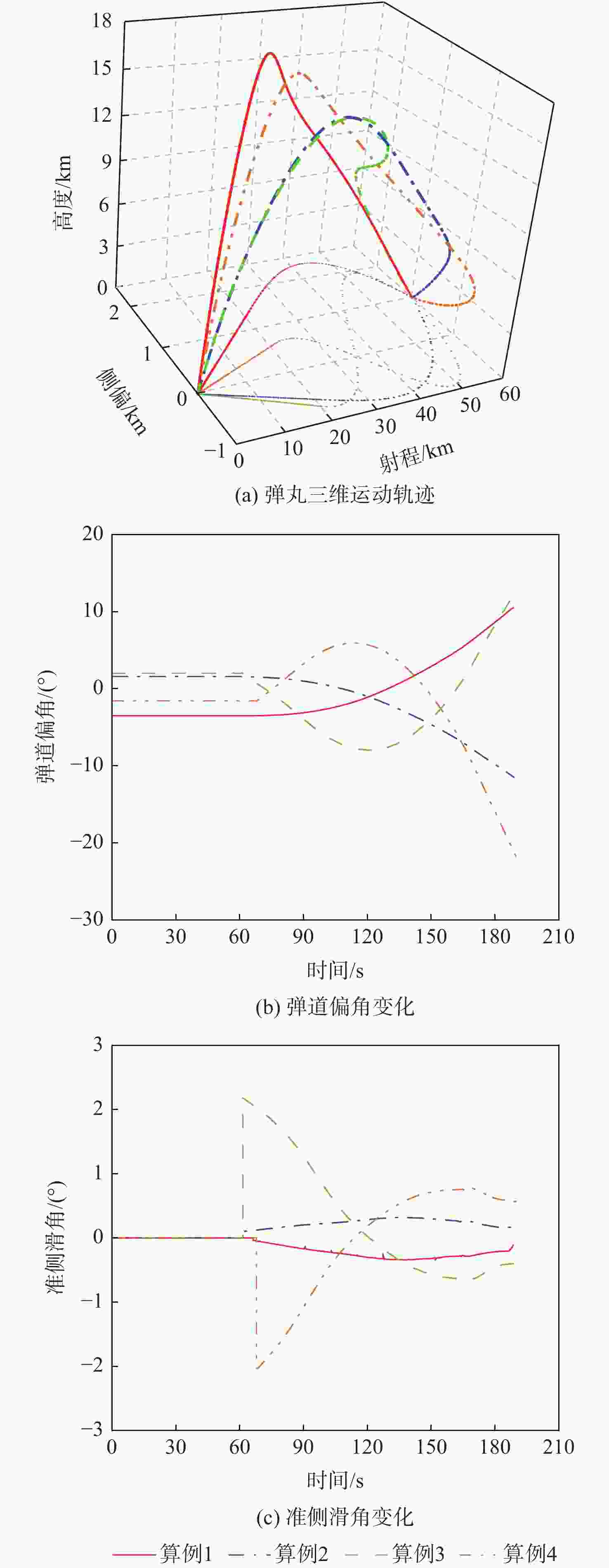
Table 8. Radar position of Scene 3

算例	雷达位置坐标/km
1	(10,0,2)，(40,0,−1)
2	(10,0,−1)，(40,0,2)
3	(15,0,20)，(50,0,−5)
4	(10,0,−20)，(50,0,10)

下载: 导出CSV

表 9 场景3全弹道规划结果

Table 9. Full trajectory programming results of Scene 3

算例	$ {\theta _0}/({\text{°}}) $	$ {\psi _{{\mathrm{v}}0}}/({\text{°}}) $	$ {t_{\mathrm{i}}}/{\mathrm{s}} $	$ {t_{\rm{o}}}/{\mathrm{s}} $	$ {t_{\mathrm{f}}}/{\mathrm{s}} $	威胁值
1	60.18	−3.51	10.80	66.33	188.56	45.93
2	60.21	1.59	10.87	61.53	188.83	45.87
3	61.99	1.99	13.65	61.42	191.05	35.39
4	61.69	−1.61	13.48	67.89	190.33	32.25

下载: 导出CSV

表 10 雷达位置

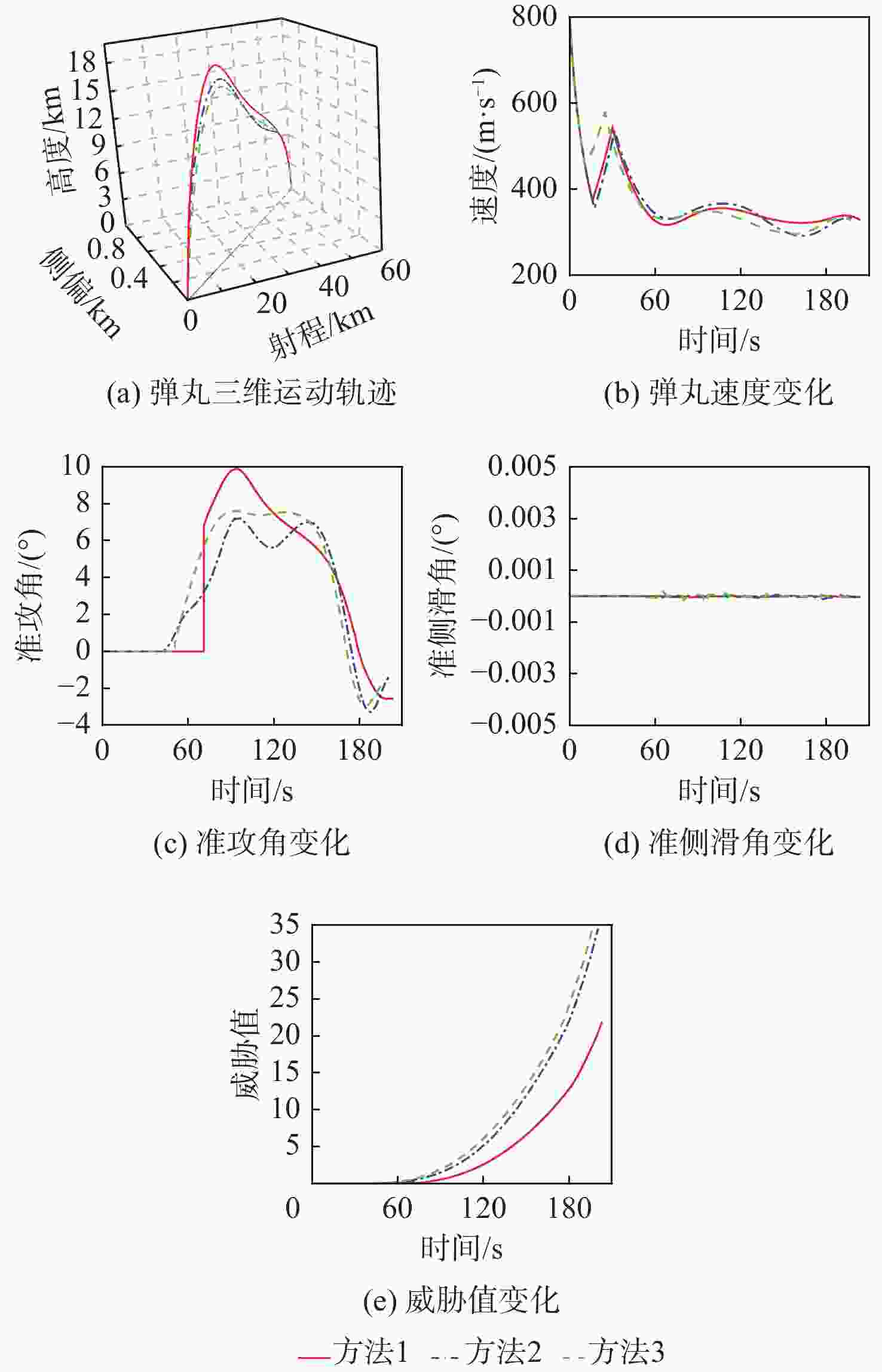
Table 10. Radar positions

算例	雷达位置坐标/km
1	(10,0,2)
2	(40,0,−1)
3	(60,0,1)
4	(15,0,20)，(50,0,−5)

下载: 导出CSV

表 11 传统方法全弹道规划结果

Table 11. Full trajectory programming results of traditional methods

方法	$ {\theta _0}/({\text{°}}) $	$ {\psi _{{\mathrm{v}}0}}/({\text{°}}) $	$ {t_{\mathrm{i}}}/{\mathrm{s}} $	$ {t_{\rm{o}}}/{\mathrm{s}} $	$ {t_{\mathrm{f}}}/{\mathrm{s}} $	能量消耗/（rad²·s）
2	63.07	−0.86	17.48	43.42	200.32	17.02
3	58.57	−0.95	10.77	50.83	196.32	22.24

下载: 导出CSV

表 12 不同算例中与传统方法对比结果

Table 12. Results compared with traditional methods in different examples

算例	威胁值			方法1的能量消耗/（rad²·s）	方法1的飞行时间/s
算例	方法1	方法2	方法3	方法1的能量消耗/（rad²·s）	方法1的飞行时间/s
1	19.51	29.65	28.69	22.51	197.76
2	28.35	41.95	42.25	24.31	202.86
3	21.79	34.46	34.51	24.93	203.07
4	34.58	53.33	53.05	24.29	200.78

下载: 导出CSV

参考文献(32)

[1]	GUO F S, LIU X X, LIU D. Review on the trajectory design of the dynamic-glider missile[J]. Procedia Engineering, 2011, 15: 1191-1195. doi: 10.1016/j.proeng.2011.08.220
[2]	陈琦. 滑翔增程制导炮弹弹道优化及制导控制方法研究[D]. 南京: 南京理工大学, 2017. CHEN Q. Investigation on trajectory optimization and guidance &control scheme for a type of gliding guided projectiles[D]. Nanjing: Nanjing University of Science and Technology, 2017(in Chinese).
[3]	CHEN Q, WANG Z Y. Optimal trajectory for time-on-target of a guided projectile using direct collocation method[C]//Proceedings of the International Conference on Mechatronic Sciences, Electric Engineering and Computer. Piscataway: IEEE Press, 2013: 2803-2806.
[4]	徐秋坪. 滑翔制导炮弹弹道规划及其自抗扰控制系统研究[D]. 南京: 南京理工大学, 2018. XU Q P. Trajectory optimization and active-disturbance-rejection control system for gliding guided projectiles[D]. Nanjing: Nanjing University of Science and Technology, 2018(in Chinese).
[5]	XIAO J K, WANG G, GUO X K, et al. Modeling on threat assessment system of reentry-course ballistic missile[J]. Advanced Materials Research, 2013, 722: 301-305. doi: 10.4028/www.scientific.net/AMR.722.301
[6]	KUMAR S, TRIPATHI B K. Modelling of threat evaluation for dynamic targets using Bayesian network approach[J]. Procedia Technology, 2016, 24: 1268-1275. doi: 10.1016/j.protcy.2016.05.112
[7]	王勃, 姚佩阳, 税冬东, 等. 基于影响网的战场威胁强度评估建模[J]. 计算机工程与设计, 2014, 35(8): 2836-2840. doi: 10.3969/j.issn.1000-7024.2014.08.043 WANG B, YAO P Y, SHUI D D, et al. Modeling of battlefield threat intensity evaluation based on influence nets[J]. Computer Engineering and Design, 2014, 35(8): 2836-2840(in Chinese). doi: 10.3969/j.issn.1000-7024.2014.08.043
[8]	LEE H, CHOI B J, KIM C O, et al. Threat evaluation of enemy air fighters via neural network-based Markov chain modeling[J]. Knowledge-Based Systems, 2017, 116: 49-57.
[9]	LIU J, LI X B, LEI Y L, et al. An index based threat modeling method for path planning[C]//Proceedings of the 2009 First International Conference on Advances in System Simulation. Piscataway: IEEE Press, 2009: 1-5.
[10]	刘娟, 赵新, 雷永林, 等. 基于指数法的导弹航迹规划空间威胁建模研究[J]. 系统仿真学报, 2009, 21(17): 5353-5356. LIU J, ZHAO X, LEI Y L, et al. Modeling of threat space for missile route planning based on index-method[J]. Journal of System Simulation, 2009, 21(17): 5353-5356(in Chinese).
[11]	刘娟, 王维平. 基于仿真数据的航迹规划威胁建模方法研究[J]. 计算机仿真, 2010, 27(9): 24-28. doi: 10.3969/j.issn.1006-9348.2010.09.007 LIU J, WANG W P. A simulation data based space threat modeling method for path planning[J]. Computer Simulation, 2010, 27(9): 24-28(in Chinese). doi: 10.3969/j.issn.1006-9348.2010.09.007
[12]	黄俊, 于雷, 李战武, 等. 对地任务规划系统威胁空间综合量化建模与仿真[J]. 系统仿真学报, 2010, 22(4): 1033-1036. HUANG J, YU L, LI Z W, et al. Integrated quantization modeling and simulation of threat space for air-to-surface mission planning system[J]. Journal of System Simulation, 2010, 22(4): 1033-1036 (in Chinese).
[13]	申舟, 谢文俊, 赵晓林, 等. 基于人工势场的无人机战场威胁建模研究[J]. 计算机仿真, 2014, 31(2): 60-64. doi: 10.3969/j.issn.1006-9348.2014.02.013 SHEN Z, XIE W J, ZHAO X L, et al. Modeling of UAV battlefield threats based on artificial potential field[J]. Computer Simulation, 2014, 31(2): 60-64(in Chinese). doi: 10.3969/j.issn.1006-9348.2014.02.013
[14]	郭志鸿. 多无人机协同的实时任务分配与航迹规划研究[D]. 重庆: 重庆理工大学, 2022. GUO Z H. Research on real-time task assignment and tracks planning for multi-UAV collaboration[D]. Chongqing: Chongqing University of Technology, 2022(in Chinese).
[15]	ZHANG R, LI S, DING Y M, et al. UAV path planning algorithm based on improved Harris Hawks optimization[J]. Sensors, 2022, 22(14): 5232. doi: 10.3390/s22145232
[16]	GUO Y C, LIU X X, ZHANG W G, et al. An improved algorithm of UAV 3D path planning[C]//Proceedings of the International Conterence on Guidance, Vavigation and Control. Berlin: Springer, 2021: 849-859.
[17]	李晓萌, 王道波, 郭继凯, 等. 基于某种生物启发式算法的无人机航迹规划[J]. 机械与电子, 2018, 36(11): 15-19. doi: 10.3969/j.issn.1001-2257.2018.11.004 LI X M, WANG D B, GUO J K, et al. Path planning of UAV based on a biological heuristic algorithm[J]. Machinery & Electronics, 2018, 36(11): 15-19(in Chinese). doi: 10.3969/j.issn.1001-2257.2018.11.004
[18]	彭建亮, 孙秀霞, 蔡满意, 等. 基于人工势场的防空威胁建模与仿真[J]. 系统工程与电子技术, 2010, 32(2): 338-341. PENG J L, SUN X X, CAI M Y, et al. Modeling and simulation of air defense threat based on artificial potential field[J]. Systems Engineering and Electronics, 2010, 32(2): 338-341(in Chinese).
[19]	ALPDEMIR M N. Tactical UAV path optimization under radar threat using deep reinforcement learning[J]. Neural Computing and Applications, 2022, 34(7): 5649-5664. doi: 10.1007/s00521-021-06702-3
[20]	温乃峰. 低空复杂环境下小型无人机的在线航迹规划算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2016. WEN N F. Research on the small UAV online path planning algorithms in complex and low-altitude environments[D]. Harbin: Harbin Institute of Technology, 2016(in Chinese).
[21]	张志伟, 蒋道刚, 袁坤刚. 低空突防航线规划研究[J]. 飞行力学, 2019, 37(4): 62-67. ZHANG Z W, JIANG D G, YUAN K G. Study on low altitude penetration route planning[J]. Flight Dynamics, 2019, 37(4): 62-67(in Chinese).
[22]	周鑫, 李新洪, 王谦. 基于威胁建模的PSO在UAV 3维航路规划中的应用[J]. 兵工自动化, 2017, 36(4): 73-76. doi: 10.7690/bgzdh.2017.04.020 ZHOU X, LI X H, WANG Q. Application of PSO based on threat modeling in 3D route planning of UAV[J]. Ordnance Industry Automation, 2017, 36(4): 73-76(in Chinese). doi: 10.7690/bgzdh.2017.04.020
[23]	LIU J S, JIANG W Z, LIU T. Penetration efficiency evaluation of missile with jammer[J]. Applied Mechanics and Materials, 2015, 719-720: 369-375. doi: 10.4028/www.scientific.net/AMM.719-720.369
[24]	唐嘉钰, 李相民, 代进进. 基于威胁建模的UCAV武器投放在线航迹规划[J]. 西北工业大学学报, 2021, 39(2): 382-391. doi: 10.3969/j.issn.1000-2758.2021.02.019 TANG J Y, LI X M, DAI J J. Online trajectory planning for UCAV performing ground attacks based on threat modeling[J]. Journal of Northwestern Polytechnical University, 2021, 39(2): 382-391(in Chinese). doi: 10.3969/j.issn.1000-2758.2021.02.019
[25]	MA M X, WU J, SHI Y, et al. Chaotic random opposition-based learning and cauchy mutation improved moth-flame optimization algorithm for intelligent route planning of multiple UAVs[J]. IEEE Access, 2022, 10: 49385-49397. doi: 10.1109/ACCESS.2022.3172710
[26]	GUO J G, HU G J, GUO Z Y, et al. Evaluation model, intelligent assignment, and cooperative interception in multimissile and multitarget engagement[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 3104-3115. doi: 10.1109/TAES.2022.3144111
[27]	CHEN Q, WANG Z Y, CHANG S J, et al. Multiphase trajectory optimization for gun-launched glide guided projectiles[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2016, 230(6): 995-1010. doi: 10.1177/0954410015602507
[28]	邱文杰, 孟秀云. 基于hp自适应伪谱法的飞行器多阶段轨迹优化[J]. 北京理工大学学报, 2017, 37(4): 412-417. QIU W J, MENG X Y. Multi-phase trajectory optimization of vehicle based on hp-adaptive pseudospectral method[J]. Transactions of Beijing Institute of Technology, 2017, 37(4): 412-417(in Chinese).
[29]	韩子鹏. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2008. HAN Z P. External ballistics of projectile and arrow[M]. Beijing: Beijing Insititute of Technology Press, 2008 (in Chinese).
[30]	任天祥, 贺建良, 邹杰. 基于改进Theta^算法的直升机三维航路规划[J]. 电光与控制, 2022, 29(2): 45-48. doi: 10.3969/j.issn.1671-637X.2022.02.010 REN T X, HE J L, ZOU J. 3D route planning for helicopters based on improved Theta^ algorithm[J]. Electronics Optics & Control, 2022, 29(2): 45-48(in Chinese). doi: 10.3969/j.issn.1671-637X.2022.02.010
[31]	卞强, 孙齐, 童余德. 一种新的改进A^算法无人机三维路径规划[J]. 武汉理工大学学报, 2022, 44(7): 80-88. doi: 10.3963/j.issn.1671-4431.2022.07.012 BIAN Q, SUN Q, TONG Y D. A new improved A^ algorithm for UAV 3D path planning[J]. Journal of Wuhan University of Technology, 2022, 44(7): 80-88(in Chinese). doi: 10.3963/j.issn.1671-4431.2022.07.012
[32]	王丽英, 张友安, 黄诘. 带约束的末制导律与伪谱法轨迹优化[M]. 北京: 国防工业出版社, 2015. WANG L Y, ZHANG Y A, HUANG J. Constrained terminal guidance law and pseudospectral trajectory optimization[M]. Beijing: National Defense Industry Press, 2015(in Chinese).