轴压铝合金蜂窝圆筒整体稳定性研究

魏家睿; 吴琼; 吴伟; 李群智; 时红伟; 张虞

doi:10.13700/j.bh.1001-5965.2023.0135

轴压铝合金蜂窝圆筒整体稳定性研究

doi: 10.13700/j.bh.1001-5965.2023.0135

魏家睿^{1, 2, 3},
吴琼^{1, 2, ,},
吴伟⁴,
李群智⁵,
时红伟⁵,
张虞^{1, 2}

1.
北京航空航天大学虚拟现实技术与系统国家重点实验室，北京 100191
2.
北京航空航天大学江西研究院景德镇分院，景德镇 333000
3.
中国航天科工集团第九总体设计部，武汉 430040
4.
北京空天技术研究所，北京 100074
5.
北京空间飞行器总体设计部，北京 100094

基金项目: 国家自然科学基金(51875024)；民用航天技术预先研究项目(D020304)

详细信息

通讯作者:
E-mail：wuqiong@buaa.edu.cn

中图分类号: TH122
计量
- 文章访问数: 195
- HTML全文浏览量: 84
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2023-03-23
- 录用日期: 2023-07-07
- 网络出版日期: 2023-08-03
- 整期出版日期: 2025-03-27

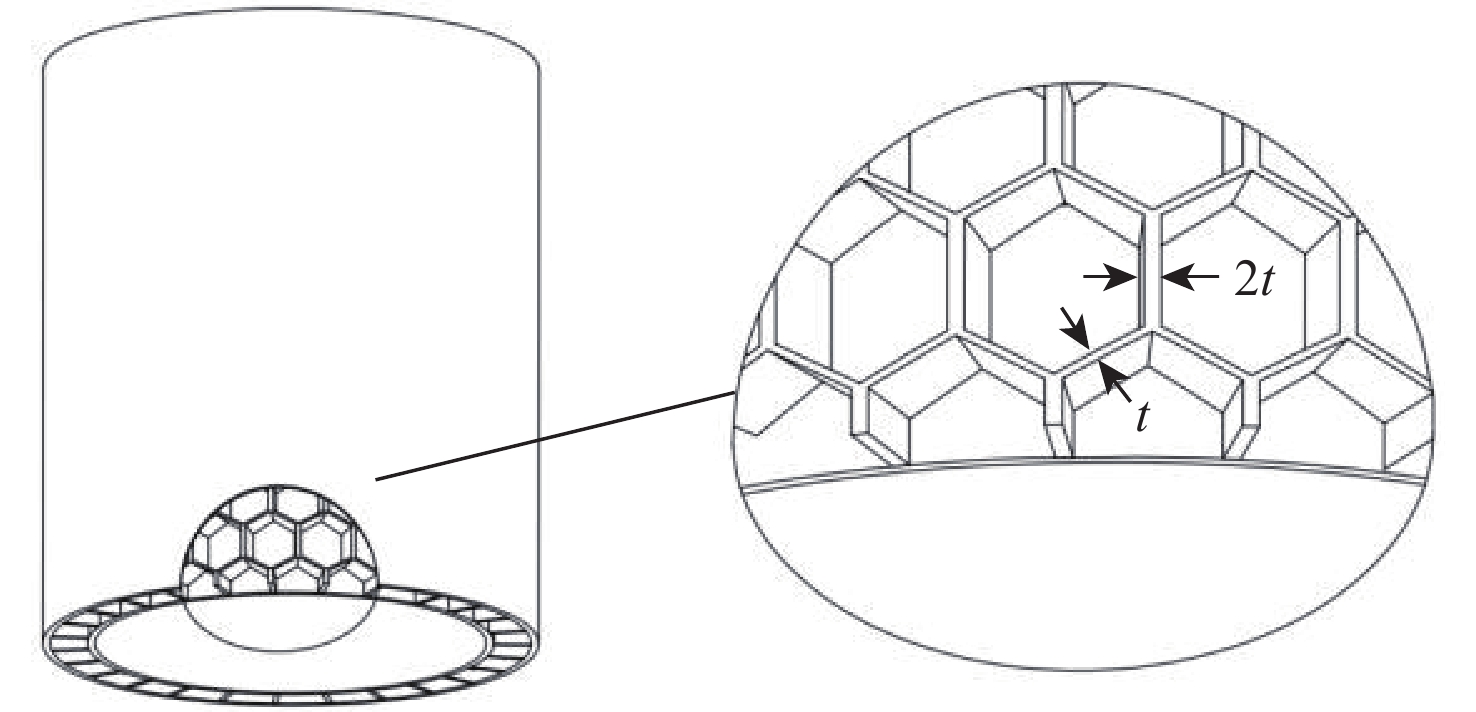
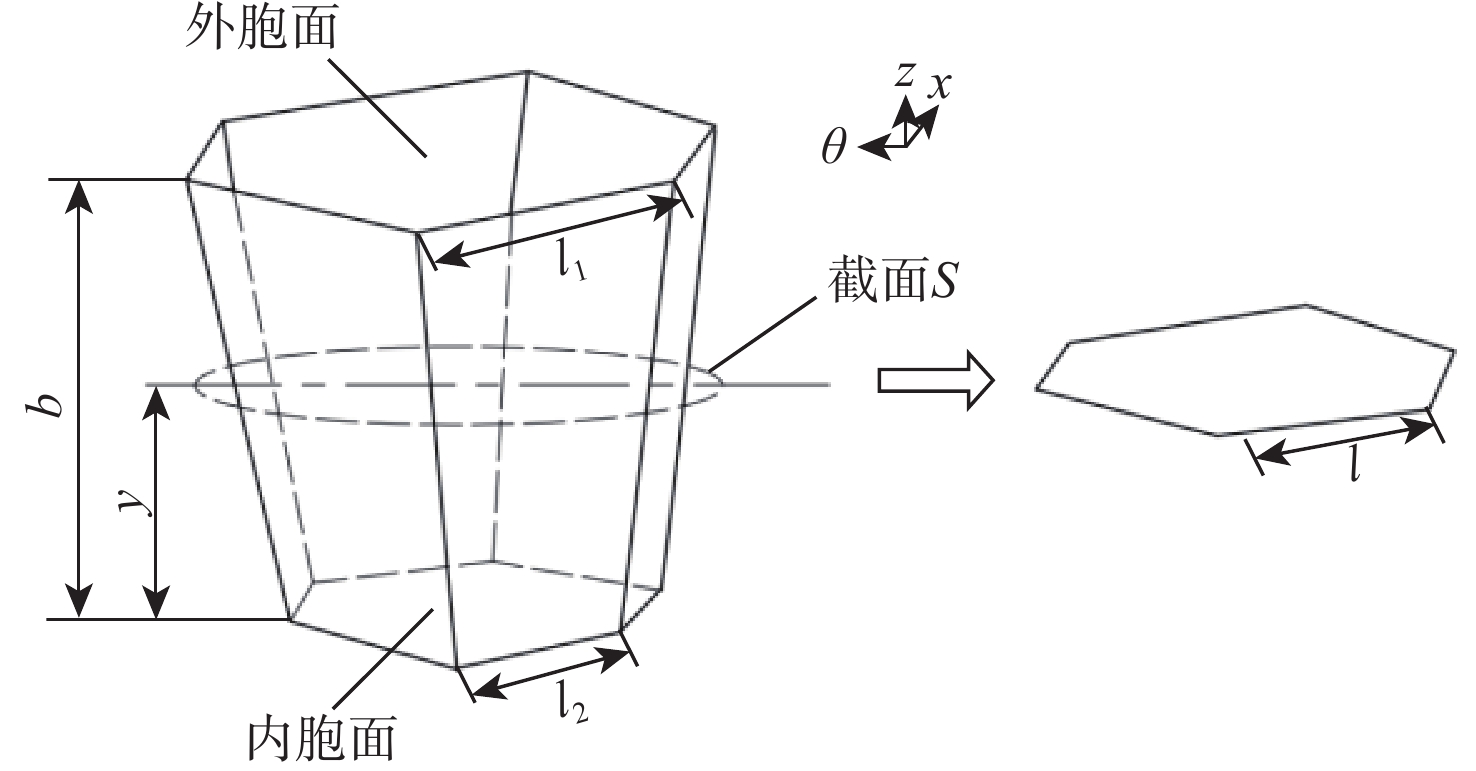
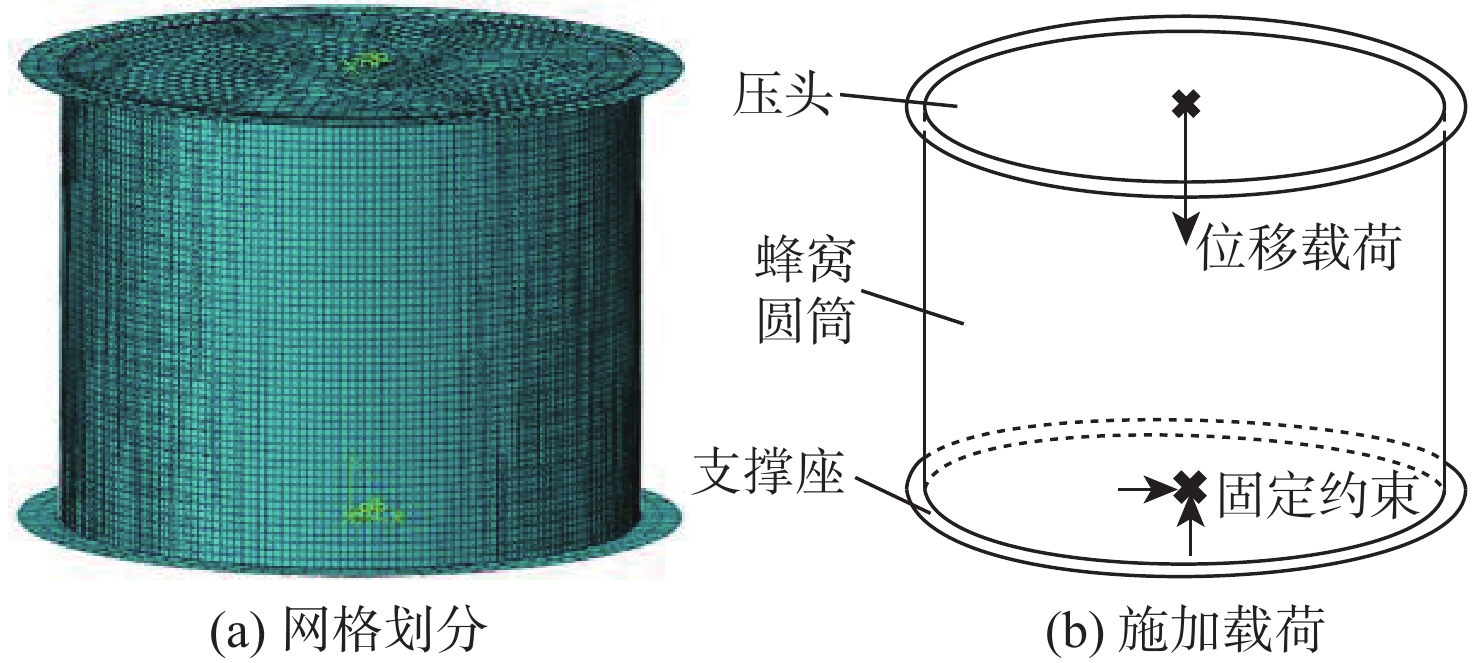
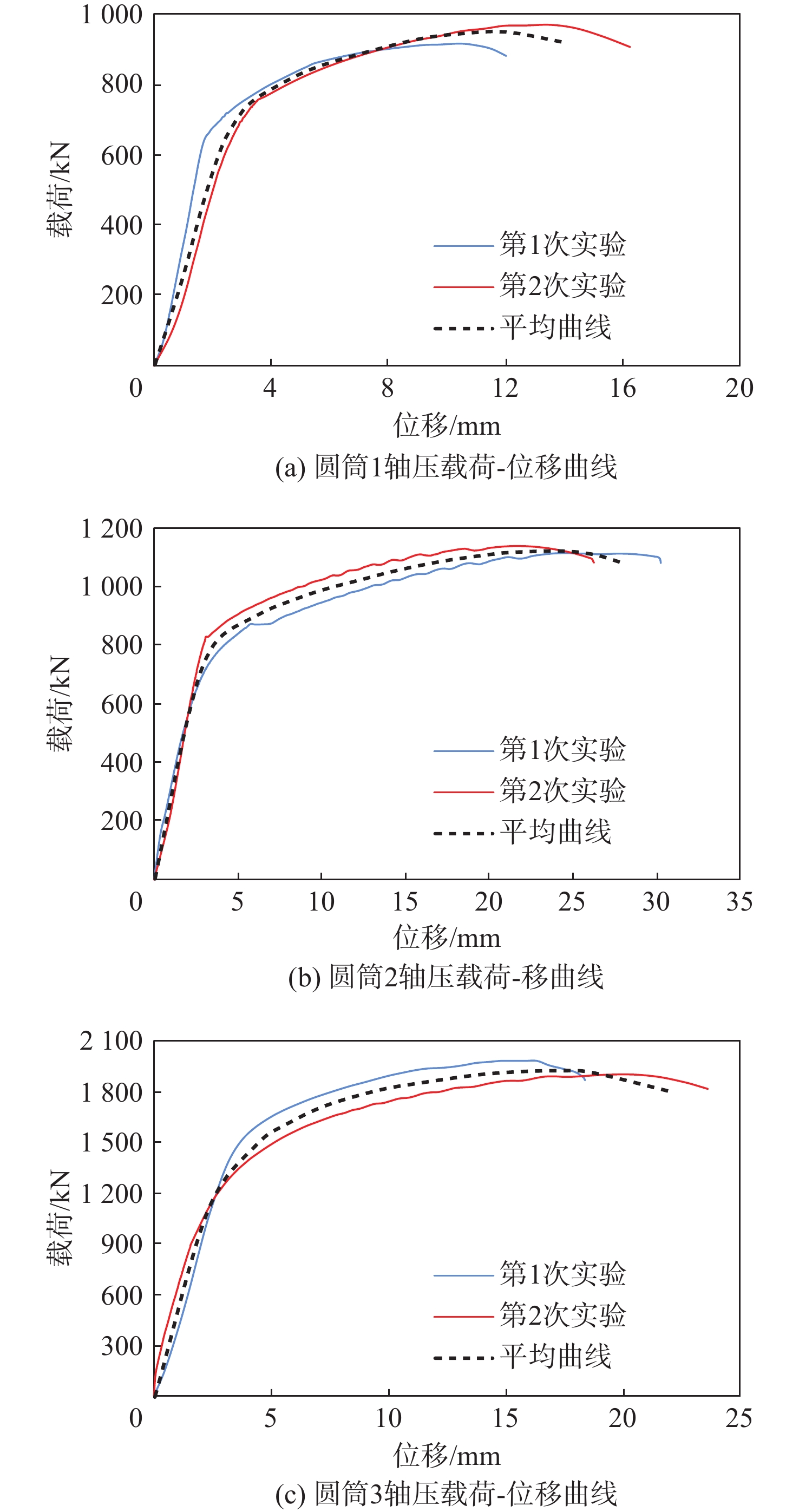
Study on global stability of aluminum alloy honeycomb cylinder under axial compression

WEI Jiarui^{1, 2, 3},
WU Qiong^{1, 2
, ,},
WU Wei⁴,
LI Qunzhi⁵,
SHI Hongwei⁵,
ZHANG Yu^{1, 2}

1.
State Key Laboratory of Virtual Reality Technology and Systems，Beihang University，Beijing 100191，China
2.
Jingdezhen Branch of Jiangxi Research Institute of Beihang University，Jingdezhen 333000，China
3.
The 9th Overall Design Department of China Aerospace Science and Industry Corporation，Wuhan 430040，China
4.
Beijing Aerospace Technology Institute，Beijing 100074，China
5.
Beijing Institute of Spacecraft System Engineering，Beijing 100094，China

Funds: National Natural Science Foundation of China (51875024); Civil Space Technology Pre-Research Program (D020304)

More Information

Corresponding author: E-mail：wuqiong@buaa.edu.cn

摘要

摘要:
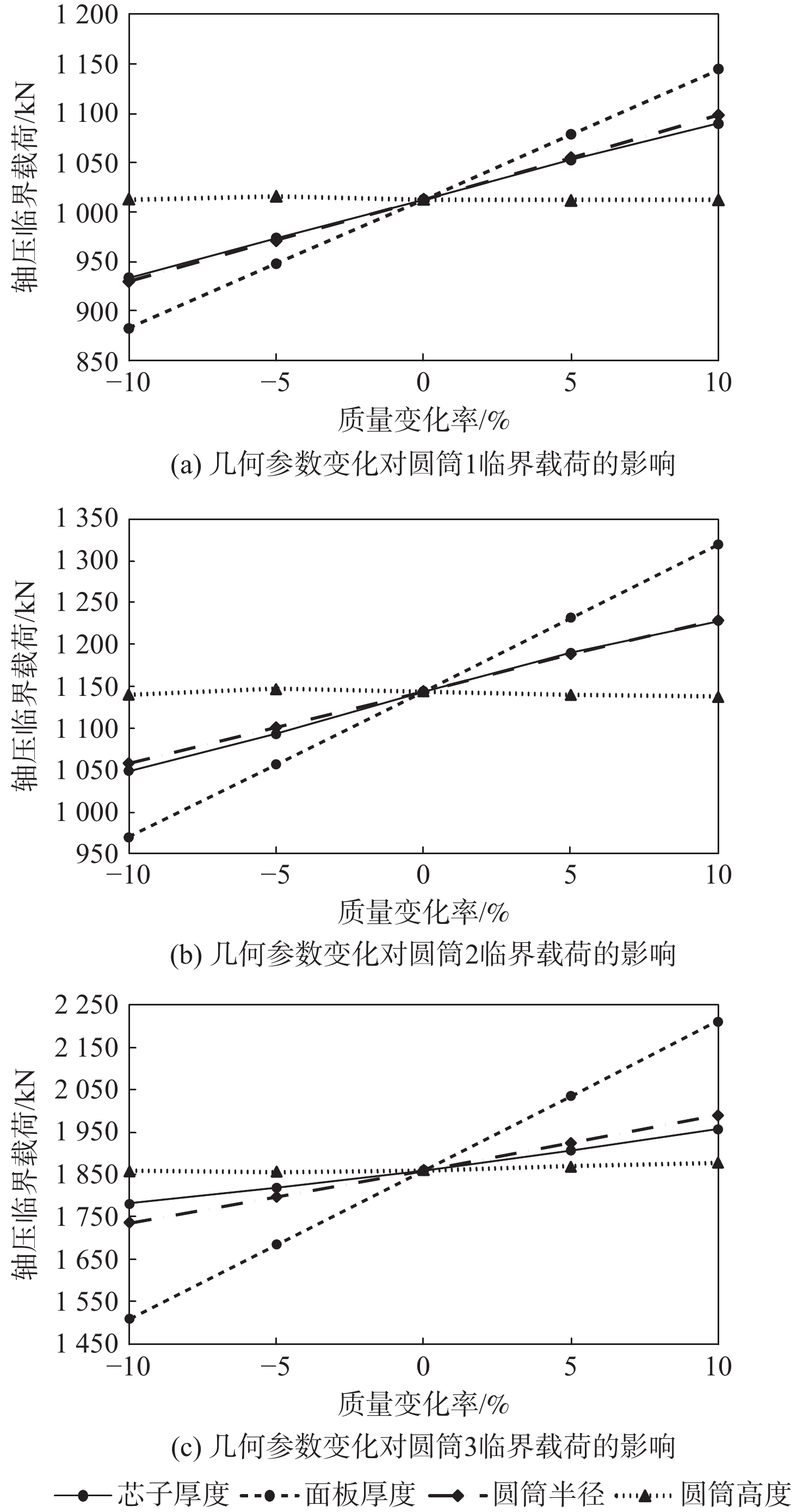
金属蜂窝圆筒结构常因轴压整体屈曲导致承载能力下降，对于其弹性屈曲问题目前已有大量研究，但在塑性屈曲问题方面的理论研究工作较少。为解决上述问题，基于蜂窝圆筒等效模型和Hamilton原理，推导了铝合金蜂窝圆筒承受轴压载荷作用时弹、塑性屈曲临界载荷的理论计算公式，并进行了轴压仿真分析和实验验证，利用理论公式讨论了蜂窝圆筒各尺寸参数对临界载荷的影响。结果表明：所提理论公式和仿真模型均能准确预测铝合金蜂窝圆筒的临界载荷，理论公式计算效率更高；圆筒质量变化±10%时，影响临界载荷的因素依次为面板厚度、圆筒半径、芯子厚度、圆筒高度；蜂窝圆筒的临界载荷与芯子厚度、面板厚度、圆筒半径近似呈线性正相关，与圆筒高度关系较弱。
- 蜂窝圆筒 /
- 整体稳定性 /
- 临界载荷 /
- 弹塑性 /
- Hamilton原理 /
- 有限元
Abstract:
Metal honeycomb cylinder structures frequently encounter a decrease in load-carrying capacity due to axial compression buckling. Extensive research has been conducted on their elastic buckling behavior. However, there are few theoretical studies on their plastic buckling behavior. To address this issue, a theoretical formula was derived for the elastic and plastic buckling critical load of the aluminum alloy honeycomb cylinder under axial compression, drawing upon the equivalent model of the honeycomb cylinder and the Hamilton principle. The simulation analysis and experimentations on the above problem were carried out. Finally, the influence of the honeycomb cylinder dimensional parameters on the critical load was discussed using the theoretical formula. The results show that both the theoretical formula and the simulation model can accurately predict the critical load of the aluminum alloy honeycomb cylinder. In comparison, the theoretical formula is calculated faster. When the cylinder mass changes within the range of ±10%, the influence degree of panel thickness, cylinder radius, core thickness and cylinder height on the critical load decreases successively. The honeycomb cylinder’s critical load exhibits a minor association with the cylinder height, but it exhibits an approximately linear positive correlation with the cylinder radius, core thickness, and panel thickness.
- honeycomb cylinder /
- global stability /
- critical load /
- elasto-plastic /
- Hamilton principle /
- finite element

HTML全文

图 1 蜂窝圆筒示意图

Figure 1. Schematic diagram of honeycomb cylinder

下载: 全尺寸图片幻灯片

图 2 蜂窝胞元排列方式

Figure 2. Honeycomb cell arrangement

下载: 全尺寸图片幻灯片

图 3 蜂窝单胞结构示意图

Figure 3. Schematic diagram of honeycomb single cell structure

下载: 全尺寸图片幻灯片

图 4 三明治夹芯等效法示意图

Figure 4. Schematic diagram of sandwich core equivalent method

下载: 全尺寸图片幻灯片

图 5 双线性硬化模型示意图

Figure 5. Schematic diagram of bilinear hardening model

下载: 全尺寸图片幻灯片

图 6 蜂窝圆筒轴压有限元分析模型

Figure 6. Finite element analysis model of honeycomb cylinder under axial compression

下载: 全尺寸图片幻灯片

图 7 蜂窝圆筒轴压实验现场

Figure 7. Honeycomb cylinder axial compression test site

下载: 全尺寸图片幻灯片

图 8 蜂窝圆筒轴压屈曲模式示意图

Figure 8. Schematic diagram of honeycomb cylinder buckling mode under axial compression

下载: 全尺寸图片幻灯片

图 9 蜂窝圆筒轴压实验载荷-位移曲线

Figure 9. Load-displacement curves of honeycomb cylindrical axial compression test

下载: 全尺寸图片幻灯片

图 10 蜂窝圆筒载荷-位移曲线汇总

Figure 10. Summary of honeycomb cylinder load-displacement curves

下载: 全尺寸图片幻灯片

图 11 蜂窝圆筒轴压临界载荷结果汇总

Figure 11. Summary of honeycomb cylinder axial compression critical load results

下载: 全尺寸图片幻灯片

图 12 几何参数变化对3种蜂窝圆筒临界载荷的影响

Figure 12. Influence of geometric parameters on critical loads of three kinds of honeycomb cylinders

下载: 全尺寸图片幻灯片

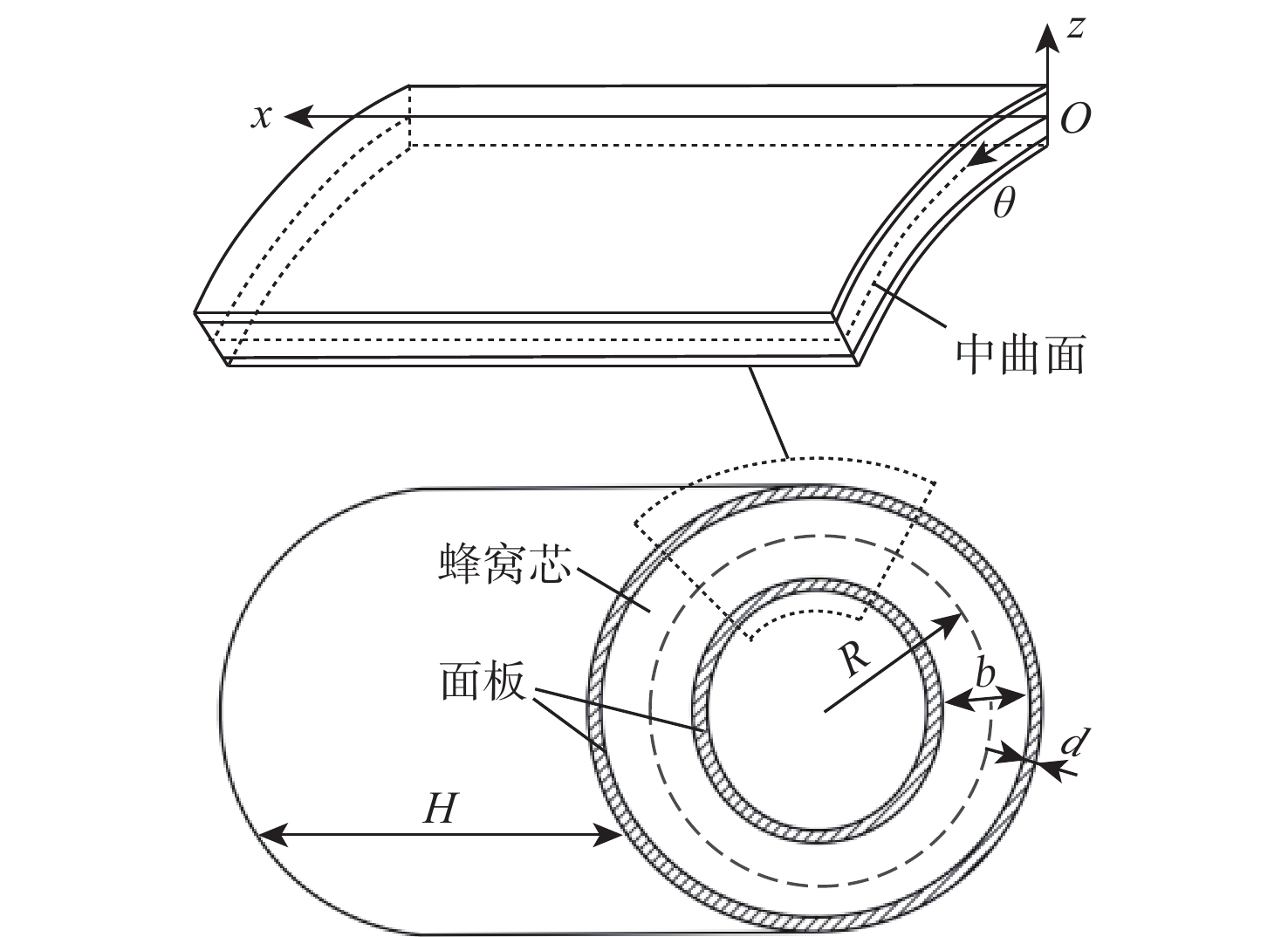
表 1 3种铝合金蜂窝圆筒的尺寸参数

Table 1. Dimensional parameters of three aluminum alloy honeycomb cylinders

圆筒编号	b/mm	d/mm	R/mm	H/mm	t/mm	l₀/mm
圆筒1	12.6	1.2	692.5	1100	0.2	6
圆筒2	22.6	1.2	687.5	1100	0.2	6
圆筒3	37.6	1.2	1140	1100	0.2	6

下载: 导出CSV

表 2 面板和蜂窝芯材料的弹性参数

Table 2. Elastic parameters of panel and honeycomb core materials

材料名称	弹性模量/MPa	泊松比	密度/（kg·m⁻³）
6A02	63000	0.33	2700
3003	69000	0.33	2730

下载: 导出CSV

表 3 蜂窝圆筒的蜂窝芯等效参数

Table 3. Equivalent parameters of honeycomb core of honeycomb cylinder

等效参数	圆筒1	圆筒2	圆筒3
E_ex/MPa	5.6926	5.5361	5.5350
E_eθ/MPa	5.8955	5.9062	5.9062
E_ez/MPa	3533.1	3526.6	3526.6
G_exθ /MPa	3.4896	3.4482	3.4479
G_exz/MPa	984.811	973.845	973.763
G_eθz/MPa	500.343	501.247	501.254
μ_exθ	0.997	0.997	0.997
μ_exz	5.32×10⁻⁴	5.18×10⁻⁴	5.18×10⁻⁴
μ_eθz	5.51×10⁻⁴	5.53×10⁻⁴	5.53×10⁻⁴
ρ_e/(kg·m⁻³)	139.31	138.67	138.66

下载: 导出CSV

表 4 质量变化率由−10%～+10%时临界载荷的变化率

Table 4. Critical load change rate when mass change rate is from −10% to +10%

参数	临界载荷变化率/%			平均值/%
参数	圆筒1	圆筒2	圆筒3	平均值/%
芯子厚度	+16.7	+17.1	+9.88	+14.6
面板厚度	+29.8	+36.1	+46.6	+37.5
圆筒半径	+18.1	+16.1	+14.6	+16.3
圆筒高度	−0.06	−0.25	+1.12	+0.27

下载: 导出CSV

表 5 蜂窝圆筒尺寸参数与临界载荷的相关系数

Table 5. Correlation coefficient between dimension parameters and critical load of honeycomb cylinder

参数	相关系数			平均值
参数	圆筒1	圆筒2	圆筒3	平均值
芯子厚度	0.999 9	0.999 0	0.998 6	0.999 2
面板厚度	0.999 9	0.999 9	0.999 9	0.999 9
圆筒半径	0.999 9	0.999 9	0.999 9	0.999 9
圆筒高度	−0.545 7	0.648 5	0.926 8	0.343 2

下载: 导出CSV

参考文献(28)

[1]	HUANG S Z, JIN Z Y, CHEN Y. Underwater blast resistance of double cylindrical shells with circular tube stiffeners[J]. Ocean Engineering, 2021, 238: 109691. doi: 10.1016/j.oceaneng.2021.109691
[2]	TENG J G, HU Y M. Behaviour of FRP-jacketed circular steel tubes and cylindrical shells under axial compression[J]. Construction and Building Materials, 2007, 21(4): 827-838. doi: 10.1016/j.conbuildmat.2006.06.016
[3]	LAN X K, FENG S S, HUANG Q, et al. A comparative study of blast resistance of cylindrical sandwich panels with aluminum foam and auxetic honeycomb cores[J]. Aerospace Science and Technology, 2019, 87: 37-47. doi: 10.1016/j.ast.2019.01.031
[4]	CAI L C, ZHANG D Y, ZHOU S H, et al. Investigation on mechanical properties and equivalent model of aluminum honeycomb sandwich panels[J]. Journal of Materials Engineering and Performance, 2018, 27(12): 6585-6596. doi: 10.1007/s11665-018-3771-2
[5]	骆洪志, 郭彦明, 吴会强. 直径五米大型箭体结构设计与优化[J]. 深空探测学报(中英文), 2021, 8(4): 380-388. LUO H Z, GUO Y M, WU H Q. Structural design and optimization of Φ5 m diameter large arrow body[J]. Journal of Deep Space Exploration, 2021, 8(4): 380-388(in Chinese).
[6]	LI Q, YANG D Q, MAO X. Pressure-resistant cylindrical shell structures comprising graded hybrid zero Poisson’s ratio metamaterials with designated band gap characteristics[J]. Marine Structures, 2022, 84: 103221. doi: 10.1016/j.marstruc.2022.103221
[7]	TIWARI G, KHAIRE N. Ballistic performance and energy dissipation characteristics of cylindrical honeycomb sandwich structure[J]. International Journal of Impact Engineering, 2022, 160: 104065. doi: 10.1016/j.ijimpeng.2021.104065
[8]	ALMROTH B O, BURNS A B, PITTNER E V. Design criteria for axially loaded cylindrical shells[J]. Journal of Spacecraft and Rockets, 1970, 7(6): 714-720. doi: 10.2514/3.30025
[9]	祝恩淳, MANDAL P, CALLADINE C R. 轴压圆柱薄壳的屈曲分析[J]. 土木工程学报, 2001, 34(3): 18-22. doi: 10.3321/j.issn:1000-131X.2001.03.004 ZHU E C, MANDAL P, CALLADINE C R. Analysis of buckling of thin cylindrical shells under axial compression[J]. China Civil Engineering Journal, 2001, 34(3): 18-22(in Chinese). doi: 10.3321/j.issn:1000-131X.2001.03.004
[10]	ANSARI Q M, TRINH L C, ZUCCO G, et al. Effect of elastic support on the linear buckling response of quasi-isotropic cylindrical shells under axial compression[J]. Engineering Structures, 2021, 244: 112796. doi: 10.1016/j.engstruct.2021.112796
[11]	LAI A D, JIA J F, ZHOU Z H, et al. Homotopic analysis for post-buckling of cylindrical shells with local thickness defects[J]. Acta Astronautica, 2022, 193: 44-55. doi: 10.1016/j.actaastro.2022.01.005
[12]	SHAMASS R, ALFANO G, GUARRACINO F. A numerical investigation into the plastic buckling paradox for circular cylindrical shells under axial compression[J]. Engineering Structures, 2014, 75: 429-447. doi: 10.1016/j.engstruct.2014.05.050
[13]	LEGENDRE J, LE GROGNEC P, DOUDARD C, et al. Analytical, numerical and experimental study of the plastic buckling behavior of thick cylindrical tubes under axial compression[J]. International Journal of Mechanical Sciences, 2019, 156: 494-505. doi: 10.1016/j.ijmecsci.2019.03.002
[14]	EVKIN A, LYKHACHOVA O. Energy barrier method for estimation of design buckling load of axially compressed elasto-plastic cylindrical shells[J]. Thin-Walled Structures, 2021, 161: 107454. doi: 10.1016/j.tws.2021.107454
[15]	RAJABIEHFARD R, DARVIZEH A, ALITAVOLI M, et al. Experimental and numerical investigation of dynamic plastic behavior of tube with different thickness distribution under axial impact[J]. Thin-Walled Structures, 2016, 109: 174-184. doi: 10.1016/j.tws.2016.08.017
[16]	张靖华, 郑武. 功能梯度圆柱壳的弹塑性屈曲[J]. 兰州理工大学学报, 2021, 47(5): 167-172. doi: 10.3969/j.issn.1673-5196.2021.05.025 ZHANG J H, ZHENG W. Elastoplastic buckling of functionally graded cylindrical shells[J]. Journal of Lanzhou University of Technology, 2021, 47(5): 167-172(in Chinese). doi: 10.3969/j.issn.1673-5196.2021.05.025
[17]	HOU X H, ZHOU S Q, CHENG Z W, et al. Buckling of regular and auxetic honeycombs under a general macroscopic stress state in symplectic system[J]. Applied Mathematical Modelling, 2022, 109: 318-340. doi: 10.1016/j.apm.2022.04.033
[18]	ZHANG C W, EYVAZIAN A, ALKHEDHER M, et al. Modified couple stress theory application to analyze mechanical buckling behavior of three-layer rectangular microplates with honeycomb core and piezoelectric face sheets[J]. Composite Structures, 2022, 292: 115582. doi: 10.1016/j.compstruct.2022.115582
[19]	赵杰, 张娟, 蒋晓琴, 等. 不同压缩工况下焊接缺陷对钎焊铝蜂窝板承载能力的影响[J]. 机械工程材料, 2020, 44(12): 97-102. ZHAO J, ZHANG J, JIANG X Q, et al. Influence of welding defects on bearing capacity of brazed aluminum honeycomb panel under different compression conditions[J]. Materials for Mechanical Engineering, 2020, 44(12): 97-102(in Chinese).
[20]	王宝芹, 王沫楠, 刘长喜. 基于多尺度方法的蜂窝夹层复合材料结构轴向压缩稳定性[J]. 复合材料学报, 2020, 37(3): 601-608. WANG B Q, WANG M N, LIU C X. Stability of honeycomb sandwich composite structure under axial compression based on multi-scale method[J]. Acta Materiae Compositae Sinica, 2020, 37(3): 601-608(in Chinese).
[21]	ZHANG Z J, WANG Y J, HUANG L, et al. Mechanical behaviors and failure modes of sandwich cylinders with square honeycomb cores under axial compression[J]. Thin-Walled Structures, 2022, 172: 108868. doi: 10.1016/j.tws.2021.108868
[22]	PAN D R, CHEN L, ZHAO Q L, et al. Local buckling theoretical calculation method of the FRP foam sandwich cylinder under axial compression[J]. Composite Structures, 2020, 246: 112371. doi: 10.1016/j.compstruct.2020.112371
[23]	王颖坚, 徐颖. 复合材料夹层板的塑性屈曲[J]. 北京大学学报(自然科学版), 1993, 29(1): 48-56. WANG Y J, XU Y. Plastic buckling of composite sandwich plates[J]. Acta Scicentiarum Naturalum Universitis Pekinesis, 1993, 29(1): 48-56(in Chinese).
[24]	刘强, 黄争呜. 金属蜂窝材料的弹塑性屈曲临界应力值[J]. 力学季刊, 2008, 29(4): 515-520. LIU Q, HUANG Z W. Elasto-plastic buckling critical stress of metal honeycomb[J]. Chinese Quarterly of Mechanics, 2008, 29(4): 515-520(in Chinese).
[25]	李贤冰, 温激鸿, 郁殿龙, 等. 蜂窝夹层板力学等效方法对比研究[J]. 玻璃钢/复合材料, 2012(增刊1): 11-15. LI X B, WEN J H, YU D L, et al. The comparative study of equivalent mechanical methods on honeycomb sandwich plate[J]. Composites Science and Engineering, 2012(Sup 1): 11-15(in Chinese).
[26]	沈元星, 侯文彬. 基于双曲面蜂窝夹层结构等效模型的研究及数值分析[J]. 计算力学学报, 2022, 39(2): 209-215. SHEN Y X, HOU W B. Equivalent models research and numerical analysis based on double curved honeycomb sandwich structure[J]. Chinese Journal of Computational Mechanics, 2022, 39(2): 209-215(in Chinese).
[27]	陈明祥. 弹塑性力学[M]. 北京: 科学出版社, 2007: 278-281. CHEN M X. Elasticity and plasticity[M]. Beijing: Science Press, 2007: 278-281(in Chinese).
[28]	闻邦椿. 机械设计手册(第1卷)[M]. 5版. 北京: 机械工业出版社, 2010: 25-26. WEN B C. Machine design handbook (Vol. 1)[M]. 5th ed. Beijing: China Machine Press, 2010: 25-26(in Chinese).