基于SSA-IWT-EMD的滚动轴承故障诊断方法

雷春丽; 焦孟萱; 樊高峰; 刘世超; 薛林林; 李建华

doi:10.13700/j.bh.1001-5965.2023.0174

基于SSA-IWT-EMD的滚动轴承故障诊断方法

doi: 10.13700/j.bh.1001-5965.2023.0174

1.
兰州理工大学机电工程学院，兰州 730050
2.
中石化英力士（天津）石化有限公司，天津 300280
3.
云南文山铝业有限公司，文山 663000

基金项目: 国家自然科学基金(51465035)；甘肃省自然科学基金(20JR5RA466)；兰州理工大学红柳一流学科建设项目

详细信息

通讯作者:
E-mail：li_jh@vip.sina.com

中图分类号: TH133.33
计量
- 文章访问数: 500
- HTML全文浏览量: 91
- PDF下载量: 4
- 被引次数: 0
出版历程
- 收稿日期: 2023-04-12
- 录用日期: 2023-06-30
- 网络出版日期: 2023-07-10
- 整期出版日期: 2025-04-30

Fault diagnosis method of rolling bearings based on SSA-IWT-EMD

1.
School of Mechanical and Electrical Engineering，Lanzhou University of Technology，Lanzhou 730050，China
2.
Ineos Sinopec Tianjin Petrochemicals Limited，Tianjin 300280，China
3.
Yunnan Wenshan Aluminum Co.，Ltd.，Wenshan 663000，China

Funds: National Natural Science Foundation of China (51465035); Natural Science Foundation of Gansu Province, China (20JR5RA466); Hongliu First-class Disciplines Development Program of Lanzhou University of Technology

More Information

Corresponding author: E-mail：li_jh@vip.sina.com

摘要

摘要:
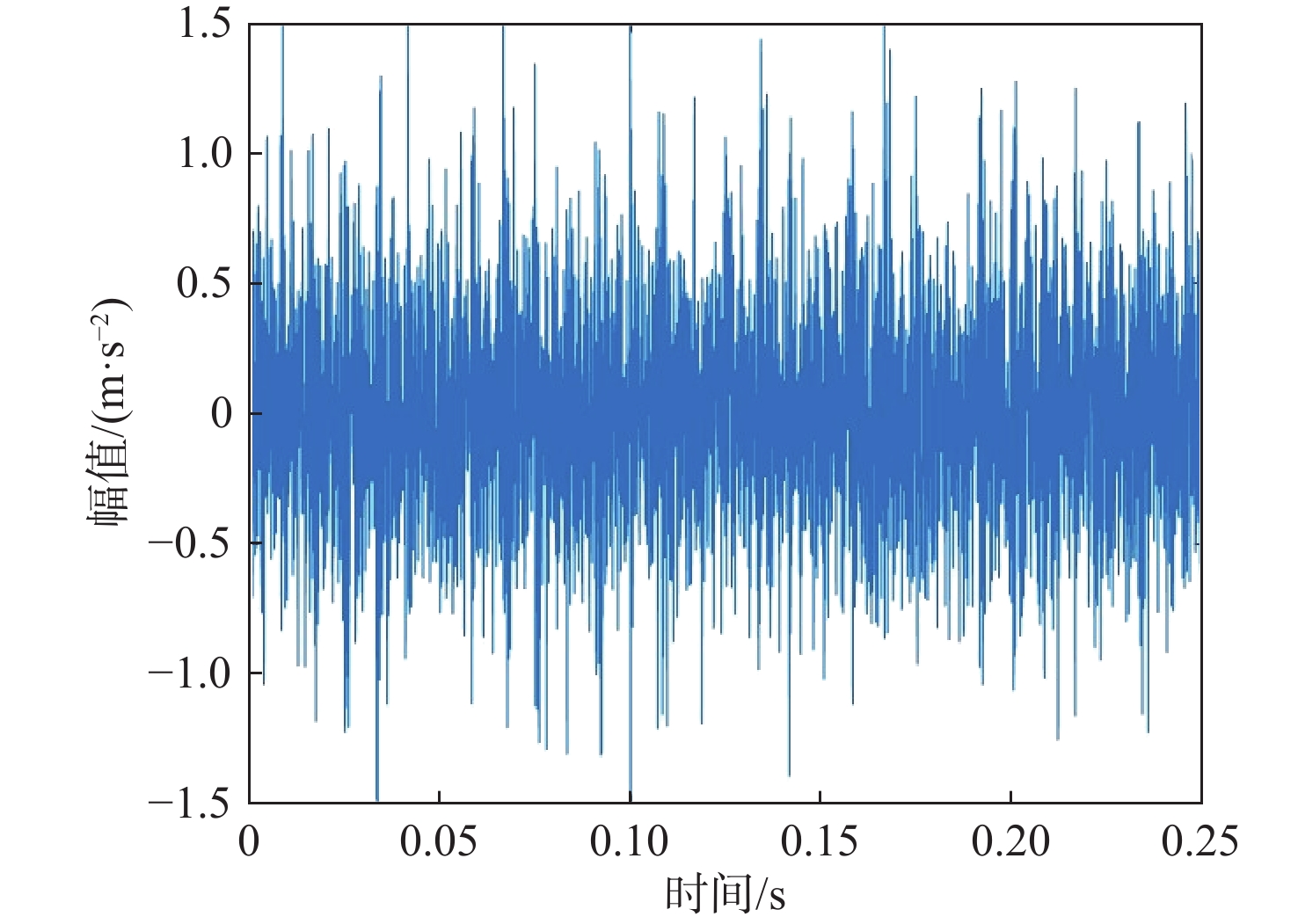
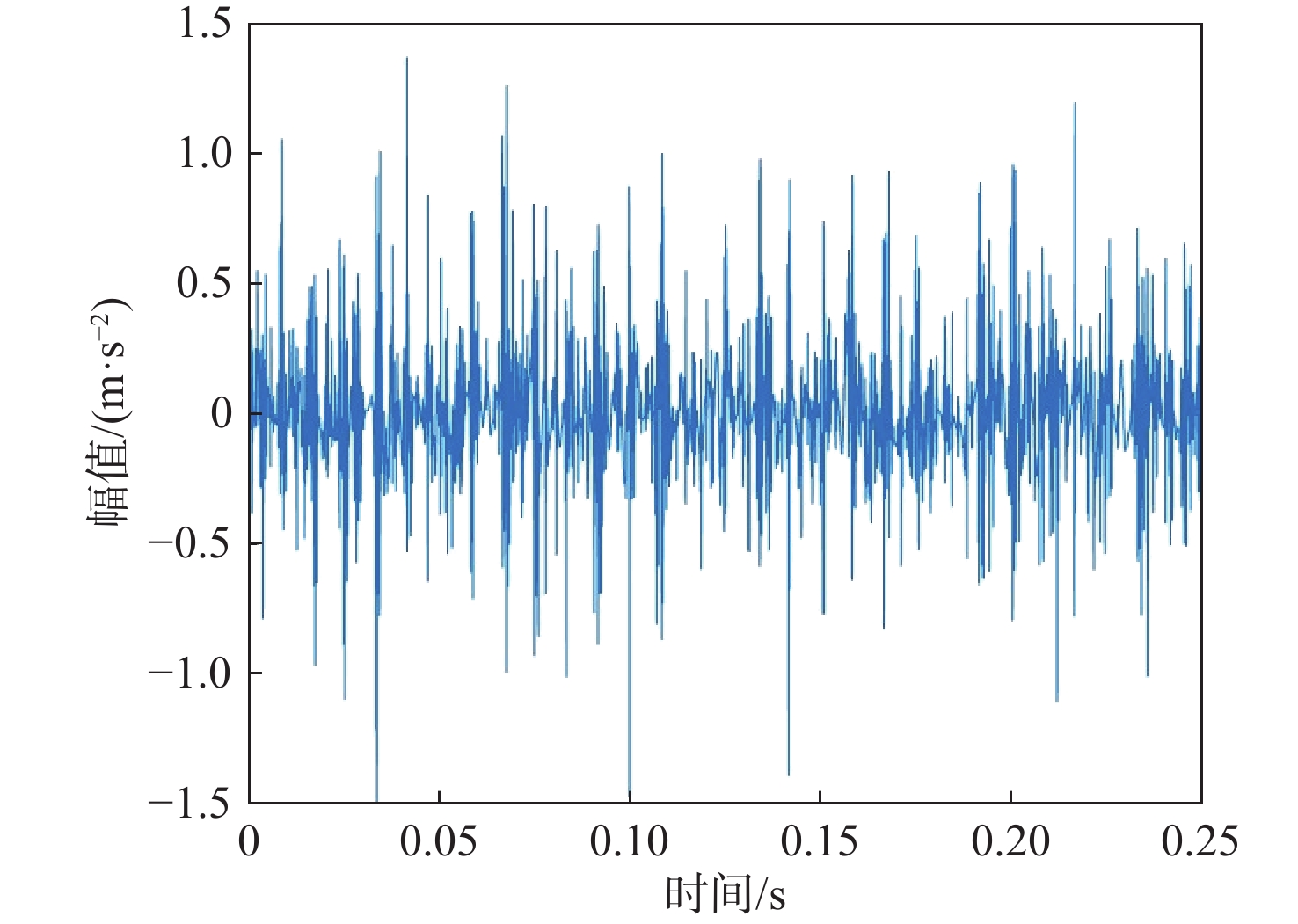
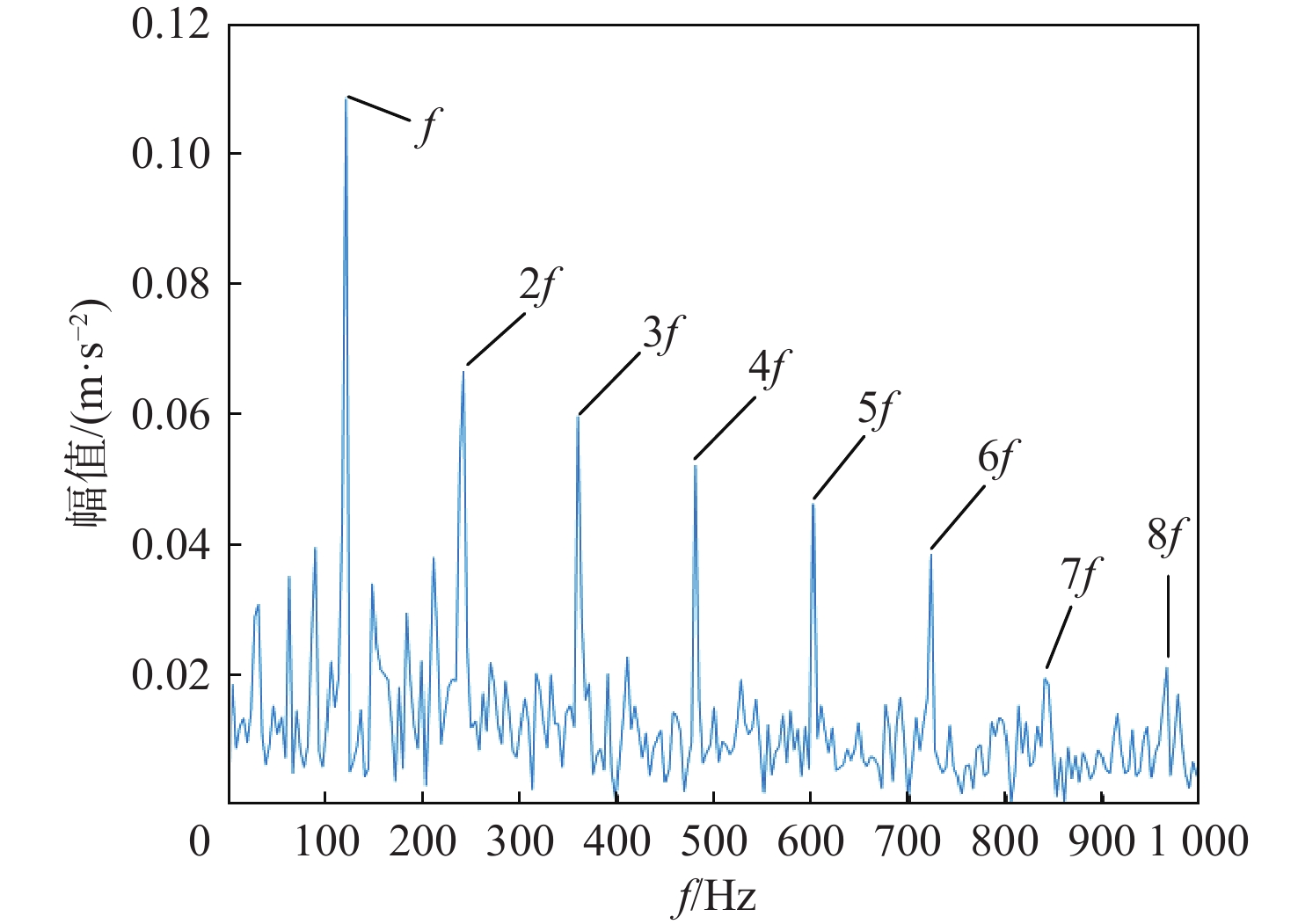
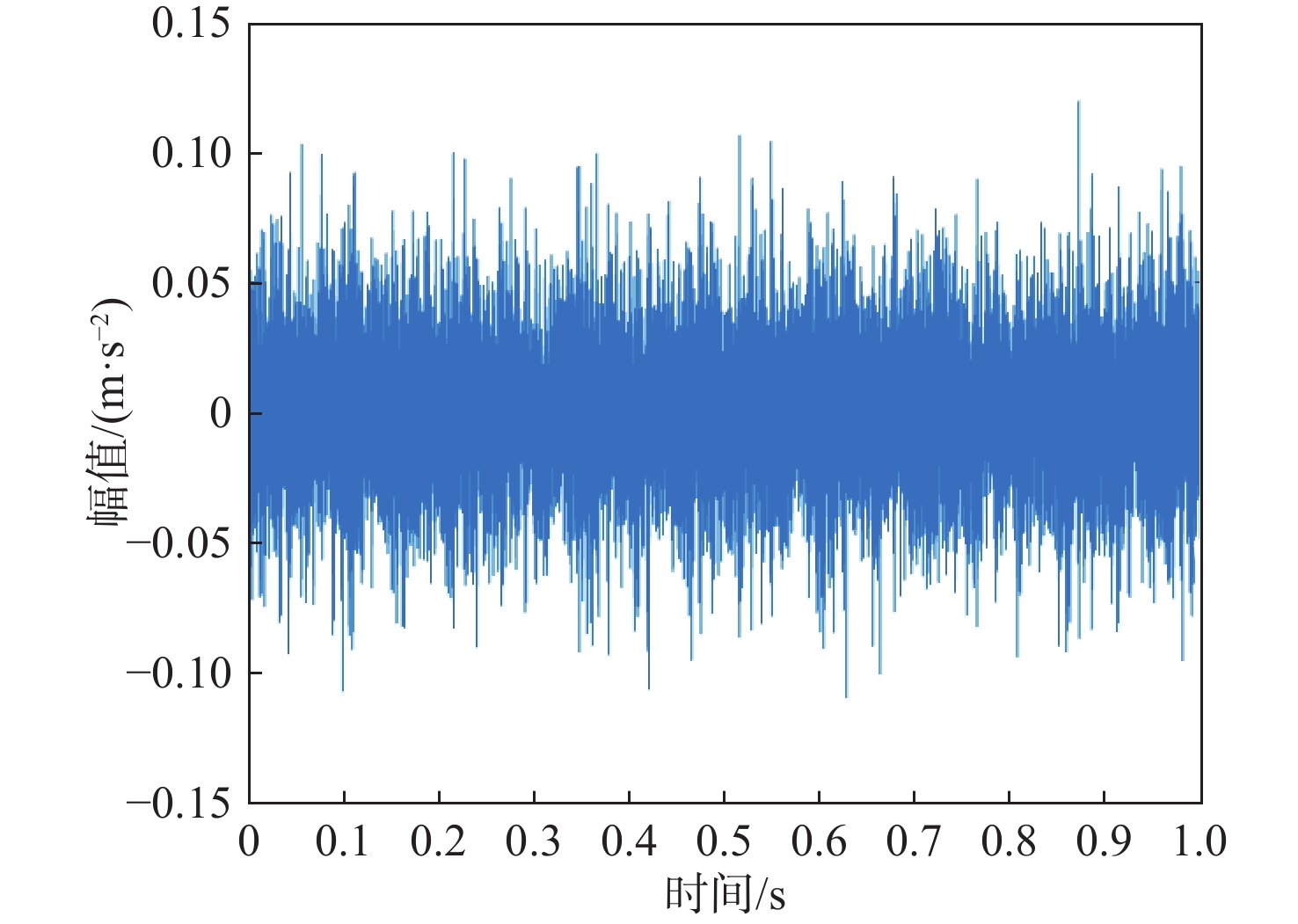
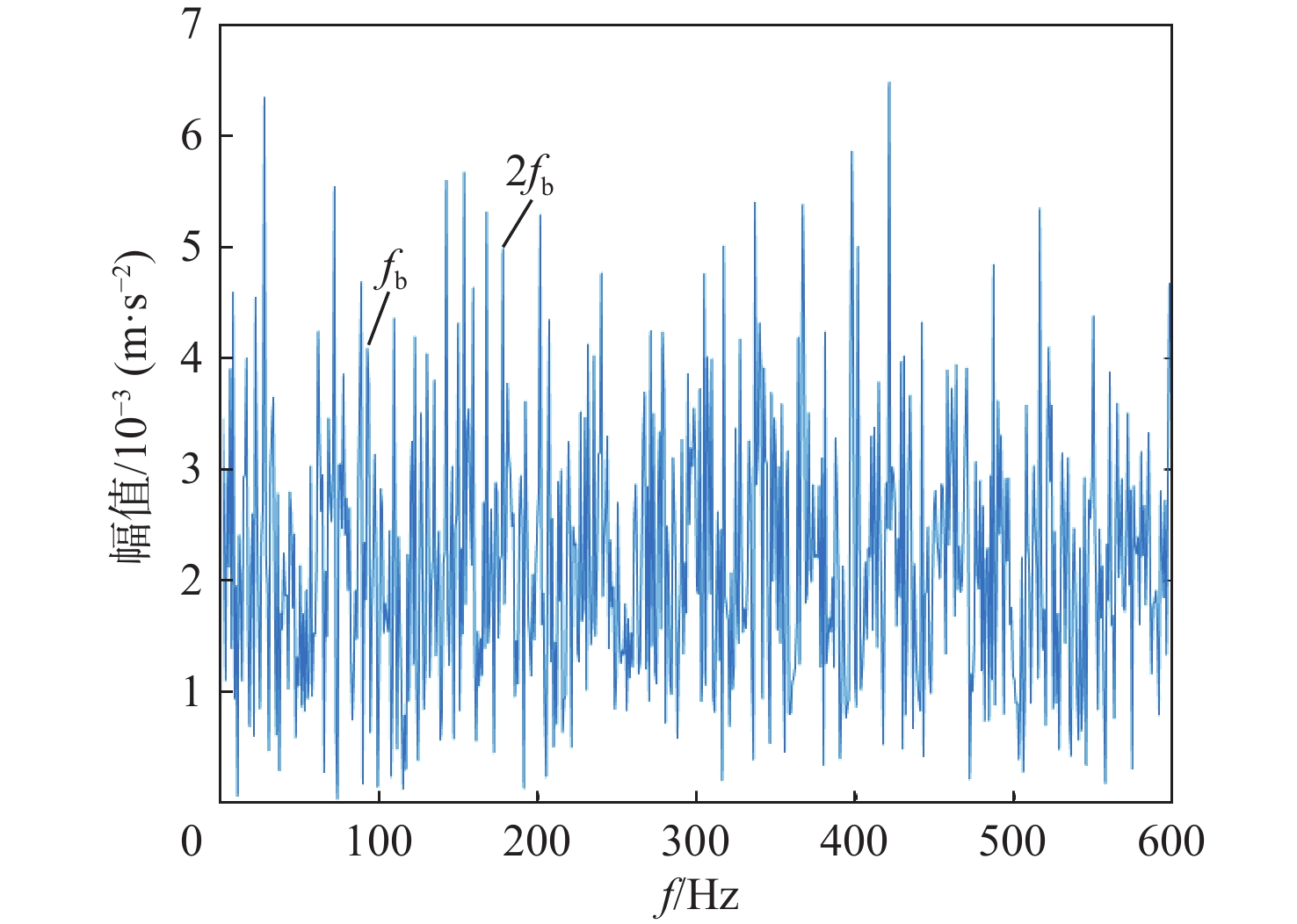
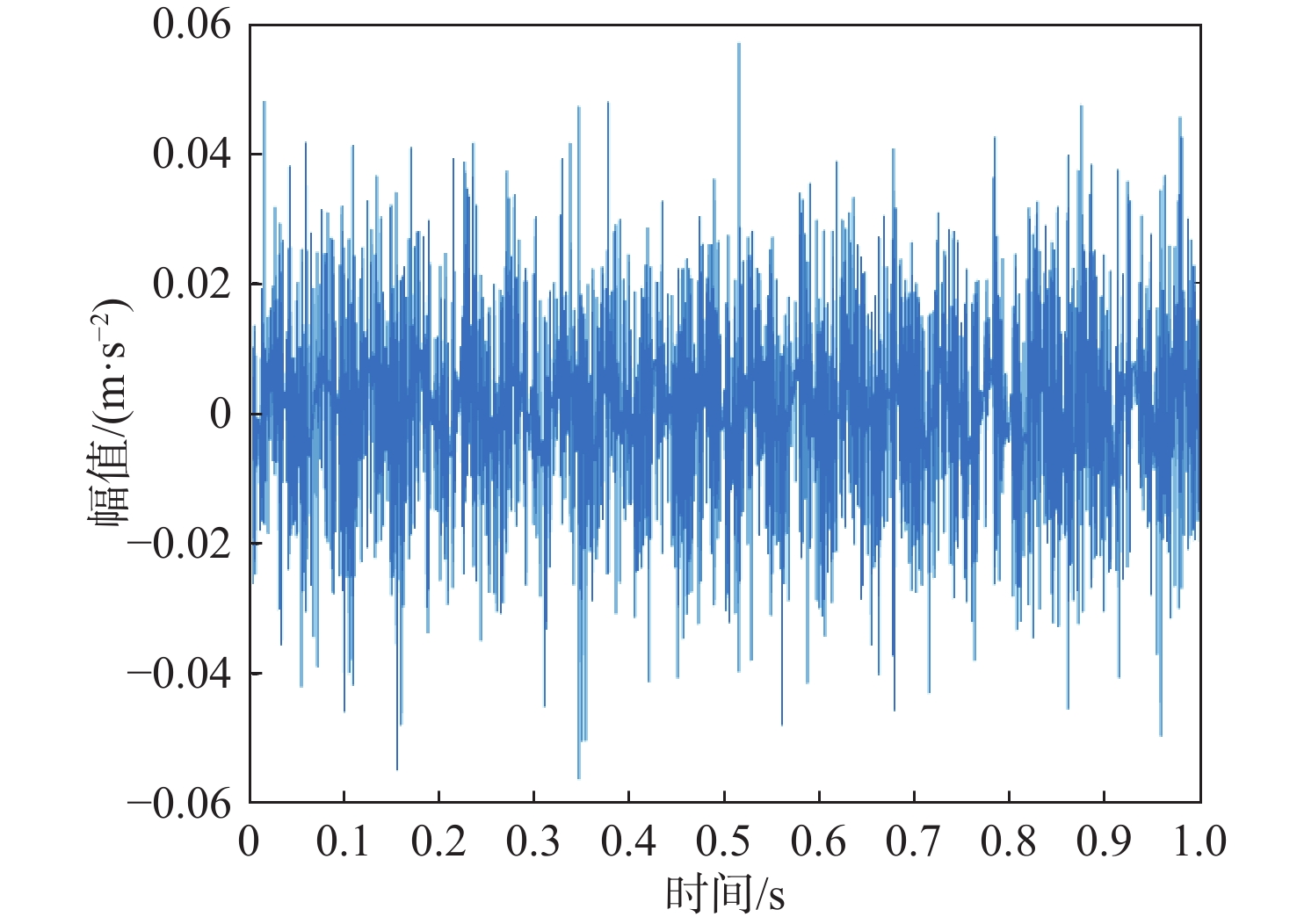
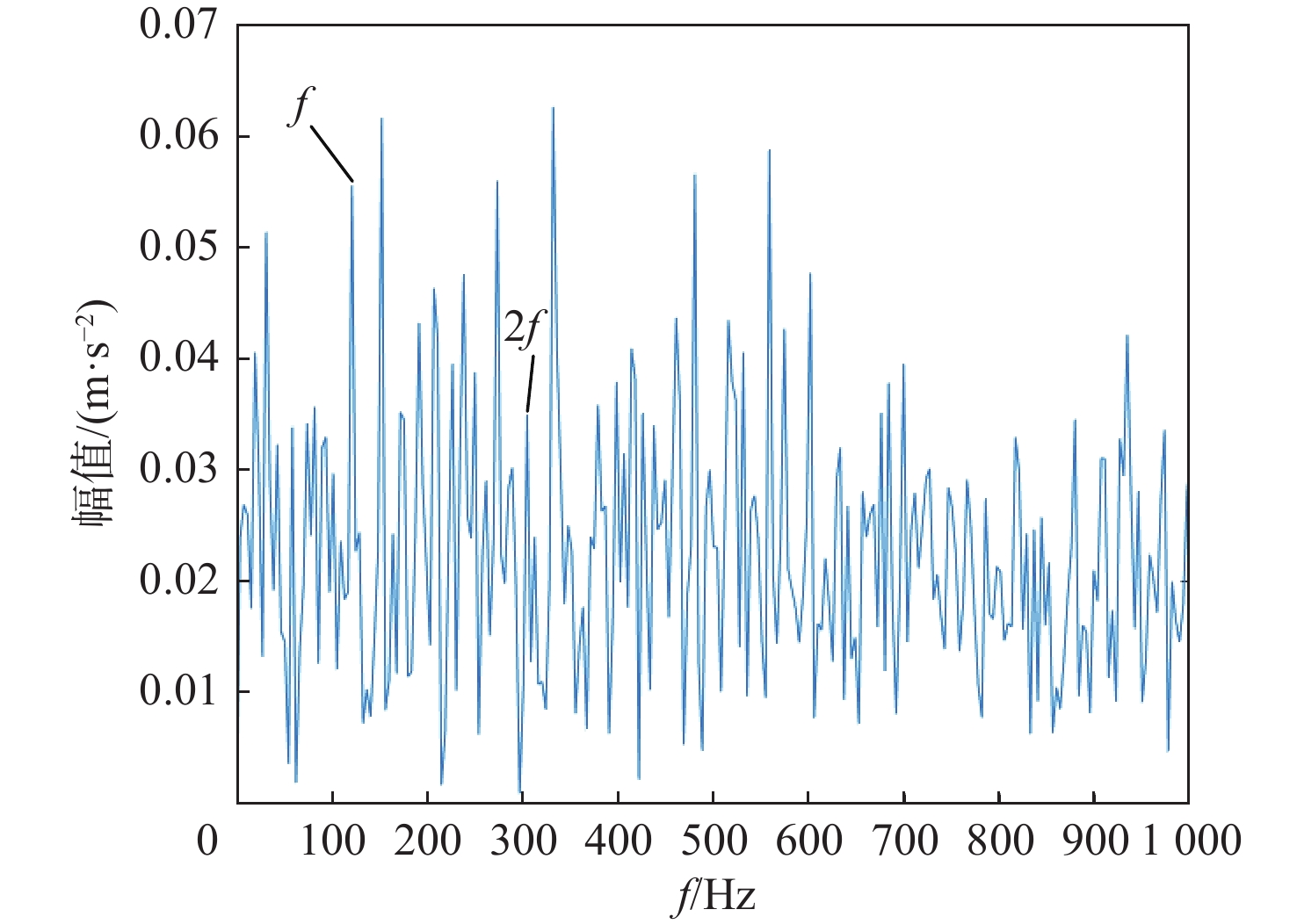
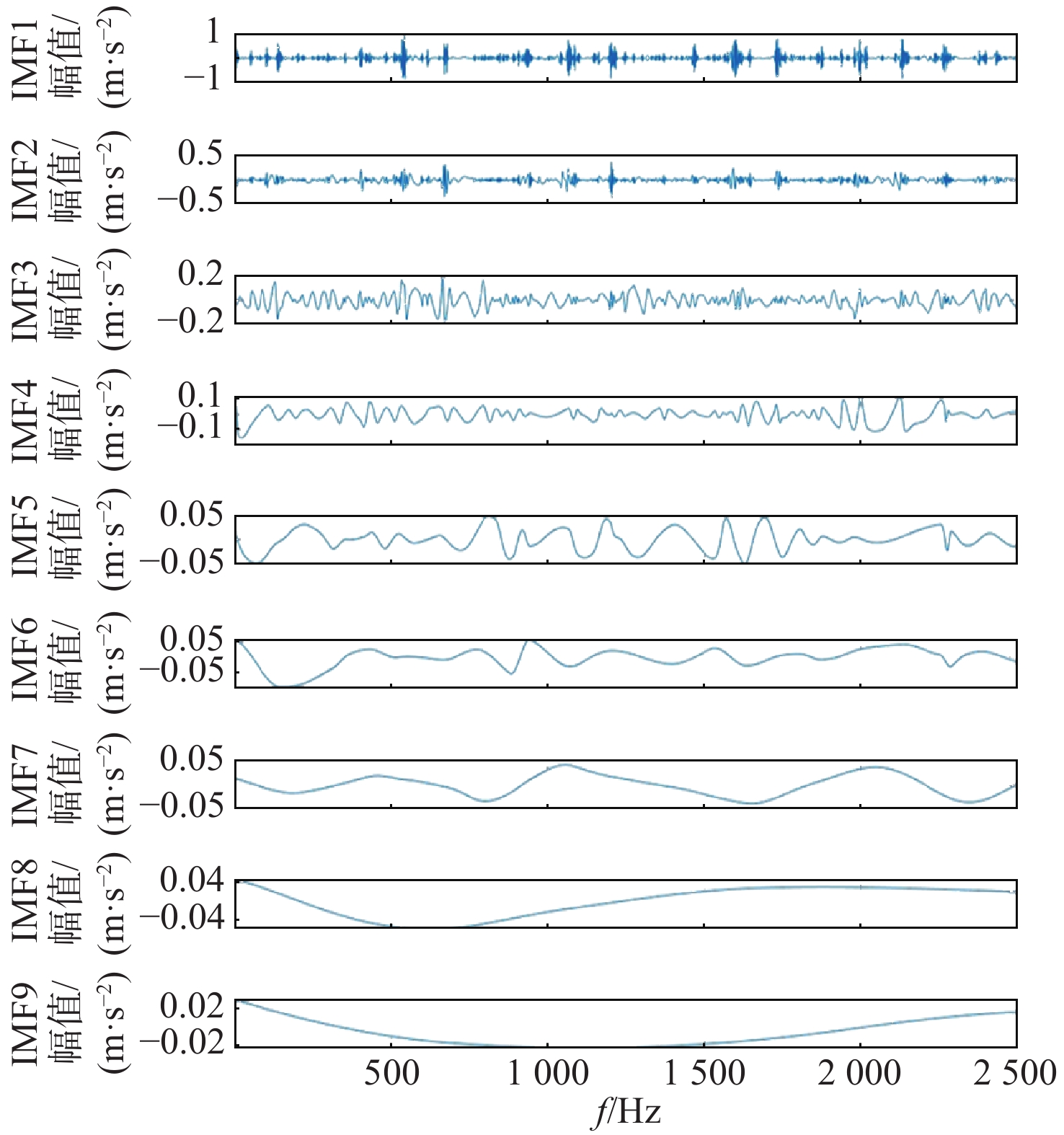
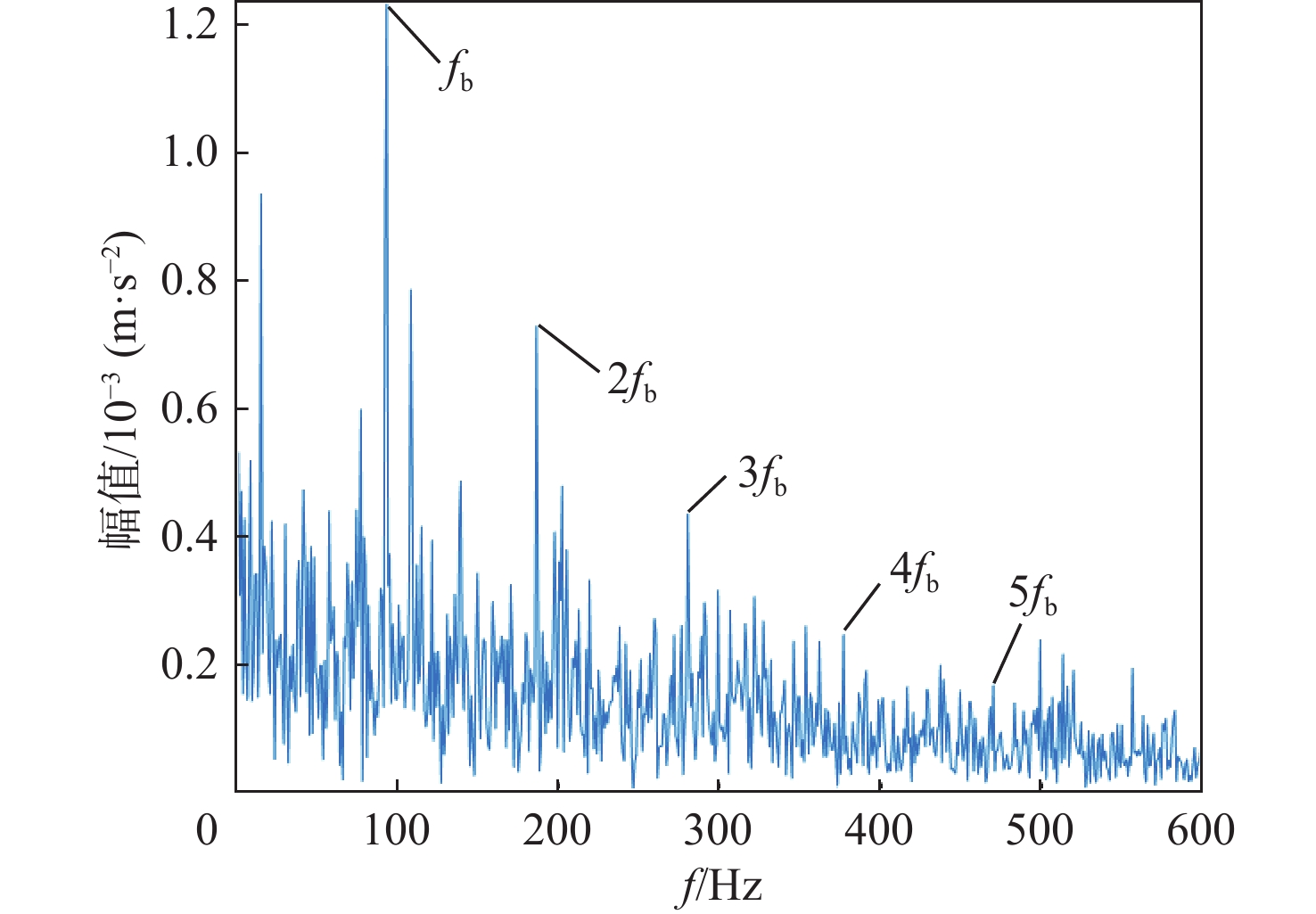
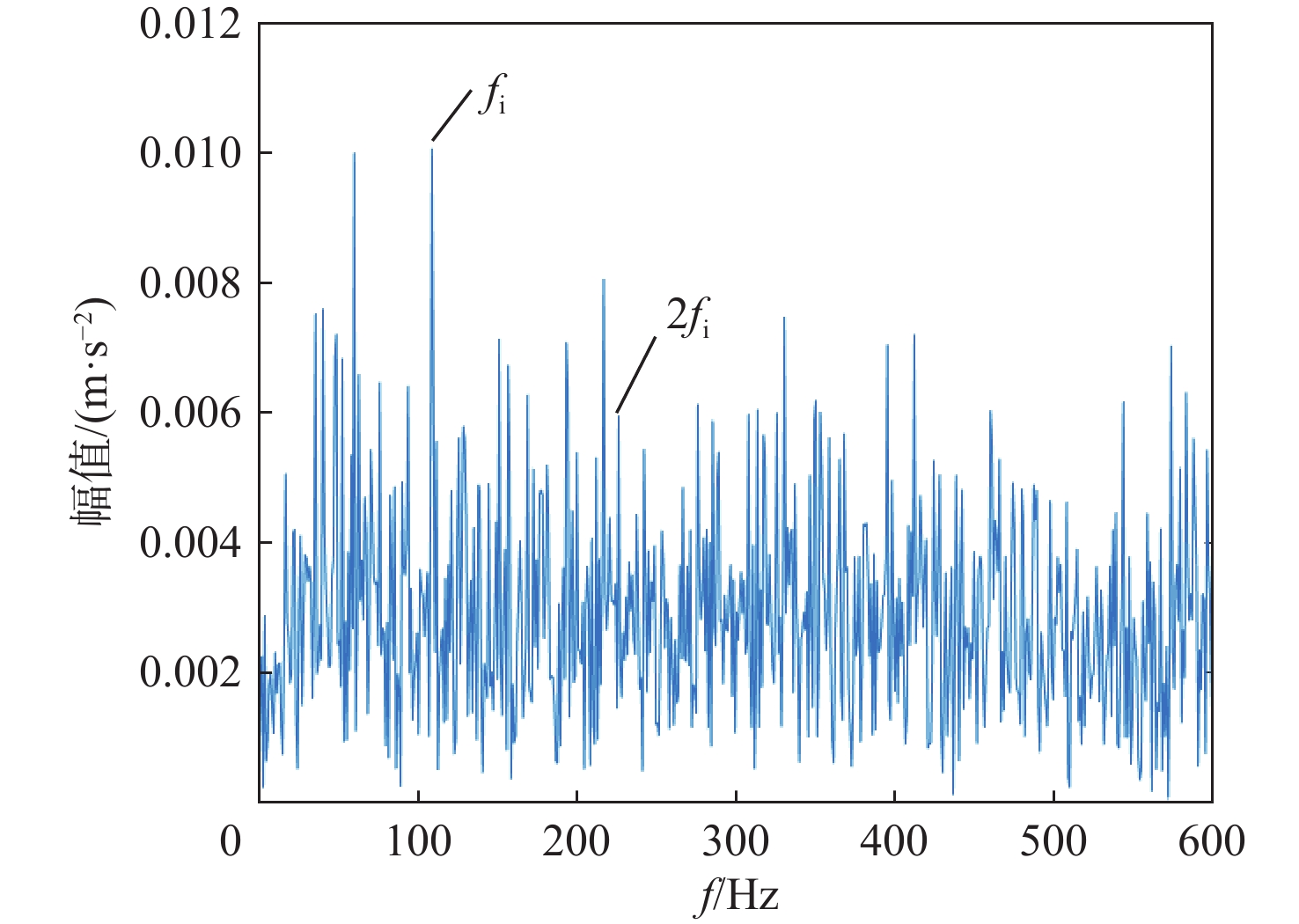
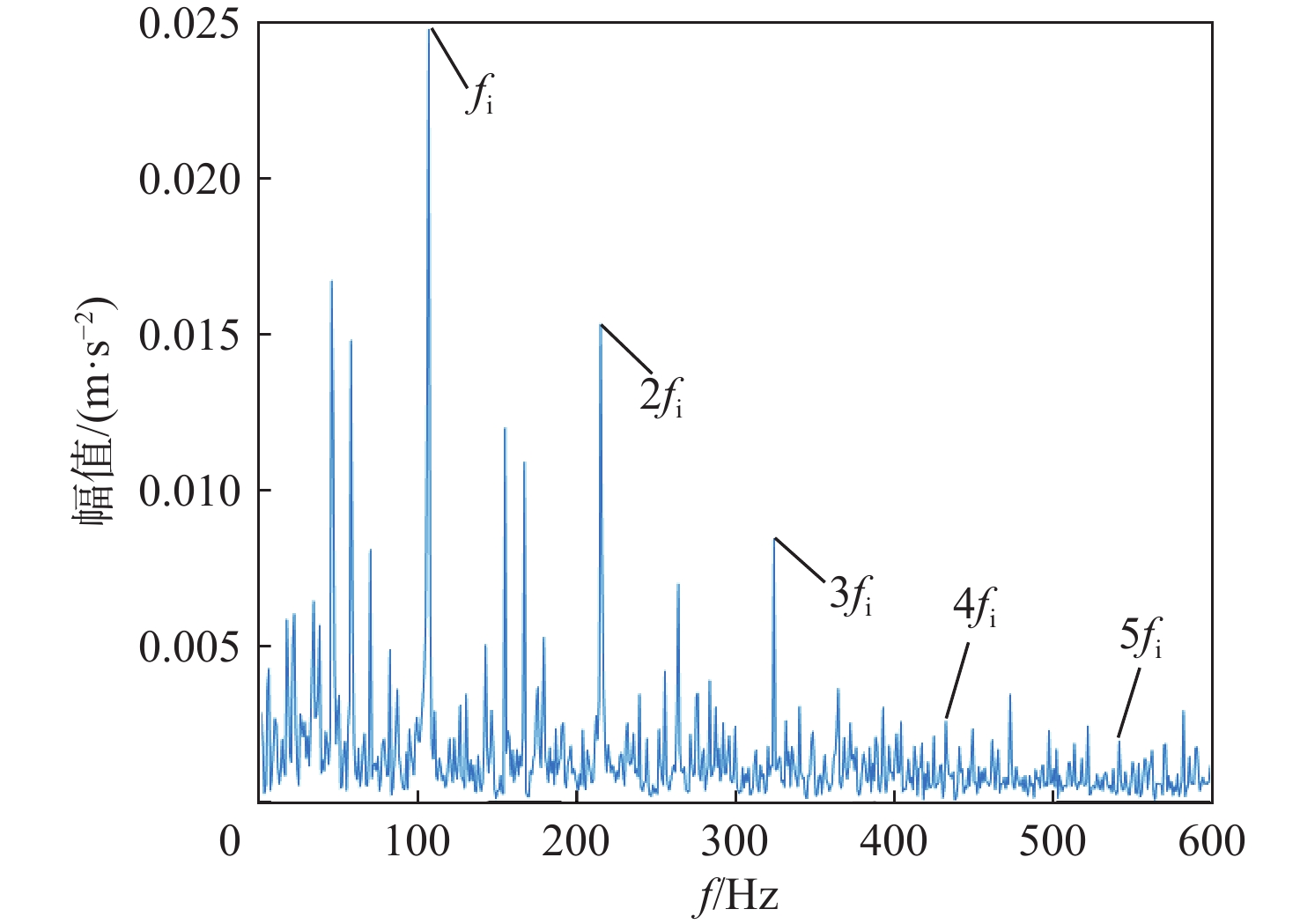
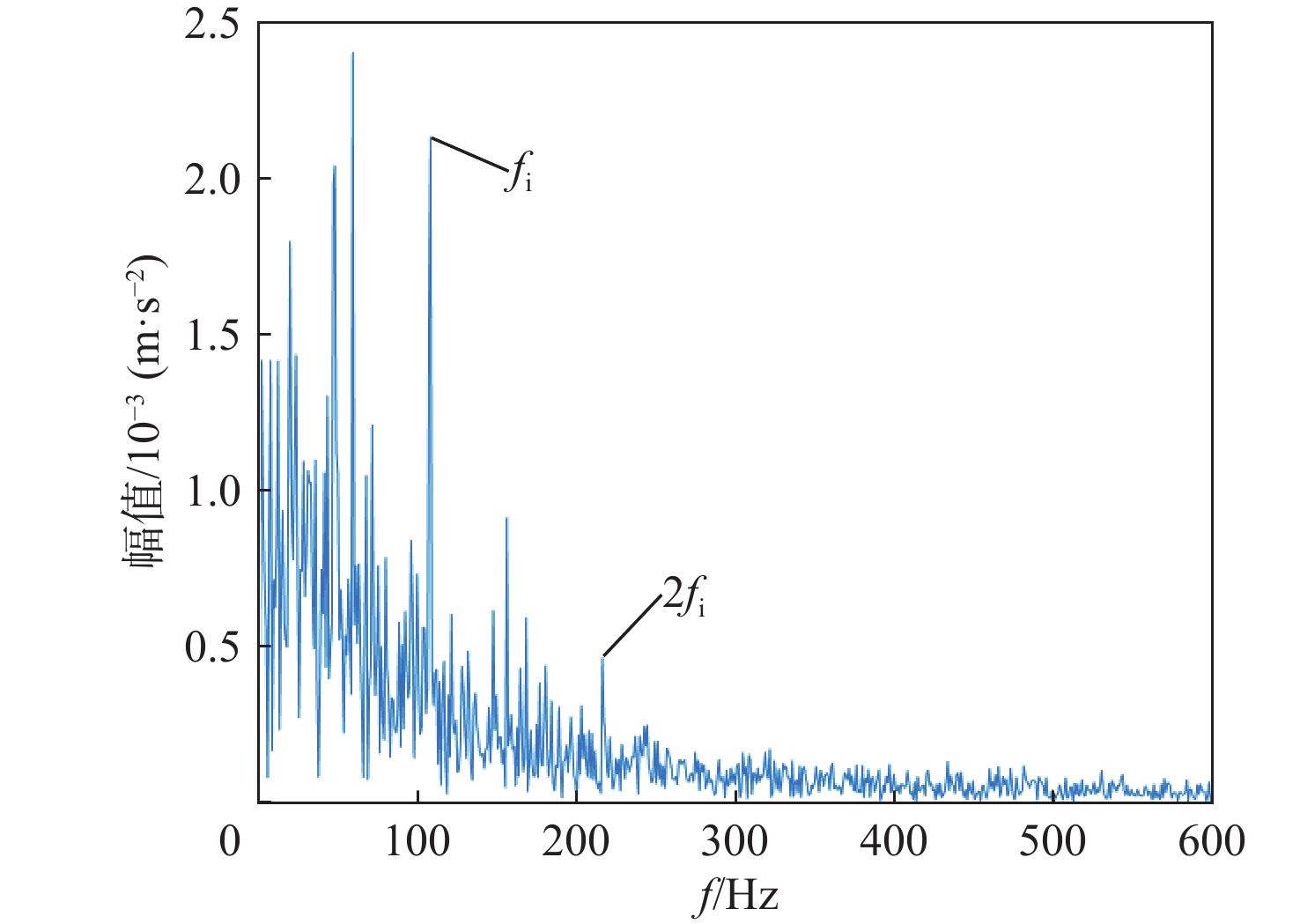
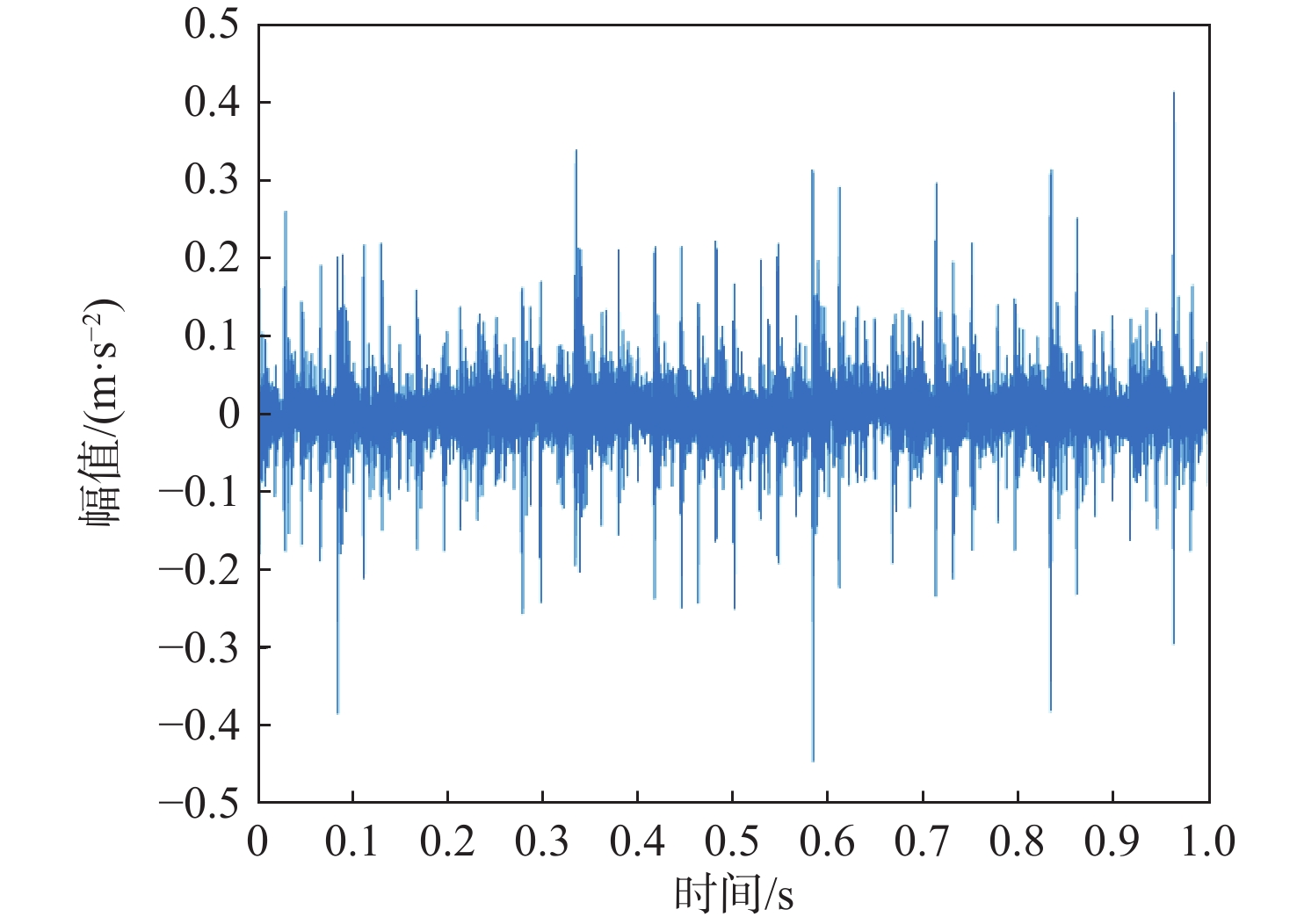
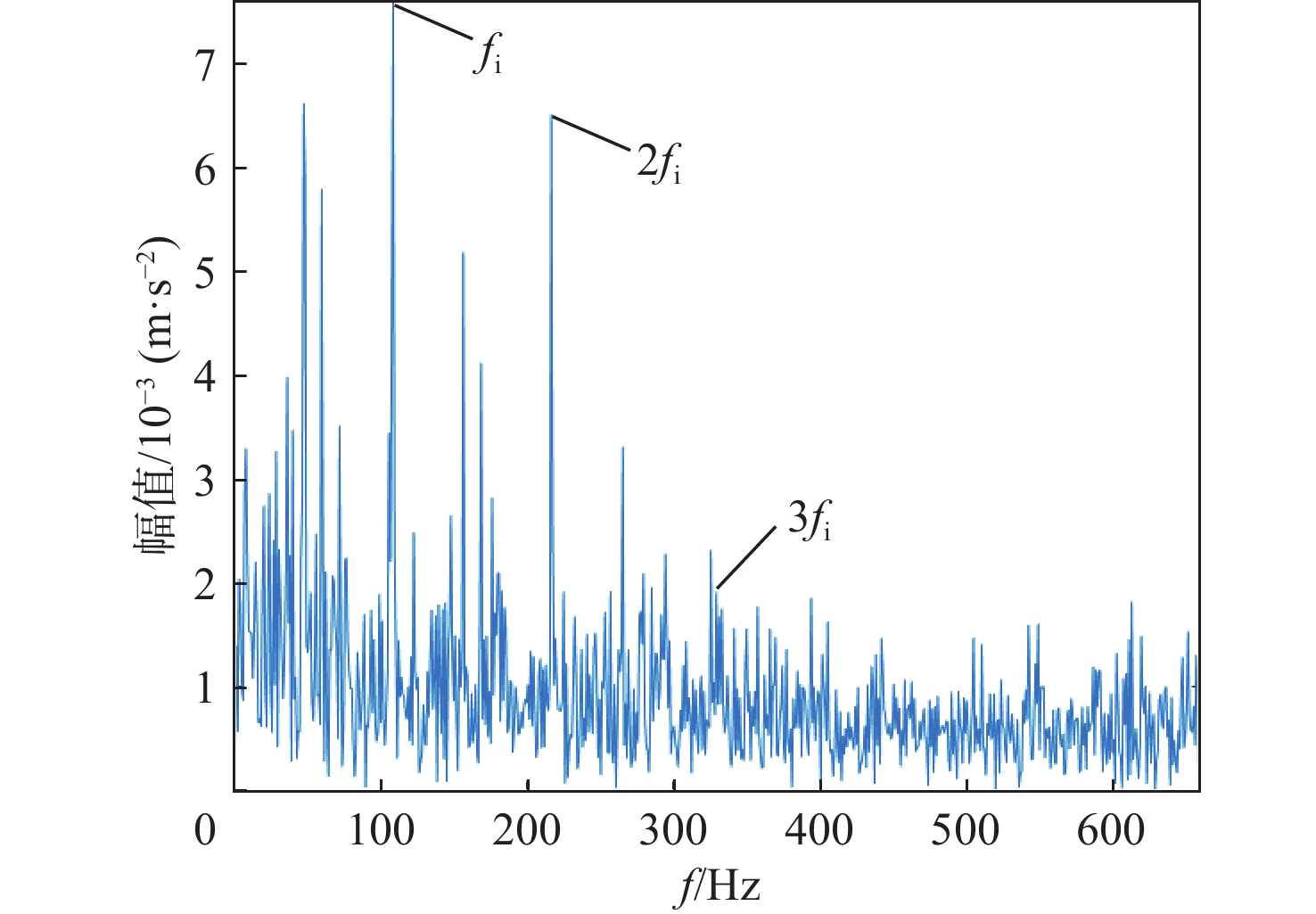
针对小波阈值降噪不充分及经验模态分解(EMD)特征频率提取不明显的问题，提出一种基于麻雀搜索算法-改进小波阈值-EMD(SSA-IWT-EMD)的滚动轴承故障诊断方法。引入2个调节因子，提出一种IWT函数，克服了传统软硬阈值的缺点，并运用SSA对其各参数进行全局寻优，实现滚动轴承信号降噪。提出一种综合指标P对EMD产生的分量进行选取重构，突出信号的故障特征信息。采用包络谱分析实现轴承的故障诊断。仿真和实测结果验证了所提方法的有效性；同时与单一指标选取分量的方法及文献方法进行对比，说明了综合指标P和所提方法具有更强的降噪能力及特征提取能力，包络谱幅值及倍频成分更明显，可以更好地实现对滚动轴承的故障诊断。
- 滚动轴承 /
- 改进阈值 /
- 综合指标 /
- 经验模态分解 /
- 故障诊断
Abstract:
Wavelet threshold denoising is insufficient, and feature frequency extraction of empirical mode decomposition (EMD) is unclear. To address these issues, a fault diagnosis method of rolling bearings based on sparrow search algorithm - improved wavelet threshold-EMD (SSA-IWT-EMD) was proposed. Firstly, two adjustment factors were introduced, and an IWT function was presented to overcome the shortcomings of traditional soft and hard thresholds. The SSA was used to globally optimize the parameters of the IWT to reduce the noise of rolling bearing signals. Secondly, a comprehensive index P was put forward to select and reconstruct the components generated by EMD, so as to highlight the fault feature information of the signals. Finally, the fault diagnosis of bearings was realized by envelope spectrum analysis. The simulation and experimental results verified the effectiveness of the proposed method. At the same time, the comparison with the single index component selection method and the literature method indicated that the comprehensive index P and the method proposed in this paper had stronger denoising ability and feature extraction ability, and the envelope spectrum amplitude and frequency doubling component were more obvious, which could better realize the fault diagnosis of rolling bearings.
- rolling bearing /
- improved threshold /
- comprehensive index /
- empirical mode decomposition /
- fault diagnosis

HTML全文

图 1 小波阈值去噪流程

Figure 1. Flow chart of wavelet threshold denoising

下载: 全尺寸图片幻灯片

图 2 基于SSA-IWT-EMD的滚动轴承故障诊断流程

Figure 2. Flow chart of fault diagnosis of rolling bearings based on SSA-IWT-EMD

下载: 全尺寸图片幻灯片

图 3 冲击信号

Figure 3. Impact signal

下载: 全尺寸图片幻灯片

图 4 仿真信号

Figure 4. Simulation signal

下载: 全尺寸图片幻灯片

图 5 原始仿真信号包络谱

Figure 5. Envelope spectrum of original simulation signal

下载: 全尺寸图片幻灯片

图 6 SSA-IWT优化后仿真信号

Figure 6. Simulation signal optimized by SSA-IWT

下载: 全尺寸图片幻灯片

图 7 仿真信号EMD分解图

Figure 7. EMD diagram of simulation signal

下载: 全尺寸图片幻灯片

图 8 SSA-IWT-EMD仿真信号包络谱

Figure 8. Envelope spectrum of SSA-IWT-EMD simulation signal

下载: 全尺寸图片幻灯片

图 9 MFS机械故障试验平台

Figure 9. MFS test platform for mechanical fault

下载: 全尺寸图片幻灯片

图 10 试验轴承原始信号1

Figure 10. Original signal 1 of test bearing

下载: 全尺寸图片幻灯片

图 11 原始试验轴承信号1包络谱

Figure 11. Envelope spectrum of original signal 1 of test bearing

下载: 全尺寸图片幻灯片

图 12 SSA-IWT优化后轴承信号1时域图

Figure 12. Time domain diagram of signal 1 of bearing optimized by SSA-IWT

下载: 全尺寸图片幻灯片

图 13 试验轴承信号1 EMD分解图

Figure 13. EMD diagram of signal 1 of test bearing

下载: 全尺寸图片幻灯片

图 14 试验轴承信号1包络谱

Figure 14. Envelope spectrum of signal 1 of test bearing

下载: 全尺寸图片幻灯片

图 15 试验轴承原始信号2

Figure 15. Original signal 2 of test bearing

下载: 全尺寸图片幻灯片

图 16 原始试验轴承信号2包络谱

Figure 16. Envelope spectrum of signal 2 of test bearing

下载: 全尺寸图片幻灯片

图 17 SSA-IWT优化后信号2

Figure 17. Signal 2 optimized by SSA-IWT

下载: 全尺寸图片幻灯片

图 18 试验轴承信号2 EMD分解图

Figure 18. EMD diagram of signal 2 of test bearing

下载: 全尺寸图片幻灯片

图 19 SSA-IWT-EMD试验轴承信号2包络谱

Figure 19. Envelope spectrum of signal 2 of bearing in SSA-IWT-EMD test

下载: 全尺寸图片幻灯片

图 20 峭度指标试验轴承信号2包络谱

Figure 20. Envelope spectrum of signal 2 of bearing in kurtosis indicator test

下载: 全尺寸图片幻灯片

图 21 文献[23]方法滤波后的实验轴承信号2

Figure 21. Signal 2 of test bearing filtered by literature [23] method

下载: 全尺寸图片幻灯片

图 22 文献[23]方法EMD分解图

Figure 22. EMD diagram of literature [23] method

下载: 全尺寸图片幻灯片

图 23 文献[23]方法实际轴承信号2包络谱

Figure 23. Envelope spectrum of signal 2 of actual bearing by literature [23] method

下载: 全尺寸图片幻灯片

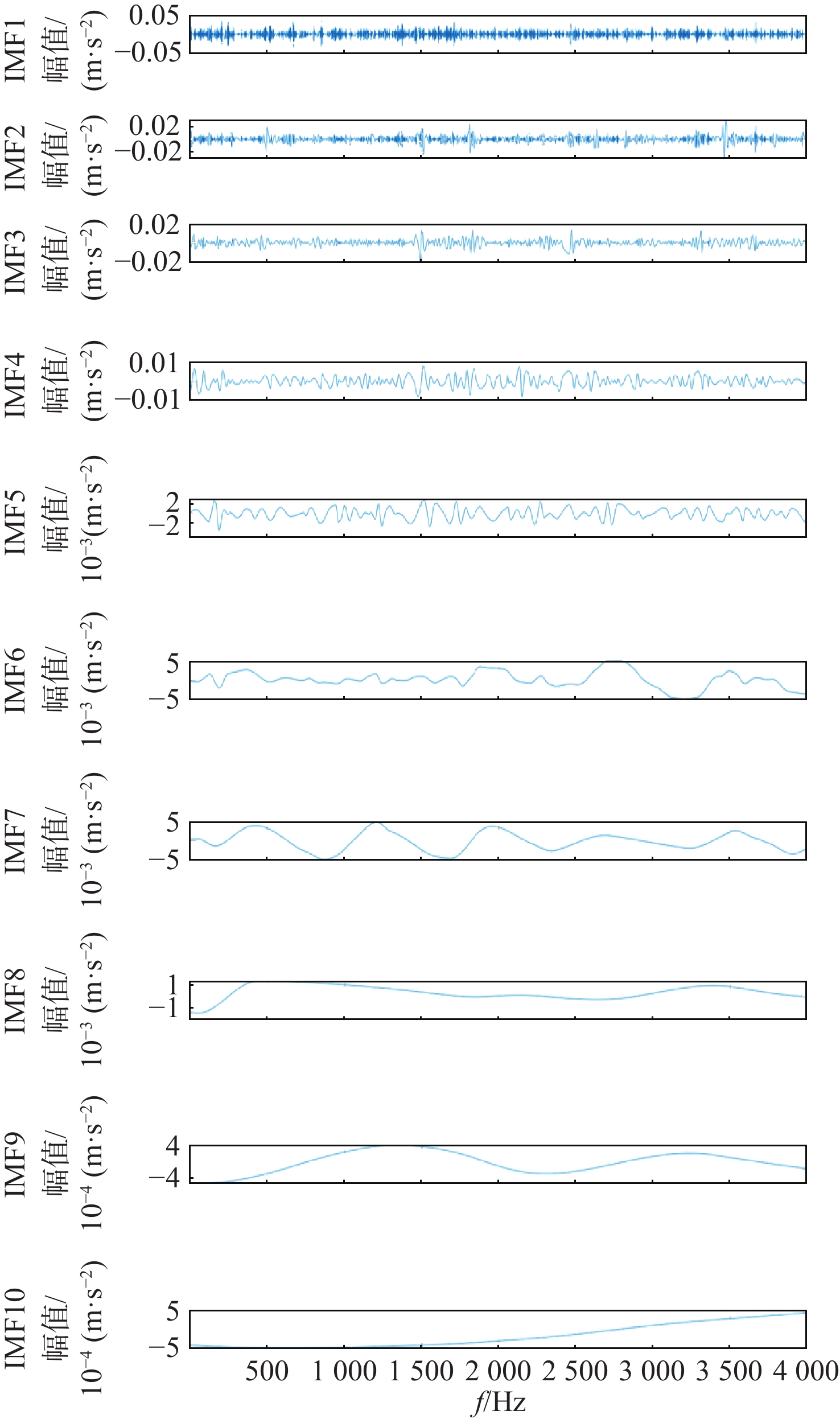
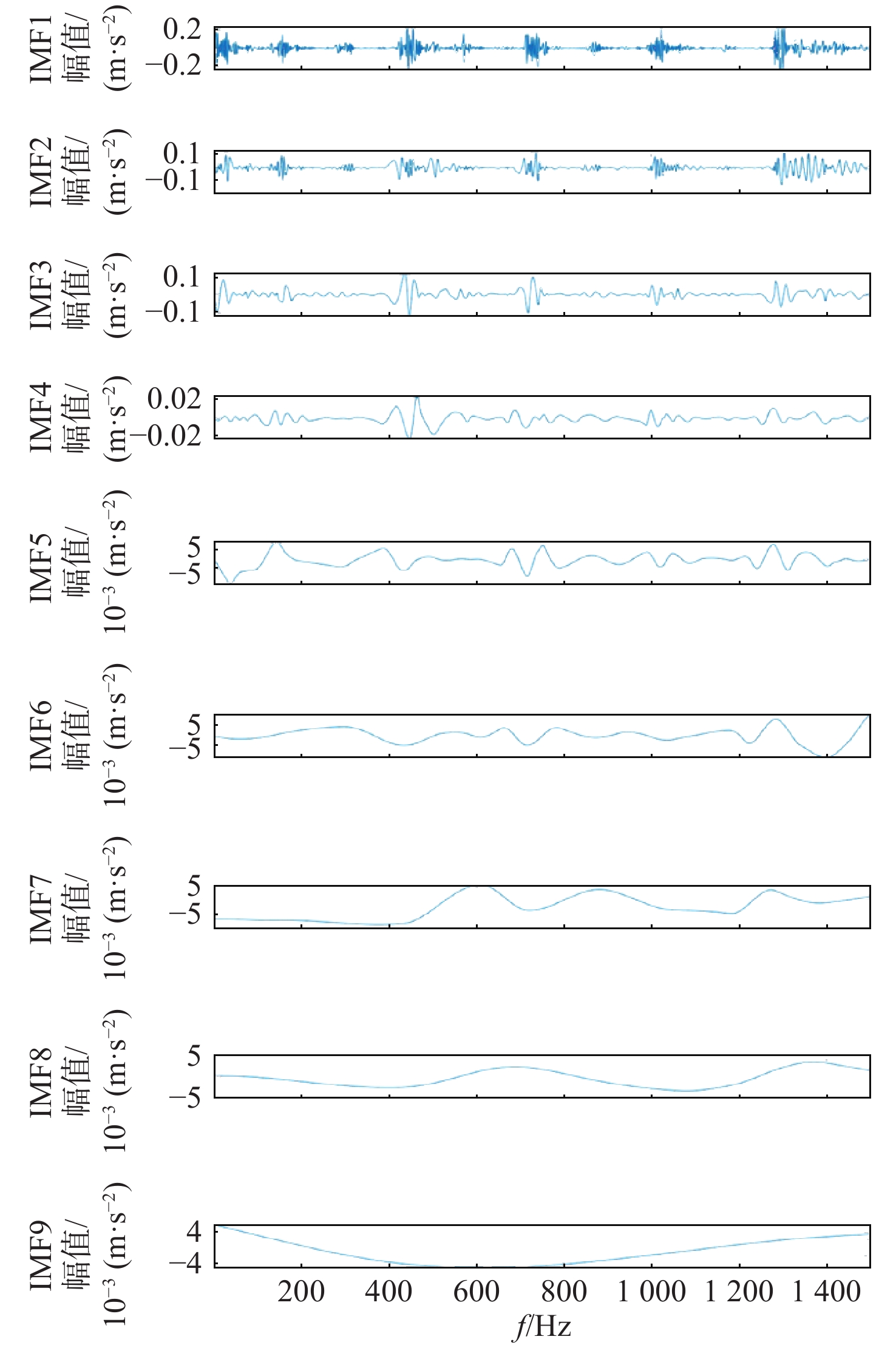
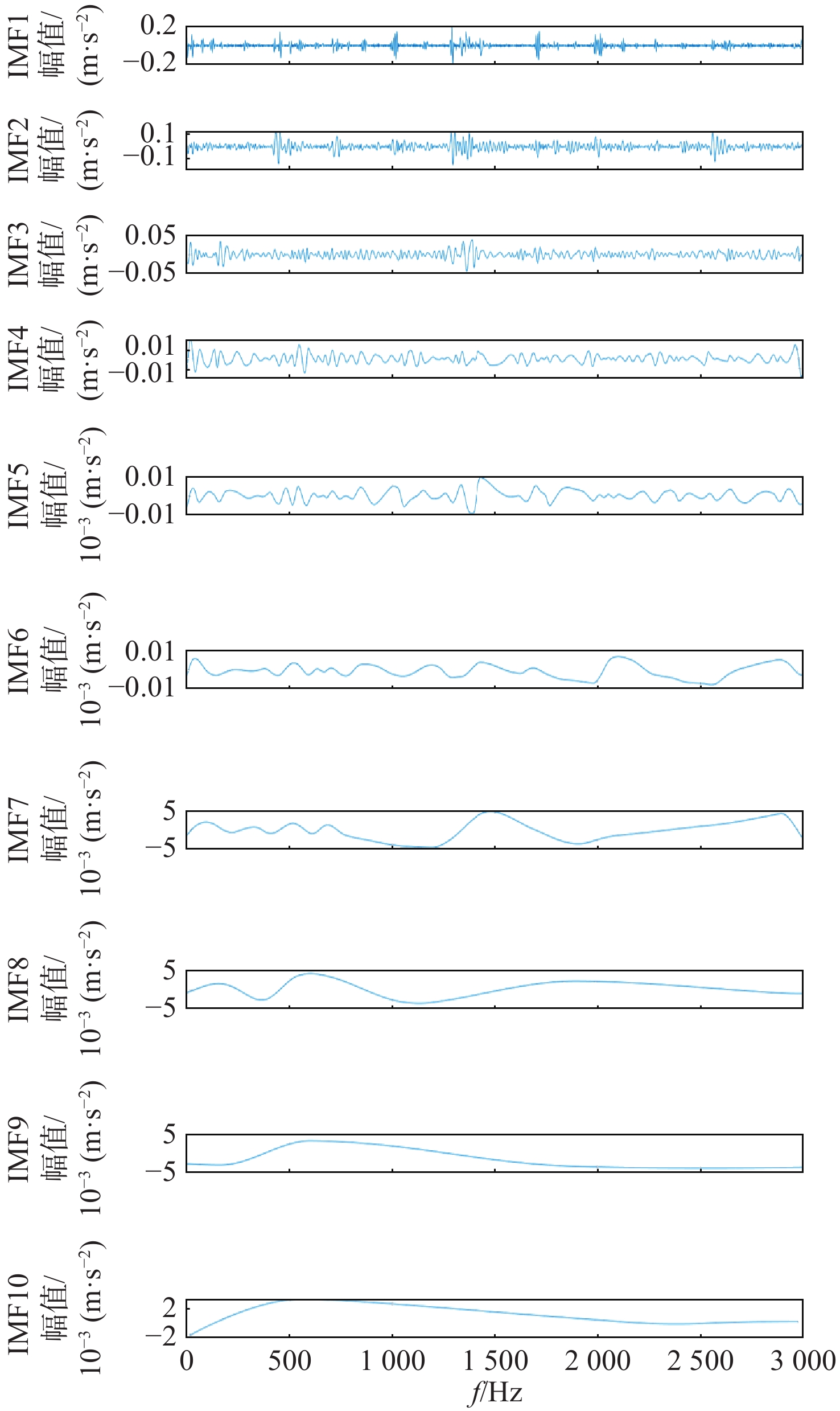
表 1 仿真信号EMD分解分量参数

Table 1. Parameters of EMD components of simulation signal

分量综合指标P 分量综合指标P 分量综合指标P

IMF1 15.517 IMF4 4.091 IMF7 2.011

IMF2 7.913 IMF5 4.798 IMF8 2.067

IMF3 9.848 IMF6 1.888 IMF9 2.307

下载: 导出CSV

表 2 ER-6k轴承参数

Table 2. Parameters of ER-6k bearing

轴承节径/mm 滚珠直径/mm 滚动体个数/个故障直径/mm

38.70 8 9 1.2

下载: 导出CSV

表 3 试验轴承信号1 EMD分解分量参数

Table 3. Parameters of EMD components of signal 1 of test bearing

分量综合指标P 分量综合指标P

IMF1 3.410 IMF6 2.981

IMF2 3.614 IMF7 1.431

IMF3 4.319 IMF8 1.643

IMF4 2.644 IMF9 1.564

IMF5 2.245 IMF10 0.941

下载: 导出CSV

表 4 试验轴承信号2 EMD分解分量参数

Table 4. Parameters of EMD components of signal 2 of test bearing

分量综合指标P 分量综合指标P 分量综合指标P

IMF1 30.614 IMF4 4.906 IMF7 2.534

IMF2 21.787 IMF5 5.401 IMF8 2.407

IMF3 4.825 IMF6 3.149 IMF9 1.557

下载: 导出CSV

表 5 试验轴承信号2EMD分解分量峭度参数

Table 5. Kurtosis parameters of EMD components of signal 2 of test bearing

分量峭度分量峭度分量峭度

IMF1 16.225 IMF4 16.772 IMF7 4.629

IMF2 14.114 IMF5 4.781 IMF8 2.686

IMF3 10.170 IMF6 5.954 IMF9 1.979

下载: 导出CSV

表 6 EMD分解分量峭度参数^[23]

Table 6. Kurtosis parameters of EMD components^[23]

分量峭度分量峭度

IMF1 18.152 IMF6 2.616

IMF2 7.099 IMF7 2.479

IMF3 6.743 IMF8 1.649

IMF4 3.680 IMF9 2.202

IMF5 2.808 IMF10 1.840

下载: 导出CSV

参考文献(23)

[1]	RAI A, UPADHYAY S H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings[J]. Tribology International, 2016, 96: 289-306. doi: 10.1016/j.triboint.2015.12.037
[2]	葛兴来, 邹丹. 多层降噪技术及Hilbert变换的轴承故障诊断方法[J]. 电机与控制学报, 2020, 24(8): 9-17. GE X L, ZOU D. Bearing fault diagnosis method of multi-layer denoising technologies and Hilbert transformation[J]. Electric Machines and Control, 2020, 24(8): 9-17(in Chinese).
[3]	SHAO R P, HU W T, LI J. Multi-fault feature extraction and diagnosis of gear transmission system using time-frequency analysis and wavelet threshold de-noising based on EMD[J]. Shock and Vibration, 2013, 20(4): 763-780. doi: 10.1155/2013/286461
[4]	王普, 李天垚, 高学金, 等. 分层自适应小波阈值轴承故障信号降噪方法[J]. 振动工程学报, 2019, 32(3): 548-556. WANG P, LI T Y, GAO X J, et al. Bearing fault signal denoising method of hierarchical adaptive wavelet threshold function[J]. Journal of Vibration Engineering, 2019, 32(3): 548-556(in Chinese).
[5]	CUI H Y, QIAO Y Y, YIN Y M, et al. An investigation on early bearing fault diagnosis based on wavelet transform and sparse component analysis[J]. Structural Health Monitoring, 2017, 16(1): 39-49. doi: 10.1177/1475921716661310
[6]	CHEN B J, SHEN B M, CHEN F F, et al. Fault diagnosis method based on integration of RSSD and wavelet transform to rolling bearing[J]. Measurement, 2019, 131: 400-411. doi: 10.1016/j.measurement.2018.07.043
[7]	崔玲丽, 高立新, 殷海晨, 等. 基于第二代小波的复合故障诊断方法研究[J]. 中国机械工程, 2009, 20(4): 442-446. doi: 10.3321/j.issn:1004-132X.2009.04.015 CUI L L, GAO L X, YIN H C, et al. Research on composite fault diagnosis method based on the second generation wavelet[J]. China Mechanical Engineering, 2009, 20(4): 442-446(in Chinese). doi: 10.3321/j.issn:1004-132X.2009.04.015
[8]	王志刚, 李友荣, 李方. 基于谐波小波分析的故障诊断方法研究[J]. 振动与冲击, 2006, 25(2): 125-128. doi: 10.3969/j.issn.1000-3835.2006.02.032 WANG Z G, LI Y R, LI F. Fault diagnosis method based on harmonic wavelet analysis[J]. Journal of Vibration and Shock, 2006, 25(2): 125-128(in Chinese). doi: 10.3969/j.issn.1000-3835.2006.02.032
[9]	张晓峰, 李功燕. 应用小波分析提取故障诊断信号的特定频段[J]. 振动与冲击, 2004, 23(4): 47-50. doi: 10.3969/j.issn.1000-3835.2004.04.011 ZHANG X F, LI G Y. Extraction of fault diagnosis signal’s frequency band with wavelet analysis[J]. Journal of Vibration and Shock, 2004, 23(4): 47-50(in Chinese). doi: 10.3969/j.issn.1000-3835.2004.04.011
[10]	邓飞跃, 强亚文, 杨绍普, 等. 一种自适应频率窗经验小波变换的滚动轴承故障诊断方法[J]. 西安交通大学学报, 2018, 52(8): 22-29. doi: 10.7652/xjtuxb201808004 DENG F Y, QIANG Y W, YANG S P, et al. A fault diagnosis method of rolling element bearings with adaptive frequency window empirical wavelet transform[J]. Journal of Xi’an Jiaotong University, 2018, 52(8): 22-29(in Chinese). doi: 10.7652/xjtuxb201808004
[11]	TUERXUN W, XU C, GUO H Y, et al. Fault diagnosis of wind turbines based on a support vector machine optimized by the sparrow search algorithm[J]. IEEE Access, 2021, 9: 69307-69315. doi: 10.1109/ACCESS.2021.3075547
[12]	REN Y, ZHANG L L, CHEN J T, et al. Noise reduction study of pressure pulsation in pumped storage units based on sparrow optimization VMD combined with SVD[J]. Energies, 2022, 15(6): 2073. doi: 10.3390/en15062073
[13]	HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A, 1998, 454(1971): 903-998. doi: 10.1098/rspa.1998.0193
[14]	KESHTAN M N, NOURI KHAJAVI M. Bearings fault diagnosis using vibrational signal analysis by EMD method[J]. Research in Nondestructive Evaluation, 2016, 27(3): 155-174. doi: 10.1080/09349847.2015.1103921
[15]	丛晓妍, 王增才, 王保平, 等. 基于 EMD 与峭度滤波的煤岩界面识别[J]. 振动、测试与诊断, 2015, 35(5): 950-954. CONG X Y, WANG Z C, WANG B P, et al. Identification of coal-rock interface based on EMD and kurtosis filtering[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(5): 950-954(in Chinese).
[16]	郭俊超, 甄冬, 孟召宗, 等. 基于WAEEMD和MSB的滚动轴承故障特征提取[J]. 中国机械工程, 2021, 32(15): 1793-1800. doi: 10.3969/j.issn.1004-132X.2021.15.004 GUO J C, ZHEN D, MENG Z Z, et al. Feature extraction of rolling bearings based on WAEEMD and MSB[J]. China Mechanical Engineering, 2021, 32(15): 1793-1800(in Chinese). doi: 10.3969/j.issn.1004-132X.2021.15.004
[17]	DENG C X, CHEN X X, LI S Q, et al. The improved wavelet threshold function and its application[J]. International Journal of Signal Processing, Image Processing and Pattern Recognition, 2016, 9(7): 79-92. doi: 10.14257/ijsip.2016.9.7.08
[18]	ZHANG Y, DING W F, PAN Z F, et al. Improved wavelet threshold for image de-noising[J]. Frontiers in Neuroscience, 2019, 13: 39. doi: 10.3389/fnins.2019.00039
[19]	MO F, MO Q, CHEN Y Y, et al. Wavelet quant, an improved quantification software based on wavelet signal threshold de-noising for labeled quantitative proteomic analysis[J]. BMC Bioinformatics, 2010, 11: 219. doi: 10.1186/1471-2105-11-219
[20]	XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
[21]	张龙, 熊国良, 黄文艺. 复小波共振解调频带优化方法和新指标[J]. 机械工程学报, 2015, 51(3): 129-138. doi: 10.3901/JME.2015.03.129 ZHANG L, XIONG G L, HUANG W Y. New procedure and index for the parameter optimization of complex wavelet based resonance demodulation[J]. Journal of Mechanical Engineering, 2015, 51(3): 129-138(in Chinese). doi: 10.3901/JME.2015.03.129
[22]	齐咏生, 樊佶, 李永亭, 等. 一种改进的解卷积算法及其在滚动轴承复合故障诊断中的应用[J]. 振动与冲击, 2020, 39(21): 140-150. QI Y S, FAN J, LI Y T, et al. An improved deconvolution algorithm and its application in compound fault diagnosis of rolling bearings[J]. Journal of Vibration and Shock, 2020, 39(21): 140-150(in Chinese).
[23]	HAN X M, XU J, SONG S N, et al. Crack fault diagnosis of vibration exciter rolling bearing based on genetic algorithm–optimized Morlet wavelet filter and empirical mode decomposition[J]. International Journal of Distributed Sensor Networks, 2022, 18(8): 155013292211145.