自适应不完备多视角聚类

陈梅; 马学艳; 张弛; 张锦宏; 钱罗雄

doi:10.13700/j.bh.1001-5965.2023.0178

自适应不完备多视角聚类

doi: 10.13700/j.bh.1001-5965.2023.0178

兰州交通大学电子与信息工程学院，兰州 730070

基金项目: 国家自然科学基金(62266029)；甘肃省重点研发计划(21YF5GA053)；甘肃省高等学校产业支撑计划(2022CYZC-36)

详细信息

通讯作者:
E-mail：chenmeilz@mail.lzjtu.cn

中图分类号: TP311
计量
- 文章访问数: 135
- HTML全文浏览量: 45
- PDF下载量: 10
- 被引次数: 0
出版历程
- 收稿日期: 2023-04-14
- 录用日期: 2023-09-14
- 网络出版日期: 2023-10-20
- 整期出版日期: 2025-04-30

Adaptive incomplete multi-view clustering

School of Electronic and Information Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China

Funds: National Natural Science Foundation of China (62266029); Gansu Key Research and Development Program (21YF5GA053); Gansu Higher Education Industry Support Program (2022CYZC-36)

More Information

Corresponding author: E-mail：chenmeilz@mail.lzjtu.cn

摘要

摘要:
高质量的完备初始图能够有效提高不完备多视角聚类的性能，缺失值填充不恰当会导致初始图丢失数据潜在的结构，同时，各视角的仿射图融合不完全会造成学习到的一致表征缺失视角间的互补信息。为此，提出自适应不完备多视角聚类(AIM)模型。在初始图构建中，AIM模型采用有效视角的相似度均值来填充对应位置的缺失值，以获取数据更加完整的潜在结构，同时引入稀疏约束来提高模型对噪声的鲁棒性；在图优化过程中，引入低秩约束捕获数据的全局结构，通过谱约束增强类内数据间的紧密性，使仿射图具有更清晰的块对角结构，并引入一致性约束最小化各视角的仿射图与一致表征之间的差异来捕获视角间的互补信息，得到具有高鉴别特征的一致鲁棒表征图。与9种不完备多视角聚类方法在真实和多种缺失率下仿真的不完备多视角数据集中进行实验对比，结果表明：AIM模型均获得了最好的聚类性能。
- 自适应构图 /
- 低秩表示 /
- 图融合 /
- 图算法 /
- 不完备多视角聚类
Abstract:
A high-quality complete initial graph can effectively improve the performance of incomplete multi-view clustering. However, inappropriate filling of missing values will lead to the initial graph losing the underlying structure of the data, and incomplete fusion of affine graphs of each view will make the unified learned representations miss the complementary information among the views. To address the aforementioned problems, an adaptive incomplete multi-view clustering (AIM) method was proposed in this paper. In the initial graph construction, AIM used the average value of similarity of valid views to fill the missing values at corresponding positions to obtain a complete potential structure of the data and introduced sparsity constraints to improve the robustness of the model to noise. In the graph optimization process, initially, low-rank constraints were introduced to capture the global structure of the data, followed by spectral constraints to enhance the closeness between data within classes to make the affine graph have a clearer block diagonal structure. The consistency constraints were introduced to minimize the differences between the affine graph and the unified representation of each view to capture the complementary information between the views. Ultimately, a unified robust representation graph with high discriminative features was obtained. The experimental comparisons with nine kinds of incomplete multi-view clustering in real and incomplete multi-view datasets simulated under multiple missing rates demonstrate that AIM obtains the best clustering performance.
- adaptive graph construction /
- low-rank representation /
- graph fusion /
- graph algorithm /
- incomplete multi-view clustering

HTML全文

图 1 AIM框架

Figure 1. Framework of AIM

下载: 全尺寸图片幻灯片

图 2 不同方法在Two-Moon数据集上可视化的一致表示

Figure 2. Consistent representation of different methods for Two-Moon dataset visualization

下载: 全尺寸图片幻灯片

图 3 缺失率为0,0.1,0.3,0.5,0.7,0.9时，不同方法在100Leaves、ORL 、Scene-15数据集上的精度

Figure 3. Accuracy of different algorithms at 100 Leaves, ORL, Scene-15 datasets with PER of 0, 0.1, 0.3, 0.5, 0.7, 0.9

下载: 全尺寸图片幻灯片

图 4 缺失率为0.3时，不同方法在ORL数据集上的混淆矩阵

Figure 4. Confusion matrix of different methods on ORL dataset with PER = 0.3

下载: 全尺寸图片幻灯片

在缺失率为0.3的ORL数据集和缺失率为0.5的100Leaves数据集上，AIM方法的归一化互信息与近邻数 $k$ 的关系

Relationship between NMI and nearest neighbor $k$ of AIM algorithm on ORL dataset with PER = 0.3 and 100Leaves dataset with PER = 0.5

下载: 全尺寸图片幻灯片

缺失率为0.3时，ORL数据集上归一化互信息与参数 ${\lambda _1}$ 、 ${\lambda _2}$ 和 ${\lambda _3}$ 的变化关系

Relationship between NMI and parameters ${\lambda _1}$ , ${\lambda _2}$ , and ${\lambda _3}$ on ORL dataset with PER = 0.3

下载: 全尺寸图片幻灯片

缺失率为0.5时，100Leaves数据集上归一化互信息与参数 ${\lambda _1}$ 、 ${\lambda _2}$ 和 ${\lambda _3}$ 的变化关系

Relationship between NMI and parameters ${\lambda _1}$ , ${\lambda _2}$ , and ${\lambda _3}$ on 100Leaves dataset with PER = 0.5

下载: 全尺寸图片幻灯片

图 8 在缺失率为0.3的ORL数据集和缺失率为0.5的100Leaves数据集上，目标函数值与迭代步数之间的变化关系

Figure 8. Relationship between object function value and iteration steps on ORL dataset with PER = 0.3 and 100Leaves dataset with PER = 0.5

下载: 全尺寸图片幻灯片

表 1 实验数据集描述

Table 1. Description of experimental dataset

数据集	n_v	c	n	d_v	类型
BBCSport	2	5	737	3183/3203	运动文档
3Sources	3	6	416	3560/3631/3068	新闻
Two-Moon	2	2	200	200/200
ORL	4	40	400	256/256/256/256	人脸图像
100Leaves	3	100	1600	64/64/64	叶片图像
Scene-15	3	15	4485	20/59/40	场景图像

下载: 导出CSV

表 2 不同方法在BBCSport、3Sources和Two-Moon数据集上的精度和归一化互信息

Table 2. Accuracy and NMI of different algorithms on BBCSport, 3Sources, and Two-Moon datasets

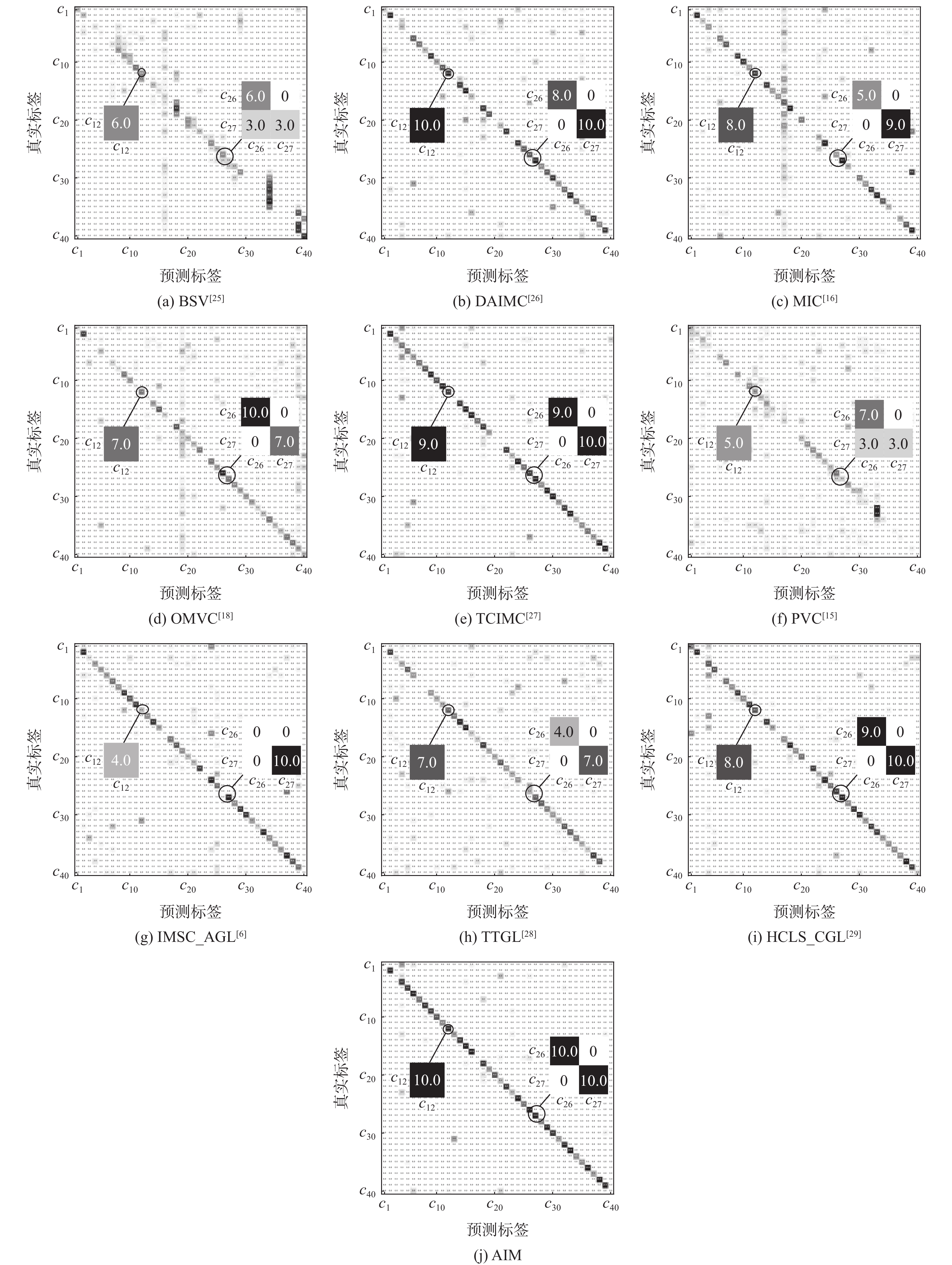
方法	精度/%			归一化互信息
方法	Two-Moon	BBCSport	3Sources	Two-Moon	BBCSport	3Sources
BSV^[25]	79.50	40.99	22.50	0.2701	0.2660	0.0530
DAIMC^[26]	73.00	75.16	58.68	0.2203	0.5780	0.4880
MIC^[16]	50.50	58.66	43.73	0.0050	0.4626	0.3894
PVC^[15]	76.50	44.33	26.45	0.2606	0.1377	0.1377
TCIMC^[27]	56.00	67.44	77.16	0.0104	0.5949	0.6763
OMVC^[18]	65.50	57.94	49.76	0.0935	0.6635	0.6635
IMSC_AGL^[6]	75.50	88.05	65.86	0.1809	0.5376	0.6198
TTGL^[28]	84.00	84.93	77.64	0.3879	0.6357	0.6011
HCLS_CGL^[29]	72.50	74.76	65.63	0.1516	0.6889	0.5724
AIM	91.00	89.55	86.15	0.5635	0.7095	0.7116

下载: 导出CSV

表 3 缺失率为0,0.1,0.3,0.5,0.7,0.9时，不同方法在100Leaves、ORL、Scene-15数据集上的归一化互信息

Table 3. NMI of different algorithms with PER of 0, 0.1, 0.3, 0.5, 0.7, 0.9 on 100Leaves、ORL、Scene-15 datasets

数据集	缺失率	归一化互信息
数据集	缺失率	BSV^[25]	DAIMC^[26]	MIC^[16]	OMVC^[18]	TCIMC^[27]	PVC^[15]	IMSC_AGL^[6]	TTGL^[28]	HCLS_CGL^[29]	AIM
100Leaves	0	0.5417	0.8754	0.8488	0.2350	0.8937	0.6600	0.9355	0.7856	0.8830	0.9536
	0.1	0.5363	0.8406	0.8170	0.5659	0.8860	0.5828	0.9247	0.7503	0.8733	0.9303
	0.3	0.4747	0.7628	0.7417	0.4952	0.6901	0.5294	0.8834	0.7320	0.8104	0.9035
	0.5	0.4359	0.6833	0.6735	0.4615	0.6982	0.4431	0.8381	0.6768	0.7986	0.8625
	0.7	0.3961	0.6302	0.6317	0.4354	0.7084	0.3981	0.8215	0.6480	0.7760	0.8405
	0.9	0.3552	0.5813	0.5944	0.4700	0.7828	0.3606	0.7663	0.6012	0.7540	0.7876
ORL	0	0.1346	0.7793	0.7869	0.7364	0.8600	0.6550	0.8351	0.7151	0.8382	0.8803
	0.1	0.4307	0.7691	0.7515	0.6910	0.8595	0.5700	0.7913	0.6902	0.8244	0.8739
	0.3	0.3946	0.7344	0.6331	0.6483	0.8236	0.4600	0.7706	0.6508	0.7932	0.8572
	0.5	0.4455	0.7096	0.5761	0.6049	0.8252	0.3550	0.7524	0.5787	0.7610	0.8450
	0.7	0.4643	0.6565	0.4910	0.5681	0.7908	0.3225	0.7227	0.5220	0.7384	0.8271
	0.9	0.4703	0.6162	0.4233	0.5563	0.7705	0.2050	0.6911	0.5054	0.7003	0.7823
Scene-15	0	0.0074	0.3048	0.3440	0.3262	0.2158	0.3336	0.4203	0.3914	0.3999	0.4634
	0.1	0.0058	0.3053	0.3241	0.2772	0.4045	0.3463	0.3994	0.3763	0.3891	0.4482
	0.3	0.0076	0.2791	0.2874	0.2540	0.4102	0.2756	0.3858	0.3336	0.3626	0.4315
	0.5	0.0075	0.2468	0.2507	0.2180	0.3994	0.2537	0.3720	0.3110	0.2959	0.4020
	0.7	0.0079	0.2092	0.2116	0.2356	0.3660	0.2604	0.3533	0.2647	0.3210	0.4053
	0.9	0.0088	0.1836	0.1921	0.2198	0.3471	0.2120	0.3382	0.2500	0.3074	0.3677

下载: 导出CSV

参考文献(29)

[1]	ZHAO J, XIE X J, XU X, et al. Multi-view learning overview: recent progress and new challenges[J]. Information Fusion, 2017, 38: 43-54. doi: 10.1016/j.inffus.2017.02.007
[2]	谢娟英, 丁丽娟. 完全自适应的谱聚类算法[J]. 电子学报, 2019, 47(5): 1000-1008. XIE J Y, DING L J. The true self-adaptive spectral clustering algorithms[J]. Acta Electronica Sinica, 2019, 47(5): 1000-1008(in Chinese).
[3]	XIA K J, GU X Q, ZHANG Y D. Oriented grouping-constrained spectral clustering for medical imaging segmentation[J]. Multimedia Systems, 2020, 26(1): 27-36. doi: 10.1007/s00530-019-00626-8
[4]	SHARMA K K, SEAL A. Multi-view spectral clustering for uncertain objects[J]. Information Sciences, 2021, 547: 723-745. doi: 10.1016/j.ins.2020.08.080
[5]	GAO H C, NIE F P, LI X L, et al. Multi-view subspace clustering[C]//Proceedings of the IEEE International Conference on Computer Vision. Piscataway: IEEE Press, 2015: 4238-4246.
[6]	WEN J, XU Y, LIU H. Incomplete multiview spectral clustering with adaptive graph learning[J]. IEEE Transactions on Cybernetics, 2020, 50(4): 1418-1429. doi: 10.1109/TCYB.2018.2884715
[7]	NISHOM M. Perbandingan akurasi Euclidean distance, Minkowski distance, Dan Manhattan distance pada algoritma K-means clustering berbasis Chi-square[J]. Jurnal Informatika: Jurnal Pengembangan IT, 2019, 4(1): 20-24. doi: 10.30591/jpit.v4i1.1253
[8]	YIN J, SUN S L. Incomplete multi-view clustering with cosine similarity[J]. Pattern Recognition, 2022, 123: 108371. doi: 10.1016/j.patcog.2021.108371
[9]	DING X J, LIU J, YANG F, et al. Random compact Gaussian kernel: application to ELM classification and regression[J]. Knowledge-Based Systems, 2021, 217: 106848. doi: 10.1016/j.knosys.2021.106848
[10]	SHANG R H, ZHANG Z, JIAO L C, et al. Self-representation based dual-graph regularized feature selection clustering[J]. Neurocomputing, 2016, 171: 1242-1253. doi: 10.1016/j.neucom.2015.07.068
[11]	WENG L B, DORNAIKA F, JIN Z. Graph construction based on data self-representativeness and Laplacian smoothness[J]. Neurocomputing, 2016, 207: 476-487. doi: 10.1016/j.neucom.2016.05.021
[12]	WANG Y, ZHANG W J, WU L, et al. Iterative views agreement: an iterative low-rank based structured optimization method to multi-view spectral clustering[C]//Proceedings of the 25th International Joint Conference on Artificial Intelligence. New York: ACM, 2016: 2153-2159.
[13]	WANG Y, WU L, LIN X M, et al. Multiview spectral clustering via structured low-rank matrix factorization[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10): 4833-4843.
[14]	ZHANG P, LIU X W, XIONG J, et al. Consensus one-step multi-view subspace clustering[J]. IEEE Transactions on Knowledge and Data Engineering, 2020, 34(10): 4676-4689.
[15]	LI S Y, JIANG Y, ZHOU Z H. Partial multi-view clustering[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2014: 1968-1974.
[16]	SHAO W, HE L. Multiple incomplete views clustering via weighted nonnegative matrix factorization with l_2,1 regularization[C]//Proceedings of the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases. Berlin: Springer, 2017: 318-334.
[17]	GAO H, PENG Y X, JIAN S L. Incomplete multi-view clustering[C]//Proceedings of the 9th IFIP TC 12 International Conference on Intelligent Information Processing VIII. Berlin: Springer, 2016: 245-255.
[18]	SHAO W X, HE L F, LU C T, et al. Online multi-view clustering with incomplete views[C]//Proceedings of the IEEE International Conference on Big Data. Piscataway: IEEE Press, 2016: 1012-1017.
[19]	CHEN J, YANG S X, PENG X, et al. Augmented sparse representation for incomplete multiview clustering[J]. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(3): 4058-4071. doi: 10.1109/TNNLS.2022.3201699
[20]	LIU X W, LI M M, TANG C, et al. Efficient and effective regularized incomplete multi-view clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(8): 2634-2646.
[21]	TRIVEDI A, RAI P, DAUMÉ H. Multiview clustering with incomplete views[C]//Proceedings of the Conference and Workshop on Neural Information Processing Systems workshop. Cambridge: MIT Press, 2010: 1-8.
[22]	LIU G C, LIN Z C, YAN S C, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 171-184. doi: 10.1109/TPAMI.2012.88
[23]	CAI J F, CANDÈS E J, SHEN Z W. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956-1982. doi: 10.1137/080738970
[24]	XIAO X L, GONG Y J, HUA Z Y, et al. On reliable multi-view affinity learning for subspace clustering[J]. IEEE Transactions on Multimedia, 2020, 23: 4555-4566.
[25]	ZHAO H D, LIU H F, FU Y. Incomplete multi-modal visual data grouping[C]//Proceedings of the 25th International Joint Conference on Artificial Intelligence. New York: ACM, 2016: 2392-2398.
[26]	HU M L, CHEN S C. Doubly aligned incomplete multi-view clustering[EB/OL]. (2019-03-07)[2023-04-01]. https://arxiv.org/abs/1903.02785v1.
[27]	XIA W, GAO Q X, WANG Q Q, et al. Tensor completion-based incomplete multiview clustering[J]. IEEE Transactions on Cybernetics, 2022, 52(12): 13635-13644. doi: 10.1109/TCYB.2021.3140068
[28]	ZHANG Z, HE W J. Tensorized topological graph learning for generalized incomplete multi-view clustering[J]. Information Fusion, 2023, 100: 101914. doi: 10.1016/j.inffus.2023.101914
[29]	WEN J, LIU C L, XU G H, et al. Highly confident local structure based consensus graph learning for incomplete multi-view clustering[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2023: 15712-15721.