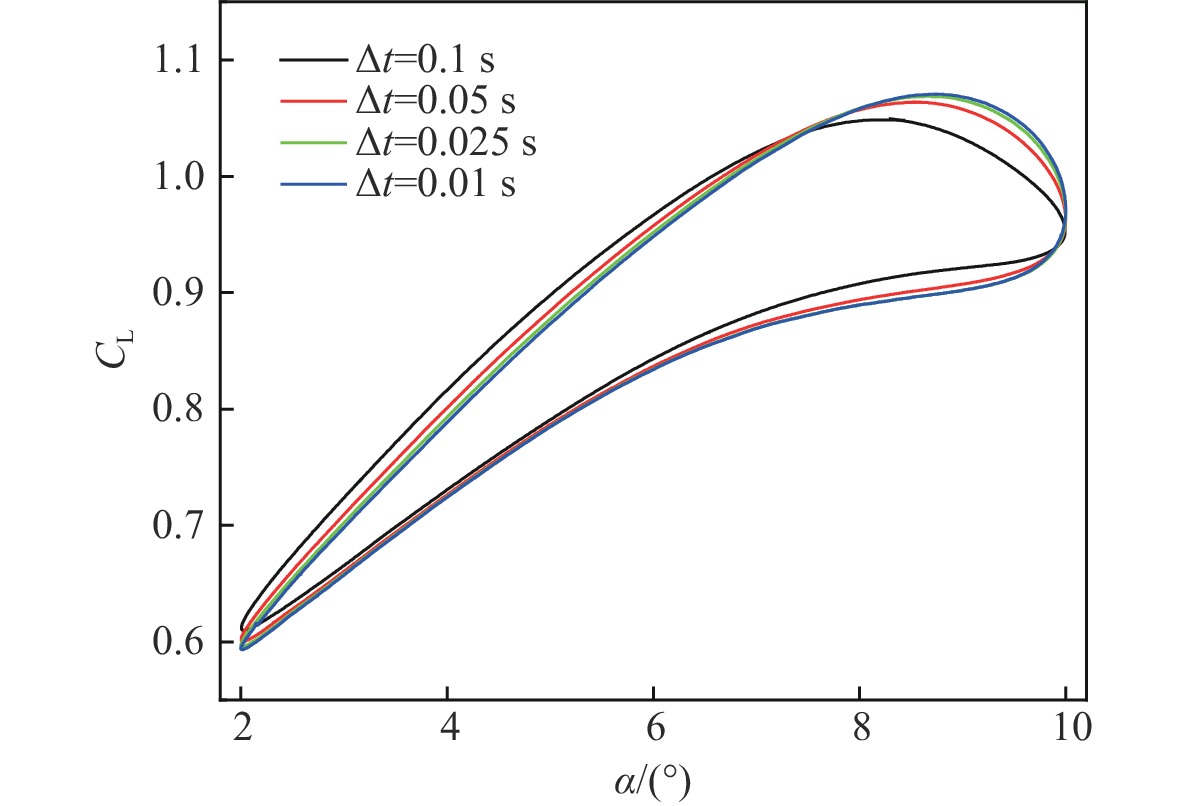
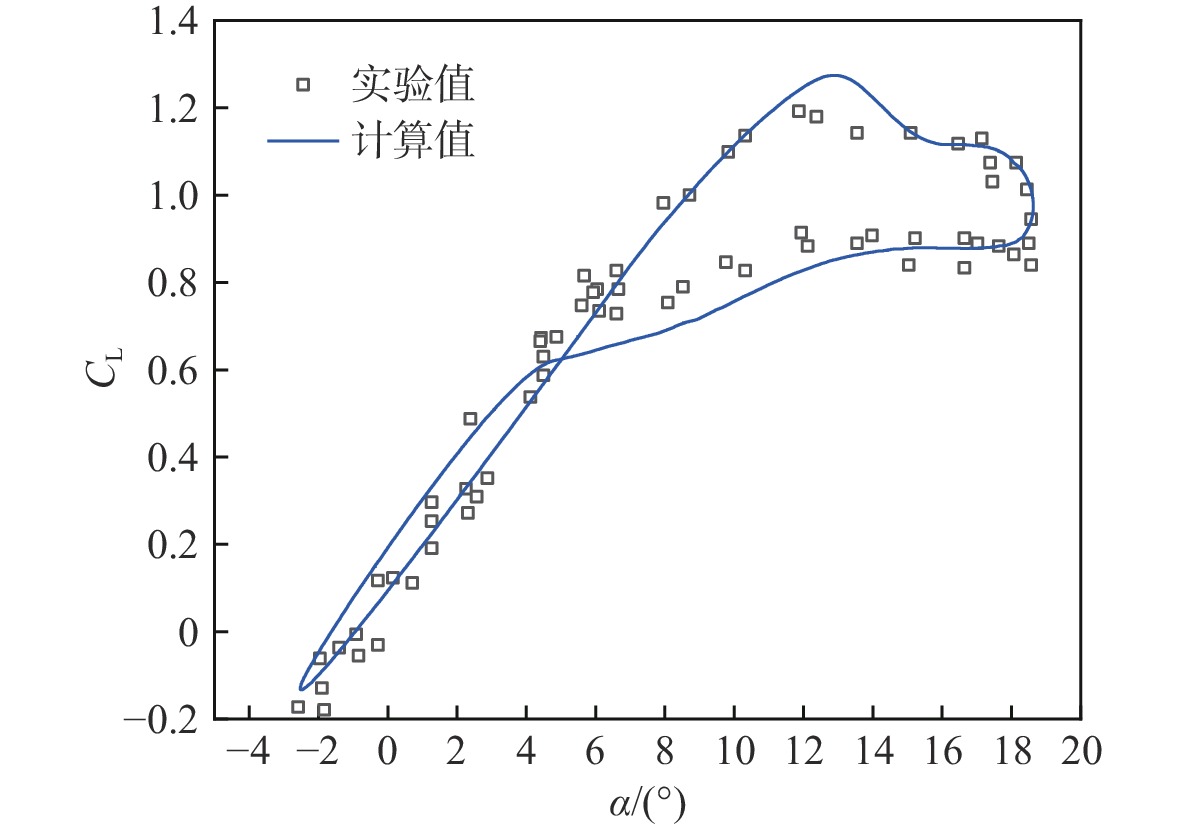
-
摘要:
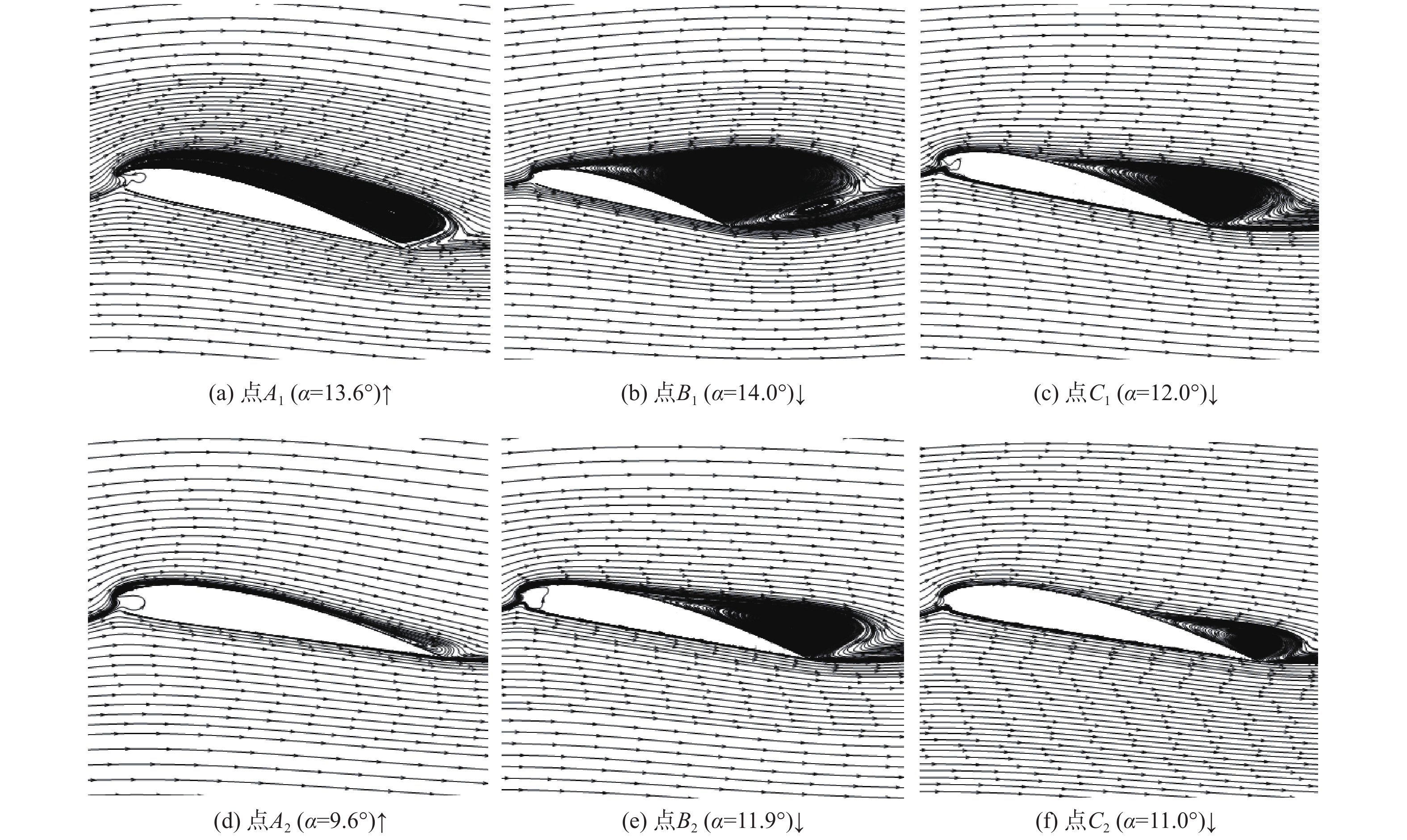
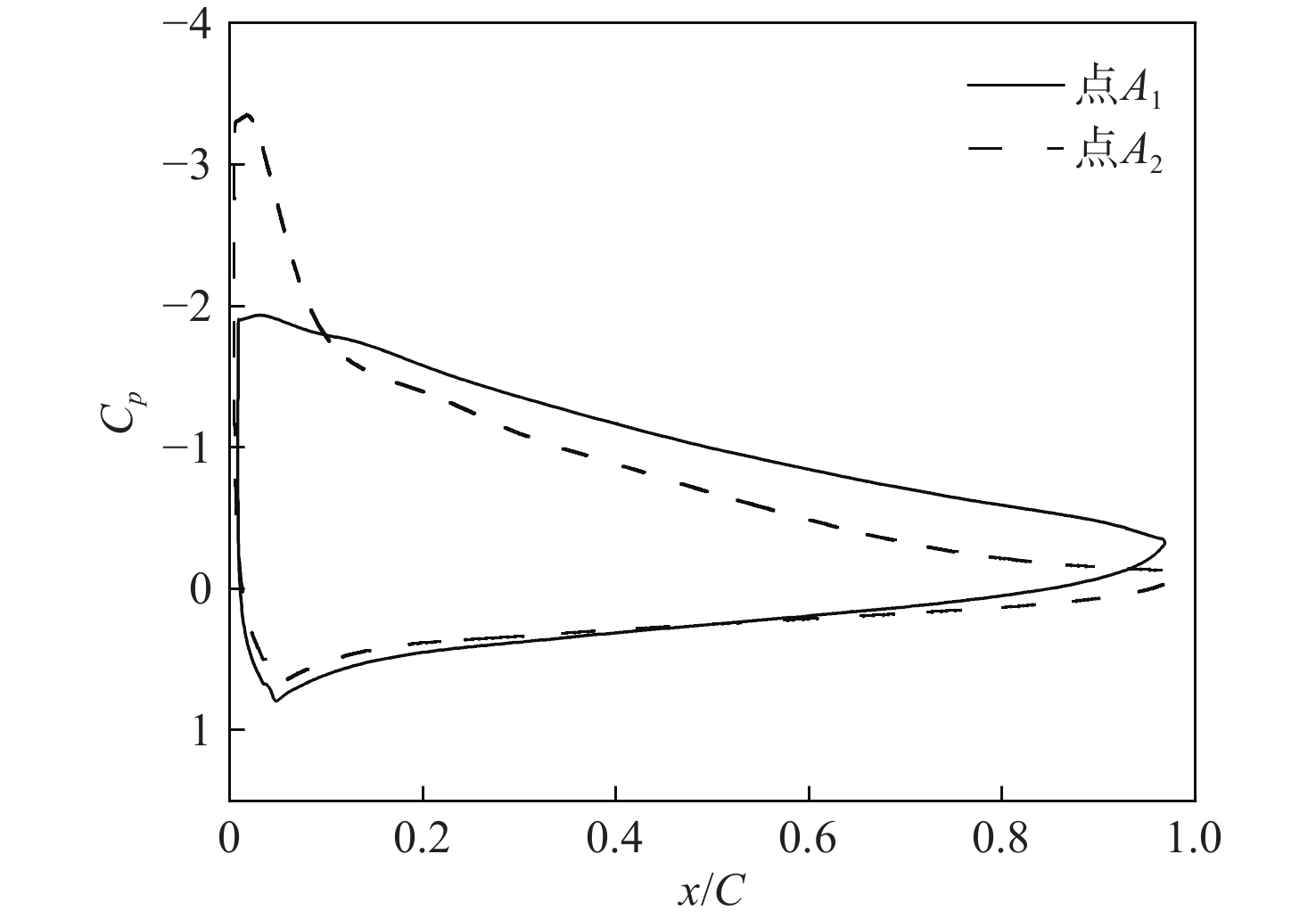
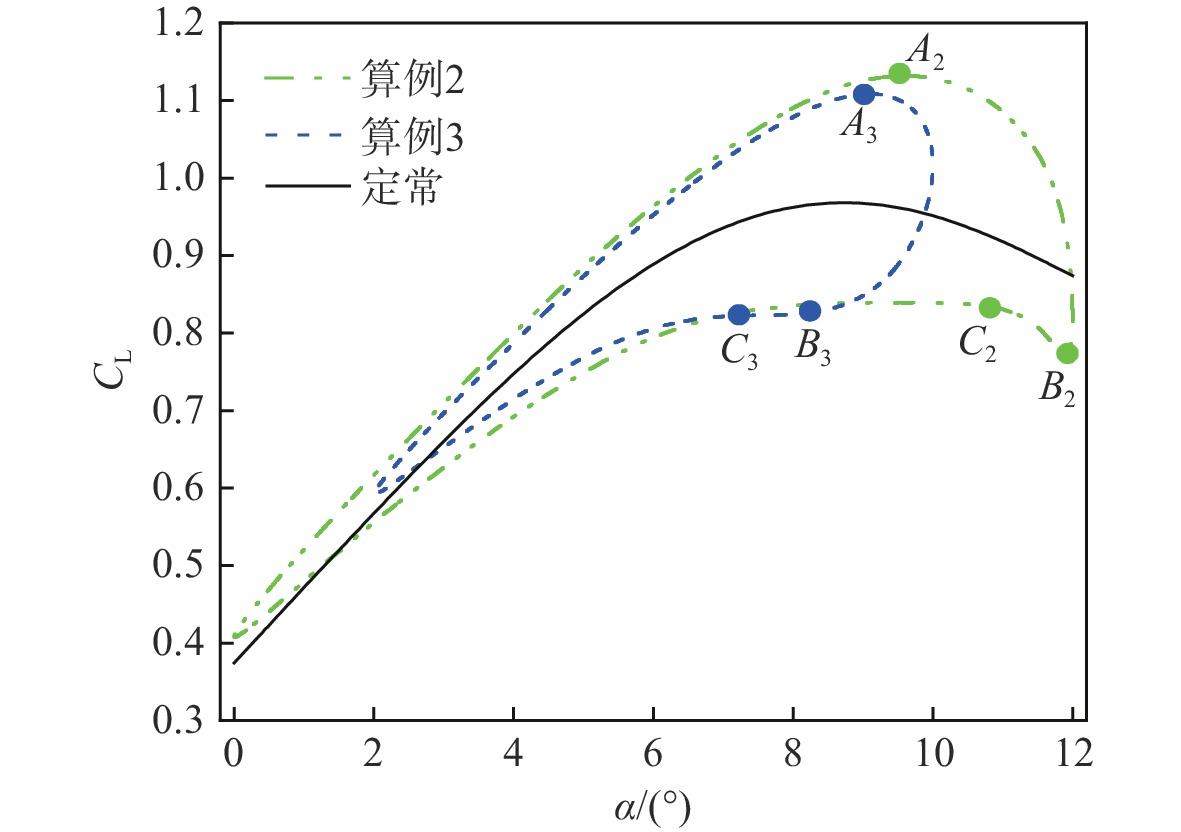
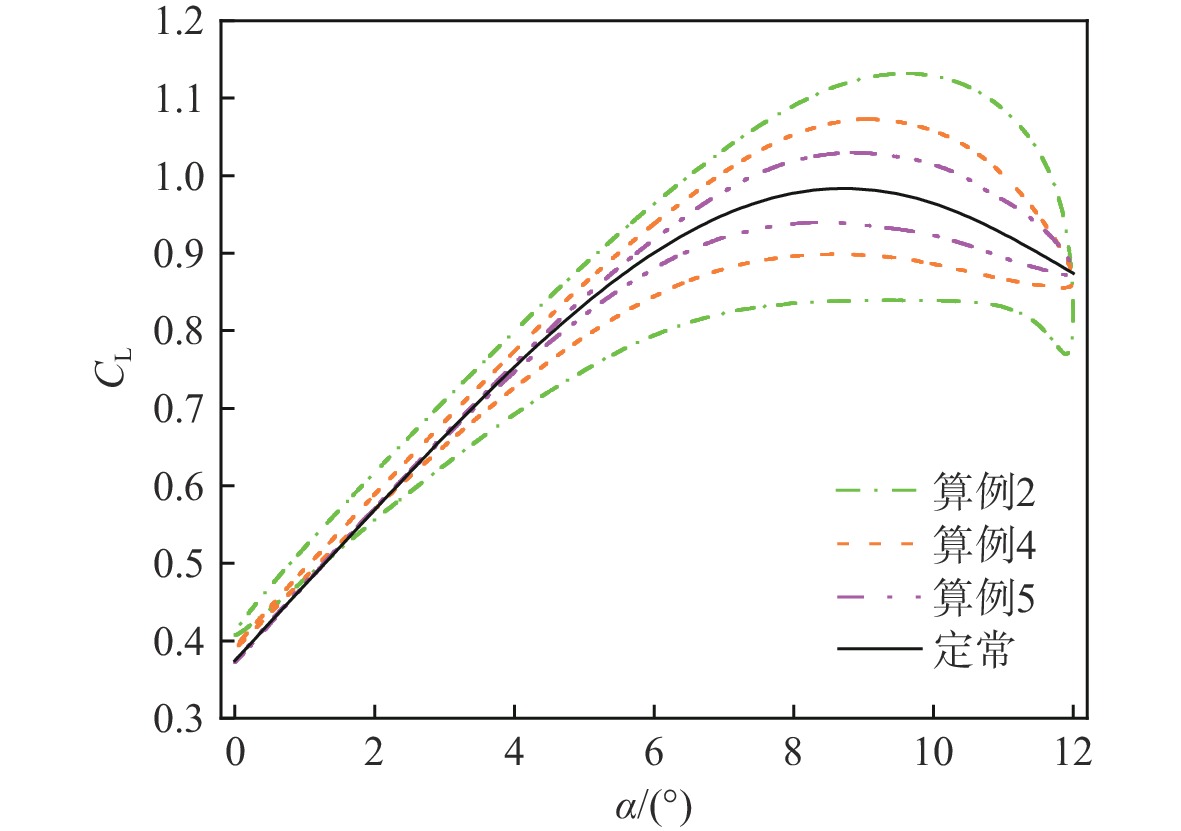
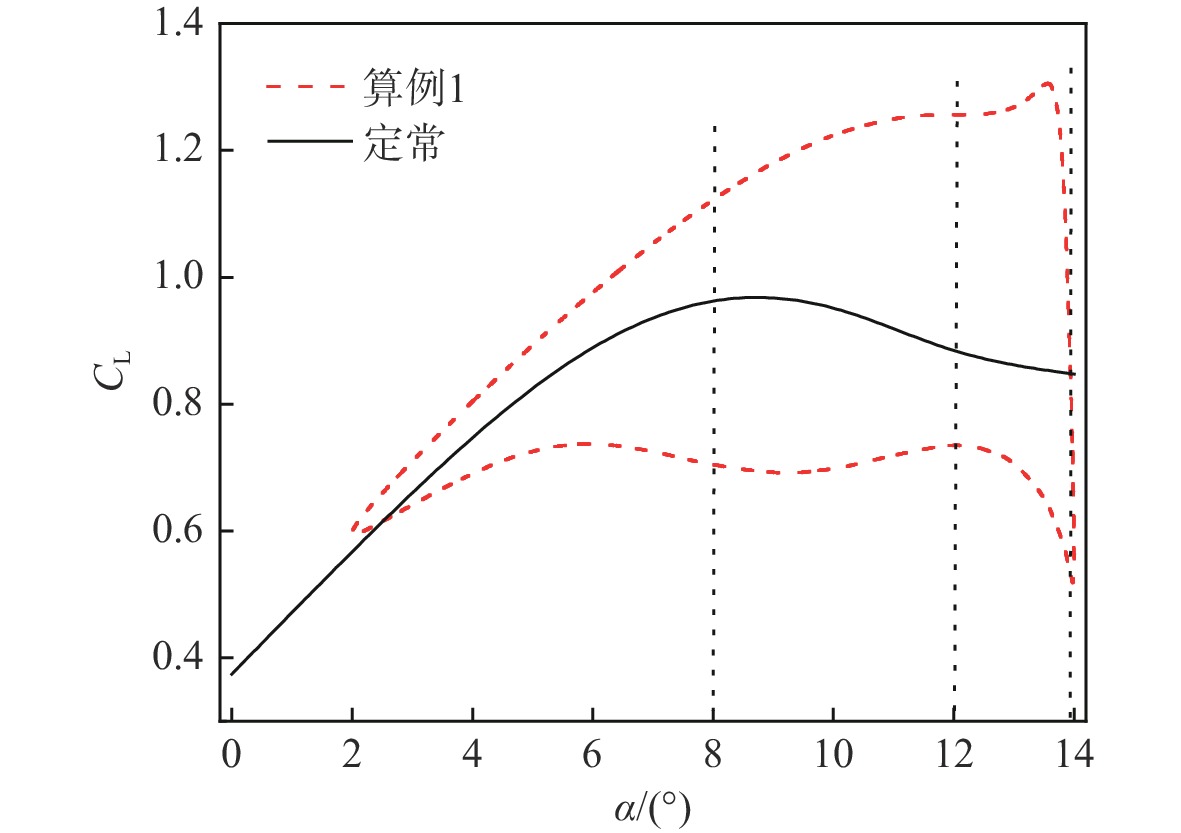
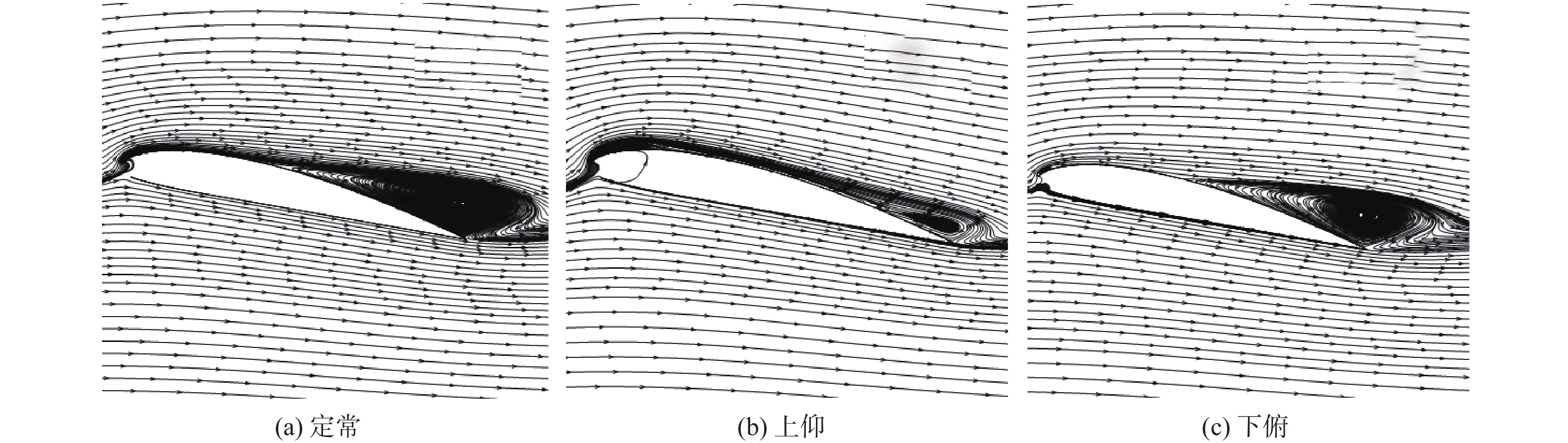
翼伞的非定常气动特性关乎飞行稳定性和飞行安全，是一个值得深入研究的问题。采用计算流体力学(CFD)方法对迎角动态变化下的翼伞翼型开展非定常数值模拟，分析平均迎角、迎角振幅和缩减频率对翼伞翼型非定常气动力和流场形态的影响。结果显示：平均迎角、迎角振幅和缩减频率3个参数中的任一个增大，都导致翼伞翼型气动力的非定常性显著增强；平均迎角与迎角振幅共同决定翼型迎角动态变化的范围，显著影响翼伞翼型的动态失速特性；缩减频率的变化对翼伞翼型的升力迟滞效应产生影响，最大升力系数随缩减频率的增加而呈线性增大。流场分析表明：翼伞翼型迎角动态增大阶段的非定常效应，延缓了翼型流动分离的发生，并使分离涡紧贴上翼面呈扁平形状，共同促使翼伞翼型的临界迎角和最大升力系数相对定常情况显著增大。研究成果有助于增进对翼伞翼型非定常气动力和流场规律的理解，为复杂风环境下的翼伞非定常气动力预测和安全性评估提供支撑。
Abstract:The unsteady aerodynamic characteristics of parafoils are a matter of flight stability and flight safety and are worthy of in-depth study. In this paper, the computational fluid dynamics (CFD) method was used to carry out an unsteady numerical simulation of the parafoil airfoil under the dynamic change of the angle of attack, so as to analyze the influence of the average angle of attack, the amplitude of the angle of attack, and the reduced frequency on the unsteady aerodynamic force and flow field pattern of the parafoil airfoil. The results show that an increase in any one of the above three parameters leads to a significant increase in the aerodynamic unsteadiness of the parafoil airfoil. The average angle of attack and the amplitude of the angle of attack amplitude jointly determine the dynamic range of the angle of attack of the airfoil, which significantly affects the dynamic stall characteristics of the parafoil airfoil; the change in reduced frequency affects the lift hysteresis effect of the parafoil airfoil, with the maximum lift coefficient increasing linearly with increasing reduced frequency. Further flow field analysis shows that the unsteady effect of the angle of attack of the parafoil airfoil in the dynamic increase stage delays the occurrence of airfoil flow separation on the one hand, and on the other hand, it flattens the separating vortex against the upper airfoil, which together contributes to a significant increase in the critical angle of attack and maximum lift coefficient of the parafoil airfoil relative to the constant case. The results of this essay will help to enhance the understanding of the unsteady aerodynamic force and flow field patterns of parafoil airfoil, support the prediction of unsteady aerodynamic forces and safety assessment of parafoil in complex wind environments.
-
Key words:
- parafoil /
- airfoil /
- aerodynamic performance /
- dynamic stall /
- reduced frequency
-
图 1 基于Clark-Y翼型的前缘开口翼型构型
Figure 1. Clark-Y-based airfoil configuration with an open leading edge
图 3 风速和风向对翼型迎角变化
Figure 3. Influence of wind speed and wind direction on change of angle of attack of airfoil
图 5 不同时间步长下数值模拟的升力系数曲线
Figure 5. Numerically simulated lift coefficient curves at different time steps
图 6 S809翼型的升力系数迟滞曲线计算值与实验值对比
Figure 6. Comparison of calculated and experimental values of lift coefficient hysteresis curves of S809 airfoil
图 8 算例1和算例2在不同迎角时的流线图
Figure 8. Streamlines for case 1 and case 2 at various angles of attack
图 9 点A1、点A2处的翼型压力分布
Figure 9. Pressure distribution at point A1 and point A2 of airfoil
图 10 算例1和算例2在相同迎角时的流线图（α=9.6°）
Figure 10. Streamlines for case 1 and case 2 at same angles of attack (α = 9.6°)
图 12 算例2和算例3在不同迎角时的流线图
Figure 12. Streamlines for case 2 and case 3 at various angles of attack
图 13 算例2、算例4和算例5的升力系数曲线
Figure 13. Lift coefficient curves for case 2, case 4, and case 5
图 14 最大升力系数随缩减频率变化曲线
Figure 14. Variation of maximum lift coefficient with reduced frequency
图 16 α=8°时，算例1与定常计算的流线图
Figure 16. Streamlines for case 1 and case of steady simulation when α = 8°
图 17 α=12°时，算例1与定常计算的流线图
Figure 17. Streamlines for case 1 and case of steady simulation when α = 12°
图 18 α=14°附近时，算例1与定常计算的流线图
Figure 18. Streamlines for case 1 and case of steady simulation when α = 14°
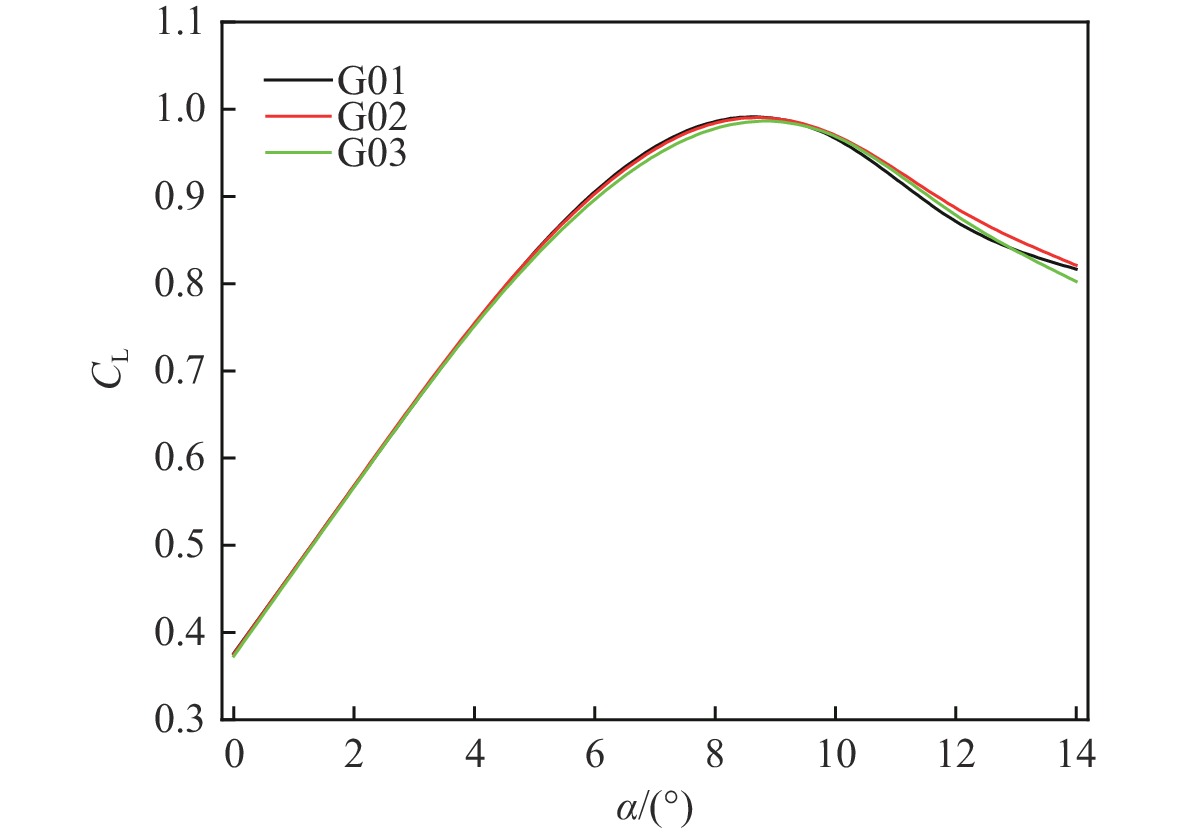
表 1 算例设置
Table 1. Computational cases
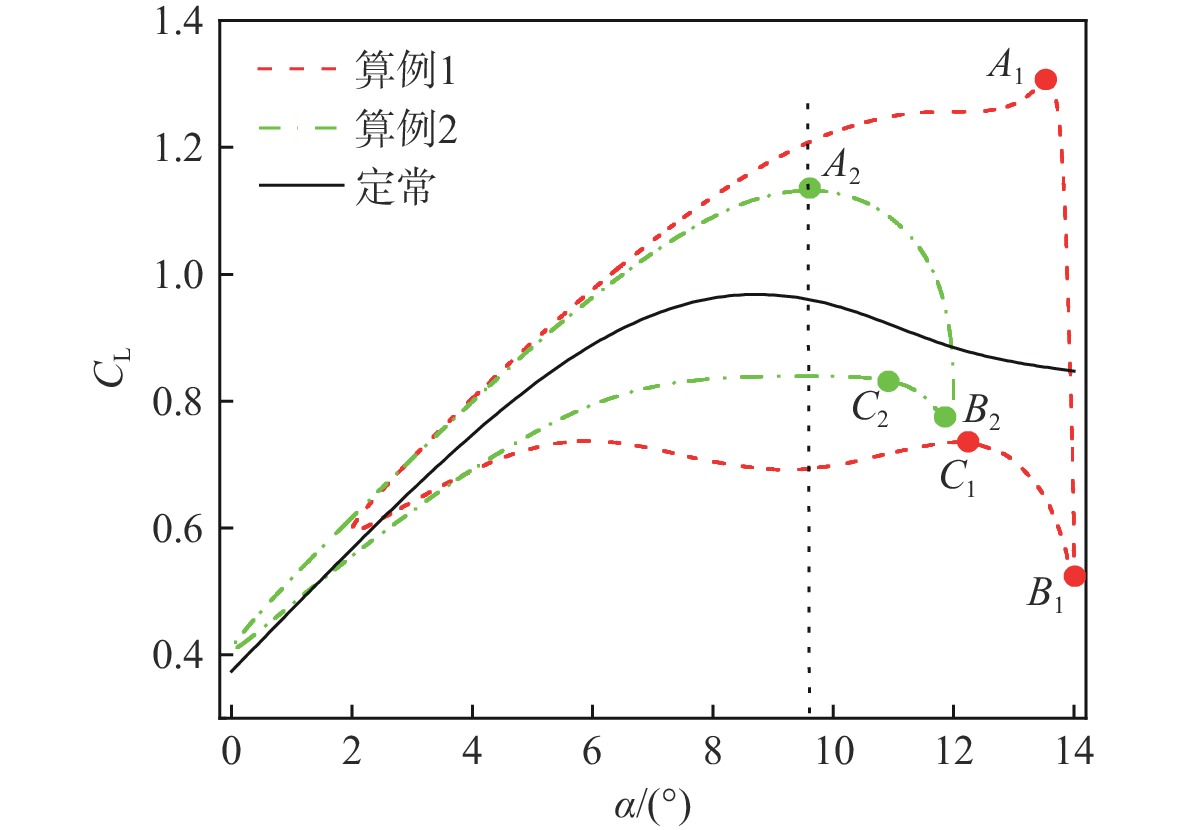
算例 平均迎角α0/(°) 迎角振幅∆α/(°) 缩减频率K 算例1 8 6 0.051 算例2 6 6 0.051 算例3 6 4 0.051 算例4 6 6 0.03 算例5 6 6 0.01 
下载: 导出CSV
表 2 用于网格无关性测试的网格参数
Table 2. Grid parameters for grid-independence testing
网格
编号壁面首层
网格高度/m翼型弦向
网格点数翼型往外的
尺度增长率网格单元
总数G01 10−5 200 1.15 2.3×104 G02 10−5 250 1.1 3.7×104 G03 10−5 300 1.05 4.9×104
下载: 导出CSV
表 3 最大升力系数随缩减频率变化的计算数据
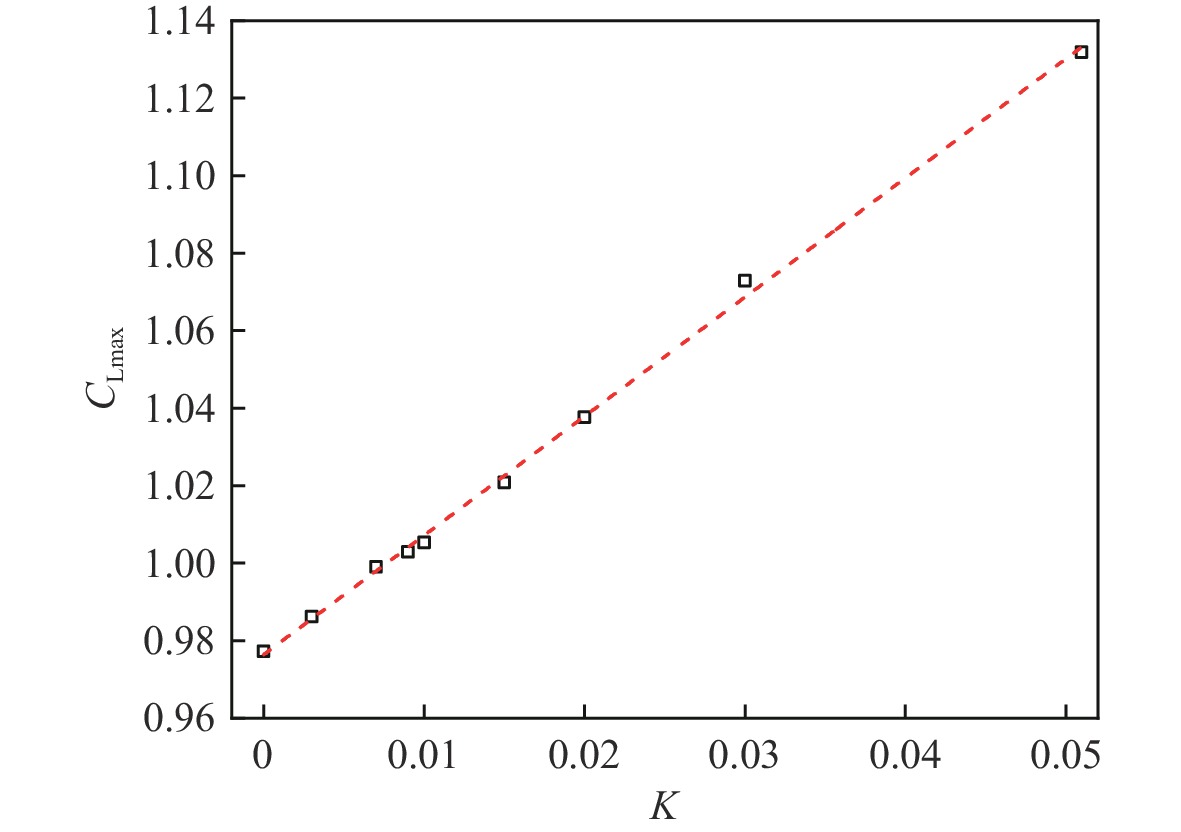
Table 3. Variation of maximum lift coefficient with reduced frequency
缩减频率/K 最大升力系数CLmax ΔCLmax/% 0（定常） 0.977 0.003 0.986 0.9 0.007 0.999 2.2 0.009 1.003 2.7 0.01 1.005 2.9 0.015 1.021 4.5 0.02 1.038 6.3 0.03 1.073 9.8 0.051 1.132 15.9
下载: 导出CSV
-
[1] 李春, 吕智慧, 黄伟, 等. 精确定点归航翼伞控制系统的研究[J]. 中南大学学报(自然科学版), 2012, 43(4): 1331-1335.LI C, LÜ Z H, HUANG W, et al. Guidance navigation & control system for precision fix-point homing parafoil[J]. Journal of Central South University (Science and Technology), 2012, 43(4): 1331-1335(in Chinese). [2] TAO J, SUN Q L, ZHU E L, et al. Quantum genetic algorithm based homing trajectory planning of parafoil system[C]//Proceedings of the 2015 34th Chinese Control Conference. Piscataway: IEEE Press, 2015: 2523-2528. [3] 高振兴. 复杂大气扰动下大型飞机飞行实时仿真建模研究[D]. 南京: 南京航空航天大学, 2009.GAO Z X. Research on real-time flight simulation of large aircraft in complex atmospheric disturbance[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009(in Chinese). [4] MITTAL S, SAXENA P, SINGH A. Computation of two-dimensional flows past ram-air parachutes[J]. International Journal for Numerical Methods in Fluids, 2001, 35(6): 643-667. doi: 10.1002/1097-0363(20010330)35:6<643::AID-FLD107>3.0.CO;2-M [5] BALAJI R, MITTAL S, RAI A K. Effect of leading edge cut on the aerodynamics of ram-air parachutes[J]. International Journal for Numerical Methods in Fluids, 2005, 47(1): 1-17. doi: 10.1002/fld.779 [6] 聂帅, 曹义华, 田似营. 前缘切口对翼伞气动性能的影响[J]. 航空动力学报, 2016, 31(6): 1477-1485.NIE S, CAO Y H, TIAN S Y. Effect on parafoil aerodynamic performance of leading edge[J]. Journal of Aerospace Power, 2016, 31(6): 1477-1485(in Chinese). [7] 李健. 前缘切口对冲压式翼伞的气动力影响[J]. 航天返回与遥感, 2005, 26(1): 36-41.LI J. The aerodynamic influence of the cutter of the front edge of parafoil[J]. Spacecraft Recovery & Remote Sensing, 2005, 26(1): 36-41(in Chinese). [8] FURFARO J, HAILEY C, BEHR V, et al. An experimental study of parafoil sections[C]//Proceedings of the14th Serodynamic Decelerator Systems Technology Conference. Reston: AIAA, 1997: 1527. [9] UDDIN M, MASHUD M. Wind tunnel test of a paraglider (flexible) wing canopy International[J]. Journal of Mechanical & Mechatronics Engineering, 2010, 10(3): 7-18. [10] 朱旭, 曹义华. 翼伞弧面下反角、翼型和前缘切口对翼伞气动性能的影响[J]. 航空学报, 2012, 33(7): 1189-1200.ZHU X, CAO Y H. Effects of arc-anhedral angle, airfoil and leading edge cut on parafoil aerodynamic performance[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1189-1200(in Chinese). [11] 王国庆, 滕海山, 王奇. 大型翼伞操纵转弯动力学研究[J]. 航天返回与遥感, 2021, 42(2): 49-58.WANG G Q, TENG H S, WANG Q. Dynamics research on maneuvering and turning of the large parafoil[J]. Spacecraft Recovery & Remote Sensing, 2021, 42(2): 49-58(in Chinese). [12] 孙青林, 梁炜, 陶金, 等. 基于CFD的风雨环境翼伞动力学建模[J]. 中南大学学报(自然科学版), 2017, 48(8): 2053-2062.SUN Q L, LIANG W, TAO J, et al. Dynamic modeling of parafoil in wind and rain environment based on CFD method[J]. Journal of Central South University (Science and Technology), 2017, 48(8): 2053-2062(in Chinese). [13] RAFFEL M, KOMPENHANS J, WERNERT P. Investigation of the unsteady flow velocity field above an airfoil pitching under deep dynamic stall conditions[J]. Experiments in Fluids, 1995, 19(2): 103-111. doi: 10.1007/BF00193856 [14] 宋红军, 王肇, 尹协振. 二维翼型非定常运动数值模拟[J]. 水动力学研究与进展(A辑), 2004, 19(增刊1): 896-903.SONG H J, WANG Z, YIN X Z. Numerical simulation on unsteady motion of 2D airfoil[J]. Chinese Journal of Hydrodynamics, 2004, 19(Sup 1): 896-903(in Chinese). [15] 闫文辉. NACA4412翼型低速绕流的定常/非定常计算对比研究[J]. 科学技术与工程, 2017, 17(2): 283-287.YAN W H. Steady/unsteady numerical study of NACA4412 airfoil around flow[J]. Science Technology and Engineering, 2017, 17(2): 283-287(in Chinese). [16] 宗涛. 风力机翼型动态失速的数值模拟[J]. 湖北电力, 2017, 41(4): 50-54.ZONG T. Numerical simulation of airfoil dynamic stall of wind turbine[J]. Hubei Electric Power, 2017, 41(4): 50-54(in Chinese). [17] 钱炜祺, 符松, 蔡金狮. 翼型动态失速的数值研究[J]. 空气动力学学报, 2001, 19(4): 427-433.QIAN W Q, FU S, CAI J S. Numerical study of airfoil dynamic stall[J]. Acta Aerodynamica Sinica, 2001, 19(4): 427-433(in Chinese). [18] TUNCER I, PLATZER M. A computational study of flow separation characteristics and wake profiles behind a flapping airfoil[C]//Proceedings of the 37th Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 1999: 648. [19] TUNCER I, WALZ R, PLATZER M. A computational study on the dynamic stall of a flapping airfoil[C]//Proceedings of the 16th AIAA Applied Aerodynamics Conference. Reston: AIAA, 1998: 2519. [20] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. doi: 10.2514/3.12149 [21] MENTER F, RUMSEY C. Assessment of two-equation turbulence models for transonic flows[C]//Proceedings of the Fluid Dynamics Conference. Reston: AIAA, 1994: 2343. [22] ELGAMMI M, SANT T. A new stall delay algorithm for predicting the aerodynamics loads on wind turbine blades for axial and yawed conditions[J]. Wind Energy, 2017, 20(9): 1645-1663. doi: 10.1002/we.2115 [23] 续荣华, 王震, 黄及水, 等. 上翼面开缝的翼伞翼型气动特性研究[J]. 航天返回与遥感, 2022, 43(3): 1-11.XU R H, WANG Z, HUANG J S, et al. Aerodynamic performance study on a parafoil airfoil with an upper surface slit[J]. Spacecraft Recovery & Remote Sensing, 2022, 43(3): 1-11(in Chinese). [24] EKATERINARIS J A, SO̸RENSEN N N, RASMUSSEN F. Numerical investigation of airfoil dynamic stall in simultaneous harmonic oscillatory and translatory motion[J]. Journal of Solar Energy Engineering, 1998, 120(1): 75-83. doi: 10.1115/1.2888050 [25] GUILMINEAU E, PIQUET J, QUEUTEY P. Unsteady two-dimensional turbulent viscous flow past aerofoils[J]. International Journal for Numerical Methods in Fluids, 1997, 25(3): 315-366. doi: 10.1002/(SICI)1097-0363(19970815)25:3<315::AID-FLD555>3.0.CO;2-L [26] RAMSAY R F, HOFFMAN M J, GREGOREK G M. Effects of grit roughness and pitch oscillation on the S809 airfoil[R]. Golden: National Renewable Energy Laboratory, 1995. -
下载:
点击查看大图
计量
- 文章访问数: 164
- HTML全文浏览量: 71
- PDF下载量: 4
- 被引次数: 0
