基于新型趋近律的AABS积分滑模控制系统设计

徐萌; 李艳; 高洁; 徐海; 高冰

doi:10.13700/j.bh.1001-5965.2023.0185

基于新型趋近律的AABS积分滑模控制系统设计

doi: 10.13700/j.bh.1001-5965.2023.0185

徐萌^{1, 2},
李艳¹,
高洁^{1, 2, ,},
徐海³,
高冰⁴

1.
中国民航大学电子信息与自动化学院，天津 300300
2.
天津市城市空中交通系统技术与装备重点实验室，天津 300300
3.
中国民用航空沈阳航空器适航审定中心，沈阳 110043
4.
中国民航大学工程技术训练中心，天津 300300

基金项目: 国家自然科学基金(51707195,62173331)；中央高校基本科研业务费专项资金(3122023016)

详细信息

通讯作者:
E-mail：jiegao@cauc.edu.cn

中图分类号: V227⁺.5
计量
- 文章访问数: 32
- HTML全文浏览量: 8
- PDF下载量: 8
- 被引次数: 0
出版历程
- 收稿日期: 2023-04-18
- 录用日期: 2023-08-02
- 网络出版日期: 2023-08-22
- 整期出版日期: 2025-04-30

Design of aircraft anti-skid braking system integral sliding mode control system based on novel reaching law

XU Meng^{1, 2},
LI Yan¹,
GAO Jie^{1, 2
, ,},
XU Hai³,
GAO Bing⁴

1.
School of Electronic Information and Automation，Civil Aviation University of China，Tianjin 300300，China
2.
Key Laboratory of Technology and Equipment of Tianjin Urban Air Transportation System，Tianjin 300300，China
3.
Shenyang Aircraft Airworthiness Certification Center of CAAC，Shenyang 110043，China
4.
Engineering Techniques Training Center，Civil Aviation University of China，Tianjin 300300，China

Funds: National Natural Science Foundation of China (51707195,62173331); The Fundamental Research Funds for the Central Universities (3122023016)

More Information

Corresponding author: E-mail：jiegao@cauc.edu.cn

摘要

摘要:
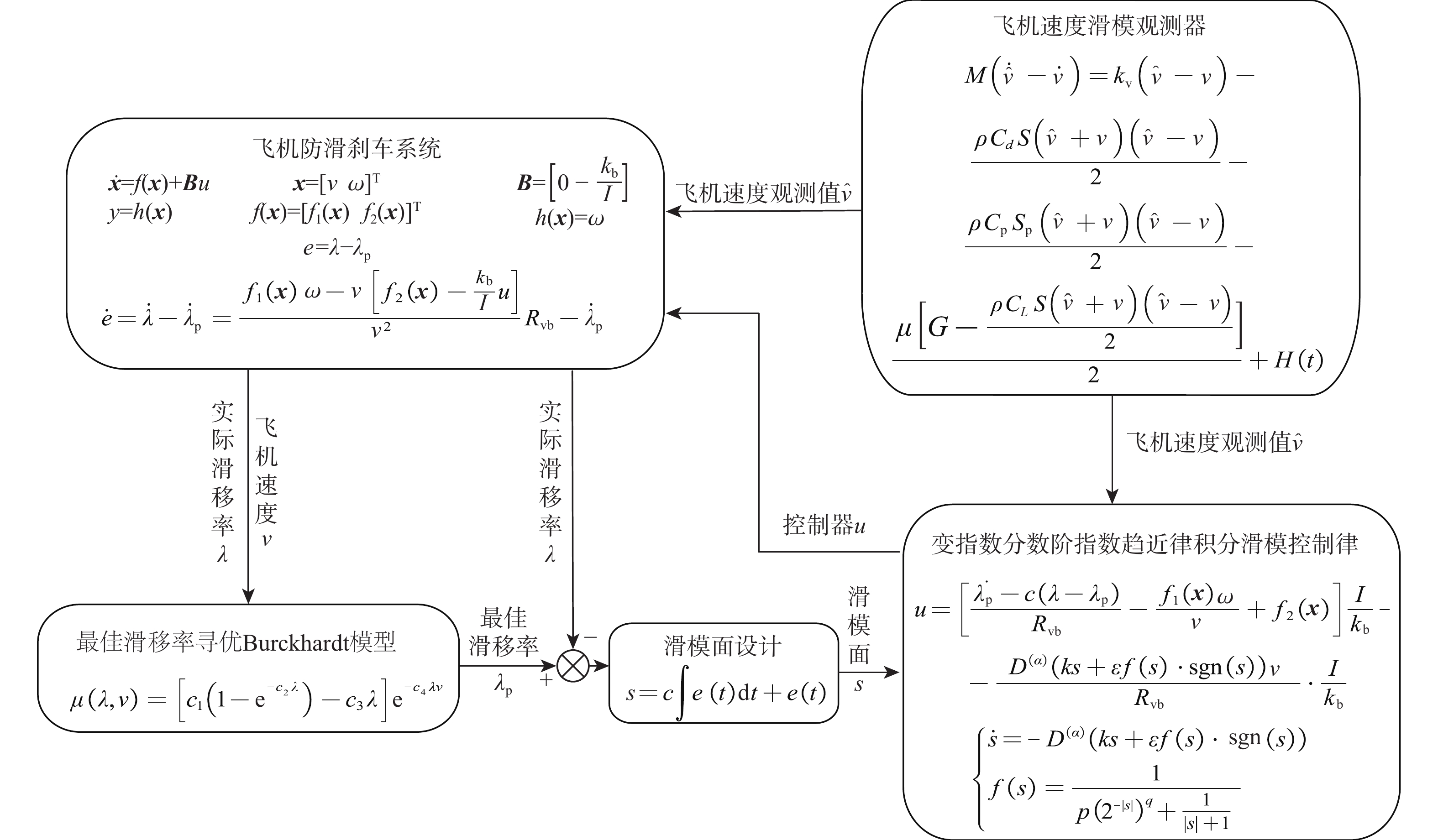
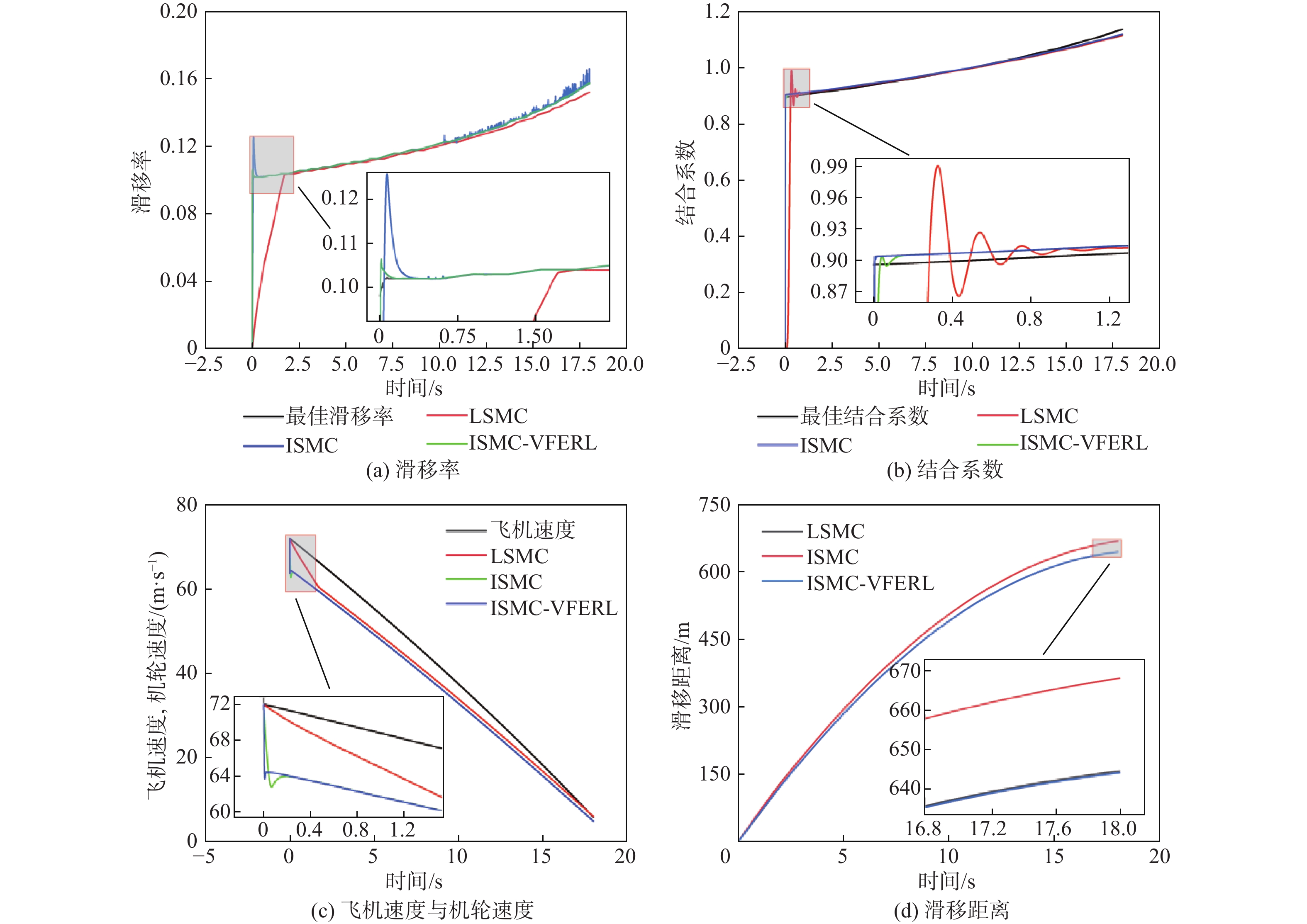
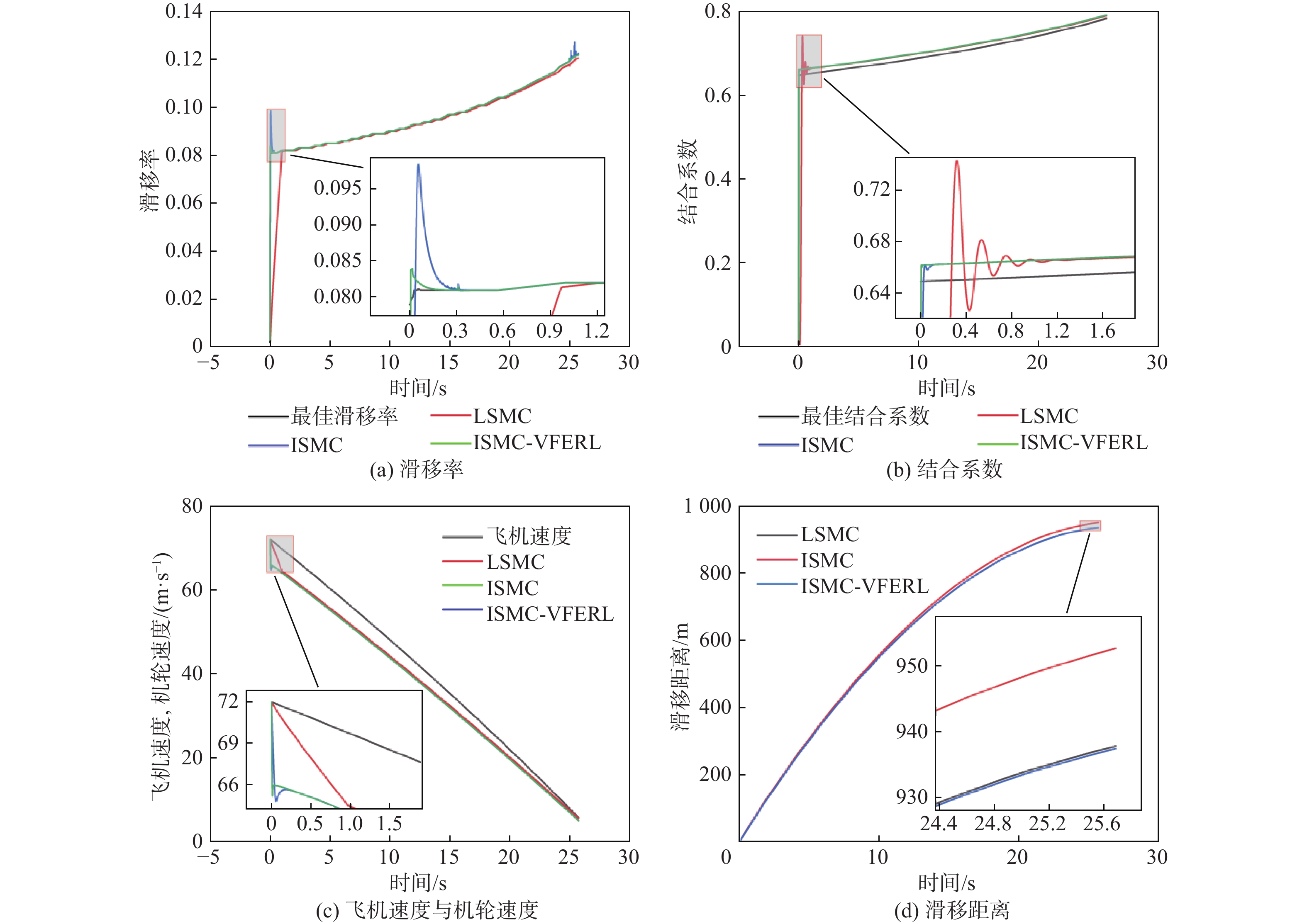
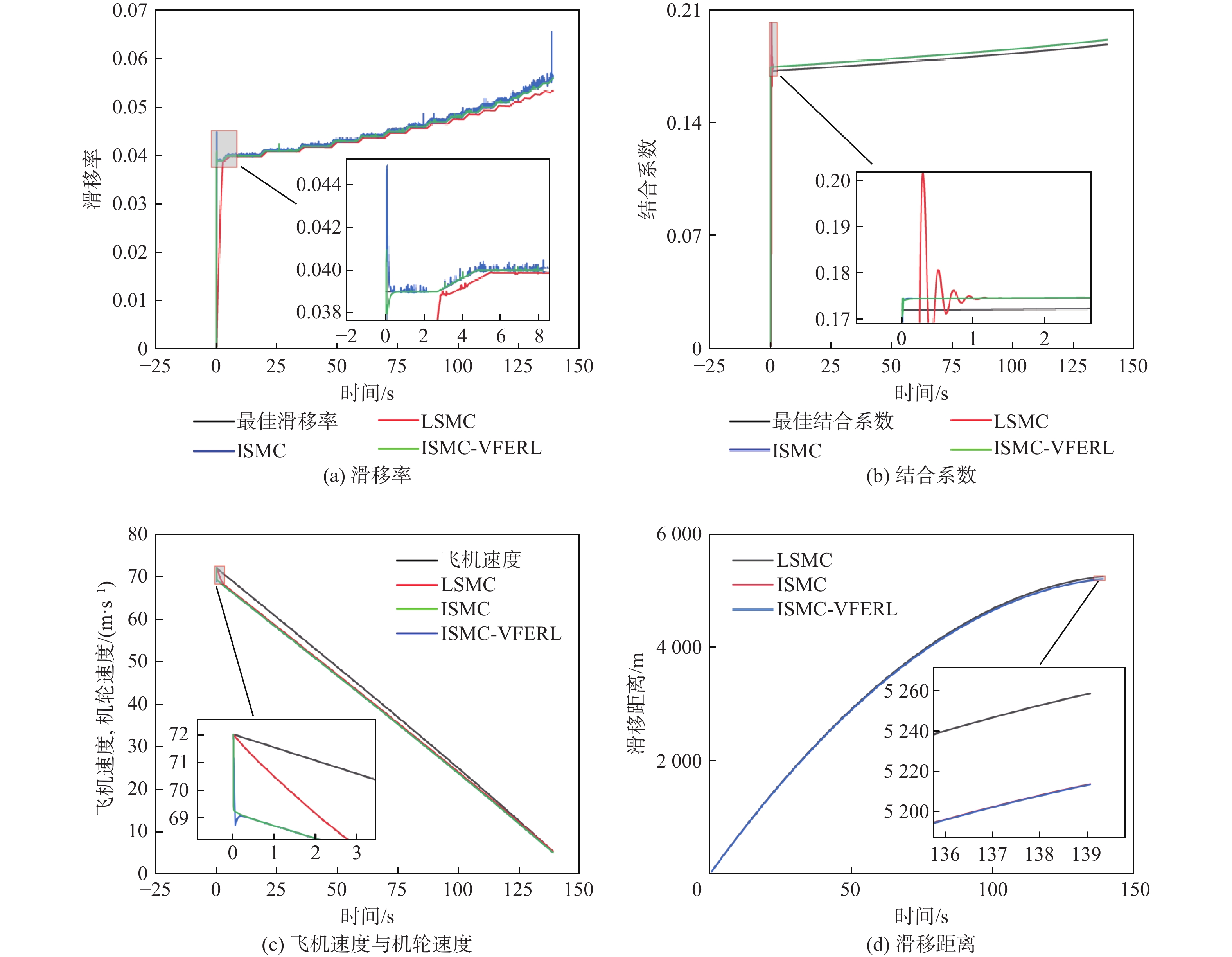
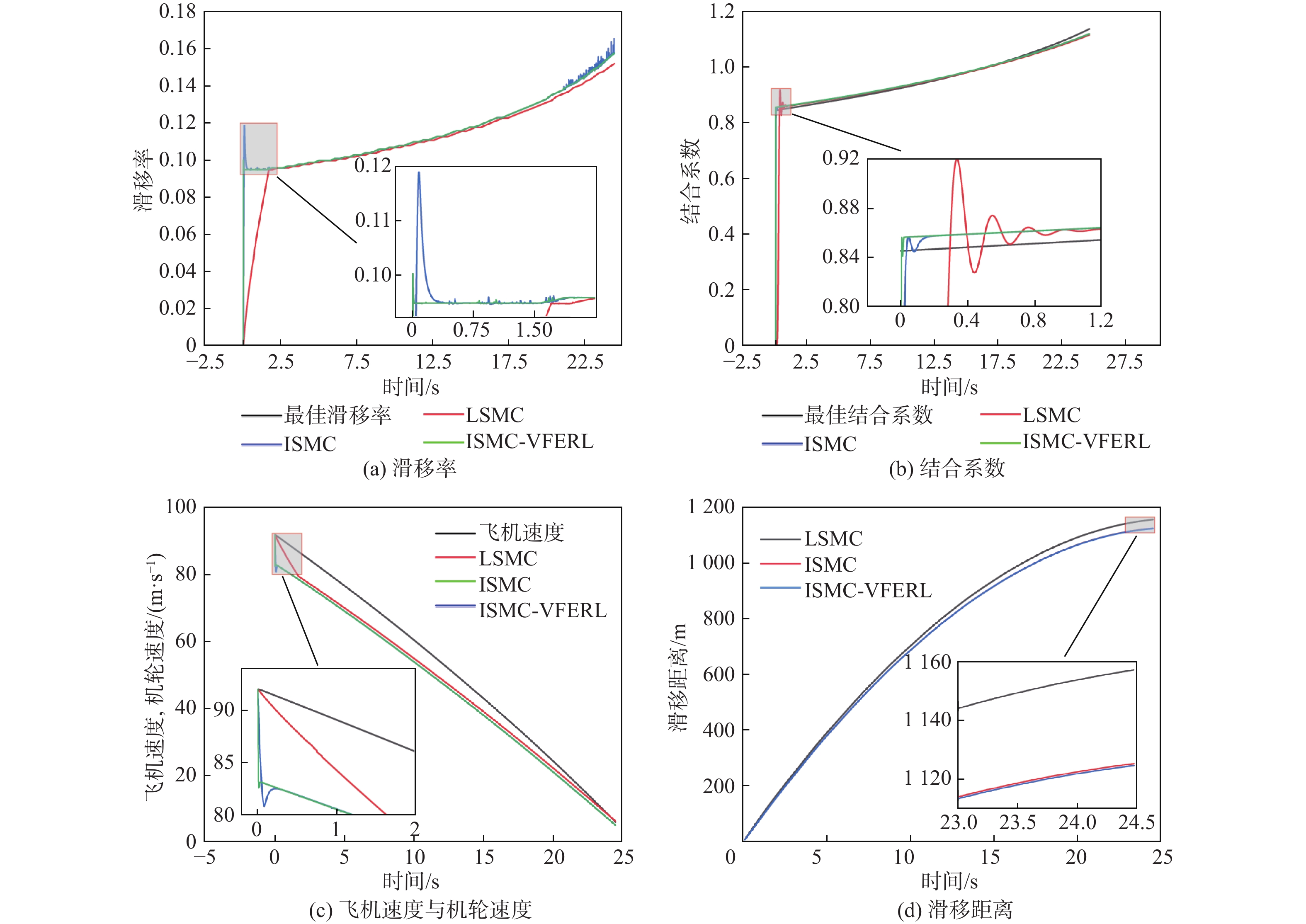
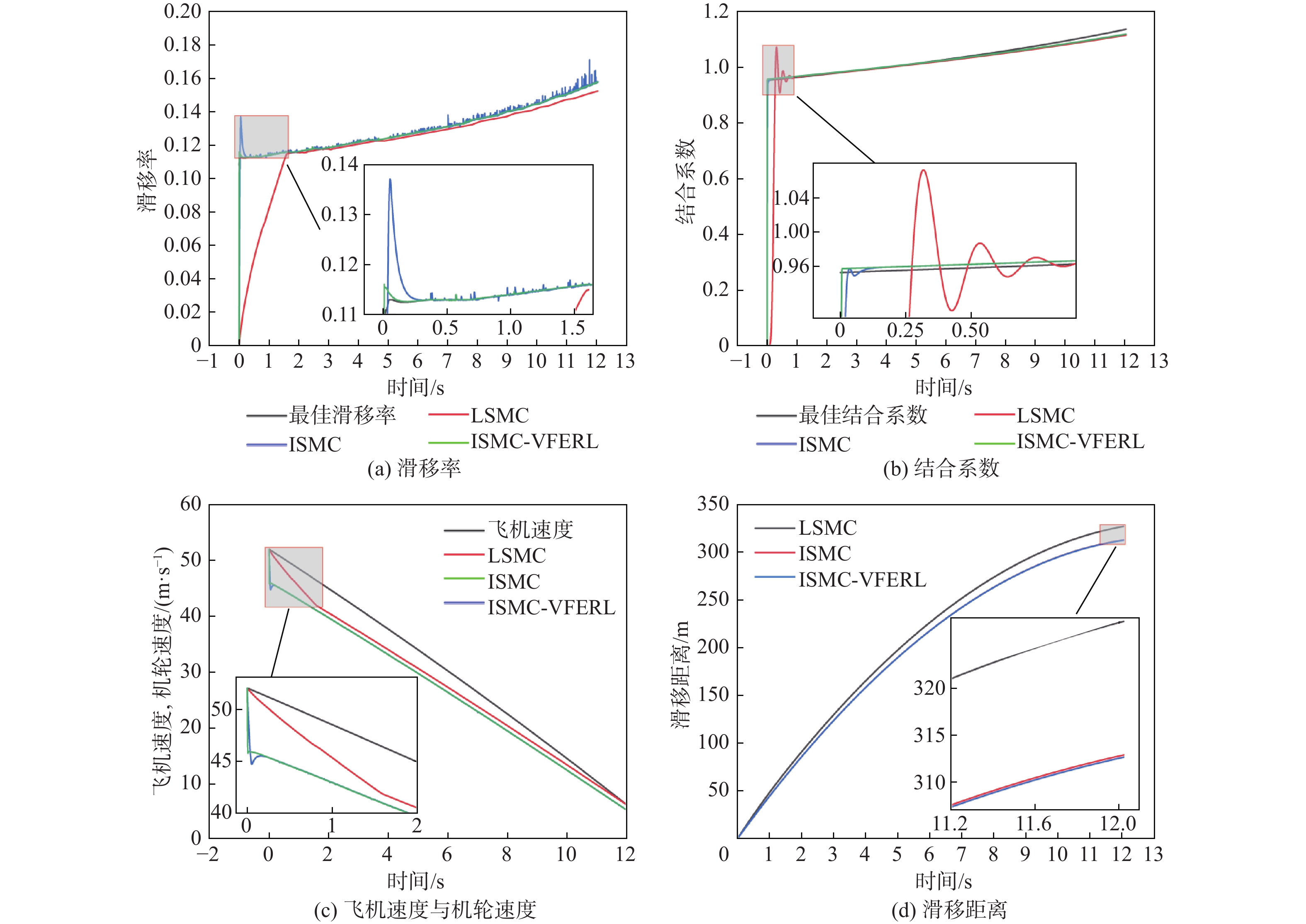
针对飞机防滑刹车系统(AABS)具有强时变性、强不可测性、内外干扰因素多的特点，提出一种变指数分数阶指数趋近律的AABS积分滑模控制(ISMC)方法。建立飞机着陆滑跑时系统的动力学模型；以提高系统快速性和鲁棒性为目标，引入变结构控制实现最佳滑移率和最大结合系数的跟踪问题；改进分数阶指数趋近律的积分滑模控制律，在抑制抖振现象的同时加快跟踪到最佳滑移率的速度；设计滑模观测器观测飞机速度，以减少存在的内外界非线性干扰；利用MATLAB仿真平台，对所提方法的可行性及有效性进行仿真验证。仿真结果表明：所设计的变指数分数阶指数趋近律的积分滑模控制器整体控制效果优于传统线性滑模控制器，滑模观测器可以精准估计飞机速度，所提方法提高了系统整体设计的鲁棒性，缩短了刹车时间和刹车距离，控制效果良好。
- 飞机防滑刹车系统 /
- 分数阶 /
- 积分滑模控制 /
- 滑移率 /
- 鲁棒性
Abstract:
Aircraft anti-skid braking system (AABS) has the characteristics of strong time variability, strong unpredictability, and many internal and external interference factors. Therefore, an integral sliding mode control (ISMC) method of AABS with variable exponential fractional order exponential reaching law was proposed. Firstly, the dynamics model of the aircraft landing system was established. Secondly, in order to improve the rapidity and robustness of the system, a variable structure control method was introduced to realize the tracking of optimal slip rate and optimal binding coefficient. Then,by improving the ISMC law of the exponential fractional order reaching law, the chattering phenomenon was suppressed, and the tracking speed to the optimal slip rate was accelerated. In addition, a sliding mode observer was designed to observe the aircraft speed to reduce the internal and external nonlinear interference. Finally, the feasibility and effectiveness of the algorithm were verified by the MATLAB simulation platform. The simulation results show that the overall control effect of the designed integral sliding mode controller with variable exponential fractional order reaching law is better than the traditional linear sliding mode controller, and the sliding mode observer can accurately estimate the aircraft speed.The method improves the robustness of the overall system design and shortens the braking time and braking distance, and the control effect is great.
- aircraft anti-skid braking system /
- fractional order /
- integral sliding mode control /
- slip rate /
- robustness

HTML全文

图 1 飞机机体受力分析

Figure 1. Force analysis of aircraft body

下载: 全尺寸图片幻灯片

${v}$ =25 m/s时不同跑道 ${\mu }$ -λ曲线

${\mu }$ -λ curves of different runways when v=25 m/s

下载: 全尺寸图片幻灯片

图 3 湿沥青跑道结合系数模型曲线

Figure 3. Binding coefficient model curves of wet asphalt runway

下载: 全尺寸图片幻灯片

图 4 飞机速度实际值与飞机速度观测值

Figure 4. Actual aircraft speed and observed aircraft speed

下载: 全尺寸图片幻灯片

图 5 飞机防滑刹车控制系统闭环控制

Figure 5. Closed-loop control diagram of AABS

下载: 全尺寸图片幻灯片

图 6 干沥青跑道下3种控制律对比

Figure 6. Comparison of three control laws under dry asphalt runway

下载: 全尺寸图片幻灯片

图 7 湿沥青跑道下3种控制律对比

Figure 7. Comparison of three control laws under wet asphalt runway

下载: 全尺寸图片幻灯片

图 8 雪跑道下3种控制律对比

Figure 8. Comparison of three control laws under snow-covered runway

下载: 全尺寸图片幻灯片

图 9 干沥青跑道顺风工况下3种控制律对比

Figure 9. Comparison of three control laws under downwind condition of dry asphalt runway

下载: 全尺寸图片幻灯片

图 10 干沥青跑道逆风工况下3种控制律对比

Figure 10. Comparison of three control laws under upwind condition of dry asphalt runway

下载: 全尺寸图片幻灯片

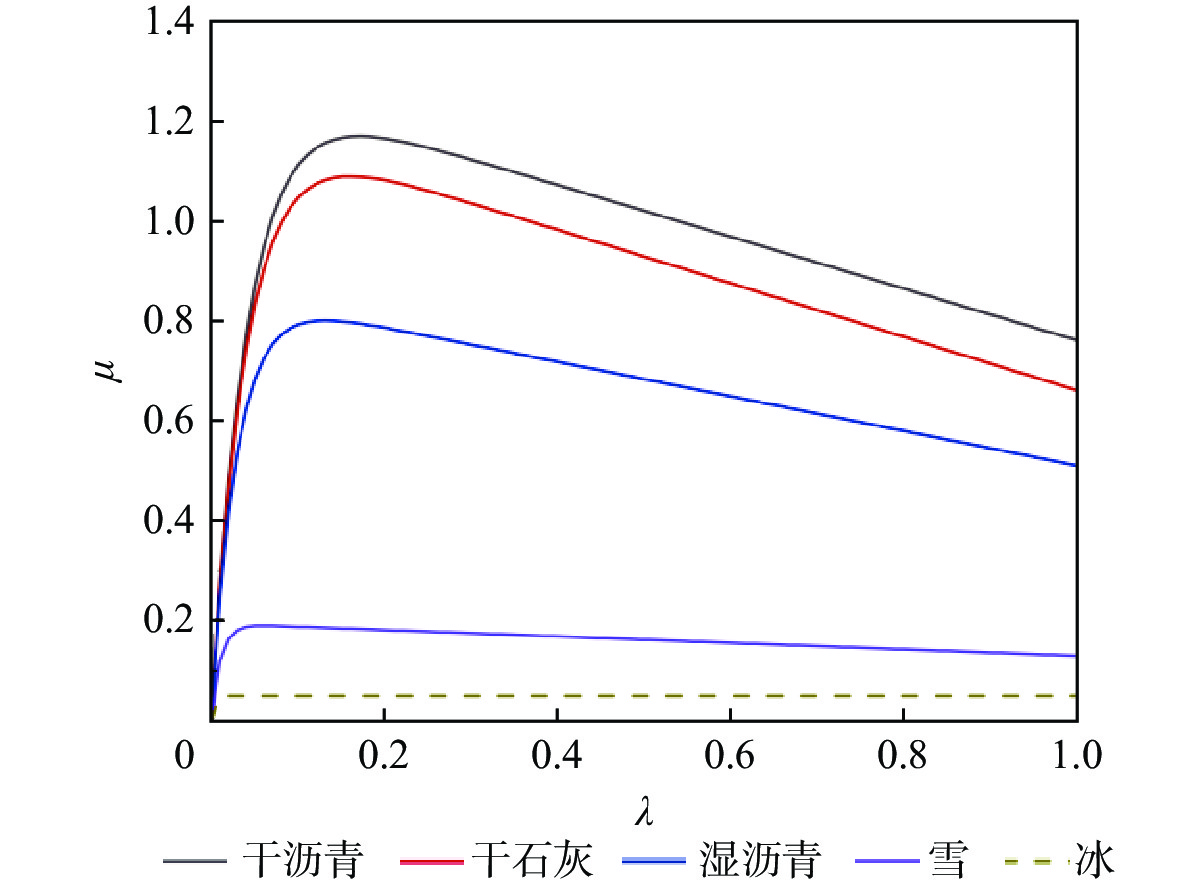
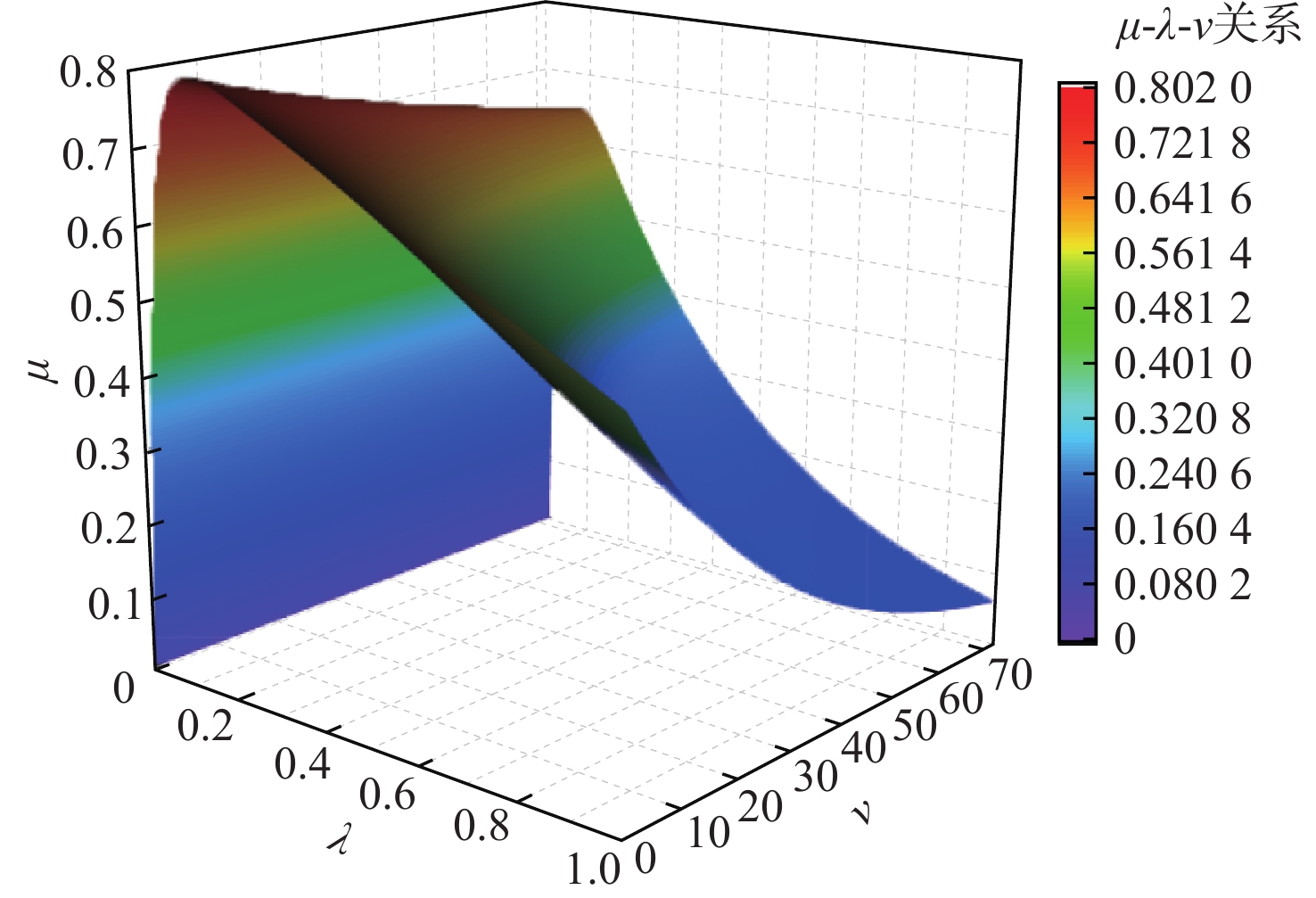
表 1 不同类型的跑道参数

Table 1. Parameters of several types of runways

跑道类型	${c_1}$	${c_2}$	${c_3}$	${c_4}$
干沥青	1.2801	23.99	0.52	0.03
干石灰	1.1973	25.168	0.5373	0.03
湿沥青	0.857	33.822	0.347	0.03
雪	0.1946	94.129	0.0646	0.03
冰	0.05	306.39	0	0.03

下载: 导出CSV

参考文献(16)

[1]	DU C L, LI F B, YANG C H, et al. Multiphase-based optimal slip ratio tracking control of aircraft antiskid braking system via second-order sliding-mode approach[J]. IEEE/ASME Transactions on Mechatronics, 2021, 27(2): 823-833.
[2]	MENG Y Z, JIANG B, QI R Y. Adaptive fault-tolerant attitude tracking control of hypersonic vehicle subject to unexpected centroid-shift and state constraints[J]. Aerospace Science and Technology, 2019, 95: 105515. doi: 10.1016/j.ast.2019.105515
[3]	JIAO Z X, SUN D, SHANG Y X, et al. A high efficiency aircraft anti-skid brake control with runway identification[J]. Aerospace Science and Technology, 2019, 91: 82-95. doi: 10.1016/j.ast.2019.05.001
[4]	QIU Y N, LIANG X G, DAI Z Y. Backstepping dynamic surface control for an anti-skid braking system[J]. Control Engineering Practice, 2015, 42: 140-152. doi: 10.1016/j.conengprac.2015.05.013
[5]	TANG Y G, ZHANG X Y, ZHANG D L, et al. Fractional order sliding mode controller design for antilock braking systems[J]. Neurocomputing, 2013, 111: 122-130. doi: 10.1016/j.neucom.2012.12.019
[6]	HUŠEK P. Adaptive sliding mode control with moving sliding surface[J]. Applied Soft Computing, 2016, 42: 178-183. doi: 10.1016/j.asoc.2016.01.009
[7]	SAVITSKI D, IVANOV V, AUGSBURG K, et al. Wheel slip control for the electric vehicle with in-wheel motors: variable structure and sliding mode methods[J]. IEEE Transactions on Industrial Electronics, 2019, 67(10): 8535-8544.
[8]	LI L B, SUN L L, ZHANG S Z. Mean deviation coupling synchronous control for multiple motors via second-order adaptive sliding mode control[J]. ISA Transactions, 2016, 62: 222-235. doi: 10.1016/j.isatra.2016.01.015
[9]	JIAO Z X, WANG Z Z, SUN D, et al. A novel aircraft anti-skid brake control method based on runway maximum friction tracking algorithm[J]. Aerospace Science and Technology, 2021, 110: 106482. doi: 10.1016/j.ast.2020.106482
[10]	D’AVICO L, TANELLI M, SAVARESI S M, et al. An anti-skid braking system for aircraft via mixed-slip-deceleration control and sliding mode observer[C]//Proceedings of the IEEE 56th Annual Conference on Decision and Control. Piscataway: IEEE Press, 2017: 4503-4508.
[11]	CHEN M Q, XU F R, LIANG X L, et al. MSD-based NMPC aircraft anti-skid brake control method considering runway variation[J]. IEEE Access, 2021, 9: 51793-51804. doi: 10.1109/ACCESS.2021.3070066
[12]	李繁飙, 黄培铭, 阳春华, 等. 基于非线性干扰观测器的飞机全电刹车系统滑模控制设计[J]. 自动化学报, 2021, 47(11): 2557-2569. LI F B, HUANG P M, YANG C H, et al. Sliding mode control design of aircraft electric brake system based on nonlinear disturbance observer[J]. Acta Automatica Sinica, 2021, 47(11): 2557-2569(in Chinese).
[13]	BAKKER E, NYBORG L, PACEJKA H B. Tyre modelling for use in vehicle dynamics studies[R]. Warrendale: SAE International, 1987: 190-204.
[14]	KIENCKE U, NIELSON L. Automotive control systems: forengine, driveline, and vehicle[J]. Measurement Science and Technology, 2000, 11(12): 1828.
[15]	林程, 梁晟, 宫新乐, 等. 面向极限工况的分布式驱动电动汽车动力学集成控制方法[J]. 汽车工程, 2022, 44(9): 1372-1385. LIN C, LIANG S, GONG X L, et al. Integrated dynamic control strategy for extreme maneuvers of 4WIDEVs[J]. Automotive Engineering, 2022, 44(9): 1372-1385(in Chinese).
[16]	EFE M O. Fractional fuzzy adaptive sliding-mode control of a 2-DOF direct-drive robot arm[J]. IEEE Transactions on Systems, Man, and Cybernetics Part B, Cybernetics, 2008, 38(6): 1561-1570. doi: 10.1109/TSMCB.2008.928227