基于异常点重构的调频引信抗扫频干扰方法

段乐帆; 郝新红; 陈齐乐

doi:10.13700/j.bh.1001-5965.2023.0199

基于异常点重构的调频引信抗扫频干扰方法

doi: 10.13700/j.bh.1001-5965.2023.0199

北京理工大学机电动态控制重点实验室，北京 100081

基金项目: 国家自然科学基金(61973037)

详细信息

通讯作者:
E-mail：haoxinhong@bit.edu.cn

中图分类号: V221⁺.3；TB553
计量
- 文章访问数: 166
- HTML全文浏览量: 79
- PDF下载量: 4
- 被引次数: 0
出版历程
- 收稿日期: 2023-04-21
- 录用日期: 2023-06-16
- 网络出版日期: 2023-07-11
- 整期出版日期: 2025-04-30

Anti-sweep jamming method for FM fuze based on outlier reconstruction

Science and Technology on Electromechanical Dynamic Control Laboratory，Beijing Institute of Technology，Beijing 100081，China

Funds: National Natural Science Foundation of China (61973037)

More Information

Corresponding author: E-mail：haoxinhong@bit.edu.cn

摘要

摘要:
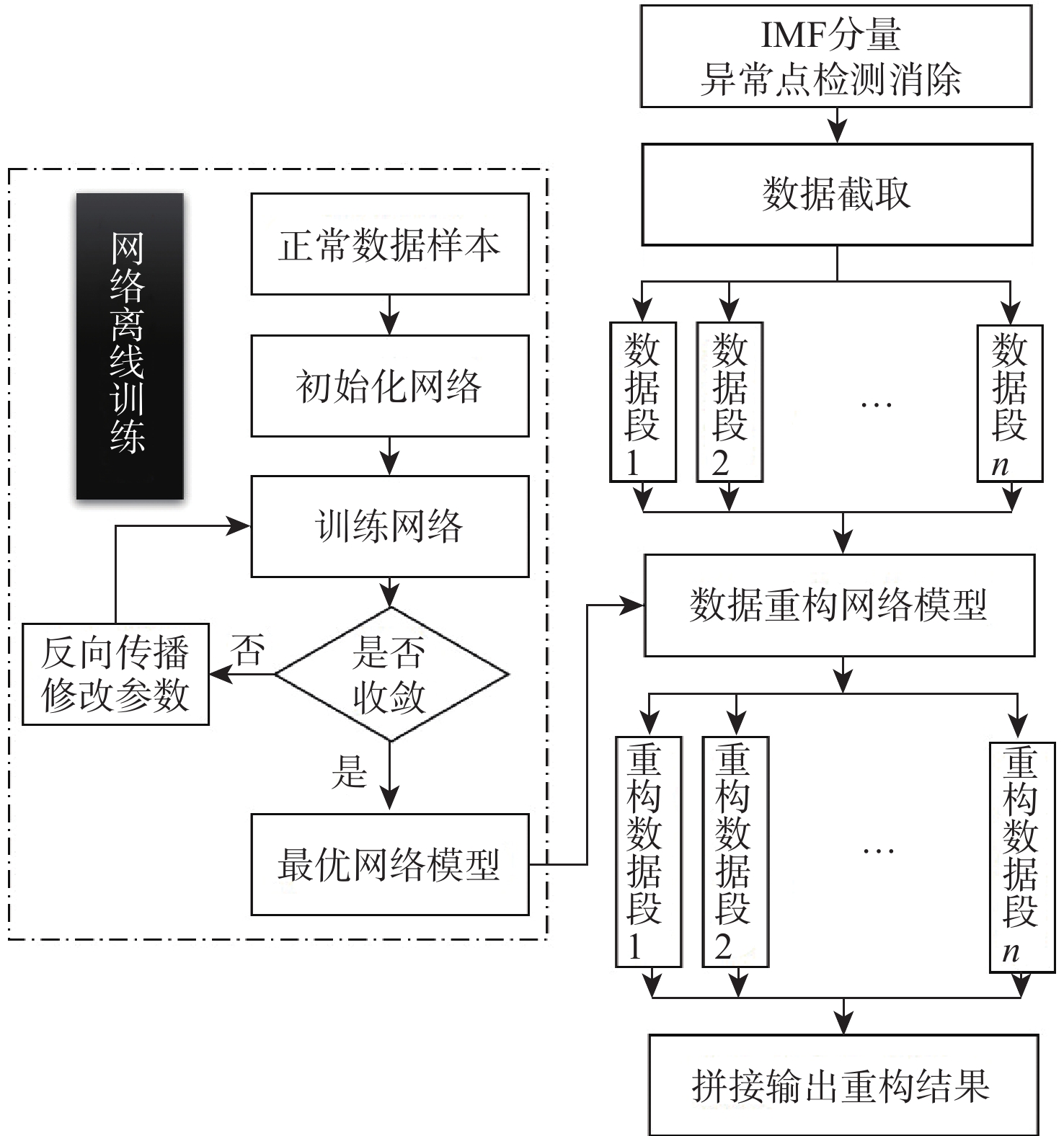
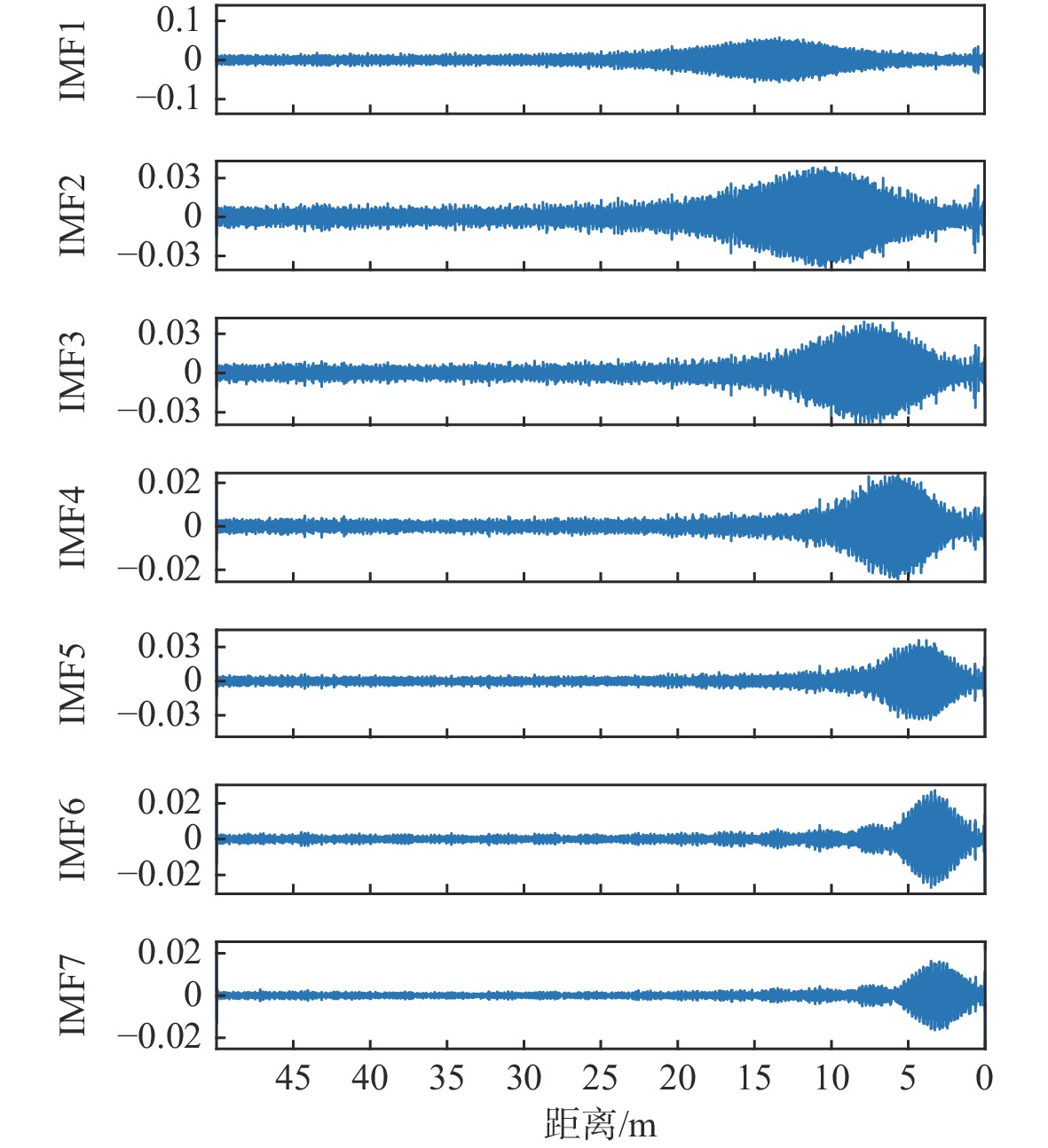
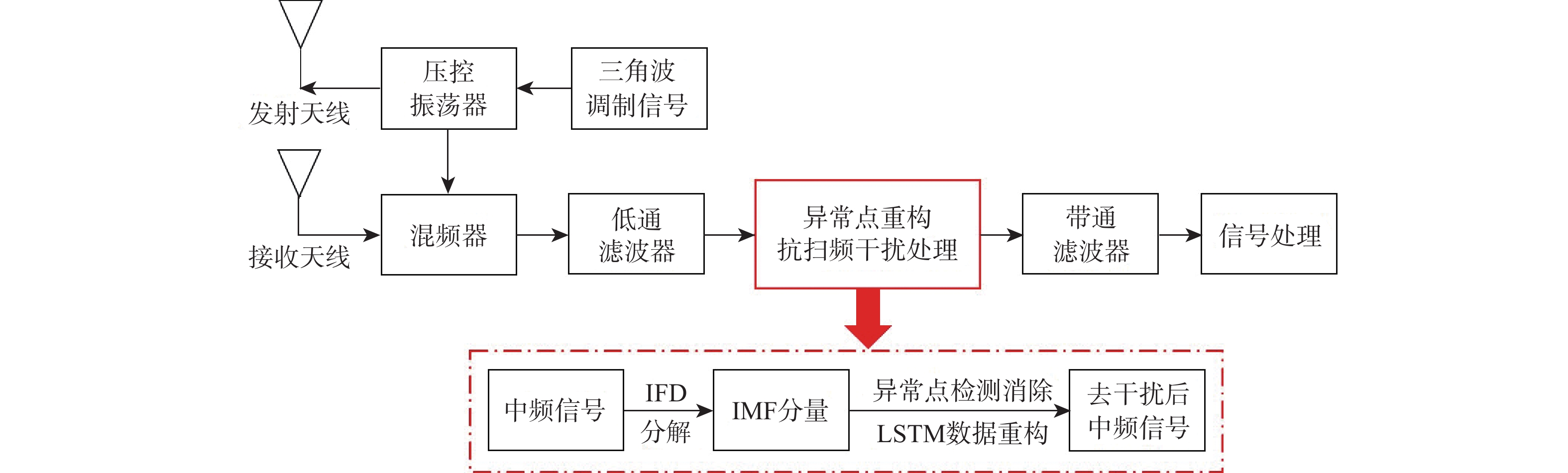
针对调频引信对抗扫频式干扰的问题，提出一种基于异常点重构的调频引信抗扫频干扰方法。该方法基于迭代滤波分解(IFD)算法，将引信中频信号分解为本征模态函数(IMF)分量；扫频干扰在IMF分量中表现为异常点，对IMF分量进行异常点检测与消除，并利用长短时记忆(LSTM)网络构建数据重构网络模型，对异常点部分进行数据重构，可以实现对扫频干扰的抑制。通过仿真验证了所提方法的有效性，结果表明该方法提高了调频引信对抗扫频式干扰的能力。
- 调频引信 /
- 扫频式干扰 /
- 抗干扰方法 /
- 异常点重构 /
- 迭代滤波分解 /
- 长短时记忆网络
Abstract:
An anti-sweep jamming method for frequency modulation (FM) fuze based on outlier reconstruction was proposed for the problem of FM fuze against sweep jamming. Based on the iterative filtering decomposition (IFD) algorithm, the intermediate frequency signal of fuze was decomposed into intrinsic mode function (IMF) components. Sweep jamming was represented as outliers in the IMF components. By detecting and eliminating outliers in the IMF components and using a long short-term memory (LSTM) network to build a data reconstruction network model, the data of outliers was reconstructed, and the sweep jamming could be suppressed. The effectiveness of the proposed method was verified by simulation. The results show that the proposed method improves the ability of FM fuze against sweep jamming.
- frequency modulation fuze /
- sweep jamming /
- anti-jamming method /
- outlier reconstruction /
- iterative filtering decomposition /
- long short-term memory network

HTML全文

图 1 抗干扰总体方案

Figure 1. General scheme of anti-jamming

下载: 全尺寸图片幻灯片

图 2 IFD算法流程

Figure 2. Flow chart of IFD algorithm

下载: 全尺寸图片幻灯片

图 3 LSTM单元结构

Figure 3. LSTM unit structure

下载: 全尺寸图片幻灯片

图 4 数据重构流程

Figure 4. Flow chart of data reconstruction

下载: 全尺寸图片幻灯片

图 5 无扫频干扰时中频信号IFD分解结果

Figure 5. IFD results of intermediate frequency signal without sweep jamming

下载: 全尺寸图片幻灯片

图 6 IMF6分量功率谱分析

Figure 6. Power spectrum analysis of IMF6 component

下载: 全尺寸图片幻灯片

图 7 扫频式干扰作用下引信输出

Figure 7. Fuze output under sweep jamming

下载: 全尺寸图片幻灯片

图 8 扫频干扰作用下中频信号IMF6分量

Figure 8. IMF6 component of intermediate frequency signal under sweep jamming

下载: 全尺寸图片幻灯片

图 9 异常点消除后的IMF6分量

Figure 9. IMF6 component after outlier removal

下载: 全尺寸图片幻灯片

图 10 数据重构后的IMF6分量

Figure 10. IMF6 component after data reconstruction

下载: 全尺寸图片幻灯片

图 11 采用异常点重构抗干扰方法的引信输出

Figure 11. Fuze output using anti-jamming method by outlier reconstruction

下载: 全尺寸图片幻灯片

表 1 仿真参数

Table 1. Simulation parameters

类别	数值
载波频率/MHz	300
调制频偏/MHz	25
调制频率/kHz	100
采样频率/MHz	5
扫频起始频率/MHz	200
扫频带宽/MHz	200
扫频点数	100
驻留时间/μs	2
干信比/dB	0

下载: 导出CSV

表 2 LSTM网络参数

Table 2. LSTM network parameters

类别	数值
输入层特征数	1
LSTM层隐含单元数	50
全连接层输出维数	1
最大训练周期	200
初始学习率	0.01
学习率折损周期	100
学习率折损因子	0.1

下载: 导出CSV

表 3 谐波信号数据重构相似度

Table 3. Similarity of harmonic signal data reconstruction

干信比/dB	数据重构相似度/%
0	93.67
5	92.53
10	90.80

下载: 导出CSV

表 4 各方法的数据重构相似度与平均处理时间

Table 4. Data reconstruction similarity and average processing time of each method

核心算法	数据重构相似度/%	平均处理时间/s
IFD	90.80	0.0027
EEMD	84.26	4.9404
SSA	87.56	1.5795

下载: 导出CSV

参考文献(20)

[1]	崔占忠, 宋世和, 徐立新. 近炸引信原理[M]. 3版. 北京: 北京理工大学出版社, 2009: 112-119. CUI Z Z, SONG S H, XU L X. Principle of proximity fuze[M]. 3rd ed. Beijing: Beijing Institute of Technology Press, 2009: 112-119 (in Chinese).
[2]	赵惠昌. 无线电引信设计原理与方法[M]. 北京: 国防工业出版社, 2012: 35. ZHAO H C. Fundamentals and methodology of radio fuze[M]. Beijing: National Defense Industry Press, 2012: 35 (in Chinese).
[3]	GIAQUINTO G, HARTLEY T. ALQ-218(V)(ICAP III)[J]. An electronic Warfare Forecast, 2012 (APR.): 23-28.
[4]	RAO G N, SASTRY C S, DIVAKAR N. Trends in electronic warfare[J]. IETE Technical Review, 2003, 20: 139-150. doi: 10.1080/02564602.2003.11417078
[5]	岳凯, 郝新红, 栗苹, 等. 基于分数阶傅里叶变换的线性调频引信定距方法[J]. 兵工学报, 2015, 36(5): 801-808. doi: 10.3969/j.issn.1000-1093.2015.05.006 YUE K, HAO X H, LI P, et al. Research on ranging method for linear frequency modulation radio fuze based on fractional Fourier transform[J]. Acta Armamentarii, 2015, 36(5): 801-808 (in Chinese). doi: 10.3969/j.issn.1000-1093.2015.05.006
[6]	张天鹏, 刘忙龙, 谢嘉. 基于FRFT的调频引信LFM干扰抑制改进方法[J]. 探测与控制学报, 2019, 41(2): 22-25. ZHANG T P, LIU M L, XIE J. Improvement of FM fuze LFM interference suppression based on FRFT[J]. Journal of Detection & Control, 2019, 41(2): 22-25(in Chinese).
[7]	孔志杰, 郝新红, 栗苹, 等. 调频引信谐波时序检测抗干扰方法及实现[J]. 北京航空航天大学学报, 2018, 44(3): 549-555. KONG Z J, HAO X H, LI P, et al. Harmonic timing sequence detection anti-jamming method and its implementation for FM fuze[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(3): 549-555(in Chinese).
[8]	陈齐乐, 郝新红, 闫晓鹏, 等. 变调制率调频引信双通道相关检测抗数字射频存储干扰方法[J]. 兵工学报, 2019, 40(3): 449-455. doi: 10.3969/j.issn.1000-1093.2019.03.001 CHEN Q L, HAO X H, YAN X P, et al. Anti-DRFM jamming method using dual-channel harmonic correlation detection for variable chirp rate FM fuze[J]. Acta Armamentarii, 2019, 40(3): 449-455(in Chinese). doi: 10.3969/j.issn.1000-1093.2019.03.001
[9]	陈齐乐, 郝新红, 闫晓鹏, 等. 基于谐波系数幅值平均的复合调制引信抗扫频式干扰方法[J]. 北京航空航天大学学报, 2020, 46(7): 1317-1324. CHEN Q L, HAO X H, YAN X P, et al. Anti sweep jamming method of hybrid modulation fuze based on harmonic coefficient amplitude averaging[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(7): 1317-1324(in Chinese).
[10]	李泽, 闫晓鹏, 栗苹, 等. 扫频式干扰对调频多普勒引信的干扰机理研究[J]. 兵工学报, 2017, 38(9): 1716-1722. doi: 10.3969/j.issn.1000-1093.2017.09.007 LI Z, YAN X P, LI P, et al. Jamming mechanism of frequency sweep jamming to FM Doppler fuze[J]. Acta Armamentarii, 2017, 38(9): 1716-1722(in Chinese). doi: 10.3969/j.issn.1000-1093.2017.09.007
[11]	LIN L, WANG Y, ZHOU H M. Iterative filtering as an alternative algorithm for empirical mode decomposition[J]. Adv Data Sci Adapt Anal, 2009, 1: 543-560. doi: 10.1142/S179353690900028X
[12]	HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A, 1998, 454(1971): 903-998. doi: 10.1098/rspa.1998.0193
[13]	CICONE A. Iterative filtering as a direct method for the decomposition of nonstationary signals[J]. Numerical Algorithms, 2020, 85(3): 811-827. doi: 10.1007/s11075-019-00838-z
[14]	CICONE A, ZHOU H M. Numerical analysis for iterative filtering with new efficient implementations based on FFT[J]. Numerische Mathematik, 2021, 147(1): 1-28. doi: 10.1007/s00211-020-01165-5
[15]	CICONE A, LIU J F, ZHOU H M. Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis[J]. Applied and Computational Harmonic Analysis, 2016, 41(2): 384-411. doi: 10.1016/j.acha.2016.03.001
[16]	HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9: 1735-1780. doi: 10.1162/neco.1997.9.8.1735
[17]	MA X L, TAO Z M, WANG Y H, et al. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data[J]. Transportation Research Part C: Emerging Technologies, 2015, 54: 187-197. doi: 10.1016/j.trc.2015.03.014
[18]	ALI M M, BABAR M I, HAMZA M, et al. Industrial financial forecasting using long short-term memory recurrent neural networks[J]. International Journal of Advanced Computer Science and Applications, 2019, 10(4): 14.
[19]	WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. doi: 10.1142/S1793536909000047
[20]	ELSNER J B, TSONIS A A. Singular Spectrum Analysis[M]. Boston: MASpringer US, 1996.