-
摘要:
全球导航卫星系统反射测量(GNSS-R)海面测高作为GNSS技术应用领域之一，其凭借全天时、低成本、高时空分辨率等特点在海洋遥感领域占据极大的优势。但受GNSS码片宽度的限制，岸基GNSS-R码延迟海面测高的最优精度仅为分米级，难以满足大地测量学领域对海面高的精度要求。提出利用傅里叶级数拟合法对码延迟测高结果进行优化，并于山东省威海市开展GNSS-R码测高实验进行验证，分别对QZSS L2C信号、QZSS L5信号及GPS L5信号的码延迟测高结果进行拟合处理并计算反演精度，对比原始测高结果发现：3段不同时长的原始测高结果经过傅里叶级数拟合优化后，其均方根误差(RMSE)从70～90 cm提升至9～15 cm。在此基础上，利用拟合所得傅里叶级数曲线对未来24 h内的海面高进行预测，与验潮站数据相比，预测结果仍保持较高精度，RMSE为13～18 cm，相关系数大于0.97。结果表明所提出的方法不仅能对码延迟测高结果进行优化，能对存在数据缺失的情况进行补充，还能对未来海面高度进行高精度的预测。
-
关键词:
- 岸基 /
- 全球导航卫星系统反射测量 /
- 码延迟 /
- 海平面高度 /
- 傅里叶级数拟合
Abstract:With the continuous innovation of GNSS technology, its application fields continue to expand. Because of its all-weather capabilities, low cost, and high spatiotemporal resolution, Global Navigation Satellite System-Reflectometry (GNSS-R) sea surface altimetry has many benefits in the field of ocean remote sensing. However, due to the limitation of GNSS chip width, the optimal accuracy of shore-based GNSS-R code-delay sea level measurements is only decimeter level, which makes it difficult to meet the accuracy requirements of Geodesy for sea surface height. In order to maximize the GNSS-R code-delay altimetry results, this research suggested using the Fourier series fitting method. To validate the suggested approach, GNSS-R code altimetry experiments were conducted in Weihai City, Shandong Province. The code-delay altimetry results of QZSS L2C signal, QZSS L5 signal and GPS L5 signal are respectively fitted and processed, and the inversion accuracy is calculated. When compared to the original altimetry findings, it is discovered that the RMSEs of the three original altimetry values with varying lengths have improved from 70-90 cm to 9-15 cm following Fourier series fitting. On this basis, the sea surface heights in the next 24 hours are predicted using the fitted Fourier series curve. Compared with the tide gauge data, the prediction results still maintain high accuracy, with RMSE of 13-18 cm and correlation a coefficient greater than 0.97. The above results indicate that the method proposed in this article can not only optimize the code-delay height measurement results and supplement the missing data, but also make high-precision predictions for future sea levels.
-
Key words:
- shore-based /
- GNSS-R /
- code delay /
- sea surface height /
- Fourier series fitting
-
由于全球变暖日益加剧，冰川融化导致海平面不断上升，因此对海平面变化的监测和研究越来越重要。海平面高度是衡量海平面变化的重要指标，对人类社会有着重要的研究意义，其观测手段也日益发展。传统监测方法有验潮站和卫星雷达测高等，其优点主要是观测精度较高，但时空分辨率低且成本较高。随着全球卫星导航系统(Global Navigation Satellite System，GNSS)的不断发展，GNSS-R(Global Navigation Satellite System-Reflectometry)技术应运而生，GNSS-R可以应用在海洋遥感方面，包括海面风场[1-5]、海面测高[6-10]、海面溢油[11-13]以及海冰监测[14-17]等不同方向。其中的GNSS-R海面测高技术与传统监测手段相比，具有低成本和高时空分辨率等优势。
随着GNSS-R技术的发展，国内外学者开展了一系列岸基、空基和星基的GNSS-R观测实验，空间分辨率不断提高。其中的岸基GNSS-R测高可以为近海海域海面高度监测提供一种新方式。由于岸基GNSS-R成本低且实验便捷，因此可以很好地解决传统监测方法成本高等问题，同时开展岸基GNSS-R研究还可以辅助星载观测。岸基GNSS-R测高是将观测设备架设在观测海域附近的海岸上来实现对海面高度的监测。根据观测量的不同，GNSS-R测高法主要有两种：一种是基于多路径信噪比的海面测高方法，即GNSS-IR (GNSS Interferometric Reflectometry) 测高法。GNSS-IR测高法仅可在卫星高度角较低时观测，且整个观测弧段得到一个反演结果，因此造成其有效观测值的数目大幅减少、时间分辨率降低。另一种是基于相位差的海面测高方法，包括载波相位法和码相位法。在基于相位差的测高方法中，当海面波动较大时，接收机无法稳定跟踪载波相位，然而码相位测高方法可以相对不受海面环境的影响。因此本文致力于开展岸基GNSS-R码相位测高方法研究。
1993年，Martin-Neira[18]提出了Paris（Passive Reflectometry and Interferometry System）概念，证实了GNSS-R的可行性。1997年9月，Martin-Neira团队在荷兰基于双天线码相位测高方法首次开展岸基海面测高实验，最终得到5 s内观测结果误差约为3.3 m，测高精度是L1C/A码片长度的1%[19]。1999年，Treuhaft等[20]通过相位测量的方法得到了误差为2 cm的湖面测高结果。2002年9月，王鑫等[21]在中国福建进行了我国首个岸基GNSS-R实验，实验最终得到有效波高参数。2010年，白伟华等[22]通过开环相位测高技术对湖面高度进行反演，其测高精度可达到厘米级。Carreno-Luengo等[8]在2012年实验通过码测高得到了亚米级的海面高结果。2015年，Zhang等[23]在浙江大洋山海域开展基于北斗二代信号的岸基海面测高研究，其结果表明测高精度达到了亚米级。2021年，储倜等[24]开展岸基GNSS-R海面测高实验，实验表明基于QZSS（Quasi-Zenith Satellite System） L1 C/A 码和L1C码的海面测高精度最优可达0.63 m和0.4 m。2022年，侯金华等[25]发现基于B1C码的GNSS-R海面测高最优精度达到分米级，据10 s观测数据的平滑结果显示：单颗卫星最优测高结果的RMSE为0.634 m，多卫星观测值加权组合最优结果的RMSE为0.538 m。
尽管GNSS-R码测高可提供高时空分辨率和稳定的测高结果，但受GNSS码片宽度限制和测量误差的影响，经过码延迟计算的岸基GNSS-R测高结果精度在米级，最优可达分米级[26,27]。这样的测高精度难以满足大地测量学研究中对海面高度精度的要求，例如，从海面高度获取海洋重力场数据往往需要海面高度的精度为厘米级。文献[6,23,24]使用滑动平均法对海面高度结果进行后处理，但其结果不能如实准确地反映海平面变化。因此，本文致力于研究GNSS-R码测高反演模型来提高海面高精度。在山东省威海市开展3次GNSS-R码测高实验，通过提出的傅里叶级数拟合法对原始测高结果进行后处理。结果发现，该方法不仅能够大幅度提高GNSS-R码测高反演精度，弥补数据缺失，还能对海平面高度进行预测。
1. GNSS-R测高
1.1 GNSS-R测高原理
GNSS-R码相位海面测高技术的关键是分别利用上视和下视的接收天线获取直、反射中频信号、通过自主研发的软件接收机[6]处理中频信号得到直、反射信号的码相位路径延迟、结合岸基GNSS-R海面测高模型由码相位路径延迟计算得到反射面到直射接收天线的高度。再通过直射天线获取的信号利用传统定位方法如精密单点定位（PPP）等得到直射天线到参考椭球面的高度H，最后计算得到海平面高度值。
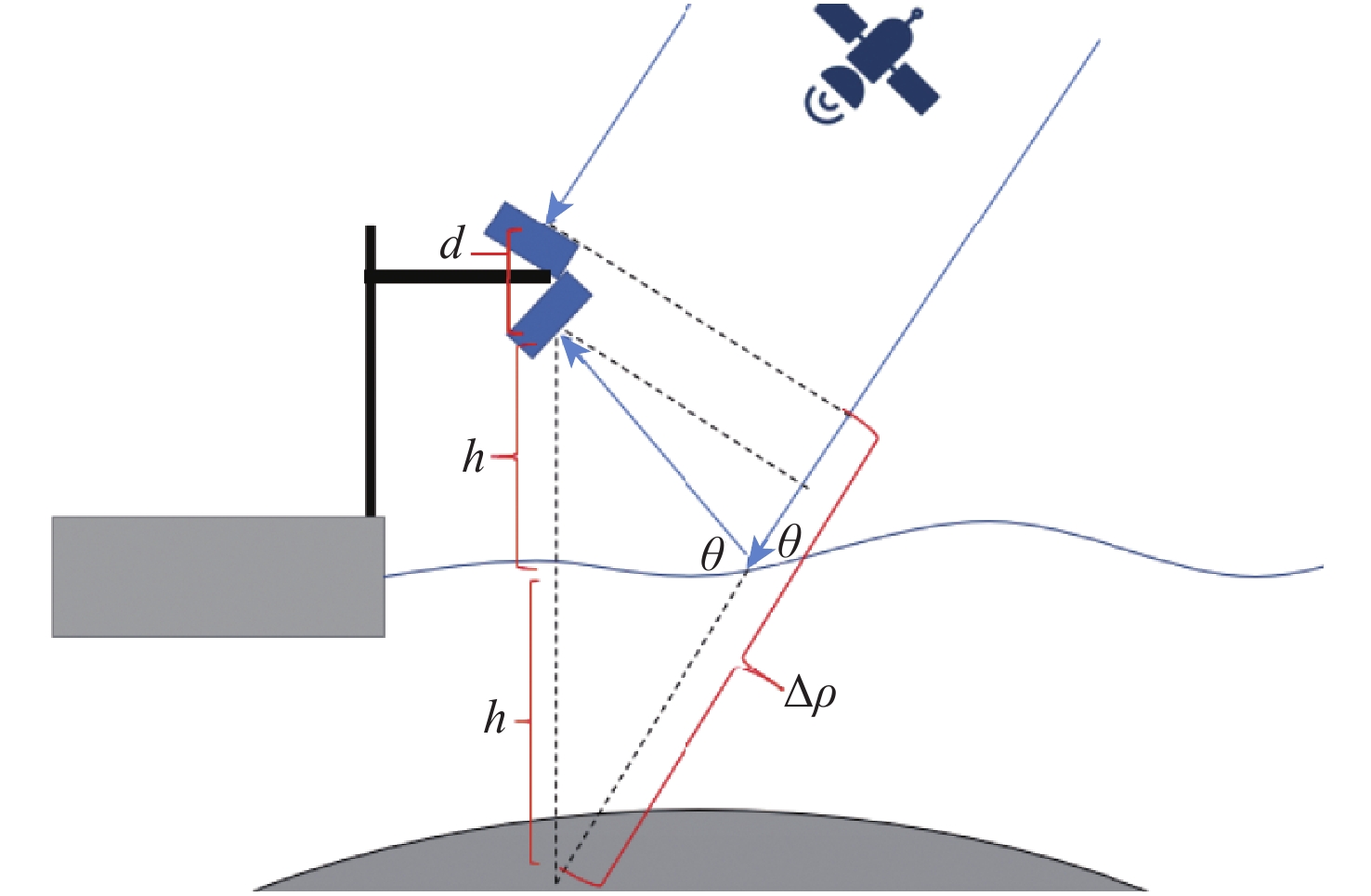
GNSS-R码相位海面测高实验的几何结构如图1所示：h是反射天线相位中心到海面的垂直高度、θ为GNSS卫星高度角、d代表直射天线和反射天线的相位中心距离、Δρ是直射信号和反射信号之间的路径延迟(上述100个路径延迟的中值)、ε为海面高度测量误差，根据图1所示的几何关系可得
图 1 岸基GNSS-R码延迟海面测高模型Figure 1. Shore-based GNSS-R code delayed sea level altimeter modelHSSH=H−Δρ−dsinθ2sinθ+ε (1) 文献[28]研究表明，高度角对GNSS-R测高结果有一定的影响，且在低高度角时误差较大。因此一般采用高高度角数据进行计算，本文数据处理限制高度角设置为30°。为保证反射信号来自海面，设置观测方位角为140°～300°。
其中，GNSS-R信号数据处理部分简述如下：直射和反射天线接收到的右旋直射信号和左旋反射信号，经过射频前端的滤波器和放大器滤波放大后，再下变频为中频信号，后经模数转换为数字中频信号。数字中频信号传至软件接收机的基带信号处理模块实现下变频，剥离载波后成为基带信号。与本地复制码进行相干积分后输出相应的多普勒频移和码相位信息，最后计算得到反射信号相对于直射信号的码延迟Δρ。本文软件接收机采用的相干积分时长为10 ms，再将1 s内所得的100个路径延迟取中值作为该秒的最终路径延迟。详细描述见文献[28]。
1.2 傅里叶级数拟合法后处理GNSS-R反演高度
通过上述GNSS-R码测高得到的海面高度最优可达分米级。在海面高度研究领域，上述所得分米级的测高结果难以满足大地测量领域的需求。同时，上述测高结果的时间分辨率是由原始中频数据的采样率和接收机对数据处理时的相干积分共同决定的。利用本文的接收机处理，得到的海面高时间分辨率为1 s。而每1 s的海面高实际上是由10 ms的信号经由数据处理得到的。10 ms的反射信号会受到海面瞬时浪高、瞬时波高等的影响进而对海面高结果产生误差。另外，受GNSS卫星分布以及限制高度角的影响，GNSS-R测高结果并不是每秒都可得到，甚至可能会出现较长时间的数据缺失。为了对GNSS-R原始码测高结果进一步处理，弥补数据缺失以及提高GNSS-R海面测高精度，我们提出利用傅里叶级数拟合法对GNSS-R原始测高数据进行建模处理。该方法的基本原理简述如下。
傅里叶级数是一种基于函数形态和函数参数拟合的方法，通过将复杂的函数分解为一系列简单的正弦周函数的级数相加，可将离散数据进行拟合、插值和滤波等，可大大提高函数拟合的精度。其表达式如下：
f(x)=m∑i=0[aicos(ixw)+bisin(ixw)] (2) 式中：x为待拟合数据；i为某一阶数；m为总阶数；w为频率；ai和bi为系数。
而在经典潮汐调和分析模型中，海平面高度可以认为是一系列余弦函数线性叠加的结果，每一个余弦函数都代表了一个分潮：
Z(t)=S0+J∑j=1(Hjcos(σjt−gj)) (3) 式中：Z(t)是时刻t观测到的水位；S0是平均海平面；σj、Hj、gj分别为第j分潮对应的角频率、振幅和迟角。
若考虑经由1.1节计算得到的GNSS-R码测高原始结果，将其视为离散数据x，代入式（2），选择阶数m， 即可得到拟合后的海面高度f(x)。对比式（2） 和式（3）可以发现，若将式（3）展开，可化为式（2）的形式，也就是说，可以用傅里叶级数（式（2））来表示GNSS-R海面高度。因此，本文提出用傅里叶级数拟合GNSS-R测高结果，以提高GNSS-R海面高观测精度。
2. GNSS-R实验概况
2.1 实验场景
为验证本文理论内容，分别采用了不同时长的3段实验数据：第1段于2020年11月5日在山东威海一栈桥处（N:37°32′ E:122°2′）开展双天线岸基GNSS-R海面测高实验采集到的GPS L5 近8 h数据。第2段于2021年3月30日在同地采集到的QZSS L2C频点 6 h数据，两次实验场地如图2所示。第3段于2023年5月27日距离栈桥直线距离约3 km外的小石岛采集到的QZSS L5 24 h数据，实验地点如图3所示。
图 2 2020年11月5日及2021年3月30日实验环境及实验地点Figure 2. Experimental environment and experimental location on 5 November 2020 and 30 March 2021
图 3 2023年5月27日实验环境及实验地点Figure 3. Experimental environment and experimental location on 27 May 2023从图2中可以看出，GNSS-R天线以及接收机架设于深入海岸线约100 m的海边栈桥，距其约20 m的位置处安置了雷达测高仪。图3中 距离该实验地点5 m处有一验潮站，采用验潮站数据作为比对数据。该实验地点与栈桥直线距离约为3 km。
3次实验的实验场地附近没有遮挡，采集数据时海面较为平静。采集到的中频数据通过笔记本电脑保存到移动硬盘中，并用1.2节所描述的软件接收机进行进一步处理，最终获得海面高度结果。
2.2 实验地点潮汐变化
中国渤海、东海、黄海的多数地点为半日潮型，即一个太阴日内出现两次高潮和两次低潮，其涨潮过程和落潮过程的时间也几乎相等约为6 h，本实验海域即为半日潮型。
表1是GNSS-R码相位海面测高实验地点附近海域在3段实验期间的潮汐变化表。
表 1 3次实验期间实验地点潮汐变化表Table 1. Table of tidal change at experimental site during the three experiments潮汐 潮时 潮高(峰值)/cm 第1段 第2段 第3段 第1段 第2段 第3段 干潮 05:35 04:29 00:40 37 45 84 满潮 11:27 10:17 07:26 222 209 239 干潮 17:53 16:06 14:26 42 55 65 满潮 23:48 22:25 20:15 221 242 196 从表1中可知：实验期间每天出现2次满潮和2次干潮，满潮与干潮时的潮高峰值第1段相差约为180 cm、第2段相差约为150 cm、第3段相差约为170 cm。为了验证所述方法的正确性，采用了包含不同海面高变化过程的3段GNSS-R数字中频信号进行处理：第1段18:00−24:00时共6 h仅包含涨潮阶段的数据，第2段14:00及22日包含部分落潮及涨潮过程的数据，第3段包含完整的涨、落潮阶段的24 h数据。
3. 实验结果分析
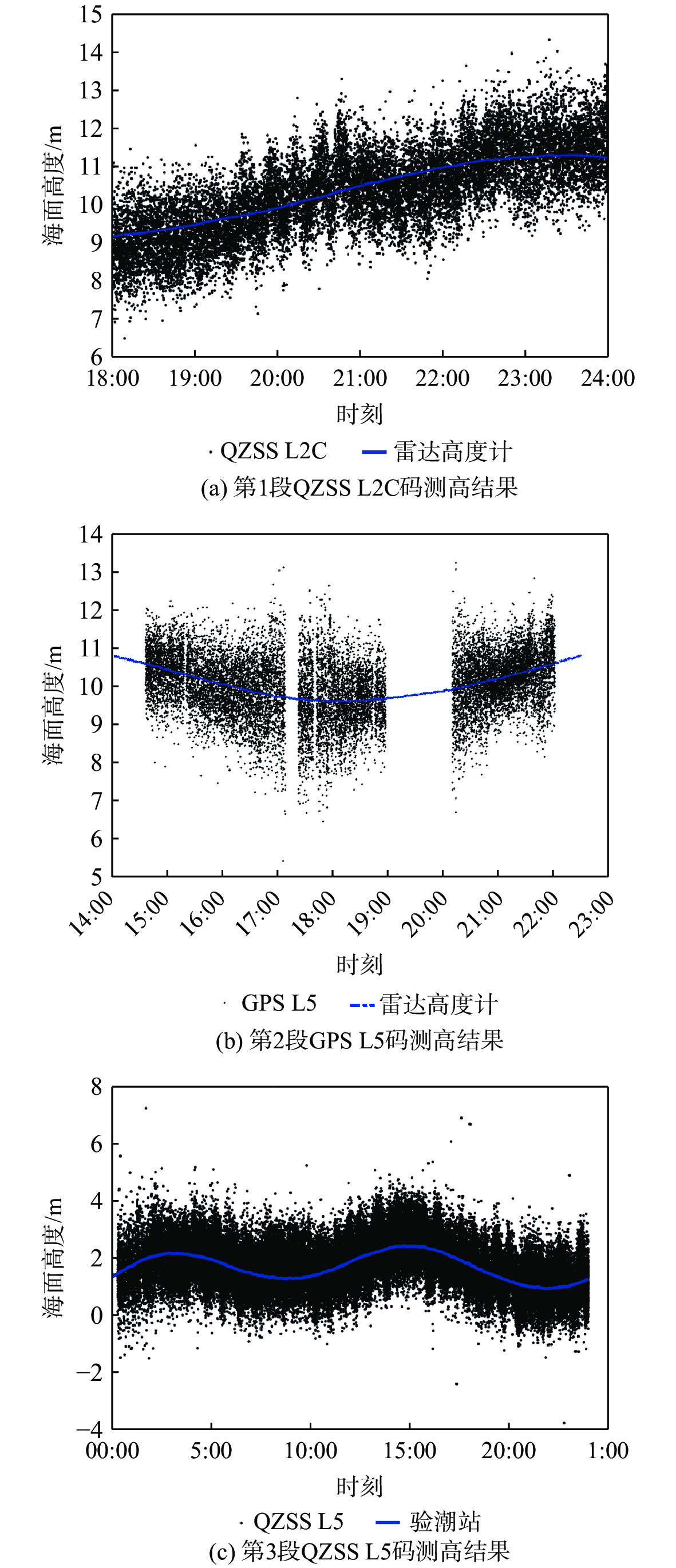
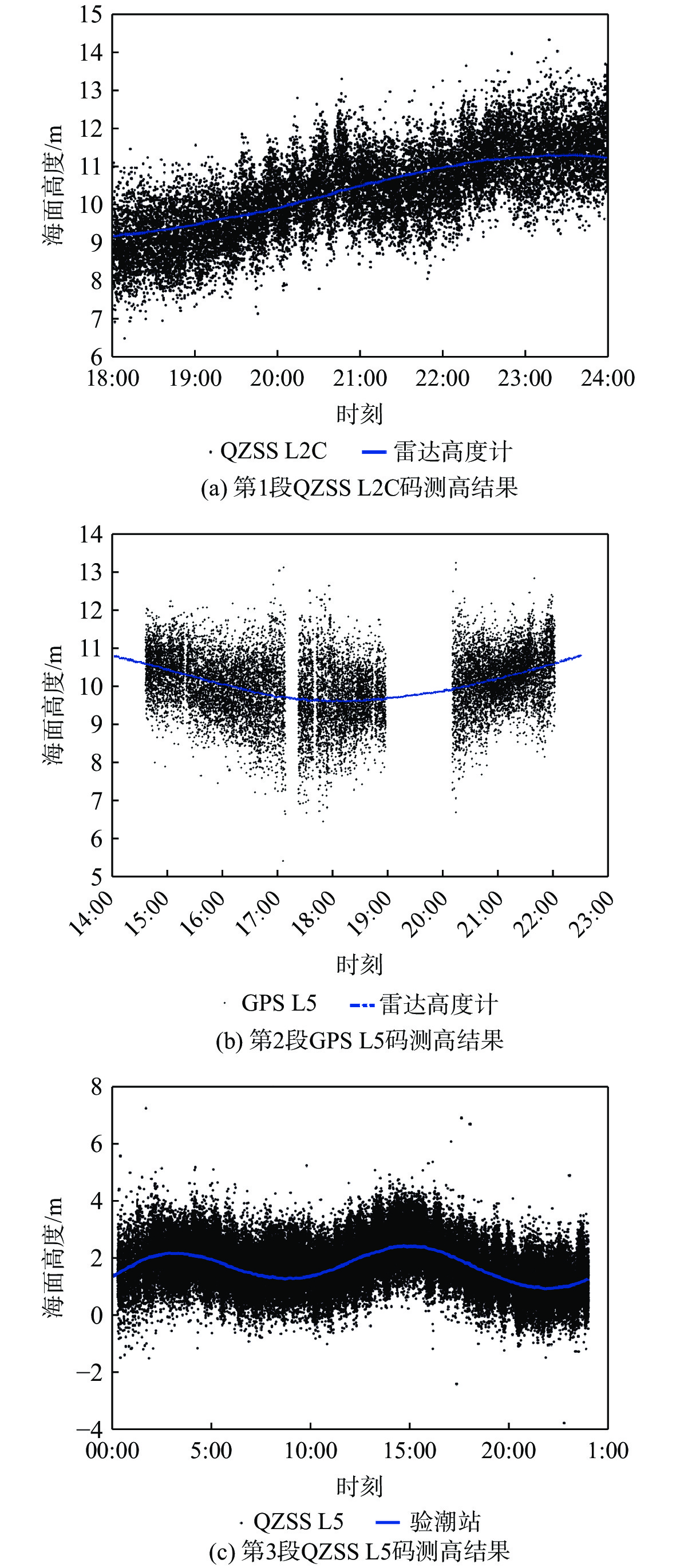
通过1.1节的原理处理3段数字中频信号得到反射信号与直射信号的路径差，再结合海面测高反演几何模型反演得到海平面高度hSSH。通过处理QZSS GEO卫星的L2C数据、GPS L5数据以及QZSS L5数据得到海平面高度结果以此验证GNSS-R码相位海面测高实验的准确性与可实用性。
图4中黑色的散点代表GNSS-R码测高中经由1.1节内容处理得到的原始海面测高结果，蓝线代表比对数据（雷达测高仪或者验潮站数据）。从图3可以看出：QZSS GEO卫星L2C码和L5码测高结果与比对数据相符合，残差值主要集中在±1 m之间。GPS L5码测高结果为当天可获取的GPS MEO卫星PRN10、PRN23、 PRN26和 PRN27卫星数据反演所得，受到实验时高度角和方位角选取的限制，当天GPS L5码仅有4颗可见卫星，其测高结果并不能覆盖全天时观测。通过3段反演的海面高度数据可以看出海平面涨潮幅度约2 m，这与当地潮汐变化表的情况基本一致。最后，经过计算得到3段GNSS-R码测高结果的精度如表2所示。由表2可知，整体而言，GNSS-R码测高精度为70～90 cm，GEO卫星测高结果均值偏差较小，而MEO卫星结果均值偏差较大。
图 4 3段数据码测高结果与海面真实高度对比Figure 4. Sea levels derived from GNSS-R code-delay altimetry of the three data codes are compared with the real sea surface height表 2 3段实验数据的GNSS-R码测高精度统计Table 2. Statistical analysis of the three experimental data for GNSS-R code-delay altimetry数据类型 均值/m RMSE/m QZSS L2C − 0.0467 0.7618 GPS L5 0.2877 0.8083 QZSS L5 − 0.0438 0.8606 3.1 傅里叶级数拟合测高结果
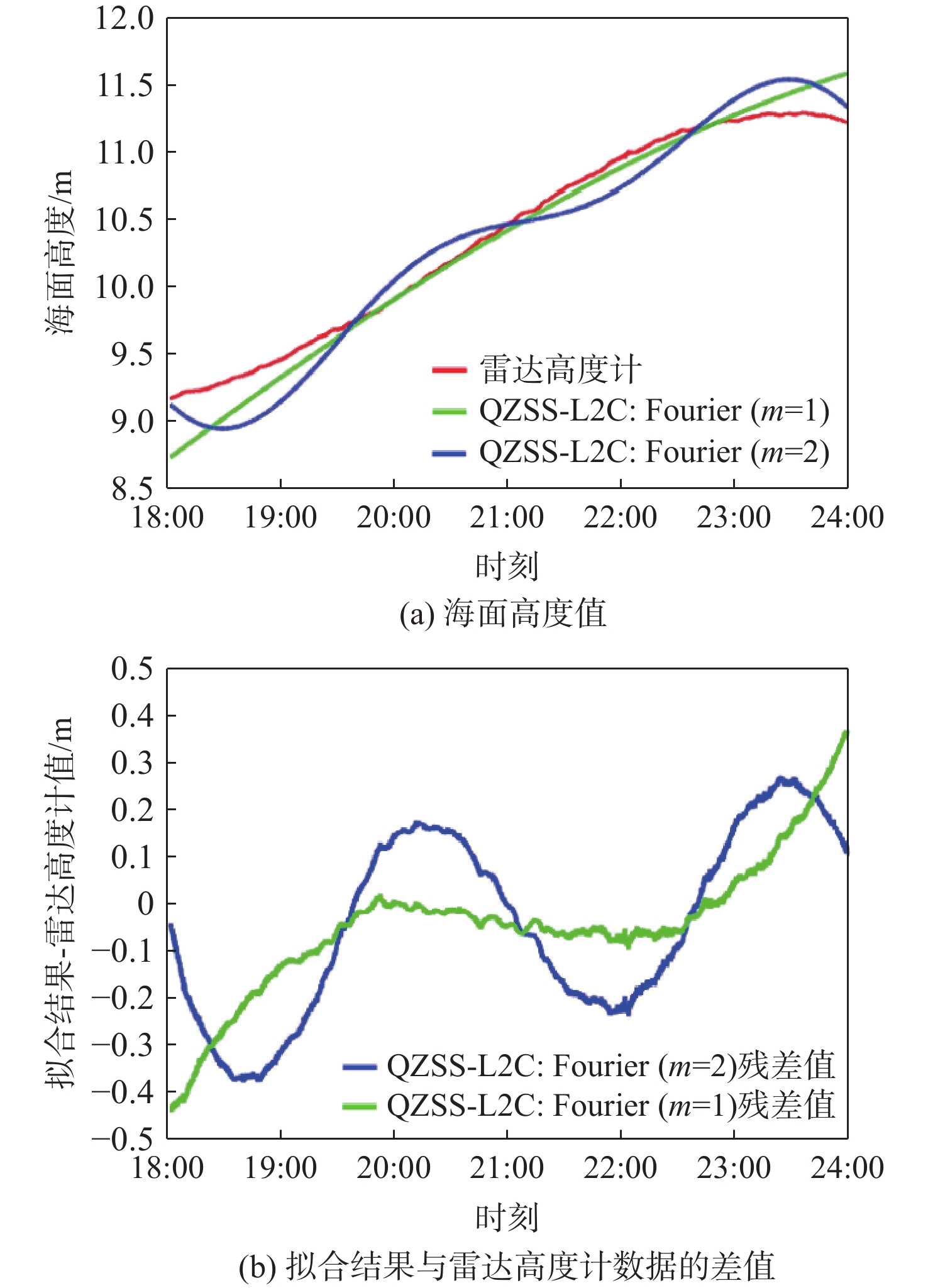
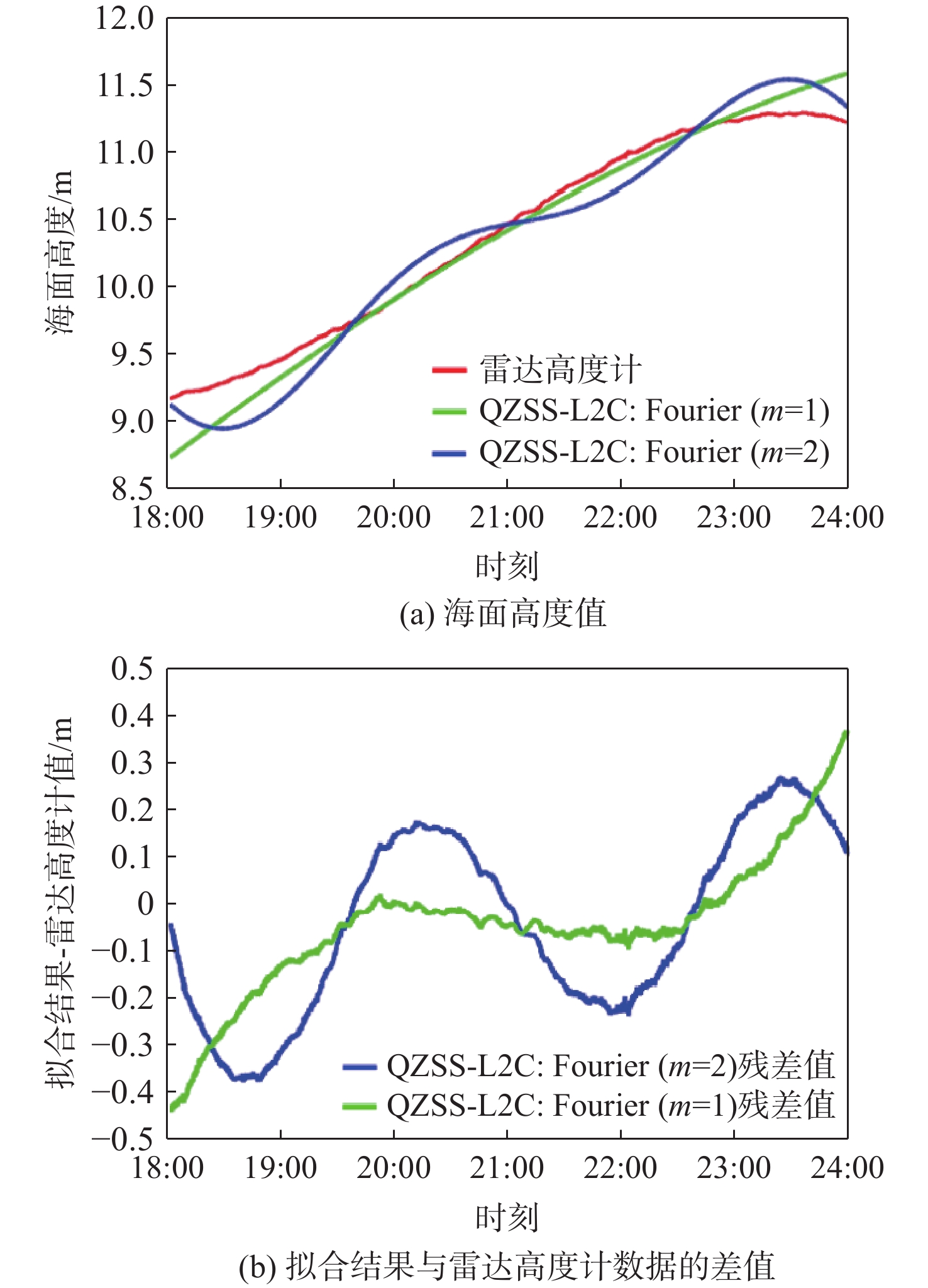
由式（2）可知，傅里叶级数随着阶数m的取值不同，拟合结果也不同，因此对于3段数据进行了不同阶数的傅里叶级数拟合。图5～图7为3段数据采用不同阶数傅里叶级数拟合GNSS-R测高结果与比对数据（雷达高度计或者验潮站数据）的比较，表3总结了3段数据的比较精度。
图 5 QZSS L2C1/2阶傅里叶级数拟合值与雷达高度计数据比较Figure 5. First- and Second-Fourier series fitting data of QZSS GEO L2C
图 6 GPS L51/2阶傅里叶级数拟合值与雷达高度计数据比较Figure 6. First- and Second-Fourier series fitting data of QZSS GPS L5
图 7 1阶、2阶和3阶傅里叶级数拟合的QZSS GEO L5码测高结果与验潮站数据对比Figure 7. First-, Second- and Third- Fourier series fitting data of QZSS GEO L5表 3 3段实验数据的傅里叶级数拟合结果与比对数据对比精度统计Table 3. Statistical analysis of the Fourier series fitting results comparing with in-situ data数据类型 均值/m RMSE/m R2/% QZSS L2C(m=1) − 0.0451 0.1481 99.33 QZSS L2C(m=2) − 0.0429 0.1961 98.14 GPS L5(m=1) 0.0256 0.1011 98.07 GPS L5(m=2) 0.0138 0.1077 97.36 QZSS L5(m=1) 0.0610 0.1861 91.60 QZSS L5(m=2) 0.0392 0.0961 97.99 QZSS L5(m=3) 0.0417 0.1016 97.76 对于第1次获取的近6 h的QZSS L2C码测高结果进行1阶和2阶傅里叶级数拟合，拟合曲线与雷达高度计结果如图5所示。从图中可以看出，相对于2阶傅里叶级数拟合，1阶级数拟合结果与雷达高度计数据更符合。
表3中加粗数据表示最优匹配统计结果。从表3可知，1阶级数拟合结果较2阶精度更高，均值偏差为−
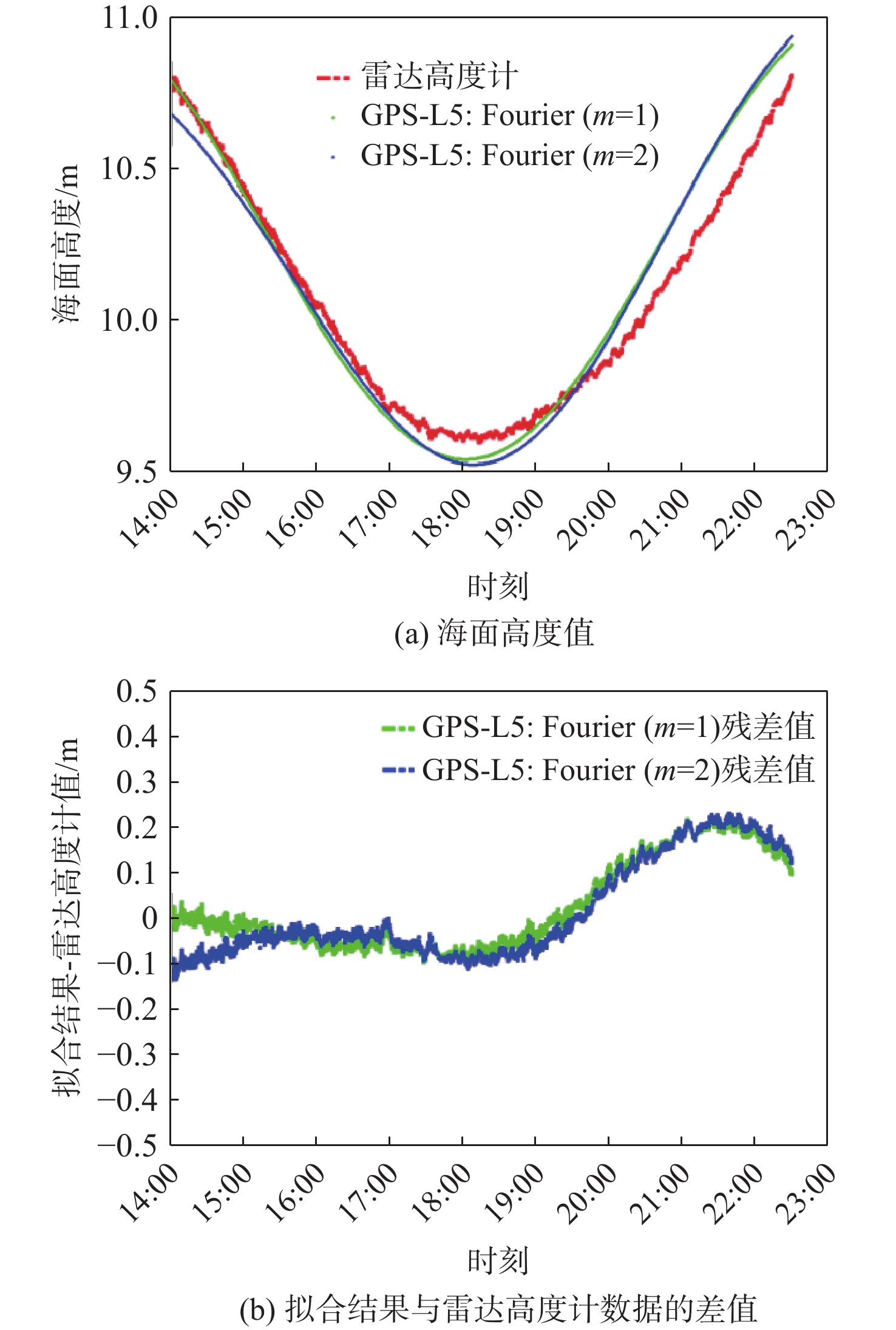
0.0451 m，均方根误差为0.1481 m，相关系数为99.33 %。对于第1段获取的近8 h的GPS L5码测高结果进行1阶和2阶傅里叶级数拟合，拟合曲线与雷达高度计结果如图6所示。从图6可以看出，2阶傅里叶级数拟合和1阶级数拟合结果相差不大，但在14:00-16:00期间，1阶傅里叶级数与雷达高度计数据更符合。从表3可知，1阶级数拟合结果较2阶精度稍高，均值偏差为
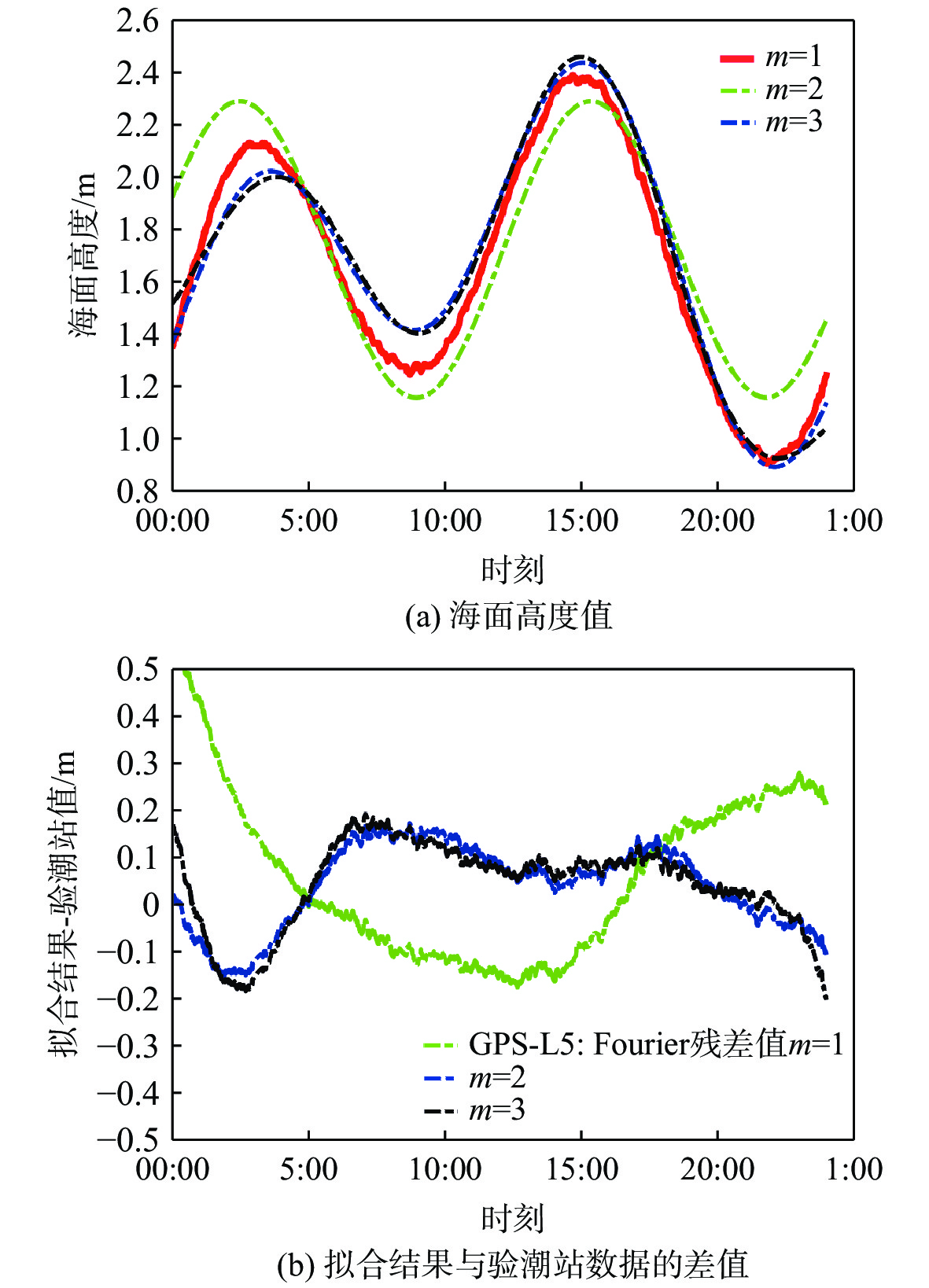
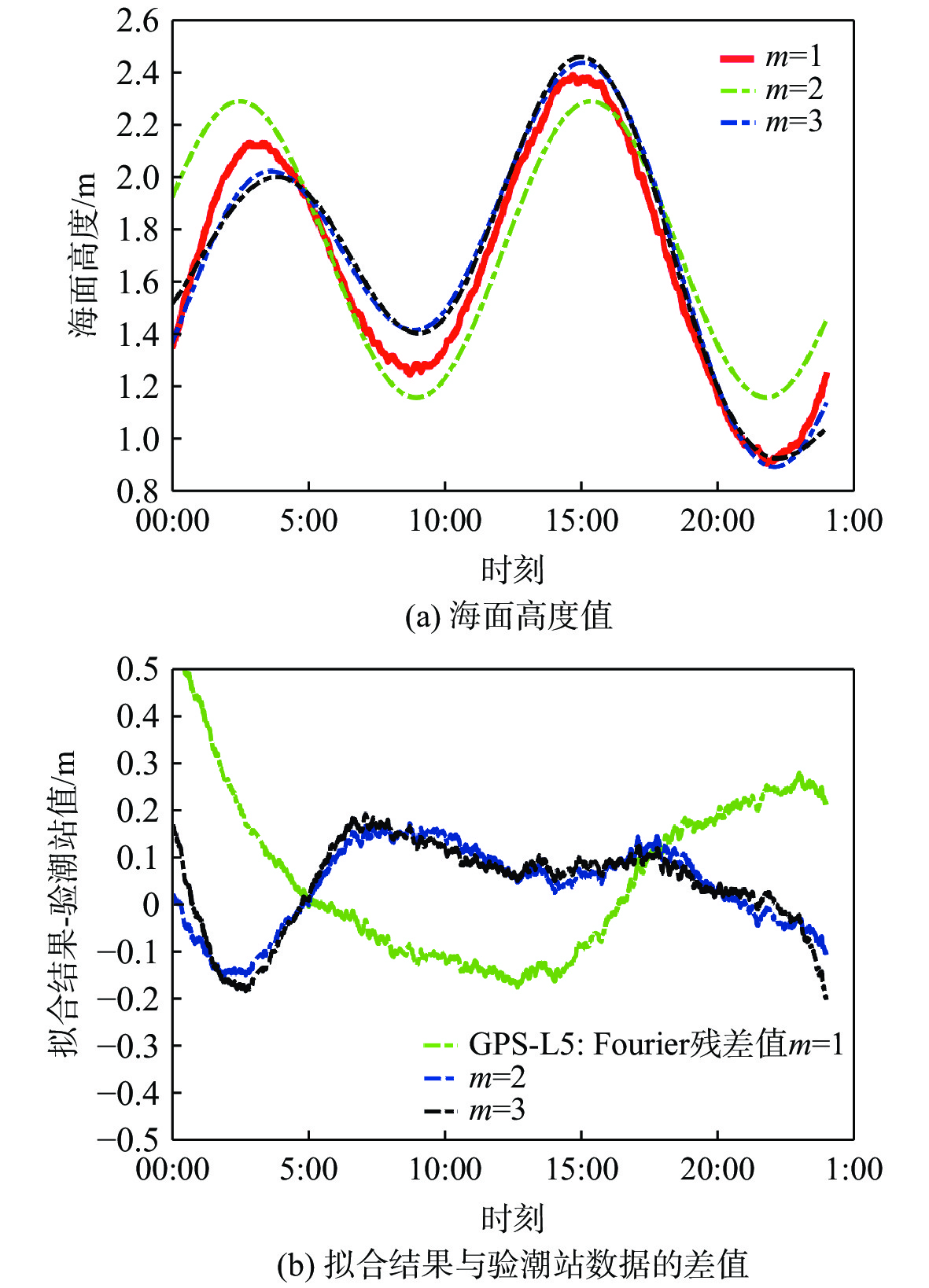
0.0256 m，均方根误差为0.1011 m，相关系数为98.07 %。第3段QZSS L5数据获得的24 h海面高结果，可以描述一整个潮汐涨落的过程。图7展示了对该GNSS-R反演结果进行1、2和3阶傅里叶级数拟合所得的曲线结果及其与验潮站数据对比的残差值。同时，图7（a）也画出了验潮站数据以进行比较。由图4可知，与验潮站峰值相比，当m=1时，拟合波形峰值存在超前/滞后现象且存在较大的偏差；而m=2和3时峰值存在较小的超前/滞后现象，但相对于m=3，m=2时偏差更小。因此取m=2时拟合波形与验潮站数据可实现最优匹配。由表3可知，m=2时，傅里叶级数拟合结果相对验潮站值的精度最高，均值偏差为
0.0392 m, 均方根误差为0.0961 m，相关系数为97.99 %。综合3段数据反演结果可知，最优傅里叶级数拟合的阶数并不是固定的，对于较短时间的6～8 h GNSS-R海面高结果来说，1阶傅里叶级数可实现最优匹配，对于24 h的海面高结果，2阶傅里叶级数可实现最优匹配。这可能与数据量的长度有关：较短时间的数据难以完全反映海面高的周期性变化，采用较低阶拟合即可实现最优匹配。因为GNSS-R测高结果存在星间偏差，对测高结果建立模型，模型的拟合系数需要根据不同导航卫星等进行调整。根据文中3段数据的分析，时间长短对拟合时最优阶数的选取有影响，因此，可以推测对同一颗卫星结果不同观测时间段数据进行拟合模型参数可能也有所差别。综合上述分析及比较表2和表3数据可得：GNSS-R码测高结果经傅里叶级数拟合后，与雷达高度计或者验潮站数据相比，精度由70～90 cm提升为9～15 cm，且相关系数大于0.97。因此，傅里叶级数拟合法不仅能大幅度提高码延迟海面测高精度，经拟合所得的海面高结果与比对数据相似且变化平滑，能如实准确地反映出海平面变化。另外，由于高度角和方位角限制，原始GPS L5码测高结果中存在有短期的数据缺失（如图4（b）17:00-17:30以及19:00-20:00区间），而采用傅里叶级数拟合后，该段数据结果仍可通过拟合曲线所得（如图6所示）。因此，傅里叶级数拟合方法也可补充原始观测结果中的数据缺失问题。
3.2 利用傅里叶级数拟合曲线进行海面高预测
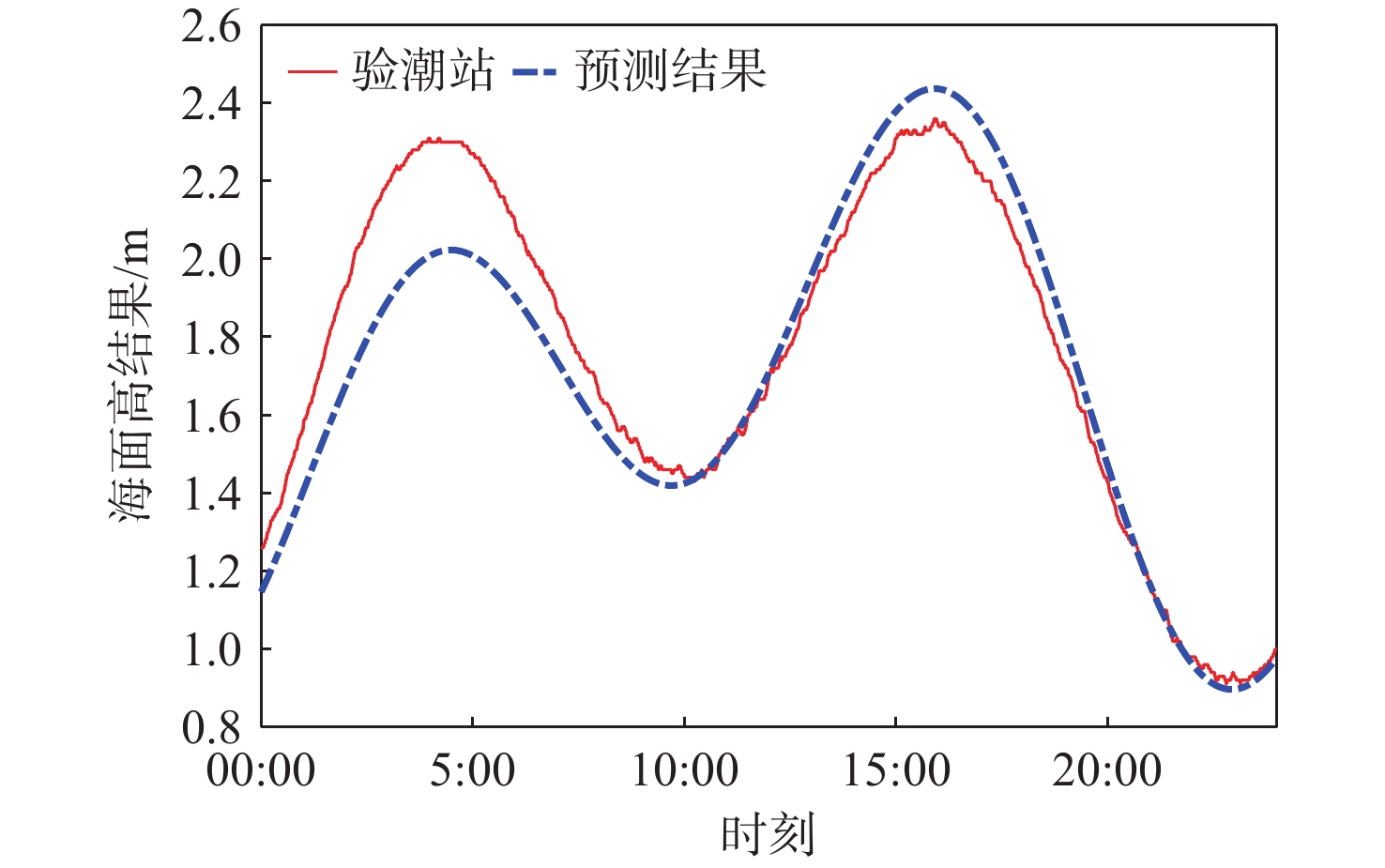
经由3.2节获取的傅里叶级数拟合曲线的自变量为时间，结果为海面高，因此，为进一步验证本文方法的正确性，采用QZSS L52阶傅里叶级数拟合曲线对海面高结果进行预测，并将预测值与验潮站数据进行比较，比较结果如图8和表4所示。图8显示：经由第3段 GNSS-R码测高数据建立的2阶傅里叶级数拟合曲线在未来24 h内（2023年5月28日）对海面高的预测结果与验潮站数据变化一致。预测结果在前12 h内存在有较大均值偏差，后12 h偏差较小，但整体海面高变化与验潮站结果保持一致。由表4可知，预测结果精度较高，均方根误差维持在13～18 cm，相关系数大于0.95。所得结果表明：傅里叶级数拟合法不仅可以提升GNSS-R码测高的精度，还可以对未来24 h内海面高度结果进行预测，且预测精度较高。
图 8 2023年5月28日2阶傅里叶级数拟合曲线计算的海面高度与验潮站数据比较Figure 8. Comparison between sea levels calculated from Second- order Fourier series fitting curve and tide gauge data on May 28th, 2023表 4 QZSS L5模型预测海面高与验潮站结果比较Table 4. Statistical analysis of the sea levels from Fourier series fitting model comparing with in-situ data时间 均值/m RMSE/m R2/% 未来1 h − 0.1307 0.1321 99.64 未来12 h − 0.1512 0.1856 97.15 未来24 h − 0.0476 0.1419 95.16 4. 结 论
伴随着GNSS的高速发展，GNSS-R的重要性日益明显，其具有全天时、低成本、高时空分辨率等优势，但受GNSS码片宽度限制和测量误差的影响，岸基GNSS-R码测高原始精度难以满足大地测量学研究中对海面高精度的要求。
本文通过岸基GNSS-R码相位海面测高实验，发现该技术原始测高结果精度为分米级。提出利用傅里叶级数拟合法建立模型对原始测高结果进行后处理，发现其能大幅度提高GNSS-R码测高反演精度并能补充GNSS-R测高缺失数据，且拟合曲线能对未来海面高度进行预测。本文的主要结论如下。
1） 通过对岸基GNSS-R码测高3段包含不同海面高变化过程的数据进行处理发现：原始测高结果的RMSE为70～90 cm，测量精度较低，且由于高度角和方位角的限制，MEO卫星结果数据存在缺失。 经过傅里叶级数拟合法建立海面高反演模型后RMSE提升为9～15 cm，且相关系数大于0.97。海面高精度得到大幅提升，且可以补充原始测高结果中的少量数据缺失。
2） 文中傅里叶级数拟合的最优阶数会随着拟合数据的长短有变化，这可能是因为较短的数据难以显示海面高的周期性变化。
3） 利用所建立的傅里叶级数拟合曲线可以实现对未来24小时内海面高度值的预测，且预测精度较高。
本文所提出的傅里叶级数拟合法可以较好地拟合用正、余弦函数表达的数据序列，因此其不仅可以与GNSS-R测高数据相结合进而提高精度，也可应用到卫星测高等数据的优化中。
致 谢 感谢威海市海洋与渔业监测减灾中心(http://www.weihai.gov.cn/art/2023/3/17/art_125777_3487711.html)提供的小石岛验潮站数据。
-
图 1 岸基GNSS-R码延迟海面测高模型
Figure 1. Shore-based GNSS-R code delayed sea level altimeter model
图 2 2020年11月5日及2021年3月30日实验环境及实验地点
Figure 2. Experimental environment and experimental location on 5 November 2020 and 30 March 2021
图 3 2023年5月27日实验环境及实验地点
Figure 3. Experimental environment and experimental location on 27 May 2023
图 4 3段数据码测高结果与海面真实高度对比
Figure 4. Sea levels derived from GNSS-R code-delay altimetry of the three data codes are compared with the real sea surface height
图 5 QZSS L2C1/2阶傅里叶级数拟合值与雷达高度计数据比较
Figure 5. First- and Second-Fourier series fitting data of QZSS GEO L2C
图 6 GPS L51/2阶傅里叶级数拟合值与雷达高度计数据比较
Figure 6. First- and Second-Fourier series fitting data of QZSS GPS L5
图 7 1阶、2阶和3阶傅里叶级数拟合的QZSS GEO L5码测高结果与验潮站数据对比
Figure 7. First-, Second- and Third- Fourier series fitting data of QZSS GEO L5
图 8 2023年5月28日2阶傅里叶级数拟合曲线计算的海面高度与验潮站数据比较
Figure 8. Comparison between sea levels calculated from Second- order Fourier series fitting curve and tide gauge data on May 28th, 2023
表 1 3次实验期间实验地点潮汐变化表
Table 1. Table of tidal change at experimental site during the three experiments
潮汐 潮时 潮高(峰值)/cm 第1段 第2段 第3段 第1段 第2段 第3段 干潮 05:35 04:29 00:40 37 45 84 满潮 11:27 10:17 07:26 222 209 239 干潮 17:53 16:06 14:26 42 55 65 满潮 23:48 22:25 20:15 221 242 196 
下载: 导出CSV
表 2 3段实验数据的GNSS-R码测高精度统计
Table 2. Statistical analysis of the three experimental data for GNSS-R code-delay altimetry
数据类型 均值/m RMSE/m QZSS L2C − 0.0467 0.7618 GPS L5 0.2877 0.8083 QZSS L5 − 0.0438 0.8606
下载: 导出CSV
表 3 3段实验数据的傅里叶级数拟合结果与比对数据对比精度统计
Table 3. Statistical analysis of the Fourier series fitting results comparing with in-situ data
数据类型 均值/m RMSE/m R2/% QZSS L2C(m=1) − 0.0451 0.1481 99.33 QZSS L2C(m=2) − 0.0429 0.1961 98.14 GPS L5(m=1) 0.0256 0.1011 98.07 GPS L5(m=2) 0.0138 0.1077 97.36 QZSS L5(m=1) 0.0610 0.1861 91.60 QZSS L5(m=2) 0.0392 0.0961 97.99 QZSS L5(m=3) 0.0417 0.1016 97.76
下载: 导出CSV
表 4 QZSS L5模型预测海面高与验潮站结果比较
Table 4. Statistical analysis of the sea levels from Fourier series fitting model comparing with in-situ data
时间 均值/m RMSE/m R2/% 未来1 h − 0.1307 0.1321 99.64 未来12 h − 0.1512 0.1856 97.15 未来24 h − 0.0476 0.1419 95.16
下载: 导出CSV
-
[1] VALENCIA E, ZAVOROTNY V U, AKOS D M, et al. Using DDM asymmetry metrics for wind direction retrieval from GPS ocean-scattered signals in airborne experiments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 52(7): 3924-3936. [2] RUF C S, GLEASON S, MCKAGUE D S. Assessment of CYGNSS wind speed retrieval uncertainty[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 12(1): 87-97. [3] RUF C S, BALASUBRAMANIAM R. Development of the CYGNSS geophysical model function for wind speed[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 12(1): 66-77. [4] FOTI G, GOMMENGINGER C, JALES P, et al. Spaceborne GNSS reflectometry for ocean winds: first results from the UK TechDemoSat-1 mission[J]. Geophysical Research Letters, 2015, 42(13): 5435-5441. [5] CLARIZIA M P, RUF C S, JALES P, et al. Spaceborne GNSS-R minimum variance wind speed estimator[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 6829-6843. doi: 10.1109/TGRS.2014.2303831 [6] GAO F, XU T H, MENG X Y, et al. A coastal experiment for GNSS-R code-level altimetry using BDS-3 new civil signals[J]. Remote Sensing, 2021, 13(7): 1378. doi: 10.3390/rs13071378 [7] ZHANG G D, XU Z C, WANG F, et al. Evaluation and correction of elevation angle influence for coastal GNSS-R ocean altimetry[J]. Remote Sensing, 2021, 13(15): 2978. doi: 10.3390/rs13152978 [8] CARRENO-LUENGO H, PARK H, CAMPS A, et al. Submeter ocean altimetry with GPS L1 C/a signal[C]// 2012 IEEE International Geoscience and Remote Sensing Symposium. Piscataway: IEEE Press, 2012: 7071-7074. [9] SOISUVARN S, JELENAK Z, SAID F, et al. The GNSS reflectometry response to the ocean surface winds and waves[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(10): 4678-4699. doi: 10.1109/JSTARS.2016.2602703 [10] RUFFINI G, SOULAT F, CAPARRINI M, et al. The Eddy Experiment: accurate GNSS-R ocean altimetry from low altitude aircraft[J]. Geophysical Research Letters, 2004, 31(12): 261-268. [11] 吴军, 张波, 洪学宝, 等. 基于北斗卫星反射信号的海面溢油探测方法及试验[J]. 北京航空航天大学学报, 2017, 43(1): 193-199.WU J, ZHANG B, HONG X B, et al. Sea surface oil spill detection method using BeiDou satellite reflected signal and its experiment[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(1): 193-199(in Chinese). [12] VALENCIA E, CAMPS A, RODRIGUEZ-ALVAREZ N, et al. Using GNSS-R imaging of the ocean surface for oil slick detection[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 6(1): 217-223. [13] LI C, HUANG W M, GLEASON S. Dual antenna space-based GNSS-R ocean surface mapping: oil slick and tropical cyclone sensing[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 8(1): 425-435. [14] ZHU Y C, TAO T Y, LI J Y, et al. Spaceborne GNSS-R for sea ice classification using machine learning classifiers[J]. Remote Sensing, 2021, 13(22): 4577. doi: 10.3390/rs13224577 [15] ZHANG Y, MENG W T, GU Q M, et al. Detection of Bohai Bay Sea ice using GPS-reflected signals[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 8(1): 39-46. [16] YAN Q Y, HUANG W M, MOLONEY C. Neural networks based sea ice detection and concentration retrieval from GNSS-R delay-Doppler maps[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(8): 3789-3798. doi: 10.1109/JSTARS.2017.2689009 [17] ALONSO-ARROYO A, ZAVOROTNY V U, CAMPS A. Sea ice detection using U. K. TDS-1 GNSS-R data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(9): 4989-5001. doi: 10.1109/TGRS.2017.2699122 [18] MARTIN-NEIRA M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry[J]. ESA Journal, 1993, 17(4): 331-355. [19] MARTIN-NEIRA M, CAPARRINI M, FONT-ROSSELLO J, et al. The PARIS concept: an experimental demonstration of sea surface altimetry using GPS reflected signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 142-150. doi: 10.1109/36.898676 [20] TREUHAFT R N, LOWE S T, ZUFFADA C, et al. 2-cm GPS altimetry over crater lake[J]. Geophysical Research Letters, 2001, 28(23): 4343-4346. doi: 10.1029/2001GL013815 [21] 王鑫, 孙强, 张训械, 等. 中国首次岸基GNSS-R海洋遥感实验[J]. 科学通报, 2008, 53(5): 589-592. doi: 10.1360/csb2008-53-5-589WANG X, SUN Q, ZHANG X X, et al. First China ocean reflection experiment using coastal GNSS-R[J]. Chinese Science Bulletin, 2008, 53(5): 589-592(in Chinese). doi: 10.1360/csb2008-53-5-589 [22] 白伟华, 孙越强, 朱光武, 等. 利用岸基GNSS-R 信号反演湖面高度[C]//第一届中国卫星导航学术年会, 2010: 496-502.BAI W H, SUN Y Q, ZHU G W, et al. Lake surface height retrieve using coastal GNSS-R signals[C]//The first China Satellite Navigation Conference, 2010: 1646-1652(in Chinese). [23] ZHANG Y, TIAN L M, MENG W T, et al. Feasibility of code-level altimetry using coastal BeiDou reflection (BeiDou-R) setups[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(8): 4130-4140. doi: 10.1109/JSTARS.2015.2446684 [24] 储倜, 贺凯飞, 高凡, 等. 基于QZSS L1信号的岸基GNSS-R码延迟海面测高[J]. 北京航空航天大学学报, 2022, 48(4): 691-697.CHU T, HE K F, GAO F, et al. Coastal GNSS-R ocean altimetry based on code delay of QZSS L1 signal[J], Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(4): 691-697(in Chinese). [25] 侯金华, 贺凯飞, 高凡, 等. 岸基BDS-R海面测高及其观测值加权方法[J]. 北京航空航天大学学报, 2024, 50(3): 1015-1026.HOU J H, HE K F, GAO F, et al. Shore-based BDS-R sea surface altimetry and weighting method of its observed values[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(3): 1015-1026(in Chinese). [26] 孟馨悦. GNSS-R实时软件接收机设计及其海陆应用[D]. 济南: 山东大学, 2022.MENG X Y. Design of GNSS-R real-time software receiver and its land and sea application[D]. Jinan: Shandong University, 2022 (in Chinese). [27] 贺匀峤. 高精度GNSS-R海面测高基带信号处理研究[D]. 济南: 山东大学, 2022.HE Y Q. Research on baseband signal processing of high precision GNSS-R sea surface altimetry[D]. Jinan: Shandong University, 2022 (in Chinese). [28] WANG N Z, HE K F, GAO F, et al. Analysis of GNSS-R code-level altimetry using QZSS C/A, L1C, and BDS B1C signals and their combinations in a coastal experiment[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2023, 16: 4549-4564. doi: 10.1109/JSTARS.2023.3274570 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 223
- HTML全文浏览量: 55
- PDF下载量: 1
- 被引次数: 0
