直驱泵阀协同式线控制动单元压力串级控制

谭草; 于鹏; 李波; 陆佳瑜; 任云云

doi:10.13700/j.bh.1001-5965.2023.0216

直驱泵阀协同式线控制动单元压力串级控制

doi: 10.13700/j.bh.1001-5965.2023.0216

谭草¹,
于鹏¹,
李波^1, ,,
陆佳瑜¹,
任云云²

1.
山东理工大学交通与车辆工程学院，淄博 255000
2.
舜泰汽车有限公司，淄博 255000

基金项目: 国家自然科学基金(51975341)；山东省优秀青年人才基金(ZR2022YQ51)；山东省的重大科技创新工程项目(2021CXGC010703)；山东省高等学校“青创科技计划”团队项目(2019KJB027,2022KJ232)；山东省青年科技人才托举工程项目(SDAST2021qt20)

详细信息

通讯作者:
E-mail：libo@sdut.edu.cn

中图分类号: U463.5；U469.72
计量
- 文章访问数: 132
- HTML全文浏览量: 79
- PDF下载量: 3
- 被引次数: 0
出版历程
- 收稿日期: 2023-04-27
- 录用日期: 2023-06-06
- 网络出版日期: 2023-06-15
- 整期出版日期: 2025-04-30

Pressure cascade control of brake-by-wire unit based on direct drive pump-valve cooperative

TAN Cao¹,
YU Peng¹,
LI Bo^{1
, ,},
LU Jiayu¹,
REN Yunyun²

1.
School of Transportation and Vehicle Engineering，Shandong University of Technology，Zibo 255000，China
2.
Shuntai Automobile Co.，Ltd.，Zibo 255000，China

Funds: National Natural Science Foundation of China (51975341); Outstanding Young Talents Foundation of Shandong Province (ZR2022YQ51); Major Scientific and Technological Innovation Project of Shandong Province (2021CXGC010703); Innovation Team Project of “Qing-Chuang Science and Technology Plan” of Colleges and Universities in Shandong Province (2019KJB027,2022KJ232); Young Technology Talent Supporting Project of Shandong Province (SDAST2021qt20)

More Information

Corresponding author: E-mail：libo@sdut.edu.cn

摘要

摘要:
针对分布式制动及高级别自动驾驶的需求，设计一种直驱泵阀协同式线控制动单元，通过电磁直线执行器直接驱动的液压泵与主动阀协调实现轮缸压力调节。为实现压力的精确控制，建立面向控制的系统动力学模型，提出一种基于外环轮缸压力控制和内环直驱泵活塞位置控制的串级控制方法。外环设计了滑模控制器提高响应速度，内环设计了自适应积分鲁棒控制器以减小参数不确定性和时变干扰的影响，证明了所提方法李雅普诺夫稳定。结果表明：直驱泵阀协同式线控制动单元为分布式制动提供一种可行的新方案，所提方法可以进一步提高制动压力的调节速度与控制精度。
- 线控制动 /
- 液压力控制 /
- 串级控制 /
- 滑模控制 /
- 自适应积分鲁棒控制
Abstract:
Aiming at the requirements of distributed braking and high-level automatic driving, a brake-by-wire unit based on a direct drive pump-valve cooperative is designed, to realize the wheel cylinder pressure regulation, the hydraulic pump directly driven by the electromagnetic linear actuator coordinates with the active valve. A control-oriented system dynamics model is established to realize the precise control of pressure, and a cascade control method is proposed, which includes an outer loop to control the cylinder pressure and an inner loop to control the plunger position in the pump. An adaptive integral robust controller is created for the inner loop to lessen the impact of time-varying interference and parameter uncertainty, while a sliding mode controller is designed for the outer loop to increase reaction speed. It is proved that the algorithm is Lyapunov stable. The results suggest that the developed brake unit is a possible novel scheme for distributed braking, and the proposed method mechanism can increase braking pressure speed and control accuracy even further.
- brake-by-wire /
- hydraulic pressure control /
- cascade control /
- sliding mode control /
- adaptive integral robust control

HTML全文

随着车辆底盘向着线控底盘、滑板底盘方向发展，对分布式制动系统的需求日益强烈；同时，高级别自动驾驶对线控系统的响应速度、控制精度提出了更高的需求^[1-2]。

电子液压式线控制动系统凭借响应迅速、功率密度高、不改变制动器结构等优势得到了广泛的青睐^[3-4]。Pan等提出一种紧凑型电子液压式线控制动系统，不需要高动力电机，且易于实现备份^[5]。余卓平等设计一种双动力源电子液压制动系统，该系统可对制动主缸液压力和踏板感觉进行独立主动控制，实现了踏板行程与液压力的解耦^[6]。胡东海和何仁提出基于安全特性的电机泵式电子液压制动系统匹配设计方法^[7]。刘兆勇等设计了一种集成式线控液压制动系统，实现该制动系统的高冗余性和4个轮缸的独立控制^[8]。各具特点的电子液压制动系统被提出，推动了线控制动技术的发展，然而难以直接用于分布式制动系统^[9]。于良耀等设计了一种分布式电液线控制动系统，通过运动转化机构将旋转电机的运动变为直线运动进而驱动液压轮缸^[10]。Gong等设计的电液制动单元采用直线电机驱动液压活塞，通过不等径的液压活塞与轮缸活塞放大电机驱动力^[11]。由上可知，现有的电子液压制动系统往往基于成熟的液压制动系统改进，仍然保留了复杂的液压管路；分布式线控系统往往需要将整个制动单元集成到制动钳上，恶化了轮边空间与簧下质量。

线控制动系统制动压力快速调节与精确控制是实现高级别制动驾驶的重要基础，也是目前的研究热点。针对不同线控系统的特点，文献[12]基于模型设计了不同的控制方法。熊璐等设计基于LuGre摩擦模型前馈补偿和死区补偿的联合控制方法，在考虑系统关键非线性特征的基础上，精确控制主缸液压力^[13]。石琴等利用径向基网络逼近连续函数特性，对与系统状态量相关的非线性摩擦力进行估计，作为反步控制器的补偿，实现线控制动系统液压精确控制^[14]。张俊智等针对线控系统中的摩擦现象，建立了一种更适用的摩擦模型，并提出了一种针对制动系统主缸压力控制的高精度压力跟踪控制方法^[15]。李波等建立了基于LuGre摩擦模型的直驱阀模型，通过串级控制实现了直驱阀控线控系统的压力精确控制^[16]。对线控系统液压力控制方法的研究主要集中在针对系统摩擦等典型非线性补偿方面，而制动系统自身的参数不确定性及面临的时变干扰也需要进一步研究^[17-19]。

综上所述，分布式制动系统需要一种降低液压管路复杂程度且不恶化轮边空间与簧下质量的制动单元；而高精度的制动液压力控制方法，则需要进一步考虑系统参数不确定性与时变干扰的影响。鉴于此，本文设计一种直驱泵阀协同式线控制动单元，通过电磁直线执行器直接驱动的液压泵与主动阀协调实现轮缸压力调节。进而设计一种基于外环轮缸压力控制和内环直驱泵柱塞位置控制的串级控制方法。通过实验验证了本文设计的制动单元和串级控制器的有效性。

1. 方案设计与工作原理

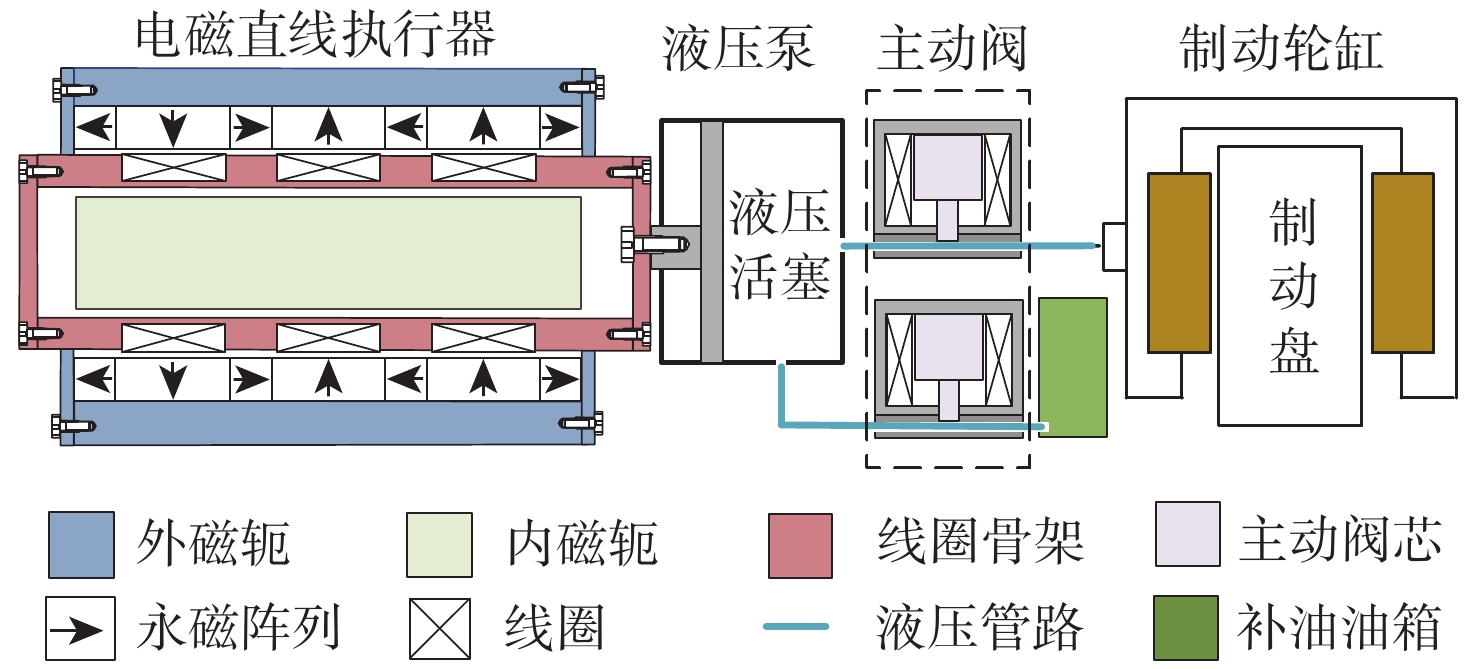
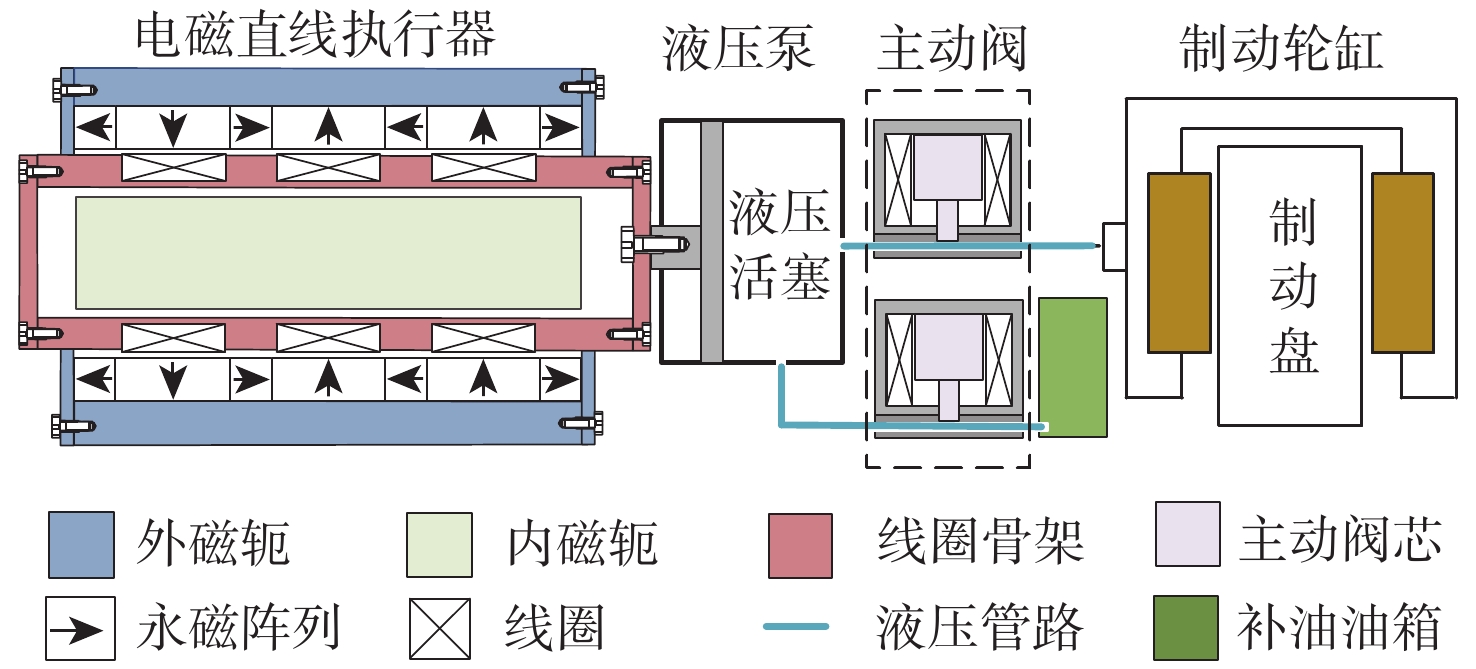
针对分布式制动及高级别自动驾驶的需求，本文设计了一种直驱泵阀协同式线控制动单元，结构示意如图1所示，主要包括电磁直线执行器、液压泵、主动阀、不改变现有结构的制动轮缸、补油油箱。电磁直线执行器、液压泵、主动阀组及补油油箱集成安装在车架上，通过油管与不改变现有结构的制动轮缸相连，有效简化制动管路，实现分布式驱动的同时不恶化轮边空间与簧下质量。其中，电磁直线执行器直接驱动的液压泵活塞往复运动，结合主动阀组的开关控制，实现制动轮缸压力的迅速调节。主动阀组由2个高速电磁阀组成，补油阀为常关阀，控制补油油箱到直驱泵之间的油路通断；保压阀为常开阀，控制直驱泵到制动轮缸之间的油路通断。设计直驱泵活塞塞直径小于轮缸活塞直径，利用不等径液压放大原理来放大直线执行器的驱动力，从而使用较小执行器获得足够的制动力。电磁直线执行器作为制动单元的动力来源，完成了电能到机械能的转换，采用高功率密度动圈式电磁直线执行器，其详细工作原理见文献[20]，省去旋转运动转换为直线运动的中间机械结构，提高了制动单元的响应速度。

图 1 直驱泵阀协同式线控制动单元原理图

Figure 1. Principle diagram of brake-by-wire unit based on direct drive pump-valve cooperative

下载: 全尺寸图片幻灯片

直驱泵阀协同式线控制动单元典型的工作过程分为调压模式、保压模式与卸压模式。卸压模式中保压阀打开、补油阀关闭，在制动轮缸压力及制动轮缸复位弹簧作用下，制动轮缸内的液压油流回液压泵、直线执行器及液压泵活塞回到初始位置；若由于液压油泄漏等原因，直线执行器未回到初始位置时，保压阀关闭、补油阀打开，直线执行器驱动液压泵活塞回到初始位置。调压模式中，保压阀打开、补油阀关闭，电磁直线执行器驱动液压活塞快速排出液压泵头中液压油流入制动轮缸、推动制动轮缸活塞消除制动间隙，进而通过控制直线电机输出力快速调节制动轮缸压力。保压模式中，保压阀、补油阀关闭，直线执行器不工作，制动轮缸压力保持不变。直驱泵阀协同式线控制动单元相较于泵控制动系统，减轻直线执行器工作负担、减小保压工况下系统的工作能耗；而相较于阀控制动系统，可更加精确地控制轮缸压力，使制动更加准确和安全。

2. 控制系统模型建立

2.1 电磁直线执行器建模

直驱泵阀协同式线控制动单元所采用的电磁直线执行器由内外磁轭、线圈骨架、线圈、永磁体组成^[19]。电磁直线执行器与液压活塞直接相连，受到摩擦力、来自活塞的液压阻力等，其机械、磁路、电路子系统耦合的模型为

$\left\{ \begin{aligned} &{M\frac{{{{\mathrm{d}}^2}x}}{{{\mathrm{d}}{t^2}}} = {F_{\mathrm{m}}} - {F_{\mathrm{f}}} - {P_1}{S_1} - {F_{{\mathrm{dis}}}}} \\ &{{F_{\mathrm{m}}} = N{B_{\mathrm{e}}}{l_{\mathrm{e}}}I = {K_{\mathrm{m}}}I} \\ & {u = IR + \frac{{{\mathrm{d}}I}}{{{\mathrm{d}}t}}L + {K_{\mathrm{e}}}v} \end{aligned} \right.$

(1)

式中：F_m为通电线圈在磁场中产生的电磁力；S₁为柱塞横截面积；N为线圈总匝数；B_e为磁场强度；l_e为线圈单匝长度；I为线圈电流；K_m为电磁力系数；M为执行器的动质量；x为动子移动位移； F_f为执行器动子移动所受到的摩擦力；F_dis为不确定性误差和干扰；u为供电电压；R和L分别为线圈电阻和电感；K_e为反电势系数；v为动子移动速度；P₁为直驱泵内部压力。

为提高建模准确性，建立一种简单而有效的摩擦力表达形式，将摩擦力看为速度的静态非线性函数，具体表达式为

${F_{\mathrm{f}}} = {B_1}\dot x + {A_{\mathrm{f}}}\arctan (\beta \dot x)$

(2)

式中：B₁为黏性系数；A_f为库伦摩擦系数，通过光滑函数arctan()来表示传统的符号函数sgn()。β为常数，设置β足够大，使得该函数保持符号函数的特性并且使摩擦力的表达更加符合实际。

2.2 液压系统建模

液压泵需在高压工况下运行，液体的可压缩性必须予以考虑。为简化直驱泵的数学模型，假设液体在流动时无局部压力损失和沿程压力损失；液压泵泵腔和液压活塞不发生形变；液压泵泵腔内各处的压力相等；整个制动单元密封良好，无液压油泄漏。液压泵的液压力变化模型为

${\dot P_1} = {\beta _{\mathrm{e}}}{({{S_1}\dot x - Q})}/{[{{S_1}(l - x)}]}$

(3)

式中：β_e为液压油有效体积弹性模量；Q为直驱泵流量； l为直驱泵腔长度。

主动阀在泵阀协同制动单元中起到了配流的作用，假设主动阀全开，此时主动阀阀芯两端压差较小，主动阀阀孔流量简化为

$Q = {k_0}{c_0}{A_0}\sqrt {\frac{2}{\rho }} \Delta P$

(4)

式中：k₀为流量线性化系数；c₀为阀口流量系数；A₀为孔口面积；ΔP为阀口液压差；ρ为液压油密度。

制动轮缸实现液压力到制动力的转化。体积模量定义为 ${\beta _{\mathrm{e}}}{S_2} \approx {k_{\mathrm{h}}}\left( {{l_{\mathrm{h}}} + {x_{\mathrm{h}}}} \right)$ ，由于活塞位移x_h较小，且轮缸压力升高时，活塞位移基本不变， ${\dot x_{\mathrm{h}}}$ 可忽略，轮缸的压力变化模型为

${\dot P_2} = {\beta _{\mathrm{e}}}\frac{Q}{{{S_2}({l_{\mathrm{h}}} + {x_{\mathrm{h}}})}}$

(5)

式中：S₂为轮缸活塞横截面积；x_h为活塞位移；l_h为轮缸腔内长度；P₂为轮缸压力。为便于液压子系统建模，设以下参数：

$\left\{ \begin{aligned} &{\xi \left( x \right) = \frac{{{\beta _{\mathrm{e}}}}}{{l - x}}} \\ & {\phi = \frac{{{k_0}{c_0}{A_0}}}{{{S_1}}}\sqrt {\frac{2}{\rho }} } \\ & {\psi =\frac{{{k_{\mathrm{h}}}{k_0}{c_0}{A_0}}}{{S_2^2}}\sqrt {\frac{2}{\rho }} } \end{aligned} \right.$

(6)

通过所设参数，直驱泵和轮缸内液压力为

$\left\{ \begin{aligned} &{{{\dot P}_1} = \xi \left( x \right)\left( {\dot x - \phi \Delta P} \right)} \\ &{{{\dot P}_2} = \psi \Delta P} \end{aligned} \right.$

(7)

由式（7）可以得到压力差表达式为

$\Delta P = \frac{{\xi \left( x \right)}}{{\xi \left( x \right)\phi + \psi }}\dot x - \frac{1}{{\xi \left( x \right)\phi + \psi }}\Delta \dot P$

(8)

根据式（8），泵内压力进一步改写为

$\left\{ \begin{aligned} & {{{\dot P}_1} = \frac{\psi }{\phi }\dot x + D} \\ & {D = \frac{{\xi \left( x \right)\phi }}{{\xi \left( x \right)\phi + \psi }}\Delta \dot P - \frac{{{\varphi ^2}}}{{{\phi ^2}\xi \left( x \right) + \phi \psi }}\dot x} \end{aligned} \right.$

(9)

2.3 制动单元状态空间模型

式(1)电路子系统中电感项 $\dfrac{{\mathrm{d}}I}{{\mathrm{d}}t}I$ 相对其他项较小，为简化模型可忽略不计，整合式(1)、式 (7)和式 (9)得到的直驱泵阀协同式线控制动单元的系统动力学模型如式（10）所示，其主要参数如表1所示。

表 1 直驱泵阀协同式线控制动单元参数

Table 1. Parameters of brake-by-wire unit based on direct drive pump-valve cooperative

结构	参数	数值
电磁直线执行器	线圈电阻R/Ω	1.40
	线圈等效电感L/mH	0.91
	反电势系数K_e/（Vs·m⁻¹）	24.61
	电磁力系数K_m/(N·A⁻¹)	24.61
直驱泵	泵腔长度l/mm	16
直驱泵	活塞面积S₁/mm²	27.5
主动阀	阀芯直径/mm	8
主动阀	阀座直径/mm	4
制动液	弹性模量β_e/MPa	1700
制动液	密度ρ/（kg·m⁻³）	1046

下载: 导出CSV

| 显示表格

$\left\{ \begin{aligned} & {{{\dot x}_1} = {x_2}} \\ & {{{\dot x}_2} = \frac{{{K_{\mathrm{m}}}}}{{MR}}u - \frac{{{K_{\mathrm{m}}}{K_{\mathrm{e}}}}}{{MR}}{x_2} - \frac{{{S_1}}}{M}{x_3} + \frac{1}{M}{F_{\mathrm{f}}} + \tilde d} \\ & {{{\dot x}_3} = \frac{\psi }{\phi }{x_2} + D} \\ & {{{\dot x}_4} = \psi \left( {{x_3} - {x_4}} \right)} \end{aligned} \right.$

(10)

式中： $\left[ {{x_1},{x_2},{x_3},{x_4}} \right] = \left[ {x,\dot x,{P_1},{P_2}} \right]$ ； $\tilde d$ 为不确定性误差和干扰F_dis所产生的不确定项。

3. 串级控制器设计

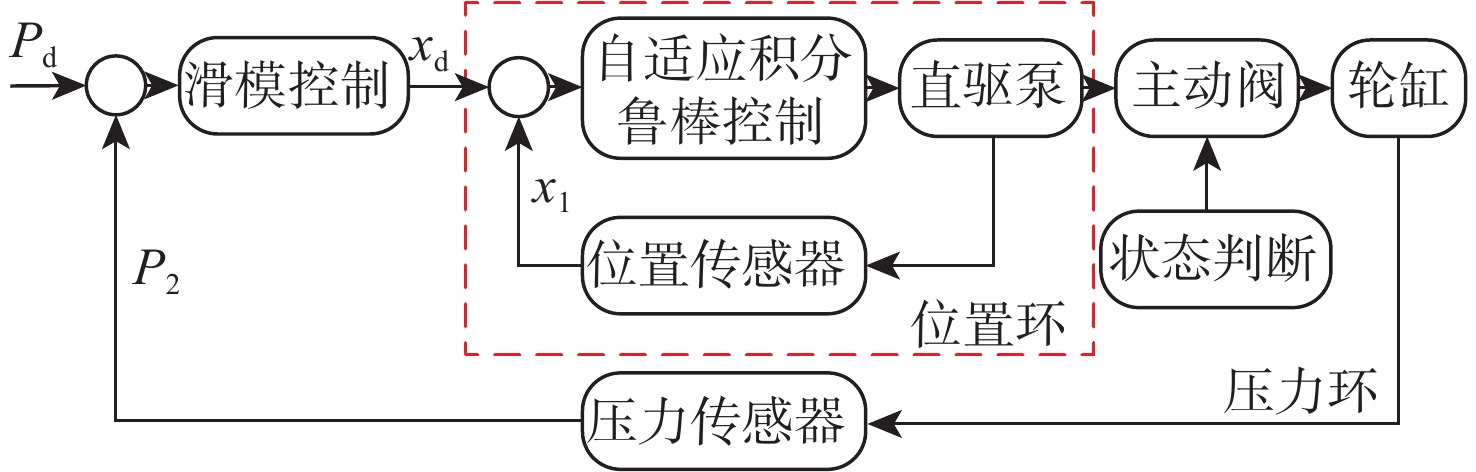
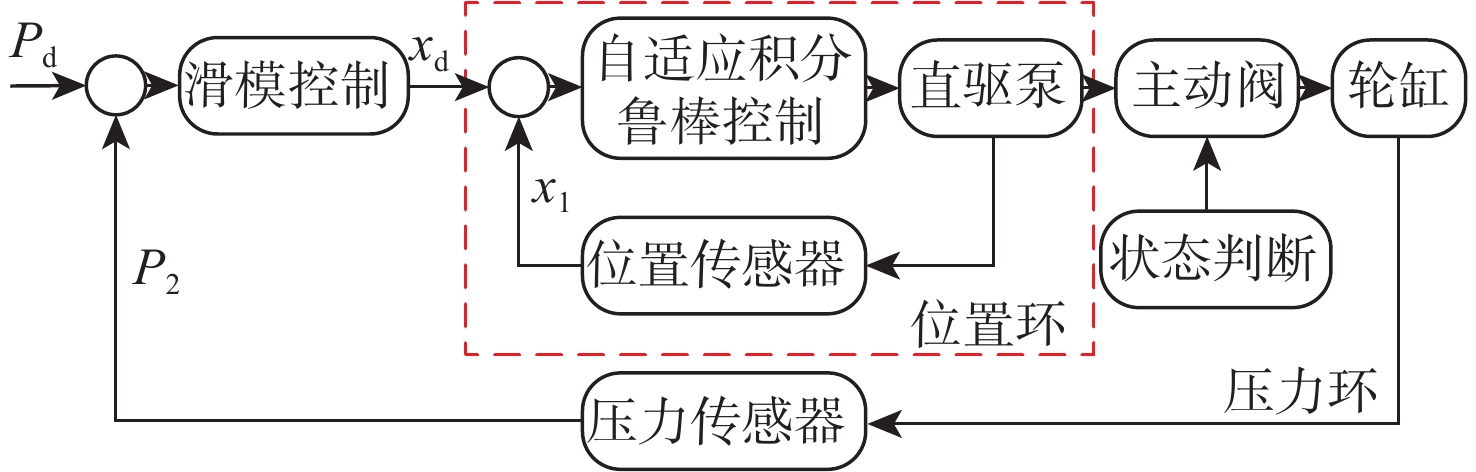
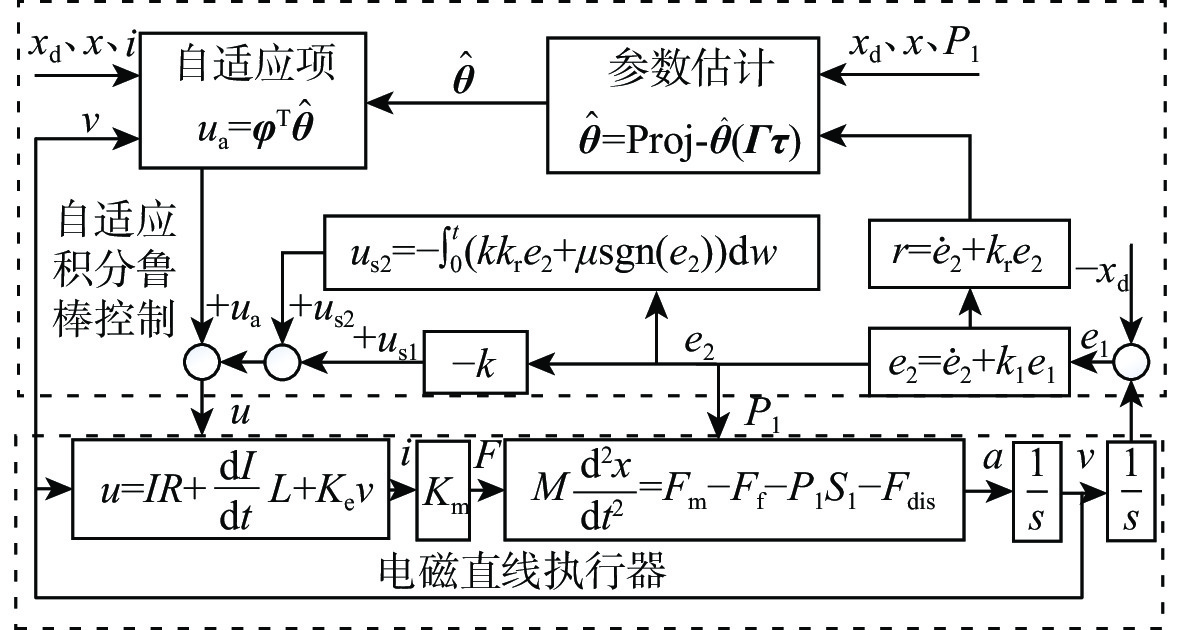
直驱泵阀协同式线控制动单元的液压力控制设计为压力环-位置环的串级控制器，其中，外环的压力环采用滑模控制，利用其控制响应快的优点，得到可以使压力快速到达目标液压力的理想时变位移。单元中电磁直线执行器与直驱泵柱塞固连，由于缺少中间缓冲环节，各种非线性和时变的内外部干扰直接作用在驱动单元上，所以需要设计合适的控制器以降低未知非线性和时变干扰对控制性能的影响。内环设计自适应积分鲁棒控制减小执行器参数不确定性和未知干扰对执行器性能的影响。本文设计的串级控制器如图2所示，其中，P_d为目标液压力；x_d为执行器目标位移。

图 2 控制系统总体框图

Figure 2. Overall block diagram of control system

下载: 全尺寸图片幻灯片

3.1 外环控制器设计

3.1.1 滑模控制器

为满足控制器设计，定义液压力误差为

$e = {P_{\mathrm{d}}} - {P_2}$

(11)

式中：P_d为目标液压力。针对制动单元的液压子系统，滑模面s设计如下^[21]：

$s = {c_{\mathrm{a}}}e + {c_{\mathrm{b}}}\int {e{\mathrm{d}}t}$

(12)

式中：c_a和c_b均为常数，为保证系统从任一点出发的状态都可到达滑模面，设计趋近律为

$\dot s = - {k_{\mathrm{h}}}s - q{\mathrm{sat}}\left( s \right)$

(13)

式中：k_h、q均为常数且均大于0；sat(s)为削弱系统抖振所设计的饱和函数，具体形式为

${\mathrm{sat}}\left( s \right) = \left\{ {\begin{array}{*{20}{c}} 1&{s \gt \delta } \\ {\dfrac{s}{\delta }}&{\left| s \right| \leqslant \delta } \\ { - 1}&{s \lt - \delta } \end{array}} \right.$

(14)

将式(12)代入式(13)得到执行器理想位移x_d：

$\begin{split}&{x_{\mathrm{d}}} =\Big[\psi \phi \Big( {c_{\mathrm{a}}}\dot e + {c_{\mathrm{b}}}{P_{\mathrm{d}}} + {k_{\mathrm{h}}}s + q{\mathrm{sat}}\left( s \right) - {c_{\mathrm{b}}}\int_0^t {D{\mathrm{d}}t } \Big) + \\ &\quad\quad \phi {c_{\mathrm{b}}}{{\dot P}_2}\Big]\Big/{{{c_{\mathrm{b}}}{\psi ^2}}} \end{split}$

(15)

3.1.2 稳定性分析

为证明系统的稳定性，构造李亚普诺夫函数如下：

${V_1} = \frac{1}{2}{s^2}$

(16)

对式（16）求导，并将式(13)代入得

${\dot V_1} = s\dot s = s\left( { - {k_{\mathrm{h}}}s - q{\mathrm{sat}}\left( s \right)} \right)$

(17)

根据饱和函数sat(s)的定义可知，式(17)恒小于0，因此，外环控制器稳定有效。

3.2 内环控制器设计

3.2.1 自适应积分鲁棒控制器设计

根据系统动力学模型式(10)，将参数定义为：θ=[θ_1, θ₂, θ₃, θ₄]^T，θ₁=MR/K_m；θ₂=K_e+B₁R/K_m；θ₃=A_fR/K_m；θ₄=S₁R/K_m，假设上述参数和不确定项范围已知，电磁直线执行器的动力学方程重新定义为

${\theta _1}{\dot x_2} = u - {\theta _2}{x_2} - {\theta _3}\arctan (\beta {x_2}) - {\theta _4}{P_1} + \tilde d$

(18)

$\left\{\begin{aligned}&\left| {\dot {\tilde d}} \right| \leqslant {\delta _1}\\ &\left| {\ddot {\tilde d}} \right| \leqslant {\delta _2} \end{aligned}\right.$

(19)

${\theta _i} \in [{\theta _{i\min }},{\theta _{i\max }}]\quad\quad i = 1,2, 3 ,4$

(20)

式中：δ₁和δ₂为已知常数。

为满足控制器设计，定义执行器位置误差e₁、滑模变量e₂和辅助变量r如下：

$\left\{\begin{aligned} &{e_1} = {x_1} - {x_{\mathrm{d}}}\\ &{e_2} = {\dot e_1} + {k_1}{e_1}\\ &r = {\dot e_2} + {k_{\rm{r}}}{e_2} \end{aligned} \right.$

(21)

式中：k₁和k_r为正增益。将这些变量进一步整合得到

$r = {\ddot x_1} - {\ddot x_{\mathrm{d}}} - k_1^2{e_1} + \left( {{k_1} + {k_{\rm{r}}}} \right){e_2}$

(22)

将式(18)代入式(22)得

$\begin{split} & {\theta _1}r = u - {\theta _1}{{\ddot x}_{\mathrm{d}}} - {\theta _2}{x_2} - {\theta _3}\arctan (\beta {x_2}) - \\ &\quad\quad {\theta _4}{P_1} + \tilde d - {\theta _1}k_1^2{e_1} + {\theta _1}\left( {{k_1} + {k_{\rm{r}}}} \right){e_2} \end{split}$

(23)

此外，通过不连续投影映射函数使参数估计值都处于有界范围内，因此，参数估计所需的投影映射函数定义为

$\tilde {\boldsymbol{\theta}} = \hat {\boldsymbol{\theta }}- {\boldsymbol{\theta}}$

(24)

$\dot {\hat {\boldsymbol{\theta}}} ={\mathrm{ Pro}}{{\mathrm{j}}{\text{-}}{\hat {\boldsymbol{\theta}} }}({\boldsymbol{\varGamma}} {\boldsymbol{\tau }})$

(25)

${\mathrm{Pro}}{{\mathrm{j}}}{{\widehat{\theta }}_{i}}\left\{{\zeta }_{i}\right\}=\left\{\begin{aligned} &0\quad\; {\widehat{\theta }}_{i}={\widehat{\theta }}_{i\mathrm{max}}\text{ }且\text{ }{\zeta }_{i} \geqslant 0\\ &0\quad\; {\widehat{\theta }}_{i}={\widehat{\theta }}_{i\mathrm{min}}\text{ }且\text{ }{\zeta }_{i} < 0\\ &{\zeta }_{i}\quad 其他\end{aligned}\right.$

(26)

式中， ${{\hat {\boldsymbol{\theta}} }}$ 和 ${{\tilde{\boldsymbol{ \theta}} }}$ 分别为参数的估计值和误差矩阵；Г为系数矩阵；τ为参数估计变量矩阵；Proj为投影映射函数，上述自适应律有以下属性：

$\left\{ \begin{aligned} & {{\theta _{i\min }} \leqslant {{\hat \theta }_i} \leqslant {\theta _{i\max }}\quad i = 1,2, \cdots ,4} \\ & {{{\tilde{\boldsymbol{ \theta}} }^{\mathrm{T}}} \left({{\boldsymbol{\varGamma}} ^{ - 1}}{\mathrm{Pro}}{{\mathrm{j}}{\text{-}}{\hat {\boldsymbol{\theta}} }}({\boldsymbol{\varGamma}} {\boldsymbol{\tau}} ) - {\boldsymbol{\tau}} \right) \leqslant 0} \end{aligned} \right.$

(27)

根据动力学方程，控制器可设计为

$\left\{\begin{aligned} & u = {u_{\mathrm{a}}} + {u_{\mathrm{s}}}\\ & {u_{\mathrm{a}}} = {{\text{φ}} ^{\mathrm{T}}}\hat {\boldsymbol{\theta}} \\ & {u_{\mathrm{s}}} = {u_{{\mathrm{s}}1}} + {u_{{\mathrm{s}}2}}\\ & {u_{{\mathrm{s}}1}} = - k{e_2} \\ \end{aligned}\right.$

(28)

式中：k为正增益；u_a为自适应补偿项；u_s为鲁棒反馈项；u_s1为用于稳定系统的比例反馈项；u_s2为积分鲁棒项；φ的具体表达式为

${\text{φ}} = {[{\ddot x_{\mathrm{d}}},{x_2},\arctan \left( {\beta {x_2}} \right),{P_1}]^{\mathrm{T}}}$

(29)

由于系统不确定的非线性因素，仅依赖线性反馈项不能达到很好的控制效果，因此，利用积分鲁棒项进一步降低模型不确定性，具体表达式为

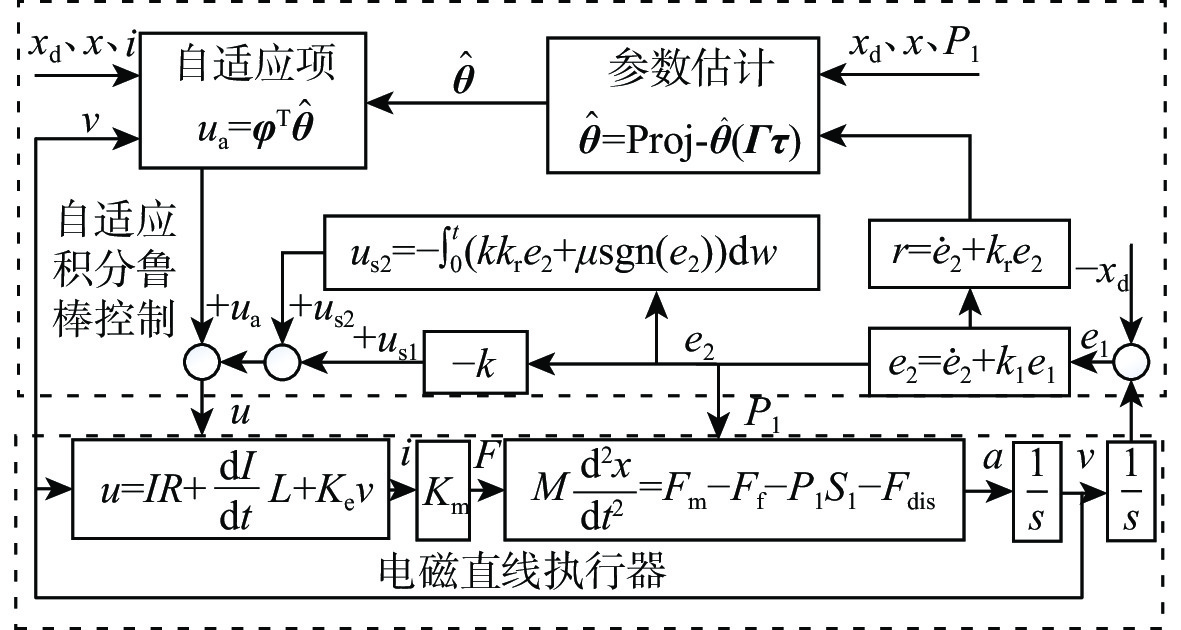
${u_{{\mathrm{s}}2}} = - \int_0^t {\left( {k{k_{\rm{r}}}{e_2} + \mu {\mathrm{sgn}}\left( {{e_2}} \right)} \right)} {\mathrm{d}}w$

(30)

式中： $\mu$ 为常数，sgn()为符号函数。自适应积分鲁棒控制的具体控制框图如图3所示。

图 3 自适应积分鲁棒控制框图

Figure 3. Adaptive integral robust control block diagram

下载: 全尺寸图片幻灯片

将控制器信号代入式(23)中得

$\begin{split} &{\theta _1}r = {{\text{φ}} ^{\mathrm{T}}}\tilde{\boldsymbol{ \theta}} - \int_0^t \left({k{k_{\mathrm{r}}}{e_2} + \mu {{\mathrm{sgn}}} \left( {{e_2}} \right)}\right) {\mathrm{d}}w + \\ &\quad\quad \tilde d - k{e_2} - {\theta _1}k_1^2{e_1} + {\theta _1}\left( {{k_1} + {k_{\mathrm{r}}}} \right){e_2} \end{split}$

(31)

为便于后续控制器稳定性分析验证，对式(31)进行求导并整理得

$\begin{split} &{\theta _1}\dot r = {{\text{φ}} ^{\mathrm{T}}}{\mathrm{Pro}}{{\mathrm{j}}{\text{-}}{\hat {\boldsymbol{\theta}} }}( - {\boldsymbol{\varGamma }}\dot {\text{φ}} r) + {{\dot {\text{φ}} }^{\mathrm{T}}}\tilde {\boldsymbol{\theta}} - kr - \\ & \quad\quad \mu {{\mathrm{sgn}}} \left( {{e_2}} \right) + \dot {\tilde d} + {\theta _1}\left( {{k_1} + {k_{\mathrm{r}}}} \right)r + \\ &\quad\quad{\theta _1}k_1^3{e_1} - \left[ {{\theta _1}k_1^2 + {\theta _1}\left( {{k_1} + {k_{\rm{r}}}} \right){k_{\mathrm{r}}}} \right]{e_2} \ \end{split}$

(32)

3.2.2 稳定性分析

首先，声明以下引理：

引理　定义辅助函数和其积分式如下：

$L\left( t \right) = - r\mu {\mathrm{sgn}}({e_2}) + r\dot{ \tilde d }$

(33)

$P = \mu \left| {{e_2}\left( 0 \right)} \right| - {e_2}\left( 0 \right)\dot {\tilde d}\left( 0 \right) - \int_0^t {L\left( w \right){\mathrm{d}}w}$

(34)

式中： $\tilde d(0)$ 和e₂(0)分别为 $\tilde d$ 和 $e_2$ 的初始值。如果控制增益满足μ>δ₁+δ₂/k_r，则函数P恒为正。

证明

对式(33)积分得

(35)

对式（35）进行分部积分得

$\begin{split} &\int_0^t {L\left( w \right)} {\mathrm{d}}w = \int_0^t {{k_{\rm{r}}}{e_2}\left( {\dot {\tilde d }- \mu {\mathrm{sgn}}({e_2})} \right)} {\mathrm{d}}w + \\ &\quad\quad {e_2}\dot{ \tilde d} - \mu (|e_2(t)|-|e_2(0)|) - {e_2}\left( 0 \right)\dot{ \tilde d}\left( 0 \right) - \int_0^t {{{\dot e}_2}\ddot {\tilde d}} {\mathrm{d}}w = \\ &\quad\quad\int_0^t {{k_{\rm{r}}}{e_2}\left( {\dot {\tilde d }- \mu {\mathrm{sgn}}({e_2})} \right)} {\mathrm{d}}w + {e_2}\dot{ \tilde d} -\\ &\quad\quad{e_2}\left( 0 \right)\dot {\tilde d}\left( 0 \right) - \mu \left| {{e_2}} \right| + \mu \left| {{e_2}\left( 0 \right)} \right| - \int_0^t {{{\dot e}_2}\ddot{ \tilde d}} {\mathrm{d}}w \end{split}$

(36)

由式（36）可得

$\begin{split} &\int_0^t {L\left( w \right)} {\mathrm{d}}w \leqslant \int_0^t {{k_{\rm{r}}}\left| {{e_2}} \right|\left( {{\delta _1} - \mu + \frac{{{\delta _2}}}{{{k_{\rm{r}}}}}} \right)} {\mathrm{d}}w + \\ & \quad\quad\left| {{e_2}} \right|\left( {{\delta _1} - \mu } \right) + \mu \left| {{e_2}\left( 0 \right)} \right| - {e_2}\left( 0 \right)\dot {\tilde d}\left( 0 \right) \end{split}$

(37)

由式（37）可以看出，若μ>δ₁+δ₂/k_r，函数P恒为正，故引理得证。

证毕

定理　若通过调整参数k、k₁、k_r，对称矩阵Λ正定，则系统(18)中所有信号均有界，且控制器可获得渐近稳定性，即t→∞时z→0，其中z=[e₁，e₂，r]^T。

${\boldsymbol{\varLambda }}= \left[ {\begin{array}{*{20}{c}} {{k_1}}&{ - \dfrac{1}{2}}&{ - \dfrac{1}{2}{c_1}} \\ { - \dfrac{1}{2}}&{{k_{\rm{r}}}}&{ - \dfrac{{1 - {c_2}}}{2}} \\ { - \dfrac{1}{2}{c_1}}&{ - \dfrac{{1 - {c_2}}}{2}}&{{k_3}} \end{array}} \right]$

(38)

定义参数：

$\left\{\begin{aligned} & {c_1} = {\theta _1}k_1^3 \\ & {c_2} = \left( {{k_1} + {k_{\rm{r}}}} \right){k_{\rm{r}}}{\theta _1} + k_1^2{\theta _1} \\ & {k_3} = k - \max \left\{ {\left| {{{\text{φ}} ^{\mathrm{T}}}\Pr {\mathrm{o}}{{\mathrm{j}}{\text{-}}{\hat {\boldsymbol{\theta}} }}\left( { -{\boldsymbol{\varGamma}} \dot {\text{φ}} } \right)} \right|} \right\} - {\theta _1}\left( {{k_1} + {k_{\rm{r}}}} \right) \end{aligned}\right.$

(39)

证明　为证明系统稳定性，定义非负函数如下：

${V_2} = \frac{1}{2}e_1^2 + \frac{1}{2}e_2^2 + \frac{1}{2}{\theta _1}{r^2} + \frac{1}{2}{\tilde {\boldsymbol{\theta}} ^{\mathrm{T}}}{{\boldsymbol{\varGamma}} ^{ - 1}}\tilde {\boldsymbol{\theta}} + P$

(40)

对式(40)求导：

${\dot V_2} = {e_1}{\dot e_1} + {e_2}{\dot e_2} + {\theta _1}r\dot r + {\tilde {\boldsymbol{\theta}} ^{\mathrm{T}}}{{\boldsymbol{\varGamma}} ^{ - 1}}\dot {\tilde {\boldsymbol{\theta}} } + \dot P$

(41)

将式(21)和式(32)代入式(41)得

$\begin{split} &{{\dot V}_2} = {e_1}\left( {{e_2} - {k_1}{e_1}} \right) + {e_2}\left( {r - {k_{\rm{r}}}{e_2}} \right) + \\ &\quad\quad r\{ {{\text{φ}} ^{\mathrm{T}}}{\mathrm{Pro}}{{\mathrm{j}}{\text{-}}{\hat {\boldsymbol{\theta}} }}\left( { -{\boldsymbol{\varGamma}} \dot {\text{φ}} r} \right) + {{\dot {\text{φ}} }^{\mathrm{T}}}\tilde {\boldsymbol{\theta}} - kr - \\ &\quad\quad\mu {{\mathrm{sgn}}} \left( {{e_2}} \right) + \dot {\tilde d }+ {\theta _1}\left( {{k_1} + {k_{\rm{r}}}} \right)r + {\theta _1}k_1^3{e_1} - \\ &\quad\quad\left[ {{\theta _1}k_1^2 + {\theta _1}\left( {{k_1} + {k_{\rm{r}}}} \right){k_{\rm{r}}}} \right]{e_2}\} + {{\tilde {\boldsymbol{\theta}} }^{\mathrm{T}}}{{\boldsymbol{\varGamma}} ^{ - 1}}\dot {\tilde {\boldsymbol{\theta}}} + \dot P \end{split}$

(42)

将式(34)中P的表达式代入式(42)并整理得

$\begin{split} &{{\dot V}_2} = - {k_1}e_1^2 - {k_{\rm{r}}}e_2^2 + {e_1}{e_2} + {e_2}r + {c_1}{e_1}r - {c_2}{e_2}r - \\ &\quad\quad k{r^2} + \left[ {{{\text{φ}} ^{\mathrm{T}}}{\mathrm{Pro}}{{\mathrm{j}}{\text{-}}{\hat {\boldsymbol{\theta}} }}\left( { -{\boldsymbol{\varGamma}} \dot {\text{φ}} } \right) + {\theta _1}\left( {{k_1} + {k_{\rm{r}}}} \right)} \right]{r^2} + \\ &\quad\quad {{\dot {\text{φ}} }^{\mathrm{T}}}\tilde {\boldsymbol{\theta}} r + {{\tilde {\boldsymbol{\theta}} }^{\mathrm{T}}}{{\boldsymbol{\varGamma}} ^{ - 1}}\dot {\tilde {\boldsymbol{\theta}}} \end{split}$

(43)

根据自适应率属性和式(39)参数得

${\dot V_2} \leqslant - {{\boldsymbol{z}}^{\rm{T}}}{\boldsymbol{\varLambda}} {\boldsymbol{z}} \leqslant - {\lambda _{\min }}\left( {\boldsymbol{\varLambda}} \right)\left( {e_1^2 + e_2^2 + {r^2}} \right)\mathop = \limits^\Delta - W$

(44)

由于V∈L_∞和W∈L₂，并且对信号z和参数的估计是有界的。那么x₁始终有界，同样控制输入u有界。根据e₁、e₂和r的计算式，可知W的导数有界，因此，W是一致连续的。根据Barbalat引理^[22]，当t→∞时W→0，故定理得证。

证毕

4. 结果与分析

4.1 试验平台

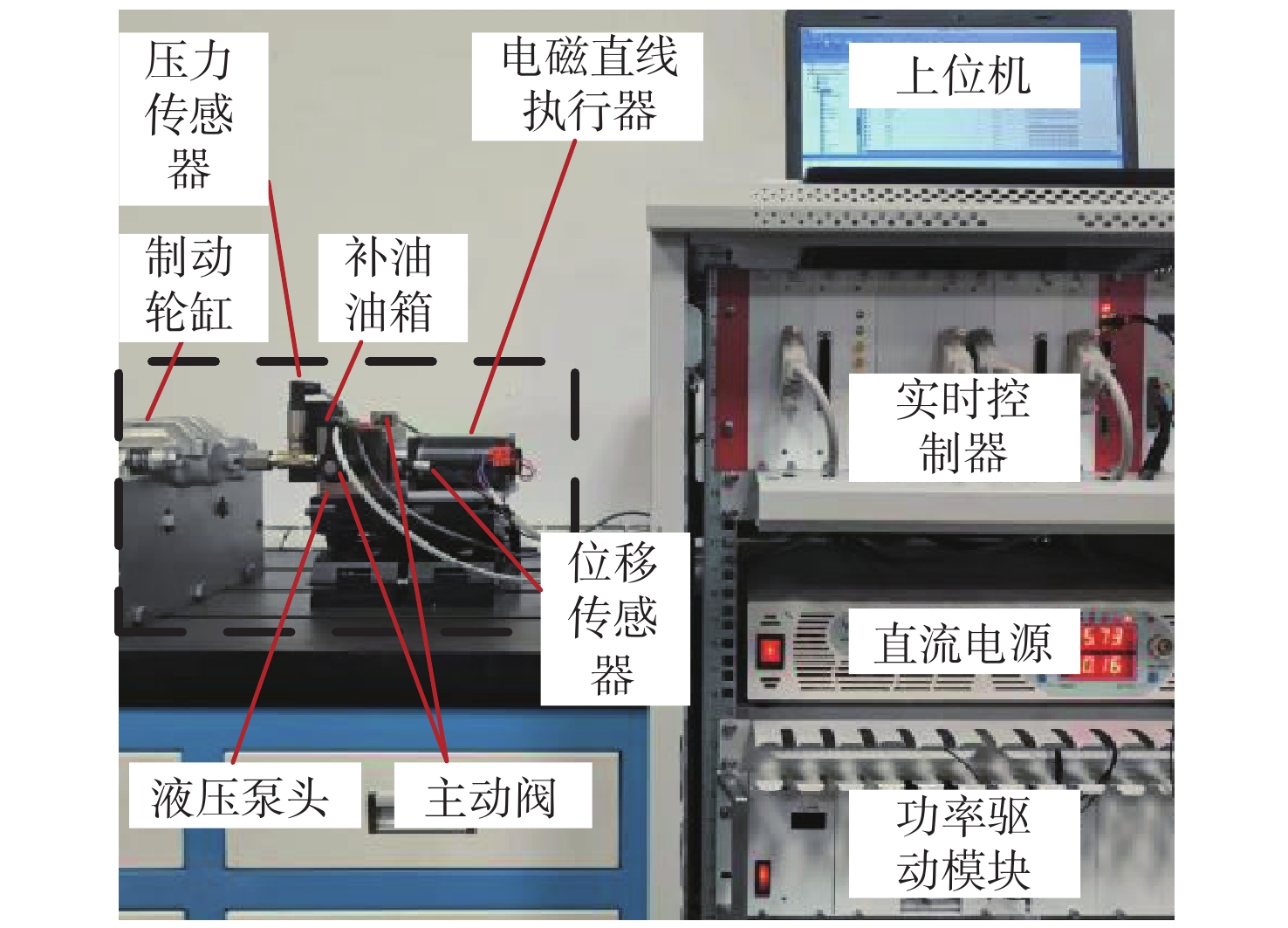
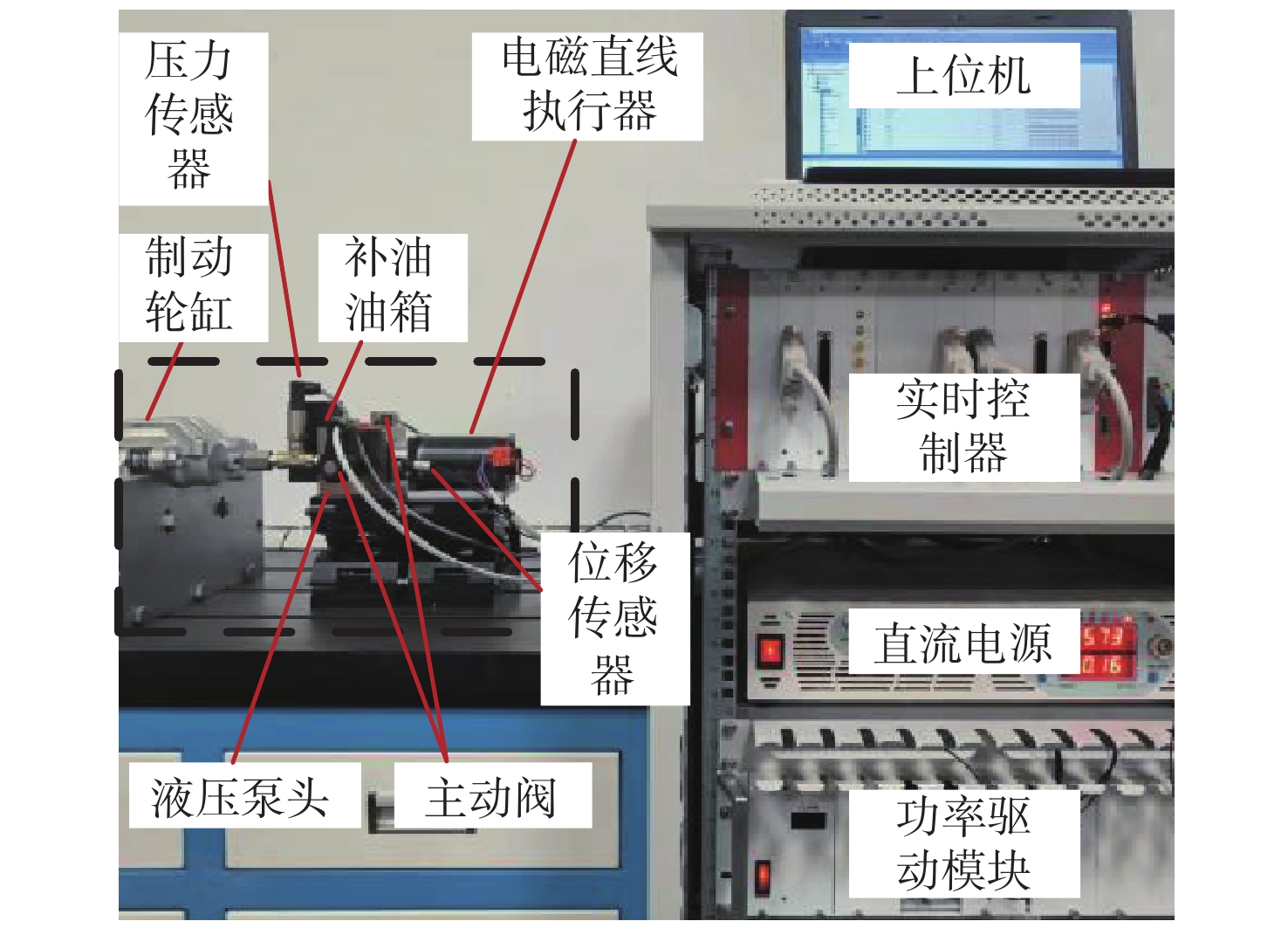
本文搭建了如图4所示的直驱泵阀协同式线控制动单元试验平台。上位机的控制信号通过以太网传送给控制器，控制器控制功率驱动模块控制电磁直线执行器的驱动电压、主动阀的开关，从而控制制动轮缸液压力。控制器采用快速控制原型系统RTU-BOX，其数字控制器采用主频率为300 MHz的32位浮点数字信号处理器TMS320C 28346。采用0.01 mm分辨率的位置传感器提供电磁直线执行器的位置反馈，具有0.01 MPa分辨率的压力传感器提供轮缸液压力反馈。

图 4 测试平台

Figure 4. Experimental platform

下载: 全尺寸图片幻灯片

将本文提出的串级控制与常用的双闭环PID控制进行比较。串级控制中，外环参数c_a=0.02，c_b=3，k_h=5，q=0.002；内环参数k=500，k₁=130，k_r=4，μ=10，θ_max=[0.1, 50, 0.5, 0.01]^T，θ_min=[0, 0, 0, 0]^T，Г=diag[0.8, 3600, 5.2, 0.02]。双闭环PID控制中外环PID参数k_p1=0.06，k_I1=0.8，k_d1=0.05；内环PID参数k_p2=600，k_I2=5000，k_d2=2000。

4.2 响应性能测试

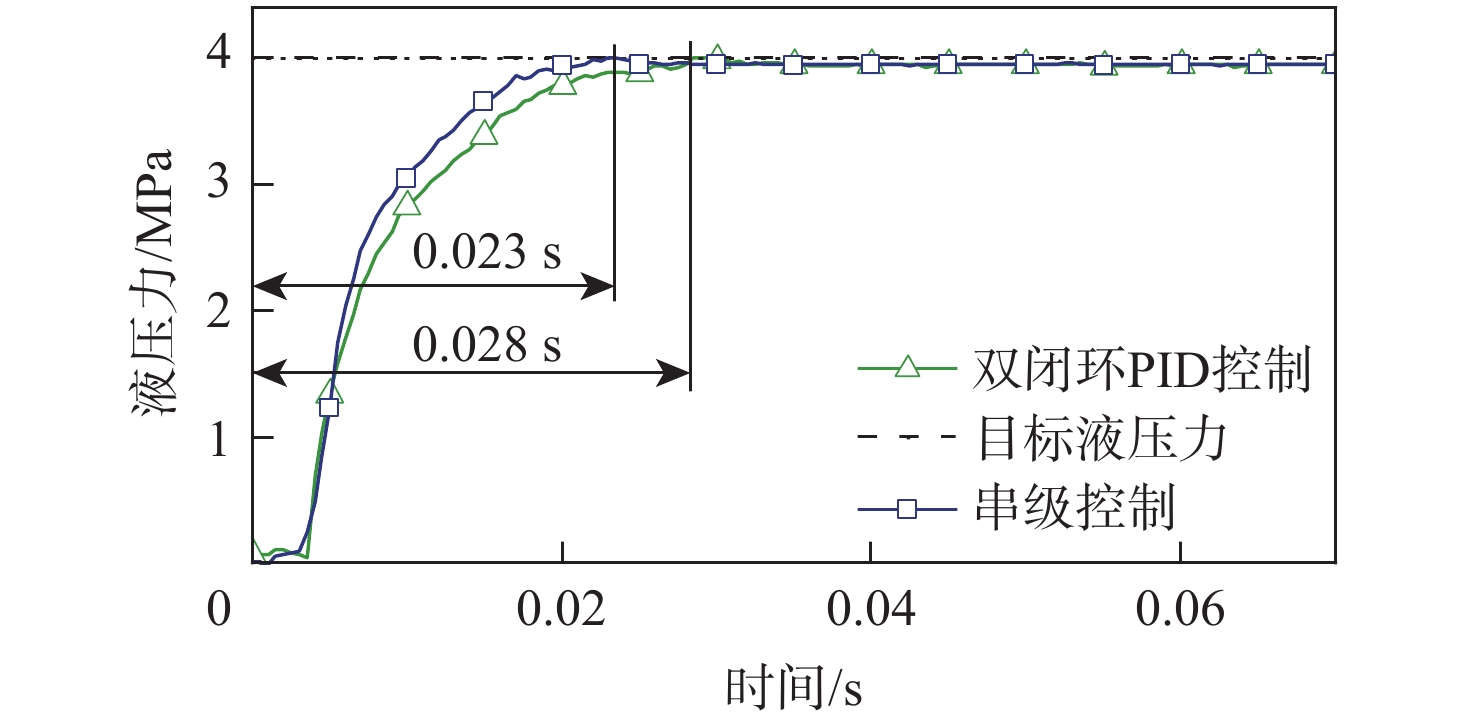
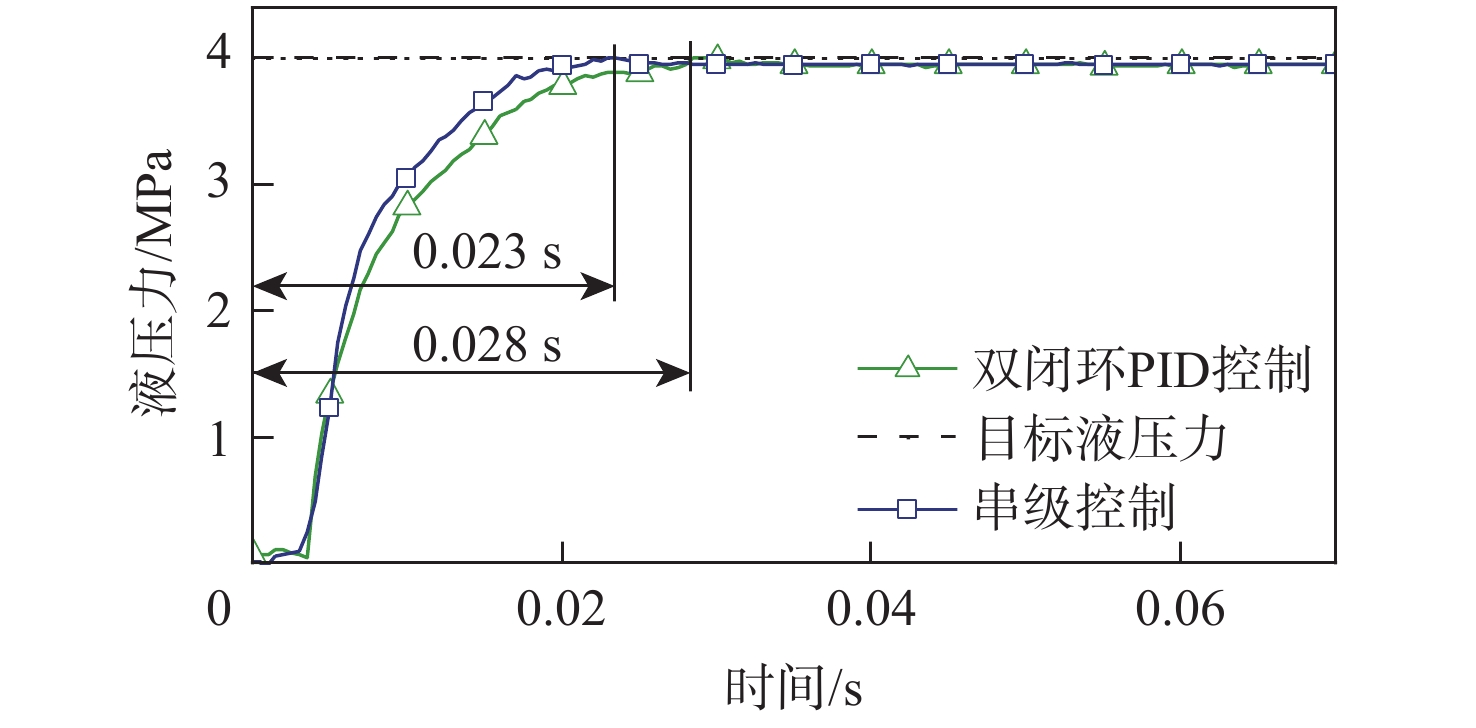
模拟目标小车紧急制动工况，设置阶跃响应目标为4 MPa，测试结果如图5所示。在2种不同控制器下，本文所设计的直驱泵阀协同式线控制动单元均可以快速达到目标值。双闭环PID控制的响应时间为0.028 s ，而串级控制的响应时间为0.023 s，相较于双闭环PID控制，响应时间提升了17.8%，证明串级控制的快速响应性能优于双闭环PID控制。

图 5 阶跃响应测试结果

Figure 5. Experimental results of step response

下载: 全尺寸图片幻灯片

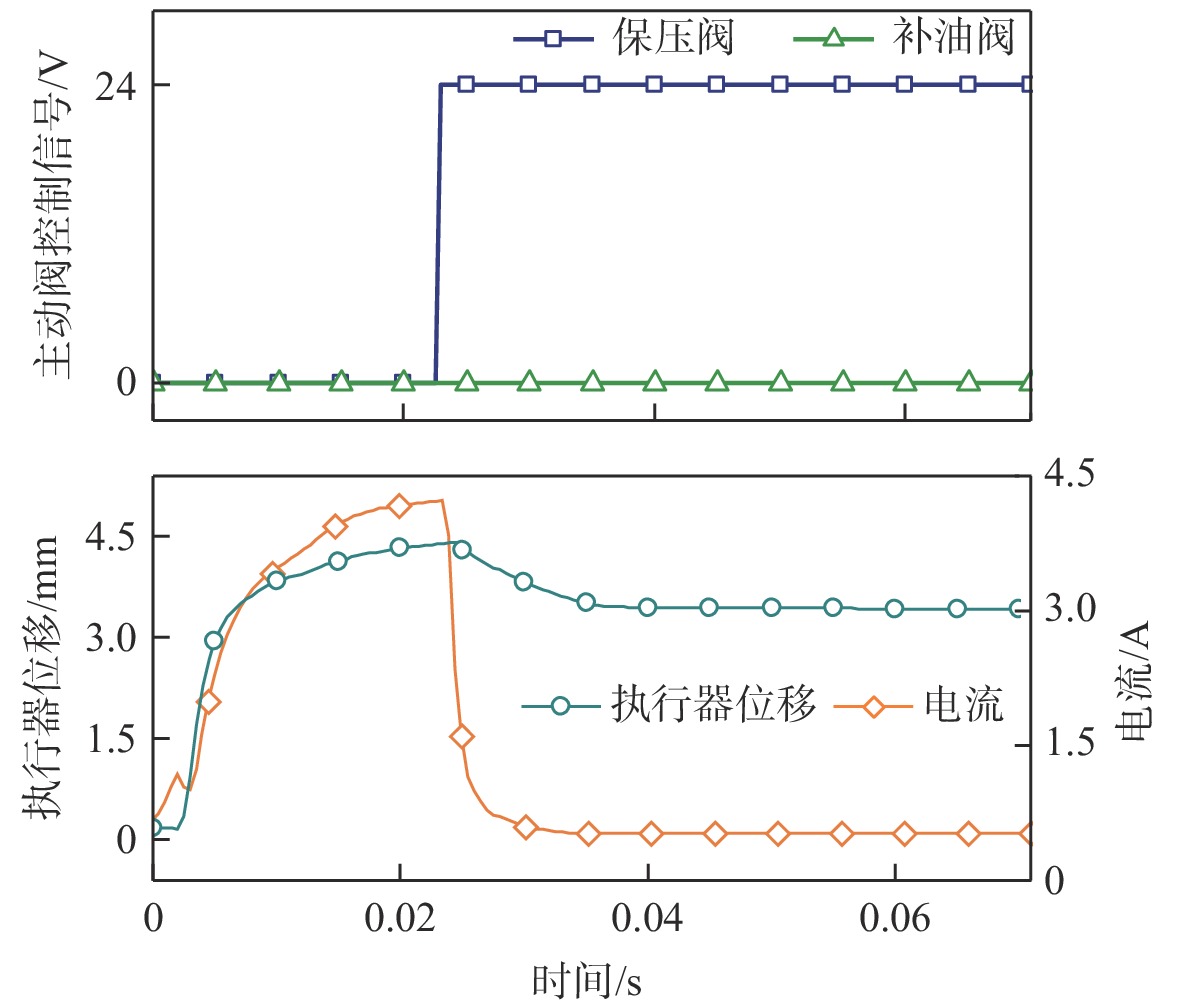
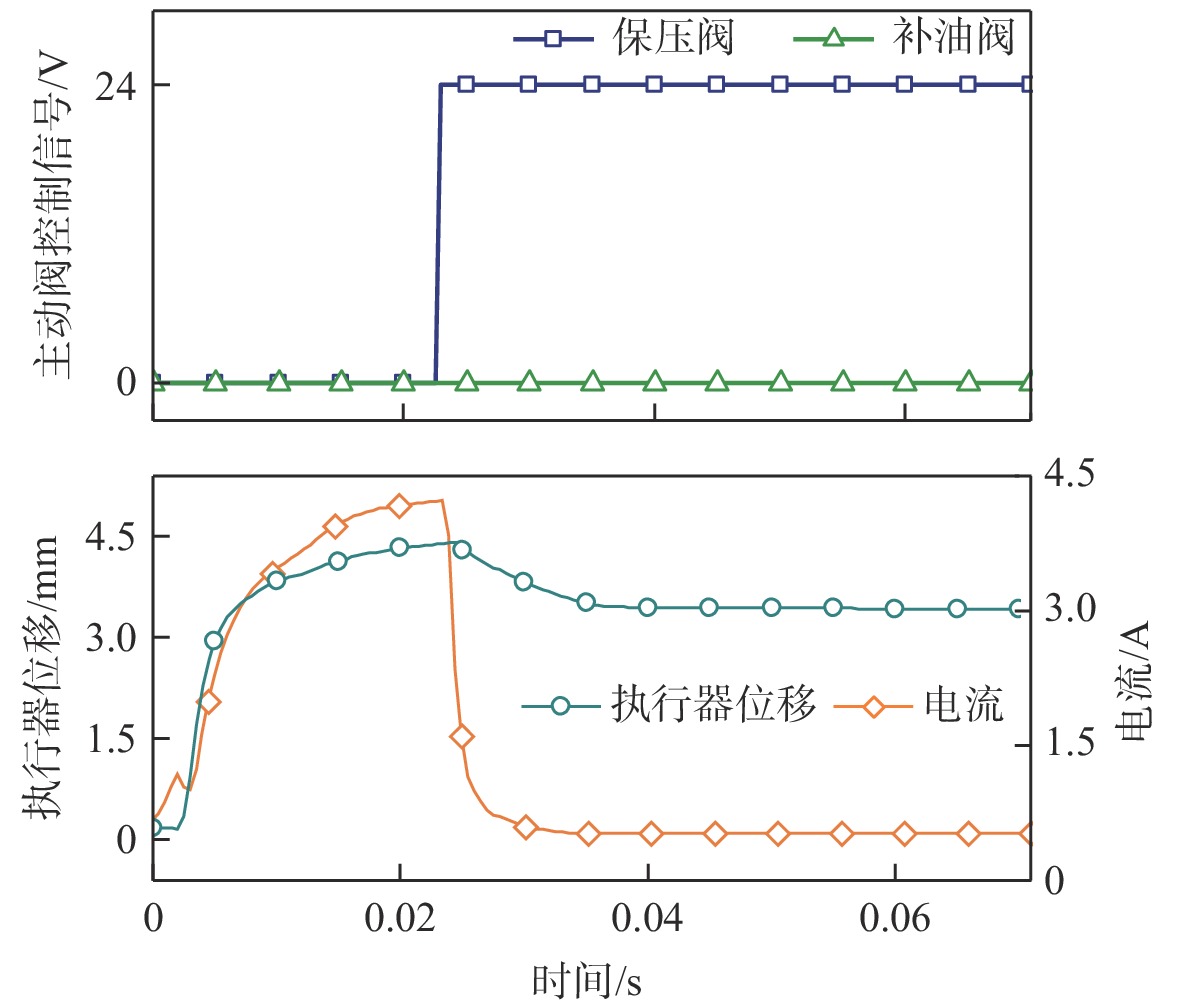
串级控制器下的电磁直线执行器及主动阀的测试结果如图6所示。系统达到目标压力且工作模式切换为保压模式时，此时保压阀关闭导致液压力出现较小的波动，同时执行器控制信号为0，电流值迅速下降，在泵腔内压力的作用下执行器向复位方向运动一段位移。

图 6 串级控制器时阶跃响应测试中直驱泵相关信号

Figure 6. Relevant signals of direct-drive pump in step response experiment with cascade controller

下载: 全尺寸图片幻灯片

4.3 跟踪性能测试

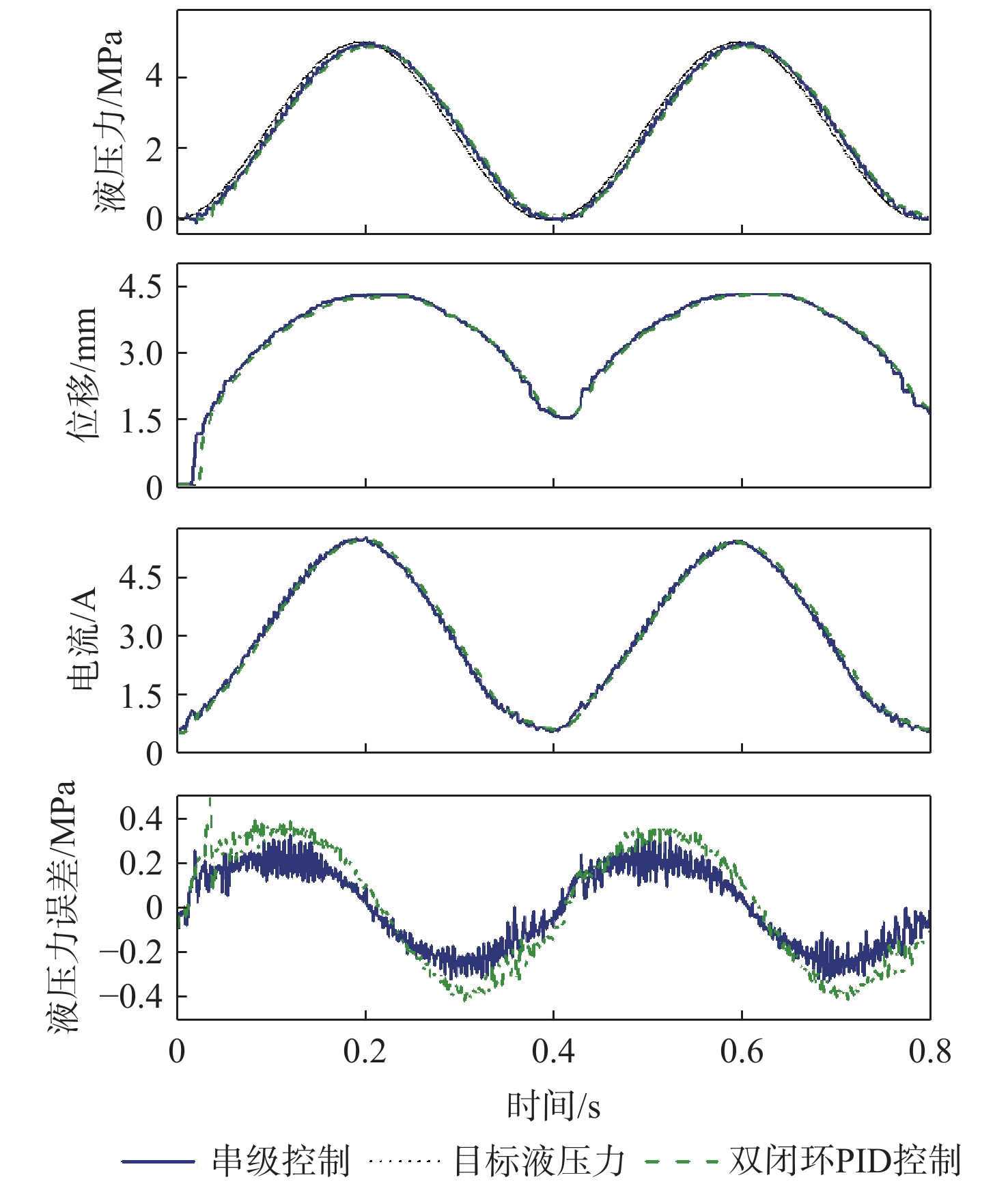
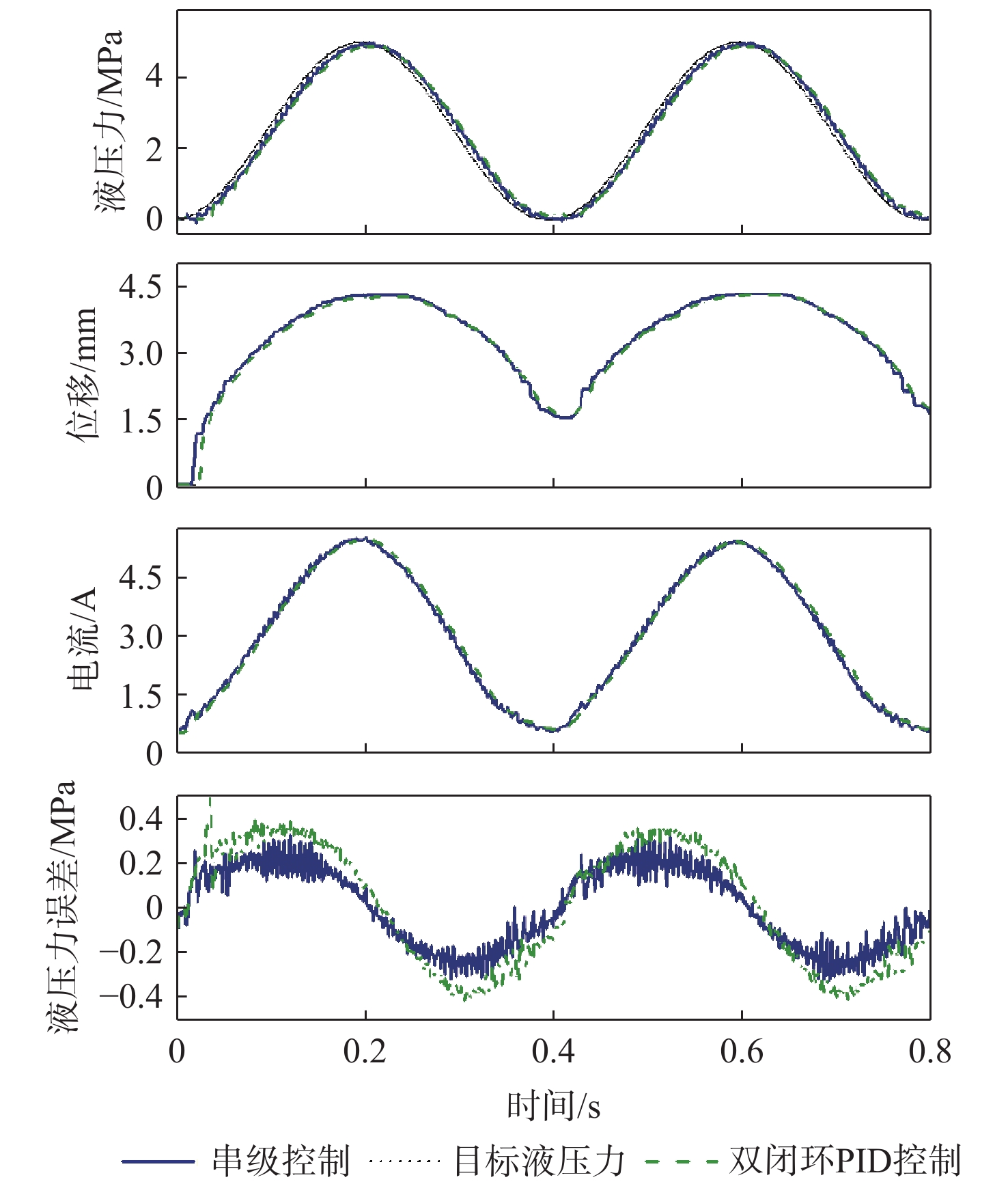
正弦制动压力工况是模拟驾驶员在某些特定工况下有规律地松踩制动踏板，设置目标正弦压力信号频率为2.5 Hz、振幅为2.5 MPa，液压力跟踪测试如图7所示。

图 7 正弦压力目标信号试验结果

Figure 7. Experimental results of sinusoidal pressure target signal

下载: 全尺寸图片幻灯片

2种控制均可以较好的跟踪正弦信号，在第1个峰值处，串级控制器和双闭环PID控制器的滞后时间分别为0.007 s和0.009 s。由于制动单元内部液压油未充满，在0.4 s处执行器动子位置高于初始状态。为进一步比较2种控制器的跟踪性能，采用液压力平均误差e_μ和误差的标准偏差e_σ来比较2种控制器的液压力跟踪性能。e_μ和e_σ的具体表达式为

$\left\{\begin{aligned} &{e_{\text{μ}} } = \left({{\displaystyle\sum\limits_{i = 1}^n {\left| {{e_i}} \right|} }}\right)\Bigg/{n}\\ &{e_{\text{σ}} } = \sqrt {\left[{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {\left| {{e_i}} \right| - {e_{\text{μ}}}} \right)}^2}} }}\right]\Bigg/{n}} \end{aligned}\right.$

(45)

在整个跟踪过程中，双闭环PID控制的e_μ为0.238 MPa，串级控制的平均误差e_μ为0.159 MPa,相比于双闭环PID控制减小了33.2%。双闭环PID控制的e_σ为0.107，串级控制的标准偏差e_σ为0.074 MPa，标准偏差e_σ为0.074 MPa，其相比于双闭环PID控制减小了30.8%。2种控制的性能参数均较小，说明2种控制均可较好的实现目标液压力的跟踪控制，同时在正弦目标液压力下，提出的串级控制器在跟踪性能上优于双闭环PID控制器。

为模拟较为缓和的制动过程，设置三角波制动目标液压力频率为2.5 Hz、振幅为2.5 MPa，2种控制器的液压力跟踪结果如图8所示。由图可知，在0.2 s和0.4 s处目标信号导数突变，但2种控制器均能较好的跟随目标液压力。

图 8 三角波压力信号试验结果

Figure 8. Experimental results of triangular wave pressure signal

下载: 全尺寸图片幻灯片

在三角波目标跟踪过程中，双闭环PID控制的平均误差e_μ为0.201 MPa，串级控制的e_μ为0.126 MPa，相较于双闭环PID控制降低了37.3%。双闭环PID控制的e_σ为0.056，串级控制的标准偏差e_σ为0.045，相比于双闭环PID控制减小了19.6%。说明相较于双闭环PID控制，串级控制在维持一定速率增加或降低液压力时有较好的准确性，也证明了在三角波目标液压力下，本文的串级控制器在跟踪性能上优于双闭环PID控制器。

5. 结　论

1）本文提出一种响应迅速、不恶化轮边空间与簧下质量的直驱泵阀协同式线控制动单元，通过电磁直线执行器直接驱动的液压泵与主动阀协调实现轮缸压力调节，为分布式制动系统提供了一种新的方案。

2）本文设计了基于外环轮缸压力和内环执行器位移的串级控制器，通过外环滑模控制得到理想执行器位移，利用内环自适应积分鲁棒控制减小执行器参数不确定性和时变干扰的影响，提高了系统响应速度与控制精度。

3）基于新的制动单元搭建了测试平台，通过阶跃响应、正弦波跟踪、三角波跟踪等工况，测试了制动单元性能，试验结果表明，在响应速度与控制精度上，本文的串级控制器优于双闭环PID控制器，为线控制动系统控制提供了一种方案。

图 1 直驱泵阀协同式线控制动单元原理图

Figure 1. Principle diagram of brake-by-wire unit based on direct drive pump-valve cooperative

下载: 全尺寸图片幻灯片

图 2 控制系统总体框图

Figure 2. Overall block diagram of control system

下载: 全尺寸图片幻灯片

图 3 自适应积分鲁棒控制框图

Figure 3. Adaptive integral robust control block diagram

下载: 全尺寸图片幻灯片

图 4 测试平台

Figure 4. Experimental platform

下载: 全尺寸图片幻灯片

图 5 阶跃响应测试结果

Figure 5. Experimental results of step response

下载: 全尺寸图片幻灯片

图 6 串级控制器时阶跃响应测试中直驱泵相关信号

Figure 6. Relevant signals of direct-drive pump in step response experiment with cascade controller

下载: 全尺寸图片幻灯片

图 7 正弦压力目标信号试验结果

Figure 7. Experimental results of sinusoidal pressure target signal

下载: 全尺寸图片幻灯片

图 8 三角波压力信号试验结果

Figure 8. Experimental results of triangular wave pressure signal

下载: 全尺寸图片幻灯片

表 1 直驱泵阀协同式线控制动单元参数

Table 1. Parameters of brake-by-wire unit based on direct drive pump-valve cooperative

结构	参数	数值
电磁直线执行器	线圈电阻R/Ω	1.40
	线圈等效电感L/mH	0.91
	反电势系数K_e/（Vs·m⁻¹）	24.61
	电磁力系数K_m/(N·A⁻¹)	24.61
直驱泵	泵腔长度l/mm	16
直驱泵	活塞面积S₁/mm²	27.5
主动阀	阀芯直径/mm	8
主动阀	阀座直径/mm	4
制动液	弹性模量β_e/MPa	1700
制动液	密度ρ/（kg·m⁻³）	1046

下载: 导出CSV

参考文献(22)

[1]	高峰, 雍加望, 丁能根, 等. 集成电液制动系统助力算法及其功能验证[J]. 北京航空航天大学学报, 2017, 43(3): 424-431. GAO F, YONG J W, DING N G, et al. Booster algorithm and functionality validation of an integrated electro-hydraulic brake system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3): 424-431(in Chinese).
[2]	ZHAO J, CHEN Z C, ZHU B, et al. Precise active brake-pressure control for a novel electro-booster brake system[J]. IEEE Transactions on Industrial Electronics, 2020, 67(6): 4774-4784. doi: 10.1109/TIE.2019.2924613
[3]	何仁, 刘学军, 刘存香. 汽车电磁-液压复合制动技术研究进展[J]. 中国公路学报, 2014, 27(11): 109-119. doi: 10.3969/j.issn.1001-7372.2014.11.015 HE R, LIU X J, LIU C X. Research progress in electromagnetic- hydraulic hybrid brake technology[J]. China Journal of Highway and Transport, 2014, 27(11): 109-119(in Chinese). doi: 10.3969/j.issn.1001-7372.2014.11.015
[4]	XIONG L, HAN W, YU Z P. Adaptive sliding mode pressure control for an electro-hydraulic brake system via desired-state and integral-antiwindup compensation[J]. Mechatronics, 2020, 68: 102359. doi: 10.1016/j.mechatronics.2020.102359
[5]	PAN N, YU L Y, WANG Z Z, et al. Design, modeling and simulation of a new compact electro-hydraulic brake system[C]//Proceedings of the SAE Technical Paper Series. Warrendale: SAE International, 2014.
[6]	余卓平, 史彪飞, 卓桂荣, 等. 集成式电子液压制动系统位移压力特性理论研究[J]. 机械工程学报, 2022, 58(22): 294-303. doi: 10.3901/JME.2022.22.294 YU Z P, SHI B F, ZHUO G R, et al. Theoretical research on pressure-position relationship of the integrated electronic-hydraulic brake system[J]. Journal of Mechanical Engineering, 2022, 58(22): 294-303(in Chinese). doi: 10.3901/JME.2022.22.294
[7]	胡东海, 何仁. 电子液压制动系统的安全设计与匹配分析[J]. 农业工程学报, 2015, 9: 77-84. doi: 10.11975/j.issn.1002-6819.2015.09.013 HU D H, HE R. Safety design and matching analysis of electronic hydraulic brake system[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 9: 77-84(in Chinese). doi: 10.11975/j.issn.1002-6819.2015.09.013
[8]	刘兆勇, 龙一鸣, 厉逸航, 等. 集成式电液制动系统设计及参数匹配的研究[J]. 汽车工程, 2022, 44(9): 1416-1424. LIU Z Y, LONG Y M, LI Y H, et al. Study on the design and parameter matching of integrated electro-hydraulic braking system[J]. Automotive Engineering, 2022, 44(9): 1416-1424(in Chinese).
[9]	陈晋市, 刘思远, 王同建, 等. 8×8全电驱动越野车电机液压联合全液压制动系统设计及性能[J]. 兵工学报, 2021, 42(02): 422-429. doi: 10.3969/j.issn.1000-1093.2021.02.019 CHEN J S, LIU S Y, WANG T J, et al. Design and performance of electro-hydraulic full hydraulic brake system for 8×8 all-electric drive off-road vehicle[J]. Acta Armamentarii, 2021, 42(02): 422-429(in Chinese). doi: 10.3969/j.issn.1000-1093.2021.02.019
[10]	WANG Z Z, YU L Y, YOU C X, et al. Fail-safe control allocation for a distributed brake-by-wire system considering the driver’s behaviour[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2014, 228(13): 1547-1567. doi: 10.1177/0954407014534225
[11]	GONG X X, QIAN L X, GE W G, et al. Research on electronic brake force distribution and anti-lock brake of vehicle based on direct drive electro hydraulic actuator[J]. International Journal of Automotive Engineering, 2020, 11(2): 22-29. doi: 10.20485/jsaeijae.11.2_22
[12]	初亮, 赵迪, 李文惠. 电-液制动系统高速开关电磁阀的建模与动态特性仿真[J]. 汽车工程, 2017, 39(1): 61-65. CHU L, ZHAO D, LI W H. Modeling and dynamic characteristics simulation for fast-switching solenoid valves in electro-hydraulic braking systems[J]. Automotive Engineering, 2017, 39(1): 61-65(in Chinese).
[13]	熊璐, 韩伟, 余卓平, 等. 考虑关键非线性特征的集成式电子液压制动系统主缸液压力精确控制[J]. 机械工程学报, 2019, 55(24): 117-126. doi: 10.3901/JME.2019.24.117 XIONG L, HAN W, YU Z P, et al. Pressure precisely control of master cylinder on integrated-electro-hydraulic brake system considering the critical nonlinear characteristics[J]. Journal of Mechanical Engineering, 2019, 55(24): 117-126(in Chinese). doi: 10.3901/JME.2019.24.117
[14]	石琴, 刘鑫, 应贺烈, 等. 电液线控制动系统压力反步控制算法研究[J]. 汽车工程, 2022, 44(5): 747-755. SHI Q, LIU X, YING H L, et al. Study on the backstepping control algorithm for the hydraulic pressure in electro-hydraulic brake-by-wire system[J]. Automotive Engineering, 2022, 44(5): 747-755(in Chinese).
[15]	JI Y, ZHANG J Z, HE C K, et al. Constraint performance pressure tracking control with asymmetric continuous friction compensation for booster based brake-by-wire system[J]. Mechanical Systems and Signal Processing, 2022, 174: 109083. doi: 10.1016/j.ymssp.2022.109083
[16]	TAN C, REN H X, LI B, et al. Design and analysis of a novel cascade control algorithm for braking-by-wire system based on electromagnetic direct-drive valves[J]. Journal of the Franklin Institute, 2022, 359(16): 8497-8521. doi: 10.1016/j.jfranklin.2022.09.006
[17]	HAN W, XIONG L, YU Z P. Braking pressure control in electro-hydraulic brake system based on pressure estimation with nonlinearities and uncertainties[J]. Mechanical Systems and Signal Processing, 2019, 131: 703-727. doi: 10.1016/j.ymssp.2019.02.009
[18]	俞军涛, 占昊, 王丽, 等. 压电式高速开关阀控液压缸位置系统[J]. 北京航空航天大学学报, 2021, 47(4): 706-714. YU J T, ZHAN H, WANG L, et al. Hydraulic cylinder position system controlled by piezoelectric high-speed on-off valve[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(4): 706-714(in Chinese).
[19]	JIANG L G, SHI Q, WEI Y J, et al. Electro-hydraulic braking dynamics for pressure demand control of brake-by-wire system[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2024, 238(4): 735-748. doi: 10.1177/09544070221135390
[20]	谭草, 鲁应涛, 葛文庆, 等. 直驱式永磁直线电机深度模糊滑模-自抗扰控制[J]. 西安交通大学学报, 2023, 57(1): 185-194. doi: 10.7652/xjtuxb202301018 TAN C, LU Y T, GE W Q, et al. Depth fuzzy sliding-mode active disturbance rejection control method of permanent magnet linear motor for direct drive system[J]. Journal of Xi’an Jiaotong University, 2023, 57(1): 185-194(in Chinese). doi: 10.7652/xjtuxb202301018
[21]	李波, 黎德祥, 葛文庆, 等. 基于直驱阀的快速响应线控制动系统液压力精确控制[J]. 中国公路学报, 2021, 34(9): 121-132. doi: 10.3969/j.issn.1001-7372.2021.09.010 LI B, LI D X, GE W Q, et al. Precision control of hydraulic pressure in fast-response brake-by-wire system based on direct-drive valve[J]. China Journal of Highway and Transport, 2021, 34(9): 121-132(in Chinese). doi: 10.3969/j.issn.1001-7372.2021.09.010
[22]	潘菲, 朱宏玉. 航天器非奇异自适应终端滑模姿轨联合控制[J]. 北京航空航天大学学报, 2020, 46(7): 1354-1362. PAN F, ZHU H Y. Spacecraft non-singular adaptive terminal sliding mode attitude-orbit coupling control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(7): 1354-1362(in Chinese).

施引文献

资源附件(0)

访问统计

点击查看大图

图(8) / 表(1)

计量

文章访问数: 132
HTML全文浏览量: 79
PDF下载量: 3
被引次数: 0

1. 方案设计与工作原理
2. 控制系统模型建立
2.1 电磁直线执行器建模
2.2 液压系统建模
2.3 制动单元状态空间模型
3. 串级控制器设计
3.1 外环控制器设计
3.2 内环控制器设计
4. 结果与分析
4.1 试验平台
4.2 响应性能测试
4.3 跟踪性能测试
5. 结　论

1. 方案设计与工作原理
2. 控制系统模型建立
2.1 电磁直线执行器建模
2.2 液压系统建模
2.3 制动单元状态空间模型
3. 串级控制器设计
3.1 外环控制器设计
3.2 内环控制器设计
4. 结果与分析
4.1 试验平台
4.2 响应性能测试
4.3 跟踪性能测试
5. 结　论

参考文献(22)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

直驱泵阀协同式线控制动单元压力串级控制

doi: 10.13700/j.bh.1001-5965.2023.0216

通讯作者:
E-mail：libo@sdut.edu.cn

计量

Pressure cascade control of brake-by-wire unit based on direct drive pump-valve cooperative

Corresponding author: E-mail：libo@sdut.edu.cn

1. 方案设计与工作原理

2. 控制系统模型建立

2.1 电磁直线执行器建模

2.2 液压系统建模

2.3 制动单元状态空间模型

3. 串级控制器设计

3.1 外环控制器设计

3.1.1 滑模控制器

3.1.2 稳定性分析

3.2 内环控制器设计

3.2.1 自适应积分鲁棒控制器设计

3.2.2 稳定性分析

4. 结果与分析

4.1 试验平台

4.2 响应性能测试

4.3 跟踪性能测试

5. 结　论

计量

目录

1. 方案设计与工作原理

2. 控制系统模型建立

2.1 电磁直线执行器建模

2.2 液压系统建模

2.3 制动单元状态空间模型

3. 串级控制器设计

3.1 外环控制器设计

3.2 内环控制器设计

4. 结果与分析

4.1 试验平台

4.2 响应性能测试

4.3 跟踪性能测试

5. 结　论

留言板

直驱泵阀协同式线控制动单元压力串级控制

doi: 10.13700/j.bh.1001-5965.2023.0216

通讯作者: E-mail：libo@sdut.edu.cn

计量

出版历程

Pressure cascade control of brake-by-wire unit based on direct drive pump-valve cooperative

Corresponding author: E-mail：libo@sdut.edu.cn

1. 方案设计与工作原理

2. 控制系统模型建立

2.1 电磁直线执行器建模

2.2 液压系统建模

2.3 制动单元状态空间模型

3. 串级控制器设计

3.1 外环控制器设计

3.1.1 滑模控制器

3.1.2 稳定性分析

3.2 内环控制器设计

3.2.1 自适应积分鲁棒控制器设计

3.2.2 稳定性分析

4. 结果与分析

4.1 试验平台

4.2 响应性能测试

4.3 跟踪性能测试

5. 结 论

计量

出版历程

目录

1. 方案设计与工作原理

2. 控制系统模型建立

2.1 电磁直线执行器建模

2.2 液压系统建模

2.3 制动单元状态空间模型

3. 串级控制器设计

3.1 外环控制器设计

3.2 内环控制器设计

4. 结果与分析

4.1 试验平台

4.2 响应性能测试

4.3 跟踪性能测试

5. 结 论

通讯作者:
E-mail：libo@sdut.edu.cn

5. 结　论

5. 结　论