作为新体制雷达的典型代表，低截获概率（low probability of intercept, LPI）雷达信号^[1]得益于其功率小、隐蔽性高、拦截率低、抗干扰能力强^[2]等特性，近年来被广泛用于舰载防空雷达、机载火控雷达。在电子对抗侦察中，电子侦察系统被视为军事作战的“千里眼”，检测和截获信号的能力是评估电子侦察系统发展进程的重要特征之一。在越来越恶化的电磁环境下，自动高效的识别低截获概率信号是现代电子侦察方向一个重要研究课题，对于战场成败具有现实意义。

雷达辐射源脉内调制方式识别的方法，基本可分为特征提取和分类器设计两大步。非平稳信号所使用的特征主要包括时频变换和高阶统计分析，其中，时频变换大多建立在魏格纳-维尔分布(Wigner-Ville distribution, WVD)的基础上。文献[3]利用短时傅里叶变换(short-time Fourier transform，STFT)和k-means算法进行信号特征分析的频谱计算，将STFT作为特征用于信号的识别。文献[4]使用崔-威廉姆斯分布(Choi-William distribution, CWD)变换将雷达信号波形转换为时频图像，并从时频图像中提取定向梯度(histogram of oriented gradients，HOG)特征和深度特征进行特征融合，进而完成对雷达信号的分类。文献[5]基于小波变换提取信号时域特征、模糊函数切片特征及循环频谱特征，并通过特征融合处理完成发射端的雷达信号分类。然而上述方法大多在信噪比(signal-to-noise ratio, SNR)高于0 dB时，识别精度较高，随着信噪比降低分类准确率会出现骤降的情况，鲁棒性较差。由于深度学习强大的特征学习能力，越来越多的研究者将其应用于雷达信号调制方式识别方面。文献[6]由残差学习卷积去噪自编码器(residual learning convolutional denoising autoencoder, RLCDAE)和基于噪声级估计(noise level estimation, NLE)的辅助分类网络构成X-net，用于强噪声背景下辐射信号的检测。文献[7]基于一维CNN网络模型，采用伪标签和自步调数据增强，提高了脉内分类的准确性。文献[8]引入一种具有2个不同网络——进化神经网络(evolutionary neural networks, ENN) 和卷积神经网络(convolutional neural networks, CNN)的混合分类器完成自动雷达波形识别系统。尽管深度学习能够对多种雷达信号实现有效的分类，但现阶段的研究工作大多为了提取信号的细微特征而设计较深的网络模型，使得算法难以在实际战场环境部署。

本文从信号的时频特性出发，提出一种基于时频重排算法和平滑伪魏格纳-威尔分布(smoothed pseudo Wigner-Ville distribution, SPWVD)的LPI雷达信号识别方法，充分利用重排算法提高时频聚集性的特点与SPWVD抑制交叉项的特性，将重排后的SPWVD时频图像作为模型的输入，利用多尺度残差网络作为分类模型，对13类常见LPI雷达信号进行有效分类识别，在信噪比大于−8 dB的情况下，整体平均识别率也可达到94%以上。

1.   雷达信号特征提取

1.1   时频特征分析

时频变换是分析诸如雷达信号等非平稳信号的有力工具，时频变换可以用来估计信号在时域和频域的联合分布情况，表征时间和频率之间的关系。常用的时频分析包括STFT、WVD、CWD等。WVD是较早提出的用于时频分析的方法，其摆脱了窗函数的束缚，同时还克服了短时傅里叶变换的缺点，信号s(t)的WVD分布定义为^[9]

式中：t为时间；f为频率；$s(\cdot)$为时间信号；“*”表示复共轭；τ为时延。

为陈述时频重排的原理，使用二次型时频分布^[10]的表达式：

式中：核函数$\phi (t,f)$为时频平面的二维低通滤波器。

由式(2)可以看出，时频平面任意点$(t,f)$的值是该点的邻近点$(t - t',f - f')$上的原信号的${\text{WVD-s}}(t,f)$经过核函数加权后的平均值。时频重排算法是通过将代表信号局部能量分布的几何中心重新定位到时频分布的能量的中心，从而提高时频图像的聚集性和可读性^[11]。时频的重排引起对时频分布的重构，移动后重心对应的坐标^[12]为

信号的WVD在时频平面的聚集性最佳，但是会导致大量交叉项的产生，对于相位调制信号而言，跳频幅度较小，而交叉项会导致细微跳频特征不清晰，进而影响相位调制信号的识别。SPWVD算法是对WVD算法进行时频域平滑的改进算法^[13]，可以独立地控制在时间和频率方向上的平滑，因为其具有可分离的核函数$\phi (t,f) = g(t)H(f)$，则可得SPWVD算法的表达式为

式中：$g(u)$为抑制时域方向交叉项的窗函数；$h(\tau )$为抑制频域方向交叉项的窗函数。该算法使用窗函数对时域和频域进行滤波，很好地抑制了交叉项的产生，但是随着平滑次数的增加，时频分辨率显著降低。

对于SPWVD而言，其重排的坐标为

式中：T_g为乘积算子；D_h为微分算子。分别定义为${T_g}(t) = tg(t)$和${D_h}(t) = \dfrac{{\mathrm{d}}}{{{\mathrm{d}}t}}h(t)$。重排后的时频分布在任意点$(t',f')$处的值是所有重排到这一点的值的和，时频重排后的 SPWVD 定义如下所示：

式中：$\delta (t)$为狄拉克冲击函数。通过使用快速傅氏变换算法，每个重排的时频分布就可以被高效计算，而不会产生很大的计算负担。任何重排分的脊可以利用脊和时频算子之间的关系得到，提取时频重排后SPWVD的脊，通过在重排后的脊上选择合适的时频点可以有效地筛选出所需信号，重排后信号的时频聚集性更强，信号所在时频域的脊和轮廓都更为明显，同时还大大降低了噪声信号的干扰，从而保证了不同调制类型信号的分辨能力，进而提高了算法的抗噪声性能。

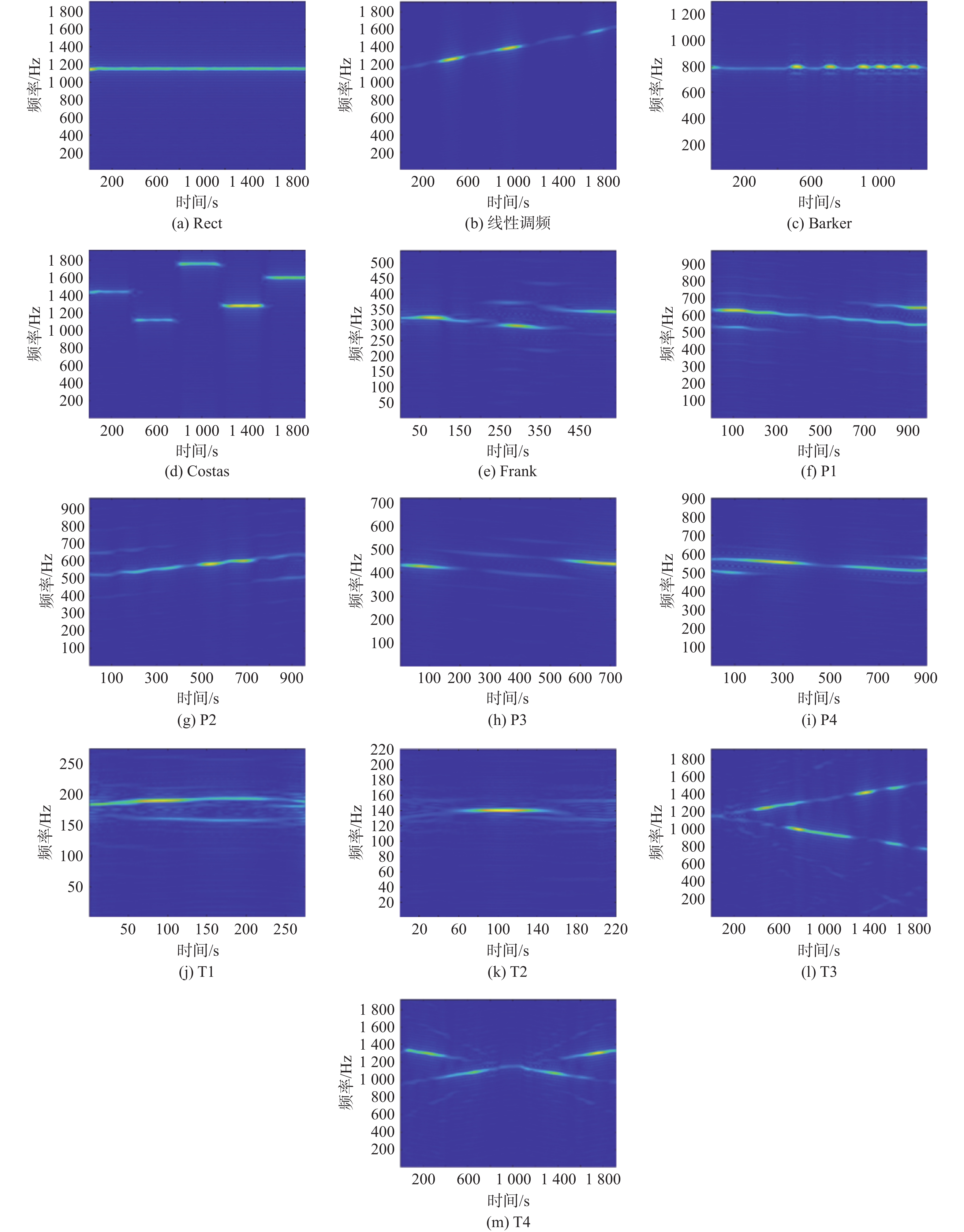
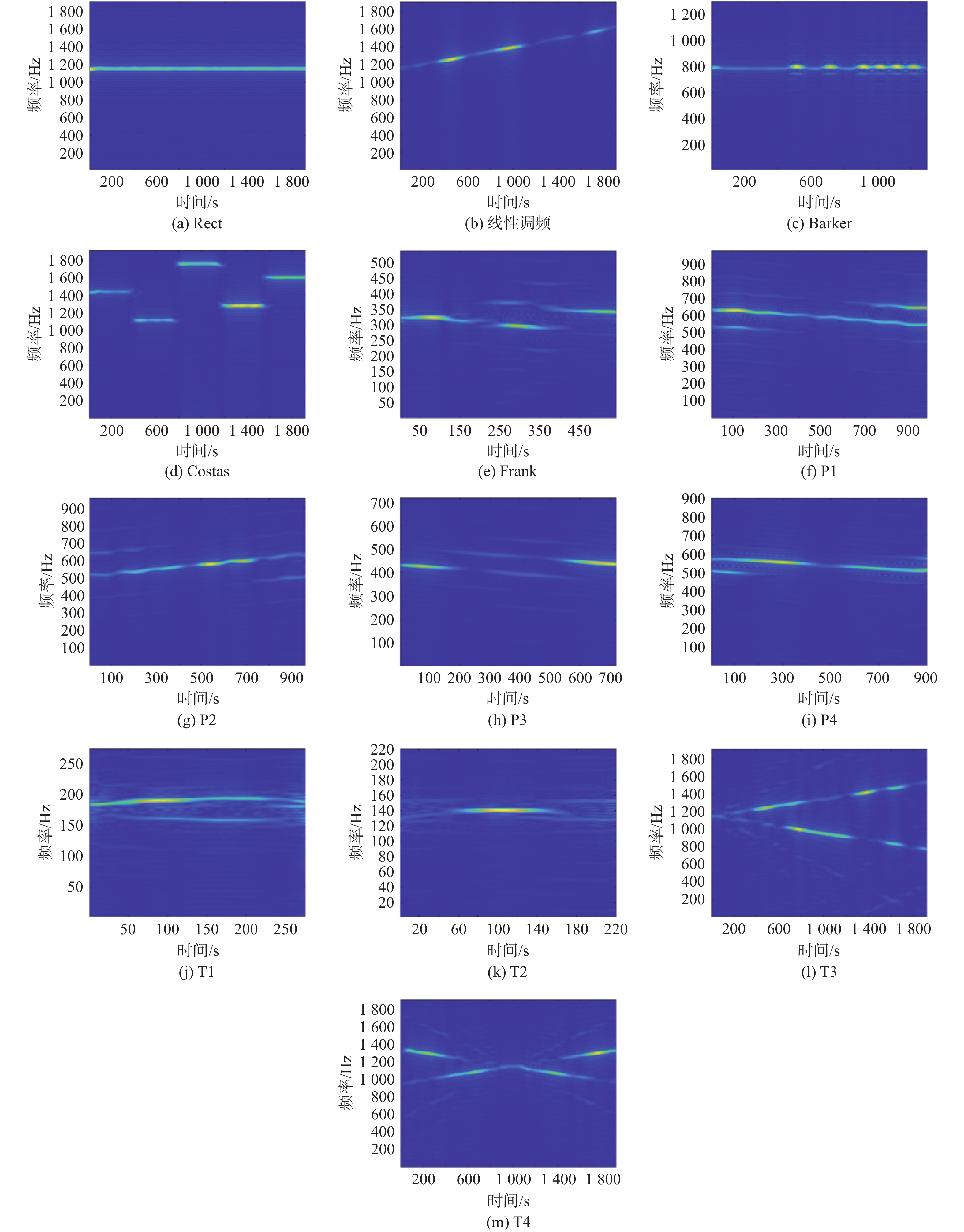
图1为信噪比为10 dB下13类LPI信号重排平滑伪维格纳维尔分布( reassigned smoothed pseudo Wigner-Ville distribution, RSPWVD)时频图像，可以看出调制方式不同的LPI雷达信号的特征差距较为显著。

图  1  SNR为10 dB时13种雷达信号的RSPWVD时频图像

Figure  1.  RSPWVD time-frequency images of 13 kinds of radar signals with SNR of 10 dB

下载: 全尺寸图片 幻灯片

1.2   时频图像预处理

雷达信号的原始时频图为RGB图像，而时频图最明显的特征是形状和数值。为区分不同信号，灰度图像足以显示这些特征。除此之外，与由R(红)、G(绿)、B(蓝)3个分量组成的RGB图像相比，灰度图像只有一个分量，彩色向灰度的转换可以大大缩小输入数据，大大降低计算成本。因此，信号经过时频处理后还需进行灰度化、二值化，以及大小的调整，再输入到分类网络进行识别。以0 dB下线性调频信号的RSPWVD时频图像为例，处理过程如图2所示，具体步骤如下。

图  2  图像预处理流程

Figure  2.  Flow chart of image preprocessing

下载: 全尺寸图片 幻灯片

步骤 1　通过计算R、G和B分量的加权和，将原始RGB时频图像转换为灰度图像，减少通道数。

步骤 2　使用全阈值二值法^[14]将灰度图像转换为二值图，进一步抑制噪声和降低计算量。

步骤 3　利用双三次插值运算将时频图像大小缩减为128像素×128像素，进一步减少数据量。

2.   基于多尺度残差网络的信号识别方法

2.1   多尺度残差网络构建

卷积神经网络因其出色的识别能力而被广泛用于图像和模式识别。CNN能够跳过复杂的数据预处理，自动提取信号特征，拥有更强大的非线性表征能力^[15]。

与传统的神经网络相比，CNN善于处理图像等高维数据。自2012年AlexNet被提出之后，CNN层数不断加深，网络拟合能力理应越来越强，但越深的网络反而训练误差越高，网络能力出现退化，识别率反而降低。残差网络由于其独特的跳跃连接设计，提供了一定程度的信息完整性，避免了在信息传递过程中，传统卷积出现的信息丢失问题，避免了网络过深导致的性能下降问题^[16]，进一步提高了目标分类和识别性能。因此，本文选择以残差结构为主体，设计出适合雷达信号识别的深度学习网络模型。

图3给出了用于LPI雷达波形识别的多尺度残差网络模型，主要基于非对称卷积核提取多尺度特征信息的思想。在捕获粗特征阶段，网络由1个3×3内核大小的卷积(conv)层和2个3×1和1×3非对称卷积核组成，与直接使用大核卷积相比，非对称卷积核可以减少训练参数的数量，但不会明显降低提取的特征质量。3×1和1×3这2个卷积核并行，用于多个尺度显式地提取特征。网络的核心组成部分为图3右侧所示的相同结构的3个处理模块，这些处理模块级联排列，以获得多尺度分辨率下的高分辨特征。每个模块都从max-pooling层开始，以降低输入特征图的空间维数，之后由2个具有非对称内核的conv层(即1×3和3×1)并行排列，几乎保持了与对称卷积相当的学习效率，两层特征映射的输出构成深度叠加层通过Depth concat连接产生输出，之后所连接的1×1单元conv层被用来控制特征的深度大小，这种跨通道参数池结构允许跨通道信息的交互。第2个Depth concat层前由类似的结构组成。Depth concat 层之间采用短连接，以避免多个层堆叠造成梯度消失，同时使模块能够学习剩余信息，而不是学习规则结构中的真实输出。特征提取层中每一个卷积层后面都连接一个批量归一化(batch normalization, BN)和指数线性单元(exponential linear unit, eLU)。最后一个模块的输出被传递到全局平均池化(global average pooling, GAP)层，通过计算输入映射的每个通道的空间维度上的平均值执行下采样，将多个特征映射到一个低维空间中。在分类网络中，GAP层通常位于全连接(fully connected, FC)层之前，以减少参数数量供下层学习^[17]。最后的Softmax层用于分类，获得13类LPI雷达信号。

图  3  多尺度残差网络模型

Figure  3.  Multi-scale residual network model

下载: 全尺寸图片 幻灯片

本文所设计的多尺度残差模型通过利用非对称卷积和跳跃连接的思想，使其拥有更为强大的特征提取性能，同时，结合时频分析图像的特点，优化模型深度及输出特征图维度，一定程度上缓解了“过拟合”问题及维度灾难问题。

2.2   信号识别流程

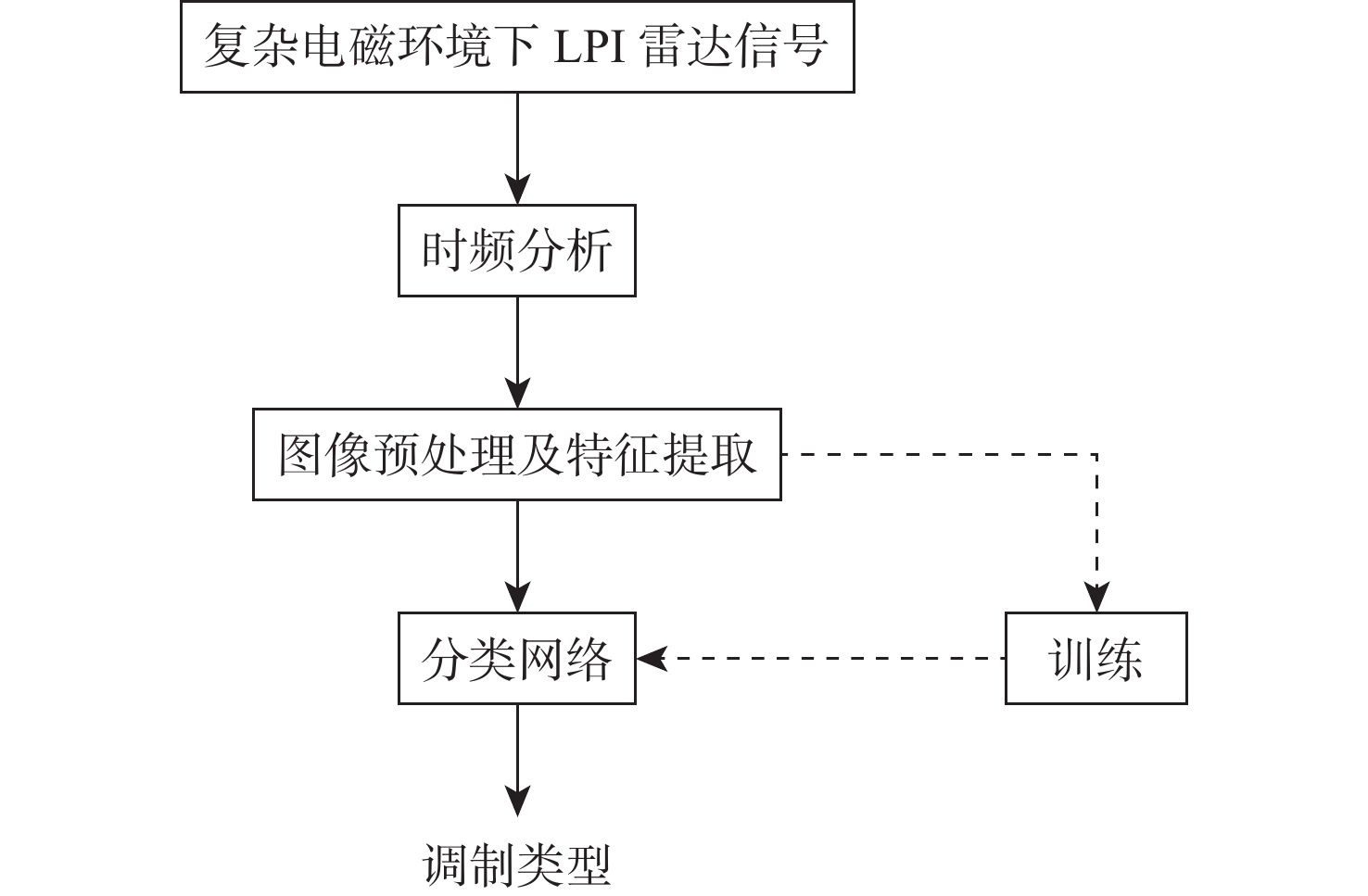
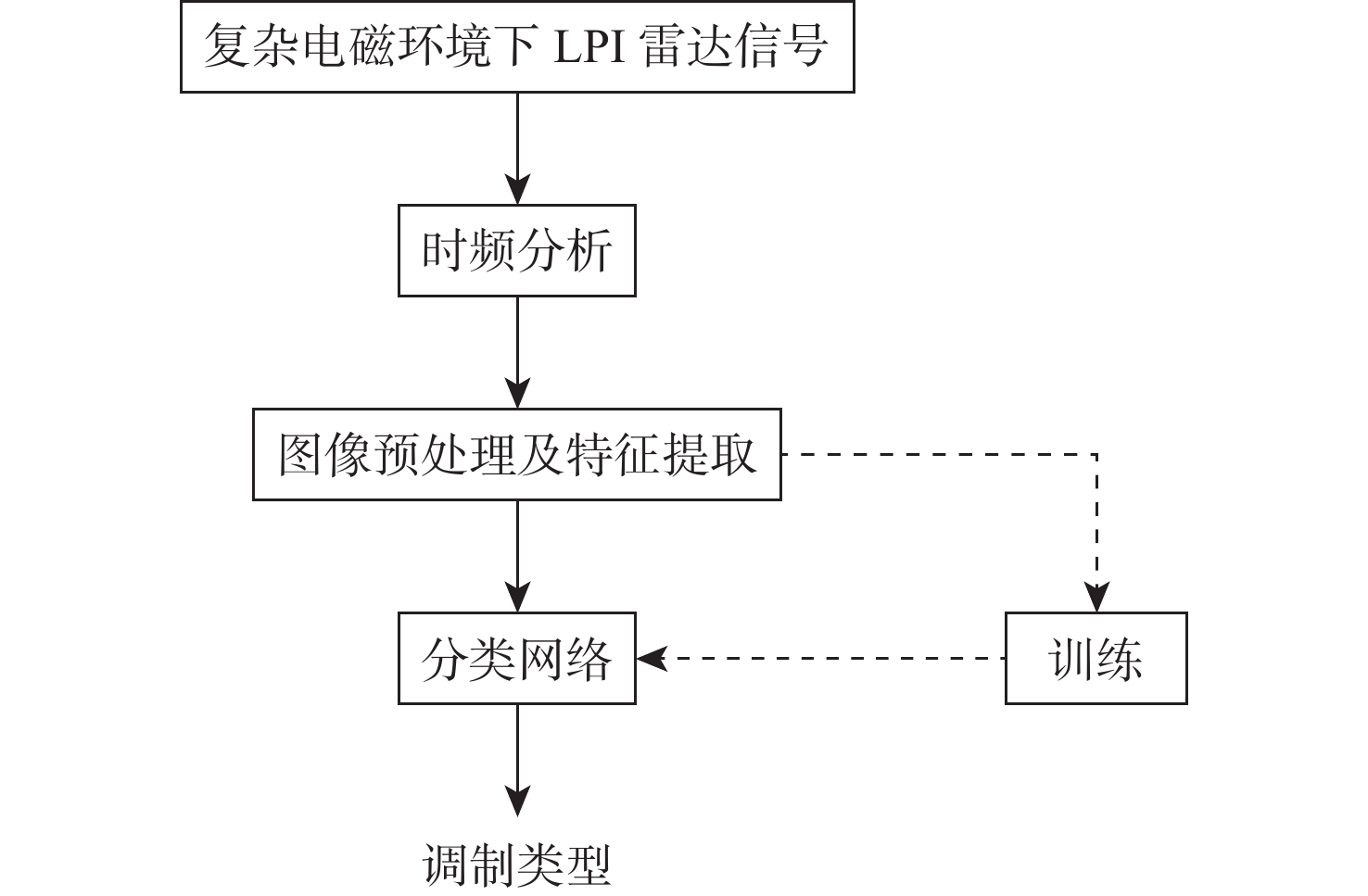
本文构建的基于时频重排和多尺度残差网络的LPI雷达信号识别方法流程如图4所示。具体步骤如下。

图  4  LPI雷达信号调制识别流程

Figure  4.  LPI radar signal modulation recognition process

下载: 全尺寸图片 幻灯片

1） 对LPI雷达信号作RSPWVD时频变换处理，获取信号相应的时频图像。

2） 对时频图像完成预处理流程，抑制噪声的同时减少数据的大小。

3） 构建多尺度残差网络模型。将预处理后的图像划分为训练集、验证集和测试集。将训练数据送入构建好的卷积神经网络完成训练，并从验证集中抽取图像进行验证。

4） 信号识别。将测试数据送入训练好的分类网络中，得到信号的调制类型。

3.   实验结果与分析

3.1   实验条件

硬件配置。Intel(R) Core(TM) i7-7700K CPU@4.20 GHz处理器，16GB内存，NVIDIA GeForce GTX 1080。

数据集。主要面向LPI雷达脉内调制信号。这类雷达大多采用频率编码、相位编码等脉冲压缩技术去完成低截获特性的要求，因此，考虑了13种常见LPI雷达波形：线性调频、矩形、Costas码、Barker码、5种多相码(Frank、P1、P2、P3和P4)和4种多时码(T1、T2、T3和T4)。各信号具体的参数设置如表1所示。网络训练时选用交叉熵损失函数，SGDM优化算法，初始学习率为0.01，epoch取值为12，batchsize设置为128。

表  1  波形参数设置

Table  1.  Waveform parameters setting

LPI信号调制样式	调制参数	取值范围
All	载频fc/Hz	U(fs /6, fs/5)
线性调频	带宽B/Hz 采样个数N	U(fs/20,fs/15) [512，1024]
Rect	采样个数N	[512，1024]
Costas	跳频序列长度 基础频率fmin/Hz 采样个数N	{3，4，5，6} U(fs/32, fs/25) [512，1024]
Barker	码长L 相位子波数cpp	{7，11，13} [2，5]
Frank	相位子波数cpp 频率步长M	[3，5] {6，7，8}
P1,P2	相位子波数cpp 频率步长M	[3，5] {6，8}
P3,P4	相位子波数cpp 子码数ns	[3，5] {36，64}
T1,T2	相位状态数Np 相位波形段数Ng 采样个数N	2 {4，5，6} [512，1024]
T3,T4	相位状态数Np 相位波形段数Ng 采样个数N 调制带宽B/Hz	2 {4，5，6} [512，1024] U(fs/20,fs/15)

下载: 导出CSV 

| 显示表格

该领域的大多数研究^[15,18-19]只考虑加性高斯白噪声(additive white Gaussian noise, AWGN)对信号产生的影响，与实际信道环境相差甚远。本文在生成数据集时，叠加范围为[f_s/6, f_s/5]的载频偏移于信号，并在AWGN的基础上叠加莱斯衰落信道去模拟真实信号的发送接收，具体信道参数如表2所示。数据集考虑了26种不同的信噪比环境，从−15 dB到10 dB，步长为1 dB。每1 dB产生1 000个样本，其中700个(70%)作为训练集，150个(15%)作为验证集，150个(15%)作为测试集。

表  2  信道参数设置

Table  2.  Channel parameters setting

信道参数	取值范围
采样频率/Hz	fs
多径衰减/ns	U(1,1000)
平均路径增益/dB	U(−20,0)
K-factor	4
最大多普勒频移/Hz	U(10, 1000)

下载: 导出CSV 

| 显示表格

3.2   实验结果分析

为了验证本文方法在LPI雷达信号识别的有效性，设置2个综合实验评估对LPI雷达波形识别的效果。

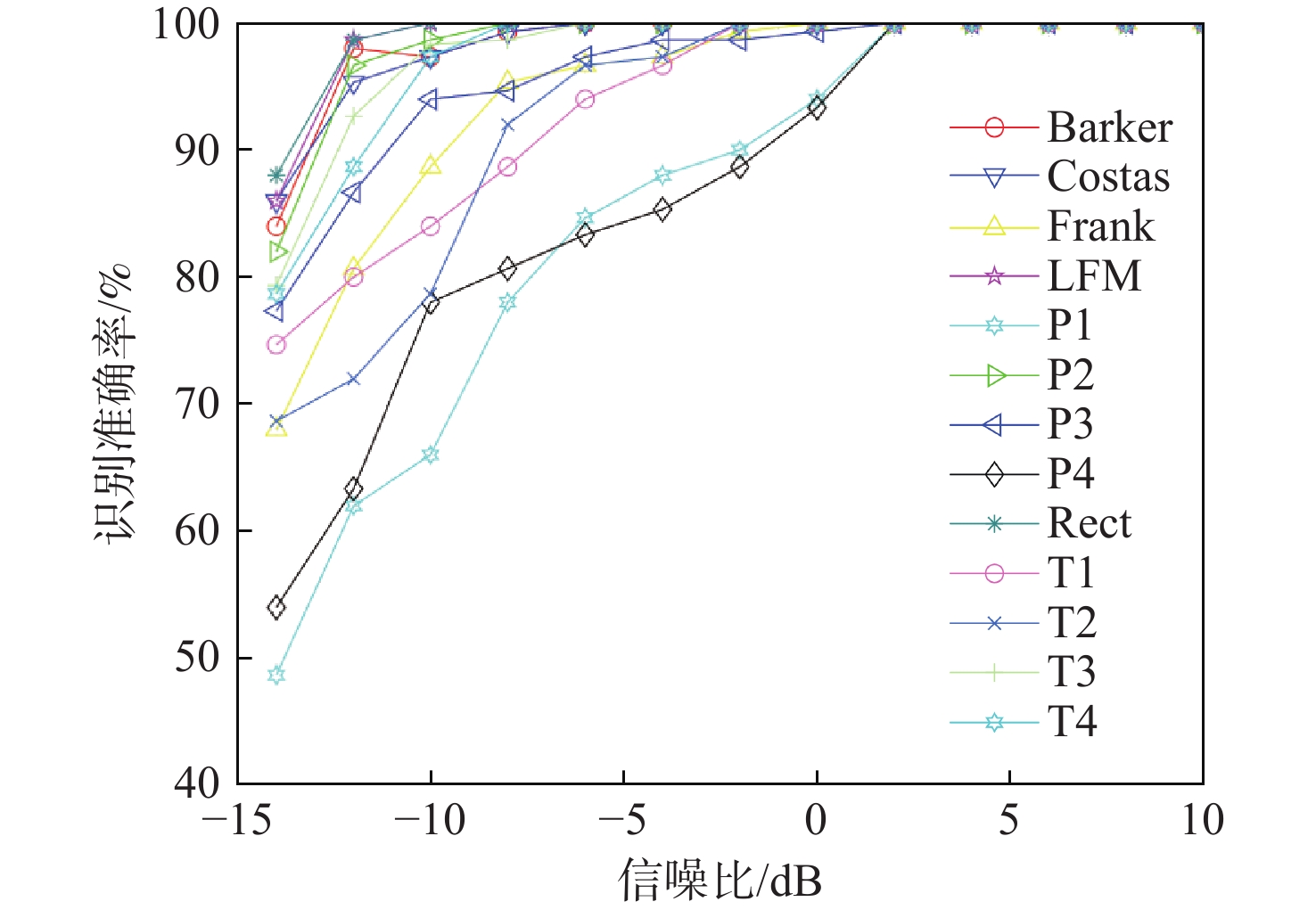
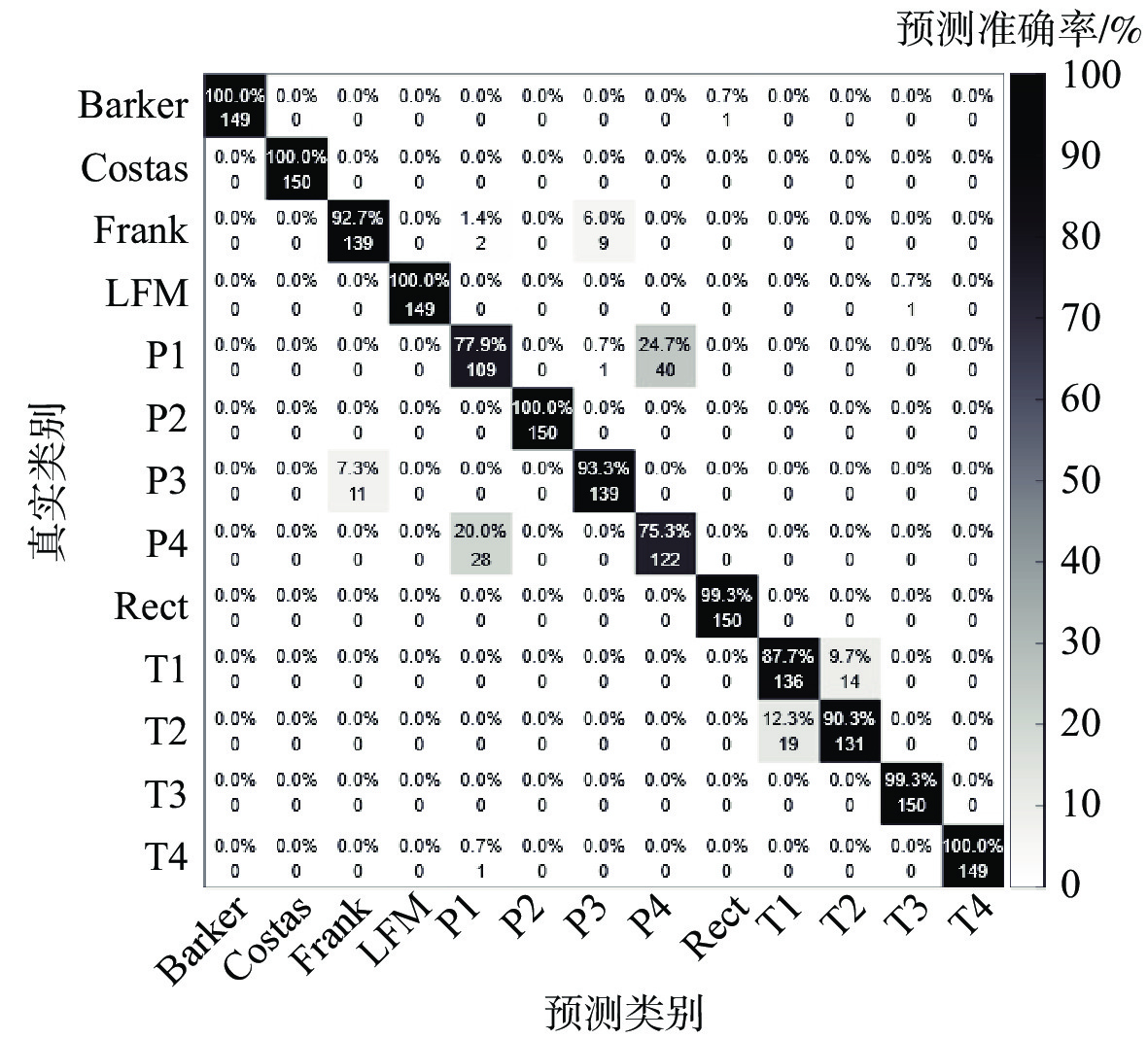
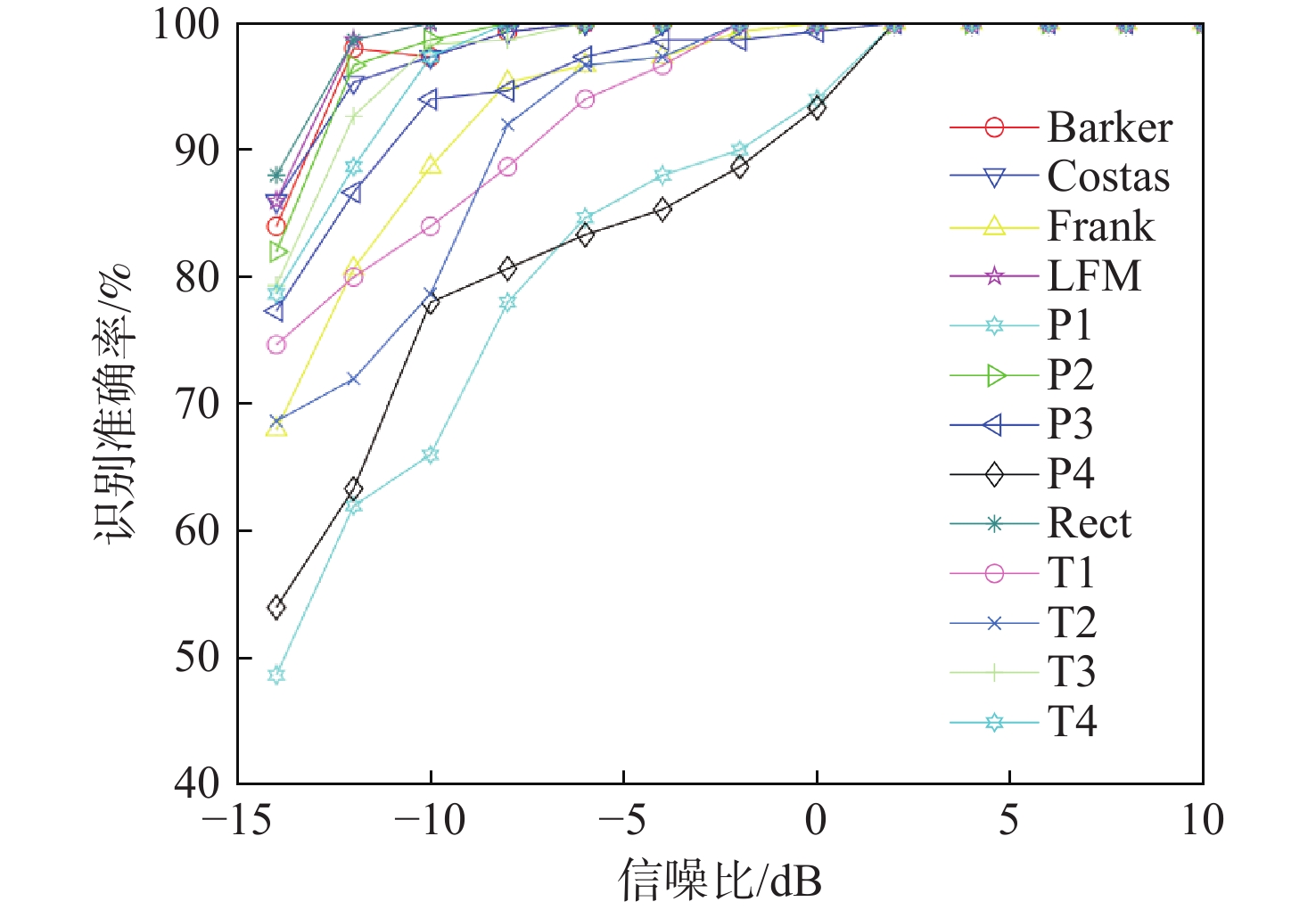
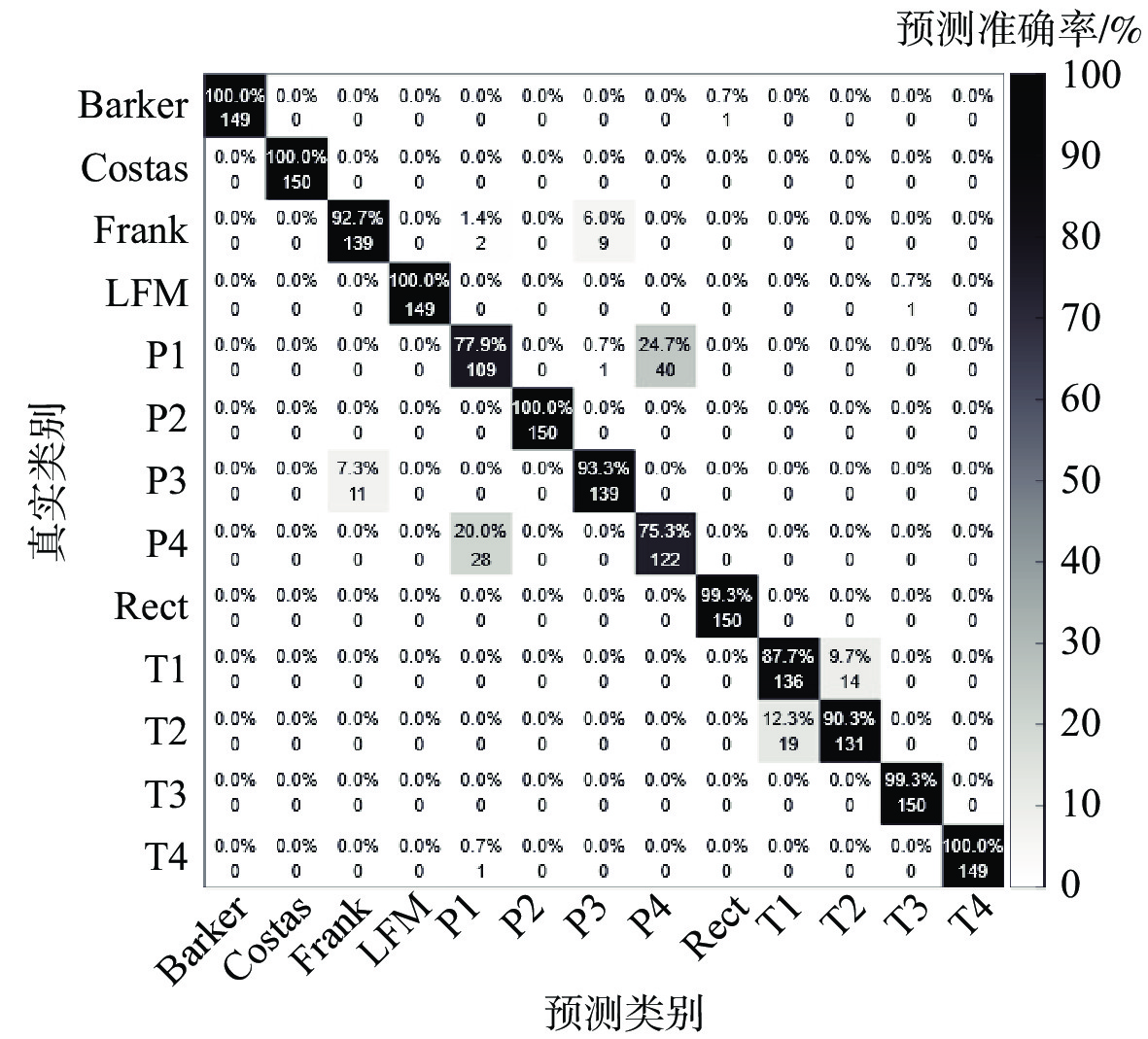
1） 实验1。该实验探究所提出的深度网络获得的13种LPI波形的识别精度。从图5的结果可见，识别率随着信噪比的增加而增加。部分调制波形，包括LFM，Costas和P2，在低信噪比下实现非常高的识别精度，在−10 dB信噪比下准确率约为97.0%。值得注意的是，Costas和LFM在−8 dB信噪比下达到了100%的正确识别率，因为其时频图像比其他波形更具鉴别性。该识别模型在−4 dB信噪比下的整体准确率达到98.8%左右。为了更细致地分析，图6提供了−8 dB信噪比下13类波形识别的混淆矩阵，Barker、Costas、LFM、P2、T4码5种信号的识别率达到100%。但由于信道恶化，多径衰落和加性噪声导致多相码Pl和P4的严重误分类(约20.0%～24.7%)。

图  5  13种雷达调制方式的识别准确率

Figure  5.  Recognition accuracy of 13 radar modulation modes

下载: 全尺寸图片 幻灯片

图  6  信号的混淆矩阵（−8 dB）

Figure  6.  Signal confusion matrix (−8 dB)

下载: 全尺寸图片 幻灯片

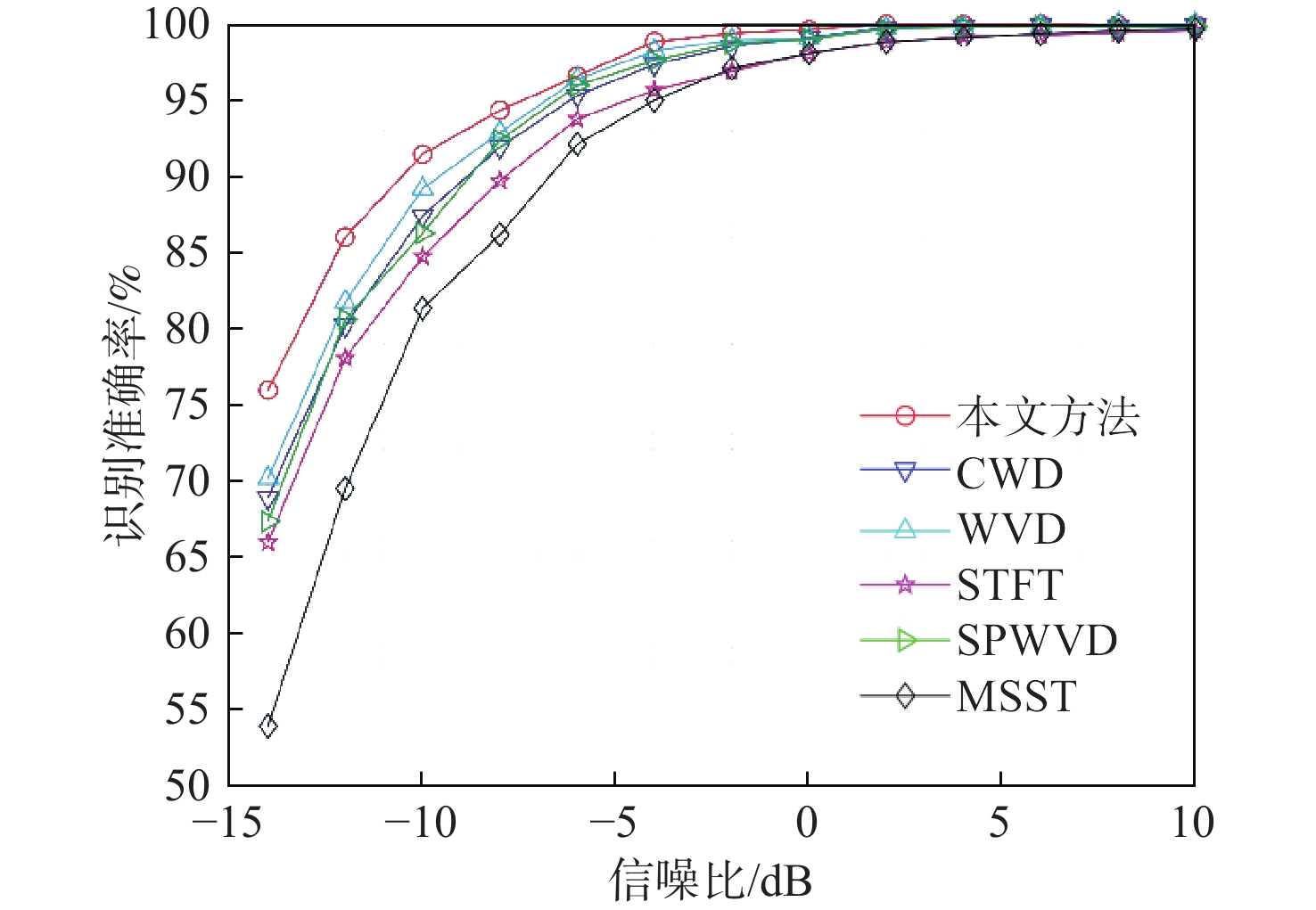
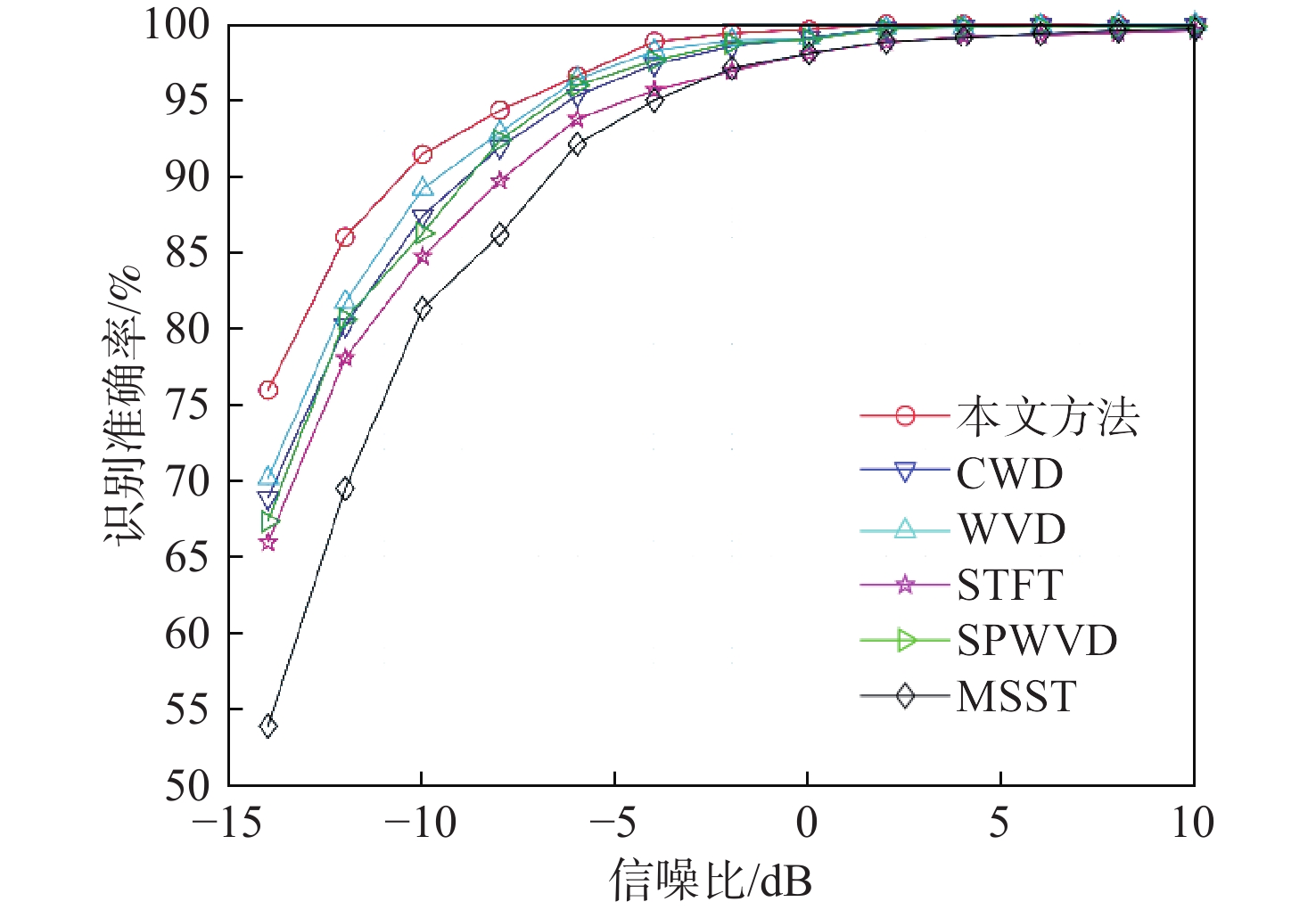
2） 实验2。时频变换方面，在同等条件下比较了本文方法和CWD、SPWVD、WVD与MSST^[20]的识别效果。运行时间对比如表3所示，本文方法基于SPWVD改进，相较SPWVD而言运行时间略有上升。对于应用最为广泛的CWD方法，单个信号执行一次耗时需要0.307 2 s左右，而执行本文方法仅需0.269 s左右，运算速度更快，在保持较好实时性的情况下提高了识别准确率。6种时频分析方法均采用设计的多尺度残差网络对数据集进行识别，如图7所示，本文方法具有较强的抑制干扰的高分辨率谱图平滑能力，比其他算法更适合分析雷达波形。重排后的时频图像要比SPWVD有更好的识别效果，当信噪比低于0 dB时，WVD的识别概率高于STFT和CWD。WVD表现出良好的性能，但随着信噪比从−2 dB开始下降后，精度迅速下降。MSST在处理T码时效果较差进而大大影响了总体识别率。总体而言，本文方法的识别准确率在信噪比较低的情况下也表现出较好的识别性能。

表  3  运行时间对比

Table  3.  Comparison of running time

时频方法	时间/s
本文方法	0.269 3
CWD	0.307 2
WVD	0.039 2
STFT	0.064 6
SPWVD	0.264 1
MSST	0.199 3

下载: 导出CSV 

| 显示表格

图  7  6种方法识别准确率对比

Figure  7.  Comparison of recognition accuracy of six methods

下载: 全尺寸图片 幻灯片

4.   结　论

针对多径条件下雷达信号时频聚集性骤降，识别准确率不高的问题，本文提出一种基于时频重排的LPI雷达信号识别方法，主要结论如下。

1） 在SPWVD时频分析的基础上引入时频重排算法，在降低交叉项的干扰的同时高效提高时频聚集性，解决了高噪声环境下时频聚集性较低的问题。

2） 在分类网络中，将多尺度残差网络模型应用于LPI雷达信号识别，借鉴残差网络ResNet的思想设计了卷积核大小、并行连接及模块间的跳连方式。

3） 实验结果表明，与传统方法相比，本文方法优于其他时频分析方法，同时还具有更高的准确率和抗噪能力，在−8 dB下信号分类准确率也可达到94%。

实际战场环境中，信号复杂多样，后续还需考虑脉冲丢失、虚假脉冲等干扰现象，以及混合调制信号的情况。