Parameter optimization method of thrust vector/pneumatic rudder composite control law for aircraft based on singular value method
-
摘要:
推力矢量/气动舵布局的先进飞机存在显著的控制耦合问题，传统的单回路控制参数设计方法在该场景下无法兼顾多控制回路的性能。因此提出一种基于回差矩阵奇异值的控制律参数优化方法，利用时域控制性能指标确定控制参数优化区间，在此基础上用奇异值方法衡量多输入多输出(MIMO)系统的稳定裕度，并建立相应的最优目标函数，从而对控制器参数寻优。采用数值仿真验证了该方法的可行性，结果显示所设计的控制参数优化算法相较于传统单回路控制参数设计方法具有更好的时域控制性能与更大的系统稳定裕度。
Abstract:Control coupling is a major problem for advanced aircraft with thrust vector/aerodynamic rudder layouts, as the performance of numerous control loops cannot be balanced using conventional single loop control parameter design techniques. Therefore, a control law parameter optimization method based on the singular value of the feedback matrix is proposed. The optimization interval of the control parameters is first established using the time domain control performance index. The stability margin of the multiple-in multiple-out (MIMO) system is then measured using the singular value method, and the corresponding optimal objective function is established to optimize the controller parameters. The feasibility of this method was verified through numerical simulation, and the results showed that the designed control parameter optimization algorithm has better time-domain control performance and a larger system stability margin compared to traditional single loop control parameter design methods.
-
图 4 不同回路控制器参数仿真包线
Figure 4. Simulation envelope of different loop controller parameters
图 5 不同组控制参数时的最小奇异值
Figure 5. Minimum singular value for different sets of control parameters
图 7 俯仰角速度环阶跃响应曲线及控制性能
Figure 7. Step response curve and control performance of pitch angular velocity loop
图 10 单输入控制设计仿真和多回路控制设计仿真速度对比结果
Figure 10. Comparison of speed results between single input control design simulation and multi loop control design simulation
图 11 单输入控制设计仿真和多回路控制设计仿真俯仰角速度对比结果
Figure 11. Comparison results of pitch angular velocity between single input control design simulation and multi loop control design simulation
图 14 加入干扰后俯仰角速度环对比曲线
Figure 14. Comparison curve of pitch angular velocity loop after adding interference
表 1 不同传递函数的分子系数
Table 1. Molecular coefficients of different transfer functions
传递函数 K4 K3 K2 K1 K0 GVδth 6.045 9.012 28.49 −0.033 0.019 Gωzδth −0.016 −0.017 0.013 −3.4×10−5 −4.95×10−20 GVδe 9.942 13.37 −52.61 22.85 0.024 Gωzδe −5.280 −2.329 −0.077 −5.196×10−5 9.712×10−18 GVδtz 0.083 −0.115 34.26 −9.072 −7.493×10−4 Gωzδtz 1.827 0.902 0.035 1.959×10−7 −1.257×10−20 
下载: 导出CSV
表 2 回路控制性能指标内容及要求
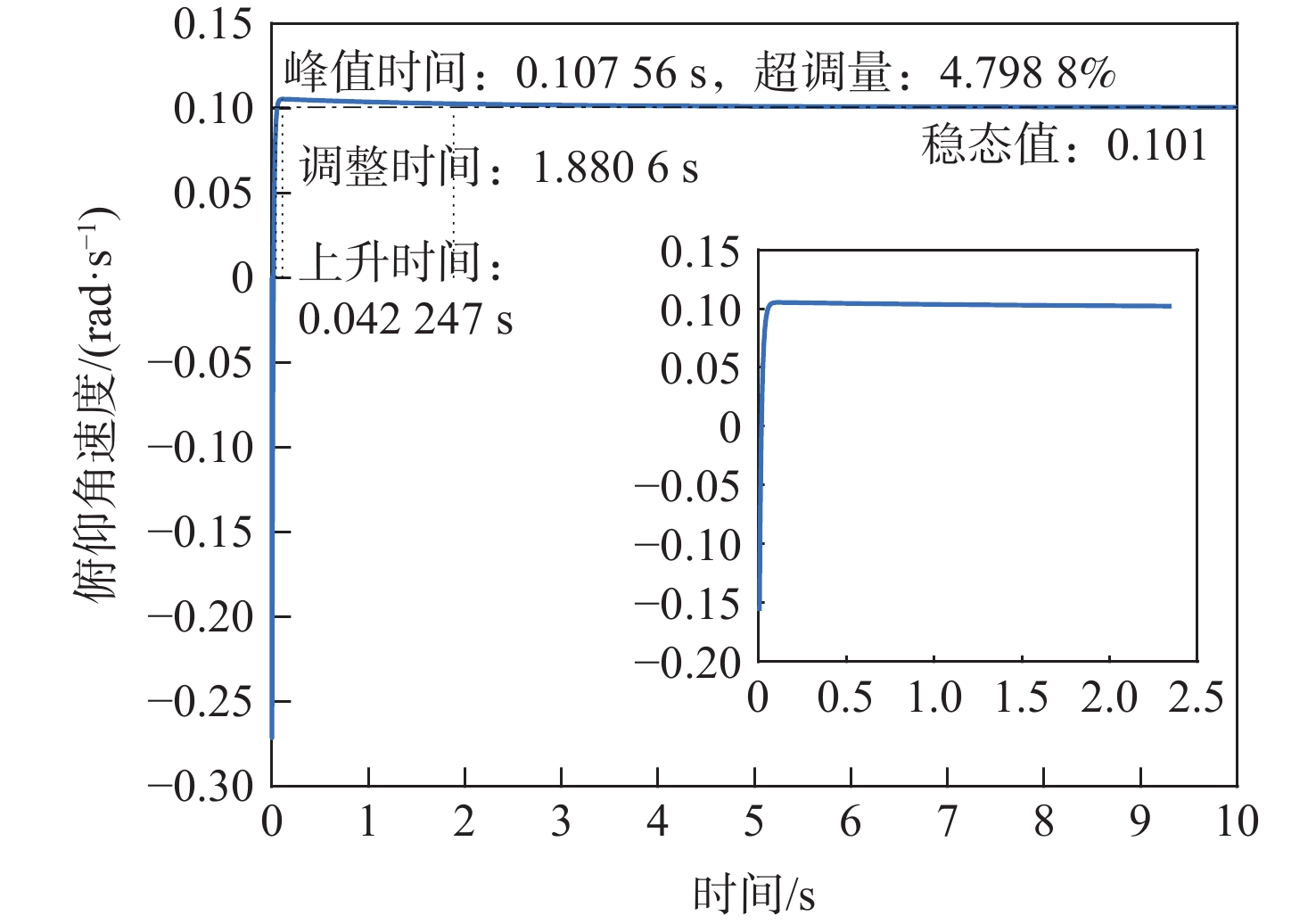
Table 2. Content and requirements of loop control performance indicators
指标要求 阶跃信号 调节时间/s 超调量/% 状态误差/% 速度回路 100 m/s 5 10 1 姿态回路 0.1 rad/s 5 10 5
下载: 导出CSV
表 3 控制参数优化区间与步长
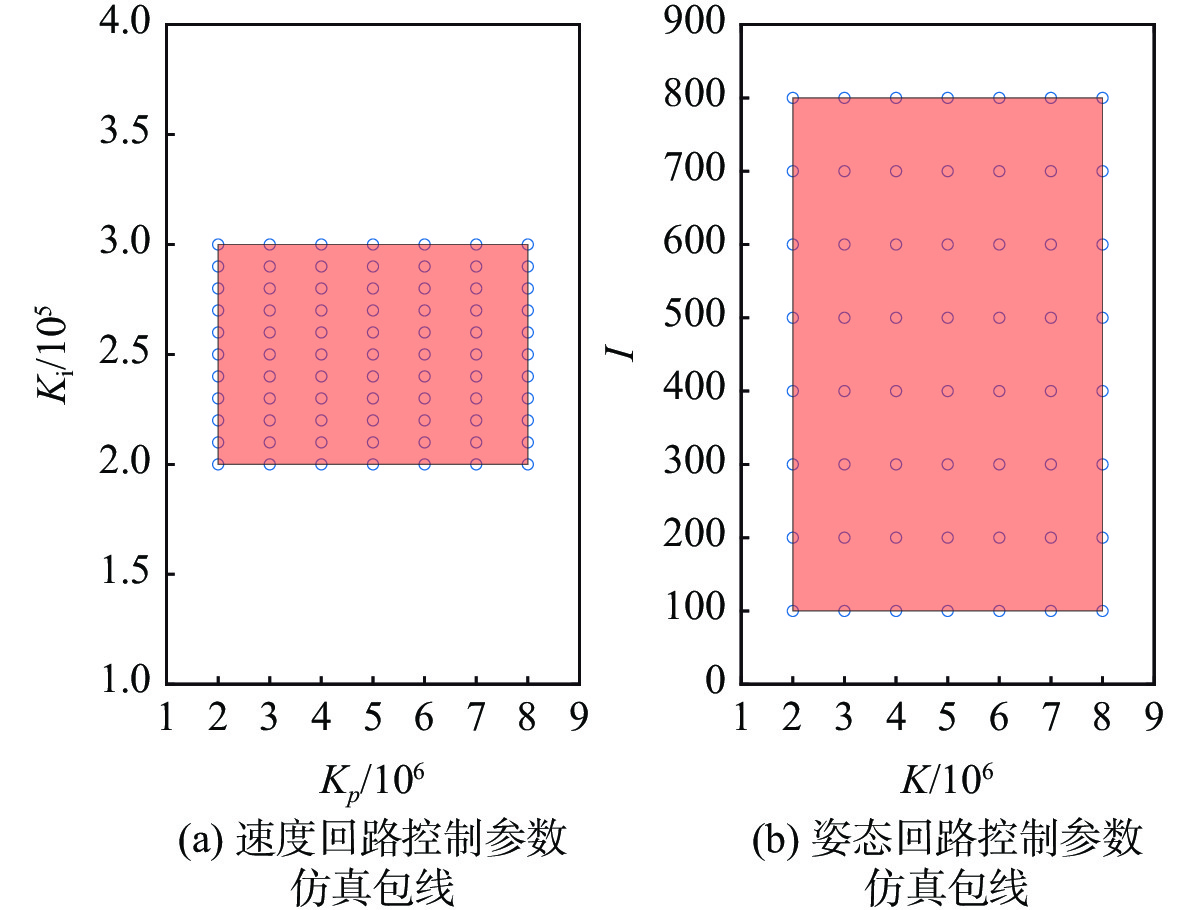
Table 3. Optimization interval and step size of control parameters
优化区间
及步长速度回路 姿态回路 Kp Ki K I 下限 2×106 2×105 2×106 1×102 上限 8×106 3×105 8×106 8×102 步长 106 104 106 102
下载: 导出CSV
表 4 最优控制器参数下的多输入多输出系统裕度
Table 4. MIMO system margin under optimal controller parameters
幅值裕度/dB 相角裕度/（°） 6.2342 63.3222
下载: 导出CSV
表 5 不同分配比例情况下的指标结果
Table 5. Indicator results under different allocation ratios
比例情况 奇异值优化结果 幅值裕度/dB 相角裕度/（°） 5∶5 1.0498 6.2342 63.3222 4∶6 1.0540 6.2520 63.6064 3∶7 1.0585 6.2708 63.9063 2∶8 1.0624 6.2875 64.1744 1∶9 1.0668 6.3060 64.4715
下载: 导出CSV
表 6 两种控制参数设计方法稳定裕度对比结果
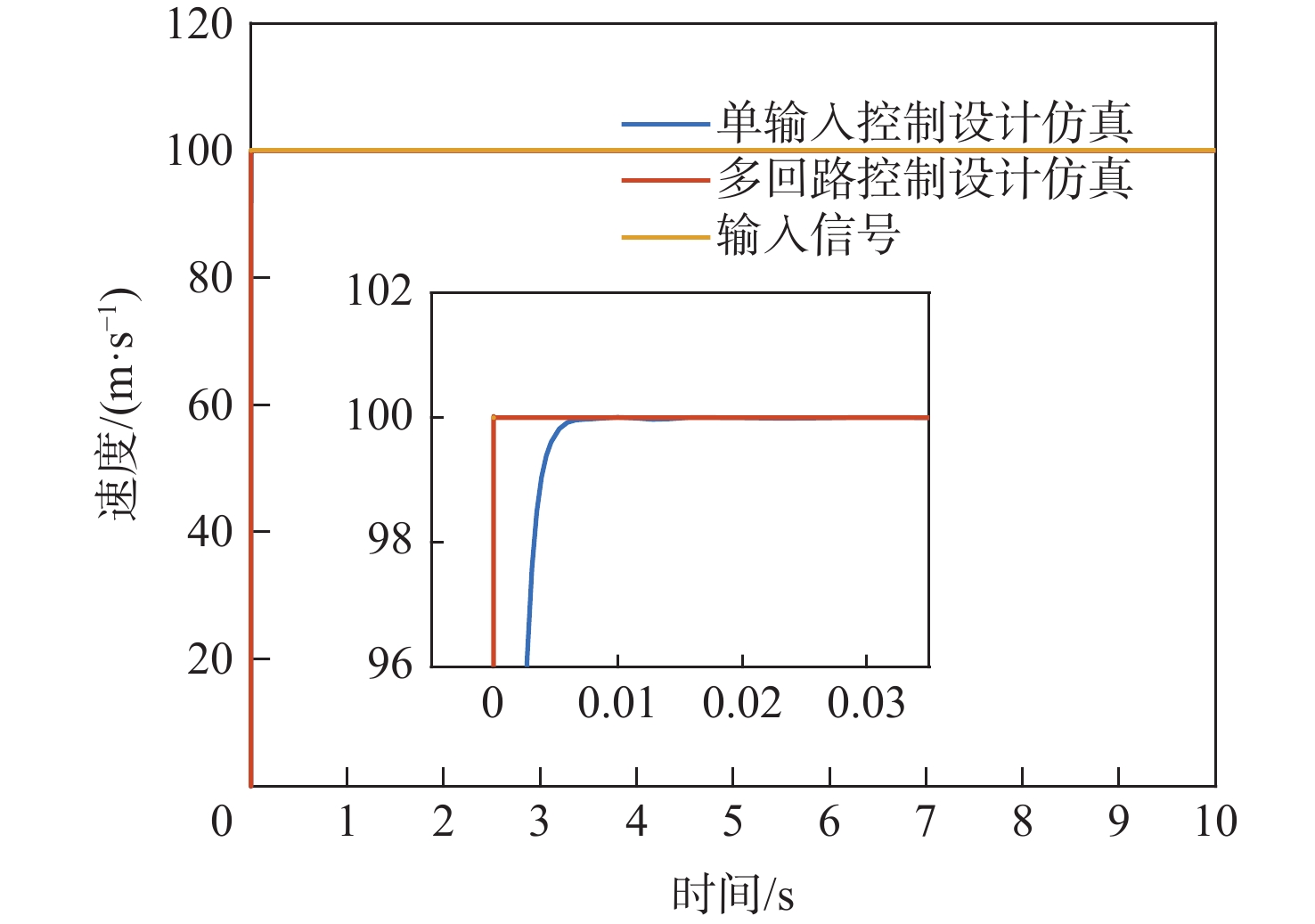
Table 6. Comparison results of stability margin between two control parameter design methods
控制参数设计方法 奇异值 幅值裕度/dB 相角裕度/（°） 单输入 0.8272 5.2355 48.8593 基于奇异值的多回路 1.0498 6.2342 63.3222 注：奇异值、幅值裕度、相角裕度的提升幅度分别为26.9%，19.1%，29.6%。
下载: 导出CSV
-
[1] LIU J J, SUN M W, CHEN Z Q, et al. Super-twisting sliding mode control for aircraft at high angle of attack based on finite-time extended state observer[J]. Nonlinear Dynamics, 2020, 99(4): 2785-2799. [2] 占正勇, 崔玉伟. 多用途作战飞机复合控制技术研究[J]. 飞行力学, 2015, 33(6): 537-541,550.ZHAN Z Y, CUI Y W. Research on complex control for multi-purpose combat aircraft[J]. Flight Dynamics, 2015, 33(6): 537-541,550(in Chinese). [3] 周大鹏, 杨大鹏, 刘然, 等. 一种面向空天飞机再入的智能自适应复合控制方法[J]. 宇航学报, 2022, 43(8): 1109-1119. doi: 10.3873/j.issn.1000-1328.2022.08.013ZHOU D P, YANG D P, LIU R, et al. An intelligent adaptive compound control method for aerospace plane reentry[J]. Journal of Astronautics, 2022, 43(8): 1109-1119(in Chinese). doi: 10.3873/j.issn.1000-1328.2022.08.013 [4] 董哲, 刘凯, 李旦伟, 等. 考虑动态控制分配的空天飞行器再入姿态复合控制设计[J]. 宇航学报, 2021, 42(6): 749-756. doi: 10.3873/j.issn.1000-1328.2021.06.008DONG Z, LIU K, LI D W, et al. A dynamic control allocation approach for reentry compound attitude control design of aerospace vehicle[J]. Journal of Astronautics, 2021, 42(6): 749-756(in Chinese). doi: 10.3873/j.issn.1000-1328.2021.06.008 [5] 董金鲁, 马悦萌, 周荻, 等. 临近空间高超声速飞行器的直接力与襟翼复合滑模控制[J]. 兵工学报, 2023, 44(2): 496-506.DONG J L, MA Y M, ZHOU D, et al. A composite sliding mode control scheme based on reaction jets and flaps for near-Space hypersonic vehicles[J]. Acta Armamentarii, 2023, 44(2): 496-506(in Chinese). [6] 郭建国, 彭谦, 周敏. 直接力/气动力复合控制技术发展综述[J]. 航空兵器, 2022, 29(1): 1-13. doi: 10.12132/ISSN.1673-5048.2021.0120GUO J G, PENG Q, ZHOU M. Review on development of direct force/aerodynamic force compound control technology[J]. Aero Weaponry, 2022, 29(1): 1-13(in Chinese). doi: 10.12132/ISSN.1673-5048.2021.0120 [7] AZARSKOV V, TUNIK A, SUSHCHENKO O. Design of composite feedback and feedforward control law for aircraft inertially stabilized platforms[J]. International Journal of Aerospace Engineering, 2020, 2020: 8853928. [8] 丁伟涛, 肖翀, 黄玉平. 直接力与推力矢量复合控制技术研究[J]. 导航定位与授时, 2017, 4(5): 27-31.DING W T, XIAO C, HUANG Y P. Researsh on the compound control of direct force and thrust vector[J]. Navigation Positioning and Timing, 2017, 4(5): 27-31(in Chinese). [9] 崔彦凯, 王志刚. 越肩发射空空导弹气动力/推力矢量复合控制器设计[J]. 宇航学报, 2010, 31(4): 1100-1104.CUI Y K, WANG Z G. Aerodynamic and thrust vector complex controller design of over the shoulder air-to-air missile[J]. Journal of Astronautics, 2010, 31(4): 1100-1104 (in Chinese). [10] GAO F, TANG S J, SHI J, et al. Compound control allocation strategy of dual aero/jet vane control missile[J]. Journal of Beijing Institute of Technology, 2012, 21(4): 434-441. [11] 苏润, 赵明. 飞艇矢量推力与舵面复合控制分配研究[J]. 电脑知识与技术, 2017, 13(24): 221-223.SU R, ZHAO M. Study on the distribution of vector thrust and rudder composite control of airship[J]. Computer Knowledge and Technology, 2017, 13(24): 221-223(in Chinese). [12] 艾尔, 王衍洋, 屈香菊. 气动/推力矢量控制面融合方式研究[J]. 飞行力学, 2005, 23(4): 20-24.AI E, WANG Y Y, QU X J. An analysis on the combination of aero/thrust vector control surfaces[J]. Flight Dynamics, 2005, 23(4): 20-24(in Chinese). [13] 李子木. 基于奇异摄动法的多变量系统稳定性测量[D]. 大连: 大连海事大学, 2017: 9-12.LI Z M. Stability measurement of multivariable systems based on singular perturbation method[D]. Dalian: Dalian Maritime University, 2017: 9-12 (in Chinese). [14] 曹玉腾, 倪少波. 再入飞行器多变量稳定裕度研究[J]. 航天控制, 2015, 33(5): 28-32.CAO Y T, NI S B. Research of reentry aerocraft multivariable stability margin[J]. Aerospace Control, 2015, 33(5): 28-32(in Chinese). [15] 瞿福存, 史忠科, 戴冠中. MIMO系统稳定裕度的几个定义[J]. 飞行力学, 2002, 20(2): 6-9. doi: 10.3969/j.issn.1002-0853.2002.02.002QU F C, SHI Z K, DAI G Z. Stability margin definitions for MIMO systems[J]. Flight Dynamics, 2002, 20(2): 6-9(in Chinese). doi: 10.3969/j.issn.1002-0853.2002.02.002 [16] LEHTOMAKI N, SANDELL N, ATHANS M. Robustness results in linear-quadratic Gaussian based multivariable control designs[J]. IEEE Transactions on Automatic Control, 2003, 26(1): 75-93. [17] 李信栋, 苟兴宇. 由回差阵奇异值求稳定裕度的退化算法[J]. 控制理论与应用, 2016, 33(4): 460-465.LI X D, GOU X Y. Degraded algorithm for determining stability margin by using singular value of the return difference matrix[J]. Control Theory & Applications, 2016, 33(4): 460-465(in Chinese). [18] SON J E, MANI A S, LATCHMAN H A. Robustness analysis for MIMO systems with unstructured uncertainties[C]// IEEE ICCA 2010. Piscataway: IEEE Press, 2010: 1333-1337. [19] 李信栋, 苟兴宇. 多体卫星MIMO控制及稳定裕度研究[J]. 航天控制, 2013, 31(5): 25-30.LI X D, GOU X Y. On MIMO control and stability margin of multi-body satellite, China[J]. Aerospace Control, 2013, 31(5): 25-30(in Chinese). [20] 吴斌, 程鹏. 多变量飞控系统的稳定裕度分析[J]. 航空学报, 1998, 19(6): 657-661.WU B, CHENG P. Stability margin analysis of multivariable flight control system[J]. Acta Aeronautica et Astronautica Sinica, 1998, 19(6): 657-661 (in Chinese). [21] 段子帆, 宁国栋, 张红文, 等. 高超声速飞行器横航向MIMO系统控制及稳定裕度评估[J]. 战术导弹技术, 2018(2): 70-79.DUAN Z F, NING G D, ZHANG H W, et al. Lateral MIMO systems control and stability margin evaluation of hypersonic vehicle[J]. Tactical Missile Technology, 2018(2): 70-79(in Chinese). [22] 李帆. 不确定性系统的解耦控制与稳定裕度分析[D]. 西安: 西北工业大学, 2001: 94-114.LI F. Decoupling control and stability margin analysis of uncertain systems[D]. Xi’an: Northwestern Polytechnical University, 2001: 94-114 (in Chinese). [23] PESCETELLI F, MINISCI E, MADDOCK C, et al. Ascent trajectory optimisation for a single-stage-to-orbit vehicle with hybrid propulsion[C]// 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference. Reston: AIAA, 2012: AIAA2012-5828. -
下载:
点击查看大图
计量
- 文章访问数: 189
- HTML全文浏览量: 66
- PDF下载量: 1
- 被引次数: 0
