近年来，民航运输业迅猛发展，同时低空空域改革为通用航空的发展带来了机遇，飞行需求不断增加，空域运行环境日趋复杂，飞行安全压力骤然加剧。为保证飞行安全的同时高效利用有限的空域资源，基于航迹运行（trajectory based operation，TBO）^[1]与自由航线空域（free route airspace，FRA）^[2]等新一代空管运行概念被提出。在TBO和FRA运行方式中，航空器可根据实际情况自主选取最优化航迹，同时允许根据航空器性能采取不同的间隔标准，大幅增加了飞行流量，提高了空域容量和飞行运行效率^[3]。然而，TBO下空域用户数量和机型种类的骤增与用户航线的自由规划，使空情变得更加复杂^[4]。因此，迫切需要一种能够反映TBO运行环境下潜在飞行冲突的模型，显示空中交通情况，辅助管制员决策指挥，以实现自由航线TBO。

在空中交通情况评估方面，国内外学者围绕空中交通管理复杂性展开了一系列研究，利用动态密度、内禀性分析和复杂系统建模等方法反映空域运行态势。1976年，Schmidt提出引入管制过程“复杂性或难度”权重系数衡量管制员工作量，由此开启复杂性研究^[5]；Delahaye等以航空器对的相对距离与相对速度为基本内禀属性，建立评价体系客观度量典型冲突场景的空中态势及其演化规律^[6]；胡明华等^[7-8]依据航空器间的迫近效应、汇聚态势和连携关系建立了空域复杂性评估模型，分析空中交通内禀性和几何结构，避免了主观因素的影响，实现了客观描述空中交通复杂性的可能。

复杂系统尤其是复杂网络理论近年来被用于描述空中交通复杂性，为分析空中交通结构和演化进程提供了一条行之有效的研究路线。复杂网络建模的核心是对复杂系统中的节点及节点之间的相互关系进行抽象。王红勇等^[9-11]提出以航空器为节点、航班之间连线为边、节点间的复杂度为权值，构建二维的加权冲突网络，用网络的节点度、连通率等衡量空中态势的局部与整体复杂性；吴明功等^[12-14]以飞机为节点，机载防撞系统(airborne collision avoidance system，ACAS)建立通信关系为连边构建飞行状态网络，选取节点强度、平均聚类系数和介数中心性等网络拓扑指标描述空中动态交通状况，使用独立主元分析法、层析分析法和熵权法等方法监控空情动态、识别关键节点，在一定程度上有效降低了主观因素带来的影响，更好地识别了空中交通复杂性；毕可心等在该基础上，引入速度障碍法优化飞行状态网络，帮助管制员提前对航空器之间的潜在冲突和空域复杂性进行分析^[15]。而在这些研究中，飞行冲突网络的连边是以通信关系或民航现行的统一间隔标准为依据判定，没有依据航空器性能采取不同的间隔标准进行判定，不能很好地适用于分析TBO运行环境下机型各异的航空器所构成的空中复杂网络。本文在传统基于概率的碰撞风险模型的基础上，综合考虑3种影响因素，构建了不同机型侧向飞行安全间隔模型，以此为依据判定飞行冲突关系，从而对飞行冲突网络结构做出优化，更适用于分析TBO运行环境下的空中交通状况。

因此，本文提出一种基于TBO不同机型的飞行冲突网络模型，基于概率论和几何法，综合考虑基于性能的通信、导航与监视(communication, navigation and surveillance, CNS)等误差影响，利用分段查找区间法求解满足目标安全等级（target level of safety，TLS）的水平安全间隔标准，构建不同机型航空器精准保护区模型。以此为依据利用速度障碍法判定网络连边，确定网络边权，引入网络拓扑指标，分析TBO运行环境下的空中交通复杂性。本文模型根据航空器性能采取不同的冲突判定间隔标准，旨在贴近TBO下的空中情况，同时增大了空域容量，为实现空域精细化运行打下基础。

1.   航空器保护区模型

TBO模式下的空中交通管理系统由7个功能模块组成，其中，冲突管理模板是针对航空器等冲突对象，通过战略冲突管理、配备合理间隔或避免潜在碰撞风险等方式，消除冲突隐患，保障飞行安全。飞行冲突探测是研究航空器未来一段时间内是否发生潜在冲突的过程，由于存在系统误差及无法消除误差的情况，航空器的探测容易受到外界因素的干扰，故采用以飞行器为中心建立航空器保护区的方法。目前，应用较为广泛的保护区模型有圆柱形和椭球形，本文采用符合实际且便于计算的椭球形保护区模型。依据国际民航组织（International Civil Aviation Organization，ICAO）规定的间隔标准，椭球体的长焦距a=10 km，短焦距d_v=300 m，当进入彼此的保护区时则存在冲突。随着CNS性能的不断增强、ACAS的不断完善，在未来TBO模式下，不能再笼统按照飞行安全间隔标准判断是否存在冲突，而应为航空器划设更为精细的保护区。

飞机期望航迹存在不确定性误差，许多不确定因素会导致飞行状态的随机性，随之影响飞行冲突的判断结果。研究表明，飞行中期望航迹与实际航迹之间的误差服从正态分布^[16]。本文运用飞机质点运动学模型，基于概率论方法，引入CNS、飞行员反应时间和气象风3个随机误差项，推导出航空器间碰撞风险模型，更加系统、有效地评估最低水平飞行安全间隔标准，得到更加精准的航空器保护区模型。

1.1   冲突解脱运动过程

飞行过程中，航空器的飞行轨迹会受到CNS性能、飞行员反应时间和气象风3个随机因素的影响，飞机的实际飞行轨迹与期望轨迹有所偏差，因此，采用概率建模。同时，2个航空器处于同一高度层时，航空器对头飞行所求得的最小安全间隔满足其他相遇场景的安全要求。因此，建立不同机型保护区模型时，应考虑对头飞行的避免碰撞运动过程。

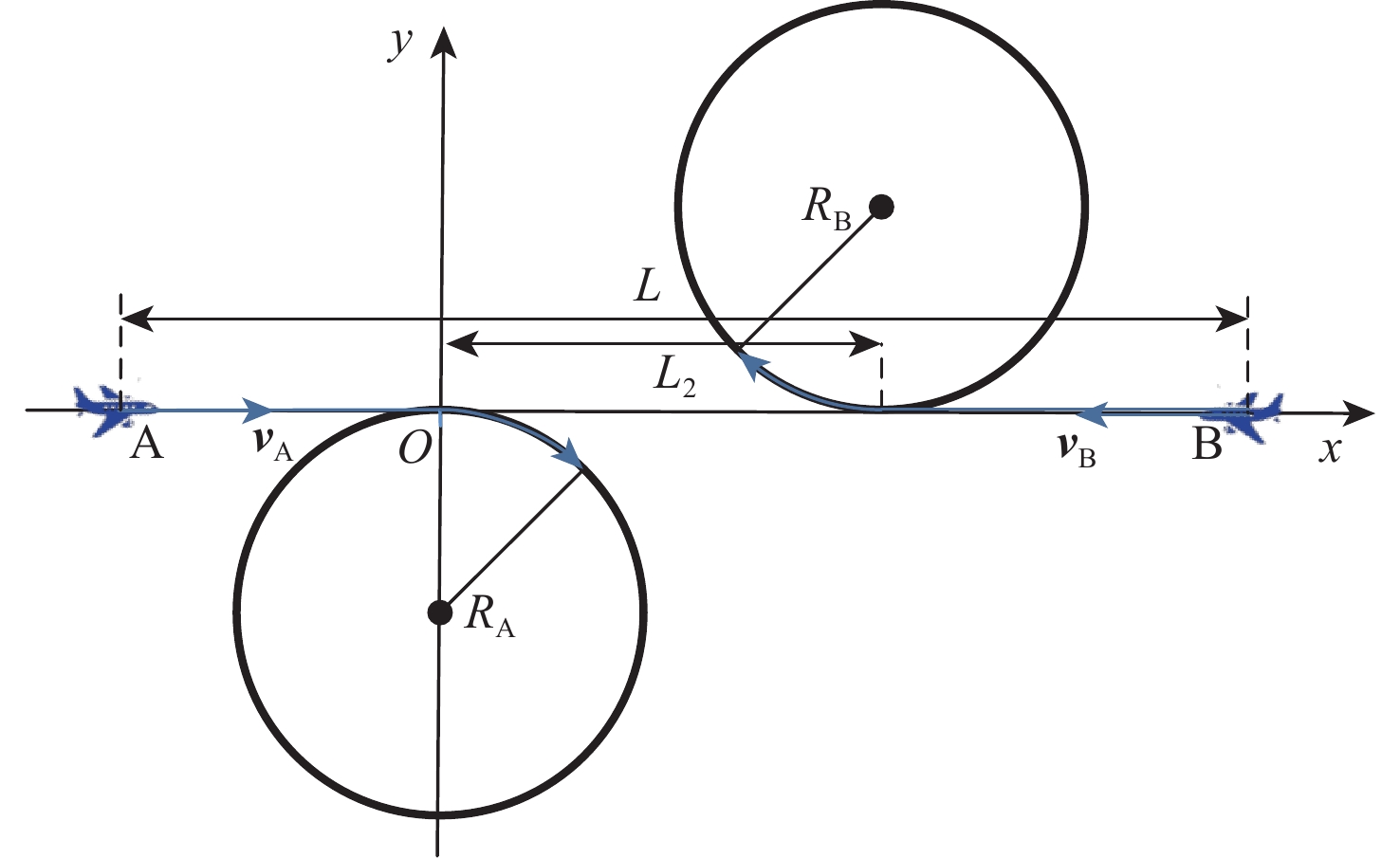
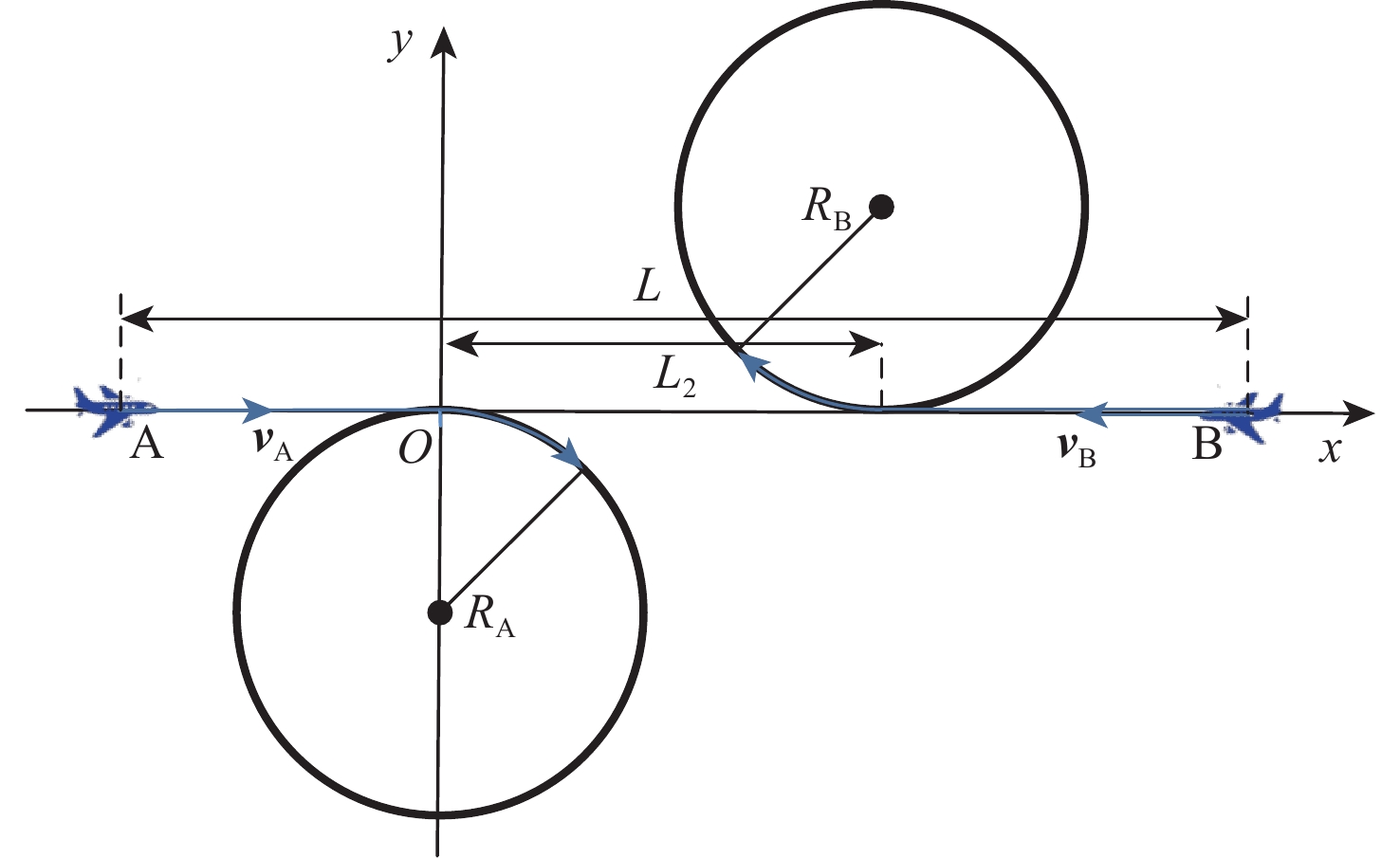
首先，对航空器冲突解脱的运动过程进行分析。在一段时间内，同一高度层、不同机型的2架航空器A、B相向匀速飞行，如图1所示，$xOy$坐标系中，航空器机载设备探测到飞行冲突时，2架航空器间的距离为L，根据飞行基本规则^[17]第71条，各自向右避让，2架航空器飞行员经过反应时间${t_{{\rm{r}}1(2)}}$决策和反应之后，采取做圆周运动的方式进行航向解脱。进而可以把航空器避免碰撞飞行运动过程分为2个阶段：第1阶段，当$t = 0$时，飞行员收到采取解脱策略指令，因为飞行员存在反应时间${t_{{\rm{r}}1(2)}}$，所以不改变航空器的航向，沿预定航迹继续飞行；第2阶段，$t = {t_{{\rm{r}}1(2)}}$时，航空器A的位置为$\left( {0,0} \right)$，航空器B的位置为$\left( {{L_2},0} \right)$,飞行员开始执行解脱策略，采取改变航向的措施，左转做匀速圆周运动。假定2架航空器的转弯半径分别为${R_{\rm{A}}}$、${R_{\rm{B}}}$,转弯的角速度分别为${\omega _{\rm{A}}}$、${\omega _{\rm{B}}}$，得到第2阶段改进的飞行运动模型为

图  1  航空器运动过程示意图

Figure  1.  Schematic diagram of the aircraft movement process

下载: 全尺寸图片 幻灯片

式中：$f\left( \cdot \right)$为飞机质点运动学模型，CNS性能满足均值为0、方差为$\sigma _{{\mathrm{cns}}}^2$的高斯分布，随机误差函数表示为$c \sim N\left( {0,\sigma _{{\mathrm{cns}}}^2} \right)$，高空风的随机扰动满足均值为0、方差为$\sigma _{\rm{w}}^2$的高斯分布，随机误差函数表示为$w \sim N\left( {{\mu _{\rm{w}}},\sigma _{\rm{w}}^2} \right)$^[18]，随机误差函数r服从伽马分布${{G}}\left( {\alpha ,\lambda } \right)$^[19]，数学期望为${\alpha }/{\lambda }$，方差为${\alpha }/{{{\lambda ^2}}}$；${D_{\rm{AB}}}$为2架航空器的水平距离，3个随机因素间及2架航空器各自所受随机因素间相互独立；Q为考虑以上3个随机因素下的实际飞机位置坐标。

1.2   碰撞风险模型

本文假定2架航空器处于同一高度层，建立碰撞风险模型，并求解2架航空器水平安全间隔标准。由于高斯随机变量之差仍服从高斯分布，2架航空器在${t_1}$时刻的间隔同样服从高斯分布，均值为2架航空器在${t_1}$时刻的理论间隔的变量，2架航空器之间的水平欧氏距离${d_{\rm{AB}}} = \sqrt {\left( {\Delta X_t^2 + \Delta Y_t^2} \right)}$, $\Delta {X_t}$与$\Delta {Y_t}$满足高斯分布：

式中：${t_1}$和${t_2}$满足$\left| {{t_{{\rm{r}}1}} - {t_{{\rm{r}}2}}} \right| = \left| {{t_1} - {t_2}} \right|$；δ_Ax为航空器A在x方向运行的随机误差。

根据文献[20]，侧向碰撞风险计算式为

式中：${N_{\mathrm{p}}}$为空域或航路上平均每飞行小时内经过的航空器数；$P\left( t \right)$为2架航空器的碰撞概率。

当${d_t} \leqslant {\lambda _{\rm{A}}} + {\lambda _{\rm{B}}}$时，则视为2架航空器发生碰撞，2架航空器的碰撞概率$P\left( t \right)$为其欧氏距离${d_t}$小于${\lambda _{\rm{A}}} + {\lambda _{\rm{B}}}$的概率，即$P(t)=\left\{d_{t} \leqslant \lambda_{{\rm{A}}}+\lambda_{{\rm{B}}}\right\}$，其中，${\lambda _{\rm{A}}}$和${\lambda _{\rm{B}}}$分别为2架航空器碰撞球半径，取其机身长、翼展长和机身高中的最大值。因此，可得第2阶段的任意时刻$t_{1}$，航空器间的碰撞概率为

$u = \Delta X_t^2 + \Delta Y_t^2$，利用概率论相关知识推导可得$u$的概率密度函数为

可得，CNS性能、飞行员反应时间和高空风导致的侧向碰撞风险$C_{\mathrm{R}}\left( t \right)$为

1.3   水平安全间隔的计算

根据ICAO对空中相撞的安全目标等级相关规定^[21]，在初始2架航空器水平安全间隔不断变化情况下，解出相应碰撞风险${C_{\mathrm{R}}}$，取${C_{\mathrm{R}}}$为5×10⁻⁹时对应的水平安全间隔值作为最低水平安全间隔标准${L_{{\mathrm{TLS}}}}$。

选择最优化方法求解最低水平安全间隔标准${L_{{\mathrm{TLS}}}}$时，粒子群算法、遗传算法和灰狼算法等最优化算法每个步骤产生的解具有随机性，且反复迭代寻找最优解相比二分法和分段查找区间法用时较长，而分段查找区间法相较二分法求解时间更短，能快速地解算不同机型航空器对间的最小安全间隔、预测潜在的飞行冲突和提供冲突解脱指令，因此，选用分段查找区间法对最低水平安全间隔进行求解，计算步骤如下：

步骤 1　确定距离查找范围$\left[0,{L}_{\mathrm{max}}\right]$及查找区间$\Delta {L_1} = 1\;000\;{\mathrm{m}}$。

步骤 2　确定第2阶段时间范围$\left[{t}_{{\mathrm{r}}},{t}_{{\mathrm{m}}}\right]$及步长$\Delta t$；计算${C_{\mathrm{R}}}\left( t \right)$，若在整个时间段满足${C_{\mathrm{R}}}\left( t \right)$小于等于目标安全等级，则输出此时的双机间距离${L_1}$，否则继续循环。

步骤 3　缩小距离查找范围$\left[{L}_{1}-\Delta {L}_{2},{L}_{1}\right]$及查找区间$\Delta {L_2} = 100\;{\mathrm{m}}$，跳至步骤2继续循环，进一步缩小查找范围及区间，直至得到符合精度要求$\varepsilon = 1\;{\mathrm{m}}$的${L_{{\mathrm{TLS}}}}$，即为所求最低水平安全间隔最优解。

定义航空器A、B的保护区为模型所求得的${L_{{\mathrm{TLS}}}}$为长轴、垂直安全间隔为300 m、300 m为短轴的椭球体。保护区长轴的大小与航空器的机型、所处的CNS环境、飞行员反应时间和高空气象风相关。

2.   基于TBO的飞行冲突网络

构建TBO运行模式下的飞行冲突网络，分析TBO模式下空中交通复杂性，需要解决航空器保护区的确定和网络连边的判断问题。飞行冲突网络$G=(V,E,W)$是以空域中航空器之间的冲突关系为研究对象的复杂网络，其中，$V = \{ {h_1},{h_2}, \cdots , {h_n}\}$为网络中由航空器组成的节点集合，$E = \{ {e_1},{e_2}, \cdots ,{e_n}\}$为反映航空器之间冲突关系的连边集合，$W = \{ {w_1},{w_2}, \cdots ,{w_n}\}$为反映潜在冲突紧迫性的连边权重集合。

2.1   TBO运行特点

TBO是以对航空器全生命周期的四维航迹为基础，在空管、航空公司、机场、航空器等相关方之间实时共享和动态维护航迹动态信息，进而实现多方协同决策。与现行基于空域扇区的运行方式相比，TBO具有如下特点：

1） 引入四维航迹管理，规划和执行飞行计划过程实现一体化，空管系统对空域资源的使用和管理更为精细。

2） 航空器可根据实际情况自主选择最优航迹，航空器之间可根据性能采取不同的间隔标准，实现航迹共享，提高飞行员情景意识。

3） 利用数据链对空指挥，实现地面空管系统与机载空管电子系统的协同。

在TBO背景下，航空器间潜在的飞行冲突是无差别的，因此，飞行冲突网络为无向网络。

2.2   冲突网络连边的确定

网络中，航空器节点构成连边需要满足以下2个条件：①位置临近，当2架航空器之间的间隔小于一定范围时，可能会发生冲突；②满足速度障碍关系，即假设一架航空器静止，并为其设置保护区，另一架航空器与其相对速度的方向在速度障碍锥内部。

在三维空域中，为航空器设置椭球形飞行保护区，当保护区内存在障碍物或其他航空器时，判定冲突发生。在TBO运行背景下，可根据航空器性能采取不同的间隔标准，椭球形保护区的长轴焦距为以上模型所求得的最小水平安全间隔${d_{\mathrm{l}}} = {L_{{\mathrm{TLS}}}}$，短轴焦距${d_{\text{v}}} = 300\;{\mathrm{m}}$。设航空器B的坐标为$\left( {{X_{\rm{B}}},{Y_{\rm{B}}},{Z_{\rm{B}}}} \right)$，则飞行保护区椭球面可表示为

航空器节点间建立连边需要通过速度障碍模型进行第2次判断。相较于车辆和机器人，航空器进行机动的空域是三维空间，因此，二维的速度障碍法无法适应航空器所有的机动行为，将其拓展至三维，如图2所示。

图  2  三维速度障碍冲突探测模型

Figure  2.  Three-dimensional speed barrier conflict detection model

下载: 全尺寸图片 幻灯片

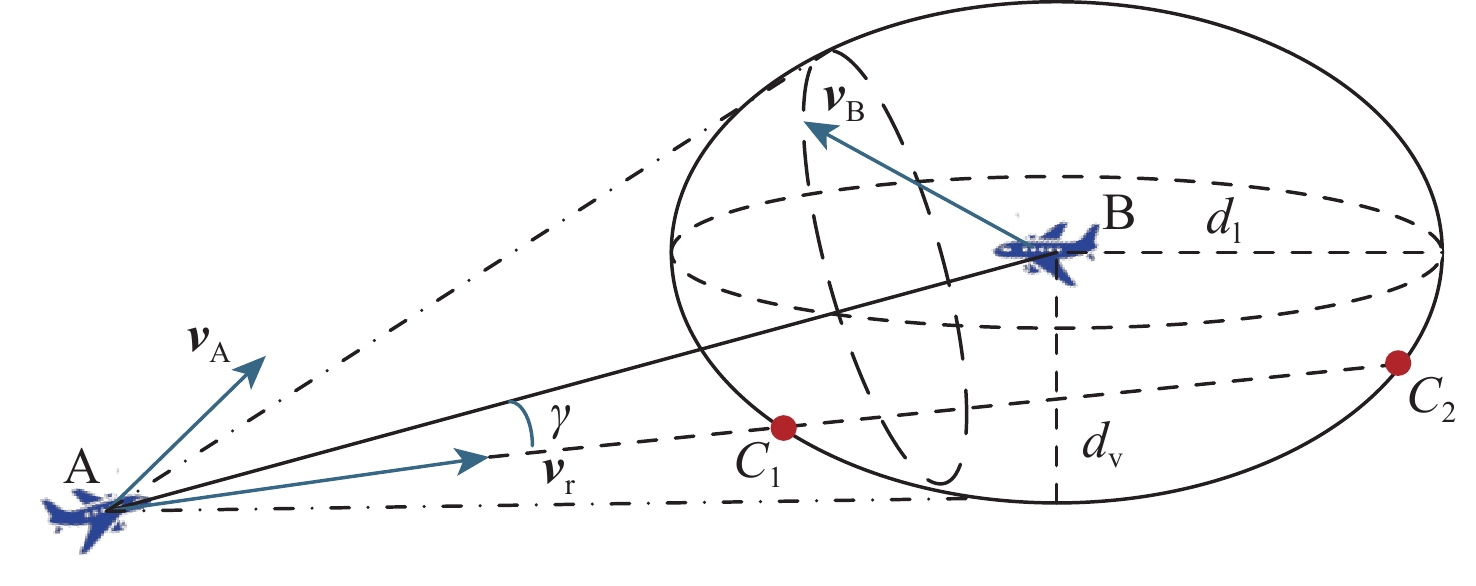
航空器A和航空器B的速度分别为${{\boldsymbol{v}}_{\rm{A}}}$和${{\boldsymbol{v}}_{\rm{B}}}$，利用矢量三角形法得出相对速度${{\boldsymbol{v}}_{\mathrm{r}}} = {{\boldsymbol{v}}_{\rm{A}}} - {{\boldsymbol{v}}_{\rm{B}}}$。由航空器A向航空器B的飞行保护区做切面，形成的区域称为速度障碍锥。当${{\boldsymbol{v}}_{\mathrm{r}}}$方向在速度障碍锥的内部时，继续飞行的航空器A将会进入航空器B的飞行保护区，如不进行调整，将会有飞行冲突发生。

${{\boldsymbol{v}}_{\mathrm{r}}}$所在的直线方程为

式中：$({X_{\rm{A}}},{Y_{\rm{A}}},{Z_{\rm{A}}})$为航空器A的坐标；$({{\boldsymbol{v}}_x},{{\boldsymbol{v}}_y},{{\boldsymbol{v}}_{\textit{z}}})$为${{\boldsymbol{v}}_{\mathrm{r}}}$的方向分量。

联立曲面方程式（8）与直线方程式（9），如果存在2个解，说明航空器B的飞行保护区与${{\boldsymbol{v}}_{\mathrm{r}}}$所在的直线有2个交点C₁和C₂；如果有$\cos \;\gamma > 0$成立，即$\gamma < 90{\textit{°}}$，则${{\boldsymbol{v}}_{\mathrm{r}}}$的方向在速度障碍锥内部，航空器A和航空器B之间构成连边：

其中：$\gamma$为相对速度${\boldsymbol{v}}_{{\rm{r}}}$与航空器A和航空器B的位置向量${{\boldsymbol{l}}_{\rm{AB}}}$的夹角；|${{\boldsymbol{l}}_{\rm{AB}}}$|为航空器A和航空器B之间的距离。

2.3   冲突网络边权的确定

飞行冲突网络的连边表示空域中航空器之间潜在的飞行冲突，而边权要能反映冲突的紧迫程度。定义$t_{\mathrm{c}}$为航空器保持当前的飞行状态，预计会发生冲突的时间。在设计连边权重时，需要满足：①航空器间距离越小，相对速度越大，冲突越紧迫，连边的权重越大，即边权随$t_{\mathrm{c}}$的减小而增大；②随着$t_{\mathrm{c}}$的减小，飞行冲突的紧迫性变化越来越剧烈，权重增加的幅度也越来越大；③考虑到速度障碍法原理和飞行冲突的现实意义，连边的权重应为正值。

图2中，相对速度延长线${{\boldsymbol{v}}_{\mathrm{r}}}$与椭球在三维空间有2个交点C₁、C₂，记航空器距2个交点距离为$\left| \overrightarrow{AC_1} \right|$、$\left| \overrightarrow{AC_2} \right|$，则有

由于可解脱时间${t_{\mathrm{c}}}$与边权是负相关的关系，结合负指数函数的性质，定义网络边权：

由于${t_{\mathrm{c}}}$为正值，其负指数函数的值域为[0,1]，可同时对飞行冲突网络的边权起到单位化的作用。

3.   实验验证与结果分析

3.1   侧向飞行安全间隔模型验证与分析

为验证本文侧向飞行安全间隔模型的有效性，即当2架航空器对头相遇时，所需的安全间隔最大，本文模型求得的最低安全间隔满足其他相遇和运动情况的安全性要求，选取A380和波音B737-800作为研究对象，具体数据如表1所示。速度均选取航空器的巡航速度，转弯坡度选取保证乘客舒适性的较大转弯坡度20°，因为2架航空器所处位置相近，所以，CNS性能均设定为RCP60、RNP10、RSP10^[17]，飞行员反应时间${t_{\mathrm{r}}}$服从伽马分布${{G}}\left( {4,5} \right)$^[18]，${N_{\mathrm{p}}}$=4架次/h^[19]。

表  1  最低安全间隔计算模型所需参数值

Table  1.  Required parameter values for the minimum safety interval calculation model

航空器	${\lambda _x}$/m	${\lambda _y}$/m	${\lambda _{\textit{z}}}$/m	$v$/(m·s−1)	$\beta$/(°)	${\sigma _{{\mathrm{cns}}}}$	${\sigma _{\rm{w}}}$	${\mu _{\rm{w}}}$	${N_{\mathrm{p}}}$
A380	72.8	79.8	24.1	251	20	64.5	10.8	60.3	16
B737-800	39.5	35.8	12.5	230	20	64.5	11.5	60.3	16

下载: 导出CSV 

| 显示表格

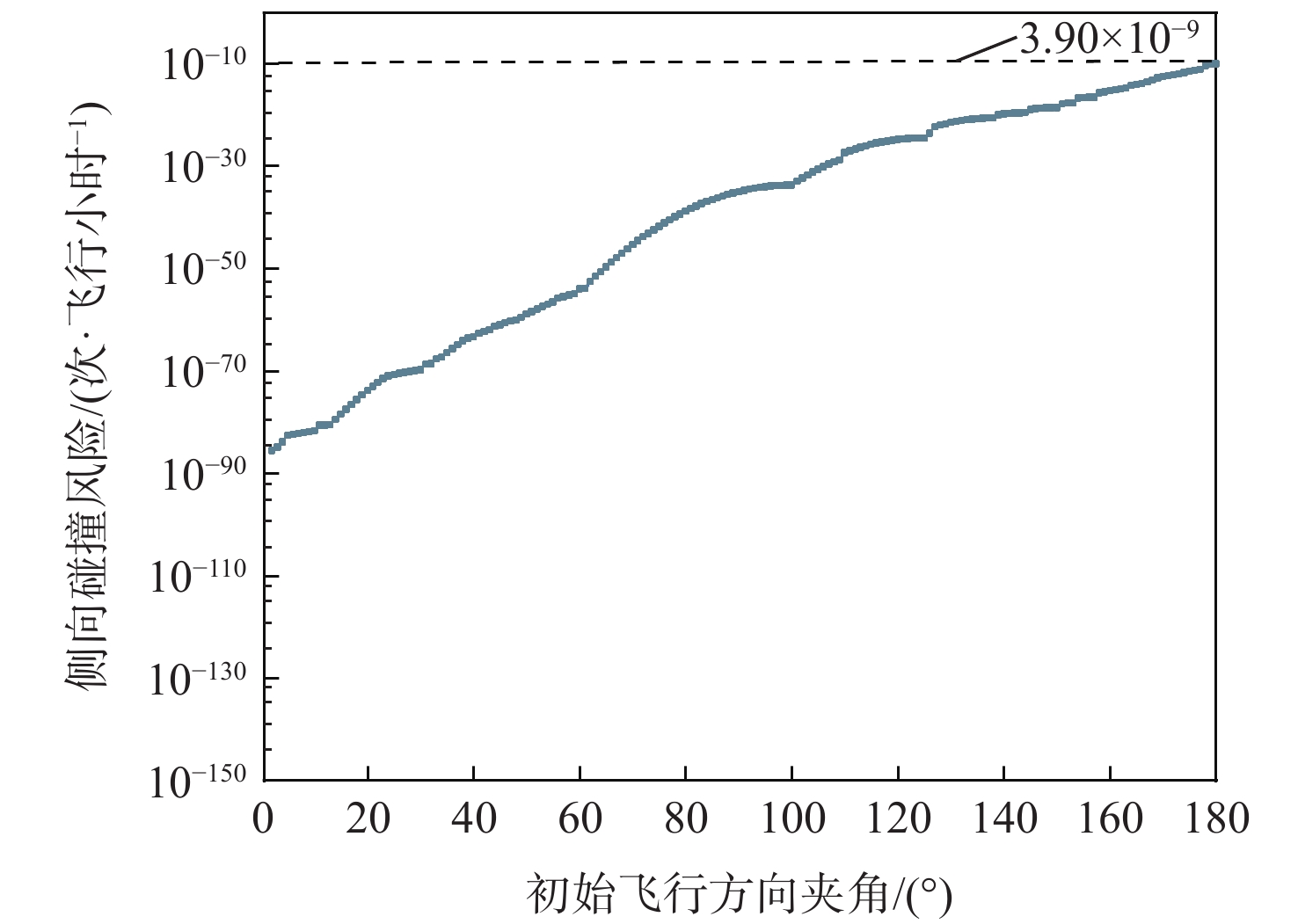
利用表1的航空器对性能参数和本文模型计算得出的最低安全间隔${d_{\mathrm{m}}}$=6227 m，将该距离作为航空器对航向解脱的初始距离，航空器初始位置确定，模拟2架航空器初始飞行方向夹角从0°变化到180°的运动过程，计算每个角度运动过程中的最大侧向碰撞风险变化如图3所示。可以看出，随着2架航空器初始飞行方向夹角变大，2架航空器间侧向碰撞风险也随之变大。当2架航空器相向飞行，即初始飞行夹角为180°时，侧向碰撞风险最大为3.90×10⁻⁹次/飞行小时。

图  3  侧向碰撞风险随初始飞行方向夹角变化

Figure  3.  Variation of lateral collision risk with initial flight direction angle

下载: 全尺寸图片 幻灯片

由图3可知，相同初始距离的条件下，双机相向避撞飞行过程中，最大侧向碰撞风险大于其他场景，所需要的安全间隔最大，验证了本文模型适用于其他的飞行场景，所求得的最低安全间隔满足其他情况的飞行安全需求。

为验证模型的安全性和有效性，通过数据模拟的方法，利用蒙特卡罗算法对该航空器对的运动过程进行仿真。将2架航空器的初始距离设置为6 227 m，对其运动过程和碰撞情况进行模拟仿真，可以得出每1×10⁸次仿真中2架航空器出现冲突的次数和平均侧向碰撞风险，如图4所示。在10×10⁸次仿真中，出现的冲突次数为1，2架航空器间的侧向碰撞风险概率始终满足小于5×10⁹次/飞行小时的飞行安全目标要求，大量的模拟运行有助于提高统计量显著性并提高置信度，验证了最低飞行安全间隔模型的安全性。

图  4  蒙特卡罗仿真

Figure  4.  Monte Carlo simulation

下载: 全尺寸图片 幻灯片

3.2   侧向飞行安全间隔模型应用分析

根据ICAO按照航空器几何尺寸进行分类的规定，中国常见民用航空器被分为等级A～F。基于本文模型，按照民用航空器等级A～F的分类标准，计算得到6个等级的航空器之间的安全间隔标准，如表2所示。计算方法为：选取6个分类等级每个等级中碰撞球半径最大的航空器机型，从等级A到等级F依次为伊尔14、雅克42、空客300、空客330-300、波音747-8和空客380；将这6个机型的性能参数代入本文模型中，其他参数同表1。

表  2  6个等级航空器间侧向安全间隔标准

Table  2.  Standards for lateral safety interval between six classes of aircraft

航空器 等级	侧向安全间隔/m
	A	B	C	D	E	F
A	2582	3779	3841	3873	3930	4028
B	3779	4836	5229	5445	5580	5643
C	3841	5229	5589	5790	5832	6186
D	3873	5445	5790	5870	5995	6223
E	3930	5580	5832	5995	6103	6252
F	4028	5643	6186	6223	6252	6365

下载: 导出CSV 

| 显示表格

国内常见不同性能民用航空器之间的侧向安全间隔标准可参照表2，进一步扩大了本文模型的应用范围，提高了参考价值。

3.3   网络性能对比

假定本文TBO模式的空域中有包括民用飞机和通用飞机5种不同机型航空器，查阅资料获取5种航空器大小、巡航速度等性能参数，其他相关参数同表1，求算出对应的最小安全间隔，如表3所示。可以看出，航空器碰撞半径越大，续航速度越快，所需的最小安全间隔越大，通用飞机由于体型小、速度慢，所需的水平安全间隔较小。同时，不同的航空器对之间的最小水平安全间隔不同，同一机型航空器A380和B737-800、A320、Cessna172、DA40的最小安全间隔不同，且均小于目前采用的国际水平安全间隔标准10 km。

表  3  不同机型组的最小安全间隔

Table  3.  Minimum safety distance for different model groups

航空器机型	最小水平安全间隔/m
	A380	B737-800	A320	Cessna172	DA40
A380	6365	6227	6222	4209	4361
B737-800	6227	6025	6017	3884	4032
A320	6222	6017	6006	6161	3875
Cessna172	4209	3884	3875	1571	1713
DA40	4361	4032	4024	1713	1856

下载: 导出CSV 

| 显示表格

为分析本文模型的性能与特性，通过MATLAB模拟航空器运行的仿真场景，构建100 km×100 km×1 km的三维空域，为模拟TBO运行环境，在4个高度层和高度层之间随机生成表3中5种不同机型航空器共40架。航空器速度设置在600～800 km/h范围内，航向任意，位置随机均匀分布。

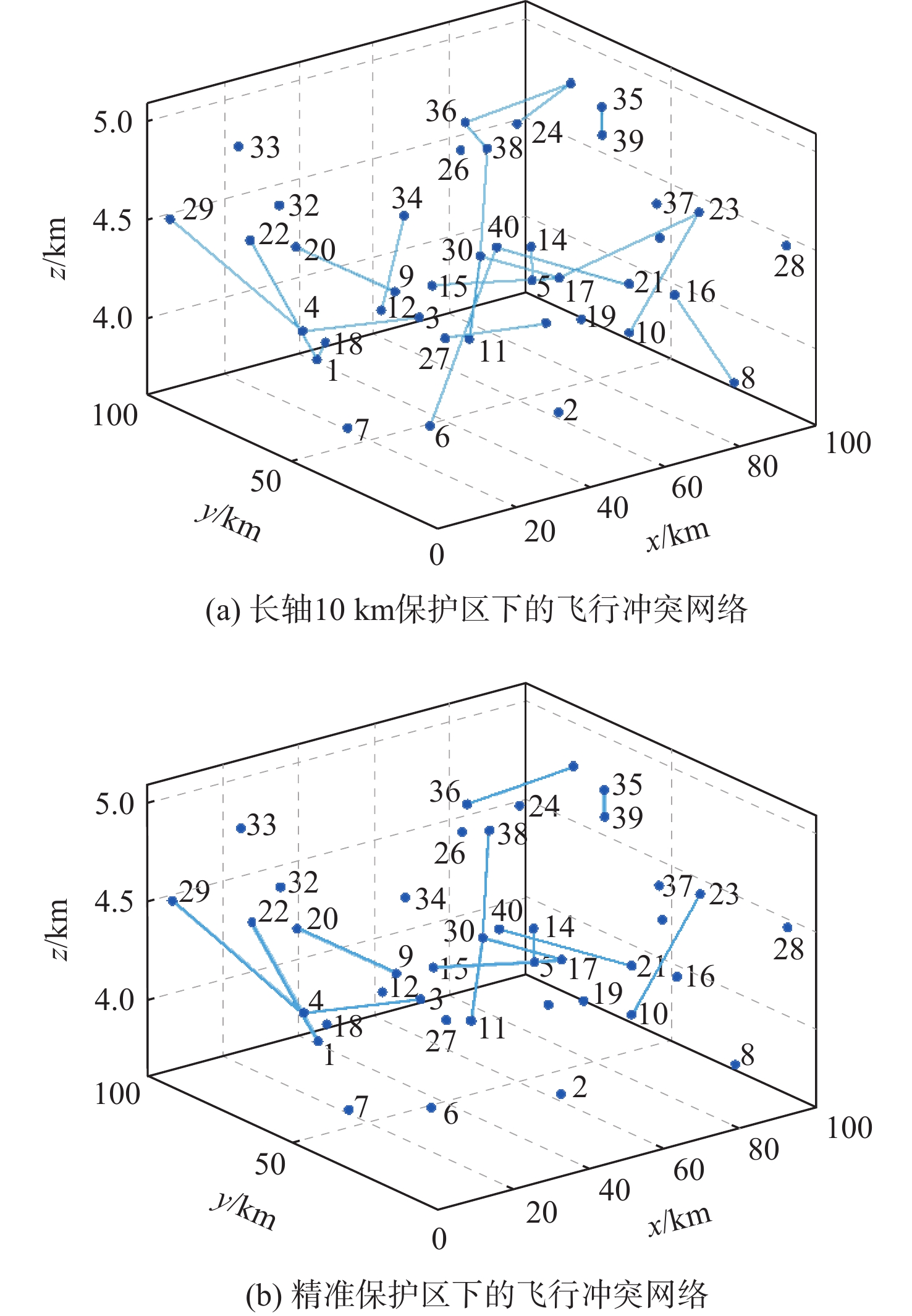
由于潜在的飞行冲突对于2架航空器是无差别的，网络中的连边也没有方向，飞行冲突网络为无向网络。图5（a）为基于速度障碍法所构建的冲突网络模型（简称冲突模型），以10 km为航空器椭球形保护区长轴所构建的冲突网络。图5（b）为以表3中不同机型组的最小安全间隔为保护区长轴所构建的冲突网络。图中节点为航空器，实线为冲突连边，两两连边越粗，表明网络边权越大，冲突越紧迫。

图  5  网络性能对比

Figure  5.  Network performance comparison

下载: 全尺寸图片 幻灯片

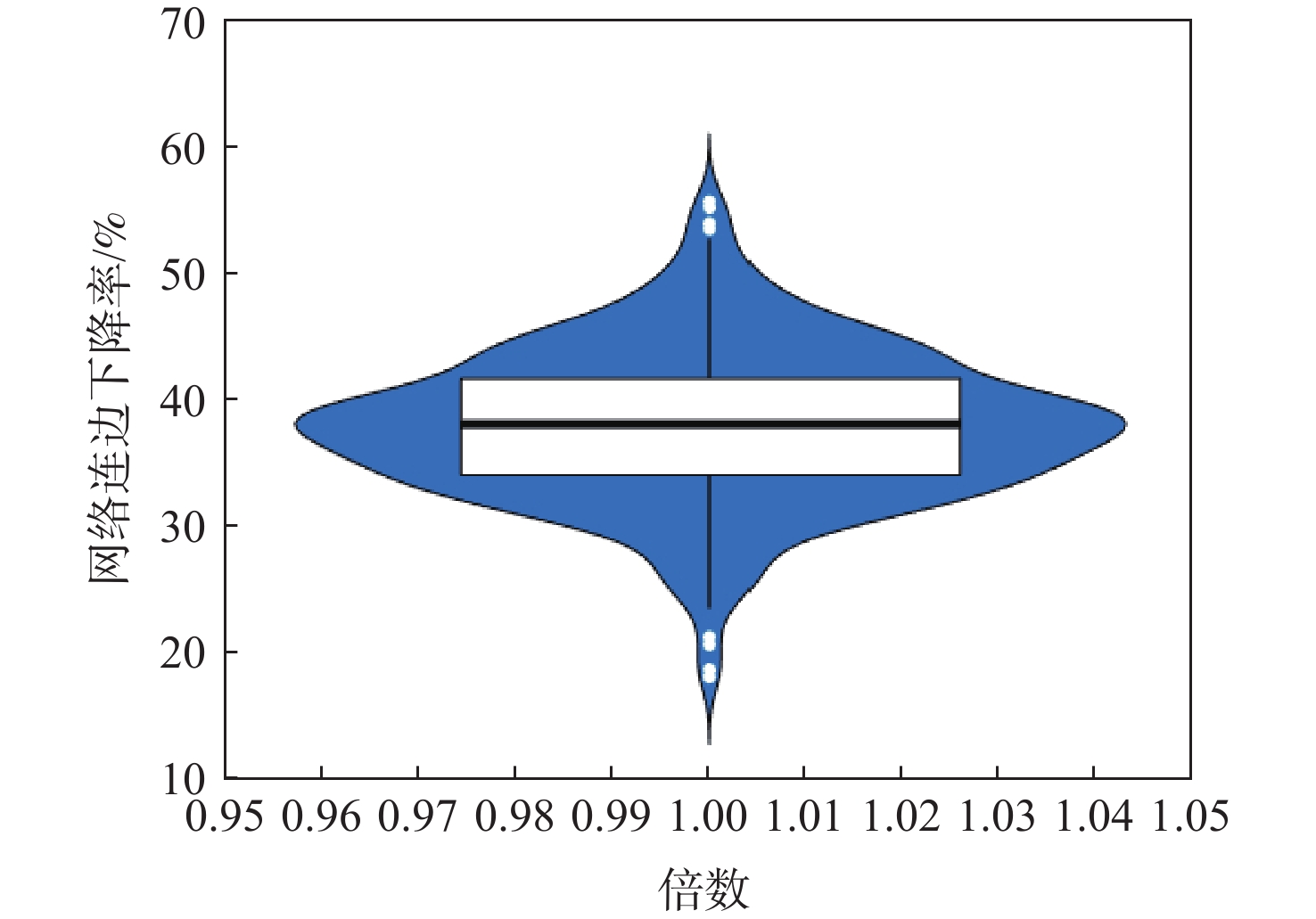
对比图5（a）和图5（b）的连边数量，长轴10 km保护区下的飞行冲突网络连边为22，精准保护区下的飞行冲突网络连边为13，相比降低了40.9%的网络连边。由于一组场景导致的数据变化有一定的偶然性，另设置200 km×200 km空域内随机生成10～70架航空器进行对比重复实验。图6为重复500次实验得出的网络连边下降率的小提琴图。图中，小提琴状区域为核密度曲线，白色矩形为25%、75%分位数，中间横线为中位数，白色点为离群值点，黑色竖线为去掉离群值点后点的上下限。可以看到，数据分布集中于30%～45%之间，总体平均值为38.1%，因此，认为TBO运行模式下，精准保护区下的冲突模型平均降低了38.1%的网络连边。

图  6  网络连边下降率分布

Figure  6.  Distribution of network connected edge decline rate

下载: 全尺寸图片 幻灯片

3.4   网络节点特征分析

针对图5所构建的2种飞行冲突网络仿真场景，考虑复杂网络指标中反映节点特征的指标：节点的度和点强，对2种冲突网络进行定量分析。

定义1　节点度${k_i}$。节点的度定义为网络中该节点和其他节点之间链接的数目，是反映网络中节点与节点连接情况的拓扑指标。在飞行冲突网络中，各航空器节点的度表示其存在的冲突数量的多少，度值越高，表示节点在网络中存在更多的邻居节点，与更多的行为单元存在关联，重要性相对更高。节点的度可表示为

式中：${k_i}$为节点度；${l_i}$为节点的连边数目。

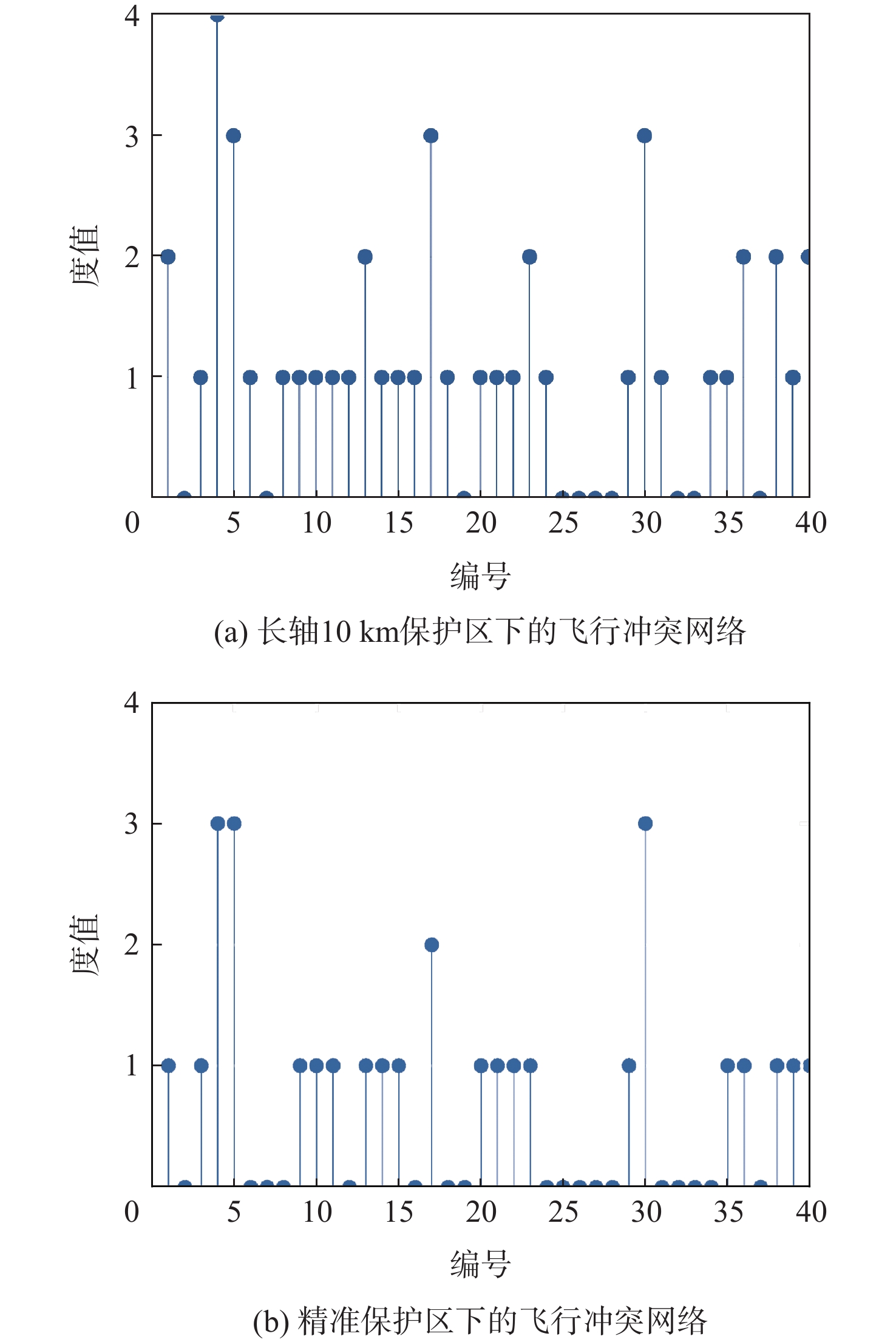
对2种保护区构建的飞行冲突网络模型节点的性质进行分析。对比分析2种网络中各个航空器对应的节点度值，如图7所示。

图  7  网络节点度值分布的对比

Figure  7.  Comparison of the distribution of degree values of network nodes

下载: 全尺寸图片 幻灯片

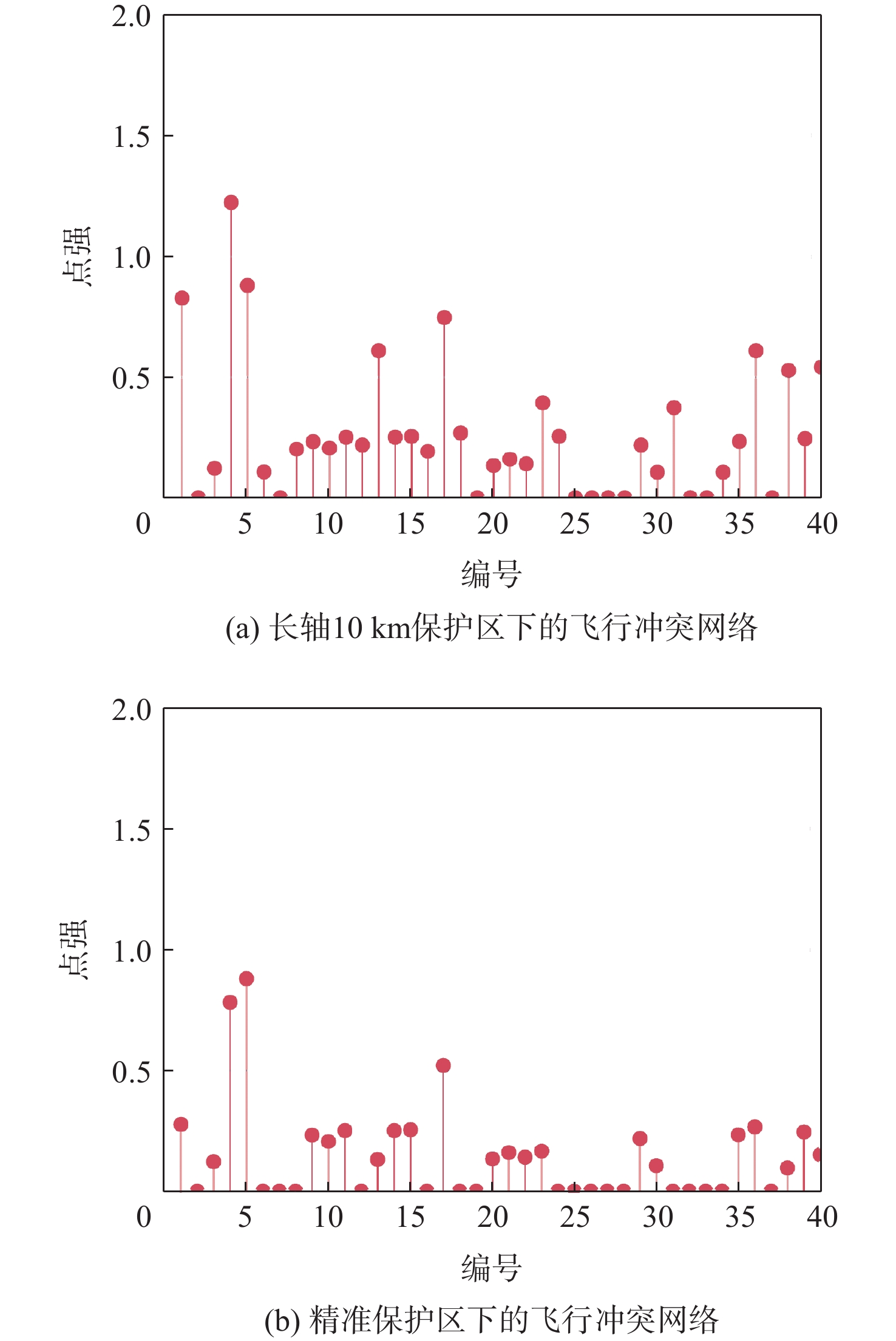
由图7可知：①长轴10 km保护区下的飞行冲突网络中，孤立节点共10个：2、7、19、25、26、27、28、32、33、37；精准保护区下的飞行冲突网络中，孤立节点共18个：2、6、7、8、16、18、19、24、25、26、27、28、31、32、33、34、37、38。孤立节点数量的增多，一定程度上缓解了空中交通拥堵情况，减轻了管制员的负荷。②长轴10 km保护区下的飞行冲突网络中度值最高的是4节点，度值为4，而精准保护区下的飞行冲突网络中度值最高的为4、5、30节点，其潜在冲突数量为3，节点度的峰值降低了25%；经过保护区变化和速度障碍法判定后，27号节点节点度值降为0，与长轴10 km保护区下的飞行冲突网络得到的结果存在较大的偏差。

定义2　点强${s_i}$。点强是与节点相连的边所对应的权值之和，该值能够反映飞机冲突态势的紧迫程度。节点的点强可表示为

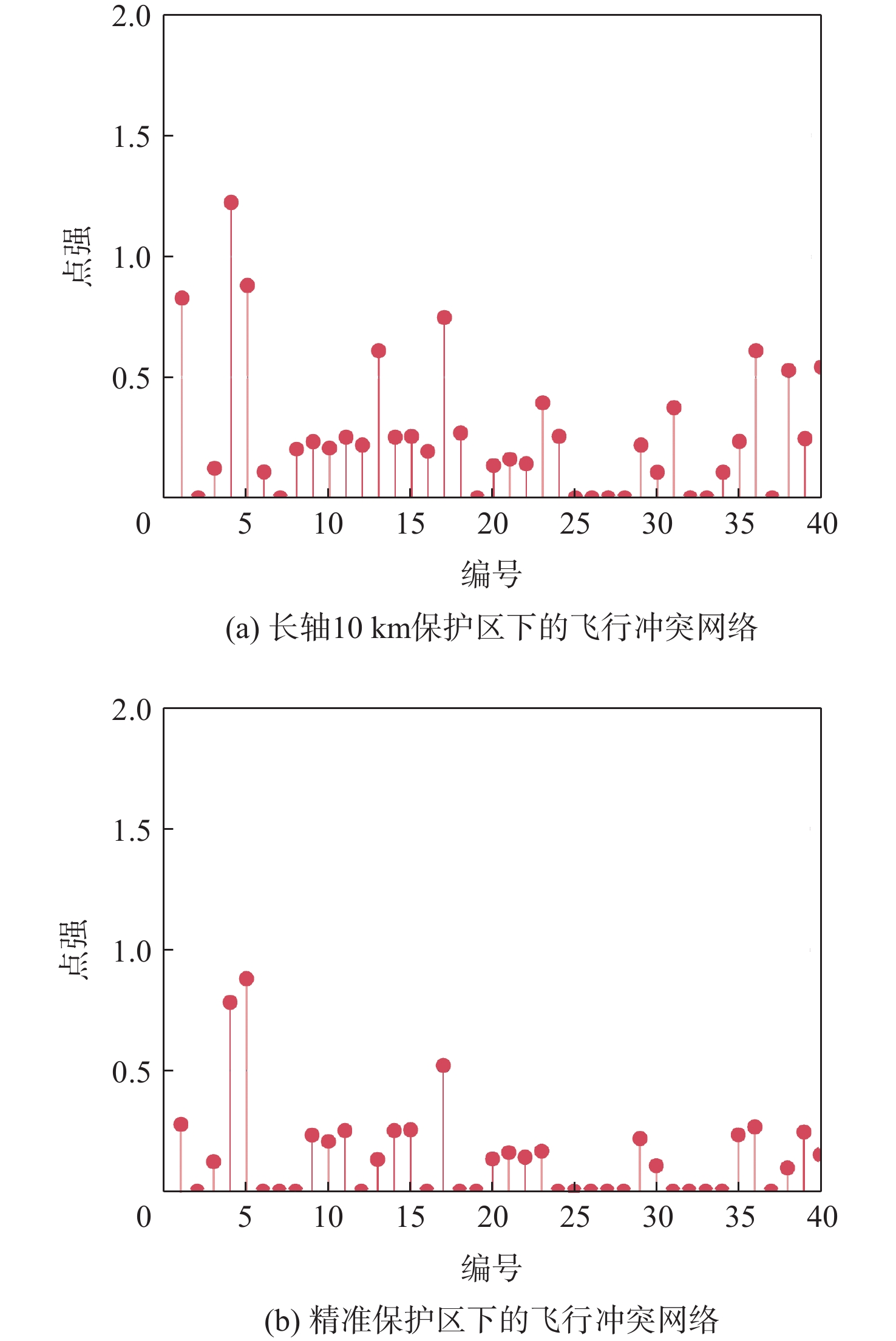
式中：${a_{ij}}$为节点$i$和节点$j$的连接关系，若相连${a_{ij}} = 1$，否则${a_{ij}} = 0$；${w_{ij}}$为节点${v_i}$和节点${v_j}$连边的权值。在飞行冲突网络中，点强反映了航空器节点潜在冲突整体的严重程度。

节点强度是由航空器节点各个冲突边的权重相加得到，可以较直观地反映航空器当前潜在的冲突情况。在相同场景下，基于不同长轴保护区形成的冲突网络点强分布如图8所示。结合图7可以看出，长轴10 km保护区下的飞行冲突网络中，4号节点的点强最高，其节点度为4，点强为1.24，对应的航空器整体潜在飞行冲突最强；相对比，精准保护区下的飞行冲突网络中，5号节点的点强最高，其节点度为3，点强为0.88。

图  8  网络节点点强分布的对比

Figure  8.  Comparison of point strength distribution of network nodes

下载: 全尺寸图片 幻灯片

综上所述，无节点度值的节点也同样无点强，节点度值较大的节点的点强也相对较大，这是因为度值较大的节点，其冲突数量较多，冲突数量多使点强增加。相较于长轴10 km保护区下的飞行冲突网络，精准保护区下的飞行冲突网络节点度值和点强都有大幅度减少。因此，精准保护区形成的冲突网络在结构上更加简单，减少单个节点的冲突数量，进而提升TBO运行模式下整个航空网络的运行效率。

3.5   网络整体特性分析

定义3　集聚系数$C$。集聚系数表示网络中的节点的邻居节点也互为邻居节点的比例，反映了网络小集群的完美程度。加权聚集系数是普通聚集系数的加权表达，定义为

式中：${a_{ij}}、{a_{jk}}、{a_{ik}}$为连通三元组的个数；$j$和$k$为节点$i$的邻居节点。

对于整个网络，平均加权集聚系数可以描述网络整体的冲突汇聚程度，用C表示：

式中：N为网络中的节点数目。

定义4　平均路径长度D。飞行冲突网络中，从节点${v_i}$和节点${v_j}$之间的路径不止一条，选取距离最短的一条为最短路径，该最短路径长度表示为

式中：L为节点${v_i}$和节点${v_j}$之间最短的一条道路；l为道路L上的一条边；${w_l}$为道路l的边权。

整个网络的平均路径长度可表示为

式中：${d_{ij}}$为节点$i$和$j$之间的最短路径。

在飞行冲突网络中，平均路径长度反映了网络中各个航空器节点间冲突的严重情况，与空域的复杂性联系密切。

定义5　网络效率N_E。网络效率能直观反映整个网络的连通度，2个节点间的效率表示为彼此距离的倒数，而整个网络的效率为每2对节点之间效率的平均值。在冲突网络中，该值能够简易地表示出航空器冲突的扩散广度，定义为

网络效率N_E越高，节点间的联系就越紧密，网络也相对更复杂。

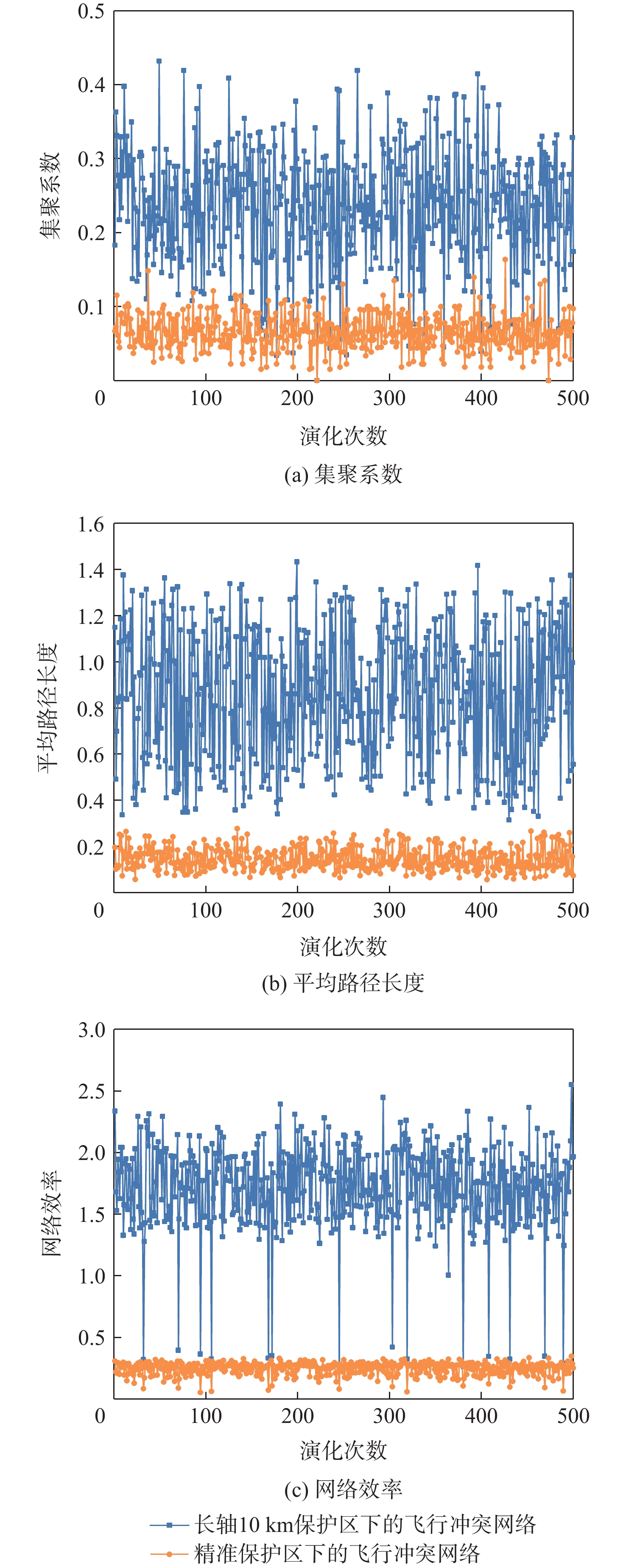
为计算和分析2种网络的整体特性指标，在已有仿真场景基础上设置网络演化规则：在MATLAB中构建仿真场景，其中，空域范围、航速、位置分布、航向均与上述仿真一致。令仿真空域随机生成50架5种机型的航空器，设置航空器演化次数为500，每次演化时间间隔为5 s（即每间隔5 s记录一次），航速与航向在每次演化过程中有30%的几率发生改变；在200 km×200 km空域范围内的航空器有50%的几率离开该空域，而在所设定空域外的航空器有50%的几率进入该空域。分别计算按照规则每步演化后2种飞行冲突网络的集聚系数、平均路径长度和网络效率，得到各指标时间序列中第1次到第500次演化的数值，绘制成折线图，如图9所示。

图  9  网络整体特性指标对比分析

Figure  9.  Comparative analysis of overall network characteristics indicators

下载: 全尺寸图片 幻灯片

由图9可知，2种保护区组成的飞行冲突网络中，各指标数值在演化过程中均在某个水平范围内波动。由长轴10 km保护区构成的飞行冲突网络中，集聚系数以0.24均线上下波动，最大值为0.43，平均路径长度以0.86均线上下波动，最大值为1.43，最小值为0.31，网络效率以1.71均线上下波动，最大值为2.55，最小值为0.24；精准保护区构成的飞行冲突网络中，集聚系数以0.07均线上下波动，最大值为0.16；平均路径长度以0.15均线上下波动，最大值为0.28，最小值为0.06，网络效率以0.25均线上下波动，最大值为0.34，最小值为0.05。可以得到结论，经过有效缩小航空器保护区范围，为不同机型航空器划定精准的保护区大小，能减少飞行冲突网络的复杂程度，降低冲突的紧迫程度，更加贴合TBO运行模式精细化、高效化、可预知的特点。

4.   实例仿真与分析

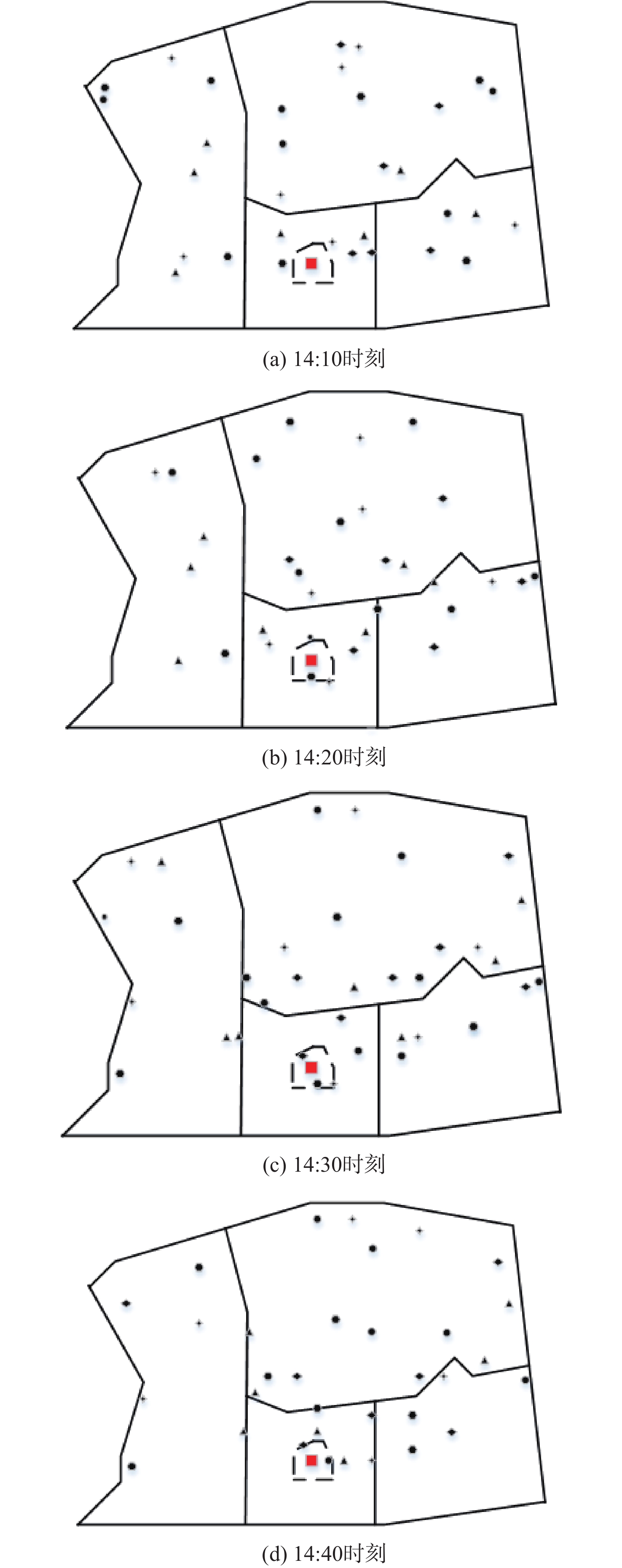
为进一步验证模型的合理性和有效性，选取厦门高崎国际机场周边管制区雷达态势作为实例进行仿真分析。厦门高崎国际机场位于福建省厦门市，是中国东南沿海重要的区域性航空枢纽，同时由于其位于中国的东南沿海，军用飞机也多将其作为任务飞行中的备降机场。以厦门高崎国际机场2021年某日14:10—14:40的飞行雷达数据作为测试样本，将该时段数据每隔10 min记录一次，记录的内容包括飞机的航速、航向和位置等，对每个时刻的空中情况通过MATLAB进行冲突网络建模，如图10所示。图中，实线表示扇区边界，虚线表示进近管制区边界，不同的实心形状表示不同机型的航空器，虚线内方块表示厦门高崎国际机场。

图  10  不同时刻空中运行态势

Figure  10.  Airborne operation situation at different moments

下载: 全尺寸图片 幻灯片

由图10可知，在30 min内，空情呈平稳态势变化，在该场景下验证本文模型的有效性。针对每个时刻的空中运行态势，分别利用现行标准间隔形成的保护区和本文提出的不同机型基准保护区判定航空期间的冲突关系，得到同一时刻2个不同的飞行冲突网络，分别对长轴10 km保护区下的飞行冲突网络和精准保护区下的飞行冲突网络的网络指标进行分析，得到的网络整体性数据如表4所示。

表  4  不同时刻的网络指标值

Table  4.  Values of network indicators at different moments

时刻	集聚系数			平均路径长度			网络效率
	长轴10 km保护区下的 飞行冲突网络	精准保护区下的 飞行冲突网络		长轴10 km保护区下的 飞行冲突网络	精准保护区下的 飞行冲突网络		长轴10 km保护区下的 飞行冲突网络	精准保护区下的 飞行冲突网络
12:10	0.4378	0.2686		0.7814	0.2578		1.6449	0.1957
12:20	0.4474	0.2793		0.6832	0.2279		1.7390	0.2189
12:30	0.4665	0.2969		0.5558	0.2360		1.3204	0.2286
12:40	0.4088	0.2329		0.6518	0.1788		1.4386	0.2310

下载: 导出CSV 

| 显示表格

由图10和表4可知，4个连续时刻的空情变化不大，基于空情构建的飞行冲突网络拓扑结构和网络指标随时间也波动较小。长轴10 km保护区得到的飞行冲突网络中，聚集系数在0.43左右，平均路径长度在0.67左右，网络效率在1.52左右。精准保护区得到的飞行冲突网络中，聚集系数在0.43上下，平均路径长度在0.67上下，网络效率在0.22上下。对比厦门高崎国际机场终端区空域仿真得到的2种飞行冲突网络的网络指标可以看出，在现行基于空域扇区运行的模式下，精准保护区模型能根据航空器性能采取不同的间隔标准，以此为基础构建的飞行冲突网络冲突连边数量和权值减小，复杂程度降低，从而可以减轻管制员工作负荷，能提高空域的运行效率。

5.   结　论

1） 航空器的临近关系是管制员判断潜在飞行冲突和空域复杂情况的重要依据，本文模型改进了使用通信关系和统一间隔标准判断冲突关系带来的空域资源浪费，更适用于未来精细化的管理模式。

2） 本文建立不同机型侧向飞行安全间隔模型，使用蒙特卡罗等方法验证了模型的安全性和有效性，以此为航空器划设精准保护区，基于速度障碍法构建飞行冲突网络，分析网络的拓扑指标衡量空中复杂性。

3） 相较于传统的建模方法，本文根据不同航空器性能得到精准的保护区模型，以此判定航空器间的冲突关系，能够减少38.1%的飞行冲突网络连边数量，降低空域的复杂程度，同时缩小了水平安全间隔标准，提高了空域的运行效率，为以TBO为核心的未来空中交通管理提供了理论支撑。