3种六自由度动力下降凸优化制导方法

王驰; 刘伟; 高扬

doi:10.13700/j.bh.1001-5965.2023.0235

3种六自由度动力下降凸优化制导方法

doi: 10.13700/j.bh.1001-5965.2023.0235

王驰^{1, 2},
刘伟^{1, 2, ,},
高扬^{1, 2}

1.
中国科学院大学航空宇航学院，北京 100049
2.
中国科学院空间应用工程与技术中心太空应用重点实验室，北京 100094

基金项目: 中国科学院青年创新促进会项目(292020000040)

详细信息

通讯作者:
E-mail：liuwei@csu.ac.cn

中图分类号: V448.131；V448.233
计量
- 文章访问数: 232
- HTML全文浏览量: 61
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2023-05-10
- 录用日期: 2023-07-21
- 网络出版日期: 2023-08-14
- 整期出版日期: 2025-04-30

Three convexification-based methods for six-degree-of-freedom powered descent guidance

WANG Chi^{1, 2},
LIU Wei^{1, 2
, ,},
GAO Yang^{1, 2}

1.
School of Aeronautics and Astronautics，University of Chinese Academy of Sciences，Beijing 100049，China
2.
Key Laboratory of Space Utilization，Technology and Engineering Center for Space Utilization，Chinese Academy of Sciences，Beijing 100094，China

Funds: Youth Innovation Promotion Association CAS (292020000040)

More Information

Corresponding author: E-mail：liuwei@csu.ac.cn

摘要

摘要:
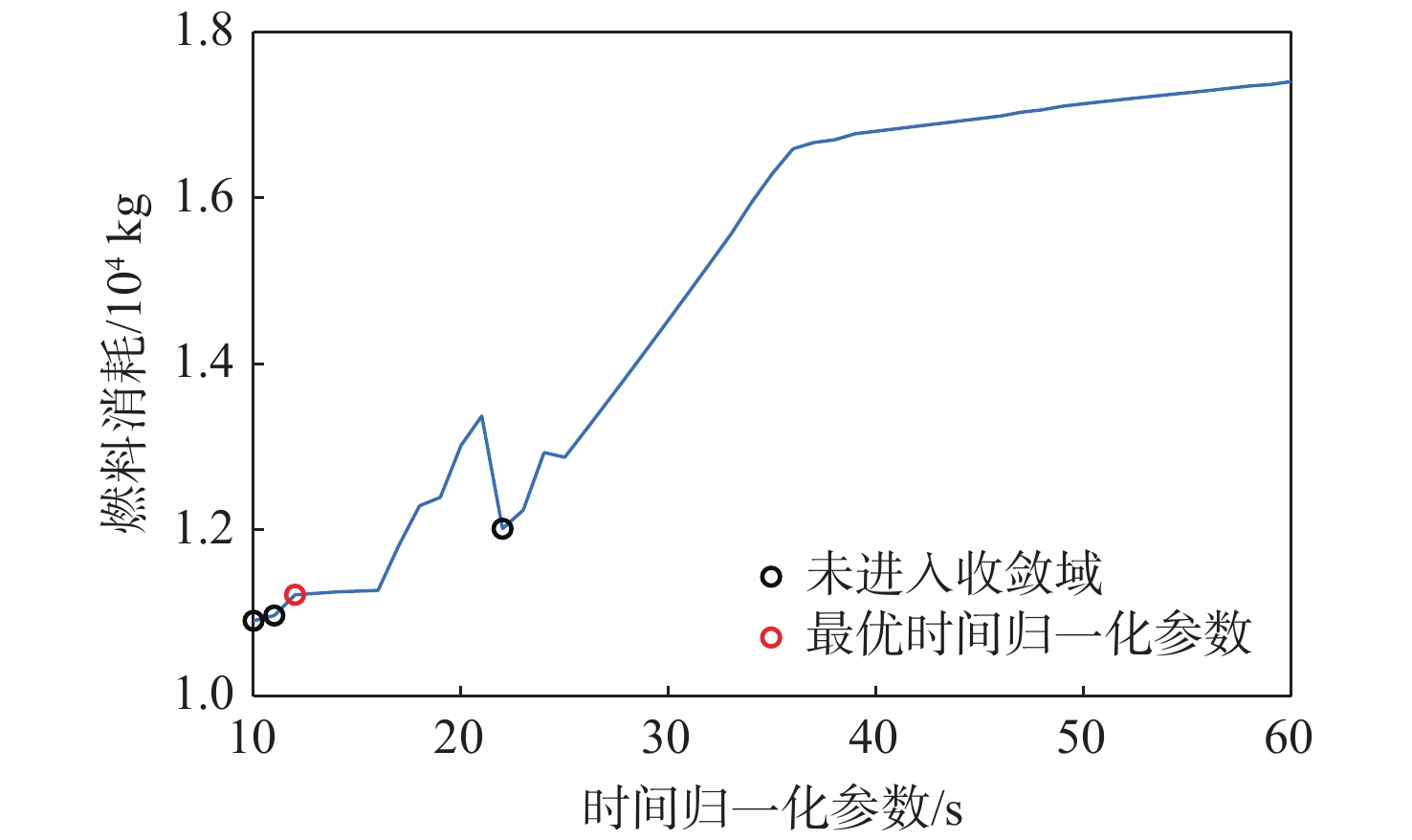
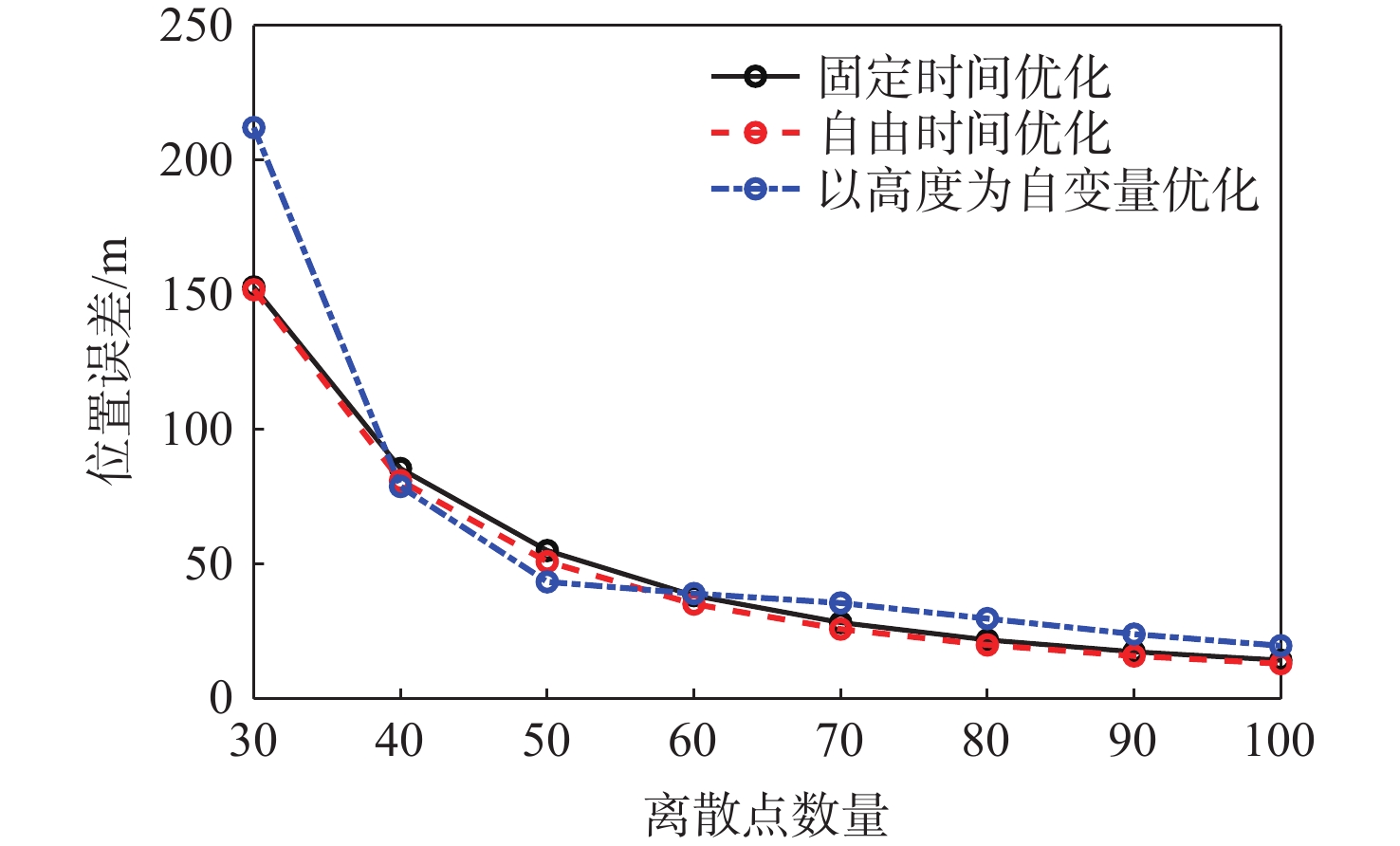
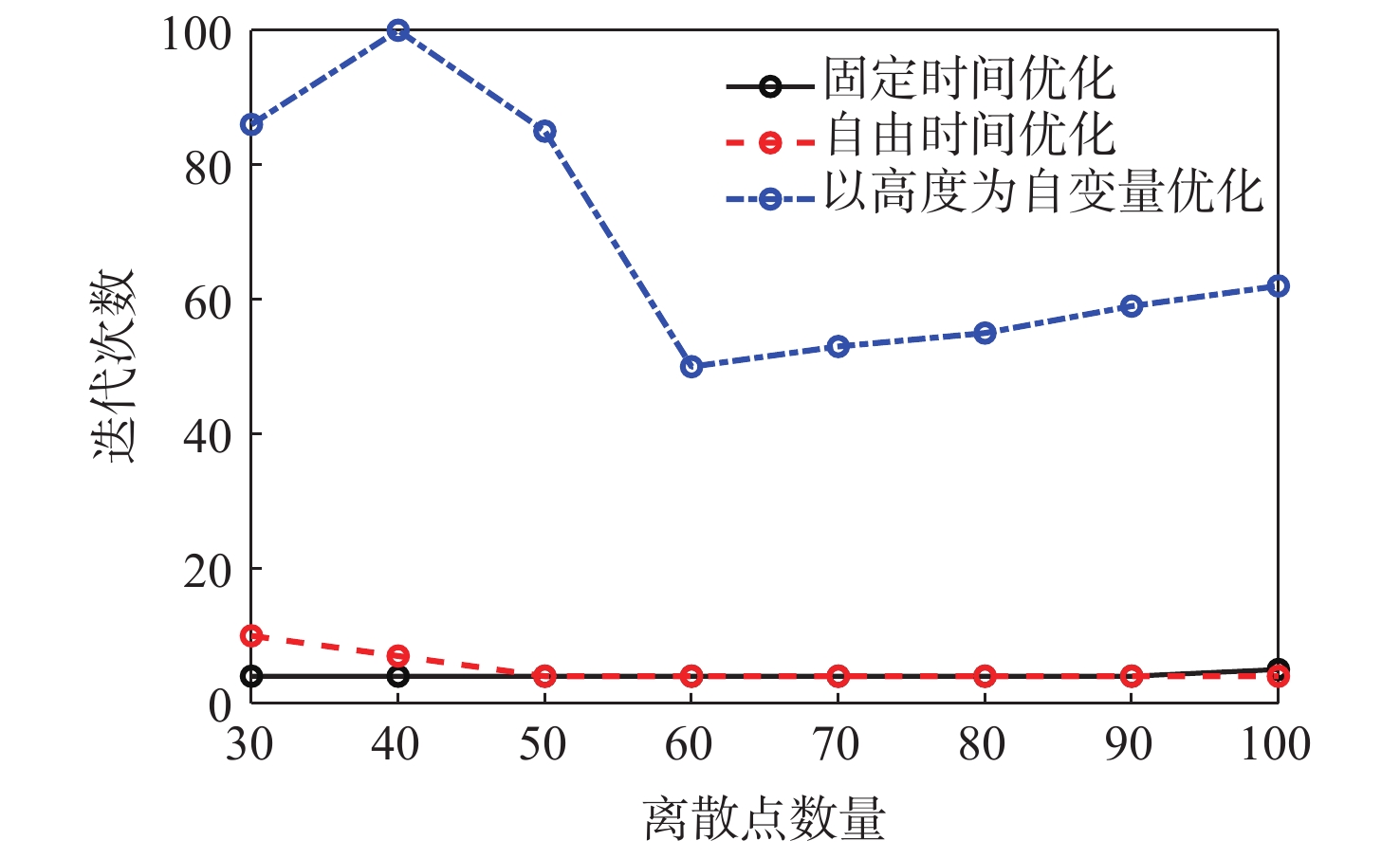
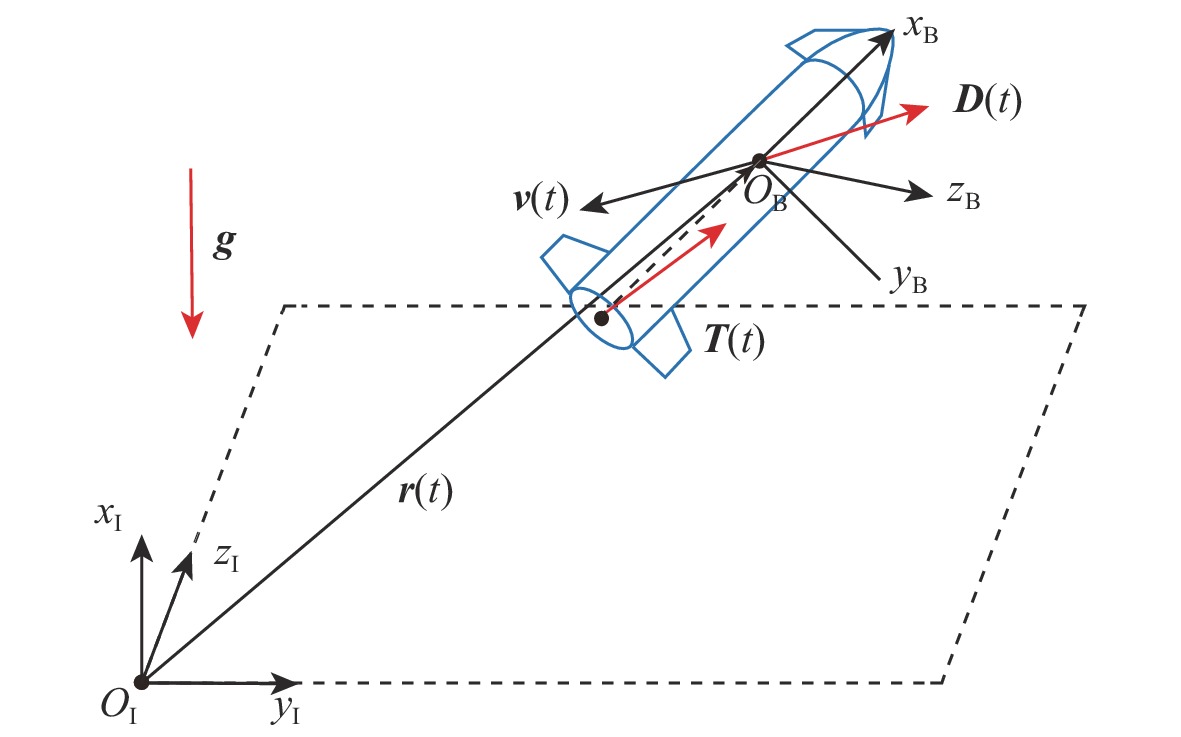
飞行器动力下降软着陆的一个关键技术在于实时求解六自由度(6-DoF)动力下降制导问题，该问题可以描述为多约束条件下的燃料最省轨迹优化问题。选取飞行时间、时间替代变量、轨迹高度3种自变量建立3种优化模型，将原始轨迹优化问题转化为序列凸优化可解形式进行迭代求解，形成了3种在线制导方法。比较3种制导方法在收敛性、实时性、最优性及求解精度上的差异，结果表明：3种制导方法均能求解六自由度动力下降问题；自变量为飞行时间的制导方法计算时间最短且燃料消耗最少，但需要预先确定动力下降飞行时间；基于其余2类自变量的制导方法能够优化动力下降飞行时间，但均为次优解，且计算时间显著增加；相同离散点数量下3种方法的求解精度相近。若采用序列凸优化作为动力下降在线制导方案，如何确定最优飞行时间、逼近燃料最优解及进一步缩短计算时间等仍有待深入研究。
- 六自由度 /
- 动力下降 /
- 自主制导 /
- 凸优化 /
- 最优飞行时间
Abstract:
A key technology for the safe landing of spacecraft in powered descent is to solve the six degrees of freedom(6-DoF) powered descent guidance problem in real time. This problem is a fuel-optimal problem with multiple constraints. In this paper, three optimization methods are established by three independent variables, namely flight time, time substitution variable, and height. Three onboard navigation techniques are created by transforming the trajectory optimization issue into a form that can be solved by successive convexification algorithms. The comparative analysis shows that all three methods can solve the 6-DoF powered descent problem. Although the flight time must be known beforehand, the optimization with flight time as an independent variable has the maximum computing efficiency and the lowest fuel use. The other two optimizations can optimize the flight time, but both are sub-optimal solutions, and the computation time is greatly increased. The accuracy of the three methods is similar under the same number of discrete points. If successive convexification algorithms are used as the online guidance algorithms for power descent, problems such as how to determine the optimal flight time, approach the optimal fuel solution and shorten the calculation time still need to be further studied.
- six degrees of freedom /
- powered descent /
- autonomous guidance /
- convex optimization /
- optimal flight time

HTML全文

图 1 飞行器本体坐标系与着陆场坐标系示意图

Figure 1. Schematic diagram of the vehicle body coordinate system and the landing site coordinate system

下载: 全尺寸图片幻灯片

图 2 不同末端时间的仿真结果

Figure 2. Simulation results for different terminal times

下载: 全尺寸图片幻灯片

图 3 本体系下的推力（控制量与状态量不解耦）

Figure 3. Thrust under the body coordinate frame(control and state are coupled)

下载: 全尺寸图片幻灯片

图 4 2种自由时间优化对比

Figure 4. Comparison of two free-final-time optimizations

下载: 全尺寸图片幻灯片

图 5 改变时间归一化参数的仿真结果（以时间替代变量为自变量优化问题）

Figure 5. Simulation results of changing the time normalization parameters (Optimisation problem with time substitution variables as independent variables)

下载: 全尺寸图片幻灯片

图 6 改变时间归一化参数的仿真结果（以高度为自变量优化问题）

Figure 6. The simulation results of changing the time normalization parameters (Optimisation problem with height as independent variables)

下载: 全尺寸图片幻灯片

图 7 离散点数量对位置误差的影响

Figure 7. Effect of the number of discrete points on the position error

下载: 全尺寸图片幻灯片

图 8 离散点数量对姿态角误差的影响

Figure 8. Effect of the number of discrete points on the attitude angle error

下载: 全尺寸图片幻灯片

图 9 离散点数量对计算时间的影响

Figure 9. Effect of the number of discrete points on the computation time

下载: 全尺寸图片幻灯片

图 10 离散点数量对迭代次数的影响

Figure 10. Effect of the number of discrete points on the number of iterations

下载: 全尺寸图片幻灯片

表 1 仿真参数

Table 1. Simulation parameters

参数	数值
初始质量 ${m_{{\text{wet}}}}$ /kg	65 170
结构质量 ${m_{{\text{dry}}}}$ /kg	25 600
圆柱体底面半径R/m	1.85
圆柱体长底L/m	41.2
最大推力 ${T_{\max }}$ /N	845 000
最小推力 ${T_{\min }}$ /N	${{845\;000}} \times 0.4$
比冲 ${I_{{\text{sp}}}}$ /s	310
质心至推力作用点位置矢量 ${\boldsymbol {r}}_{\text{T}}$ /m	$[ \begin{array}{*{20}{c}} { - 20}&0&0 \end{array} ]$
大气密度 $\rho$ /(kg·m⁻³)	1.225
阻力系数 ${C_{{{\mathrm{d}}}}}$	1.3
参考面积 $S$ /m²	${\text{π}} {r^2},r = 1.85{\text{ m}}$

下载: 导出CSV

表 2 状态参数

Table 2. State parameters

状态参数	数值
初始位置 ${{\boldsymbol {r}}_0}$ /m	$[ \begin{array}{*{20}{c}} {5\;000}&{1\;000}&0 \end{array} ]$
初始速度 ${{\boldsymbol {v}}_0}$ /(m·s⁻¹)	$[ \begin{array}{*{20}{c}} { - 100}&{ - 10}&0 \end{array} ]$
初始姿态四元数 ${\boldsymbol {q}}_0$	${ [ \begin{array}{{20}{c}} 1&0&{\begin{array}{{20}{c}} 0&0 \end{array}} \end{array} ]}$
初始姿态角速度 ${{\text{ω}}_0}$ /（rad·s⁻¹）	$[ \begin{array}{*{20}{c}} 0&0&0 \end{array} ]$
末端位置 ${{\boldsymbol {r}}_{\text{f}}}$ /m	$[ \begin{array}{*{20}{c}} 0&0&0 \end{array} ]$
末端速度 ${{\boldsymbol {v}}_{\text{f}}}$ /(m·s⁻¹)	$[ \begin{array}{*{20}{c}} { - 1}&0&0 \end{array} ]$
末端姿态四元数 ${{\boldsymbol {q}}_{\text{f}}}$	$[ \begin{array}{{20}{c}} 1&0&{\begin{array}{{20}{c}} 0&0 \end{array}} \end{array} ]$
末端姿态角速度 ${{\text{ω}}_{\text{f}}}$ /（rad·s⁻¹）	$[ \begin{array}{*{20}{c}} 0&0&0 \end{array} ]$
路径角 $\gamma$ /(°)	4
最大姿态角 ${\theta _{\max }}$ /(°)	30
最大姿态角速度 ${\omega _{\max }}$ /((°)·s⁻¹）	5
最大推力摆角 ${\delta _{\max }}$ /(°)	20

下载: 导出CSV

表 3 固定时间序列凸优化参数

Table 3. Fixed time sequential convex optimization parameters

参数	数值
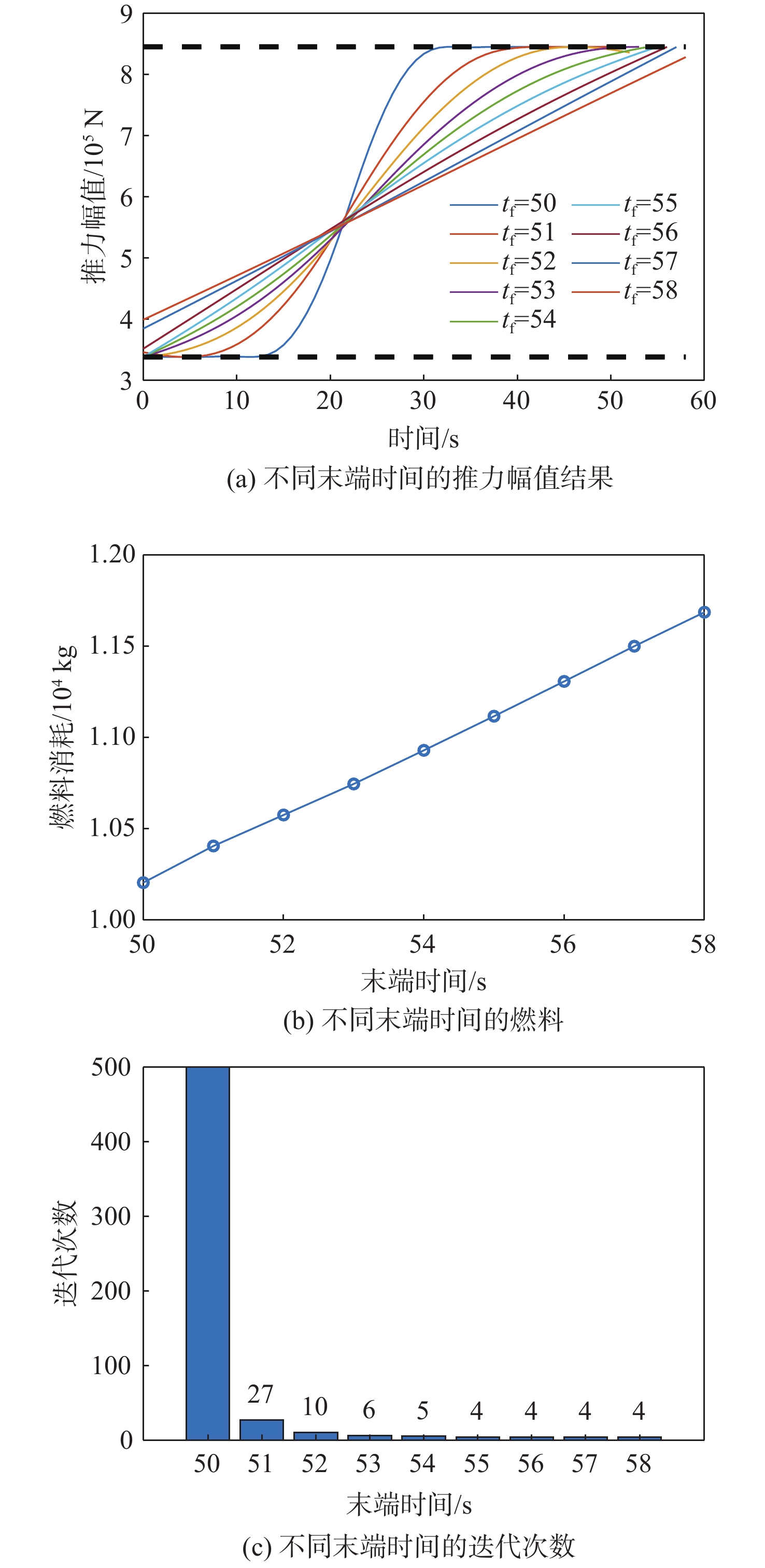
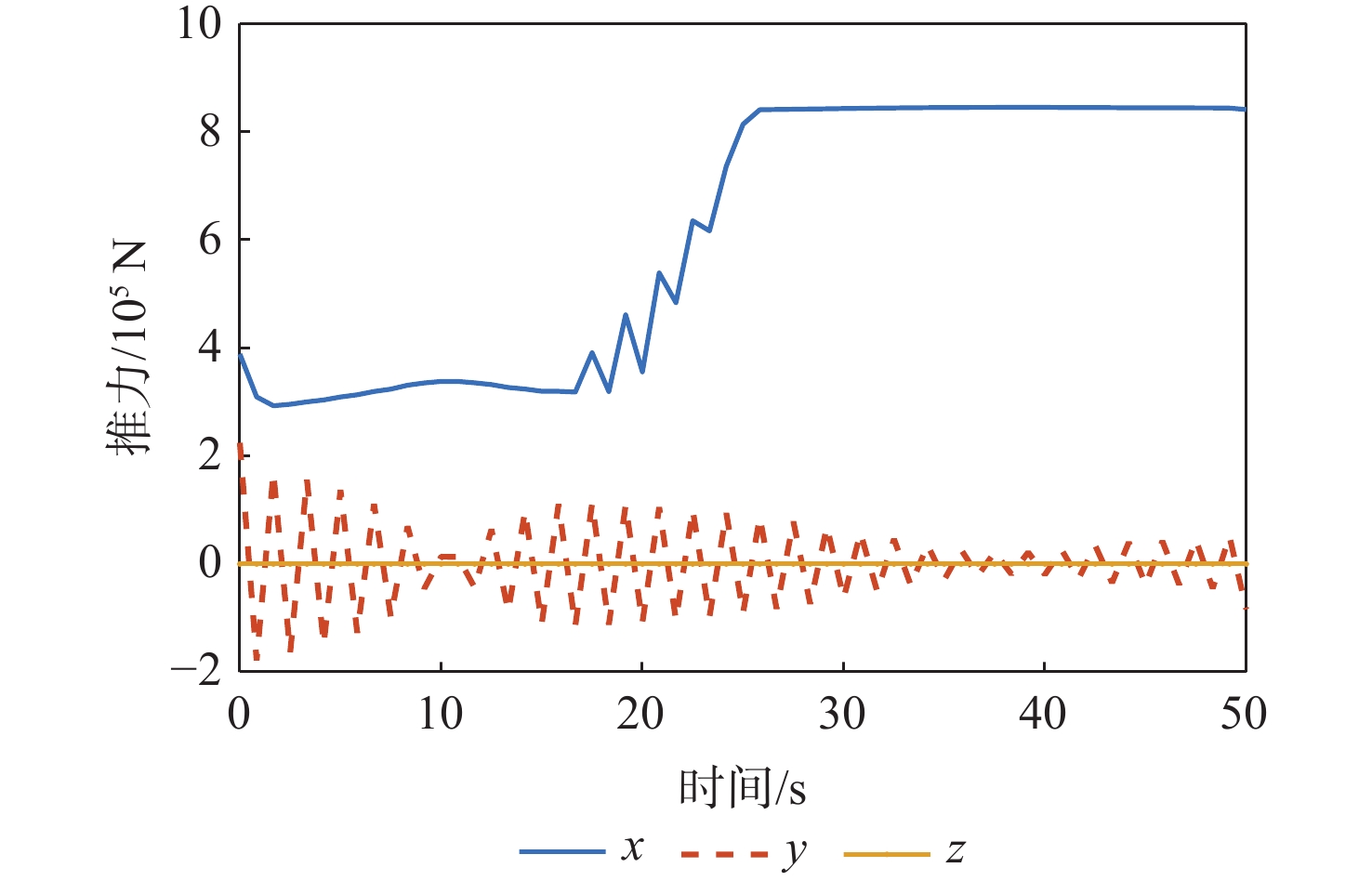
时间 ${t_{\text{f}}}$ /s	$50,51,\cdots ,58$
归一化距离 ${l_{\text{s}}}$ /m	5 000
归一化时间 ${t_{\text{s}}}$ /s	$50,51,\cdots ,58$
归一化推力 ${T_{\text{s}}}$ /N	845000
离散点个数 $K$	60
信任域罚函数系数 ${w_{\boldsymbol{\eta}}}$	1
线性化误差罚函数系数 ${w_{\boldsymbol{\kappa}}}$	10⁴
最大迭代次数 ${i_{\max }}$	500
信任域误差限 ${\varepsilon _{\boldsymbol{\eta}}}$	10⁻⁴
线性化误差限 ${\varepsilon _{\boldsymbol{\kappa}}}$	10⁻⁸

下载: 导出CSV

表 4 不同末端时间着陆误差

Table 4. Landing error for different terminal times

末端时间/s	位置误差/m	速度误差/(m·s⁻¹)	姿态角误差/(°)	角速度误差/((°)·s⁻¹）
50	256.94	19.80	4.06	0.046 2
51	95.81	7.40	1.52	0.024
52	55.59	4.29	0.87	0.014 8
53	45.27	3.46	0.68	0.008 5
54	41.46	3.11	0.59	0.005 6
55	38.25	2.83	0.52	0.003 2
56	35.00	2.56	0.46	0.001 4
57	34.03	2.46	0.43	0.000 87
58	34.39	2.43	0.42	0.000 769

下载: 导出CSV

表 5 序列凸优化参数（以时间替代变量为自变量）

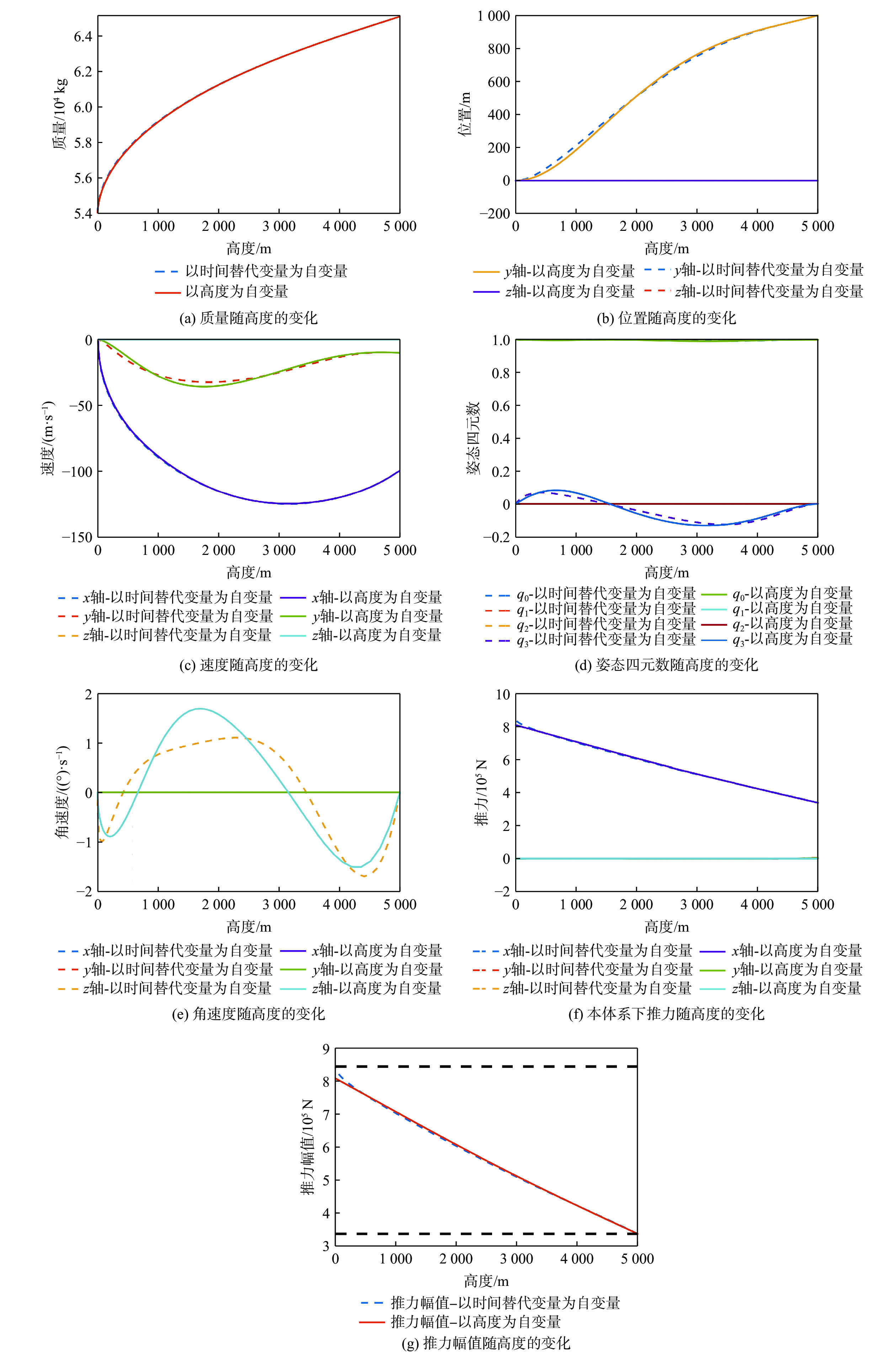
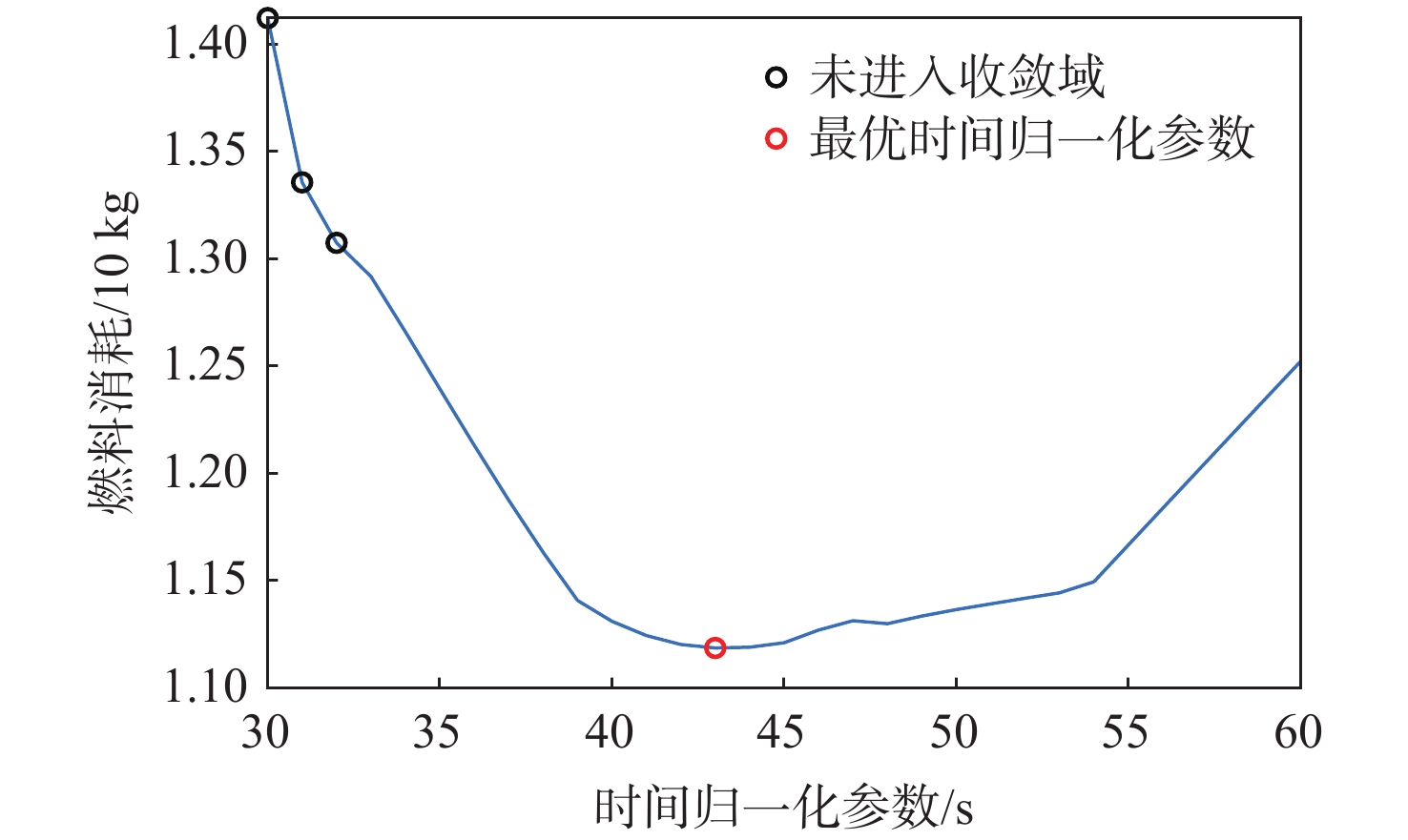
Table 5. Successive convex optimization parameters (with time substitution variables as independent variables)

参数	数值
归一化距离 ${l_{\text{s}}}$ /m	5 000
归一化时间 ${t_{\text{s}}}$ /s	43
归一化推力 ${T_{\text{s}}}$	845000
离散点个数 $K$	60
$\lambda$ 罚函数系数 ${w_{\lambda}}$	10
信任域罚函数系数 ${w_{\boldsymbol{\eta }}}$	0.1
线性化误差罚函数系数 ${w_{\boldsymbol{\kappa }}}$	10⁴
最大迭代次数 ${i_{\max }}$	500
信任域误差限 ${\varepsilon _{\boldsymbol{\eta}}}$	10⁻⁴
线性化误差限 ${\varepsilon _{\boldsymbol{\kappa }}}$	10⁻⁸

下载: 导出CSV

表 6 序列凸优化参数（以高度为自变量）

Table 6. Successive convex optimization parameters(with height as independent variables)

参数	数值
归一化距离 ${l_{\text{s}}}$ /m	5 000
归一化时间 ${t_{\text{s}}}$ /s	12
归一化推力 ${T_{\text{s}}}$	845000
离散点个数K	60
信任域罚函数系数 ${w_{\boldsymbol{\eta }}}$	1
线性化误差罚函数系数 ${w_{\boldsymbol{\kappa }}}$	10⁴
最大迭代次数 ${i_{\max }}$	500
信任域误差限 ${\varepsilon _{\boldsymbol{\eta }}}$	10⁻⁴
线性化误差限 ${\varepsilon _{\boldsymbol{\kappa }}}$	10⁻⁸

下载: 导出CSV

表 7 自由时间优化末端着陆误差对比

Table 7. Comparison of landing errors for free-final-time optimization

自变量	燃料消耗/kg	位置误差/m	速度误差/(m·s⁻¹)	姿态角误差/(°)	角速度误差/((°)·s⁻¹）
时间替代变量	11185.7	35.1070	2.6270	0.4812	0.0041
高度	11008.0	39.0043	5.9782	0.47074	0.11541

下载: 导出CSV

表 8 计算时间对比

Table 8. Comparision of computation time

优化方法	迭代次数	平均单次迭代时间/s	总时间/s
固定时间优化（55 s）	4	0.62	2.46
自由时间优化	4	7.64	30.57
以高度为自变量优化	50	0.44	21.82
自由时间优化（*）	1	7.80	2.46+7.80
以高度为自变量优化（*）	33	0.41	2.46+13.45
注：带*仿真选取55 s固定时间优化结果作为初值。

下载: 导出CSV

参考文献(27)

[1]	SONG Z Y, WANG C, THEIL S, et al. Survey of autonomous guidance methods for powered planetary landing[J]. Frontiers of Information Technology & Electronic Engineering, 2020, 21(5): 652-674.
[2]	LIU X F, LU P, PAN B F. Survey of convex optimization for aerospace applications[J]. Astrodynamics, 2017, 1(1): 23-40. doi: 10.1007/s42064-017-0003-8
[3]	LU P, LIU X F. Autonomous trajectory planning for rendezvous and proximity operations by conic optimization[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(2): 375-389. doi: 10.2514/1.58436
[4]	TANG G, JIANG F H, LI J F. Fuel-optimal low-thrust trajectory optimization using indirect method and successive convex programming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(4): 2053-2066. doi: 10.1109/TAES.2018.2803558
[5]	邓雁鹏, 穆荣军, 彭娜, 等. 月面着陆动力下降段最优轨迹序列凸优化方法[J]. 宇航学报, 2022, 43(8): 1029-1039. doi: 10.3873/j.issn.1000-1328.2022.08.005 DENG Y P, MU R J, PENG N, et al. Sequential convex optimization method for lunar landing during powered descent phase[J]. Journal of Astronautics, 2022, 43(8): 1029-1039(in Chinese). doi: 10.3873/j.issn.1000-1328.2022.08.005
[6]	徐西宝, 白成超, 陈宇燊, 等. 月/火探测软着陆制导技术发展综述[J]. 宇航学报, 2020, 41(6): 719-729. doi: 10.3873/j.issn.1000-1328.2020.06.009 XU X B, BAI C C, CHEN Y S, et al. A survey of guidance technology for Moon/Mars soft landing[J]. Journal of Astronautics, 2020, 41(6): 719-729(in Chinese). doi: 10.3873/j.issn.1000-1328.2020.06.009
[7]	HARRIS M W, AÇıKMEŞE B. Maximum divert for planetary landing using convex optimization[J]. Journal of Optimization Theory and Applications, 2014, 162(3): 975-995. doi: 10.1007/s10957-013-0501-7
[8]	BLACKMORE L, ACIKMESE B, SCHARF D P. Minimum-landing-error powered-descent guidance for Mars landing using convex optimization[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1161-1171. doi: 10.2514/1.47202
[9]	ACIKMESE B, PLOEN S R. Convex programming approach to powered descent guidance for Mars landing[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1353-1366. doi: 10.2514/1.27553
[10]	PINSON R, LU P. Rapid generation of optimal asteroid powered descent trajectories via convex optimization[C]//Proceedings of the AAS/AIAA Astrodynamics Specialist Conference. Reston: AIAA, 2015.
[11]	PINSON R M, LU P. Trajectory design employing convex optimization for landing on irregularly shaped asteroids[J]. Journal of Guidance, Control, and Dynamics, 2018, 41(6): 1243-1256. doi: 10.2514/1.G003045
[12]	LIU X F, SHEN Z J, LU P. Entry trajectory optimization by second-order cone programming[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(2): 227-241. doi: 10.2514/1.G001210
[13]	SCHARF D P, AÇIKMEŞE B, DUERI B, et al. Implementation and experimental demonstration of onboard powered-descent guidance[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(2): 213-229. doi: 10.2514/1.G000399
[14]	SZMUK M, ACIKMESE B, BERNING A W. Successive convexification for fuel-optimal powered landing with aerodynamic drag and non-convex constraints[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2016.
[15]	WANG Z B, GRANT M J. Constrained trajectory optimization for planetary entry via sequential convex programming[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(10): 2603-2615. doi: 10.2514/1.G002150
[16]	MAO Y Q, SZMUK M, AÇıKMEŞE B. Successive convexification of non-convex optimal control problems and its convergence properties[C]// Proceedings of the IEEE 55th Conference on Decision and Control. Piscataway: IEEE Press, 2016: 3636-3641.
[17]	LIU X F, LU P. Solving nonconvex optimal control problems by convex optimization[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 750-765. doi: 10.2514/1.62110
[18]	YANG R Q, LIU X F. Fuel-optimal powered descent guidance with free final-time and path constraints[J]. Acta Astronautica, 2020, 172: 70-81. doi: 10.1016/j.actaastro.2020.03.025
[19]	SZMUK M, EREN U, ACIKMESE B. Successive convexification for Mars 6-DoF powered descent landing guidance[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2017.
[20]	SZMUK M, ACIKMESE B. Successive convexification for 6-DoF Mars rocket powered landing with free-final-time [C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2018.
[21]	REYNOLDS T P, SZMUK M, MALYUTA D, et al. Dual quaternion-based powered descent guidance with state-triggered constraints[J]. Journal of Guidance, Control, and Dynamics, 2020, 43(9): 1584-1599. doi: 10.2514/1.G004536
[22]	KAMATH A G, ELANGO P, MCEOWEN S, et al. Customized real-time first-order methods for onboard dual quaternion-based 6-DoF powered-descent guidance[C]//Proceedings of the AIAA SCITECH 2023 Forum. Reston: AIAA, 2023.
[23]	CHEN Y S, YANG G W, WANG L, et al. A fast algorithm for onboard atmospheric powered descent guidance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 6112-6123.
[24]	MAO Y Q, DUERI D, SZMUK M, et al. Successive convexification of non-convex optimal control problems with state constraints[J]. IFAC-PapersOnLine, 2017, 50(1): 4063-4069. doi: 10.1016/j.ifacol.2017.08.789
[25]	MALYUTA D, REYNOLDS T, SZMUK M, et al. Discretization performance and accuracy analysis for the rocket powered descent guidance problem[C]//Proceedings of the AIAA Scitech 2019 Forum. Reston: AIAA, 2019.
[26]	MATTINGLEY J, BOYD S. CVXGEN: A code generator for embedded convex optimization[J]. Optimization and Engineering, 2012, 13(1): 1-27. doi: 10.1007/s11081-011-9176-9
[27]	TOH K C, TODD M J, TÜTÜNCÜ R H. On the implementation and usage of SDPT3–A Matlab software package for semidefinite-quadratic-linear programming, version 4.0[M]// Handbook on Semidefinite, Conic and Polynomial Optimization. Berlin: Springer, 2011: 715-754.