Stability control of vehicles powered by non-pneumatic wheels based on robust optimal sliding mode
-
摘要:
机械弹性电动轮是一种新式非充气轮胎，具有防爆、防胎刺等优点，文章中基于匹配该电动轮的分布式汽车，提出了一种鲁棒最优滑模(ROSM)控制策略，以便提高车辆转向时的横摆稳定性。针对线性二自由度模型，为实现最优控制采用线性二自由度调节器(LQR)，输出初始的附加横摆力矩；考虑到实际行驶中车辆状态是复杂的非线性系统，建立包含不确定参数的车辆动力学模型，并在初始最优控制量的基础上设计一种鲁棒积分滑模控制器，该控制器对不确定参数与外部干扰具有良好的鲁棒性，且仍能实现最优控制；通过MATLAB/Simulink和Carsim联合仿真，对控制方法进行仿真验证，结果表明：双移线工况中，ROSM控制下横摆角速度的平均绝对误差(MAE)、均方根误差(RMSE)与LQR控制相比分别下降了63.83%、65.33%；蛇形工况中，其分别降低了58.38%、60.02%。
Abstract:Mechanical elastic electric wheel is a new type of non-pneumatic tire, which has the advantages of explosion-proof, anti-puncture, etc. In this paper, based on the distributed vehicle matching with the electric wheel, a robust optimal sliding mode (ROSM) control strategy is proposed to improve the yaw stability of the vehicle. Firstly, the initial additional yaw moment is calculated using a linear 2-DOF regulator (LQR) control rule for the linear 2-DOF model. Secondly, considering the complex nonlinearity of the actual vehicle system, a vehicle dynamics model with uncertain parameters is established. And a robust integral sliding mode controller is designed on the basis of the initial optimal control law. The improved controller has good robustness to uncertain parameters and external disturbances, which could still achieve optimal control effectiveness. Finally, the control scheme is verified by co-simulations of MATLAB/Simulink and Carsim. The findings demonstrate that, in the simulation of double lane change, the mean absolute error (MAE) and root mean square error (RMSE) of the yaw rate under ROSM control are decreased by 63.83% and 65.33%, respectively, in comparison to LQR control. As for the serpentine condition, they respectively decreased by 58.38% and 60.02%.
-
Key words:
- non-pneumatic wheels /
- direct yaw moment /
- LQR /
- robust optimal control /
- sliding mode control
-
随着世界各国对环境的日渐重视，不少欧洲国家相继颁布未来燃油车禁售令，纯电动汽车的应用与普及已成为必然趋势。分布式轮毂电机驱动作为新兴的驱动结构，具有四轮转矩独立可控、结构紧凑、智能网联适配性强等优点，极大地提高了车辆稳定性控制的灵活性。
车轮是保证分布式电动车稳定行驶的基础部件，传统充气轮胎在恶劣路面有穿刺、爆胎的风险，南航赵又群团队[1]研制的机械弹性电动轮（mechanical elastic electric wheel，MEEW）具有防爆、防胎刺等优点，并在重型卡车上完成了实车验证。Deng等[2]对机械弹性车轮的结构、力学特性进行了深入研究，张陈曦等[3]充分考虑了该车轮衍生的免充气轮胎的径向刚度特性，运用半逆解法优化尺寸设计，提高了车辆行驶的平顺性；张晨等[4]运用疲劳试验方法对该车轮的耐久性进行了研究。
直接横摆力矩控制(direct yaw moment control，DYC)是辅助驾驶中控制车辆稳定性的常见方法，其关键是准确计算出附加横摆力矩值，常用算法包括模糊控制[5]、PID控制[6]、滑模控制[7]和模型预测控制[8]。Liu 等[9]构建了基于无味粒子滤波观测器的前馈系统，通过实时观测车辆横摆角速度与质心侧偏角，计算出精确的附加横摆力矩，提高了车辆稳定行驶的跟踪精度。林棻等[10]采用分层控制器控制车辆的横摆稳定性，上层基于积分联合终端的滑模控制器，获得期望的横摆力矩，下层基于纵向力轴载比例合理分配力矩。Zhu 等[11]设计了一种基于粒子群优化的非线性模型预测控制方法，控制精度较高，但计算复杂耗时，难以满足车辆辅助驾驶的实时性要求。
滑模控制由于其实现简单、响应迅速、鲁棒性强等优点，广泛应用于系统工程中的非线性扰动控制。Yan等[12]、Rangel等[13]为了使水下车辆在复杂多变的环境中跟踪三维轨迹，设计了基于积分滑模的鲁棒控制器。Norsahperi等[14]提出了一种改进的最优积分滑模控制策略，使得机器人在耦合效应、参数变化和外界干扰下仍能保持较高的跟踪性能。Xu 等[15]针对分布式电动车动力学参数不确定与扰动问题，提出了最优控制与高阶滑模相结合的鲁棒控制算法。丛森森等[16]针对底盘横纵向稳定性问题，以滑模面构建了车辆动态稳定域，滑模动态控制器始终控制车辆维持在稳定状态，保证行驶的安全性。梁宝钰等[17]为了保持车辆在侧风干扰下行驶的稳定性，基于滑模理论计算出汽车高速行进时所需的附加横摆力矩，有效提高了车辆抗侧风干扰能力。陈特等[18]基于非奇异终端滑模控制，在状态观测基础上实现了主动前轮转向功能，大大提高了轨迹跟踪的精度。
在上述研究基础上，本文基于匹配机械弹性车轮的分布式汽车，提出了一种鲁棒最优滑模[12-19] (ROSM)的控制策略，以便提高车辆转向时的横摆稳定性。首先，基于线性二自由度车辆模型，设计线性二自由度调节器(LQR)控制器，输出初始最优附加横摆力矩值；其次，由于机械弹性车轮实际行驶中侧偏刚度存在不确定性摄动，且路面状态复杂多变，从而引入参数不确定的非线性动力学模型，在此基础上设计了一种基于初始最优控制量的鲁棒最优积分滑模控制策略，该策略不仅可以实现最优控制目标，且对不确定参数与外部干扰具有良好的鲁棒性；最后基于二次规划，将附加横摆力矩合理分配至各轮胎。
1. 动力学模型搭建
1.1 车辆动力学模型建立
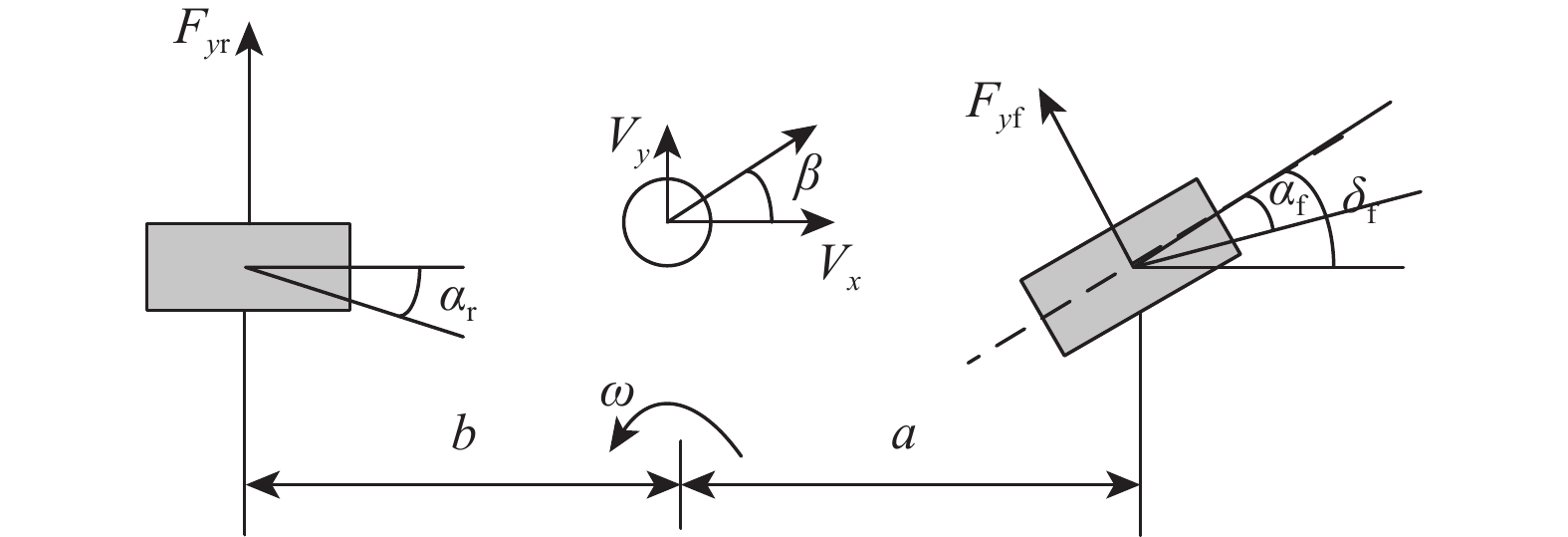
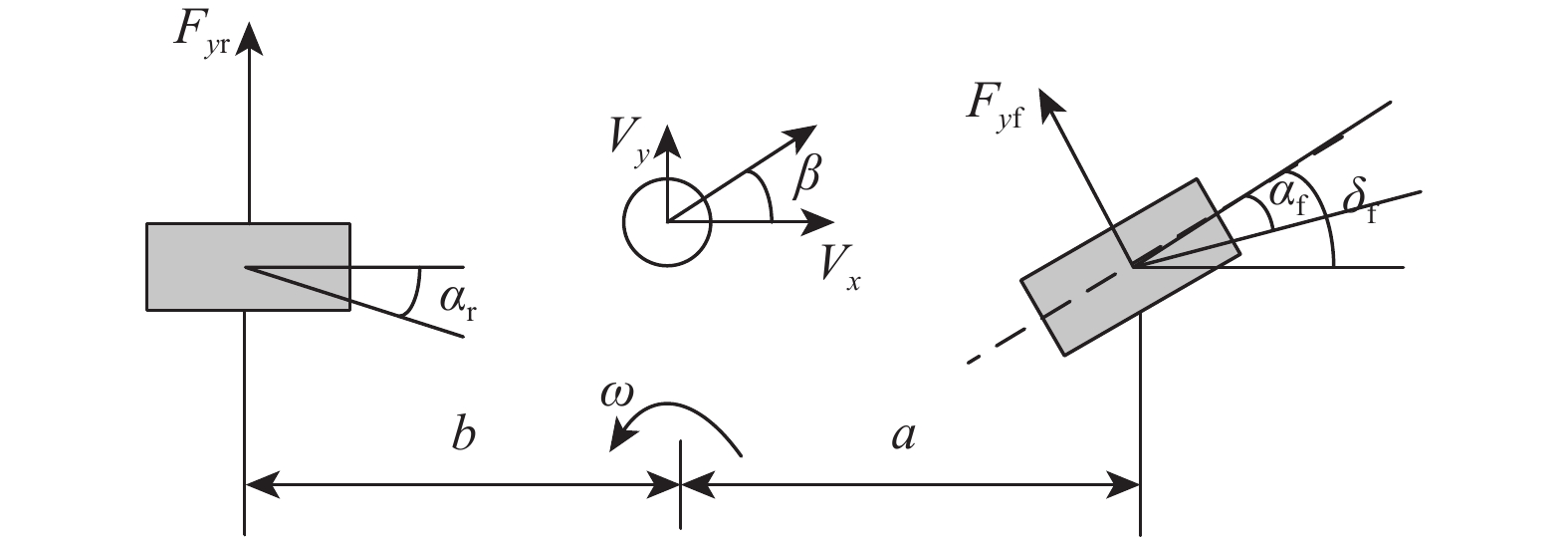
本文选取理想的车辆二自由度模型作为参考模型，如图1所示。
其动力学方程为
[˙β˙ω]=[kf+krmVxakf−bkrmVx2−1akf−bkrIza2kf+b2krIzVx][βω]+[−kfmVx−akfIz]δf (1) 式中：β为质心侧偏角；ω为横摆角速度；Vx为车辆纵向车速；a、b为车辆质心至前、后轴距离；m为整车质量；Iz为横摆转动惯量；δf为前轮转角；kf、kr为车辆在理想状态下的前、后轴侧偏刚度。
一般而言，理想质心侧偏角可以取为0，而期望的横摆角速度为
ωd=Vx/L1+KsVx2δf (2) 式中：L为车辆前后轴距；Ks为车辆不足转向参数，Ks = mL2(akr−bkf)。
由于轮胎附着极限的存在，理想横摆角速度有一个上限值，可以表示为
ωm=μgVx (3) 式中：μ为路面附着系数。
综上，理想横摆角速度和质心侧偏角可表示为
{ωd={ω|ω|<ωmωmsign(ω)|ω|>ωm βd=0 (4) 1.2 非充气轮胎动力学模型
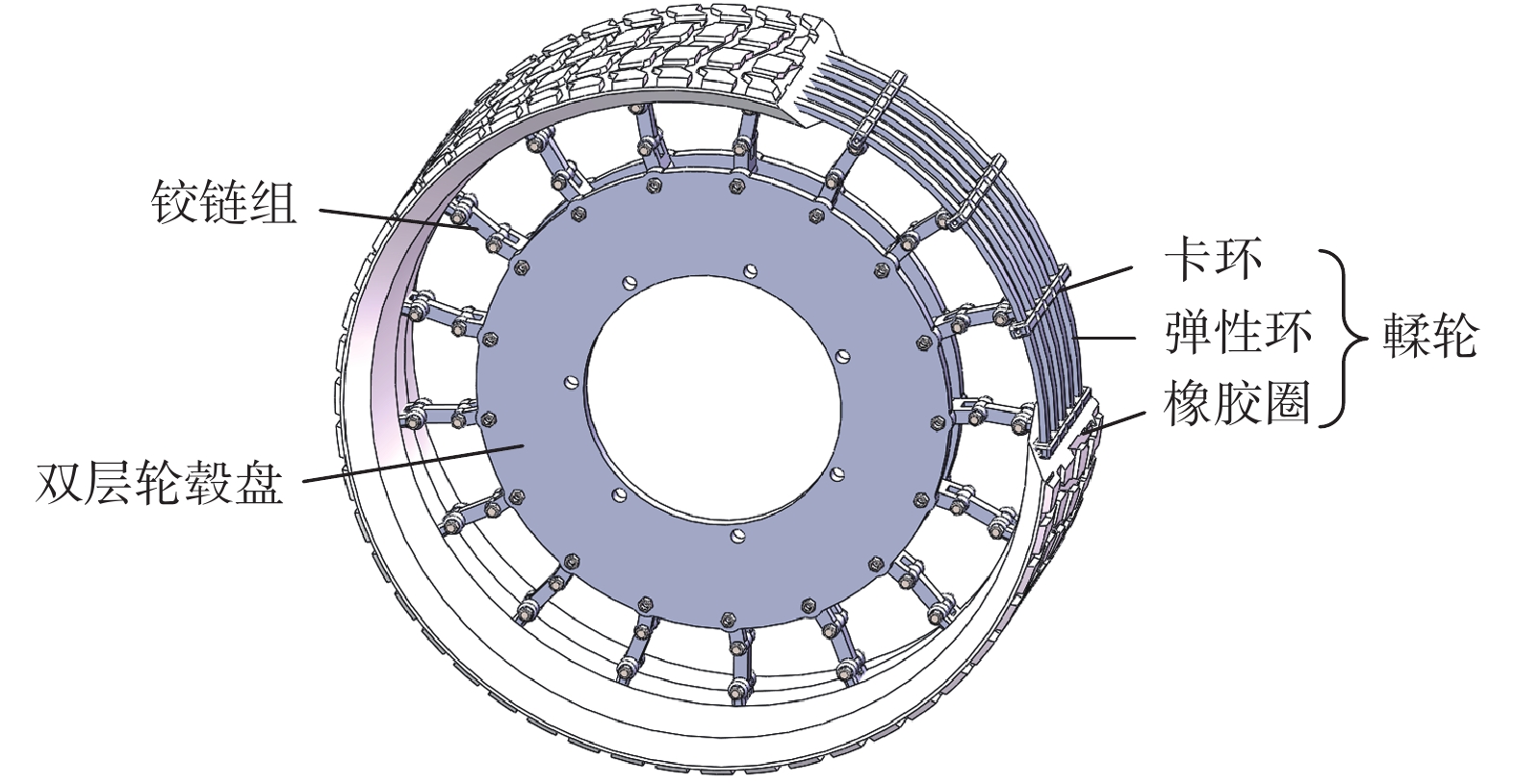
南航赵又群团队研制的机械弹性电动轮（MEEW）[20]具有防爆、防胎刺等优点，能够承受较大的径向载荷，选取该非充气轮胎作为本文的研究对象。MEEW结构与试验台如图2、图3所示，MEEW由轮毂、铰链组、輮轮组成，橡胶层经硫化处理覆在卡环、弹性环上形成輮轮。
为具象表达MEEW的轮胎特性，引入“魔术公式”[21]，分别建立MEEW纵向力Fx与侧向力Fy的力学模型。
{Fx=Dxsin[Cxarctan(Bxϕx)]+Svxϕx=(1−Ex)λ+(Ex/Bx)arctan(Bxλ) (5) {Fy=Dysin[Cyarctan(Byϕy)]+Svyϕy=(1−Ey)α+(Ey/By)arctan(Byα) (6) 式中：Bx、By分别为纵向力、侧向力的刚度因子；Cx、Cy分别为纵向力、侧向力曲线的形状因子；Dx、Dy分别为纵向力、侧向力的峰值因子；Ex、Ey分别为纵向力、侧向力曲线的曲率因子；λ为纵向滑移率，α为轮胎的侧偏角；Svx为纵向力曲线的水平方向漂移，Svy为侧向力曲线的垂直方向漂移。具体为
{Bx=rx/(CxDx)Cx=b0Dx=b1F2z+b2Fzrx=(b3F2z+b4Fz)e−b5FzEx=b6F2z+b7Fz+b8 (7) {By=ry/(CyDy)Cy=a0Dy=a1F2z+a2Fzry=a3sin(2arctan(Fz/a4))Ey=a6Fz+a7 (8) 式中：Fz为MEEW承受的径向载荷；rx、ry分别为纵向力、侧向力曲线过原点的斜率。
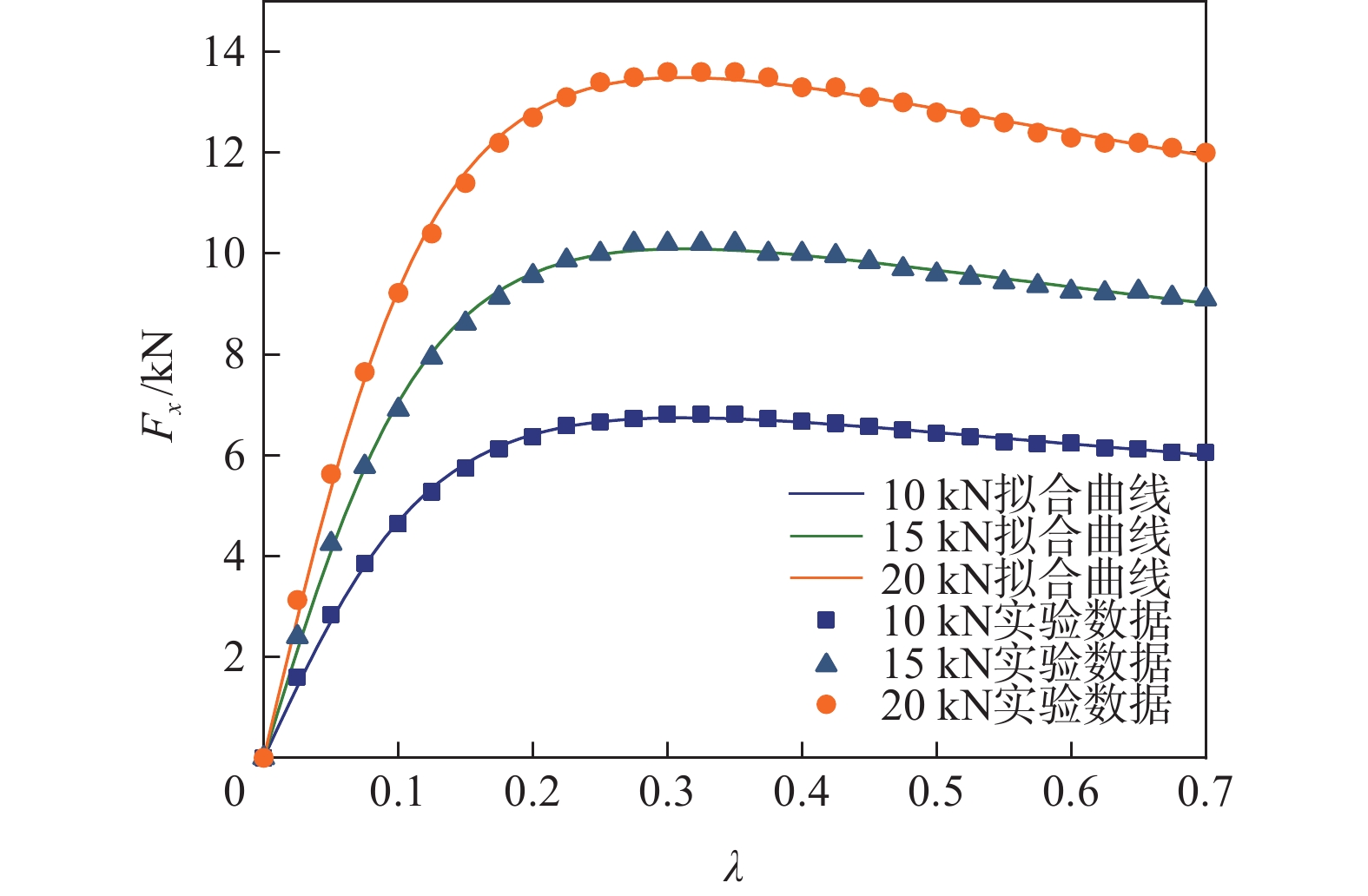
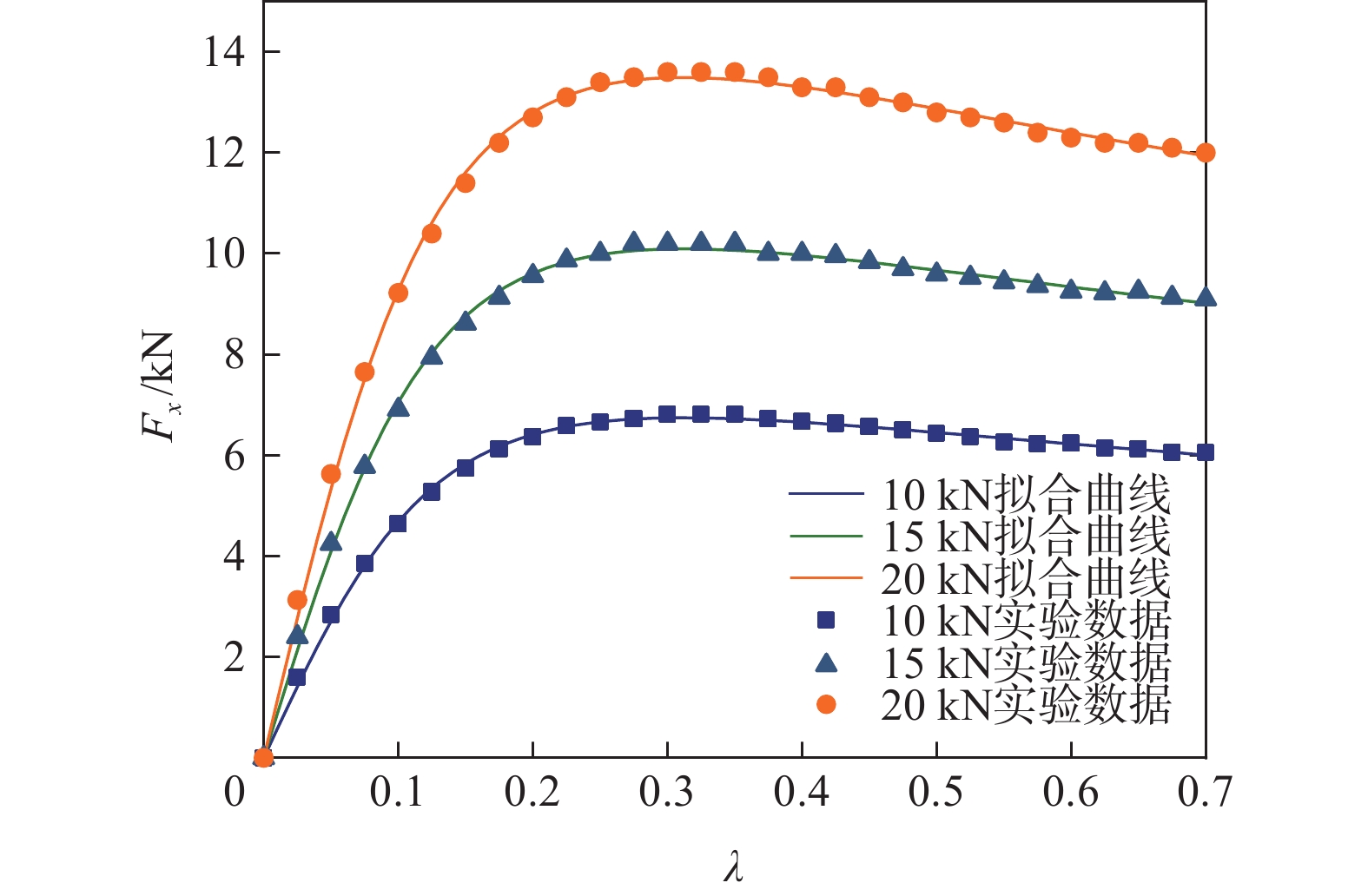
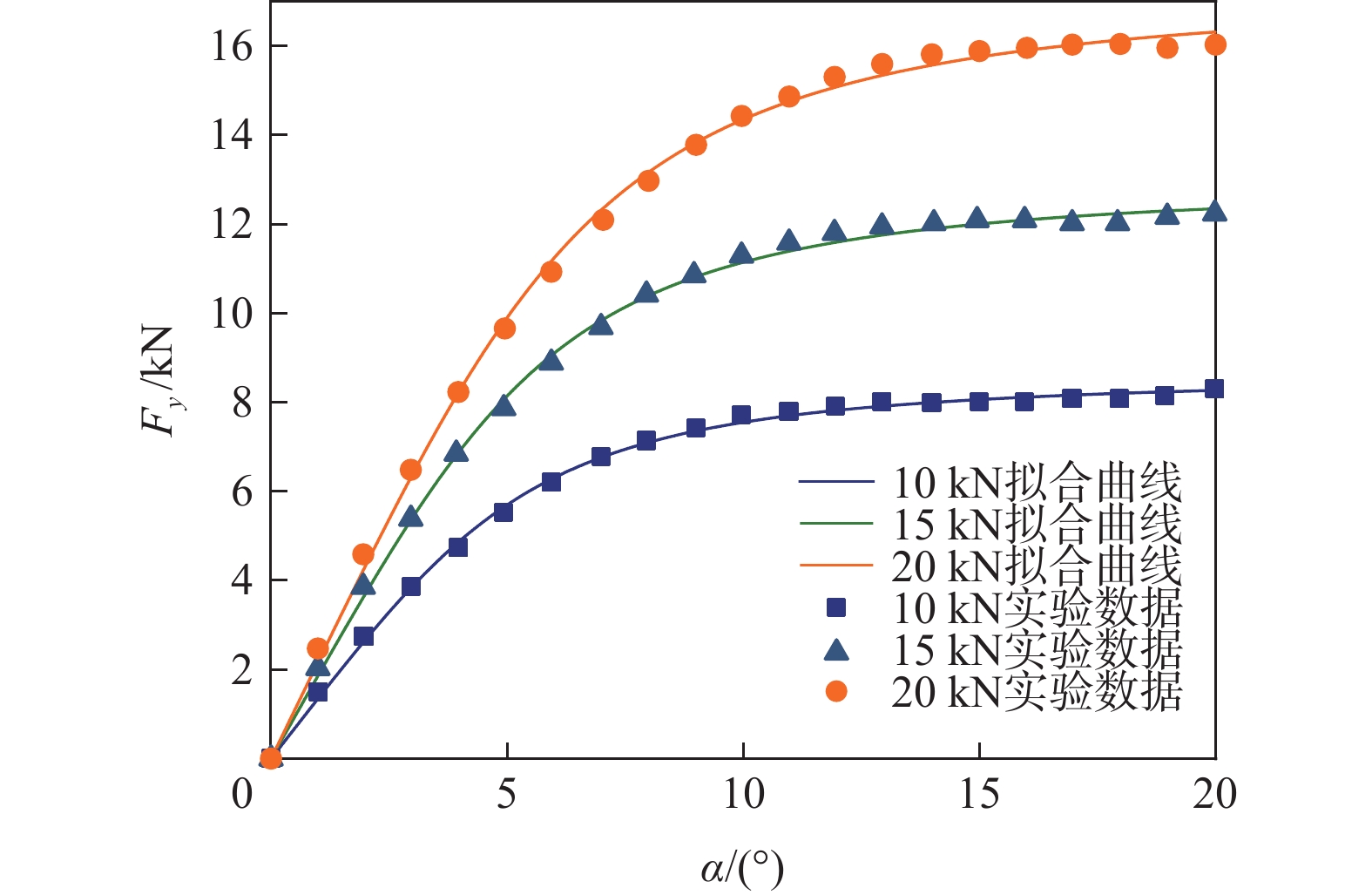
在样机实验中对MEEW分别施加10 kN、15 kN、20 kN的径向载荷，并拟合实验结果数据，得到纵向力Fx与侧向力Fy的拟合曲线如图4、图5所示，魔术轮胎公式参数辨识结果如表1所示。
表 1 MEEW参数拟合结果Table 1. Parameter fitting resultsFz/kN Bx Cx Dx Ex By Cy Dy Ey 10 4.9477 1.7216 6795.14 0.4541 0.1364 1.2682 8150 − 0.0988 15 3.9323 2.1252 10103.66 0.8742 0.1271 1.2682 12200 − 0.0952 20 4.8070 1.7390 13495.56 0.4411 0.1116 1.2682 16310 − 0.0914 2. 基于鲁棒最优滑模的上层控制器设计
2.1 基于线性二自由度模型的LQR控制方法
轮胎侧偏特性在非线性区域时，轮胎侧偏刚度也随着侧偏角的增大而不断变化，通常为简化问题，假使其依旧保持原有的等效侧偏刚度，本节基于线性二次型(LQR)设计直接横摆力矩控制器[22]。基于线性二自由度模型，理想的质心侧偏角与横摆角速度为
[˙βd˙ωd]=[kf+krmVxakf−bkrmVx2−1akf−bkrIza2kf+b2krIzVx][βdωd]+[−kfmVx−akfIz]δf (9) 为保持车身稳定，轮毂电机驱动对四轮施加直接横摆力矩，总附加横摆力矩ΔM作用后，动力学方程更新为
[˙β˙ω]=[kf+krmVxakf−bkrmVx2−1akf−bkrIza2kf+b2krIzVx][βω]+[−kfmVx−akfIz]δf+[01Iz]ΔM (10) 定义理想质心侧偏角与实际响应值的差为Δβ，理想横摆角速度与实际响应值的差为Δω，具体为
{Δβ=βd−βΔω=ωd−ω (11) 式(9)与式(10)相减得
[Δ˙βΔ˙ω]=[kf+krmVxakf−bkrmVx2−1akf−bkrIza2kf+b2krIzVx][ΔβΔω]+[0−1Iz]ΔM (12) 令A=[kf+krmVxakf−bkrmVx2−1akf−bkrIza2kf+b2krIzVx]，B=[0−1Iz]，X=[ΔβΔω]T ，U=ΔM，则式(12)可化成标准形式：
˙X=AX+BU (13) 为消除误差，求出附加横摆力矩最优解U∗，基于LQR理论设计控制方程：
{min (14) 式中：{\boldsymbol {K}}为反馈系数矩阵， {{\boldsymbol {Q}}_{\text{k}}} 矩阵能使系统误差快速逼近0，{{\boldsymbol {R}}_{\text{k}}}矩阵限制系统最大量，避免输出超出轮毂电机负载的横摆力矩。 {{\boldsymbol {P}}_{\text{k}}} 为Riccati方程的解，Riccati方程为
\begin{split} &{{\boldsymbol {A}}^{{\mathrm{T}}}}{{\boldsymbol {P}}_{\text{k}}} + {{\boldsymbol {P}}_{\text{k}}}{\boldsymbol {A}} + {{\boldsymbol {Q}}_{\text{k}}} - {{\boldsymbol {P}}_{\text{k}}}{\boldsymbol {BR}}_{\text{k}}^{{ - 1}}{{\boldsymbol {B}}^{{\mathrm{T}}}}{{\boldsymbol {P}}_{\text{k}}} = \\ &\quad\quad {{\boldsymbol {A}}^{{\mathrm{T}}}}{{\boldsymbol {P}}_{\text{k}}} + {{\boldsymbol {P}}_{\text{k}}}{\boldsymbol {A}} + {{\boldsymbol {Q}}_{\text{k}}} - {{\boldsymbol {P}}_{\text{k}}}{\boldsymbol {BK}} = {{\boldsymbol{0}}} \end{split} (15) 为证明LQR控制的稳定性，定义李雅普诺夫函数为
V({\boldsymbol {X}}) = {{\boldsymbol {X}}^{\text{T}}}{{\boldsymbol {P}}_{\text{k}}}{\boldsymbol {X}} > 0 (16) 对V(X)求导得
\dot V({\boldsymbol {X}}) = {{\boldsymbol {\dot X}}^{\text{T}}}{{\boldsymbol {P}}_{\text{k}}}{\boldsymbol {X}} + {{\boldsymbol {X}}^{\text{T}}}{{\boldsymbol {P}}_{\text{k}}}{\boldsymbol {\dot X}} (17) 当 U = {U^ * } 时，
{\boldsymbol {\dot X}} = {\boldsymbol {AX}} + {\boldsymbol {B}}( - {\boldsymbol {KX}}) = ({\boldsymbol {A}} - {\boldsymbol {BK}}){\boldsymbol {X}} (18) 将上式代入式(17)，\dot V({\boldsymbol {X}})可更新为
\begin{split} & \dot V({\boldsymbol {X}}) = {\left( {{\boldsymbol {AX}} - {\boldsymbol {BKX}}} \right)^{\text{T}}}{{\boldsymbol {P}}_{\text{k}}}{\boldsymbol {X}} + {{\boldsymbol {X}}^{\text{T}}}{{\boldsymbol {P}}_{\text{k}}}\left( {{\boldsymbol {AX}} - {\boldsymbol {BKX}}} \right) =\\ &\quad\quad {{\boldsymbol {X}}^{\text{T}}}\left( {{{\boldsymbol {P}}_{\text{k}}}{\boldsymbol {A}} + {{\boldsymbol {A}}^{\text{T}}}{{\boldsymbol {P}}_{\text{k}}} - {{\boldsymbol {P}}_{\text{k}}}{\boldsymbol {BK}} - {\boldsymbol {K}}_{}^{\text{T}}{{\boldsymbol {B}}^{\text{T}}}{{\boldsymbol {P}}_{\text{k}}}} \right){\boldsymbol {X}} =\\ &\quad\quad {{\boldsymbol {X}}^{\text{T}}}\left( { - {{\boldsymbol {Q}}_{\text{k}}} - {\boldsymbol {K}}_{}^{\text{T}}{{\boldsymbol {B}}^{\text{T}}}{{\boldsymbol {P}}_{\text{k}}}} \right){\boldsymbol {X}} =\\ &\quad\quad {{\boldsymbol {X}}^{\text{T}}}\left( { - {{\boldsymbol {Q}}_{\text{k}}} - {{\left( {{{\boldsymbol {B}}^{\text{T}}}{{\boldsymbol {P}}_{\text{k}}}} \right)}^{\text{T}}}{\boldsymbol {R}}_{\text{k}}^{ - 1}\left( {{{\boldsymbol {B}}^{\text{T}}}{{\boldsymbol {P}}_{\text{k}}}} \right)} \right){\boldsymbol {X}} < 0 \end{split} (19) 根据李雅普诺夫稳定性理论， \dot V({\boldsymbol{X}}) 负定，基于LQR的闭环动态控制系统趋于稳定。
2.2 基于非线性二自由度模型的鲁棒最优滑模控制
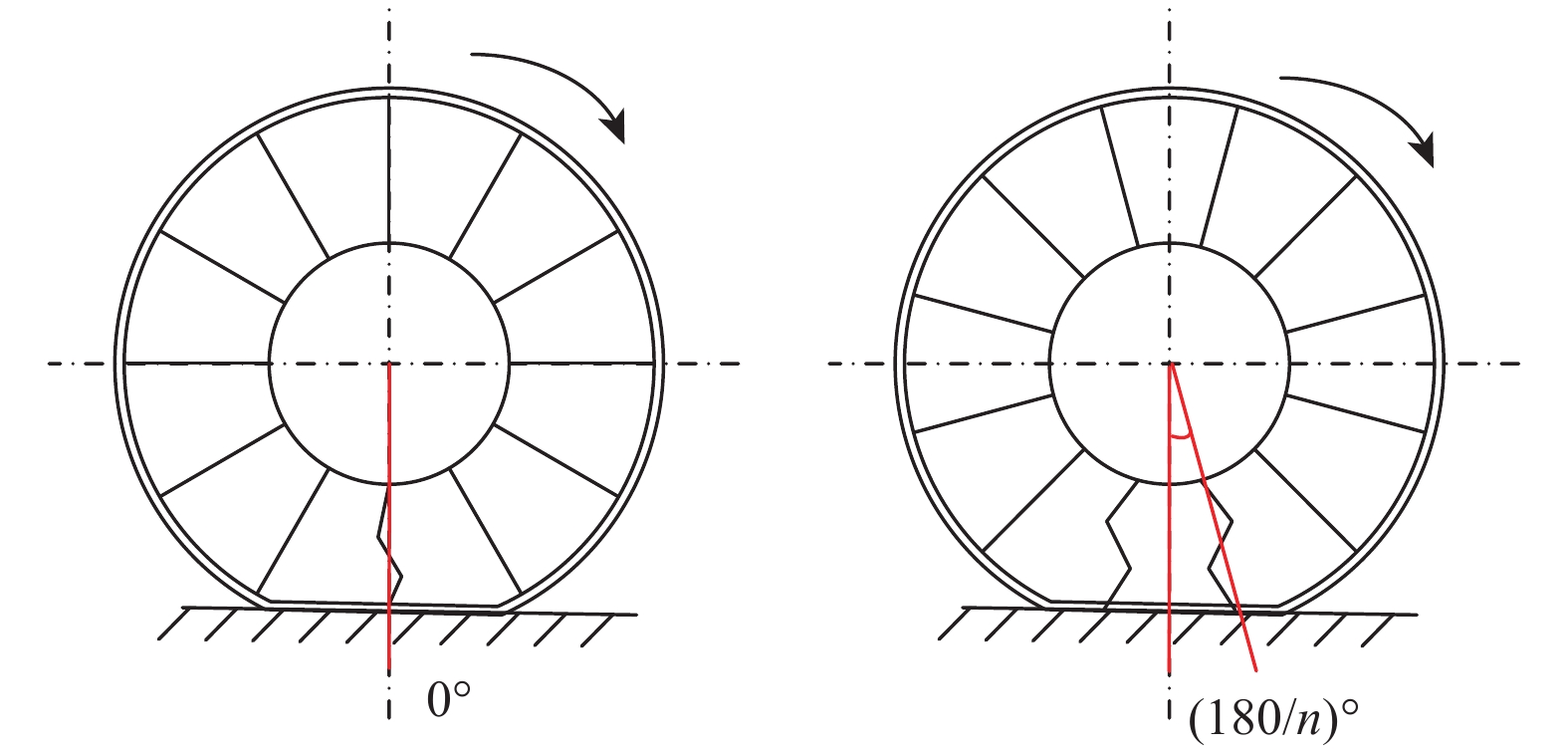
实际行驶中，车辆轮胎是一个复杂的非线性系统。与普通充气轮胎通过胎压向地面传递力不同，机械弹性电动轮的接地状态复杂多变，是由铰链组挤压弹性环来实现触地区域力的传递。如图6所示，假设轮胎的扁平程度不变，触地区域中线与铰链最小夹角变化范围为0～(180/n)°（n为铰链组数），整个过程轮胎侧偏刚度一直变化[23]且摄动程度高于普通轮胎，因而基于线性模型的稳定性控制缺乏准确性与鲁棒性。
考虑轮胎侧偏刚度、路面状态等因素的变化，将式(13)更新为非线性二自由度模型如下：
{\boldsymbol {\dot X'}} = ({\boldsymbol {A}} + \Delta {\boldsymbol {A}}){\boldsymbol {X}} + ({\boldsymbol {B}} + \Delta {\boldsymbol {B}})U + {\boldsymbol {N}} (20) 为表征参数的不确定性，引入时变函数\Delta {\boldsymbol {A}}、\Delta {\boldsymbol {B}}；为描述随机的路面干扰，引入时变函数{\boldsymbol {N}}。针对该不确定车辆模型，若仍沿用前文线性模型下的LQR控制器，则无法保证车辆极限工况下稳定性的控制效果。对此本文设计了一种鲁棒最优滑模控制方法，与传统的滑模控制不同，积分滑模控制中避免了趋近阶段。因此，积分滑模的优点是控制系统总是从初始状态开始就在滑模表面上运行，可以实现整个动态响应过程的鲁棒性[24]。为该不确定模型设计积分滑模面，如下所示：
S(t) = {\boldsymbol {W}}({\boldsymbol {X'}}(t) - {\left. {{\boldsymbol {X}}(t)} \right|_{U = {U^ * }}}) (21) 式中，{\boldsymbol{W}}为常数矩阵，且满足：\left| {{\boldsymbol{WB}}} \right| \ne 0
对式(21)求导得
\begin{split} &\dot S(t) = {\boldsymbol {W}}(({\boldsymbol {A}} + \Delta {\boldsymbol {A}}){\boldsymbol {X}} + ({\boldsymbol {B}} + \Delta {\boldsymbol {B}})U + {\boldsymbol {N}} - ({\boldsymbol {A}} - {\boldsymbol {BK}}){\boldsymbol {X}})= \\ &\quad\quad {\boldsymbol {W}}(({\boldsymbol {A}} + {\boldsymbol {BK}}){\boldsymbol {X}} + ({\boldsymbol{B}} + \Delta {\boldsymbol {B}})U + {\boldsymbol {N}}) \end{split} (22) 为使切换函数滑动模态稳定，令\dot S(t) = 0，可得等效控制率：
\begin{split} &{U_{{\mathrm{eq}}}} = - {({\boldsymbol {W}}({\boldsymbol {B}} + \Delta {\boldsymbol {B}}))^{ - 1}} \cdot ({\boldsymbol {W}}(\Delta {\boldsymbol {A}} + {\boldsymbol {BK}}){\boldsymbol {X}} + {\boldsymbol {WN}})= \\ &\quad\quad - {({\boldsymbol {B}} + \Delta {\boldsymbol {B}})^{ - 1}} \cdot ((\Delta {\boldsymbol {A}} + {\boldsymbol {BK}}){\boldsymbol {X}} + {\boldsymbol {N}}) \end{split} (23) 将其代入不确定系统(20)得到：
\begin{split} & {\boldsymbol {\dot X'}} = ({\boldsymbol {A}} + \Delta {\boldsymbol {A}}){\boldsymbol{X}} + ({\boldsymbol {B}} + \Delta {\boldsymbol {B}}){U_{{\text{eq}}}} + {\boldsymbol {N}} =\\ &\quad\quad ({\boldsymbol {A}} + \Delta {\boldsymbol {A}}){\boldsymbol {X}} - ({\boldsymbol {B}} + \Delta {\boldsymbol {B}}){({\boldsymbol{B}} + \Delta {\boldsymbol {B}})^{ - 1}} \cdot\\ &\quad\quad ((\Delta {\boldsymbol {A}} + {\boldsymbol {BK}}){\boldsymbol {X}} + {\boldsymbol {N}}) + {\boldsymbol {N}} =\\ &\quad\quad ({\boldsymbol {A}} - {\boldsymbol {BK}}){\boldsymbol {X}} \end{split} (24) 可以看出，式(24)与式(18)一致，表明当不确定系统在所设计的积分滑模面(21)运行时，两者系统状态空间方程相同，未受不确定参数\Delta {\boldsymbol {A}}、\Delta {\boldsymbol {B}}、{\boldsymbol {N}}的影响，即在不确定系统下仍能实现式（14）中目标函数的优化，仍能实现最优控制。在此基础上构造滑模控制率：
\left\{\begin{aligned} & U = {U^ * } - {({\boldsymbol {WB}})^{ - 1}}f(x){{\mathrm{sgn}}} (s) =\\ &\quad\quad -{\boldsymbol {KX}} - {({\boldsymbol {WB}})^{ - 1}}f(x){{\mathrm{sgn}}} (s) \\ & f(x) = {\eta _1}\left\| {\left. {{\boldsymbol {WB}}} \right\|} \right.\left\| {\left. {\boldsymbol {X}} \right\|} \right. + {\eta _2}\left\| {\left. {{\boldsymbol {WB}}} \right\|} \right. + {\eta _3} \end{aligned}\right. (25) 式中： {\eta _1} 、 {\eta _2} 、 {\eta _3} 为给定大于0的常数。
为削弱抖振，用饱和函数 {\text{sat}}(s) 代替式(25)中的符号函数 {{\mathrm{sgn}}} (s) ，饱和函数表达式为
{\text{sat}}(s) = \left\{ \begin{aligned} &1\quad\quad\quad {s_2} > \varDelta \\ & s/\varDelta\quad\quad \left| {{s_2}} \right| \leqslant \varDelta \\ & - 1\quad\quad {s_2} < - \varDelta \end{aligned} \right. (26) 式中： \varDelta 为边界层厚度。
2.3 鲁棒最优滑模控制器稳定性证明
为证明鲁棒最优滑模控制的稳定性，定义李雅普诺夫函数为
V = \frac{1}{2}{S^2} (27) 对其求导得
\begin{split} &\dot V = S\dot S = S{\boldsymbol {W}}(({\boldsymbol {A}} + {\boldsymbol {BK}}){\boldsymbol {X}} + ({\boldsymbol {B}} + \Delta {\boldsymbol {B}})U + {\boldsymbol {N}}) =\\ &\quad\quad S{\boldsymbol {W}}(\Delta {\boldsymbol {AX}} + \Delta {\boldsymbol {B}}U + {\boldsymbol {N}}) + S{\boldsymbol {WB}}({\boldsymbol {KX}} + U) \end{split} (28) 在实际行车环境中，不确定项\Delta {\boldsymbol{A}}、\Delta {\boldsymbol{B}}、{\boldsymbol{N}}都是有界的，那么可以定义
\left\{ \begin{aligned} & {\Delta {\boldsymbol {A}}(t) = {\boldsymbol {B}}\Delta {\boldsymbol {A'}}(t)} \\ & {\Delta {\boldsymbol {B}}(t) = {\boldsymbol {B}}\Delta {\boldsymbol {B'}}(t)} \\ & {{\boldsymbol {N}}(t) = {\boldsymbol {B}}\Delta {\boldsymbol {N'}}(t)} \end{aligned} \right. (29) 式中：\Delta {\boldsymbol {A'}}、\Delta {\boldsymbol {B'}}、{\boldsymbol {N'}}为未知矩阵函数。由于\Delta {\boldsymbol {A}}、\Delta {\boldsymbol {B}}、{\boldsymbol {N}}是有界的，{\boldsymbol {B}}为已知实矩阵，显然\Delta {\boldsymbol {A'}}、\Delta {\boldsymbol {B'}}、{\boldsymbol {N'}}也是有界的，不妨定义总的不确定干扰项{\boldsymbol{\xi}} (t)，具体形式为
{\boldsymbol{\xi}} (t) = \Delta {\boldsymbol {A'}}(t){\boldsymbol {X}}(t) + \Delta {\boldsymbol {B'}}(t)U(t) + {\boldsymbol {N'}}(t) (30) 由于{\boldsymbol{\xi}} (t)表达式中各项都是有界的，因此可以假定
\left\| {\left. {{\boldsymbol{\xi}} (x,t)} \right\|} \right. \leqslant {\eta _1}\left\| {\left. {{\boldsymbol {X}}(t)} \right\|} \right. + {\eta _2} (31) 将式(29)代入式(28)可得
\begin{split} & \dot V = S{\boldsymbol {W}}({\boldsymbol {B}}\Delta {\boldsymbol {A'X}} + {\boldsymbol {B}}\Delta {\boldsymbol {B'}}U + {\boldsymbol {BN'}}) +\\ & \quad\quad S{\boldsymbol {WB}}({\boldsymbol {KX}} + U) \end{split} (32) 在满足式(31)的条件下，将控制率式(25)代入式(32)得
\begin{split} & \dot V = S{\boldsymbol {W}}({\boldsymbol {B}}\Delta {\boldsymbol {A'X}} + {\boldsymbol {B}}\Delta {\boldsymbol {B'}}U + B{\boldsymbol {N'}}) + \\ &\quad\quad S{\boldsymbol {WB}}({\boldsymbol {KX}} - {\boldsymbol {KX}} - {({\boldsymbol {WB}})^{ - 1}}f(x){{\mathrm{sgn}}} (s)) =\\ &\quad\quad S{\boldsymbol {WB}}(\Delta {\boldsymbol {A'X}} + \Delta {\boldsymbol {B'}}U + {\boldsymbol {N'}}) - S \cdot f(x){{\mathrm{sgn}}} (s)\leqslant \\ &\quad\quad S{\boldsymbol {WB}}({\eta _1}\left\| {\left. {\boldsymbol {X}} \right\|} \right. + {\eta _2}) -\\ & \quad\quad S({\eta _1}\left\| {\left. {{\boldsymbol {WB}}} \right\|} \right.\left\| {\left. {\boldsymbol {X}} \right\|} \right. + {\eta _2}\left\| {\left. {{\boldsymbol {WB}}} \right\|} \right. + {\eta _3}){{\mathrm{sgn}}} (s) \leqslant\\ &\quad\quad - \left\| {\left. S \right\|} \right. \cdot {\eta _3} \leqslant 0 \\ \end{split} (33) 综上，根据 李雅普诺夫稳定性理论，基于鲁棒最优滑模的闭环动态控制系统趋于稳定。
3. 基于二次规划的下层控制器设计
利用分布式电动车各轮毂电机独立可控的特点，采用二次规划算法对上层控制器输出的总附加横摆力矩 U 进行分配。轮胎附着利用率 \eta 是能表征车辆稳定性的参数之一， \eta 越小，车辆越不易抱死，稳定性越强，其表达式为
\eta {\text{ = }}\frac{{{F_{xi}}^2 + F_{yi}^2}}{{{{(\mu {F_{{\textit{z}}i}})}^2}}}\begin{array}{*{20}{c}} {}&{i = {\text{fl,fr,rl,rr}}} \end{array} (34) 式中： {F_{{{x}}i}} 、 {F_{{{y}}i}} 、 {F_{{\textit{z}}i}} 分别代表各轮的纵向力、侧向力、垂向力； \mu 为路面附着系数。
由于直接横摆力矩控制各轮纵向力，故以优化轮胎附着利用率 \eta 为目标，设计二次规划目标函数如下：
\min J = \min \sum\limits_i \eta = \min \sum\limits_i {\frac{{F_{xi}^2 + F_{yi}^2}}{{{{(\mu {F_{{\textit{z}}i}})}^2}}}} (35) 依托分布式电动车四轮转矩独立可控的特点，本文中设计的控制器主要通过控制四轮的纵向力分配来达到稳定性控制效果。由于轮胎侧向力与前轮转角、侧偏角等因素相关，DYC无法直接控制其大小，无法进行优化，因此可以将轮胎利用率改写为[25]
\min J = \min \sum\limits_i {\frac{{F_{xi}^2}}{{{{(\mu F_{{\textit{z}}i}^{})}^2}}}} = \min \sum\limits_i {\frac{{T_{xi}^2}}{{{{(\mu F_{{\textit{z}}i}^r)}^2}}}} (36) 式中： T_{xi}^{} 为各轮纵向驱动力； r 为车轮滚动半径。车轮总纵向力矩 T_x^{} 与总附加横摆力矩 U 存在如下关系：
\left\{ \begin{aligned} & {{T_x} = {T_{x{\text{fl}}}} + {T_{x{\text{fr}}}} + {T_{x{\text{rl}}}} + {T_{x{\text{rr}}}}} \\ &{U = \frac{d}{{2r}}( - {T_{x{\text{fl}}}} + {T_{x{\text{fr}}}} - {T_{x{\text{rl}}}} + {T_{x{\text{rr}}}})} \end{aligned} \right. (37) 式中： d 为轮距。令 {\boldsymbol {x}} = {[\begin{array}{*{20}{c}} {{T_{x{\text{fl}}}}}&{{T_{x{\text{fr}}}}}&{{T_{x{\text{rl}}}}}&{{T_{x{\text{rr}}}}} \end{array}]^{\text{T}}} ，{{\boldsymbol {b}}_{{\text{eq}}}} = {[\begin{array}{*{20}{c}} {{T_x}}&U \end{array}]^{\text{T}}}， {{\boldsymbol {A}}_{{\text{eq}}}} = \left[ {\begin{array}{*{20}{l}} 1&1&1&1 \\ { - \dfrac{d}{{2r}}}&{\dfrac{d}{{2r}}}&{ - \dfrac{d}{{2r}}}&{\dfrac{d}{{2r}}} \end{array}} \right] ，则
{{\boldsymbol {A}}_{{\text{eq}}}}{\boldsymbol {x}} = {{\boldsymbol {b}}_{{\text{eq}}}} (38) 考虑到轮胎力不得超过路面提供的附着力，设置约束条件：
- \mu {F_{zi}}r \leqslant T_{{{x}}i}^{} \leqslant \mu {F_{{\textit{z}}i}}r\begin{array}{*{20}{c}} {}&{i = {\text{fl,fr,rl,rr}}} \end{array} (39) 考虑驱动轮的理想输出转矩不得超过轮毂电机的最大输出转矩，设置约束条件：
- {T_{\max }} \leqslant {T_{xi}} \leqslant {T_{\max }} (40) 式中， {T_{\max }} 由电机外特性曲线得到。
综上所述，可将式(36)的二次规划问题描述成标准形式：
\left\{ \begin{aligned} & \min\; J = \min {{\boldsymbol {x}}^{\text{T}}}{\boldsymbol {Gx}} \\ & \quad\quad{{\text{s}}{\text{.t}}{\text{.}}}\quad {{\boldsymbol {A}}_{{\text{eq}}}}{\boldsymbol {x}} = {{\boldsymbol {b}}_{{\text{eq}}}} \\ &\quad\quad\quad\quad \max ( - \mu {F_{{\textit{z}}i}}r, - {T_{\max }}) \leqslant {T_{{{x}}i}} \leqslant \min (\mu {F_{{\textit{z}}i}}r,{T_{\max }}) \end{aligned} \right. (41) 式中：
{\boldsymbol {G}} = {\text{diag}}\left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{{(\mu {F_{z{\text{fl}}}}r)}^2}}}}&{\dfrac{1}{{{{(\mu {F_{z{\text{fr}}}}r)}^2}}}}&{\dfrac{1}{{{{(\mu {F_{z{\text{rl}}}}r)}^2}}}}&{\dfrac{1}{{{{(\mu {F_{z{\text{rr}}}}r)}^2}}}} \end{array}} \right]该二次规划问题可在MATLAB中调用quadprog函数求解。
4. 仿真验证
为了验证本文设计的鲁棒最优滑模控制器的有效性，利用MATLAB/Simulink与车辆动力学仿真软件Carsim搭建联合仿真平台进行试验验证。在Carsim中搭建MEEW车辆模型，具体参数如表2所示。本文中ROSM控制器参数为 {\eta }_{1}\text{=100} ，{\eta }_{{2}}= 3\;000 ，{\eta }_{\text{3}}\text{=100} ，{{\boldsymbol {R}}_k} = {\text{3}} \times {10^{ - 5}}，{{\boldsymbol {Q}}_k} = {\text{diag}}(20\;000,20\;000)，边界层厚度\varDelta = 10。
表 2 车辆参数Table 2. Vehicle parameters参数 数值 车辆质量 m/kg 1610 转动惯量 Iz/(kg·m2 ) 2059.2 质心到前轴距离 a/m 1.05 质心到后轴距离 b/m 1.61 轮距 d/m 1.565 轮胎滚动半径 R/m 0.35 前轮等效刚度 kf /(N·rad−1 ) − 87002 后轮等效刚度 kr /(N·rad−1 ) − 79240 4.1 双移线工况
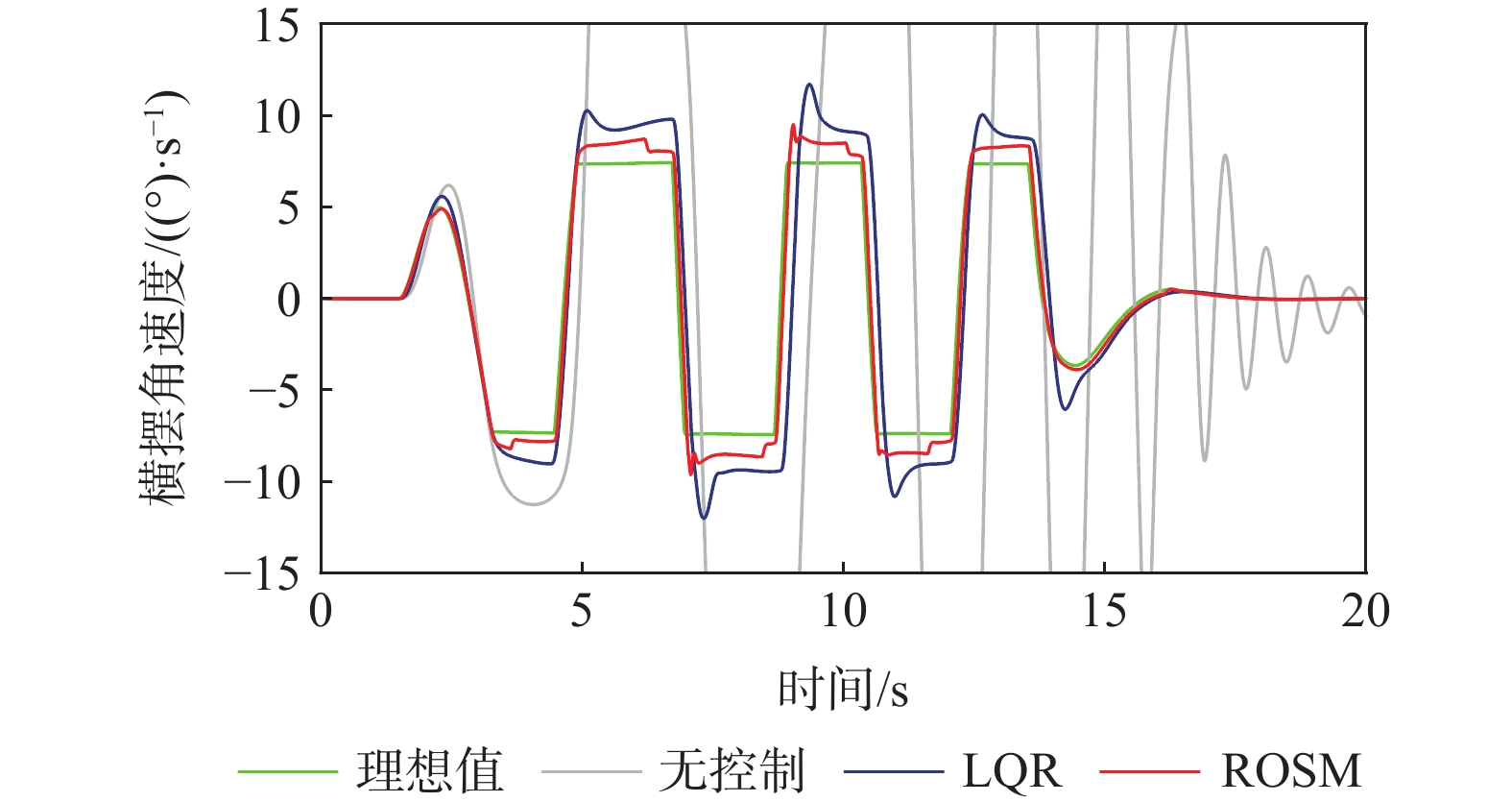
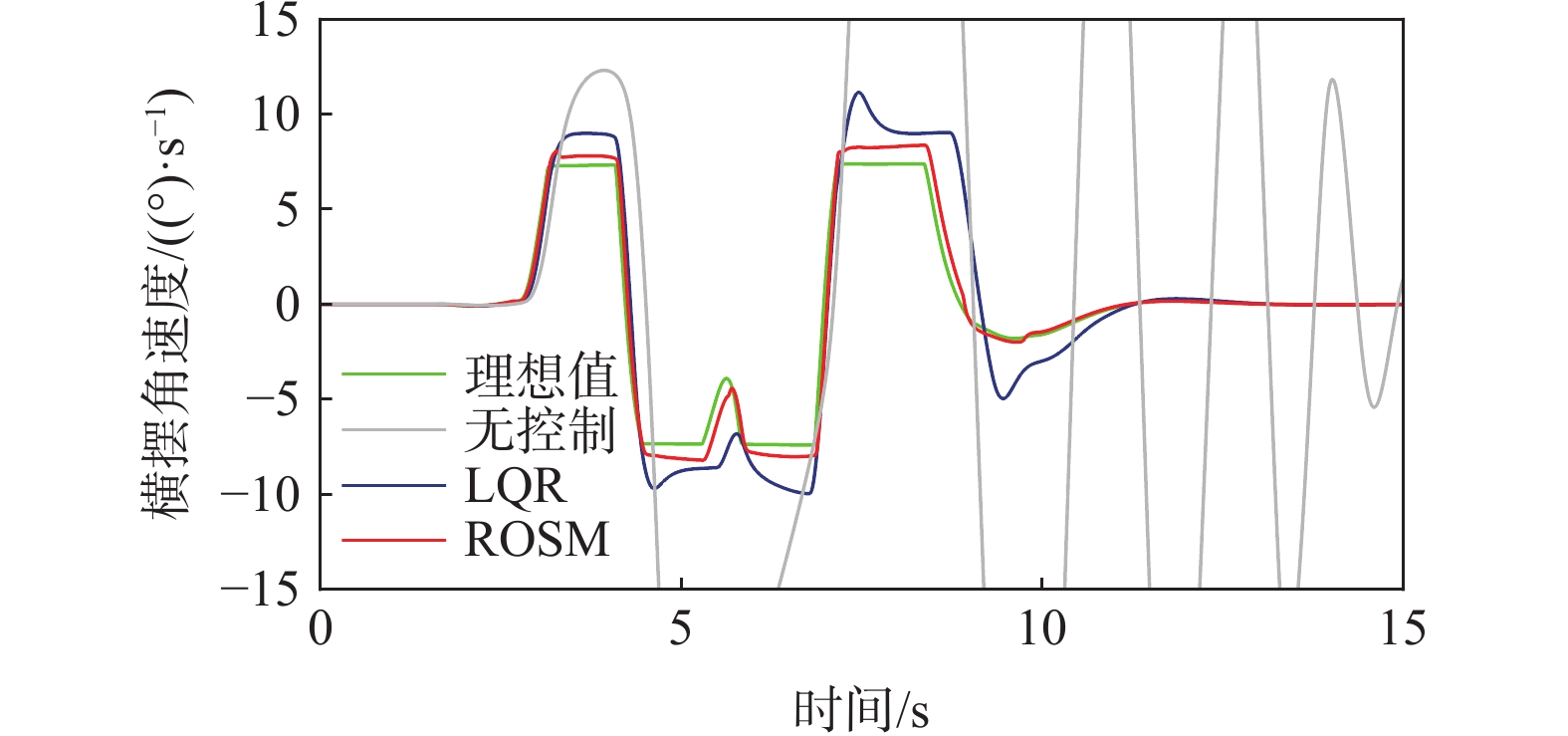
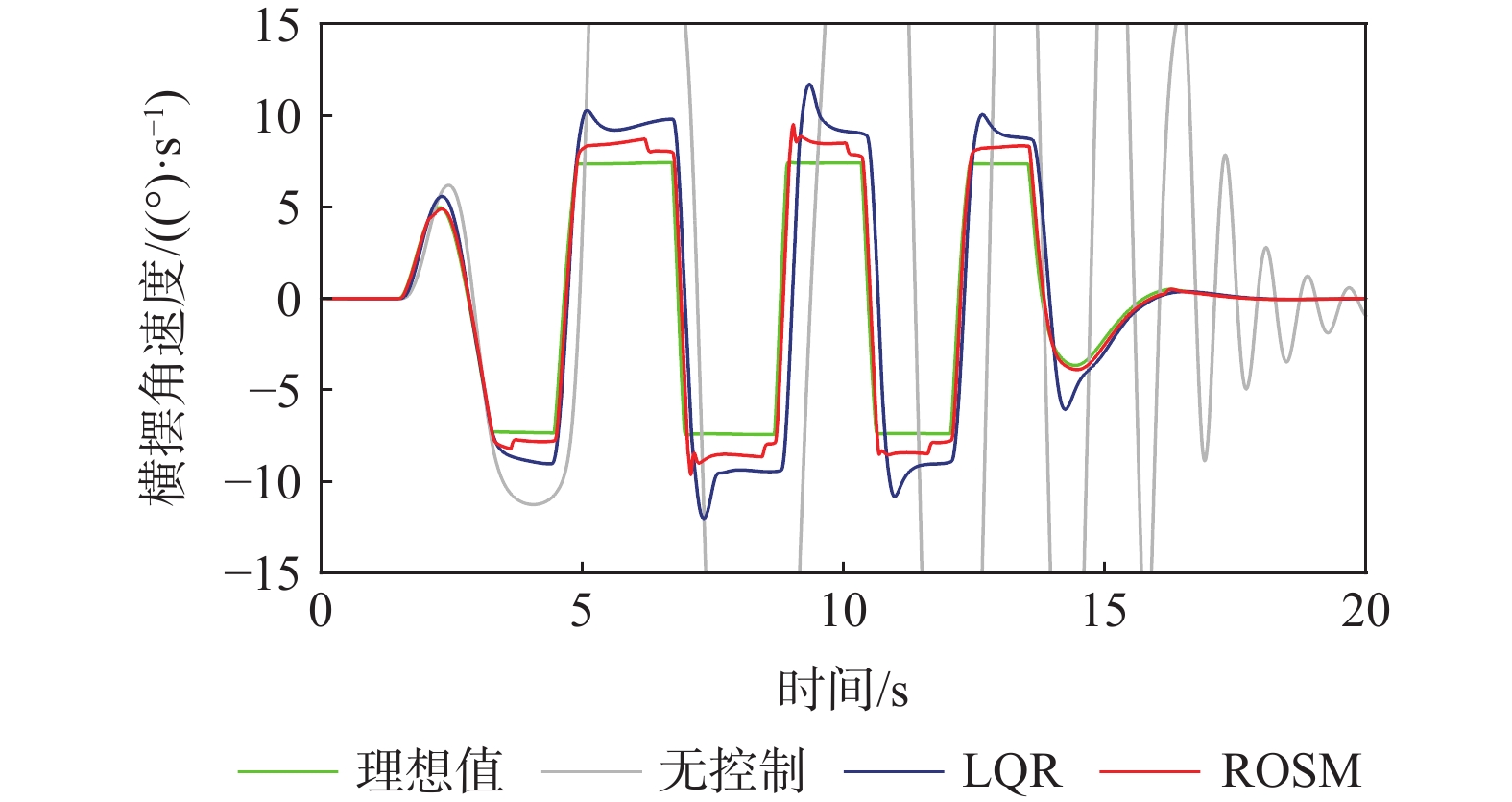
设置车速为72 km/h，路面附着系数为0.3的双移线工况。图7为横摆角速度对比图，当无控制时，曲线发散，车辆失稳。单一LQR控制与鲁棒最优滑模控制都能极大改善车辆行驶的稳定性，但可明显看出鲁棒最优滑模控制效果曲线更贴近理想值，横摆角速度与理想值的误差峰值仅为0.94(°)/s，而单一LQR控制误差峰值为3.75(°)/s，降低了74.93%。
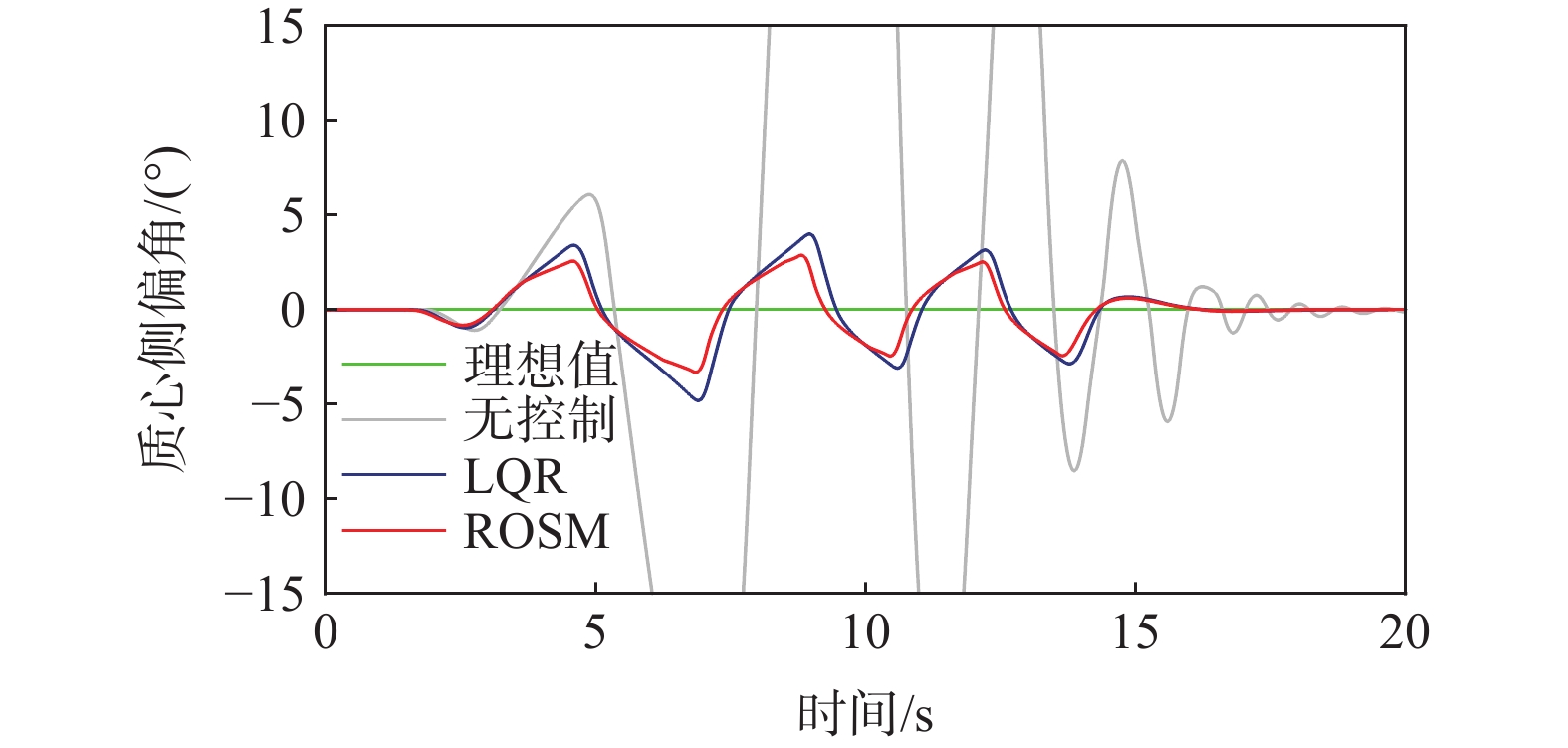
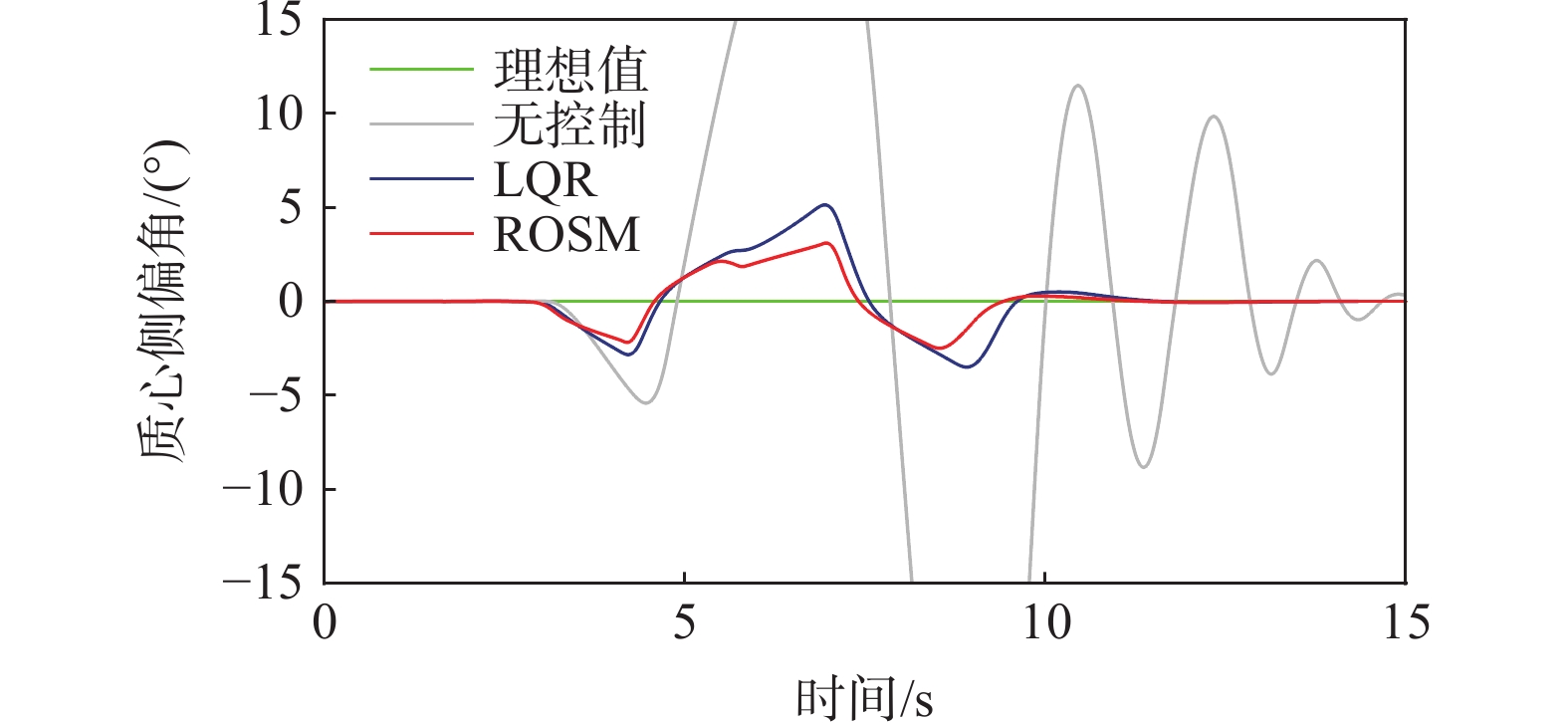
图8为质心侧偏角对比图，可明显看出鲁棒最优滑模控制效果更好，质心侧偏角与理想值的误差峰值仅为3.03°，而单一LQR控制误差峰值为5.04°，峰值降低了39.88%。
图9为鲁棒最优滑模控制下的车辆四轮转矩图。车辆在低附着路面转向时易侧滑、倾翻，由图可看出在4 s与7 s左右转向时，电机执行器动态补偿了轮胎转矩，极大提升了车辆的稳定性。
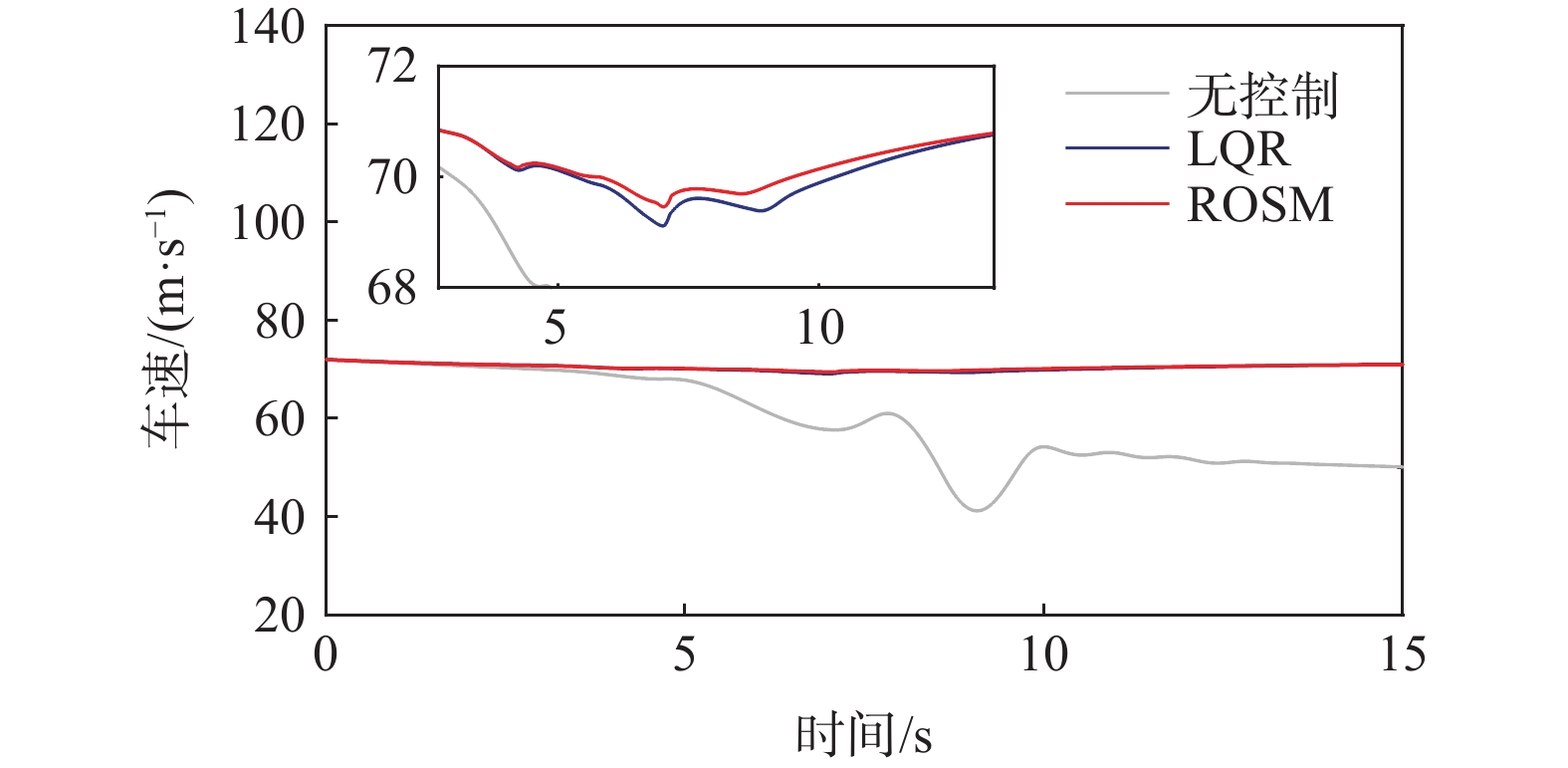
图 9 四轮转矩变化（鲁棒最优滑模控制）Figure 9. Four -wheel torque variation (robust optimal sliding mode control)图10为车速变化对比图，期望车速为72 km/h，LQR控制器与鲁棒最优滑模控制器都能很好地稳定车速，保证车辆的平顺性与驾驶人的乘坐体验。
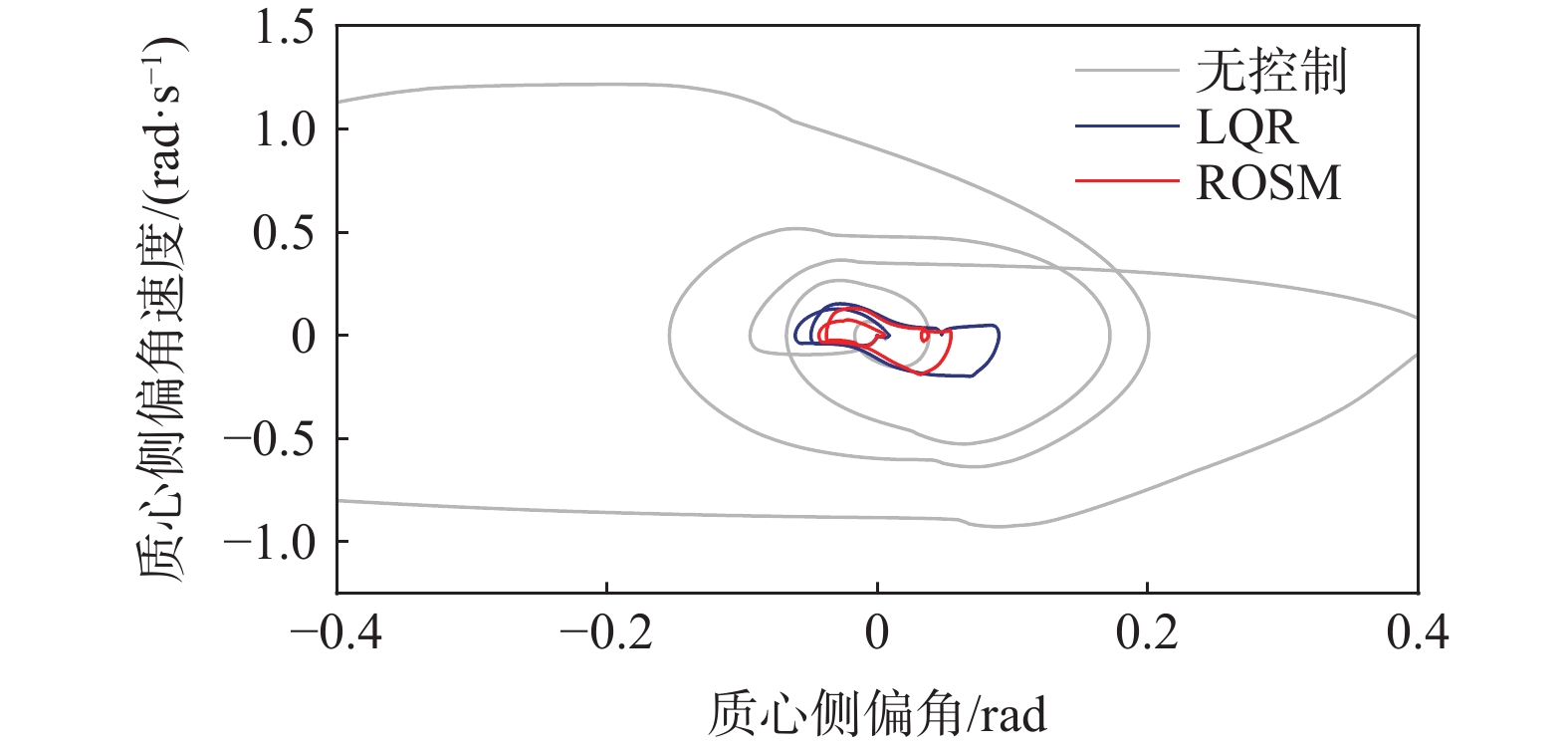
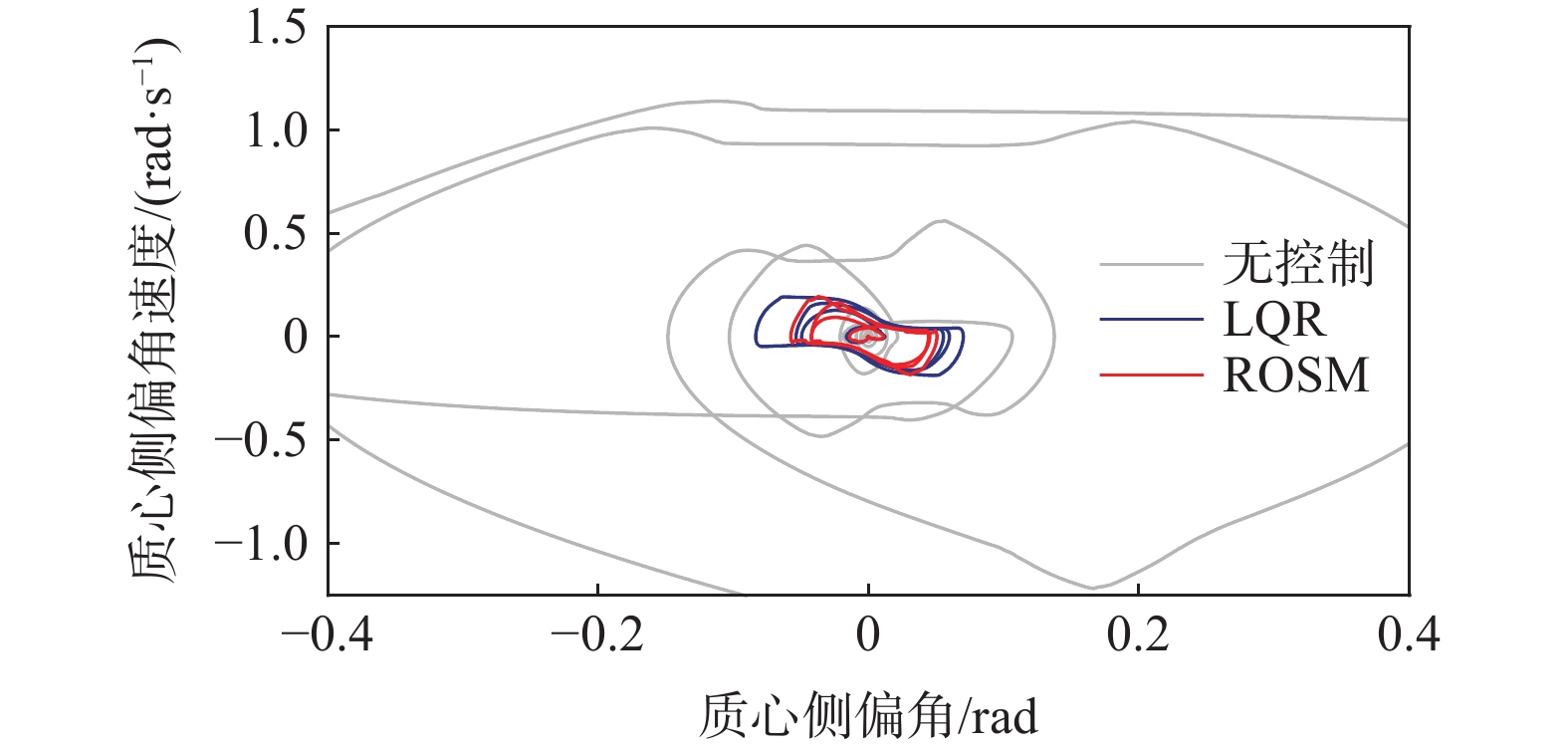
图11为不同控制下的“质心侧偏角-质心侧偏角速度”相图。无控制时，参数发散，车辆失稳；LQR控制与鲁棒最优滑模控制都能使曲线收敛，但鲁棒最优滑模控制收敛速度更快、半径更小、效果更佳。
图 11 “质心侧偏角-质心侧偏角速度”相图Figure 11. ‘Centre-of-mass lateral deflection angle - centre-of-mass lateral deflection angular velocity’ phase Diagrams4.2 蛇形工况
设置车速为72km/h，路面附着系数为0.3的蛇形工况。从图12、图13可知，在蛇形工况下，ROSM控制下的质心侧偏角、横摆角速度曲线仍更贴合理想值，说明ROSM的稳定性控制效果优于LQR控制。从图14可知，控制器在蛇形转弯处补偿转矩，保证了车辆的操稳性。图15、图16与双移线工况类似，ROSM控制下，车速保持效果略好于LQR控制，相图中ROSM控制效果最佳。
图 14 四轮转矩变化（鲁棒最优滑模控制）Figure 14. Four -wheel torque variation (robust optimal sliding mode control)
图 16 “质心侧偏角-质心侧偏角速度”相图Figure 16. ‘Centre-of-mass lateral deflection angle - centre-of-mass lateral deflection angular velocity’ phase Diagrams横摆角速度与质心侧偏角是评估车辆稳定性的两个重要指标，为了评估二者跟踪理想值的效果，引入平均绝对误差(MAE)δMAE和均方根误差(RMSE)δRMSE的评估指标，具体为
\delta_{\text{MAE}} = \frac{1}{k}\sum\limits_{i = 1}^k {\left| {x - {x_{\text{d}}}} \right|} (42) \delta_{\text{RMSE}} = \sqrt {\frac{1}{k}\sum\limits_{i = 1}^k {{{\left( {x - {x_{\text{d}}}} \right)}^2}} } (43) 式中： x 指代\omega 或\beta ；{x_{\text{d}}}为理想值；k为采样样本数，计算结果如表3所示。
表 3 评估指标对比Table 3. Comparison of evaluation indicators工况 \omega δMAE \omega δRSME \beta δMAE \beta δRSME 双移线LQR 1.0161 1.8285 1.0270 1.7139 双移线ROSM 0.3675 0.6339 0.7070 1.1663 蛇形LQR 1.4944 2.2791 1.2446 1.7863 蛇形ROSM 0.6220 0.9111 0.9732 1.3679 从表中可明显看出，无论双移线工况还是蛇形工况，鲁棒最优滑模控制下\omega 与\beta 的δMAE与δRSME都小于相同工况下的单一LQR控制，更能保证车辆在极限工况下行驶的稳定性。双移线工况中，ROSM控制下横摆角速度的δMAE、δRSME与LQR控制相比分别下降了63.83%、65.33%；蛇形工况中，其分别降低了58.38%、60.02%，说明文中设计的ROSM控制器控制效果较之LQR控制有明显提升。质心侧偏角方面，双移线下其δMAE、δRSME与LQR控制相比分别下降了31.16%、31.95%，而蛇形工况下，其分别下降了21.81%、23.42%，说明鲁棒最优控制器能有效改善车辆的操稳性。
5. 结 论
本文针对匹配机械弹性电动轮(MEEW)车辆转向时的横摆稳定性控制问题，提出了一种鲁棒最优滑模的控制策略。首先，基于线性二自由度车辆模型，设计线性二自由度调节器(LQR)控制器，输出初始最优控制量；其次，考虑到轮胎侧偏刚度、路面状态等因素的变化，引入参数不确定的非线性动力学模型，为了处理参数的不确定性与外部干扰，设计了一种基于初始最优控制量的鲁棒最优积分滑模控制策略(ROSM)，该策略不仅可以实现最优控制目标，而且对不确定参数与外部干扰具有良好的鲁棒性；最后通过MATLAB/Simulink和Carsim联合仿真，对控制方法进行仿真验证，结果表明：在双移线与蛇形工况下，鲁棒最优滑模控制车辆稳定性，其横摆角速度、质心侧偏角与理想值的平均绝对误差、均方根误差皆小于相同工况下的LQR控制，跟踪理想值精度高于LQR控制，控制效果更佳。
-
图 9 四轮转矩变化（鲁棒最优滑模控制）
Figure 9. Four -wheel torque variation (robust optimal sliding mode control)
图 11 “质心侧偏角-质心侧偏角速度”相图
Figure 11. ‘Centre-of-mass lateral deflection angle - centre-of-mass lateral deflection angular velocity’ phase Diagrams
图 14 四轮转矩变化（鲁棒最优滑模控制）
Figure 14. Four -wheel torque variation (robust optimal sliding mode control)
图 16 “质心侧偏角-质心侧偏角速度”相图
Figure 16. ‘Centre-of-mass lateral deflection angle - centre-of-mass lateral deflection angular velocity’ phase Diagrams
表 1 MEEW参数拟合结果
Table 1. Parameter fitting results
Fz/kN Bx Cx Dx Ex By Cy Dy Ey 10 4.9477 1.7216 6795.14 0.4541 0.1364 1.2682 8150 − 0.0988 15 3.9323 2.1252 10103.66 0.8742 0.1271 1.2682 12200 − 0.0952 20 4.8070 1.7390 13495.56 0.4411 0.1116 1.2682 16310 − 0.0914 
下载: 导出CSV
表 2 车辆参数
Table 2. Vehicle parameters
参数 数值 车辆质量 m/kg 1610 转动惯量 Iz/(kg·m2 ) 2059.2 质心到前轴距离 a/m 1.05 质心到后轴距离 b/m 1.61 轮距 d/m 1.565 轮胎滚动半径 R/m 0.35 前轮等效刚度 kf /(N·rad−1 ) − 87002 后轮等效刚度 kr /(N·rad−1 ) − 79240
下载: 导出CSV
表 3 评估指标对比
Table 3. Comparison of evaluation indicators
工况 \omega δMAE \omega δRSME \beta δMAE \beta δRSME 双移线LQR 1.0161 1.8285 1.0270 1.7139 双移线ROSM 0.3675 0.6339 0.7070 1.1663 蛇形LQR 1.4944 2.2791 1.2446 1.7863 蛇形ROSM 0.6220 0.9111 0.9732 1.3679
下载: 导出CSV
-
[1] 赵又群. 非充气机械弹性安全车轮理论与方法[M]. 北京: 科学出版社, 2020: 12-28.ZHAO Y Q. Theory and method for non-pneumatic mechanical elastic safety wheel[M]. Beijing: Science Press, 2020: 12-28 (in Chinese). [2] DENG Y J, ZHAO Y Q, XU H, et al. Finite element modeling of interaction between non-pneumatic mechanical elastic wheel and soil[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2019, 233(13): 3293-3304. doi: 10.1177/0954407018821555 [3] 张陈曦, 赵又群, 冯世林, 等. 伪刚体-柔体耦合的新式免充气轮胎刚度分析[J]. 中国机械工程, 2021, 32(9): 1051-1060,1072.ZHANG C X, ZHAO Y Q, FENG S L, et al. Stiffness analysis of new type non-pneumatic tires based on pseudo-rigid-flexible body coupling model[J]. China Mechanical Engineering, 2021, 32(9): 1051-1060,1072(in Chinese). [4] 张晨, 赵又群, 郑鑫, 等. 随机载荷下机械弹性车轮的热力耦合耐久性研究[J]. 中国机械工程, 2021, 32(14): 1669-1676.ZHANG C, ZHAO Y Q, ZHENG X, et al. Study on thermal coupling durability of mechanical elastic wheels under random loads[J]. China Mechanical Engineering, 2021, 32(14): 1669-1676(in Chinese). [5] WANG Q G, ZHUANG Y, WEI J N, et al. A driver model–based direct yaw moment controller for in-wheel motor electric vehicles[J]. Advances in Mechanical Engineering, 2019, 11(9): 1687814019877319. [6] GAN L. Study on yaw moment control for electric vehicle with four-wheel in-wheel motor based on fuzzy PI control[J]. Machinery Design & Manufacture, 2015, 7: 103-107. [7] ASIABAR A N, KAZEMI R. A direct yaw moment controller for a four in-wheel motor drive electric vehicle using adaptive sliding mode control[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2019, 233(3): 549-567. doi: 10.1177/1464419318807700 [8] 段敏, 孙小松, 张博涵. 基于模型预测控制与离散线性二次型调节器的智能车横纵解耦跟踪控制[J]. 汽车技术, 2022(8): 38-46.DUAN M, SUN X S, ZHANG B H. Horizontal and vertical decoupling tracking control based on MPC and DLQR[J]. Automobile Technology, 2022(8): 38-46(in Chinese). [9] LIU D Y, HUANG S, WU S, et al. Direct yaw-moment control of electric vehicle with in-wheel motor drive system[J]. International Journal of Automotive Technology, 2020, 21(4): 1013-1028. doi: 10.1007/s12239-020-0096-6 [10] 林棻, 蔡亦璋, 赵又群, 等. 匹配机械弹性车轮的分布式驱动电动汽车稳定性控制[J]. 机械工程学报, 2022, 58(8): 236-243. doi: 10.3901/JME.2022.08.236LIN F, CAI Y Z, ZHAO Y Q, et al. Lateral stability control of distributed drive electric vehicle with mechanical elastic wheel[J]. Journal of Mechanical Engineering, 2022, 58(8): 236-243(in Chinese). doi: 10.3901/JME.2022.08.236 [11] ZHU J J, WANG Z P, ZHANG L, et al. Braking/steering coordination control for in-wheel motor drive electric vehicles based on nonlinear model predictive control[J]. Mechanism and Machine Theory, 2019, 142: 103586. doi: 10.1016/j.mechmachtheory.2019.103586 [12] YAN Z P, WANG M, XU J. Robust adaptive sliding mode control of underactuated autonomous underwater vehicles with uncertain dynamics[J]. Ocean Engineering, 2019, 173: 802-809. [13] RANGEL M A G, MANZANILLA A, SUAREZ A E Z, et al. Adaptive non-singular terminal sliding mode control for an unmanned underwater vehicle: real-time experiments[J]. International Journal of Control, Automation and Systems, 2020, 18(3): 615-628. doi: 10.1007/s12555-019-0674-4 [14] NORSAHPERI N M H, DANAPALASINGAM K A. An improved optimal integral sliding mode control for uncertain robotic manipulators with reduced tracking error, chattering, and energy consumption[J]. Mechanical Systems and Signal Processing, 2020, 142: 106747. doi: 10.1016/j.ymssp.2020.106747 [15] XU T, ZHAO Y Q, DENG H F, et al. Integrated optimal control of distributed in-wheel motor drive electric vehicle in consideration of the stability and economy[J]. Energy, 2023, 282: 128990. doi: 10.1016/j.energy.2023.128990 [16] 丛森森, 高峰, 许述财. 基于动态稳定域的车辆横纵向稳定性协同控制[J]. 汽车工程, 2022, 44(6): 900-908.CONG S S, GAO F, XU S C. Cooperative control of vehicle lateral and longitudinal stability based on dynamic stability region[J]. Automotive Engineering, 2022, 44(6): 900-908(in Chinese). [17] 梁宝钰, 汪怡平, 刘珣, 等. 基于滑模理论的高速车辆侧风稳定性控制研究[J]. 汽车工程, 2022, 44(1): 123-130.LIANG B Y, WANG Y P, LIU X, et al. Study on crosswind stability control of high-speed vehicle based on sliding mode theory[J]. Automotive Engineering, 2022, 44(1): 123-130(in Chinese). [18] 陈特, 徐兴, 蔡英凤, 等. 基于状态估计的无人车前轮转角与横摆稳定协调控制[J]. 北京理工大学学报, 2021, 41(10): 1050-1057.CHEN T, XU X, CAI Y F, et al. Coordinated control of front-wheel steering angle and yaw stability for unmanned ground vehicle based on state estimation[J]. Transactions of Beijing Institute of Technology, 2021, 41(10): 1050-1057(in Chinese). [19] BAI R, WANG H B. Robust optimal control for the vehicle suspension system with uncertainties[J]. IEEE Transactions on Cybernetics, 2022, 52(9): 9263-9273. doi: 10.1109/TCYB.2021.3052816 [20] DENG H F, ZHAO Y Q, FENG S L, et al. Torque vectoring algorithm based on mechanical elastic electric wheels with consideration of the stability and economy[J]. Energy, 2021, 219: 119643. doi: 10.1016/j.energy.2020.119643 [21] PACEJKA H. Tire and vehicle dynamics[M]. Amsterdam: Elsevier, 2005: 27-29. [22] 龙文, 刘豪. 车辆稳定性控制系统LQR算法设计[J]. 汽车实用技术, 2021, 46(23): 76-79,110.LONG W, LIU H. Design of vehicle system dynamics control algorithm based on LQR method[J]. Automobile Applied Technology, 2021, 46(23): 76-79,110(in Chinese). [23] 郑鑫, 赵又群, 王秋伟, 等. 匹配机械弹性车轮的电子稳定控制器参数分析[J]. 中国机械工程, 2020, 31(23): 2883-2890.ZHENG X, ZHAO Y Q, WANG Q W, et al. Parameter analysis of electronic stability controller matching mechanical elastic wheels[J]. China Mechanical Engineering, 2020, 31(23): 2883-2890(in Chinese). [24] ALI MASOOD CHEEMA M, FLETCHER J E, FARSHADNIA M, et al. Sliding mode based combined speed and direct thrust force control of linear permanent magnet synchronous motors with first-order plus integral sliding condition[J]. IEEE Transactions on Power Electronics, 2018, 34(3): 2526-2538. [25] 王文伟, 赵一凡, 张伟, 等. 多轴轮边驱动铰接客车的横摆稳定性控制策略[J]. 机械工程学报, 2020, 56(14): 161-172. doi: 10.3901/JME.2020.14.161WANG W W, ZHAO Y F, ZHANG W, et al. Yaw stability control strategy of multi-wheel independent electric articulated bus[J]. Journal of Mechanical Engineering, 2020, 56(14): 161-172(in Chinese). doi: 10.3901/JME.2020.14.161 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 104
- HTML全文浏览量: 38
- PDF下载量: 1
- 被引次数: 0
