Flexible arrival trajectory optimization at terminal airspace based on mixed integer programming
-
摘要:
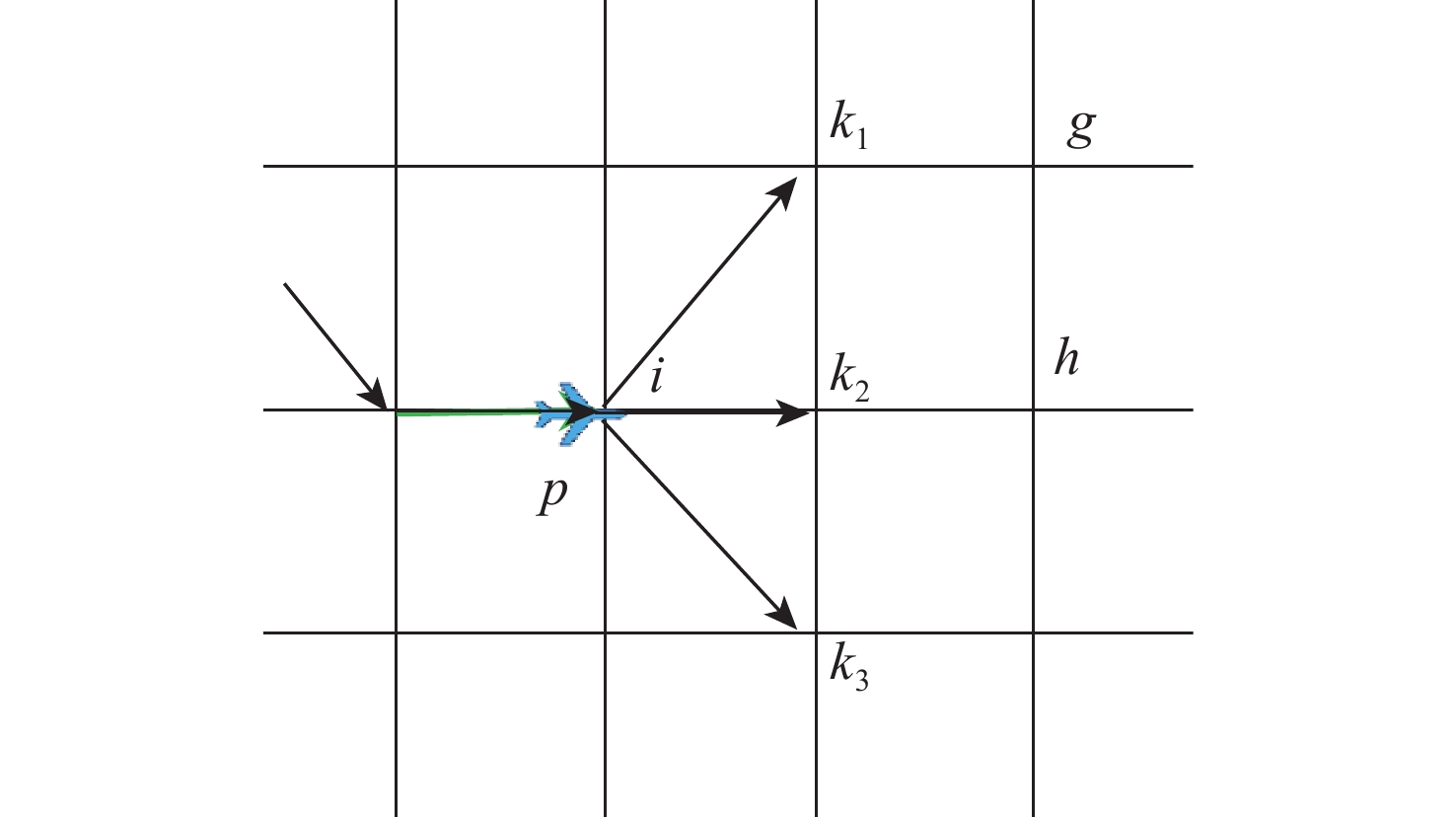
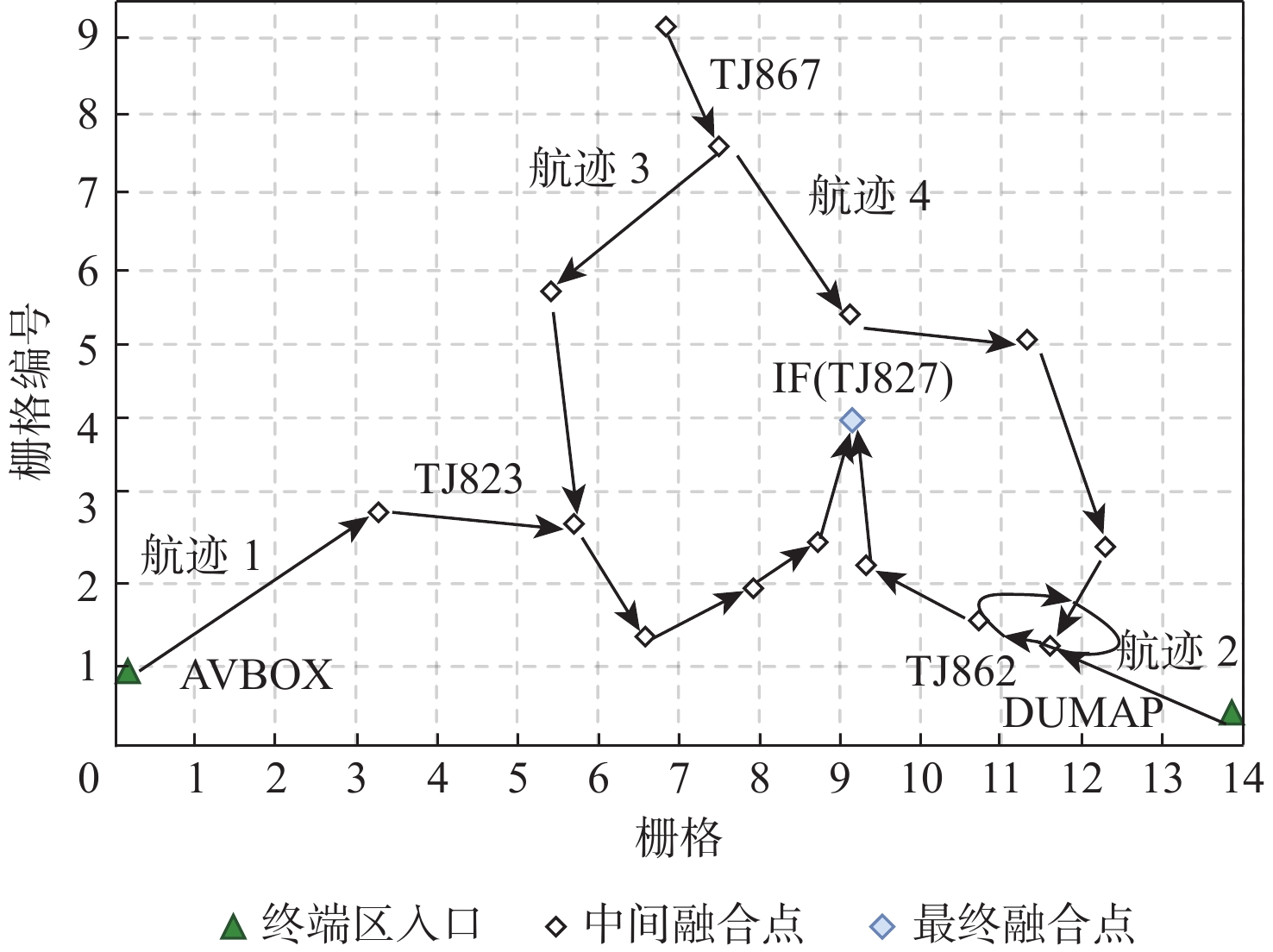
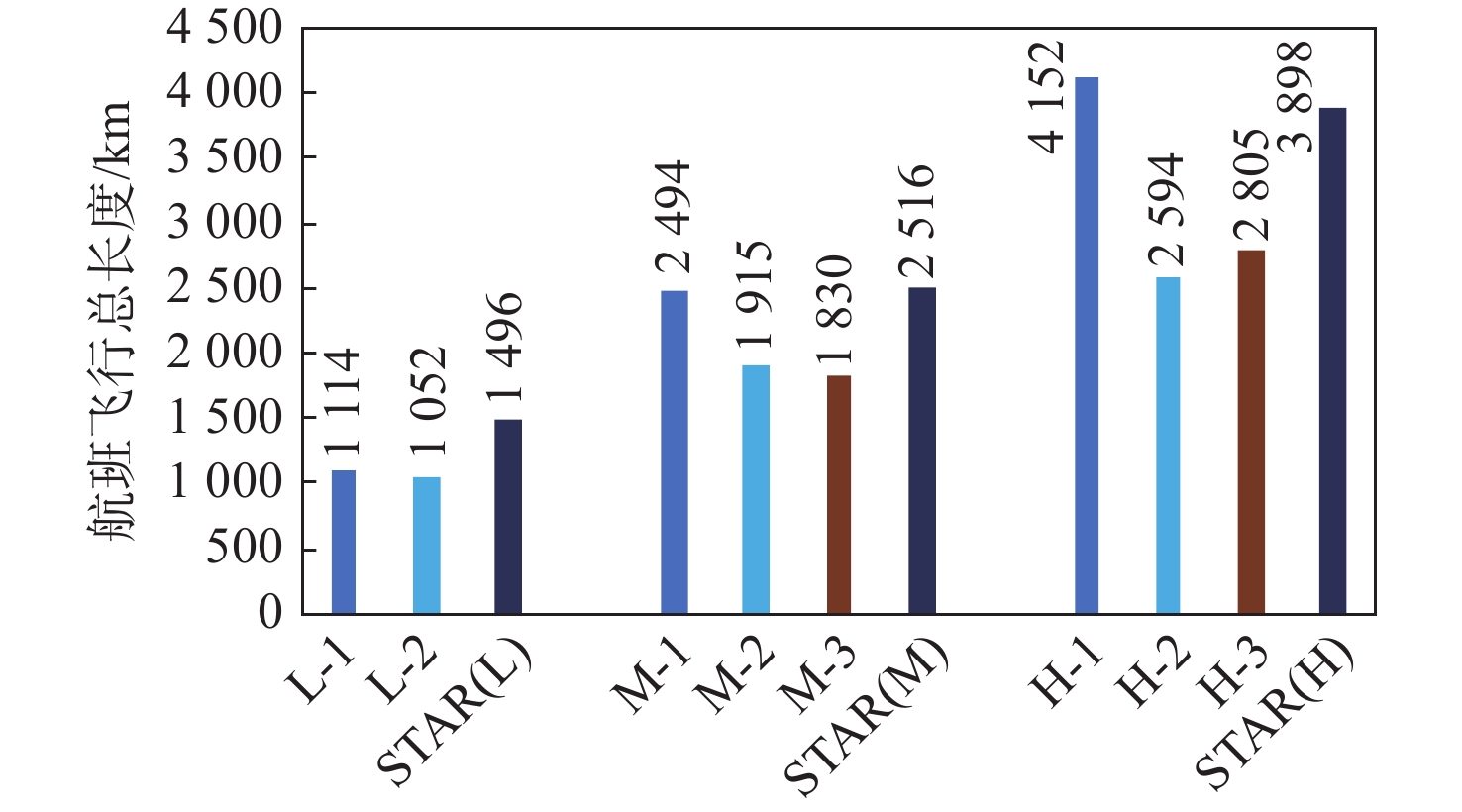
随着航空运输量持续增长和空域容量日渐饱和，固定进场程序对航班调配缺乏灵活性，潜在冲突多、调配困难、等待时间长、碳排放量大等问题日趋凸显。综合考虑多航班在终端区的进场、进近、排序、汇聚等运行过程，提出和描述了基于柔性进场航迹优化解决方案。基于终端区和航空器运行特征，设计终端区航班进场时空离散网络栅格。以航迹和总飞行长度最短为目标，建立柔性进场航迹的混合整数规划模型，分别考虑网络栅格规则、航空器转弯特性、飞行冲突、安全间隔、航迹连续性等限制条件，以天津机场终端区为例，基于不同的交通密度等级和终端区入口时间窗，设置多组典型实验案例，使用商业求解器Gurobi对所建模型进行求解验证。结果表明：柔性进场航迹较标准仪表进场程序(STAR)，航迹长度平均缩短127.375 km，飞行总长度平均降低534.75 km，航班进场时间平均减少6.24 min；且在相同交通密度等级，入口时间窗设置合理的情况下，柔性进场航迹对航班量的小幅波动具有一定的鲁棒性。
Abstract:Problems with flight conflicts, difficult deployment, lengthy wait times, and high carbon emissions are becoming more frequent as a result of the continuous growth in air traffic, the saturation of available airspace, and the rigidity of the conventional fixed approach procedure used in the terminal area. A solution based on flexible approach trajectory optimization is developed and detailed, taking into account the operating processes of multiple flights such as descent, approach, sequencing, and margining in the terminal area. A spatiotemporal discrete network grid of flight approaches in the terminal area is created based on the characteristics of the terminal and aircraft operation. A mixed integer programming model is developed with the objective of minimizing the trajectory and overall flight length, as well as being constrained by factors including grid regulations, airplane turning characteristics, flying conflicts, safety separation, and trajectory continuity. The model is solved and validated using the commercial solver Gurobi, and multiple sets of typical experimental scenarios are put up depending on different traffic density levels and the entrance time frame, using the Tianjin Airport terminal area as an example. The results show that the flexible approach trajectory length is decreased by an average of 127.375 km and the total flight length is reduced by 534.75 km compared with the standard instrument approach procedure (STAR), with an average reduction of 6.24 min in flight arrival times. Additionally, with the same traffic density level and a fair entrance time window setting, the flexible approach trajectory is resilient enough to handle slight variations in the number of flights.
-
图 7 最终融合点栅格对应的3个可用对角航迹段
Figure 7. Three available diagonal trajectory segments in each final merge point grid
图 15 不同时间窗的进场航迹长度
Figure 15. Length of arrival trajectory based on different time window
图 18 中交通密度下不同测试的航迹
Figure 18. Trajectories for different tests in medium traffic density
图 19 高交通密度下不同测试的航迹
Figure 19. Trajectories for different tests in high traffic density
表 1 不同测试场景的案例数据
Table 1. Case data in different test scenarios
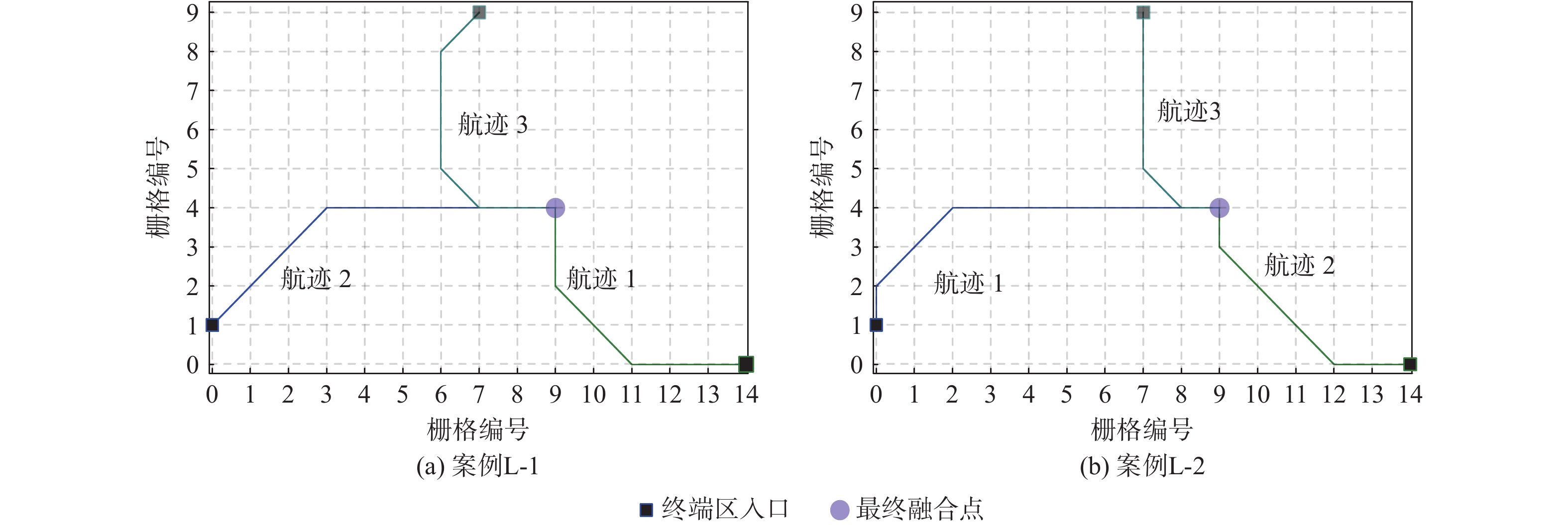
测试案例 密度 航班量 时间窗/min 三入口航班量 L-1 低 13 0 4-5-4 L-2 低 13 1 4-5-4 M-1 中 22 0 8-8-6 M-2 中 22 1 8-8-6 M-3 中 22 2 8-8-6 H-1 高 32 2 10-10-12 H-2 高 32 3 10-10-12 H-3 高 32 4 10-10-12 
下载: 导出CSV
表 2 优化航迹相对原进场程序的长度变化
Table 2. Changes in the length of arrival trajectory
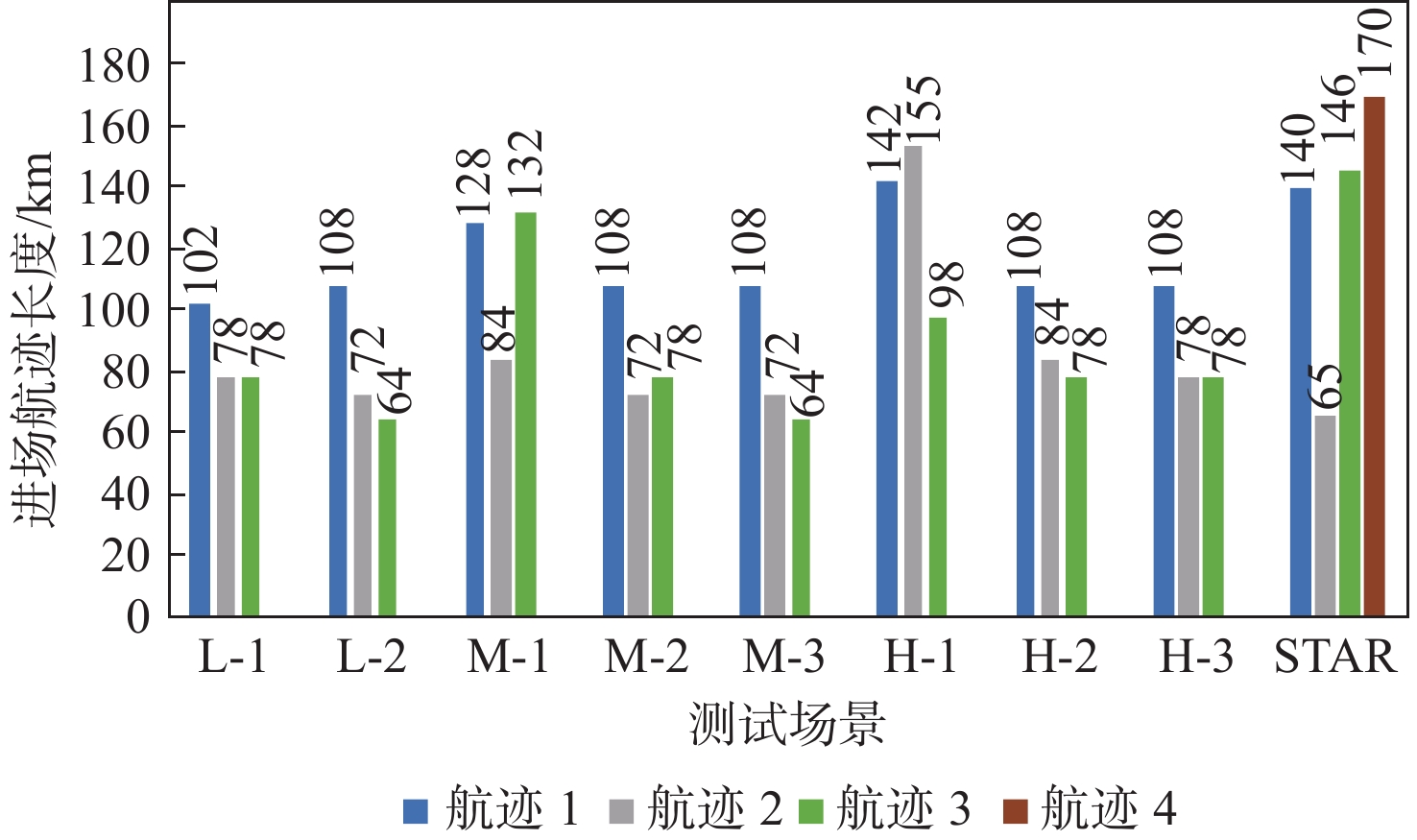
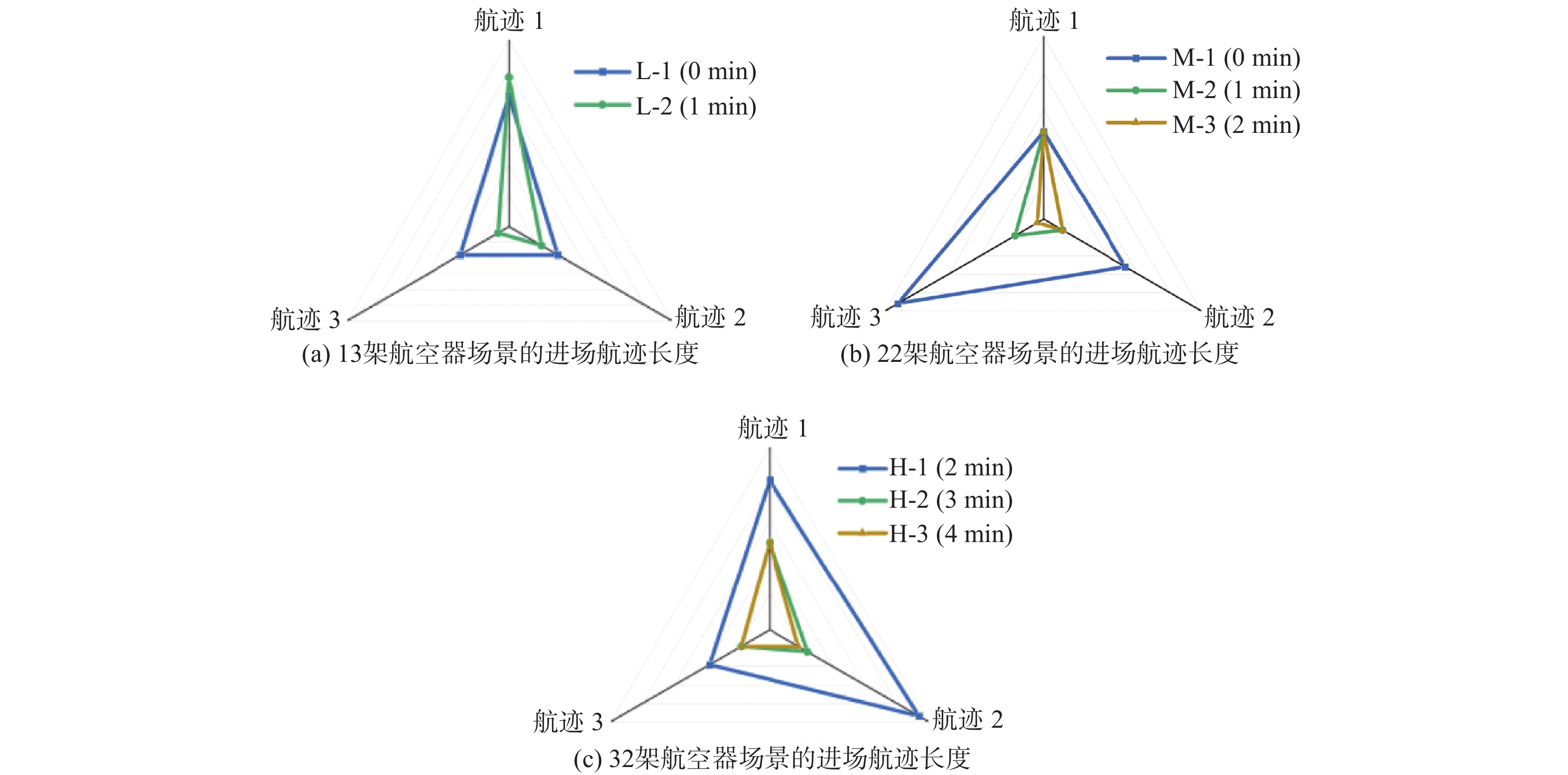
案例 航迹1
长度/km航迹2
长度/km航迹3
长度/km航迹4
长度/km总长度/
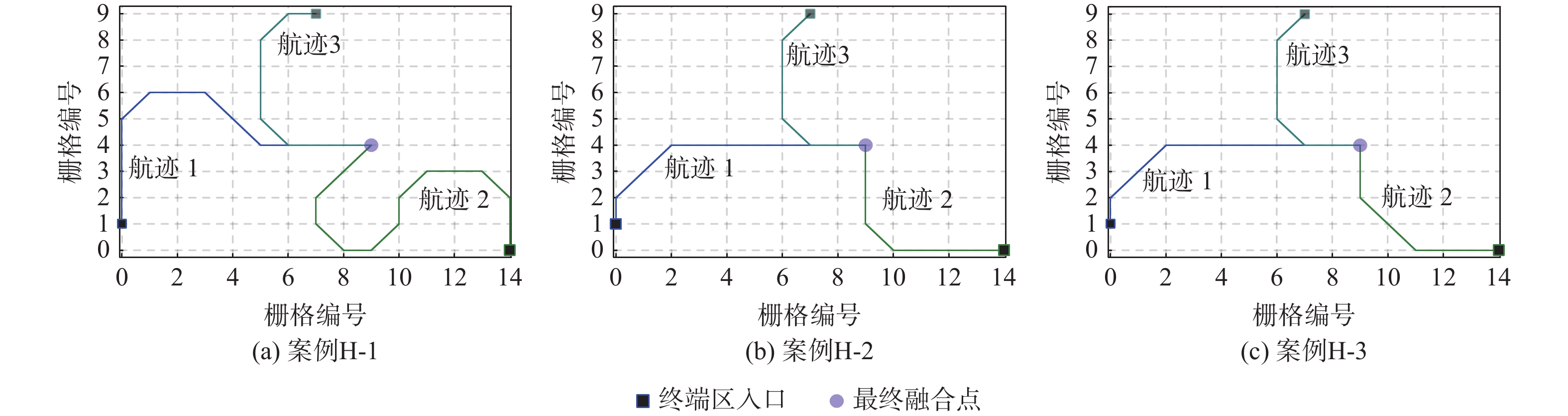
kmL-1 −37 +14 −67 −90 L-2 −31 +9 −82 −104 M-1 −11 +19 −13 −5 M-2 −31 +9 −67 −89 M-3 −31 +9 −82 −104 H-1 +3 +90 −47 −170 −124 H-2 −31 +19 −67 −170 −249 H-3 −31 +14 −67 −170 −254
下载: 导出CSV
表 3 最后一架航班到达最终融合点的时间
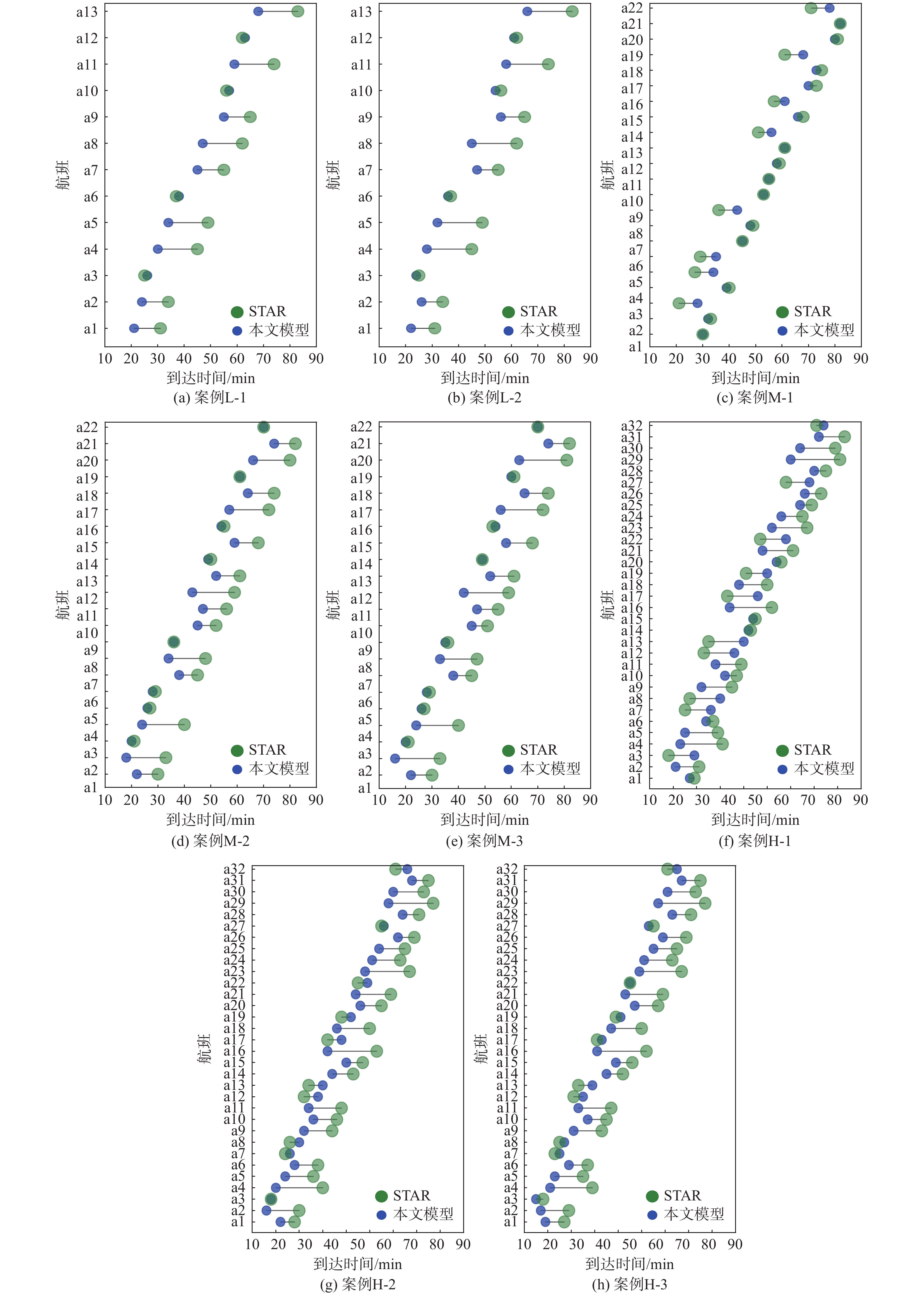
Table 3. Time when the last flight arrived at the final merge point
min 测试场景 本文模型 STAR L-1 66 83 L-2 66 83 M-1 78 82 M-2 74 82 M-3 74 82 H-1 84 87 H-2 78 87 H-3 77 87
下载: 导出CSV
表 4 不同测试案例的数据
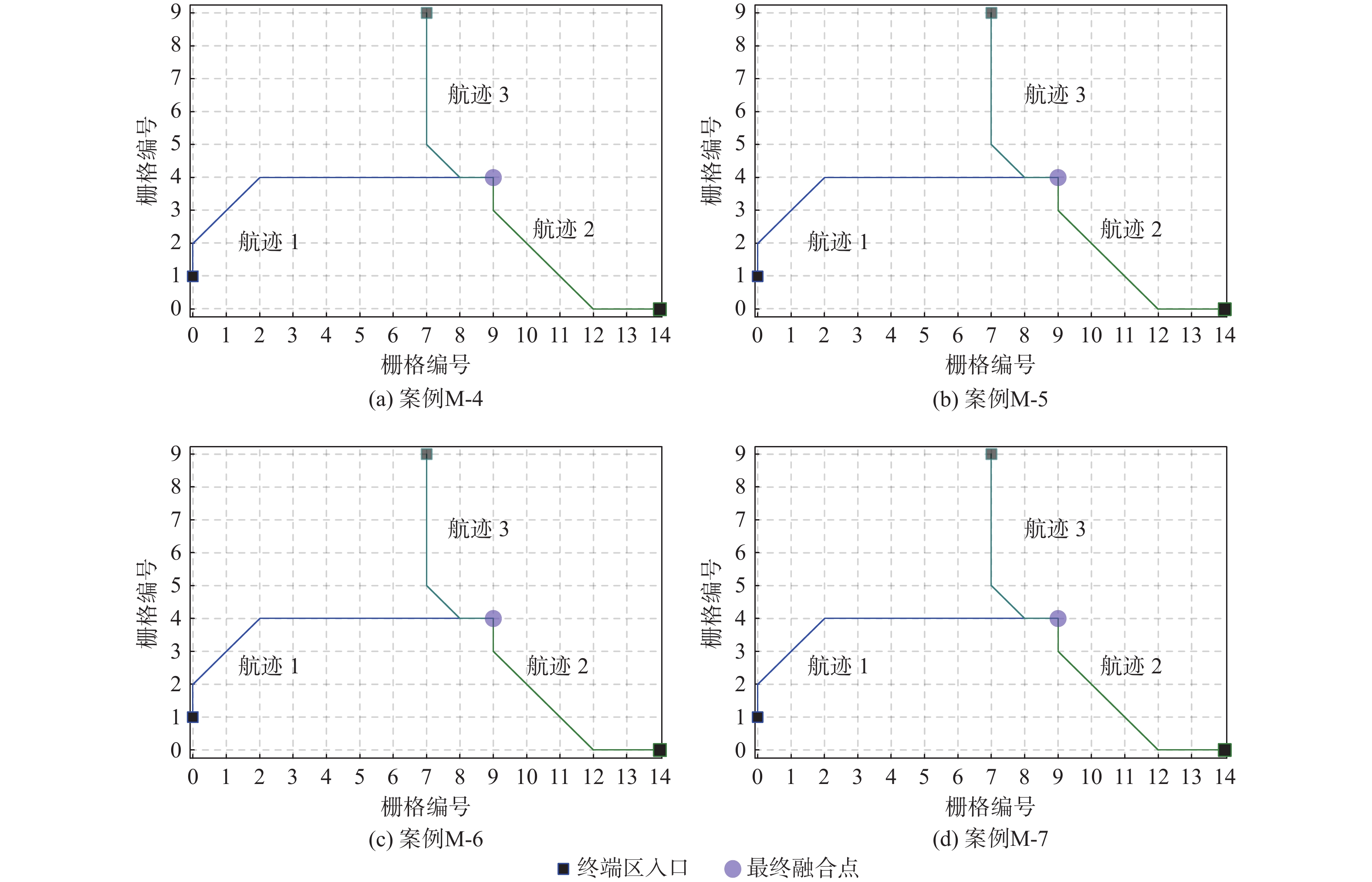
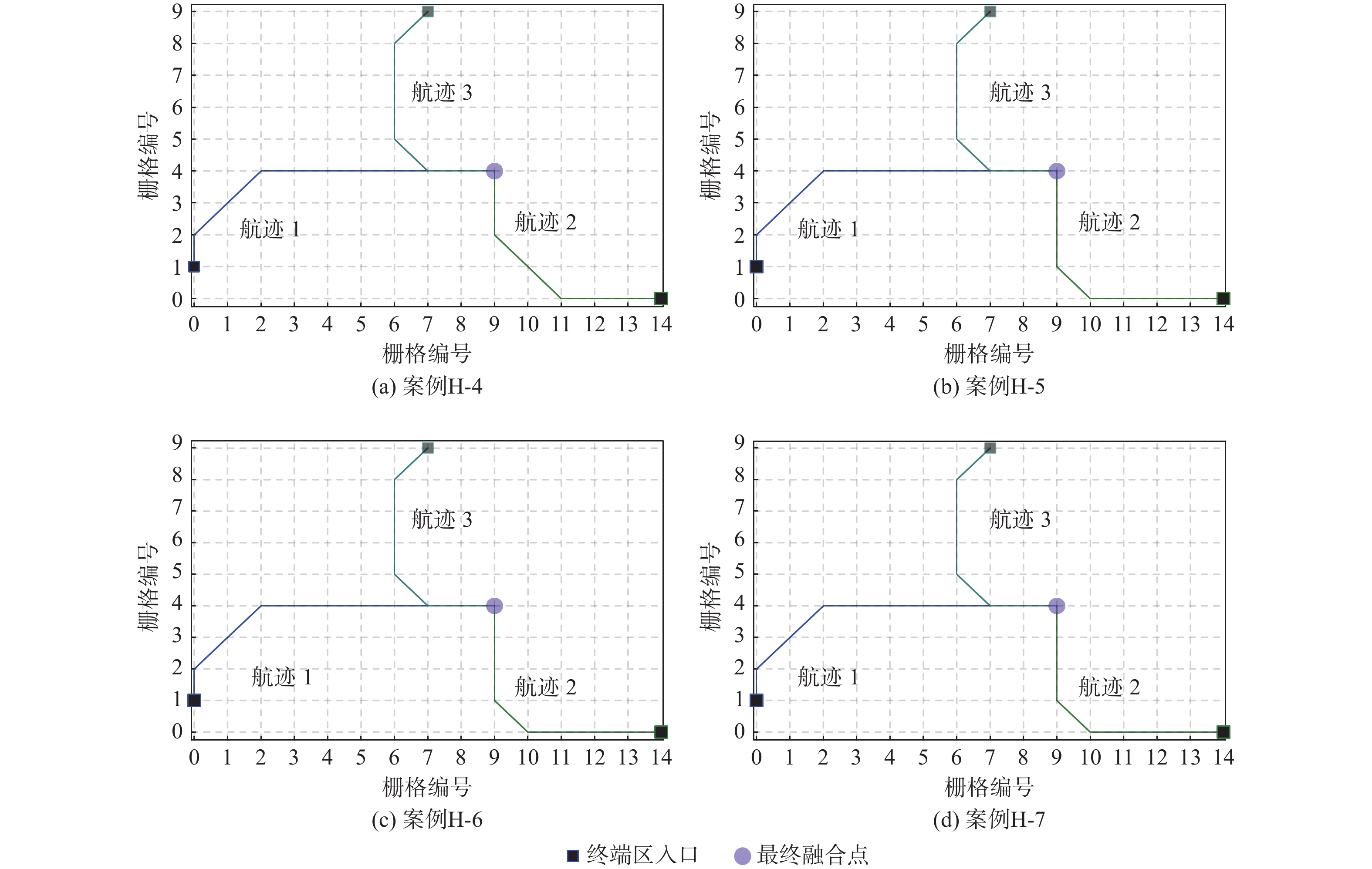
Table 4. Data for different test cases
测试 密度 航班量 时间窗/min 三入口航班量 L-3 低 14 1 4-6-4 L-4 低 15 1 4-7-4 L-5 低 13 1 6-4-3 L-6 低 13 1 4-4-5 M-4 中 21 1 8-8-5 M-5 中 23 1 9-9-5 M-6 中 22 1 9-7-6 M-7 中 22 1 8-9-5 H-4 高 31 3 10-10-11 H-5 高 33 3 10-11-12 H-6 高 32 3 11-10-11 H-7 高 32 3 11-11-10
下载: 导出CSV
-
[1] BENTRUP L, HONFFMANN M. Free routing airspace in Europe[C]//Proceedings of the International Conference on Research in Air Transportation. Drexel: ICRAT, 2016. [2] Eurocontrol. Point merge integration of arrival flows enabling extensive RNAV application and continuous descent - operational services and environment definition (V2.0) [EB/OL]. (2010-07-19)[2023-04-20]. https://www.eurocontrol.int/concept/point-merge. [3] 张军峰, 游录宝, 周铭, 等. 基于点融合系统的多目标进场排序与调度[J]. 北京航空航天大学学报, 2023, 49(1): 66-73.ZHANG J F, YOU L B, ZHOU M, et al. Multi-objective arrival sequencing and scheduling based on point merge system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(1): 66-73(in Chinese). [4] 赵向领, 雷碧玉. 点汇聚进近飞行程序近地风险评估方法研究[J]. 中国安全科学学报, 2017, 27(3): 157-162.ZHAO X L, LEI B Y. Research on method for assessing risk in ground approach under point merging procedure[J]. China Safety Science Journal, 2017, 27(3): 157-162(in Chinese). [5] CECEN R K. Multi-objective TMA management optimization using the point merge system[J]. Aircraft Engineering and Aerospace Technology, 2021, 93(1): 15-24. doi: 10.1108/AEAT-09-2019-0181 [6] LEE S, HONG Y, KIM Y. Optimal scheduling algorithm in point merge system including holding pattern based on mixed-integer linear programming[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2020, 234(10): 1638-1647. doi: 10.1177/0954410019830172 [7] 戴喜妹. 基于分派规则的航班排序与调度研究[D]. 南京: 南京航空航天大学, 2019: 4-50.DAI X M. Research on flight sequencing and scheduling based on assignment rules[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2019: 4-50(in Chinese) . [8] 刘继新, 江灏, 董欣放, 等. 基于空中交通密度的进场航班动态协同排序方法[J]. 航空学报, 2020, 41(7): 279-294. doi: 10.7527/S1000-6893.2020.23717LIU J X, JIANG H, DONG X F, et al. Dynamic collaborative sequencing method for arrival flights based on air traffic density[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(7): 279-294(in Chinese). doi: 10.7527/S1000-6893.2020.23717 [9] 乐美龙, 吴宪晟, 胡钰明. 基于滚动时域控制的多路径进场航班排序优化[J]. 北京航空航天大学学报, 2023, 49(12): 3222-3229.LE M L, WU X S, HU Y M. Arrival flights optimal sequencing based on path selection and rolling horizon control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(12): 3222-3229(in Chinese). [10] 张军峰, 游录宝, 杨春苇, 等. 基于多目标帝国竞争算法的进场排序与调度[J]. 航空学报, 2021, 42(6): 464-476.ZHANG J F, YOU L B, YANG C W, et al. Arrival sequencing and scheduling based on multi-objective Imperialist competitive algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(6): 464-476(in Chinese). [11] SAMÀ M, D’ARIANO A, CORMAN F, et al. Metaheuristics for efficient aircraft scheduling and re-routing at busy terminal control areas[J]. Transportation Research Part C: Emerging Technologies, 2017, 80: 485-511. doi: 10.1016/j.trc.2016.08.012 [12] LIANG M, DELAHAYE D, MARÉCHAL P. Integrated sequencing and merging aircraft to parallel runways with automated conflict resolution and advanced avionics capabilities[J]. Transportation Research Part C: Emerging Technologies, 2017, 85: 268-291. doi: 10.1016/j.trc.2017.09.012 [13] HONG Y, CHOI B, KIM Y. Two-stage stochastic programming based on particle swarm optimization for aircraft sequencing and scheduling[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(4): 1365-1377. doi: 10.1109/TITS.2018.2850000 [14] SALEHIPOUR A, MODARRES M, MOSLEMI NAENI L. An efficient hybrid meta-heuristic for aircraft landing problem[J]. Computers & Operations Research, 2013, 40(1): 207-213. [15] 张洪海, 汤一文, 许炎. TBO模式下终端区进场交通流优化模型与仿真分析[J]. 航空学报, 2020, 41(7): 319-332.ZHANG H H, TANG Y W, XU Y. Optimizing arrival traffic flow in airport terminal airspace under trajectory based operations[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(7): 319-332(in Chinese). [16] 杨磊, 李文博, 刘芳子, 等. 柔性空域结构下连续下降航迹多目标优化[J]. 航空学报, 2021, 42(2): 200-216.YANG L, LI W B, LIU F Z, et al. Multi-objective optimization of continuous descending trajectories in flexible airspace[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(2): 200-216(in Chinese). [17] 陈昇, 周隽, 胡小兵, 等. 基于混合模拟退火算法的机场进场程序优化[J]. 计算机应用, 2022, 42(2): 606-615.CHEN S, ZHOU J, HU X B, et al. Optimization of airport arrival procedures based on hybrid simulated annealing algorithm[J]. Journal of Computer Applications, 2022, 42(2): 606-615(in Chinese). [18] CECEN R K. A stochastic programming model for the aircraft sequencing and scheduling problem considering flight duration uncertainties[J]. The Aeronautical Journal, 2022, 126(1304): 1736-1751. doi: 10.1017/aer.2022.17 [19] CECEN R K. A path stretching model for effective terminal airspace management[J]. International Journal of Aeronautical and Space Sciences, 2022, 23(5): 1043-1052. doi: 10.1007/s42405-022-00486-z [20] LEE H, BALAKRISHNAN H. A study of tradeoffs in scheduling terminal-area operations[J]. Proceedings of the IEEE, 2008, 96(12): 2081-2095. doi: 10.1109/JPROC.2008.2006145 [21] ZHANG H H, YANG X L, FAN W, et al. Guidance control strategy for air traffic flow in terminal areas[J]. Advances in Mechanical Engineering, 2016, 8(10): 1-12. [22] SÁEZ R, PRATS X, POLISHCHUK T, et al. Traffic synchronization in terminal airspace to enable continuous descent operations in trombone sequencing and merging procedures: an implementation study for Frankfurt Airport[J]. Transportation Research Part C: Emerging Technologies, 2020, 121: 102875. doi: 10.1016/j.trc.2020.102875 [23] CHIDA H, ZUNIGA C, DELAHAYE D. Topology design for integrating and sequencing flows in terminal maneuvering area[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2016, 230(9): 1705-1720. doi: 10.1177/0954410016636155 [24] SÁEZ R, POLISHCHUK T, SCHMIDT C, et al. Automated sequencing and merging with dynamic aircraft arrival routes and speed management for continuous descent operations[J]. Transportation Research Part C: Emerging Technologies, 2021, 132: 103402. doi: 10.1016/j.trc.2021.103402 [25] SÁEZ R, PRATS X, POLISHCHUK T, et al. Automation for separation with continuous descent operations: dynamic aircraft arrival routes[J]. Journal of Air Transportation, 2020, 28(4): 144-154. doi: 10.2514/1.D0176 [26] LIU J M, GUO Z, YU B. Optimising Gate assignment and taxiway path in a discrete time–space network: integrated model and state analysis[J]. Transportmetrica B: Transport Dynamics, 2023, 11(1): 1-23. doi: 10.1080/21680566.2022.2036650 [27] 中国民用航空局. 民用航空空中交通管理规则: CCAR-93-R5[S]. 北京: 中国民用航空局, 2018: 86-91.Civil Aviation Administration of China. Civil aviation air traffic management rules: CCAR-93-R5[S]. Beijing: Civil Aviation Administration of China, 2018: 86-91(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 265
- HTML全文浏览量: 39
- PDF下载量: 7
- 被引次数: 0
