Dual-phase scheduling of apron support vehicles considering multi-vehicle coordination
-
摘要:
大型机场机坪保障车辆一直面临较大运行压力,而多种机坪保障服务的配合约束和动态航班信息对车辆调度提出更高挑战。考虑连续工作、容量限制的连续工作和往返工作3种不同模式车辆运行约束差异,以车辆数量最少和行驶总距离最小为目标,建立多车型协同的机坪保障车辆调度模型。根据机场实际运行情况,对该模型进行双阶段求解,在静态阶段设计一种融合局部搜索的非支配排序遗传算法Ⅱ(LS-NSGA Ⅱ),在动态阶段设计一种类邻域搜索算法求解多车型协同调度问题。数据仿真结果表明:所建模型静态调度阶段结果相对于先到先服务(FCFS),车辆数量和行驶总距离分别降低了18.9%和8.9%;动态调度阶段结果能保持原调度计划车辆数量,行驶距离调整量相较于大规模邻域搜索算法降低了25.8%。研究结果可以为大型机场机坪保障车辆调度管理和决策提供一定的指导。
Abstract:The coordination restrictions of several apron support services and dynamic flight information have resulted in increased operational demand on large airport apron support vehicles and more difficulties with vehicle scheduling. Considering the difference of vehicle operation constraints in three different modes of continuous operation, capacity-limited continuous operation and round-trip operation, a multi-vehicle cooperative apron support vehicle scheduling model is established with the goal of minimizing the number of vehicles and the total driving distance. The model is solved in two stages according to the actual operation of the airport. In the static stage, a local search non-dominated corting genetic algorithms Ⅱ (LS-NSGA II) algorithm integrating local search is designed. In the dynamic stage, a similar neighborhood search algorithm is designed. The static results show that the number of vehicles and the total driving distance are reduced by 18.9% and 8.9% respectively compared with the first-come-first-served. In comparison to the big neighborhood search technique, the dynamic results can keep the number of cars in the static scheduling plan while reducing the adjusted driving distance by 25.8%. The research results can provide a certain guiding significance for the scheduling management and decision-making of large airport apron support vehicles.
-
机坪保障车辆作为保障航班服务质量和时效性的重要支持设备,现阶段普遍采用基于先到先服务(first-come-first-served,FCFS)的人工指派调度[1-3],而这种调度策略已经无法满足日趋繁忙的大型枢纽机场,亟待寻求科学高效的机坪保障车辆调度策略。由于航空器机坪服务所需保障车辆类型众多、服务种类多样、车辆服务时间约束迥异、车载资源受限,因此,若能根据不同车型工作方式设置独特约束条件,再将所有车辆看作一个整体进行统一调度,则能进一步提高保障车辆的服务效率。
国内外众多学者对大型机场机坪保障车辆调度策略已经进行了大量研究,绝大多数学者的主要研究对象为某类单一车型,并考虑单车型的独特运行模式[4-5],如加油车[6-7]、摆渡车[8-9]、行李车[10]、除冰车[11]等。
关于多车型协同的机坪保障车辆调度研究发展迅速。多车型协同是指将2种或2种以上的车型作为一个整体进行协同配置,以实现更大范围的高效率机坪保障车辆调度。Zhao等[12]以摆渡车和牵引车为研究对象,以车辆数量最少和任务均衡量最大为目标建立双目标混合整数规划(mixed integer programming,MIP)模型。Zhu等[13]以加油车和摆渡车为研究对象,设计了考虑两者时间约束的多目标混合整数规划模型,并使用CPLEX求解器进行求解。
在机场的实际运行过程中,机坪保障车辆调度可以分为2个阶段:静态调度阶段和动态调度阶段。上述研究[12-13]主要针对静态阶段,而针对动态阶段的车辆调度策略研究逐渐成为近年来的研究热点。在机坪保障车辆动态调度问题中很多相关信息是不确定且随机的,如服务航班的进离港时间发生变化[14-15]或航班更改停靠机坪[16]等,因此,在调度保障车辆时须根据实时信息对车辆路径进行及时调整。大型机场机坪保障车辆动态调度问题的本质是带时间窗的动态车辆路径问题(dynamic vehicle routing problem with time windows, DVRPTW),因此,可以参考这一领域内的相关研究[17-19]。
综上,目前已有的研究中多车型协同主要体现在车型种类,鲜有从车辆工作方式的角度出发进行研究;在动态调度研究中,大都是将动态问题直接转化为静态模型并使用传统DVRPTW的求解算法和思路,未考虑机坪保障车辆实时调度场景的适用性。因此,本文基于对机坪保障车辆工作方式的分析,选取代表性车型进行协同调度研究,并设计双阶段算法进行求解。
1. 问题描述
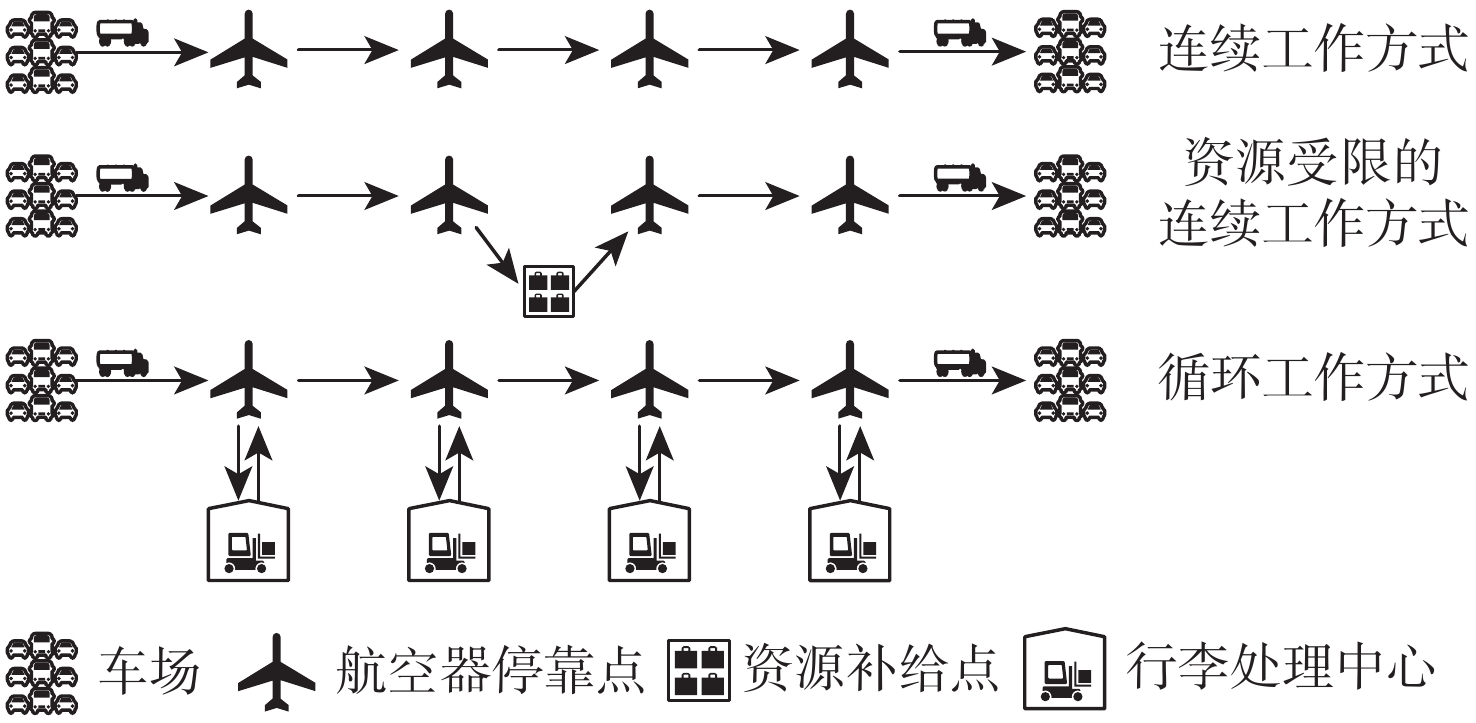
所有类型的机坪保障车辆都必须按照民用机场规定的运行模式进行调度和服务。本文分析了机坪保障车辆的工作方式并将其分为3类,如图1所示。
连续工作方式指机坪保障车辆从车场出发后前往服务点进行地面保障服务,结束任务后继续前往下一服务点直至完成所有任务后返回车场;资源受限的连续工作方式指当剩余车载资源无法满足下一个服务点的需求,必须返回补给点补充资源后再执行后续任务;循环工作方式是指机坪保障车辆在进行服务需要往返于多个服务点,是最复杂的车辆工作方式。
本文以传送带车、清水车和行李牵引车3种典型车辆为研究对象,主要功能是完成进离港航班的行李服务和清水服务,且传送带车和行李牵引车需要相互协同配合工作,从而完成机坪保障服务。
机坪保障车辆从航班i停靠点到航班j停靠点转场时的行驶距离与车辆工作方式有关。本文使用希腊字母α、β和γ分别表示行李牵引车、传送带车和清水车。调度有向图G中,dij表示航班i停靠点到航班j停靠点的实际距离,sqij表示q类型车辆从航班i停靠点到航班j停靠点的转场距离,a、b和c分别表示清水补给点、行李中心停靠点和车场。
行李牵引车为循环工作方式,其转场距离与航班性质有关,具体如表1所示。传送带车为连续工作方式车辆,其转场距离sβij=dij。清水车为资源受限的连续工作方式,当资源不够需要前往补给点时,其转场距离sγij=dia+daj,其余情况sγij=dij。
表 1 行李牵引车转场距离Table 1. Luggage tractor transfer distance前序航班i性质 后序航班j性质 车辆转场方向 转场距离sαij 进港 进港 行李中心→停机位 dbj 进港 离港 行李中心→行李中心 0 离港 进港 停机位→停机位 dij 离港 离港 停机位→行李中心 dib 2. 机坪保障车辆协同调度模型
2.1 模型假设
1) 航班机型及车辆基本信息完备无误,且不会发生变更。
2) 机坪保障车辆一旦开始服务,不会因任何情况中断直至该项任务结束。
3) 同类型的机坪保障车辆性能相同,车辆操作人员的工作能力和效率相同。
4) 车辆均从车场出发,完成所有任务后再次返回车场,且行驶速度不变。
2.2 单车型调度模型
机坪保障车辆单车型调度模型目标函数如下:
Zq1 = min∑k∈Nqyqk (1) Zq2=min∑k∈Nq∑i,j∈Hqsqijxqijk (2) 式中:Nq为q车型车辆集合;Hq为q车型需要服务的航班集合。式(1)表示q车型车辆数目最少;式(2)表示q车型行驶距离最小。
式(3)~式(9)为通用约束。式(3)表示每个航班只接受一次q类型车辆的服务;式(4)~式(6)表示车辆路的流量限制,即车辆最多同时服务一个航班;式(7)表示使用的机坪保障车辆不能超过可用车辆数量;式(8)表示车辆k到达航空器j停靠点的时间不晚于该航空器服务开始时间;式(9)表示q车型开始服务航班i的时间必须在该类型服务开始时间窗内。
∑k∈Nqzqik=1∀i∈Hq (3) ∑i∈Hqxqcik⩽ (4) {\displaystyle \sum _{j\in {H}^{q}}{x}_{ijk}^{q}}-{\displaystyle \sum _{j\in {H}^{q}}{x}_{jik}^{q}}=0\quad\quad \forall k\in {N}^{q},\forall i\in {H}^{q} (5) \sum\limits_{i \in {H^q}} {x_{ick}^q} \leqslant 1\quad\quad \forall k \in {N^q} (6) \sum\limits_{k \in {N^q}} {y_k^q \leqslant {U^q}} (7) E_{ik}^q + \frac{{s_{ij}^q}}{v} - (1 - x_{ijk}^q)M \leqslant S_{jk}^q\quad\quad \forall k \in {N^q},{\text{ }}\forall i,j \in {H^q} (8) {A}_{i}^{q}{{\textit{z}}}_{ik}^{q}\leqslant {S}_{ik}^{q}{{\textit{z}}}_{ik}^{q}\leqslant {B}_{i}^{q}{{\textit{z}}}_{ik}^{q}\quad\quad \forall k\in {N}^{q},\text{ }\forall i\in {H}^{q} (9) 式中: {\textit{z}}_{ik}^q 为决策变量;{U^q}为q车型可用车辆数量;E_{ik}^q为q车型车辆k结束服务航班i的时间;S_{ jk}^q为q车型车辆k开始服务航班j的时间;v为机坪保障车辆行驶速度;M为无穷大正数; A_i^q 为q车型服务航班i的最早开始时间; B_i^q 为q车型服务航班i的最晚开始时间。
式(10)~式(11)为清水车特定约束。式(10)表示清水车从车场出发时为空载状态;式(11)表示清水车在运行过程中剩余清水量不小于0也不超过最大容积。
{c}_{ck}^{\gamma}{y}_{k}^{\gamma}=0\quad\quad \forall k\in {N}^{\gamma} (10) 0\leqslant {c}_{ik}^{\gamma}{{\textit{z}}}_{ik}^{\gamma}\leqslant P\quad\quad\forall i\in {H}^{\gamma},\text{ }\forall k\in {N}^{\gamma} (11) 式中: c_{ck}^\gamma 为清水车k服务完航班i后的剩余清水容量;P为清水车最大容量。
x_{ijk}^q 为0-1决策变量,当q车型的车辆k依次服务航班i、j时其值为1,否则为0; y_k^q 为0-1决策变量,当q车型的车辆k被启用时其值为1,否则为0; {\textit{z}}_{ik}^q 为0-1决策变量,当q车型的车辆k服务航班i时其值为1,否则为0。
2.3 多车型协同调度模型
在机场地面保障实际运行环节中,需要不同车型相互配合完成服务。本文主要考虑传送带车和行李牵引车之间的协同配合。
机坪保障车辆多车型协同调度的目标函数如下:
{Z_1}{\text{ = }}\min \sum\limits_{k \in {N^q}} {\sum\limits_{q \in Q} {y_k^q} } (12) {Z}_{2}\text=\mathrm{min}{\displaystyle \sum _{k\in {H}^{q}}{\displaystyle \sum _{i,j\in {H}^{q}}{\displaystyle \sum _{q\in Q}{s}_{ij}^{q}{x}_{ijk}^{q}}}} (13) 式中:Q为机坪保障车辆类型集合。
式(12)表示所有机坪保障车辆数量最少;式(13)表示所有机坪保障车辆行驶总距离最小。最小化车辆数量是为探索完成保障所必须的资源支持数量,最小化行驶总距离是为减少车辆运行成本的同时尽可能避免车辆在飞行区大面积活动。
在行李装卸服务中,行李牵引车和传送带车必须同时抵达服务地点才可以工作。因此,协同调度在满足单车型调度约束式(3)~式(11)外,还需要满足如下约束条件:
{T}_{ik}^{\alpha}\geqslant {T}_{il}^{\beta}\quad\quad \forall i\in H,\forall k\in {N}^{\alpha},\forall l\in {N}^{\beta} (14) \begin{array}{l}{S}_{ik}^{\alpha}={S}_{il}^{\beta}= \left\{ \begin{array}{cc}{T}_{ik}^{\alpha}\qquad {T}_{ik}^{\alpha} \gt {A}_{i}^{\alpha}\\ {A}_{i}^{\alpha}\qquad {T}_{ik}^{\alpha}\leqslant {A}_{i}^{\alpha}\end{array}\quad\quad \right.\\ \quad\quad \forall i\in H,\forall k\in {N}^{\alpha},\forall l\in {N}^{\beta}\end{array} (15) {E}_{ik}^{\alpha}={E}_{il}^{\beta}\quad\quad \forall i\in H,\forall k\in {N}^{\alpha},\forall l\in {N}^{\beta} (16) 式中: T_{ik}^q 为q车型车辆k到达航班i停靠点的时间。式(14)~式(16)为车辆协同约束。式(14)表示传送带车必须在行李牵引车前抵达;式(15)表示只有传送到车和行李牵引车同时到达服务点才可以开始行李服务;式(16)表示服行李牵引车结束服务后传送带车方可结束服务。
3. 双阶段调度求解方法
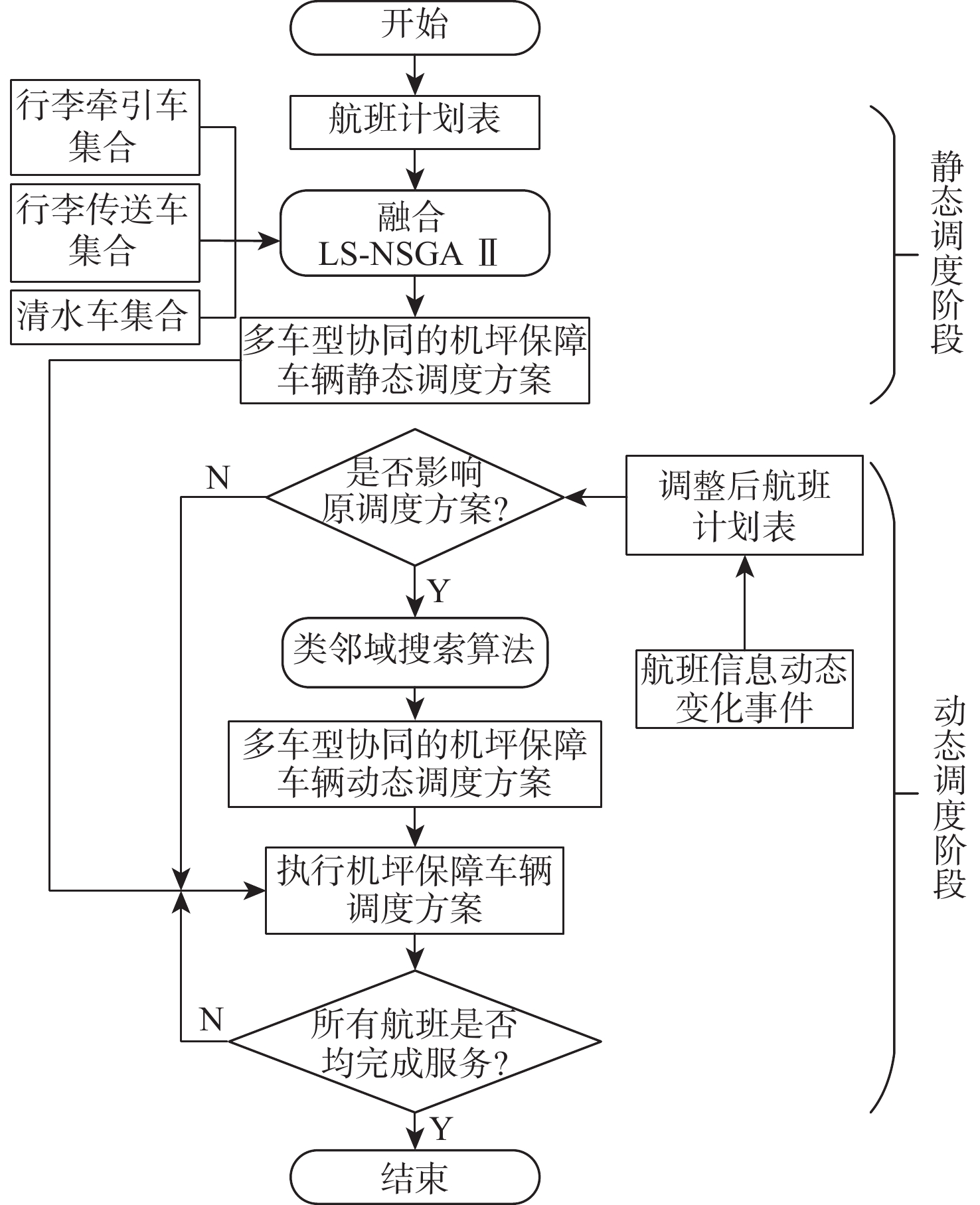
机坪保障车辆调度分为双阶段,即静态调度和动态调度。静态调度是指根据待执行的航班计划表求解多车型协同配合的机坪保障车辆调度方案。动态调度是根据临时发生的航班信息变化对静态调度方案进行实时调整,快速高效地得到新调度方案。本文设计的多车型协同的机坪保障车辆双阶段求解流程如图2所示。
针对多车型协同的机坪保障车辆静态调度,本文采用融合局部搜索的非支配排序遗传算法Ⅱ(local search non-dominated sorting genetic algorithms Ⅱ,LS-NSGA Ⅱ)。首先,采用节约里程算法构建初始解以保证初始解质量;其次,使用LS-NSGA Ⅱ对初始解进行迭代计算,得到Pareto最优解集;最后,使用多属性决策中有序加权平均算子得到满足协同约束的多车型调度问题的最优解。
针对多车型协同的机坪保障车辆动态调度,本文参考邻域搜索算法中的破坏和修复理念设计类邻域搜索(similar neighborhood search,SNS)算法。首先,判断原有的调度计划是否满足变化的航班计划表;其次,筛选出原方案中需要调整服务车辆的航班;最后,将需要调整的航班按照新时间窗和协同约束插入到车辆路径中,以达到快速响应的目的。
3.1 静态调度阶段算法设计
本文在传统NSGA Ⅱ基础的交叉变异操作后增加局部搜索操作,在保证算法具备全局搜索能力的同时提高局部搜索能力,能更快贴近最优解,提高求解质量和效率。
局部搜索操作的核心是破坏操作和修复操作。通过破坏算子筛选出种群中需要调整的航班,再根据修复算子将这些航班重新插入车辆路径中,得到新调度方案。根据机坪保障车辆调度模型的特点,引入随机移除和最差值移除2种破坏算子,以及最小插入成本、最大遗憾值2种修复算子,且根据新个体的质量选择破坏算子和修复算子。LS-NSGA Ⅱ主函数伪代码如下:
输入 迭代前种群C,迭代次数{\mathrm{gen}},交叉概率P_{\mathrm{c}},变异概率P_{\mathrm{m}},航班信息集合{{s}},停机位间距离矩阵 \boldsymbol{d} ,清水车容量限制P。
输出 迭代后种群C'。
1. F←C //生成父代初始种群F
2. 对F进行非支配排序和拥挤度计算
3. t←1
4. while t \leqslant {\mathrm{gen}}
5. Q←\varnothing
6. for i←1 to {\mathrm{length}}[F]
7. 使用二元锦标赛方法对F进行选择操作,选出个体f
8. Q←Q \cup f
9. end for
10. for j←1 to {\mathrm{length}}[Q]
11. g←Q(j,:) //提取第j个个体
12. 对g进行交叉、变异、局部搜索操作,生成新个体g'
13. Q(j,:)←g'
14. end for
15. W←Q \cup F
16. 对W进行非支配排序计算
17. F←对W进行精英选择策略,得到新父代种群
18. t←t + 1
19. end while
20. C'←F
21. return C'
3.2 动态调度阶段算法设计
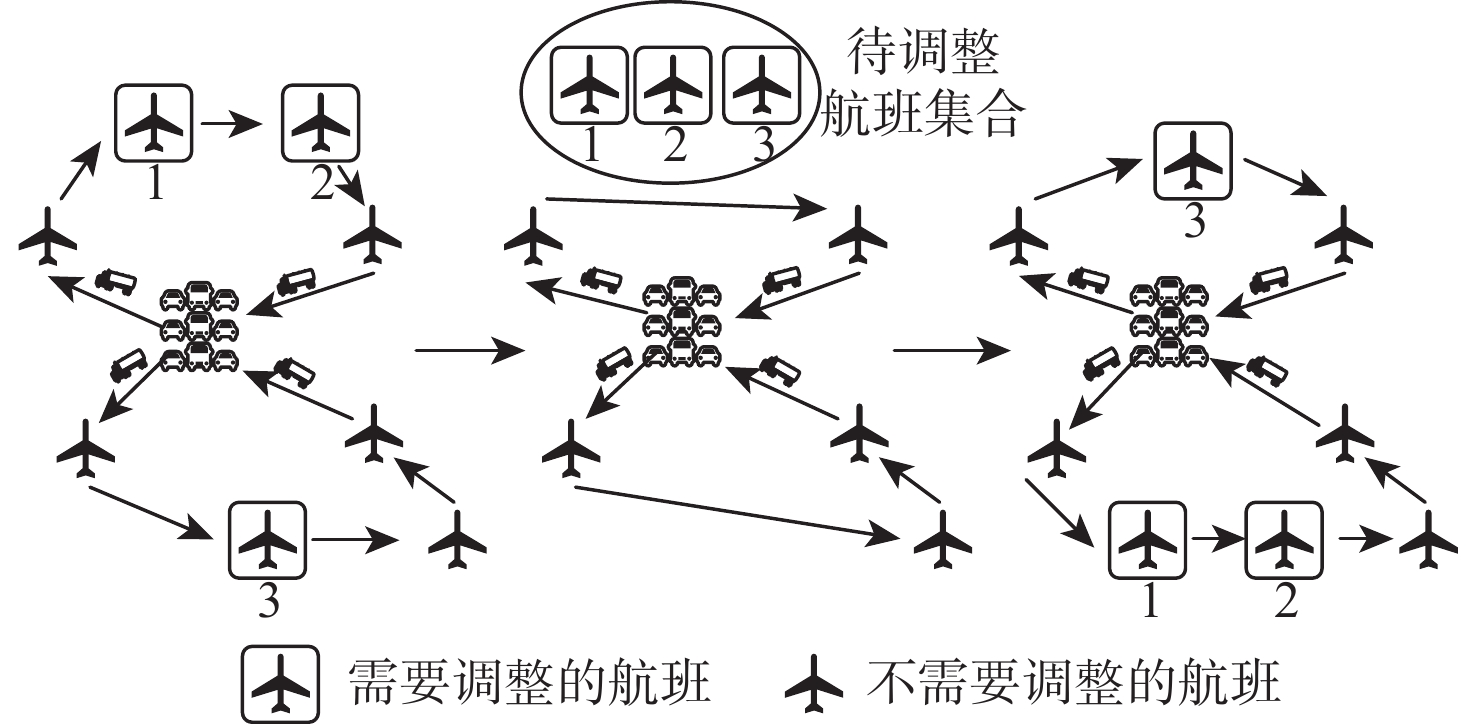
本文设计了一种类邻域搜索算法,SNS算法的整体思想如图3所示。航班信息发生变化后,将需要调整保障车辆的航班移动至待调度航班集合 H_{\rm{adjust}}^q 中,完成破坏操作;再将待调度航班插入至新路径中,完成修复操作。为满足动态调度的时效性,若调整结果没有违反任何单车型调度和协同调度约束条件,则完成动态调度,不再进行迭代寻找最优解。
本文假设在开始动态调整时,已经完成或正在进行的调度计划不会发生变化。SNS算法主函数伪代码如下:
输入 原始调度方案X,原始航班信息集合{{s}},动态航班信息集合{{s}}',停机位间距离矩阵\boldsymbol{d} ,清水车容量限制P。
输出 动态调度方案X'。
1. H_{{\mathrm{adjust}}}^\alpha ;H_{{\mathrm{adjust}}}^\beta ;H_{{\mathrm{adjust}}}^\gamma ←{{s}},{{s}}',X
//得到待重新调整的航班集合
2. [{{V}}^\alpha ;{{V}}^\beta ;{{V}}^\gamma ]←X //各车型原始调度路径
3. while H_{{\mathrm{adjust}}}^\alpha \ne \varnothing &&H_{{\mathrm{adjust}}}^\beta \ne \varnothing && H_{{\mathrm{adjust}}}^\gamma \ne \varnothing
4. while H_{\rm{adjust}}^\alpha \ne \varnothing
5. {V}^{\alpha}\leftarrow\mathrm{repair}(H_{\rm{adjust}}^{\alpha}) //行李牵引车动态调度
6. end while
7. while H_{\rm{adjust}}^\gamma \ne \varnothing
8. {{V}}^\gamma \leftarrow {\mathrm{repair}}(H_{\rm{adjust}}^\gamma )//清水车动态调度
9. end while
11. while H_{\rm{adjust}}^\beta \ne \varnothing
12. {{V}}^\beta \leftarrow {\mathrm{repair}}(H_{\rm{adjust}}^\beta ) //清水车动态调度
13. end while
14. X'←[{{V}}^\alpha ;{{V}}^\beta ;{{V}}^\gamma ]
15. if X'中有违反任意多车型协同调度模型约束的航班
16. H_{\rm{adjust}}^q ←违反约束条件的航班
17. end if
18. end while
19. return X'
4. 实例分析
4.1 实验数据
本文以中国某大型机场T2航站楼实际运行数据为例,选取国庆假期某日高峰时刻进离港航班数据,验证多车型协同机坪保障车辆调度模型和双阶段求解算法的可靠性。
4.1.1 航班与车辆信息
本文共选取145个航班,其中,进港航班67个,离港航班78个,始发航班11个,过站航班共有67对。航班计划表要素如表2所示。
表 2 航班计划表(示例)Table 2. Flight schedule (example)航班编号 机型 机位 计划进/离港时刻 航班性质 过站时长/min 1 A32B 268 10:00 进港 65 2 ERJ190 434 10:00 离港 65 车辆信息主要包括车辆可用数量、车辆所需数量和工作时长,如表3所示。
表 3 车辆所需数量和服务时长Table 3. Number of vehicles required and minutes of service机型 车辆所需数量/台 服务时长/min 行李牵引车 传送带车 清水车 行李牵引车 传送带车 清水车 进港 离港 进港 离港 C 1 1 1 15 25 15 25 5 D 2 1 1 15 25 15 25 7 E 2 1 1 15 25 15 25 7 F 3 2 1 20 30 20 30 9 4.1.2 算法参数
本文设计的算法均在MATLAB平台上实现,LS-NSGA Ⅱ相关参数设置如表4所示。
表 4 LS-NSGA Ⅱ参数设置Table 4. LS-NSGA Ⅱ parameters settings参数 数值 LS-ANSGA Ⅱ迭代次数 300 LS-ANSGA Ⅱ种群大小 150 交叉概率 0.7 变异概率 0.05 目标函数权重 0.5 4.1.3 动态调度信息
本文设计的动态情景为得知未来2 h内发生的航班变动信息,表5为不同类型航班信息变化数量。变化出现频率及变更时长符合该机场历史数据,因此,本文设计的动态情景能在一定程度上还原实际运行中的动态变化。
表 5 动态变化的航班数量Table 5. Number of dynamic change flights航班性质 航班数量 时间变更 停机位变更 航班取消 进港 33 2 1 离港 14 2 1 4.2 静态调度结果分析
4.2.1 静态调度算法对比
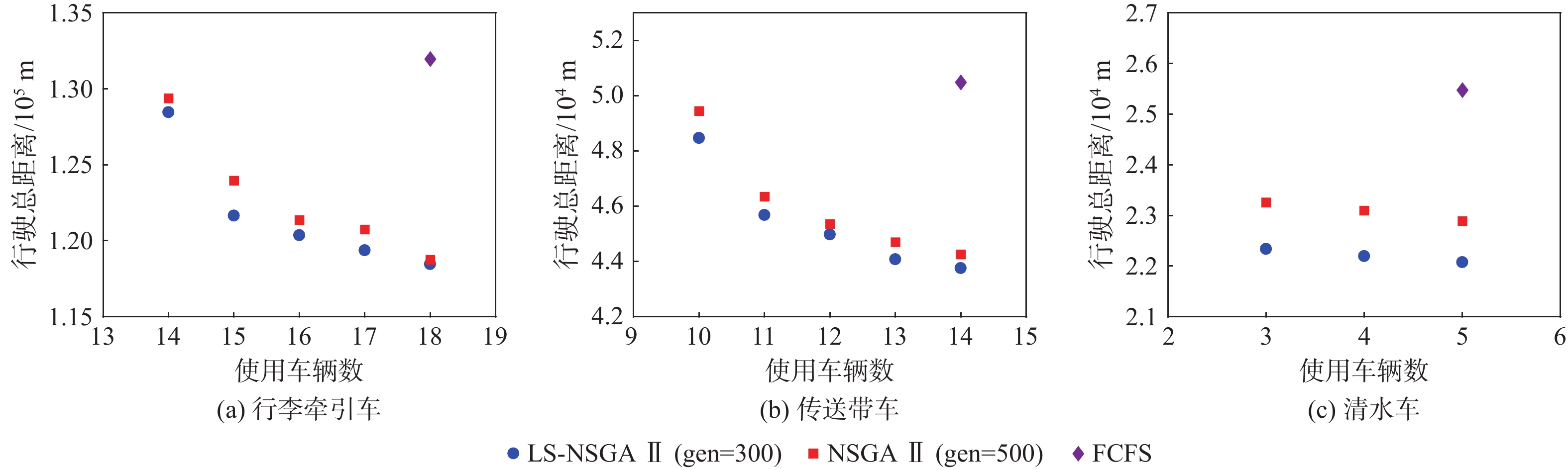
使用LS-NSGA Ⅱ对静态阶段求解得到Pareto最优解集,并与传统NSGA Ⅱ结果进行比较如表6所示,计算结果散点图如图4所示。其中,NSGA Ⅱ相关参数的设置与LS-NSGA Ⅱ一致。
表 6 LS-NSGA Ⅱ、NSGA Ⅱ和FCFS结果对比Table 6. LS-NSGA II,NSGA II and FCFS results comparison车辆类型 Z_1^i /台 Z_2^i /m 行李牵引车 传送带车 清水车 行李牵引车 传送带车 清水车 LS-NSGA Ⅱ 14 10 3 128456 48467 22336 15 11 4 121648 45679 22194 16 12 5 120358 44974 22074 17 13 119365 44075 18 14 118453 43754 NSGA Ⅱ 14 10 3 129375 49447 23257 15 11 4 123956 46346 23071 16 12 5 121365 45355 22887 17 13 120745 44698 18 14 118753 44256 FCFS 18 14 5 131965 50486 25476 通过有序加权平均算子得到多车型协同的整体最佳调度方案,最优结果在表6中加粗显示。同时与FCFS进行对比,对比结果如表7所示。
表 7 最优解对比Table 7. Comparison of optimal solutions算法 {Z_1} /台 {Z_2} /m LS-NSGA Ⅱ 30 189521 NSGA Ⅱ 30 193373 FCFS 37 207927 由图4可知,LS-NSGA Ⅱ求得的Pareto最优解集整体优于FCFS算法求得的唯一解,并通过更少的迭代次数获得比NSGA Ⅱ更好的优化结果。
由表7可知,LS-NSGA Ⅱ相较于FCFS算法需要的车辆总数减少7辆,降幅18.9%;行驶总距离减少18 406 m,降幅8.9%,这是由于FCFS策略只按照时间序列进行车辆调度,没有全局优化理念。相较于传统的NSGA Ⅱ,本文设计的LS-NSGA Ⅱ使用更少时间求解出相同车辆数目,并将行驶总距离减少了3 852 m,这是由于增加了局部搜索操作,在保证原有全局搜索能力的基础上加速局部搜索效率,加速了求解速度并提高结果质量。
综上,本文所建立的静态阶段算法在质量和效率上均优于对比的基准算法。
4.2.2 协同调度与顺序调度对比
表8为顺序调度和协同调度结果对比。顺序调度是指按照单车型调度模型分别求解3种车型调度结果,其中,传送带车需根据行李牵引车的调度结果进行求解以满足行李装卸服务的协同约束条件。
表 8 顺序调度与协同调度结果对比Table 8. Comparison of sequential scheduling and collaborative scheduling调度模式 {Z_1} /台 {Z_2} /m Z_1^i /台 Z_2^i /m 行李牵引车 传送带车 清水车 行李牵引车 传送带车 清水车 顺序调度 32 191873 16 12 4 122515 47033 22325 协同调度 30 189521 15 11 4 121648 45679 22194 由表8可知,相较于顺序调度,本文建立的协同调度模型车辆使用数减少了2辆,降幅6.3%,车辆行驶距离减少了2 352 m。其中,行李牵引车和传送带车的数量均减少1辆;行李牵引车、传送带车和清水车的行驶距离分别减少了867 m、
1354 m和131 m。这是由于顺序调度中传送带车在行李牵引车之后求解,为迎合牵引车的时间窗协同完成行李装卸服务,才造成传送带车数量上涨。而清水车没有协同约束条件,因此,其数量与顺序调度一样,车辆行驶距离仅有小幅降低。综上,本文建立的多车型协同调度模型能对机坪保障车辆进行更系统化的求解,并对2个目标函数的优化效果均优于独立调度。
4.3 动态调度结果分析
4.3.1 动态调度算法对比
对本文4.1.3节设置的动态情景求解,并与文献[20]中的自适应大邻域搜索(adaptive large neighborhood search,ALNS)算法进行对比,结果如表9所示。2种算法的车辆数涨幅相同,但与静态调度行驶距离的差值SNS算法比ALNS算法少25.8%。并且SNS算法能够使用更短的时间获得与ALNS算法所得相近的实时调度方案,结果表明,本文设计的SNS算法能根据航班动态信息快速高效获得实时调度方案,且调整速度满足机场实际运行需求。
表 9 SNS和ALNS算法结果对比Table 9. SNS and ALNS algorithms results comparison动态调度算法 {Z_1} /台 与静态调度差值/台 {Z_2} /m 与静态调度差值/m 计算时间/s SNS 32 +2 217111 + 27590 6.53 ALNS[20] 32 +2 228146 + 38625 142.72 4.3.2 动态调度与静态调度对比
使用SNS算法进行动态求解后结果与静态调度结果对比如表10所示。3种车型行驶总距离均有所增长,平均每辆行李牵引车增加约429 m,平均每辆传送带车增加582 m,平均每辆清水车增加372 m。2种车型使用数量均增加1辆,其中,清水车数量与原方案相同。
表 10 动态调度与静态调度结果对比Table 10. Comparison of dynamic scheduling and static scheduling调度模式 {Z_1} /台 {Z_2} /m Z_1^i /台 Z_2^i /m 行李牵引车 传送带车 清水车 行李牵引车 传送带车 清水车 动态调度 32 217111 16 12 4 136614 56816 23681 静态调度 30 189521 15 11 4 121648 45679 22194 为分析各车型机坪保障车辆路径变化情况,表11统计了不同信息变更情景下的航班数量。清水车调度中调整的航班数量不多,这是因为该车型主要服务离港航班,通常在发生延误前就已经完成清水操作,无需因延误调整调度计划,只有在停机位变更和航班取消时才必须做出实时调整。行李牵引车和传送带车的时间窗与计划进港/离港时间关系密切,几乎所有的航班信息变更情况都需要这2类车调整调度结果,因此,需要调整的航班数量较多,并且会影响到一部分正常航班。
表 11 动态调度中不同情景下的航班数量Table 11. Number of flights under different scenarios in dynamic scheduling机坪保障车辆
类型航班信息改变 航班信息未改变 保障车辆改变 保障车辆未改变 保障车辆改变 保障车辆未改变 行李牵引车 37 16 24 68 传送带车 28 25 15 77 清水车 3 14 0 61 为研究车辆服务过程中在场面的流动情况,本文将航站楼分为7个区域。由于优化目标包含最小化车辆行驶距离,会使调度结果中车辆呈现分区服务的状态,因为这样可以减少车辆在场面大面积和长距离流通,从而达到降低行驶距离的目的。由于行李牵引车使用数量最多且需要调整的航班最多,因此,以行李牵引车为例分析动态调度与静态调度车辆服务范围对比,结果如表12所示。其中,车辆16是在动态阶段的新增车辆,因此,该车无静态调度范围。
表 12 行李牵引车双阶段调度结果对比Table 12. Comparison of two-stage scheduling results of luggage tractor车辆序号 航站楼分区 1 2 3 4 5 6 7 1 √ √ ○ ○ 2 √ √ ○ ○ ○ 3 √ ○ ○ ○ 4 √ √ √ ○ 5 √ √ √ ○ ○ ○ 6 √ √ √ ○ ○ ○ ○ ○ ○ ○ 7 √ √ √ √ √ √ √ ○ ○ ○ ○ ○ ○ ○ 8 √ √ ○ ○ 9 √ √ ○ ○ ○ 10 √ √ √ √ √ √ √ ○ ○ ○ 11 √ ○ ○ 12 √ √ √ ○ ○ ○ 13 √ √ ○ ○ 14 √ √ ○ 15 √ √ ○ ○ 16 ○ ○ ○ 注:√表示静态调度,○表示动态调度。 综上,本文提出的SNS算法对连续工作方式和资源受限的连续工作方式的机坪保障车辆仍能保持原有的服务范围;对于循环工作方式的车辆虽然相较于静态方案有所改变,但仍能与原方案服务范围保持较高的相似度。
5. 结 论
分析机坪保障车辆工作方式、车辆转场距离、车辆特定运行规则、协同运行规则等车辆约束条件,在此基础上建立考虑多车型的机坪保障车辆协同调度模型,根据机场实际运行特点设计静态调度和动态调度双阶段求解算法。以中国某大型机场实际运行数据为案例,验证了本文模型和算法的有效性。本文主要结论如下。
1) 本文建立的多车型协同调度模型与各车型独立调度相比,车辆数量降低了6.3%,且每种车辆的行驶距离均有所下降。
2) 静态调度阶段在传统的NSGA Ⅱ基础上加入局部搜索操作,在保证算法全局搜索能力的同时加速局部搜索效率。与传统的先到先服务策略相比,能减少18.9%的车辆数量和8.9%的行驶总距离。
3) 动态阶段的SNS算法能满足机场实际动态变化情景,在计算时间和与原计划差值上均优于对比算法,并且动态调度结果能在车辆服务范围上与原计划保持高相似度。
机坪保障车辆系统不是独立运行的,停机位分配方案可能会使车辆调度计划无法满足服务需求。未来研究可以针对机坪保障车辆资源和停机位资源进行联合调度研究,分析联合调度的耦合因素和求解策略。对推动智慧机场发展,提高机场运营管理水平具有重要意义。
-
表 1 行李牵引车转场距离
Table 1. Luggage tractor transfer distance
前序航班i性质 后序航班j性质 车辆转场方向 转场距离 s_{ij}^\alpha 进港 进港 行李中心→停机位 {d_{bj}} 进港 离港 行李中心→行李中心 0 离港 进港 停机位→停机位 {d_{ij}} 离港 离港 停机位→行李中心 {d_{ib}} 表 2 航班计划表(示例)
Table 2. Flight schedule (example)
航班编号 机型 机位 计划进/离港时刻 航班性质 过站时长/min 1 A32B 268 10:00 进港 65 2 ERJ190 434 10:00 离港 65 表 3 车辆所需数量和服务时长
Table 3. Number of vehicles required and minutes of service
机型 车辆所需数量/台 服务时长/min 行李牵引车 传送带车 清水车 行李牵引车 传送带车 清水车 进港 离港 进港 离港 C 1 1 1 15 25 15 25 5 D 2 1 1 15 25 15 25 7 E 2 1 1 15 25 15 25 7 F 3 2 1 20 30 20 30 9 表 4 LS-NSGA Ⅱ参数设置
Table 4. LS-NSGA Ⅱ parameters settings
参数 数值 LS-ANSGA Ⅱ迭代次数 300 LS-ANSGA Ⅱ种群大小 150 交叉概率 0.7 变异概率 0.05 目标函数权重 0.5 表 5 动态变化的航班数量
Table 5. Number of dynamic change flights
航班性质 航班数量 时间变更 停机位变更 航班取消 进港 33 2 1 离港 14 2 1 表 6 LS-NSGA Ⅱ、NSGA Ⅱ和FCFS结果对比
Table 6. LS-NSGA II,NSGA II and FCFS results comparison
车辆类型 Z_1^i /台 Z_2^i /m 行李牵引车 传送带车 清水车 行李牵引车 传送带车 清水车 LS-NSGA Ⅱ 14 10 3 128456 48467 22336 15 11 4 121648 45679 22194 16 12 5 120358 44974 22074 17 13 119365 44075 18 14 118453 43754 NSGA Ⅱ 14 10 3 129375 49447 23257 15 11 4 123956 46346 23071 16 12 5 121365 45355 22887 17 13 120745 44698 18 14 118753 44256 FCFS 18 14 5 131965 50486 25476 表 7 最优解对比
Table 7. Comparison of optimal solutions
算法 {Z_1} /台 {Z_2} /m LS-NSGA Ⅱ 30 189521 NSGA Ⅱ 30 193373 FCFS 37 207927 表 8 顺序调度与协同调度结果对比
Table 8. Comparison of sequential scheduling and collaborative scheduling
调度模式 {Z_1} /台 {Z_2} /m Z_1^i /台 Z_2^i /m 行李牵引车 传送带车 清水车 行李牵引车 传送带车 清水车 顺序调度 32 191873 16 12 4 122515 47033 22325 协同调度 30 189521 15 11 4 121648 45679 22194 表 9 SNS和ALNS算法结果对比
Table 9. SNS and ALNS algorithms results comparison
动态调度算法 {Z_1} /台 与静态调度差值/台 {Z_2} /m 与静态调度差值/m 计算时间/s SNS 32 +2 217111 + 27590 6.53 ALNS[20] 32 +2 228146 + 38625 142.72 表 10 动态调度与静态调度结果对比
Table 10. Comparison of dynamic scheduling and static scheduling
调度模式 {Z_1} /台 {Z_2} /m Z_1^i /台 Z_2^i /m 行李牵引车 传送带车 清水车 行李牵引车 传送带车 清水车 动态调度 32 217111 16 12 4 136614 56816 23681 静态调度 30 189521 15 11 4 121648 45679 22194 表 11 动态调度中不同情景下的航班数量
Table 11. Number of flights under different scenarios in dynamic scheduling
机坪保障车辆
类型航班信息改变 航班信息未改变 保障车辆改变 保障车辆未改变 保障车辆改变 保障车辆未改变 行李牵引车 37 16 24 68 传送带车 28 25 15 77 清水车 3 14 0 61 表 12 行李牵引车双阶段调度结果对比
Table 12. Comparison of two-stage scheduling results of luggage tractor
车辆序号 航站楼分区 1 2 3 4 5 6 7 1 √ √ ○ ○ 2 √ √ ○ ○ ○ 3 √ ○ ○ ○ 4 √ √ √ ○ 5 √ √ √ ○ ○ ○ 6 √ √ √ ○ ○ ○ ○ ○ ○ ○ 7 √ √ √ √ √ √ √ ○ ○ ○ ○ ○ ○ ○ 8 √ √ ○ ○ 9 √ √ ○ ○ ○ 10 √ √ √ √ √ √ √ ○ ○ ○ 11 √ ○ ○ 12 √ √ √ ○ ○ ○ 13 √ √ ○ ○ 14 √ √ ○ 15 √ √ ○ ○ 16 ○ ○ ○ 注:√表示静态调度,○表示动态调度。 -
[1] KUHN K, LOTH S. Airport service vehicle scheduling[J]. Air Traffic Control Quarterly, 2010, 18(1): 63-83. doi: 10.2514/atcq.18.1.63 [2] NORIN A, GRANBERG T A, YUAN D, et al. Airport logistics–a case study of the turn——around process[J]. Journal of Air Transport Management, 2012, 20: 31-34. [3] NORIN A, YUAN D, GRANBERG T A, et al. Scheduling de-icing vehicles within airport logistics: a heuristic algorithm and performance evaluation[J]. Journal of the Operational Research Society, 2012, 63(8): 1116-1125. doi: 10.1057/jors.2011.100 [4] DU J Y, BRUNNER J O, KOLISCH R. Planning towing processes at airports more efficiently[J]. Transportation Research Part E: Logistics and Transportation Review, 2014, 70: 293-304. doi: 10.1016/j.tre.2014.07.008 [5] 王博, 王剑辉, 彭笑非, 等. 基于机场协同决策系统的机坪牵引车调度方法[J]. 科学技术与工程, 2021, 21(4): 1667-1673. doi: 10.3969/j.issn.1671-1815.2021.04.061WANG B, WANG J H, PENG X F, et al. The method for scheduling towing tractors based on A-CDM system[J]. Science Technology and Engineering, 2021, 21(4): 1667-1673(in Chinese). doi: 10.3969/j.issn.1671-1815.2021.04.061 [6] GAMAYANTI N, SAHAL M, WIBISONO A. Optimization of vehicle routing problem with tight time windows, short travel time and re-used vehicles (vrptsr) for aircraft refueling in airport using ant colony optimization algorithm[J]. Journal on Advanced Research in Electrical Engineering, 2018, 2(1): 43-46. [7] 衡红军, 戚馨桐. 考虑任务均衡的加油车动态调度问题[J]. 计算机工程与科学, 2020, 42(5): 923-930.HENG H J, QI X T. Dynamic refueling vehicle scheduling considering task balance[J]. Computer Engineering & Science, 2020, 42(5): 923-930(in Chinese). [8] ZHAO P X, HAN X, WAN D. Evaluation of the airport ferry vehicle scheduling based on network maximum flow model[J]. Omega, 2021, 99: 102178. doi: 10.1016/j.omega.2019.102178 [9] HAN X, ZHAO P X, KONG D X. Two-stage optimization of airport ferry service delay considering flight uncertainty[J]. European Journal of Operational Research, 2023, 307(3): 1103-1116. doi: 10.1016/j.ejor.2022.09.023 [10] GUO W A, XU P, ZHAO Z, et al. Scheduling for airport baggage transport vehicles based on diversity enhancement genetic algorithm[J]. Natural Computing, 2020, 19(4): 663-672. doi: 10.1007/s11047-018-9703-0 [11] 袁成斌. 基于启发式算法的机场除冰资源调度策略研究[D]. 武汉: 华中科技大学, 2020: 51-63.YUAN C B. Research on airport deicing resource scheduling strategy based on heuristic algorithm[D]. Wuhan: Huazhong University of Science and Technology, 2020: 51-63(in Chinese). [12] ZHAO P X, GAO W Q, HAN X, et al. Bi-objective collaborative scheduling optimization of airport ferry vehicle and tractor[J]. International Journal of Simulation Modelling, 2019, 18(2): 355-365. doi: 10.2507/IJSIMM18(2)CO9 [13] ZHU S R, SUN H J, GUO X. Cooperative scheduling optimization for ground-handling vehicles by considering flights’ uncertainty[J]. Computers & Industrial Engineering, 2022, 169: 108092. [14] GUIMARANS D, PADRÓN S. A stochastic approach for planning airport ground support resources[J]. International Transactions in Operational Research, 2022, 29(6): 3316-3345. doi: 10.1111/itor.13104 [15] 吴枕. 大型机场地面保障车辆协同与动态调度研究[D]. 北京: 北京交通大学, 2021: 27-38.WU Z. Research on coordination and dynamic scheduling of ground support vehicles in large airports[D]. Beijing: Beijing Jiaotong University, 2021: 27-38(in Chinese) . [16] 蔡畅. 枢纽机场摆渡车动态调度方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2021: 31-44.CAI C. Research on dynamic dispatching method of hub airport car ferry[D]. Harbin: Harbin Institute of Technology, 2021: 31-44(in Chinese) . [17] XUE G Q, WANG Y, GUAN X Y, et al. A combined GA-TS algorithm for two-echelon dynamic vehicle routing with proactive satellite stations[J]. Computers & Industrial Engineering, 2022, 164: 107899. [18] 王庞伟, 邓辉, 于洪斌, 等. 车路协同系统下区域路径实时决策方法[J]. 北京航空航天大学学报, 2019, 45(7): 1349-1360.WANG P W, DENG H, YU H B, et al. Real-time regional path decision method in cooperative vehicle infrastructure system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(7): 1349-1360(in Chinese). [19] 范厚明, 张跃光, 田攀俊, 等. 时变路网下异型车辆动态配置与路径优化[J]. 系统工程理论与实践, 2022, 42(2): 455-470. doi: 10.12011/SETP2020-0017FAN H M, ZHANG Y G, TIAN P J, et al. Dynamic vehicle routing problem of heterogeneous fleets with time-dependent networks[J]. Systems Engineering-Theory & Practice, 2022, 42(2): 455-470(in Chinese). doi: 10.12011/SETP2020-0017 [20] CHEN S F, CHEN R, WANG G G, et al. An adaptive large neighborhood search heuristic for dynamic vehicle routing problems[J]. Computers & Electrical Engineering, 2018, 67: 596-607. -








 下载:
下载:



 下载:
下载: