Coordinated control of transition flight position and attitude for a quad tilt-rotor UAV
-
摘要:
针对四倾转旋翼无人机倾转过渡飞行控制问题，提出一种基于指定时间预设性能控制（ATPPC）的过渡飞行位姿协调控制方法。分析四倾转旋翼无人机六自由度非线性运动/动力学模型，完成仿射非线性处理；为准确呈现倾转过程与气动特性的关系，在传统的“短舱角-飞行速度”二维过渡走廊的基础上，增加迎角为过渡走廊的第三维度，建立“短舱角-飞行速度-迎角”三维安全过渡走廊，通过合理匹配飞行速度、短舱倾角与迎角确保无人机的过渡安全；针对倾转过渡过程中的固定翼/旋翼异构冗余操纵高效分配问题，采用序列二次规划算法，将操纵分配问题转化为带有多约束条件的非线性优化问题，通过求解优化问题最优解，实现控制力和力矩到旋翼转速、舵面等执行机构的准确映射；通过在三维过渡走廊内设计一条安全剖面作为位姿协调控制指令，将所提控制方法与非线性动态逆方法进行对比仿真实验。结果表明：所提控制方法在实现四倾转旋翼无人机过渡飞行控制方面不仅具有可行性，而且相较于传统方法，具有更显著的优势。
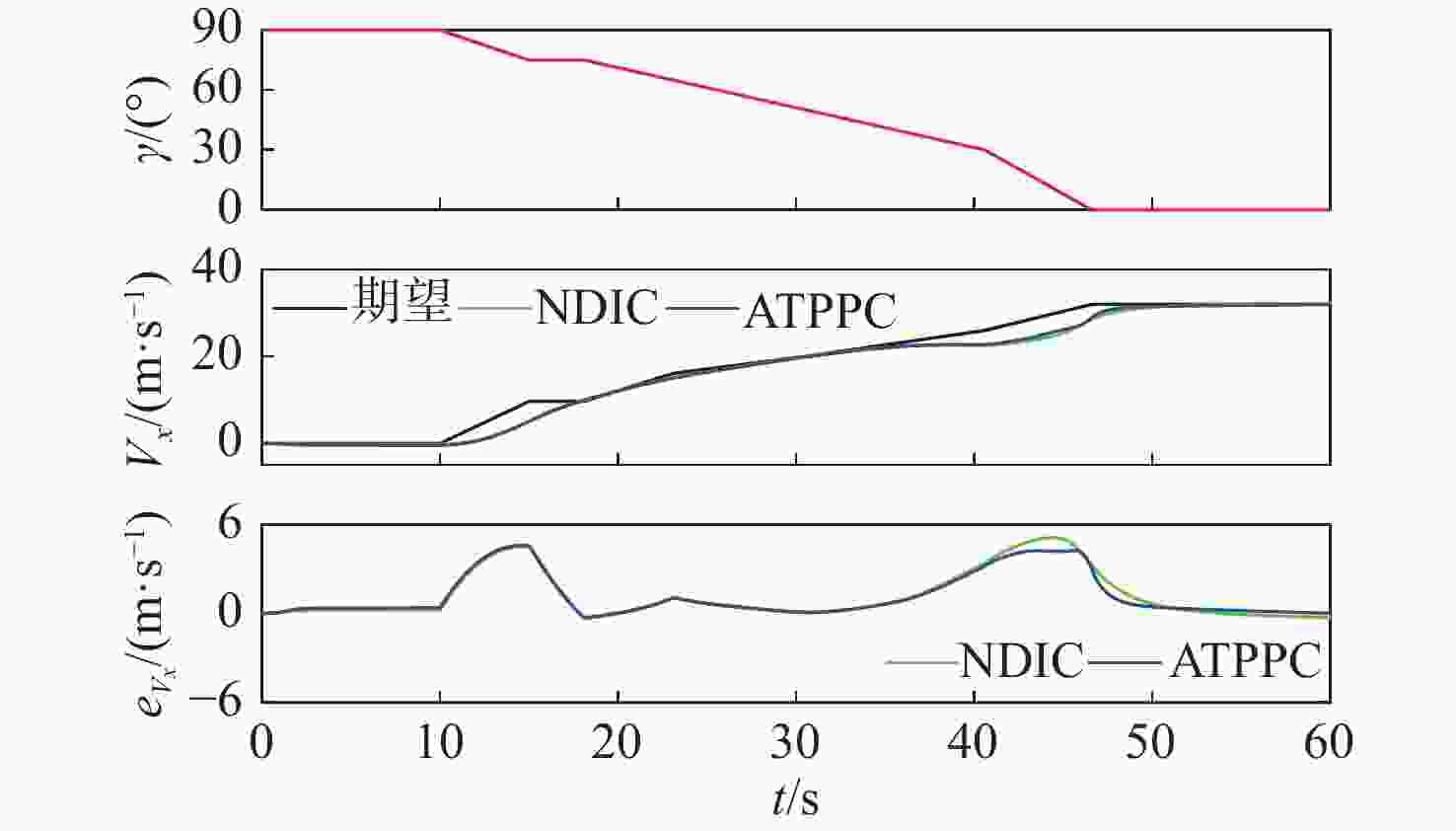
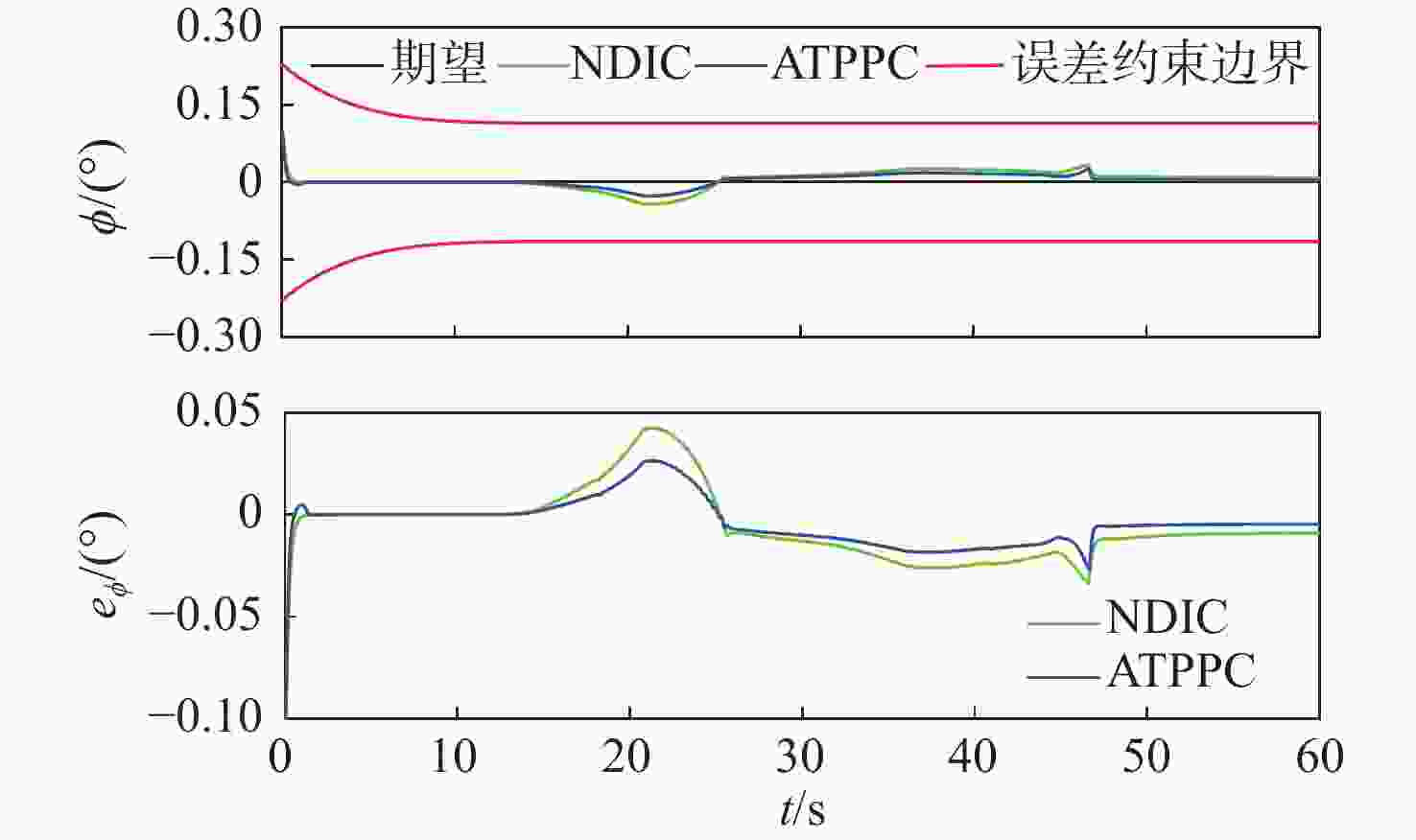
Abstract:Abstract: In this paper, a coordinated control method for transition flight position and attitude based on appointed-time prescribed performance control（ATPPC） is proposed for the tilt transition flight control problem of quad tilt-rotor UAVs. Firstly, establish a six degree of freedom nonlinear motion/dynamics model for a quad tilt-rotor UAV and complete affine nonlinear processing. Second, a three-dimensional safe transition corridor of "nacelle angle flight speed angle of attack" is established to ensure the transition safety of the UAV through reasonable matching of flight speed, nacelle inclination angle, and angle of attack. This is done by adding the angle of attack as the third dimension to the traditional two-dimensional transition corridor of "nacelle angle flight speed" in order to accurately present the relationship between the tilting process and aerodynamic characteristics with these characteristics. Then, in response to the efficient allocation problem of the fixed wing/rotor heterogeneous redundant control during the tilt transition process, a sequential quadratic programming algorithm is used to transform the control allocation problem into a nonlinear optimization problem with multiple constraints. By solving the optimal solution of the optimization problem, accurate mapping of control force and torque to the rotor speed, rudder surface, and other executing mechanisms is achieved. On this basis, a position and attitude coordination control method for quad tilt-rotor UAVs based on appointed-time prescribed performance control is proposed, and the stability of the closed-loop system is analyzed. Finally, a safety profile is designed within the three-dimensional transition corridor as a position and attitude coordination control command. The proposed control method is compared with the nonlinear dynamic inverse method in simulation experiments. The findings shown that the suggested approach provides benefits over conventional techniques in addition to being practical for attaining transition flight control of quad tilt-rotor UAVs. -
图 5 SQP算法求解异构操纵问题流程
Figure 5. Flow of SQP algorithm for solving heterogeneous manipulation problems
图 6 四倾转旋翼无人机过渡飞行控制框图
Figure 6. Block diagram of quad tilt-rotor UAV transition flight control
图 10 $ {V}_{x}、\gamma 、\alpha $指令与跟踪三维曲线
Figure 10. 3D curve of $ {V}_{x}、\gamma 、\alpha $ instruction and tracking
图 15 $T$与${\boldsymbol{M}}$指令与跟踪曲线
Figure 15. $T$ and ${\boldsymbol{M}}$ instruction and tracking curves
表 1 四倾转旋翼无人机过渡飞行期望指令
Table 1. Desired commands for transition flight of quad tilt-rotor UAV
短舱角$\gamma $/(°) 速度指令${V_x}$/(m·s−1) 角位置$\theta $/(°) 0 32 2 10 30 1 20 28 1 30 26 1 50 20.06 2 65 16.12 3 90 0 0 
下载: 导出CSV
表 2 四倾转旋翼无人机参数
Table 2. Parameters of quad tilt-rotor UAV
参数 数值 飞行高度$H$/m 1000 无人机质量${{m}}$/kg 100 参考面积${S_{{\mathrm{ref}}}}$/m2 2.317 平均气动展长$b$/m 1.5 平均气动弦长$\bar c$/m 0.55 旋翼转速范围$\omega $/(r·min−1) 0～ 5500 舵面偏转范围${\delta _u}$/(°) −20～20
下载: 导出CSV
表 3 四倾转旋翼无人机过渡飞行控制参数
Table 3. Transition flight control parameters of quad tilt-rotor UAV
参数 数值 NDIC的控制增益 ${{\boldsymbol{K}}_1} = {\mathrm{diag}}\left( {0.8,0.8} \right),{{\boldsymbol{K}}_2} = {\mathrm{diag}}\left( {6,6} \right)$
${K_{V_x}} = 2,{{\boldsymbol{K}}_3} = {\mathrm{diag}}\left( {9,9,9} \right)$, ${{\boldsymbol{K}}_4} = {\mathrm{diag}}\left( {40,40,40} \right)$NDIC的DSC
时间常数${\tau _2} = {\tau _4} = 0.005$ ATPPC的控制增益 ${{\boldsymbol{K}}_1} = {\mathrm{diag}}\left( {0.8,0.8} \right),{{\boldsymbol{K}}_2} = {\mathrm{diag}}\left( {6,6} \right)$
${K_{V_x}} = 2,{{\boldsymbol{K}}_3} = {\mathrm{diag}}\left( {9,9,9} \right)$
${{\boldsymbol{K}}_4} = {\mathrm{diag}}\left( {40,40,40} \right)$, ${\varepsilon _1} = 0.01$,${\varepsilon _3} = 0.06$ATPPC的DSC
时间常数${\tau _2} = {\tau _4} = 0.005$ ATPPC指定时间 ${T_{{\text{con}}}}{\text{ = }}20$ 操纵分配权重${{\boldsymbol{W}}_1}$ ${\mathrm{diag}}\left( {1,15,60,10} \right) \times {10^4}$ 操纵分配权重${{\boldsymbol{W}}_2}$ $ \left\{ \begin{gathered} 100{\mathrm{diag}}(1,1,1,1,1,1,1) \qquad 0 ^\circ \leqslant \gamma \leqslant 60^\circ \\ 100{\mathrm{diag}}(1,1,1,1) \qquad \qquad \;\; 60 ^\circ < \gamma \leqslant 90^\circ \\ \end{gathered} \right. $
下载: 导出CSV
-
[1] 袁涛, 单俊杰, 刘明, 等. 舰载无人直升机的作战应用及其关键技术[J]. 直升机技术, 2020(4): 61-64. doi: 10.3969/j.issn.1673-1220.2020.04.014YUAN T, SHAN J J, LIU M, et al. Operation application and the key technology of carrier-based unmanned helicopter[J]. Helicopter Technique, 2020(4): 61-64(in Chinese). doi: 10.3969/j.issn.1673-1220.2020.04.014 [2] 苏子康, 李春涛, 余跃, 等. 绳系拖曳飞行器高抗扰轨迹跟踪控制[J]. 北京航空航天大学学报, 2021, 47(11): 2234-2248.SU Z K, LI C T, YU Y, et al. High anti-disturbance trajectory tracking control for cable towed vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(11): 2234-2248(in Chinese). [3] 沙虹伟. 无人倾转旋翼机飞行力学建模与姿态控制技术研究[D]. 南京: 南京航空航天大学, 2007.SHA H W. Research on flight mechanics modeling and attitude control technology of unmanned tilt-rotor aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007(in Chinese). [4] 黄利龙. 四倾转旋翼无人机控制系统设计与实现[D]. 沈阳: 东北大学, 2017.HUANG L L. Design and implementation of control system for four tilt rotor UAV[D]. Shenyang: Northeastern University, 2017(in Chinese). [5] SHEN S Y, XU J F, CHEN P, et al. Adaptive neural network extended state observer-based finite-time convergent sliding mode control for a quad tiltrotor UAV[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 6360-6373. [6] LEBACQZ J V, SCOTT B C. Ground-simulation investigation of VTOL airworthiness criteria for terminal area operations[J]. Journal of Guidance, Control, and Dynamics, 1985, 8(6): 761-767. doi: 10.2514/3.20052 [7] SONG Y G, WANG H J. Design of flight control system for a small unmanned tilt rotor aircraft[J]. Chinese Journal of Aeronautics, 2009, 22(3): 250-256. doi: 10.1016/S1000-9361(08)60095-3 [8] 俞志明, 陈仁良, 孔卫红. 倾转四旋翼飞行器倾转过渡走廊分析方法[J]. 北京航空航天大学学报, 2020, 46(11): 2106-2113.YU Z M, CHEN R L, KONG W H. Analysis method for conversion corridor of quad tilt rotor aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(11): 2106-2113 (in Chinese). [9] 夏济宇, 周洲, 王正平, 等. 倾转动力无人机三维过渡走廊研究[J]. 北京航空航天大学学报, 2024, 50(3): 886-895.XIA J Y, ZHOU Z, WANG Z P, et al. The research on three-dimensional transition corridor of tilt-propulsion UAV[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(3): 886-895(in Chinese). [10] KANG Y, PARK B, YOO C, et al. Control law modification according to flight test of small scaled tilt rotor UAV[C]//Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit. Reston: AIAA, 2008. [11] 周玙, 刘莉. 倾转旋翼无人机最优过渡倾转角曲线[J]. 北京航空航天大学学报, 2019, 45(11): 2277-2283.ZHOU Y, LIU L. Optimal transition tilt angle curve of tiltrotor UAV[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(11): 2277-2283(in Chinese). [12] 王东升, 郭剑东, 浦黄忠. 无人倾转旋翼机过渡模式舵面分配及自抗扰控制[J]. 电光与控制, 2019, 26(4): 23. doi: 10.3969/j.issn.1671-637X.2019.04.005WANG D S, GUO J D, PU H Z. Rudder distribution and active disturbance rejection control of unmanned tiltrotor aircraft in transition mode[J]. Electronics Optics & Control, 2019, 26(4): 23(in Chinese). doi: 10.3969/j.issn.1671-637X.2019.04.005 [13] 吴瑷菁. 垂起倾转旋翼无人机过渡模式控制系统设计[D]. 哈尔滨: 哈尔滨工业大学, 2020: 39-44.WU A J. Design of transition mode control system for vertical tilt-rotor UAV[D]. Harbin: Harbin Institute of Technology, 2020: 39-44(in Chinese). [14] 严旭飞, 陈仁良. 倾转旋翼机动态倾转过渡过程的操纵策略优化[J]. 航空学报, 2017, 38(7): 520865. doi: 10.7527/S1000-6893.2017.520865YAN X F, CHEN R L. Control strategy optimization of dynamic conversion procedure of tilt-rotor aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 520865(in Chinese). doi: 10.7527/S1000-6893.2017.520865 [15] 李继财. 基于反步与QP联合的倾转四旋翼运动控制研究[D]. 长春: 吉林大学, 2021: 39-56.LI J C. Research on motion control of tilting quadrotor based on backstepping and QP[D]. Changchun: Jilin University, 2021: 39-56(in Chinese). [16] ZHEN P, WANG W H, SONG S Y, et al. Nonlinear attitude control of tiltrotor aircraft based on active disturbance rejection sliding mode method[C]//Proceedings of the IEEE Chinese Guidance, Navigation and Control Conference. Piscataway: IEEE Press, 2016: 1351-1356. [17] ONER K T, CETINSY E, SIRIMOGLU E, et al. LQR and SMC stabilization of a new unmanned aerial vehicle[J]. World Academy of Science Engineering and Technology, 2009, 3(10): 554-559. [18] KANG Y, KIM N, KIM B S, et al. Autonomous waypoint guidance for tilt-rotor unmanned aerial vehicle that has nacelle-fixed auxiliary wings[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014, 228(14): 2695-2717. doi: 10.1177/0954410014525127 [19] 陈永, 龚华军, 王彪. 倾转旋翼机过渡段纵向姿态控制技术研究[J]. 飞行力学, 2011, 29(1): 30-33.CHEN Y, GONG H J, WANG B. Research on longitudinal attitude control technology of tilt rotor during transition[J]. Flight Dynamics, 2011, 29(1): 30-33(in Chinese). [20] 郭建东, 宋彦国, 夏品奇. 小型无人倾转旋翼机全模式飞行操纵控制[J]. 南京航空航天大学学报, 2009, 41(4): 439-444. doi: 10.3969/j.issn.1005-2615.2009.04.004GUO J D, SONG Y G, XIA P Q. Full envelope flight control method for small unmanned tilt rotor aircraft[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(4): 439-444(in Chinese). doi: 10.3969/j.issn.1005-2615.2009.04.004 [21] LOMBAERTS T, KANESHIGE J, SCHUET S, et al. Dynamic inversion based full envelope flight control for an eVTOL vehicle using a unified framework[C]//Proceedings of the AIAA Scitech 2020 Forum. Reston: AIAA, 2020. [22] WANG Z G, LI J B, DUAN D Y. Manipulation strategy of tilt quad rotor based on active disturbance rejection control[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2020, 234(3): 573-584. doi: 10.1177/0954410019875534 [23] 肖业伦, 金长江. 大气扰动中的飞行原理[M]. 北京: 国防工业出版社, 1993: 27-48.XIAO Y L, JIN C J. Flight theory in atmosphere turbulence[M]. Beijing: National Defense Industry Press, 1993: 27-48(in Chinese). [24] SU Z K, LI C T, WANG H L. Barrier Lyapunov function-based robust flight control for the ultra-low altitude airdrop under airflow disturbances[J]. Aerospace Science and Technology, 2019, 84: 375-386. doi: 10.1016/j.ast.2018.10.008 [25] SANNER R M, SLOTINE J E. Gaussian networks for direct adaptive control[J]. IEEE Transactions on Neural Networks, 1992, 3(6): 837-863. doi: 10.1109/72.165588 [26] 李森, 胡军. 基于序列二次规划的推力矢量控制分配方法[J]. 空间控制技术与应用, 2009, 35(4): 17-21. doi: 10.3969/j.issn.1674-1579.2009.04.004LI S, HU J. Sequential quadratic programming-based thrust vector control allocation[J]. Aerospace Control and Application, 2009, 35(4): 17-21(in Chinese). doi: 10.3969/j.issn.1674-1579.2009.04.004 [27] 李岳明, 王小平, 张军军, 等. 基于改进二次规划算法的X舵智能水下机器人控制分配[J]. 上海交通大学学报, 2020, 54(5): 524-531.LI Y M, WANG X P, ZHANG J J, et al. X-rudder autonomous underwater vehicle control allocation based on improved quadratic programming algorithm[J]. Journal of Shanghai Jiao Tong University, 2020, 54(5): 524-531(in Chinese). [28] 蓝雪. 船舶动力定位系统推力分配及控制方法研究[D]. 上海: 上海交通大学, 2018: 38-41.LAN X. Study on control and thrust allocation of vessels with dynamic positioning system[D]. Shanghai: Shanghai Jiao Tong University, 2018: 38-41(in Chinese). [29] LI L N, LIU Z X, GUO S F, et al. Adaptive neural learning prescribed-time control for teleoperation systems with output constraints[C]//Proceedings of the IECON 48th Annual Conference of the IEEE Industrial Electronics Society. Piscataway: IEEE Press, 2022: 1-6. [30] SWAROOP D, HEDRICK J K, YIP P P, et al. Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2002, 45(10): 1893-1899. -
下载:
点击查看大图
计量
- 文章访问数: 545
- HTML全文浏览量: 74
- PDF下载量: 12
- 被引次数: 0
