Finite element simulation for ultrasonic testing of materials with coarse-grained tissue
-
摘要:
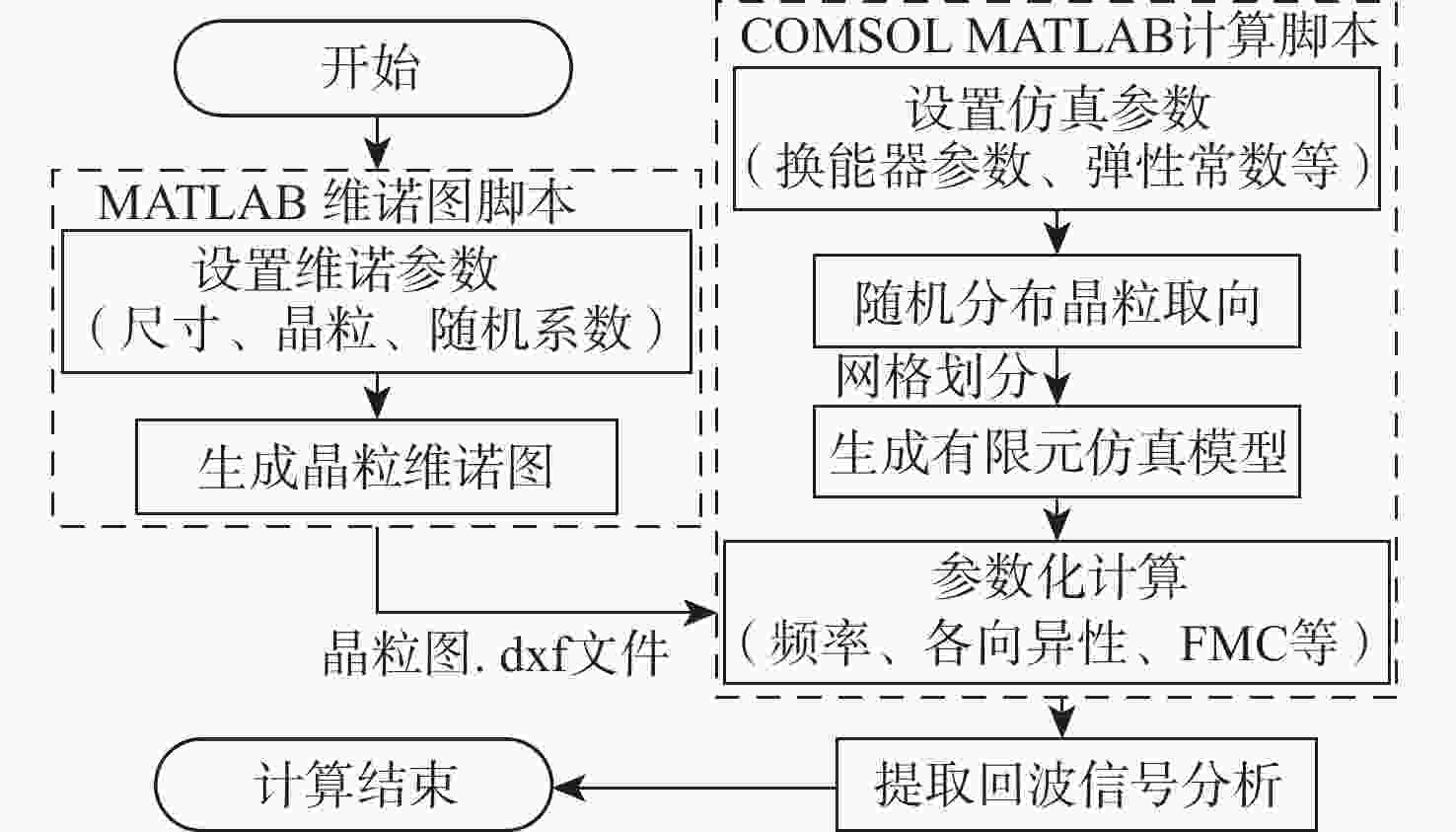
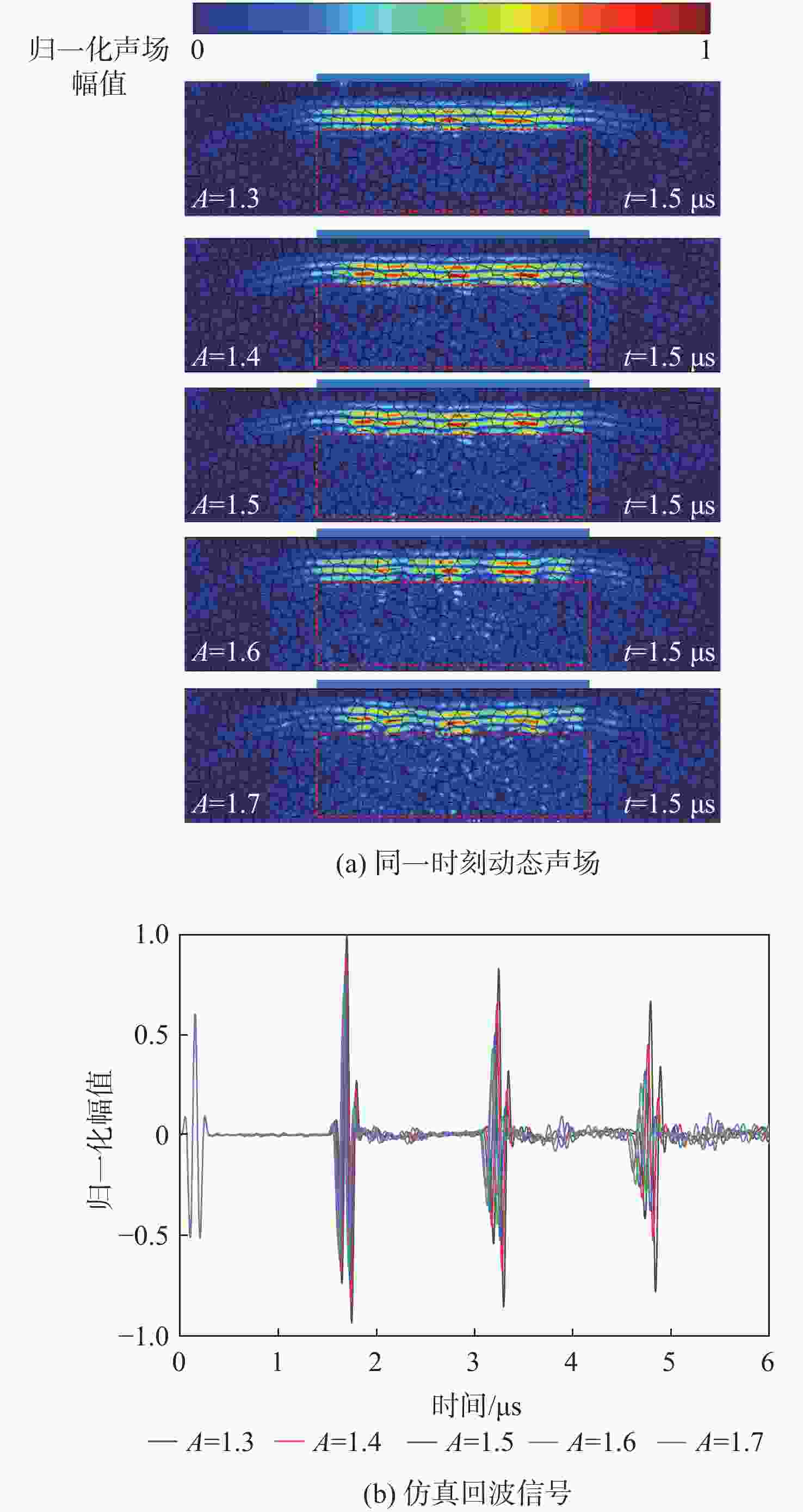
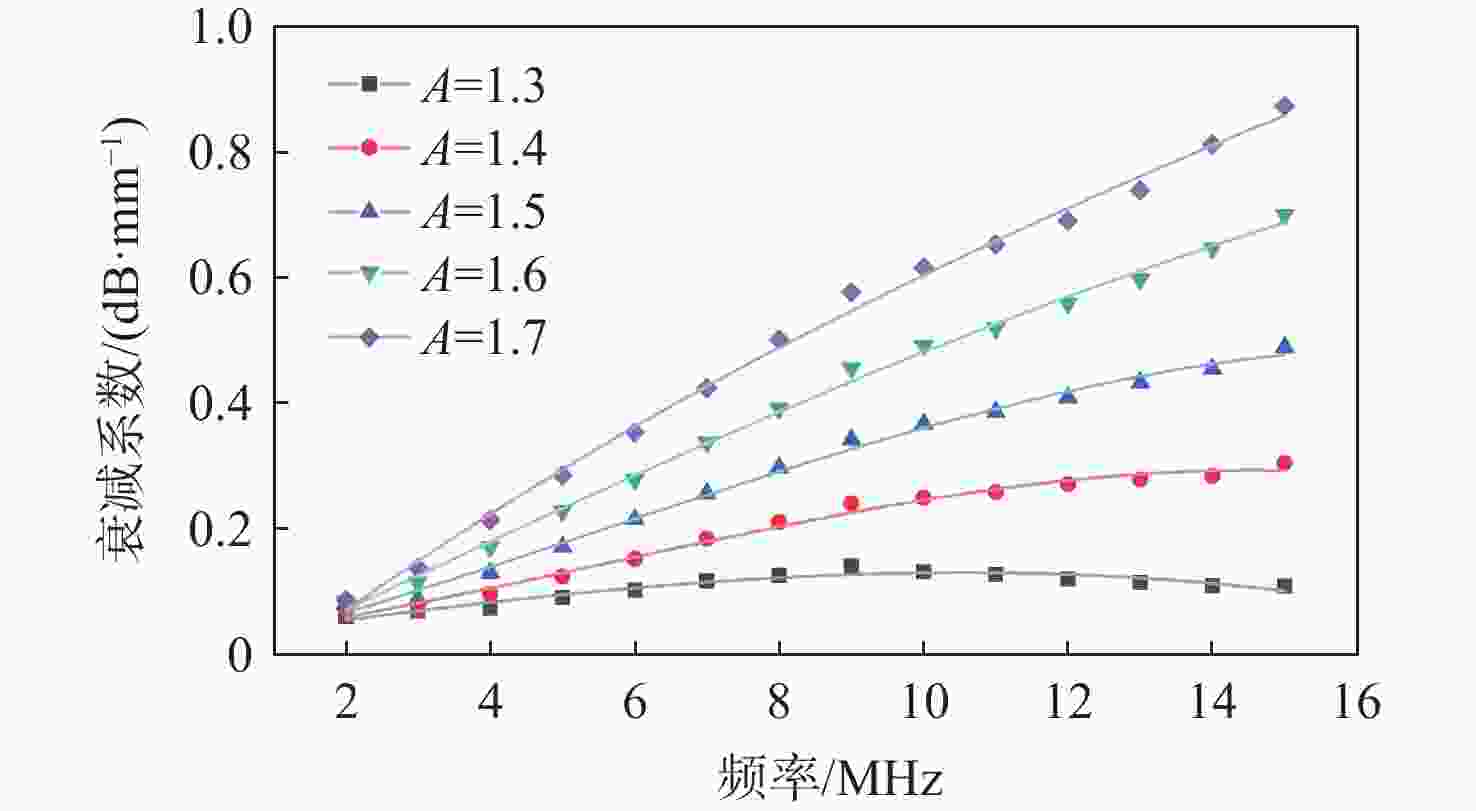
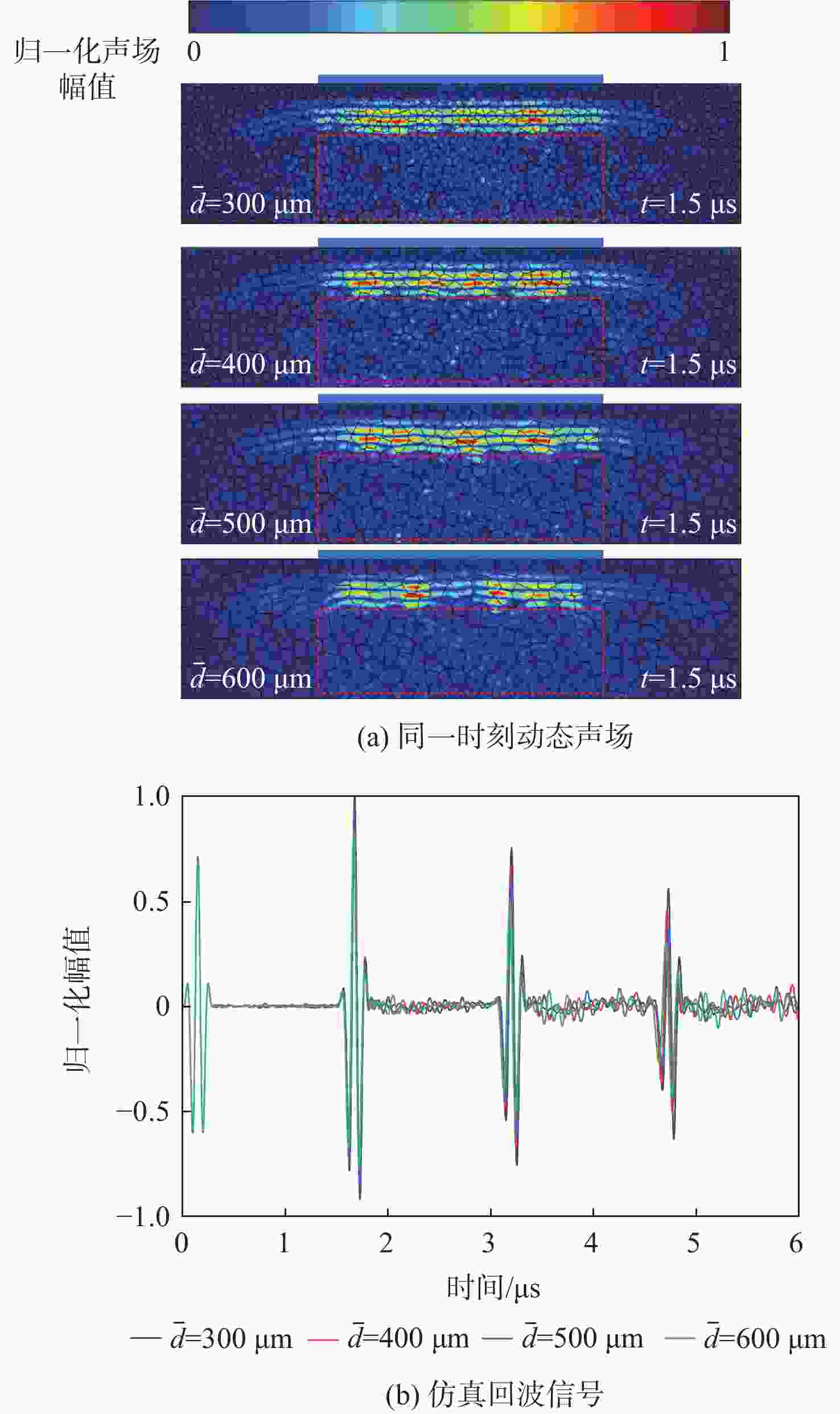
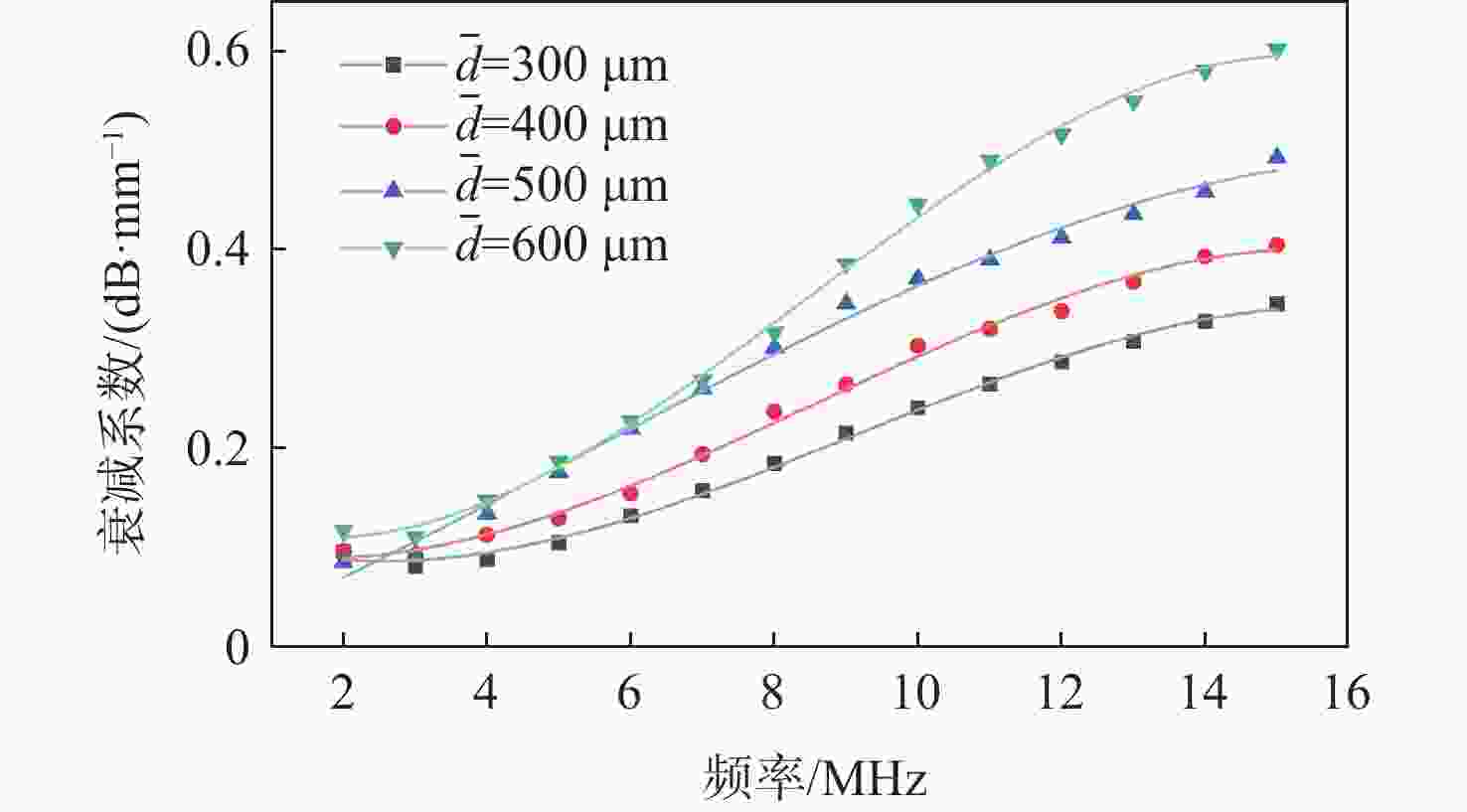
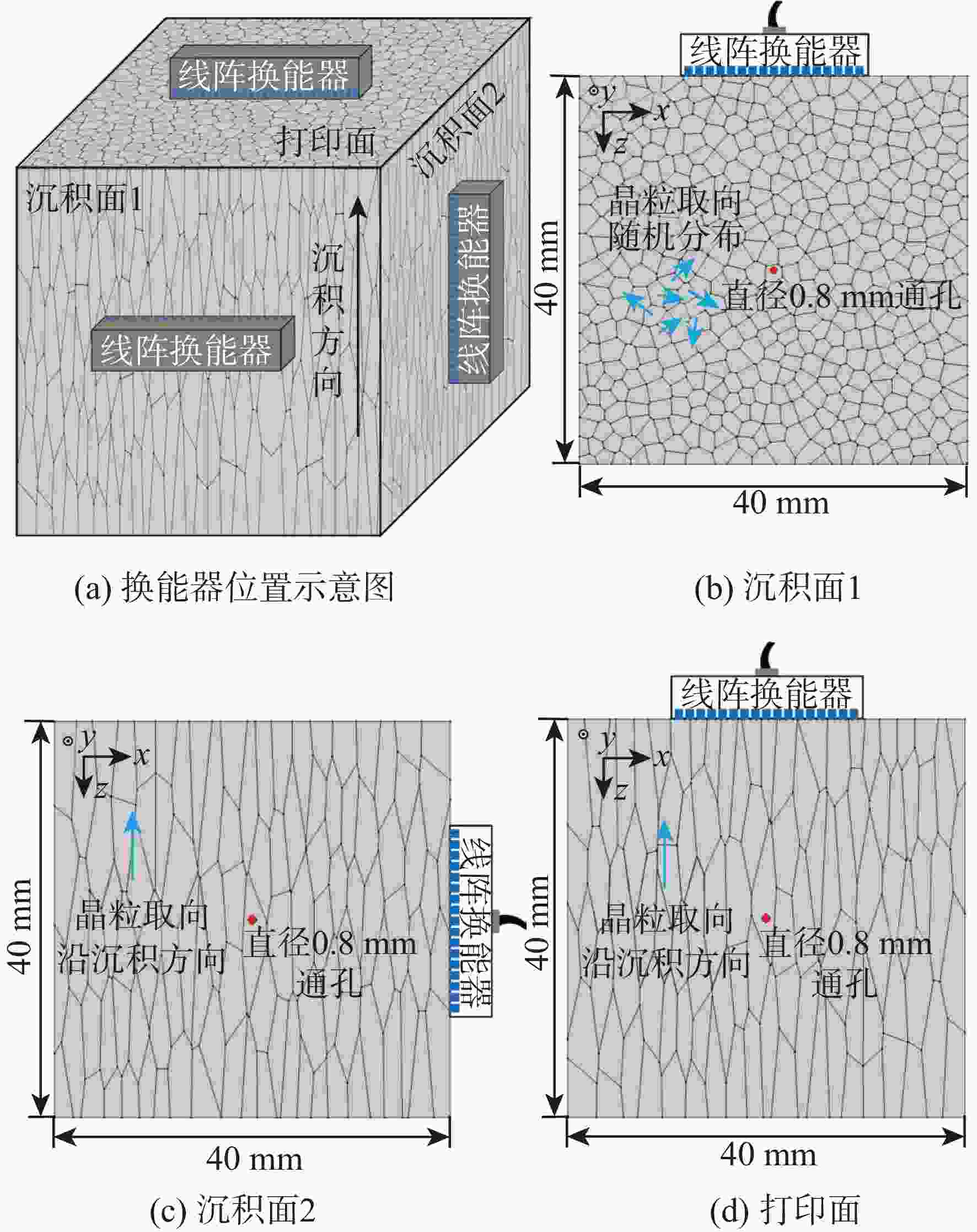
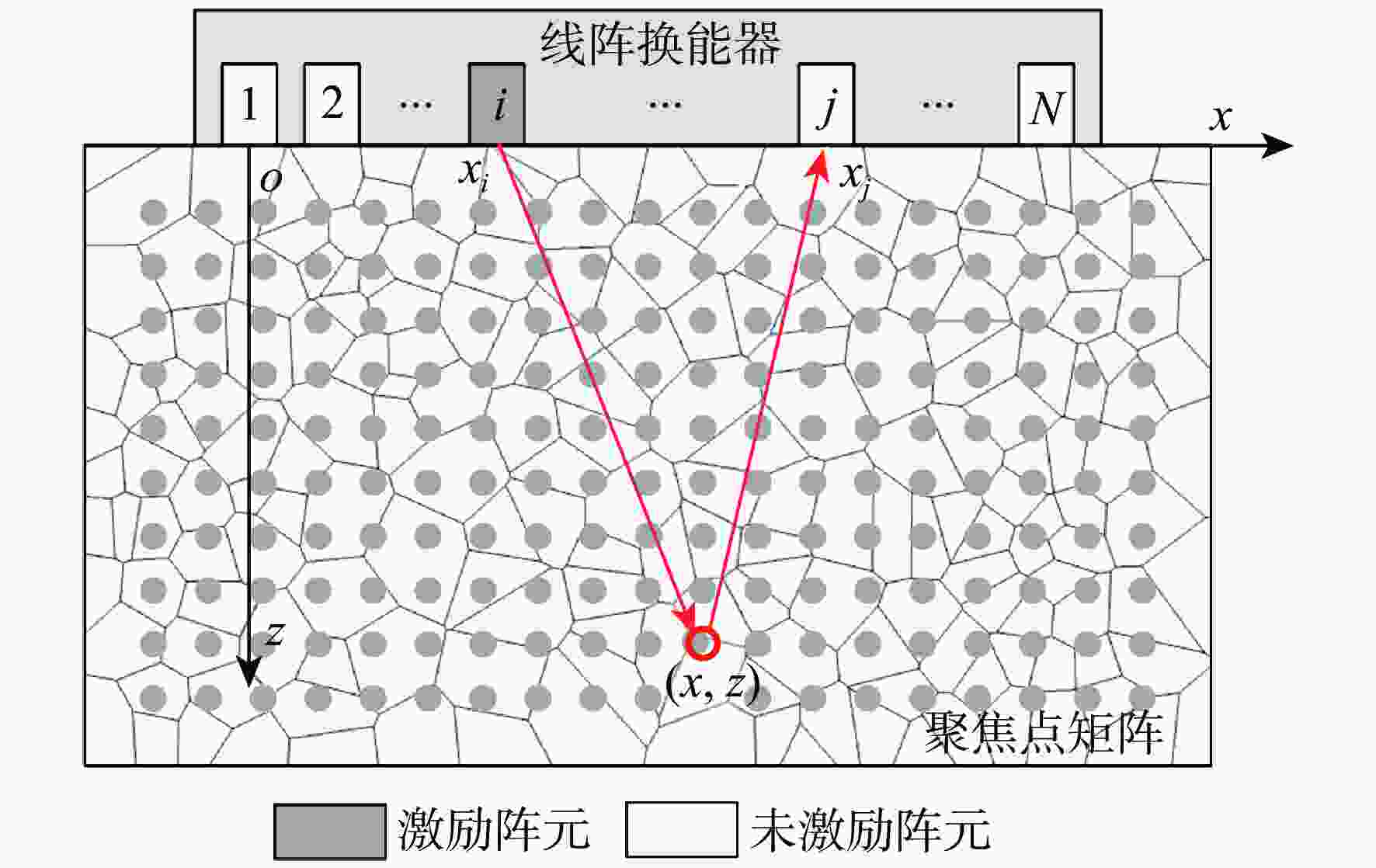
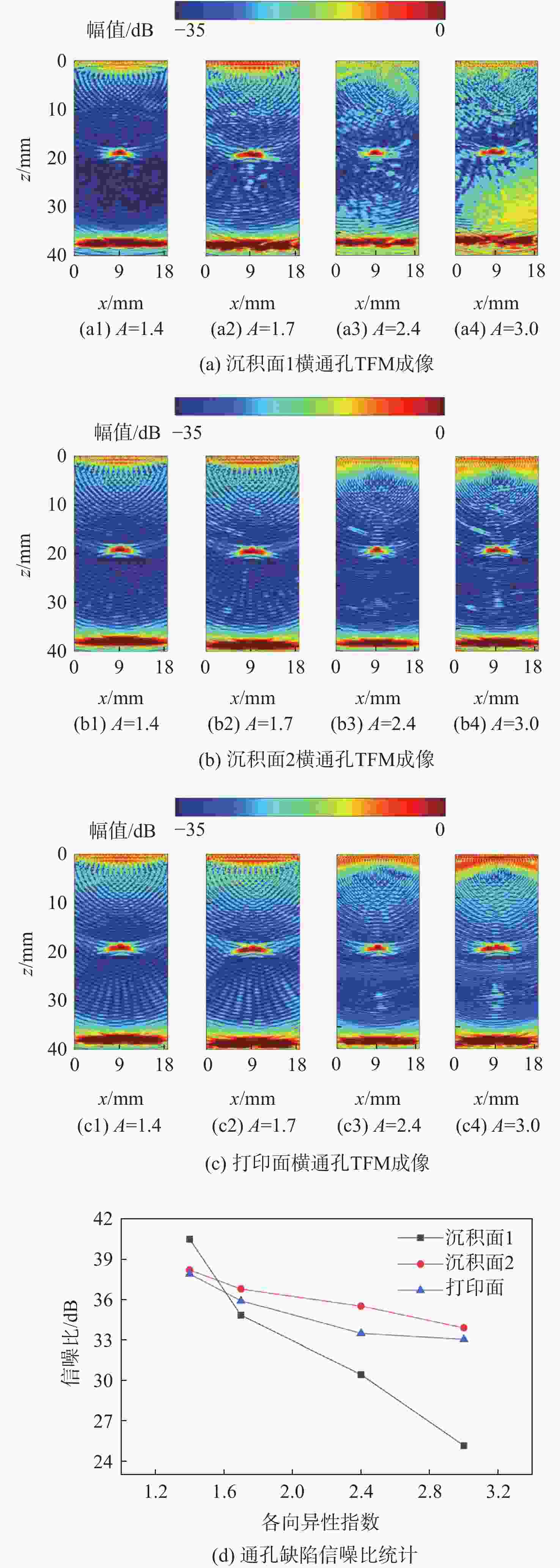
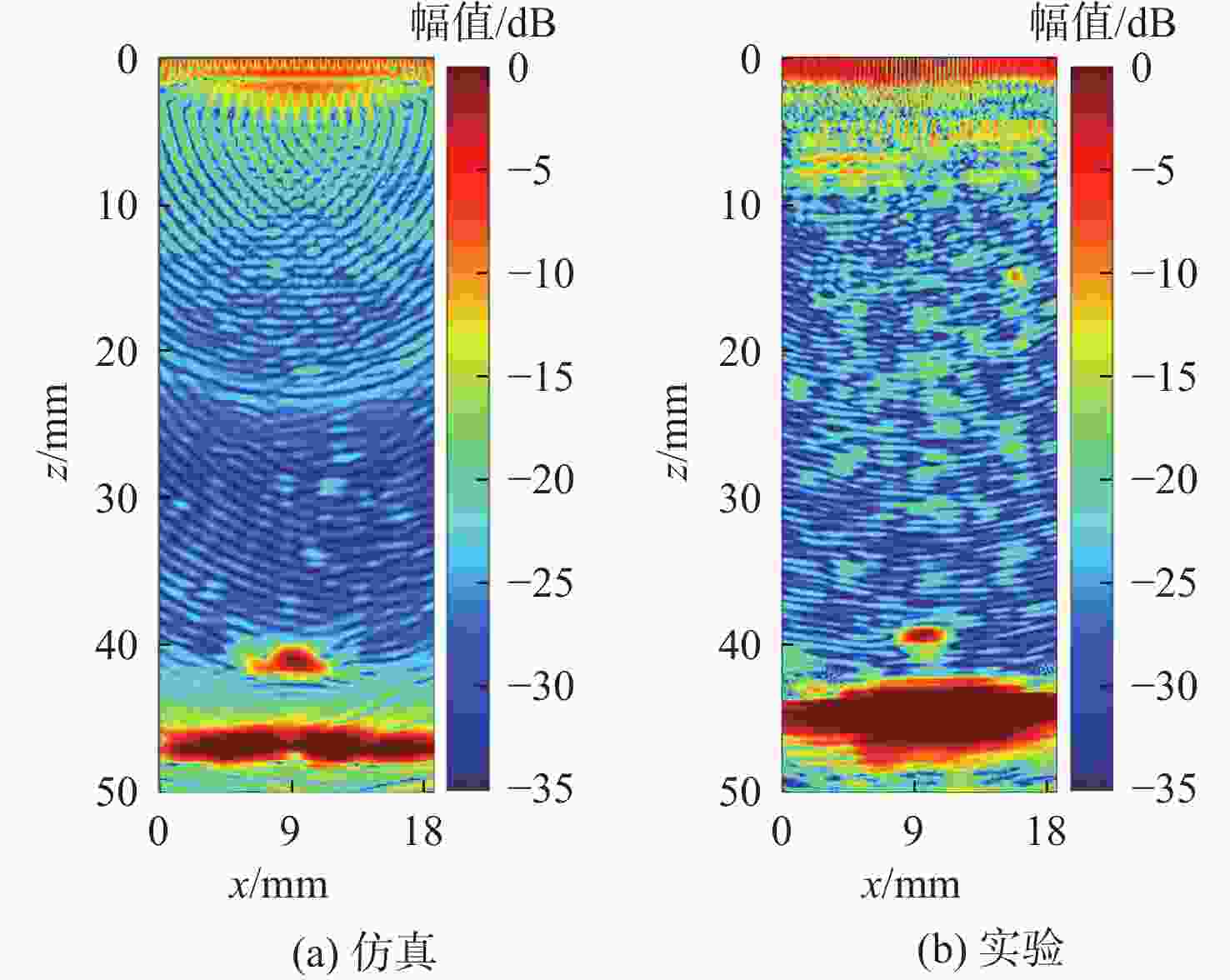
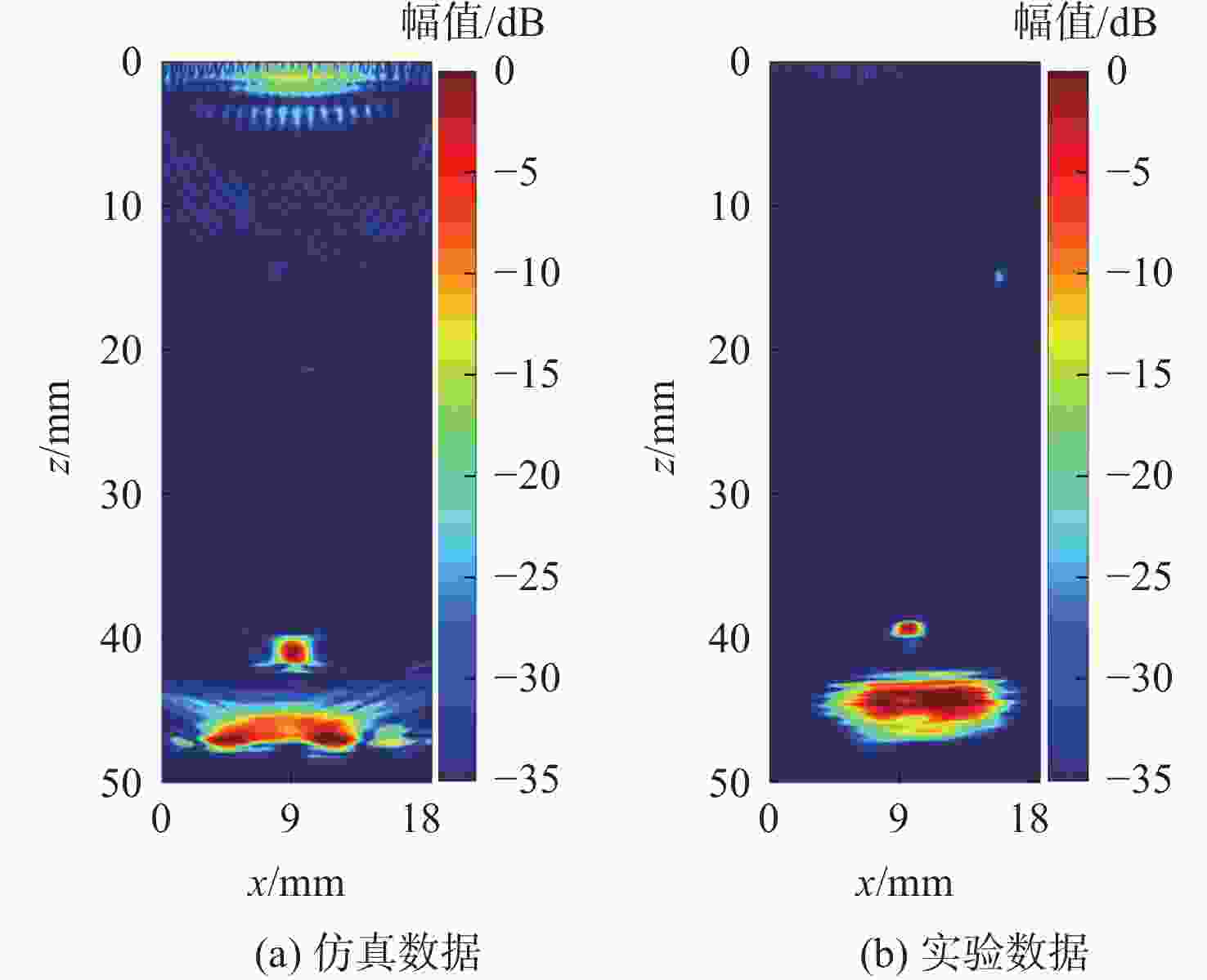
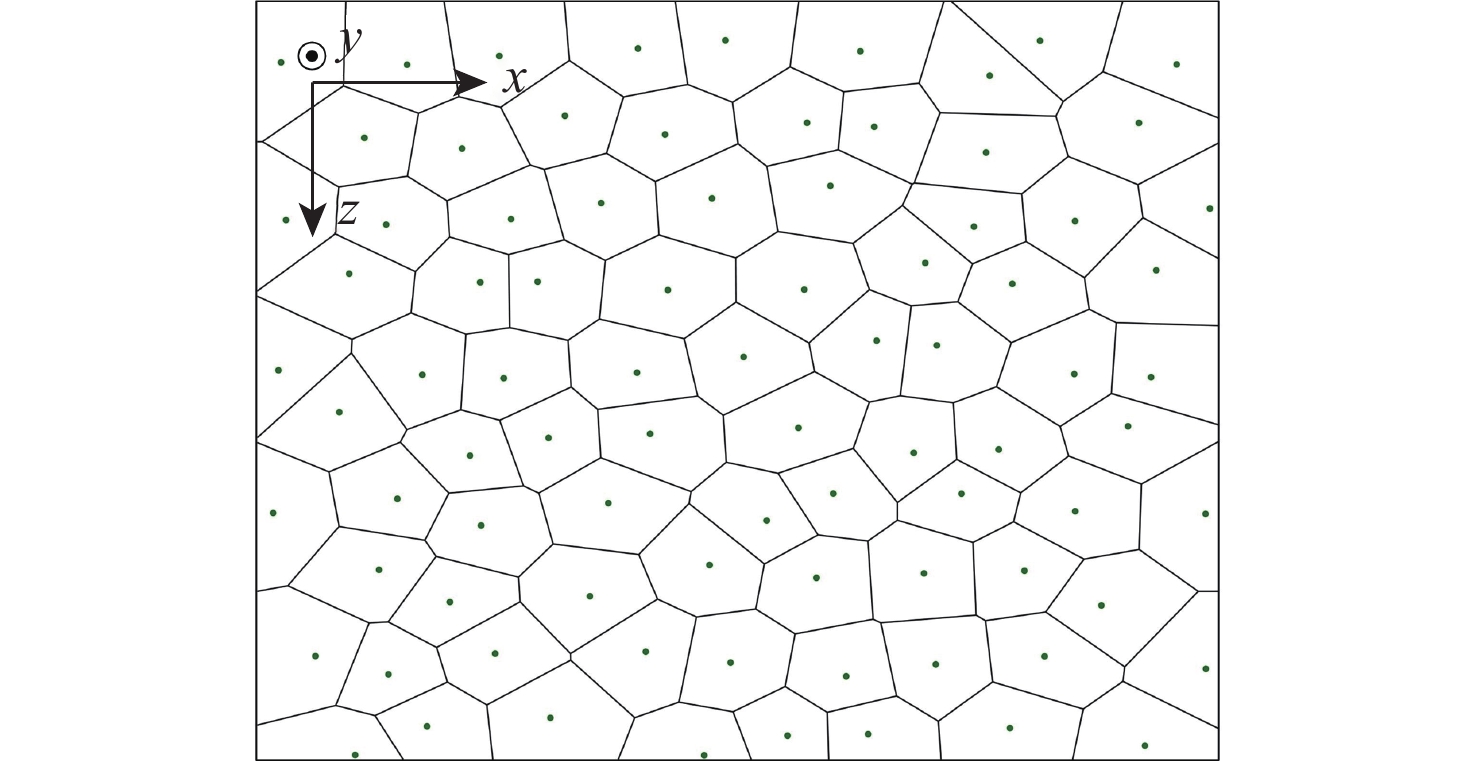
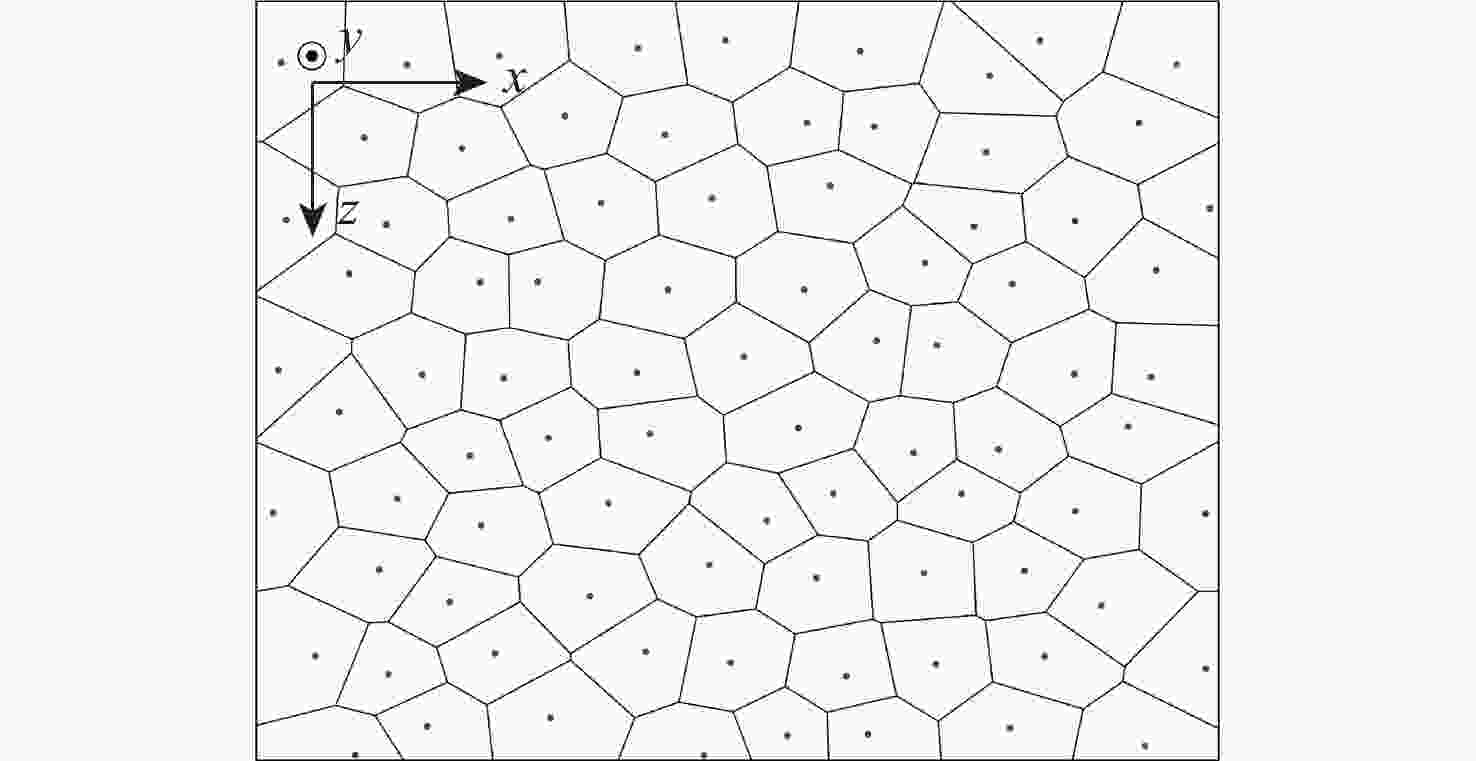
粗晶组织金属材料具有晶粒粗大、声学各向异性、结构非均匀性等特点，超声波在其内部传播时，会引起强烈的波形畸变、声能衰减及结构声散射，导致超声检测回波信号信噪比差。为掌握超声波在粗晶组织材料中的传播规律，并为超声检测方案提供理论指导，研究粗晶组织材料的超声检测有限元仿真方法。基于维诺图算法生成材料二维晶粒模型，通过材料弹性张量的形式对晶粒的各向异性取向进行定义，建立可实现参数化计算的有限元声学仿真模型。基于提出的有限元声学仿真模型，从单声束超声检测和阵列超声检测2个方面展开仿真方法研究：以具备等轴晶结构特征的镍基高温合金GH4169和具备柱状晶结构特征的增材制造钛合金为例，建立单声束声衰减反射法测量仿真模型和阵列超声全矩阵采集(FMC)数据采集仿真模型；仿真分析不同各向异性指数及平均晶粒尺寸下不同频率超声波的声衰减规律，计算不同各向异性指数及不同检测方向下全聚焦方法(TFM)成像的信噪比，并进行相位相干因子(PCF)成像降噪。仿真和实验的PCF成像结果相对于TFM的信噪比分别提升了23.52 dB和24.72 dB。对GH4169试样及增材制造钛合金试样的实验结果证明了该规律，验证了仿真方法的有效性。
Abstract:The acoustic characteristics of coarse-grained metal materials are complex due to the coarse grain, anisotropy, and non-uniformity. Ultrasonic testing has a poor signal to noise ratio because of severe waveform distortion, energy attenuation, and structural scattering that occur when ultrasonic waves propagate inside it. To investigate the propagation law of ultrasonic waves in coarse-grained materials and provide theoretical guidance for the ultrasonic testing scheme, a finite element simulation modeling method for ultrasonic testing of coarse-grained materials was proposed. A two-dimensional grain model of the material was generated based on the Voronoi diagram algorithm. The anisotropic orientation of the grains was defined through the form of the material elasticity tensor. A finite element acoustic simulation method that enables parametric calculations was established. The simulation modeling research was carried out in terms of both acoustic attenuation and full matrix capture (FMC). A simulation model of the acoustic attenuation measurement of nickel-based high-temperature alloy GH4169 was established. A comprehensive matrix capture data acquisition simulation model was developed for titanium alloys using additive manufacturing, and the acoustic attenuation patterns of ultrasonic waves of various frequencies at various anisotropy indexes and grain sizes were simulated and examined. The signal-to-noise ratios of total focusing method (TFM) imaging at different anisotropy indexes and different detection directions were simulated and analyzed. The phase coherence factor (PCF) denoising imaging was performed on the TFM imaging results of flat bottom hole defects. The signal-to-noise ratio of simulated and experimental flat bottom hole defects is improved by 23.52 dB and 24.72 dB, respectively. GH4169 specimens with different average grain sizes were prepared by heat treatment. The simulation approach’s validity is confirmed by the results of the acoustic attenuation measurement experiments conducted on GH4169 specimens and the TFM imaging studies conducted on a titanium alloy specimen employing additive manufacturing.
-
图 2 粗晶组织材料声学仿真模型计算流程
Figure 2. Flowchart of calculation for coarse grain materials acoustic simulation model
图 3 声衰减反射法测量仿真模型
Figure 3. Simulation model for measurement of acoustic attenuation by pulse reflection method
图 4 不同各向异性指数下10 MHz超声波的传播 ($ \overline d = 500{\text{ μm}} $)
Figure 4. Propagation of ultrasonic waves at 10 MHz with different anisotropy indexes ($ \overline d = 500{\text{ μm}} $)
图 5 不同频率下声衰减与各向异性指数的关系 ($ \overline d = 500{\text{ μm}} $)
Figure 5. Curves of acoustic attenuation versus anisotropy index at different frequencies ($ \overline d = 500{\text{ μm}} $)
图 6 不同平均晶粒尺寸下10 MHz超声波的传播(A=1.5)
Figure 6. Propagation of ultrasonic waves at 10 MHz with different average grain sizes (A=1.5)
图 7 不同频率下声衰减与平均晶粒尺寸的关系(A = 1.5)
Figure 7. Curves of acoustic attenuation versus average grain size at different frequencies (A=1.5)
图 8 不同热处理参数下GH4169晶粒组织金相图
Figure 8. Metallographic photos of GH4169 grain structure under different heat treatment parameters
图 9 增材制造钛合金柱状晶结构
Figure 9. Columnar crystal structure of titanium alloy by additive manufacturing
图 10 增材制造钛合金全矩阵数据采集有限元模型
Figure 10. Finite element model of FMC for titanium alloy by additive manufacturing
图 12 不同各向异性指数下的横通孔缺陷仿真成像
Figure 12. Simulation imaging of drill hole defects under different anisotropy indexes
图 13 增材制造粗晶试样超声检测实验和有限元仿真模型
Figure 13. Ultrasonic testing experiment and FE simulation model of coarse-grained specimen by additive manufacturing
图 14 平底孔缺陷仿真与实验的TFM成像对比
Figure 14. Comparison of TFM imaging for simulation and experiment of flat bottom hole defects
图 15 平底孔缺陷的PCF降噪成像结果
Figure 15. PCF denoising imaging results of flat bottom hole defects
表 1 GH4169的晶粒弹性常数和各向异性指数
Table 1. Single-crystal elastic constants and anisotropy index of GH4169
晶粒弹性常数/GPa 各向异性指数 C11 C12 C44 181.73 77.88 51.92 1.00 
下载: 导出CSV
表 2 不同热处理参数下GH4169试样声衰减反射法测量实验数据
Table 2. Acoustic attenuation measurement experiment data of GH4169 specimens by pulse reflection method under different heat treatment parameters
热处理参数 平均晶粒
尺寸/μm2.25 MHz测量衰减
系数/(dB·mm−1)5 MHz测量衰减
系数/(dB·mm−1)10 MHz测量衰减
系数/(dB·mm−1)15 MHz测量衰减
系数/(dB·mm−1)1050 ℃, 1 h水淬120 0.1915 0.2011 0.2419 0.3430 1080 ℃, 1 h水淬188 0.2054 0.2397 0.2749 0.3740 1100 ℃, 1 h水淬271 0.2044 0.2586 0.2929 1130 ℃, 1 h水淬320 0.1825 0.2656 0.3029 1150 ℃, 1 h水淬360 0.2108 0.2712 0.3178
下载: 导出CSV
表 3 线阵换能器参数
Table 3. Parameters of the linear array transducer
参数 数值 中心频率/MHz 5 阵元数量 32 阵元间距/mm 0.6 阵元宽度/mm 0.5
下载: 导出CSV
表 4 不同钛/钛合金的晶粒弹性常数和各向异性指数
Table 4. Single-crystal elastic constants and anisotropy index of pure titanium and alloys
材料 晶粒弹性常数/GPa 各向异性指数 C11 C12 C44 Ti-17 174 116 41 1.4 Ti-17 167 115 44 1.7 Ti-5533 100 70 36 2.4 纯钛 134 110 36 3
下载: 导出CSV
表 5 平底孔缺陷TFM和PCF成像信噪比
Table 5. Signal-to-noise ratios for TFM and PCF imaging of flat bottom hole defects
方法 信噪比/dB 信噪比提升/dB TFM PCF 仿真 31.67 55.19 23.52 实验 31.46 56.18 24.72
下载: 导出CSV
-
[1] HONARVAR F, VARVANI-FARAHANI A. A review of ultrasonic testing applications in additive manufacturing: defect evaluation, material characterization, and process control[J]. Ultrasonics, 2020, 108: 106227. doi: 10.1016/j.ultras.2020.106227 [2] 林珊珊, 康达, 王宏宝, 等. 增材制造高温合金的相控阵超声检测[J]. 无损检测, 2021, 43(4): 62-65.LIN S S, KANG D, WANG H B, et al. Phased array ultrasonic testing of high temperatrue alloy fabricated by additive manufacturing[J]. Nondestructive Testing Technologying, 2021, 43(4): 62-65(in Chinese). [3] 马立印, 李洋, 周正干. 整体叶盘叶片焊缝裂纹相控阵超声检测[J]. 北京航空航天大学学报, 2017, 43(9): 1900-1908.MA L Y, LI Y, ZHOU Z G. Detection of welding crack in blisk blade based on ultrasonic phased array[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(9): 1900-1908(in Chinese). [4] 徐娜, 何方成, 周正干. 基于动态孔径聚焦的L型构件相控阵超声检测[J]. 北京航空航天大学学报, 2015, 41(6): 1000-1006.XU N, HE F C, ZHOU Z G. Ultrasonic phased array inspection of L-shaped components based on dynamic aperture focusing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(6): 1000-1006(in Chinese). [5] ROKHLIN S I, BOLLAND T K, ADLER L. High-frequency ultrasonic wave propagation in polycrystalline materials[J]. The Journal of the Acoustical Society of America, 1992, 91(1): 151-165. doi: 10.1121/1.402764 [6] BLOXHAM H A, VELICHKO A, WILCOX P D. Combining simulated and experimental data to simulate ultrasonic array data from defects in materials with high structural noise[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2016, 63(12): 2198-2206. doi: 10.1109/TUFFC.2016.2614492 [7] VAN PAMEL A, HUTHWAITE P, BRETT C R, et al. Numerical simulations of ultrasonic array imaging of highly scattering materials[J]. NDT & E International, 2016, 81: 9-19. [8] 陈尧, 罗忠兵, 张东辉, 等. 基于EBSD技术构建弹性各向异性粗晶材料超声仿真模型的研究[J]. 机械工程学报, 2016, 52(18): 24-30.CHEN Y, LUO Z B, ZHANG D H, et al. Research on modeling of ultrasonic propagation in anisotropic coarse-grained materials based on EBSD technique[J]. Journal of Mechanical Engineering, 2016, 52(18): 24-30(in Chinese). [9] LHUILLIER P E, CHASSIGNOLE B, OUDAA M, et al. Investigation of the ultrasonic attenuation in anisotropic weld materials with finite element modeling and grain-scale material description[J]. Ultrasonics, 2017, 78: 40-50. doi: 10.1016/j.ultras.2017.03.004 [10] NAKAHATA K, SUGAHARA H, BARTH M, et al. Three dimensional image-based simulation of ultrasonic wave propagation in polycrystalline metal using phase-field modeling[J]. Ultrasonics, 2016, 67: 18-29. doi: 10.1016/j.ultras.2015.12.013 [11] GEZAEI ABERA A, SONG S J, KIM H J, et al. Prediction of grain orientation in dissimilar metal weld using ultrasonic response of numerical simulation from deliberated scatterers[J]. International Journal of Pressure Vessels and Piping, 2018, 168: 1-10. doi: 10.1016/j.ijpvp.2018.09.001 [12] LI W T, ZHU B G, ZHOU Z G, et al. Simulation and experiment of ultrasonic phased array for additive manufacturing titanium alloy with columnar crystal structure[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2022, 64(5): 262-269. doi: 10.1784/insi.2022.64.5.262 [13] 李文涛, 周正干. 激光增材制造钛合金构件的阵列超声检测方法研究[J]. 机械工程学报, 2020, 56(8): 141-147. doi: 10.3901/JME.2020.08.141LI W T, ZHOU Z G. Research on ultrasonic array testing methods of laser additive-manufacturing titanium alloy[J]. Journal of Mechanical Engineering, 2020, 56(8): 141-147(in Chinese). doi: 10.3901/JME.2020.08.141 [14] 周正干, 王俊, 李洋, 等. 多层黏接结构的阵列超声检测评价方法[J]. 北京航空航天大学学报, 2023, 49(12): 3207-3214.ZHOU Z G, WANG J, LI Y, et al. Ultrasonic array testing and evaluation method of multilayer bonded structures[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(12): 3207-3214(in Chinese). [15] ERWIG M. The graph Voronoi diagram with applications[J]. Networks, 2000, 36(3): 156-163. doi: 10.1002/1097-0037(200010)36:3<156::AID-NET2>3.0.CO;2-L [16] AULD B A. Acoustic fields and waves in solids[M]. New York: Wiley, 1973. [17] YUAN G J, WANG R Z, GONG C Y, et al. Investigations of micro-Notch effect on small fatigue crack initiation behaviour in nickel-based alloy GH4169: experiments and simulations[J]. International Journal of Fatigue, 2020, 136: 105578. doi: 10.1016/j.ijfatigue.2020.105578 [18] HOLMES C, DRINKWATER B, WILCOX P. The post-processing of ultrasonic array data using the total focusing method[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2004, 46(11): 677-680. doi: 10.1784/insi.46.11.677.52285 [19] WU J G, ZHAO H W, WANG Y, et al. Micro mechanical property investigations of Ni-based high-temperature alloy GH4169 based on nanoindentation and CPFE simulation[J]. International Journal of Solids and Structures, 2022, 258: 111999. doi: 10.1016/j.ijsolstr.2022.111999 [20] ZHU W F, XIANG Y X, ZHANG H Y, et al. Super-resolution ultrasonic Lamb wave imaging based on sign coherence factor and total focusing method[J]. Mechanical Systems and Signal Processing, 2023, 190: 110121. doi: 10.1016/j.ymssp.2023.110121 -
下载:
点击查看大图
计量
- 文章访问数: 347
- HTML全文浏览量: 109
- PDF下载量: 4
- 被引次数: 0
