用于天基机会信号定位的NC-LEO卫星单站TLE估计

秦红磊; 邓若凡; 吕红丽

doi:10.13700/j.bh.1001-5965.2023.0684

用于天基机会信号定位的NC-LEO卫星单站TLE估计

doi: 10.13700/j.bh.1001-5965.2023.0684

秦红磊^1, ,,
邓若凡¹,
吕红丽^{2, 3}

1.
北京航空航天大学电子信息工程学院，北京 100191
2.
陕西省组合与智能导航重点实验室，西安 710068
3.
中国电子科技集团公司第二十研究所，西安 710068

基金项目:

陕西省组合与智能导航重点实验室开放基金(SKLIIN-20190107)

详细信息

通讯作者:
E-mail：qhlmmm@sina.com

中图分类号: P228.1；TN966
计量
- 文章访问数: 272
- HTML全文浏览量: 147
- PDF下载量: 27
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-24
- 录用日期: 2024-02-23
- 网络出版日期: 2024-03-11
- 整期出版日期: 2025-12-31

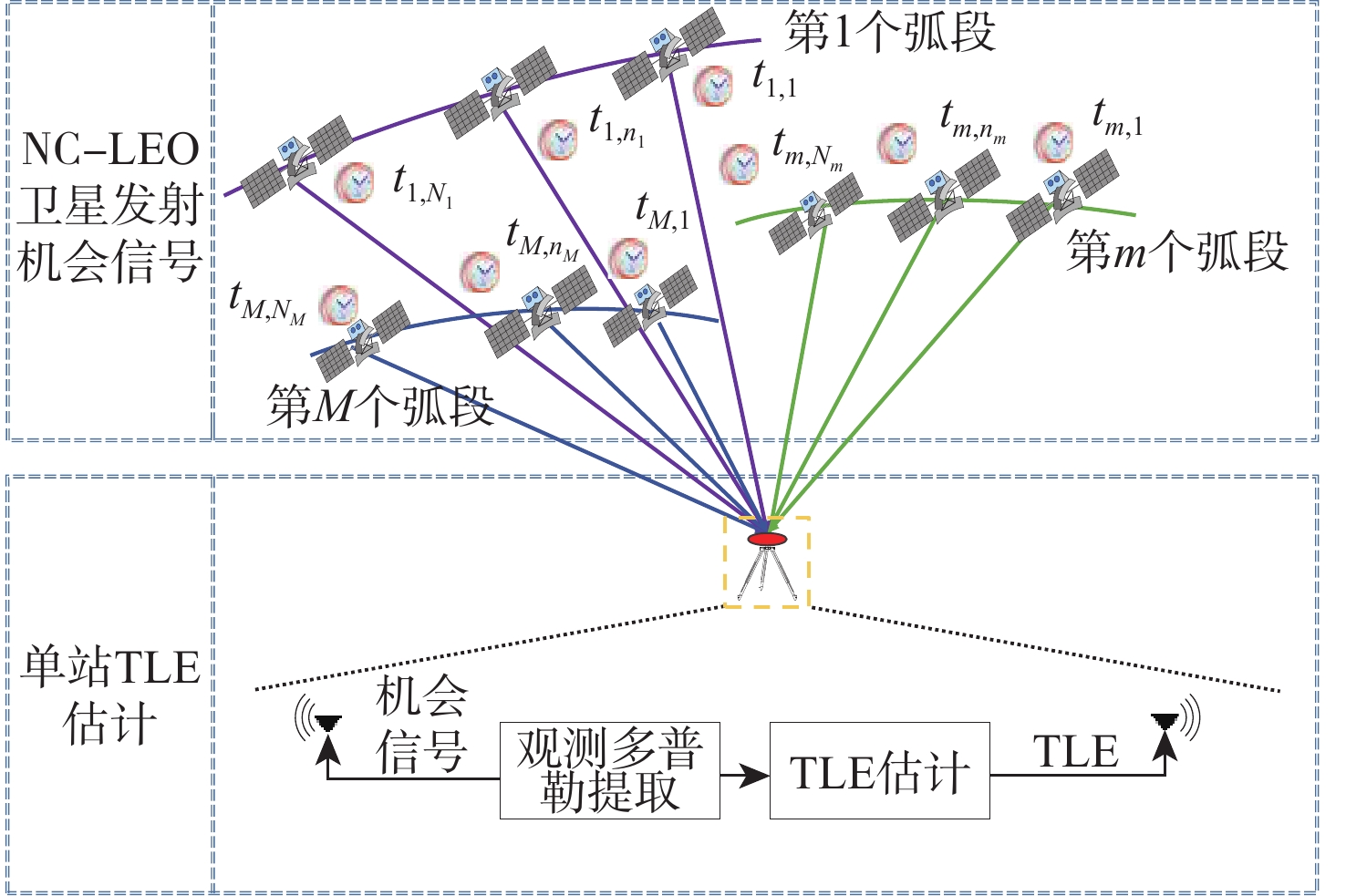
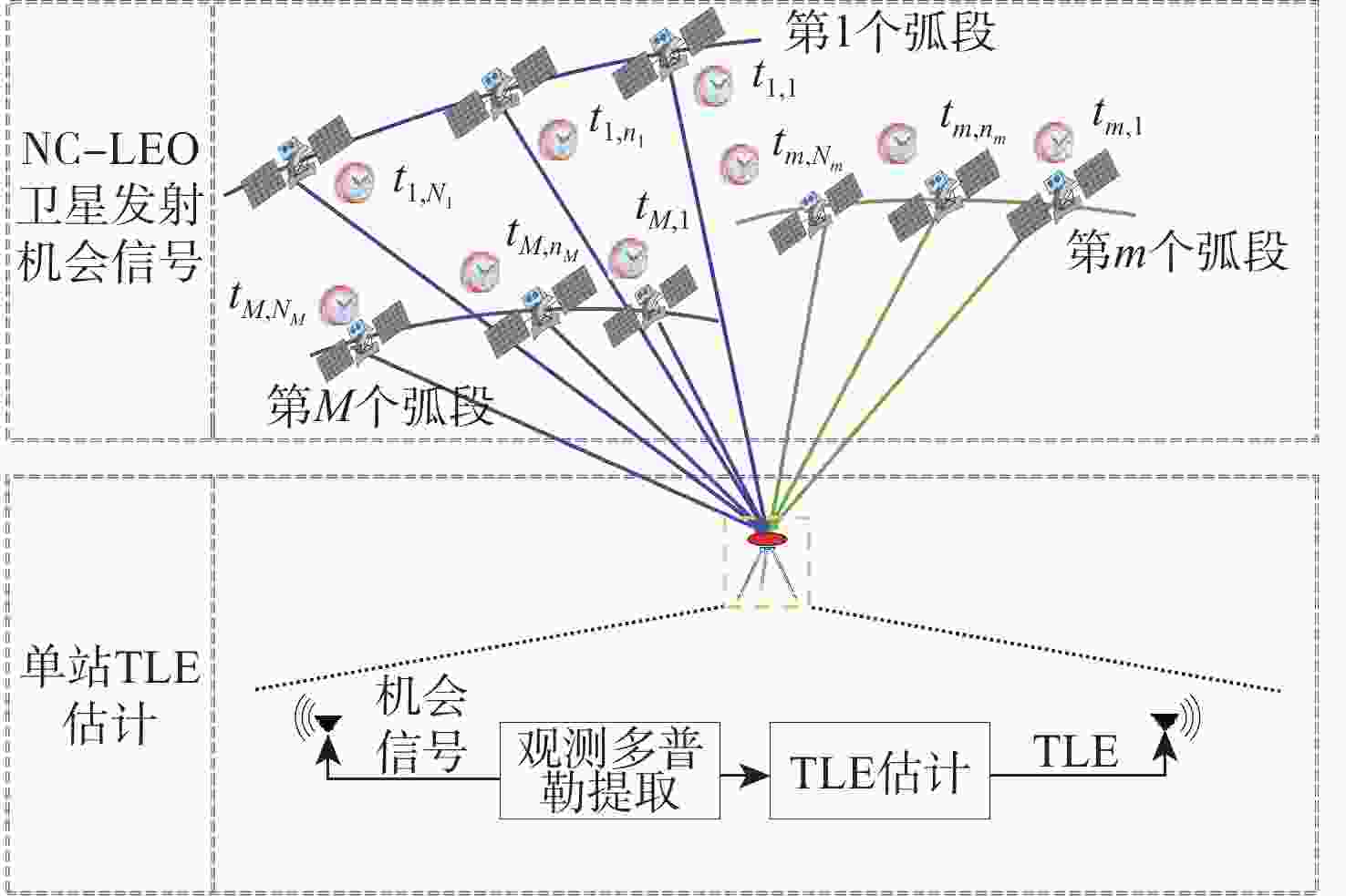
Single-station TLE estimation of NC-LEO satellite for space-based opportunistic positioning

QIN Honglei^{1
, ,},
DENG Ruofan¹,
LYU Hongli^{2, 3}

1.
School of Electronic and Information Engineering，Beihang University，Beijing 100191，China
2.
Shaanxi Key Laboratory of Integrated and Intelligent Navigation，Xi’an 710068，China
3.
Xi’an Research Institute of Navigation Technology，Xi’an 710068，China

Funds:

Foundation of Shaanxi Key Laboratory of Integrated and Intelligent Navigation (SKLIIN-20190107)

More Information

Corresponding author: E-mail：qhlmmm@sina.com

摘要

摘要:
天基机会信号定位是弹性定位、导航与授时(PNT)体系的重要部分，当前大部分定位终端所用的非合作低轨(NC-LEO)卫星轨道可靠性和精度差。为解决该问题，提出NC-LEO卫星单站两行轨道根数(TLE)估计的体系结构，通过单站提取的多普勒观测量和星座设计轨道参数获取精密TLE。同时，提出基于多初始化策略的遗传算法-岭估计的TLE估计算法，实现在先验轨道不完备和法方程病态的情况下获取精密TLE。实际试验证明：相比基于NORAD公开的TLE定位，基于所提方法获取的TLE定位精度更高。
- 天基机会信号定位 /
- 非合作低轨卫星 /
- 单站 /
- 两行轨道根数估计 /
- 轨道确定
Abstract:
The space-based opportunistic positioning is an integral part of the resilient positioning, navigation, and timing (PNT) system. At the moment, most space-based opportunistic positioning terminals depend on the non-cooperative low Earth orbit (NC-LEO) satellite’s unreliable and imprecise orbit. To address this problem, this paper presents a framework for single-station two line element (TLE) estimation of non-cooperative low Earth orbit satellites. The precise TLE is obtained using Doppler observations from a single-station and the orbital parameters for constellation design. Additionally, a TLE estimation algorithm is proposed based on a genetic algorithm-ridge estimation approach with multiple initialization strategies. This method facilitates the acquisition of accurate TLE even in situations where prior orbit information is incomplete, and when the problem is ill-conditioned. Finally, real-world tests confirm that using TLEs computed using the suggested method leads to improved accuracy when compared to placement based on NORAD’s publicly available TLEs.
- space-based opportunistic positioning /
- non-cooperative low Earth orbit satellite /
- single-station /
- two line element estimation /
- orbit determination

HTML全文

图 1 NC-LEO卫星单站TLE估计体系结构示意图

Figure 1. Diagram of single-station TLE estimation for NC-LEO satellite

下载: 全尺寸图片幻灯片

图 2 SGP4模型根据平均轨道根数计算瞬时轨道根数流程

Figure 2. Flowchart for calculating instantaneous orbital elements based on average orbital elements of SGP4 model

下载: 全尺寸图片幻灯片

图 3 不同种群规模对应的算法收敛后适应度函数MC结果

Figure 3. MC results of fitness function after algorithm convergence corresponding to different population sizes

下载: 全尺寸图片幻灯片

图 4 不同种群规模对应的升交点赤经及近地点幅角与平近点角之和的MC结果

Figure 4. MC results of ascending node right ascension and sum of argument of perigee and mean anomaly corresponding to different population sizes

下载: 全尺寸图片幻灯片

图 5 精密TLE位置、速度RMSE标准差随岭参数变化曲线

Figure 5. Curves of RMSE standard deviation of precision TLE position velocity with ridge parameters

下载: 全尺寸图片幻灯片

图 6 等定位误差面

Figure 6. Iso-position error plane

下载: 全尺寸图片幻灯片

图 7 不同方向和基线距离的定位误差

Figure 7. Position error for different directions and baseline distances

下载: 全尺寸图片幻灯片

图 8 NC-LEO卫星TLE估计系统实物图

Figure 8. Physical diagram of NC-LEO satellite TLE estimation system

下载: 全尺寸图片幻灯片

图 9 用于估计目标卫星TLE的观测多普勒

Figure 9. Observation Doppler for estimating TLE of target satellites

下载: 全尺寸图片幻灯片

图 10 目标卫星精密TLE的残差分布直方图

Figure 10. Residual distribution histogram of precision TLE for target satellite

下载: 全尺寸图片幻灯片

图 11 不同时间内基于不同方法获取的TLE定位RMSE

Figure 11. Positioning RMSE based on TLE by different methods in different time

下载: 全尺寸图片幻灯片

图 12 相比基于公开TLE，基于估计TLE定位的精度提高比例

Figure 12. Compared to positioning based on public TLE, proportion of position accuracy improvement based on estimated TLE

下载: 全尺寸图片幻灯片

表 1 2颗目标卫星的轨道参数

Table 1. Orbital parameters of two target satellites

卫星编号	一天绕地球圈数	轨道倾角/（°）	偏心率	升交点赤经/（°）	近地点幅角/（°）	平近点角/（°）	弹道系数
41919卫星	14.34220991	86.3975	0.0002160	228.0428	91.9051	26.7190	−0.00179080
43577卫星	14.34217309	86.4037	0.0002372	196.3858	100.9897	346.6261	0.00089653

下载: 导出CSV

参考文献(33)

[1]	MORTON Y J, VAN DIGGELEN F, SPILKER J J, et al. Position, navigation, and timing technologies in the 21st Century: integrated satellite navigation, sensor systems, and civil applications, volume 1[M]. Hoboken: John Wiley & Sons, 2021: 3-4.
[2]	IANNUCCI P A, HUMPHREYS T E. Fused low-Earth-orbit GNSS[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(4): 3730-3749. doi: 10.1109/TAES.2022.3180000
[3]	PROL F S, FERRE R M, SALEEM Z, et al. Position, navigation, and timing (PNT) through low Earth orbit (LEO) satellites: a survey on current status, challenges, and opportunities[J]. IEEE Access, 2022, 10: 83971-84002. doi: 10.1109/ACCESS.2022.3194050
[4]	秦红磊, 李志强, 赵超. Iridium/ORBCOMM机会信号融合定位技术[J]. 北京航空航天大学学报, 2022, 48(10): 1845-1853. QIN H L, LI Z Q, ZHAO C. Fusion positioning based on Iridium/ORBCOMM signals of opportunity[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(10): 1845-1853(in Chinese).
[5]	秦红磊, 武宁, 赵超. 基于视向矢量修正的 Iridium 机会信号多普勒差分定位技术[J]. 北京航空航天大学学报, 2024, 50(3): 748-756. QIN H L, WU N, ZHAO C. Differential positioning with Doppler measurements from Iridium based on lines of sight correction[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(3): 748-756(in Chinese).
[6]	NEINAVAIE M, KHALIFE J, KASSAS Z M. Acquisition, Doppler tracking, and positioning with starlink LEO satellites: first results[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(3): 2606-2610. doi: 10.1109/TAES.2021.3127488
[7]	LEE B S. NORAD TLE conversion from osculating orbital element[J]. Journal of Astronomy and Space Sciences, 2002, 19(4): 395-402. doi: 10.5140/JASS.2002.19.4.395
[8]	KRAG H, KLINKRAD H, ALARCÓN-RODRIGUEZ J R. Assessment of orbit uncertainties for collision risk predictions at ESA[C]//Proceedings of the 2nd IAASS Conference “Space Safety in a Global World”. [S. l. ]: International Association for the Advancement of Space Safety, 2007: 14-16.
[9]	VALLADO D A, CRAWFORD P. SGP4 orbit determination: AIAA 2008-6770[R]. Reston: AIAA, 2008.
[10]	WANG R, LIU J, ZHANG Q M. Propagation errors analysis of TLE data[J]. Advances in Space Research, 2009, 43(7): 1065-1069. doi: 10.1016/j.asr.2008.11.017
[11]	SPERETTA S, SUNDARAMOORTHY P P, GILL E K A. Long-term performance analysis of NORAD two-line elements for CubeSats and PocketQubes[C]//Proceedings of the Small Satellites for Earth Observation. Berlin: DLR, 2017.
[12]	KAHR E, MONTENBRUCK O, O’KEEFE K P G. Estimation and analysis of two-line elements for small satellites[J]. Journal of Spacecraft and Rockets, 2013, 50(2): 433-439. doi: 10.2514/1.A32352
[13]	MONTENBRUCK O. An epoch state filter for use with analytical orbit models of low Earth satellites[J]. Aerospace Science and Technology, 2000, 4(4): 277-287. doi: 10.1016/S1270-9638(00)00133-4
[14]	张耀, 刘静. 基于角度转化的空间碎片测角数据精密定轨方法[J]. 北京航空航天大学学报, 2023, 49(7): 1600-1605. ZHANG Y, LIU J. Precise orbit determination method for angle-only observation data of space debris based on angle conversion theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(7): 1600-1605(in Chinese).
[15]	李庆扬, 莫孜中, 祁力群. 非线性方程组的数值解法[M]. 北京: 科学出版社, 1987. LI Q Y, MO Z Z, QI L Q. Numerical solution of nonlinear equations[M]. Beijing: Science Press, 1987(in Chinese).
[16]	MORALES-FERRE R, LOHAN E S, FALCO G, et al. GDOP-based analysis of suitability of LEO constellations for future satellite-based positioning[C]//Proceedings of the IEEE International Conference on Wireless for Space and Extreme Environments. Piscataway: IEEE Press, 2020: 147-152.
[17]	耿涛, 刘经南, 赵齐乐, 等. 星地监测网下的北斗导航卫星轨道确定[J]. 测绘学报, 2011, 40(S1): 46-51. GENG T, LIU J N, ZHAO Q L, et al. Compass precise orbit determination based on space-ground monitoring network[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 46-51(in Chinese).
[18]	李斐, 郝卫峰, 王文睿, 等. 非线性病态问题解算的扰动分析[J]. 测绘学报, 2011, 40(1): 5-9. LI F, HAO W F, WANG W R, et al. The perturbation analysis of nonlinear ill conditioned solution[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 5-9(in Chinese).
[19]	李文华, 袁建平. 单站多普勒跟踪定轨的优化算法[J]. 宇航学报, 2001, 22(3): 69-73. doi: 10.3321/j.issn:1000-1328.2001.03.011 LI W H, YUAN J P. Optimal algorithm of orbit tracking and determination by single station Dopper radar[J]. Journal of Astronautics, 2001, 22(3): 69-73(in Chinese). doi: 10.3321/j.issn:1000-1328.2001.03.011
[20]	LOVELL T A. Application of genetic algorithms to state estimation of tethered systems[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(15): 1799-1819. doi: 10.1016/S0045-7825(03)00202-0
[21]	BAJPAI P, KUMAR M. Genetic algorithm: an approach to solve global optimization problems[J]. Indian Journal of Computer Science and Engineering, 2010, 1(3): 199-206.
[22]	HOERL A E, KENNARD R W. Ridge regression: biased estimation for nonorthogonal problems[J]. Technometrics, 1970, 12(1): 55-67. doi: 10.1080/00401706.1970.10488634
[23]	JANG D H, ANDERSON-COOK C M. Visualization approaches for evaluating ridge regression estimators in mixture and mixture-process experiments[J]. Quality and Reliability Engineering International, 2015, 31(8): 1483-1494. doi: 10.1002/qre.1683
[24]	OU J K, DING W W, LIU J H, et al. An improved algorithm for autonomous orbit determination of navigation satellite constellation[J]. Survey Review, 2011, 43(322): 361-369. doi: 10.1179/003962611X13055561708669
[25]	胡敏, 曾国强. 平均轨道根数与密切轨道根数的互换[J]. 飞行器测控学报, 2012, 31(2): 77-81. HU M, ZENG G Q. Transformation between mean and osculating orbital elements[J]. Journal of Spacecraft TT& C Technology, 2012, 31(2): 77-81(in Chinese).
[26]	刘一帆. 基于 SGP4 模型的低轨道航天器轨道预报方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2009: 27-33. LIU Y F. Research on low Earth orbit spacecraft orbit prediction strategy based on SGP4 model[D]. Harbin: Harbin Institute of Technology, 2009: 27-33(in Chinese).
[27]	PRATT J, AXELRAD P, LARSON K M, et al. Satellite clock bias estimation for iGPS[J]. GPS Solutions, 2013, 17(3): 381-389. doi: 10.1007/s10291-012-0286-4
[28]	MORALES J J, KHALIFE J, SANTA CRUZ U, et al. Orbit modeling for simultaneous tracking and navigation using LEO satellite signals[C]//Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation. Manassas: ION, 2019: 2090-2099.
[29]	曲国庆, 孙振, 苏晓庆, 等. 非线性参数估计的自适应松弛正则化算法[J]. 武汉大学学报(信息科学版), 2019, 44(10): 1491-1497. QU G Q, SUN Z, SU X Q, et al. Adaptive relaxation regularization algorithm for nonlinear parameter estimation[J]. Geomatics and Information Science of Wuhan University, 2019, 44(10): 1491-1497 (in Chinese).
[30]	梁亚澜, 聂长海. 覆盖表生成的遗传算法配置参数优化[J]. 计算机学报, 2012, 35(7): 1522-1538. doi: 10.3724/SP.J.1016.2012.01522 LIANG Y L, NIE C H. The optimization of configurable genetic algorithm for covering arrays generation[J]. Chinese Journal of Computers, 2012, 35(7): 1522-1538(in Chinese). doi: 10.3724/SP.J.1016.2012.01522
[31]	ANSALONE L, CURTI F. A genetic algorithm for initial orbit determination from a too short arc optical observation[J]. Advances in Space Research, 2013, 52(3): 477-489. doi: 10.1016/j.asr.2013.04.004
[32]	HANSEN P C, O’LEARY D P. The use of the L-curve in the regularization of discrete ill-posed problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1487-1503. doi: 10.1137/0914086
[33]	MORTLOCK T, KASSAS Z M. Assessing machine learning for LEO satellite orbit determination in simultaneous tracking and navigation[C]//Proceedings of the IEEE Aerospace Conference. Piscataway: IEEE Press, 2021: 1-8.