融合多项式差分学习与逐维变异的混沌蜉蝣算法

毛清华; 赵冰; 李阳

doi:10.13700/j.bh.1001-5965.2023.0698

融合多项式差分学习与逐维变异的混沌蜉蝣算法

doi: 10.13700/j.bh.1001-5965.2023.0698

燕山大学经济管理学院，秦皇岛 066004

详细信息

通讯作者:
E-mail：maoqh@ysu.edu.cn

中图分类号: TP18
计量
- 文章访问数: 208
- HTML全文浏览量: 68
- PDF下载量: 14
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-27
- 录用日期: 2024-02-23
- 网络出版日期: 2024-06-28
- 整期出版日期: 2025-12-31

Chaos ephemeran algorithm combining polynomial difference learning and dimensional variation

School of Economics and Management，Yanshan University，Qinhuangdao 066004，China

More Information

Corresponding author: E-mail：maoqh@ysu.edu.cn

摘要

摘要:
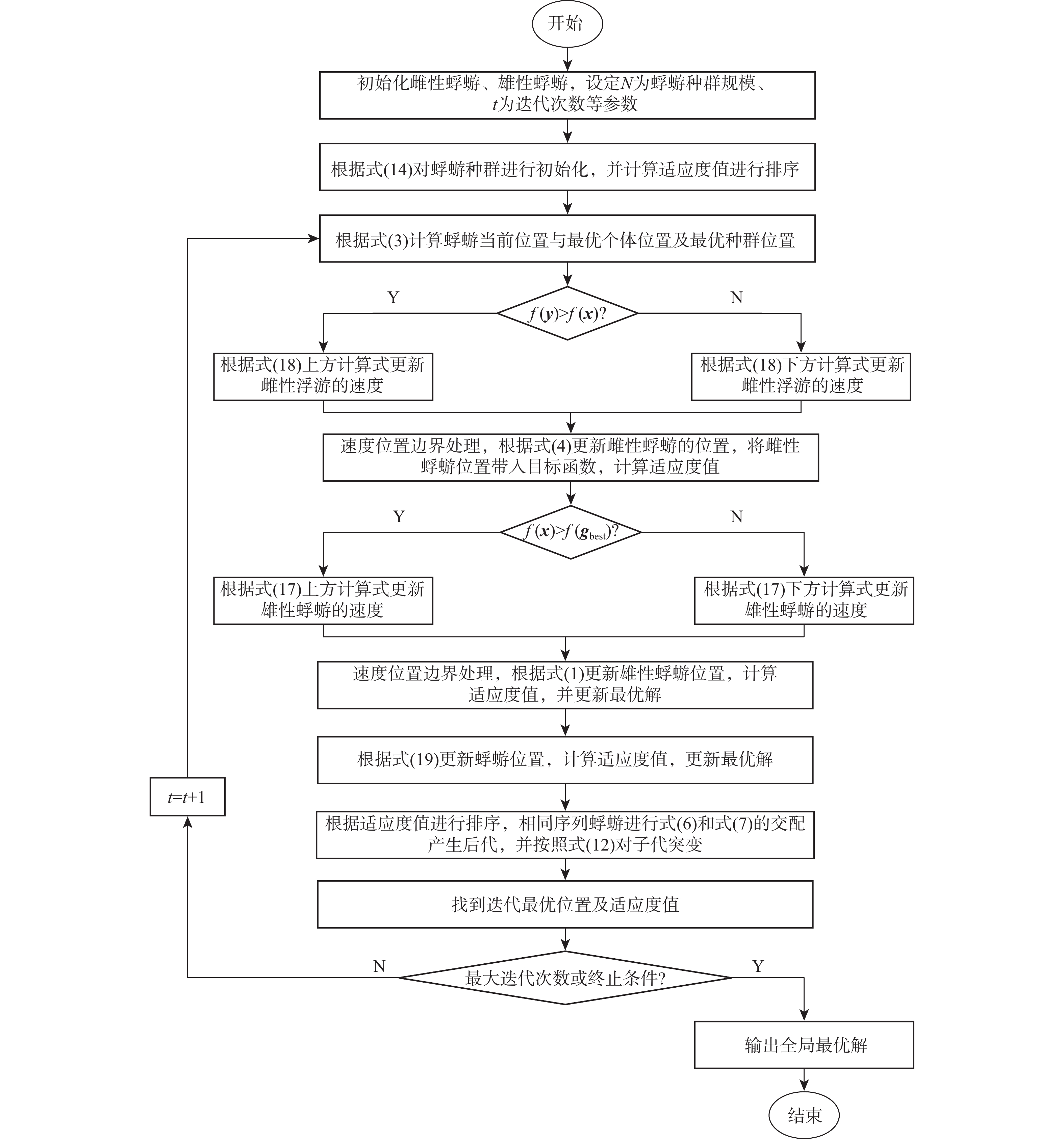
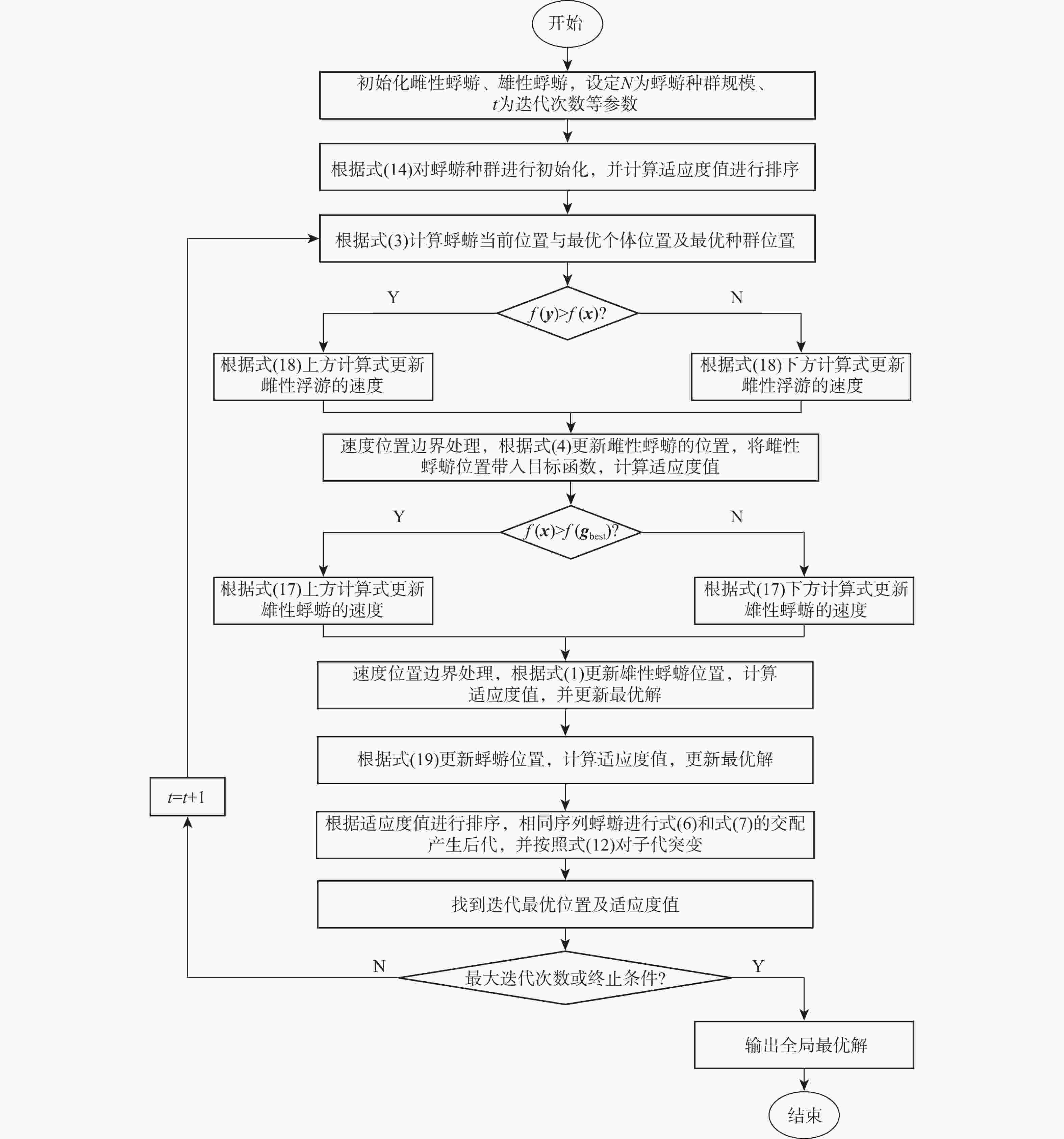
由于蜉蝣算法(MA)前期收敛速度缓慢，后期收敛精度也不高。基于此，将多项式差分学习和逐维变异相结合，构造一种融合多项式差分学习和逐维变异策略的混沌蜉蝣算法(LOPMA)。该算法提出改进Logistic混沌使初始解均匀分布，避免算法出现早熟现象；采用逐维变异策略，防止算法受不同维度之间影响陷入局部最优；采用多项式差分策略对蜉蝣算法进行改进，通过改善种群间信息交流来提升算法的寻优精度。并将3种改进策略分别引入仿真，进行消融实验对比分析，证明每种改进策略的有效性。在12个可变维度的基准测试函数上对LOPMA进行仿真对比分析，在CEC2017测试函数上将其他6种智能优化算法与较为新颖的其他策略改进的蜉蝣算法与LOPMA进行对比实验。结果表明：将多项式差分学习和逐维变异相结合，使LOPMA具有更好的稳定性、更快的收敛速度和更高的精度。
- 蜉蝣算法 /
- 改进型Logistic混沌 /
- 逐维变异 /
- 多项式差分学习 /
- CEC2017测试函数
Abstract:
Due to the slow convergence speed in the early stages and low convergence accuracy in the later stages of the Mayfly Algorithm (MA), a chaotic mayfly algorithm incorporating polynomial differential learning and dimension-wise mutation, named LOPMA, is proposed. This algorithm introduces an improved Logistic chaotic mapping to ensure uniform distribution of initial solutions, thereby avoiding premature convergence. A dimension-wise mutation strategy is adopted to prevent the algorithm from being trapped in local optima due to inter-dimensional interference. Furthermore, a polynomial differential learning strategy is integrated to enhance the information exchange among individuals, thereby improving the optimization precision. Each of the three improvement strategies was individually implemented and evaluated through ablation experiments to demonstrate their respective effectiveness. Comparative simulations of LOPMA were conducted on 12 benchmark functions with variable dimensions. On the CEC2017 test functions, LOPMA was compared with six other intelligent optimization algorithms as well as other recently proposed variants of mayfly algorithms. The results show that the combination of polynomial differential learning and dimension-wise mutation enables LOPMA to achieve better stability, faster convergence speed, and higher accuracy.
- ephemera algorithm /
- improved Logistic chaos /
- dimensional variation /
- polynomial difference learning /
- CEC2017 test function

HTML全文

图 1 LOPMA流程图

Figure 1. LOPMA flow chart

下载: 全尺寸图片幻灯片

图 2 引入改进Logistic映射前后寻优对比

Figure 2. Comparison of optimization before and after introducing improved Logistic mapping

下载: 全尺寸图片幻灯片

图 3 引入逐维变异寻优结果对比

Figure 3. Introduction of dimension-by-dimension variation optimization results comparison

下载: 全尺寸图片幻灯片

图 4 引入多项式差分学习寻优结果对比

Figure 4. Comparison of optimization results using polynomial difference learning

下载: 全尺寸图片幻灯片

图 5 标准测试函数平均收敛曲线

Figure 5. Standard test function average convergence curves

下载: 全尺寸图片幻灯片

表 1 标准测试函数

Table 1. Standard test functions

函数	名称	取值范围	最优解
f₁	Sphere	[−100,100]	0
f₂	Schwefel’s 2.22	[−10,10]	0
f₃	Schwefel’s 1.2	[−100,100]	0
f₄	Schwefel’s 2.21	[−100,100]	0
f₅	Rosenbrock’s	[−30,30]	0
f₆	Step	[−100,100]	0
f₇	Quartic	[−1.28,1.28]	0
f₈	Rastrigin’s	[−5.12,5.12]	0
f₉	Ackely ’s	[−32,32]	0
f₁₀	Griewank’s	[−600,600]	0
f₁₁	P enalized 1	[−50,50]	0
f₁₂	Penalized 2	[−50,50]	0

下载: 导出CSV

表 2 部分CEC2017测试函数

Table 2. Part of CEC2017 test functions

函数	特征	取值范围	最优解
CEC03	UN	[−100,100]	300
CEC06	MN	[−100,100]	600
CEC09	MN	[−100,100]	900
CEC12	HF	[−100,100]	1200
CEC15	HF	[−100,100]	1500
CEC18	HF	[−100,100]	1800
CEC21	CF	[−100,100]	2100
CEC24	CF	[−100,100]	2400
CEC27	CF	[−100,100]	2700

下载: 导出CSV

表 3 消融实验在基准函数下的对比分析

Table 3. Comparative analysis of ablation experiments under reference function

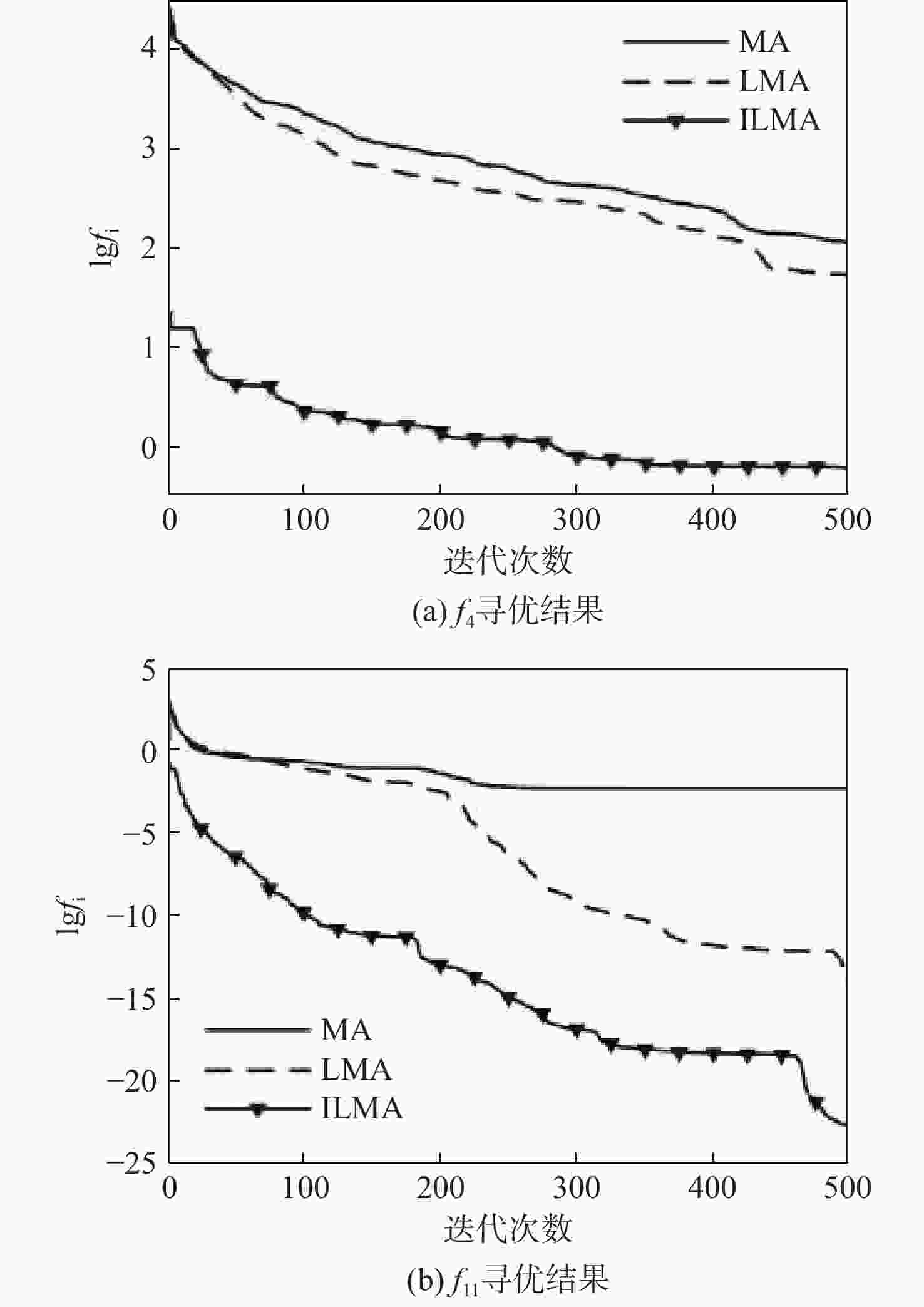
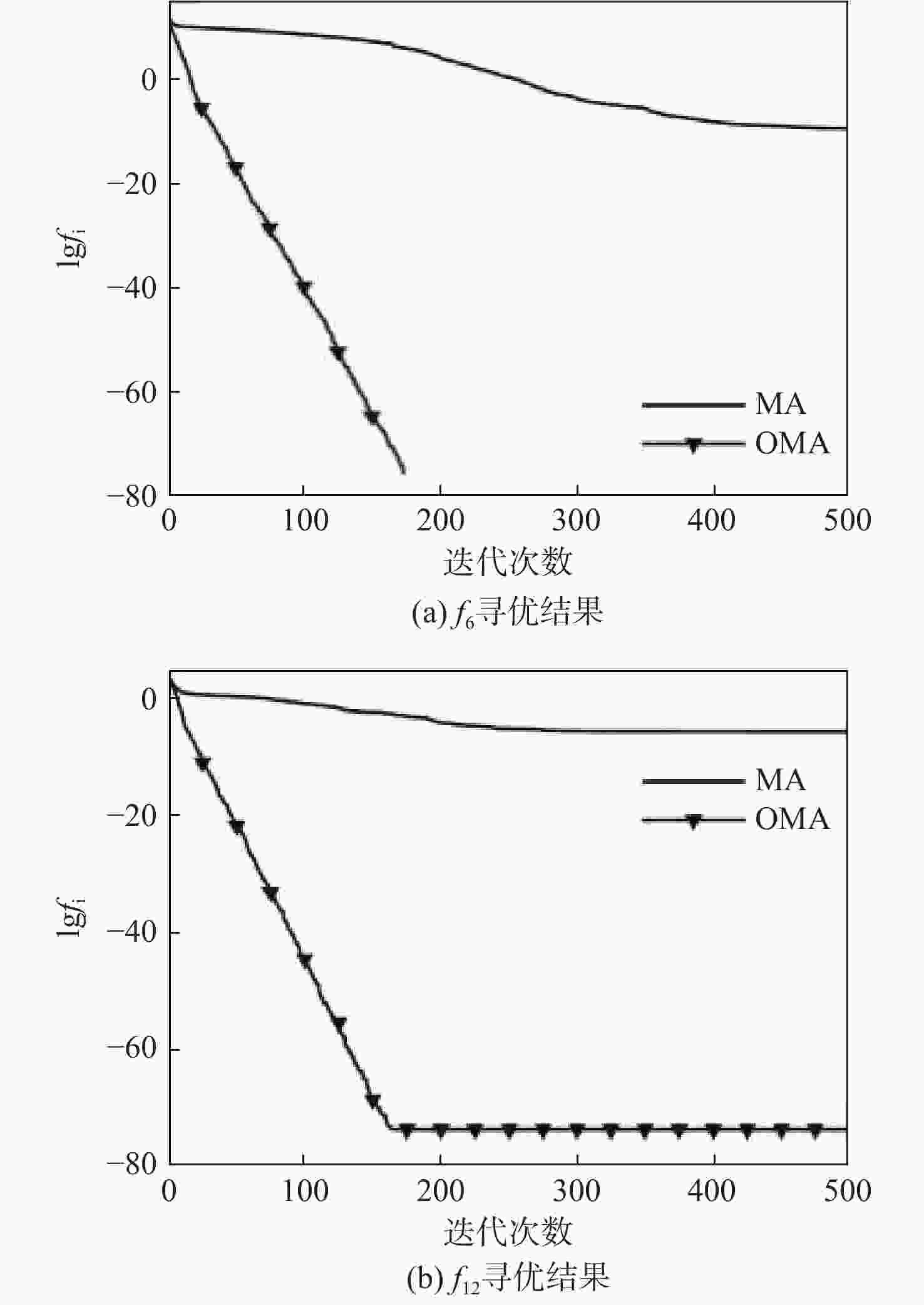
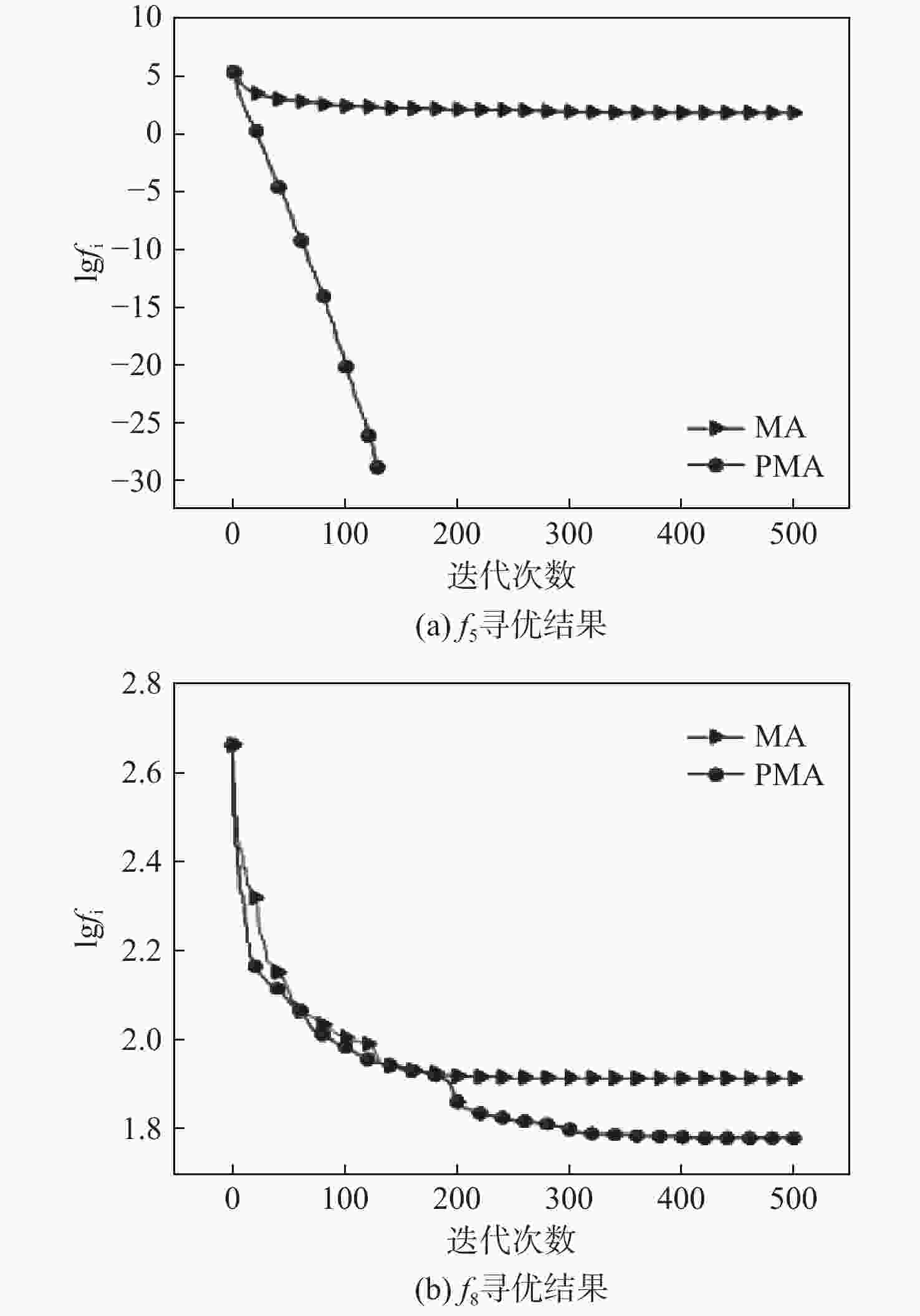
函数	算法	平均值			标准差
函数	算法	d'=10	d'=50	d'=100	d'=10	d'=50	d'=100
f₁	MA	2.58×10⁻³⁵	2.58×10⁻³⁵	1.38×10²	1.12×10⁻³²	1.12×10⁻³⁴	1.53×10²
	ILMA	1.08×10⁻³⁶	1.07×10⁻⁶⁶	8.42×10⁻⁵⁰	4.65×10⁻³⁵	2.46×10⁻⁶⁶	1.95×10⁻⁴⁹
	OMA	6.55×10⁻⁷⁴	6.55×10⁻⁷⁴	4.43×10⁻⁵⁰	3.57×10⁻⁷³	3.57×10⁻⁷³	5.59×10⁻⁵⁰
	PMA	1.61×10⁻¹⁴⁰	1.37×10⁻¹²⁷	3.26×10⁻¹²⁷	6.30×10⁻¹⁴⁰	6.80×10⁻¹²⁷	1.49×10⁻¹²⁶
	LOPMA	3.99×10⁻¹⁴¹	9.76×10⁻¹²⁸	2.28×10⁻¹²⁷	1.31×10⁻¹⁴⁰	1.88×10⁻¹²⁷	6.27×10⁻¹²⁷
f₃	MA	4.38×10⁻¹³	4.38×10⁻¹³	2.51×10⁴	9.97×10⁻¹³	9097×10⁻¹³	8.20×10³
	ILMA	7.36×10⁻¹⁴	1.08×10⁻⁶¹	2.64×10⁻⁴⁴	3.78×10⁻¹⁴	2.74×10⁻⁶¹	1.41×10⁻⁴³
	OMA	1.12×10⁻⁶²	3.84×10⁻²⁶	2.44×10⁻⁴⁵	4.05×10⁻⁶²	1.19×10⁻²⁵	4.72×10⁻⁴⁵
	PMA	9.47×10⁻¹⁴²	4.86×10⁻¹³¹	3.25×10⁻¹³⁰	4.71×10⁻¹⁴¹	1.53×10⁻¹³⁰	1.28×10⁻¹²⁹
	LOPMA	1.25×10⁻¹⁴⁰	3.43×10⁻¹³¹	3.74×10⁻¹³¹	4.78×10⁻¹⁴⁰	1.13×10⁻¹³⁰	1.95×10⁻¹³⁰
f₄	MA	3.50×10⁻⁴	1.79×10¹	2.98×10¹	5.91×10⁻⁴	4.75	3.96
	ILMA	1.00×10⁻⁶	3.81×10⁻²⁶	7.29×10⁻²⁶	1.20×10⁻⁶	8.89×10⁻²⁶	1.07×10⁻²⁵
	OMA	9.32×10⁻³³	3.84×10⁻²⁶	5.81×10⁻²⁶	3.96×10⁻³²	1.19×10⁻²⁵	9.53×10⁻²⁶
	PMA	1.17×10⁻⁷¹	9.35×10⁻⁶⁷	3.20×10⁻⁶⁵	2.50×10⁻⁷¹	1.76×10⁻⁶⁶	1.27×10⁻⁶⁴
	LOPMA	9.03×10⁻⁷⁴	4.85×10⁻⁶⁸	6.82×10⁻⁶⁶	3.47×10⁻⁷³	1.25×10⁻⁶⁷	1.64×10⁻⁶⁵
f₆	MA	1.66×10⁻³⁰	2.79×10⁻²	1.36×10²	6.85×10⁻³⁰	5.17×10⁻²	4.54×10²
	ILMA	1.08×10⁻³¹	1.03×10⁻³⁴	2.05×10⁻³⁴	4.65×10⁻³²	5.63×10⁻³⁴	7.81×10⁻³⁴
	OMA	0	3.08×10⁻³⁴	1.03×10⁻³⁴	0	9.40×10⁻³⁴	5.63×10⁻³⁴
	PMA	0	0	0	0	0	0
	LOPMA	0	0	0	0	0	0
f₈	MA	3.16	6.32×10¹	1.54×10²	2.83	1.65×10¹	3.71×10¹
	ILMA	4.90×10⁻¹	5.17×10¹	1.10×10²	1.80	1.64×10¹	2.83×10¹
	OMA	7.31×10⁻¹	1.03×10¹	5.61×10¹	1.01	4.25	1.38×10¹
	PMA	5.42	5.06×10¹	9.51×10¹	2.08	1.78×10¹	2.45×10¹
	LOPMA	6.63×10⁻¹	8.71	4.63×10¹	1.12×10⁻¹	3.17	8.60
f₁₁	MA	2.07×10⁻²	5.92×10⁻²	1.92×10⁻¹	7.89×10⁻²	1.01×10⁻¹	1.71×10⁻¹
	ILMA	1.04×10⁻²	4.20×10⁻³	1.00×10⁻³	5.68×10⁻²	1.58×10⁻²	5.70×10⁻³
	OMA	5.45×10⁻¹⁶	4.10×10⁻³	4.71×10⁻³³	2.98×10⁻¹⁵	1.58×10⁻²	7.38×10⁻³⁶
	PMA	2.07×10⁻²	2.10×10⁻³	4.71×10⁻³³	7.89×10⁻²	1.14×10⁻²	1.39×10⁻⁴⁸
	LOPMA	1.04×10⁻²	1.70×10⁻³	3.67×10⁻³³	5.68×10⁻²	1.17×10⁻³	1.25×10⁻⁴⁹

下载: 导出CSV

表 4 算法参数设置

Table 4. Algorithm parameter settings

算法	参数设置
LOPMA	$ \begin{aligned}& a_1=1, a_2=1.5, \beta=2, f_{\rm{l}}=1 \\& d_{\text{damp}}=0.8, f_{\text{damp}}^{{\rm{l}}}=0.99, d'=5\end{aligned} $
WOA	$ a_{\max }=2, a_{\min }=0 $
GA	$ p_{1}=0.9, p_{2}=0.1 $
GWO	$ a_{\max }=2, a_{\min }=0, r_{1}, r_{2} \in[0,1] $
PSO	$ \omega=0.9, c_{1}=c_{2}=1.5 $

下载: 导出CSV

表 5 标准测试函数寻优结果

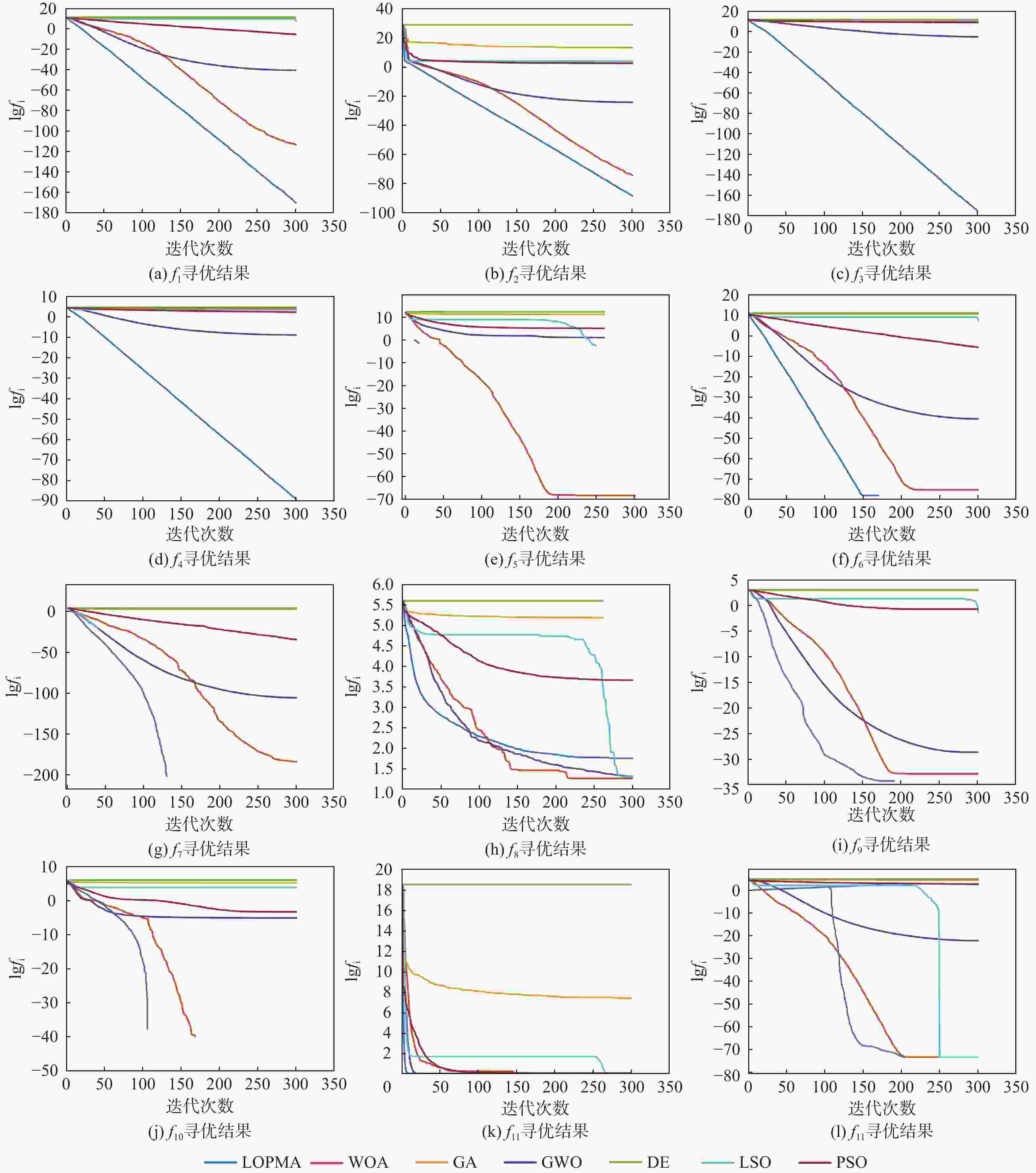
Table 5. Optimization results of standard test functions

函数	算法	最优值	平均值	标准差	函数	算法	最优值	平均值	标准差
f₁	LOPMA	2.80×10⁻²⁰⁵	2.33×10⁻¹⁶⁹	0	f₇	LOPMA	0	0	0
	WOA	7.50×10⁻⁷⁸	3.19×10⁻⁶⁹	1.51×10⁻⁶⁸		WOA	2.20×10⁻¹²³	9.30×10⁻⁹⁷	5.09×10⁻⁹⁶
	GA	4.36×10⁴	3.88×10⁴	4.75×10³		GA	4.86×10¹	4.20×10¹	8.36
	GWO	2.90×10⁻²⁵	1.99×10⁻²⁵	2.72×10⁻²⁵		GWO	2.63×10⁻⁴⁶	4.43×10⁻⁴⁷	1.28×10⁻⁴⁶
	DE	7.07×10⁴	6.31×10⁴	7.54×10³		DE	4.51×10¹	4.04×10¹	8.96
	LSO	2.27×10³	9.34×10²	1.10×10³		LSO	0	7.58×10⁻¹⁶	2.21×10⁻¹⁵
	PSO	1.43×10⁻³	4.59×10⁻⁴	8.16×10⁻⁴		PSO	2.68	2.06	3.50
f₂	LOPMA	6.86×10⁻⁹⁶	6.75×10⁻⁸⁸	3.68×10⁻⁸⁷	f₈	LOPMA	0	0	0
	WOA	9.12×10⁻⁵²	4.41×10⁻⁴⁹	2..04×10⁻⁴⁸		WOA	0	7.49	4.10×10¹
	GA	4.01×10⁵	5.21×10⁶	1.24×10⁷		GA	3.56×10²	3.31×10⁻²	2.34×10¹
	GWO	7.20×10⁻¹⁶	1.14×10⁻¹⁵	7.02×10⁻¹⁶		GWO	2.84×10⁻¹³	3.42	5.18
	DE	6.59×10¹²	1.69×10¹²	3.63×10¹²		DE	2.90×10²	2.70×10²	1.62×10¹
	LSO	4.28×10¹	2.86×10¹	1.95×10¹		LSO	2.85	3.69	2.02×10¹
	PSO	1.99×10¹	9.66	8.71		PSO	7.77×10¹	9.97×10¹	3.07×10¹
f₃	LOPMA	2.49×10⁻¹⁹⁸	1.17×10⁻¹³⁰	6.39×10⁻¹³⁰	f₉	LOPMA	8.88×10⁻¹⁶	8.88×10⁻¹⁶	0
	WOA	6.12×10⁴	5.04×10⁴	1.22×10⁴		WOA	4.44×10⁻¹⁵	4.80×10⁻¹⁵	2.16×10⁻¹⁵
	GA	5.48×10⁴	4.82×10⁴	6.79×10³		GA	1.98×10¹	1.96×10¹	2.96×10⁻¹
	GWO	1.50×10⁻⁵	4.60×10⁻⁵	9.57×10⁻⁵		GWO	2.42×10⁻¹³	2.08×10⁻¹³	5.72×10⁻¹⁴
	DE	1.46×10⁵	1.18×10⁵	3.10×10⁴		DE	2.00	2.00	4.17×10⁻²
	LSO	3.73×10³	2.02×10³	2.88×10³		LSO	8.88×10⁻¹⁶	2.16×10⁻¹	1.18
	PSO	1.63×10⁴	6.70×10³	5.68×10³		PSO	1.65	4.00	2.44
f₄	LOPMA	5.52×10⁻¹¹⁹	7.06×10⁻⁸⁵	3.81×10⁻⁸⁴	f₁₀	LOPMA	0	0	0
	WOA	0.89×10²	0.49×10²	0.28×10²		WOA	0	6.90×10⁻³	3.78×10⁻²
	GA	0.72×10²	0.72×10²	4.02		GA	3.94×10²	3.50×10²	4.28×10¹
	GWO	1.15×10⁻⁶	3.50×10⁻⁶	3.29×10⁻⁶		GWO	0	3.90×10⁻³	1.04×10⁻²
	DE	8.75×10¹	8.59×10¹	3.34		DE	3.88×10²	3.48×10²	4.11×10¹
	LSO	2.33×10¹	1.78×10¹	5.98		LSO	3.26	4.08	1.32×10¹
	PSO	0.12×10²	9.90	3.53		PSO	7.90×10⁻²	8.09×10⁻²	1.36×10⁻¹
f₅	LOPMA	0	0	0	f₁₁	LOPMA	1.57×10⁻³²	1.57×10⁻³²	5.57×10⁻⁴⁸
	WOA	0	4.12×10⁻³¹	1.57×10⁻³⁰		WOA	1.57×10⁻³²	1.57×10⁻³²	5.57×10⁻⁴⁸
	GA	9.55×10⁴	7.64×10⁴	1.71×10⁴		GA	9.29	1.20×10¹	2.23
	GWO	1.03×10⁻¹⁵	0.39×10⁻²	2.16×10⁻²		GWO	1.82×10⁻²⁹	3.15×10⁻²⁹	3.34×10⁻²⁹
	DE	2.46×10⁵	2.05×10⁵	4.78×10⁴		DE	1.31×10¹	1.84×10¹	3.07
	LSO	2.60	1.38×10¹	3.15		LSO	2.36×10⁻³²	2.36×10⁻³²	8.35×10⁻⁴⁸
	PSO	0.27×10²	1.39×10²	3.04×10²		PSO	2.86×10⁻⁹	1.59×10⁻¹	3.02×10¹
f₆	LOPMA	0	0	0	f₁₂	LOPMA	1.35×10⁻³²	1.35×10⁻³²	5.57×10⁻⁴⁸
	WOA	0	2.05×10⁻³⁴	7.82×10⁻³⁴		WOA	1.35×10⁻³²	1.35×10⁻³²	5.57×10⁻⁴⁸
	GA	4.36×10⁴	3.88×10⁴	4.75×10³		GA	1.49×10¹	1.52×10¹	2.75
	GWO	3.00×10⁻²⁵	1.99×10⁻²⁵	2.72×10⁻²⁵		GWO	2.13×10⁻²⁹	1.38×10⁻²⁸	2.22×10⁻²⁸
	DE	70.7×10⁴	6.31×10⁴	7.54×10³		DE	1.45×10²	1.34×10²	1.71×10¹
	LSO	2.27×10³	9.34×10²	1.01×10³		LSO	1.35×10⁻³²	1.35×10⁻³²	5.57×10⁻⁴⁸
	PSO	0.14×10⁻²	4.60×10⁻⁴	8.16×10⁻⁴		PSO	3.50×10⁻⁶	1.82×10⁻²	4.18×10⁻²

下载: 导出CSV

表 6 LOPMA与其他算法的显著性差异检验结果

Table 6. Significance difference test results between LOPMA and other algorithms

函数	p
函数	LOPMA和WOA	LOPMA和GA	LOPMA和GWO	LOPMA和MA	LOPMA和DE	LOPMA和LSO	LOPMA和PSO
f₁	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	1.90×10⁻³	3.02×10⁻¹¹
f₂	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	6.61×10⁻¹	3.02×10⁻¹¹
f₃	3.01×10⁻¹¹	3.01×10⁻¹¹	3.01×10⁻¹¹	3.01×10⁻¹¹	3.02×10⁻¹¹	1.90×10⁻³	3.01×10⁻¹¹
f₄	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹
f₅	6.54×10⁻¹	2.16×10⁻⁸	2.16×10⁻⁸	2.16×10⁻⁸	3.26×10⁻¹¹	1.61×10⁻¹¹	2.16×10⁻⁸
f₆	1.67×10⁻¹	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.70×10⁻⁸	1.21×10⁻¹²
f₇	5.31×10⁻¹⁰	5.31×10⁻¹⁰	5.31×10⁻¹⁰	5.31×10⁻¹⁰	9.10×10⁻⁹	1.18×10⁻¹²	5.31×10⁻¹⁰
f₈	2.17×10⁻¹⁰	3.02×10⁻¹¹	9.49×10⁻⁷	3.02×10⁻¹¹	3.02×10⁻¹¹	1.55×10⁻¹⁰	3.02×10⁻¹¹
f₉	6.42×10⁻⁸	9.16×10⁻¹	9.16×10⁻¹	9.16×10⁻¹	9.19×10⁻⁷	7.68×10⁻¹³	9.16×10⁻¹
f₁₀	1.17×10⁻¹³	4.57×10⁻¹²	4.91×10⁻¹³	4.57×10⁻¹²	7.72×10⁻⁵	7.72×10⁻⁵	4.57×10⁻¹²
f₁₁	1.61×10⁻¹	2.37×10⁻¹²	1.24×10⁻⁹	4.40×10⁻¹¹	2.372×10⁻¹²	1.61×10⁻¹	2.07×10⁻¹⁰
f₁₂	1.35×10⁻⁸	3.31×10⁻¹¹	3.31×10⁻¹¹	3.31×10⁻¹¹	3.37×10⁻¹¹	5.55×10⁻¹¹	3.31×10⁻¹¹

下载: 导出CSV

表 7 与其他改进蜉蝣算法性能对比

Table 7. Compared with other improved in the performance of the ephemera algorithms

函数	平均值				标准差
	对照组1		对照组2		对照组1		对照组2
	LOPMA	MIWMA^[26]	LOPMA	MIMA^[27]	LOPMA	MIMA^[26]	LOPMA	MIMA^[27]
f₁	3.65×10⁻¹²⁴	1.40×10⁻¹³⁵	2.89×10⁻²⁶²	1.49×10⁻¹⁹²	2.01×10⁻¹²⁵	6.50×10⁻¹³⁴	0	0
f₂	9.02×10⁻⁶⁵	2.05×10⁻⁶⁰	9.59×10⁻¹³³	7.61×10⁻⁹⁸	2.23×10⁻⁶⁴	9.61×10⁻⁶⁰	5.54×10⁻¹³²	1.16×10⁻⁹⁷
f₃	3.73×10⁻¹²⁹	2.55×10⁻¹¹³	6.81×10⁻²⁶⁸	9.82×10⁻⁶⁴	1.37×10⁻¹²⁸	1.70×10⁻¹¹²	0	4.28×10⁻⁶³
f₄	4.81×10⁻⁶⁵	1.88×10⁻⁶⁰	1.32×10⁻¹³⁴	4.93×10⁻³⁴	1.64×10⁻⁶⁴	1.17×10⁻⁵⁹	3.90×10⁻¹³⁴	2.42×10⁻³³
f₇	1.65×10⁻⁵	5.62×10⁻⁵	3.59×10⁻³	1.25×10⁻⁴	2.44×10⁻⁶	4.08×10⁻⁵	2.64×10⁴	1.32×10⁻⁴
f₈	0	0	0	0	0	0	0	0
f₉	8.88×10⁻¹⁶	8.88×10⁻¹⁶	8.88×10⁻¹⁶	8.88×10⁻¹⁶	0	0	0	0
f₁₀	0	0	0	0	0	0	0	0
f₁₁	6.23×10⁻¹⁴	6.43×10⁻¹³	1.24×10⁻³²	2.38×10⁻³²	4.40×10⁻¹³	6.72×10⁻¹³	4.26×10⁻³³	5.83×10⁻³⁴

下载: 导出CSV

表 8 CEC2017寻优结果

Table 8. CEC2017 optimization results

函数	平均值						标准差
函数	AFSMA^[28]	I-GWO^[29]	WOA	LSO	MA	LOPMA	AFSMA^[28]	I-GWO^[29]	WOA	LSO	MA	LOPMA
CEC03	4.80×10⁴	1.84×10⁴	2.67×10⁵	1.30×10⁵	1.35×10⁵	6.64×10⁴	1.44×10⁴	3.46×10³	7.62×10⁴	3.94×10⁴	6.39×10⁴	2.78×10³
CEC06	6.24×10²	7.02×10²	6.83×10²	6.77×10²	6.67×10²	6.41×10²	1.02×10¹	1.11×10²	1.36×10¹	1.15×10¹	9.50×10⁰	8.61×10⁰
CEC09	5.05×10³	1.14×10³	1.15×10⁴	1.04×10⁴	6.03×10³	3.42×10³	1.56×10³	3.32×10³	3.83×10³	1.97×10³	1.25×10³	1.29×10³
CEC12	3.37×10⁶	4.86×10⁶	4.28×10⁸	4.82×10⁹	1.43×10⁷	2.78×10⁶	3.13×10⁶	4.14×10⁶	2.55×10⁸	1.63×10⁹	1.55×10⁷	3.06×10⁶
CEC15	1.33×10⁴	6.04×10⁴	1.08×10⁷	4.55×10⁸	2.23×10⁴	5.41×10³	1.33×10⁴	4.06×10⁴	1.89×10⁷	5.20×10⁸	1.82×10⁴	5.94×10³
CEC18	2.45×10⁶	4.56×10⁵	1.16×10⁷	3.98×10⁷	2.02×10⁵	1.62×10⁵	2.72×10⁶	2.91×10⁵	1.22×10⁷	2.02×10⁵	1.96×10⁵	1.68×10⁵
CEC21	2.45×10³	3.21×10³	2.66×10³	2.67×10³	2.73×10³	2.45×10³	3.67×10¹	1.31×10²	6.48×10¹	3.35×10¹	5.01×10¹	3.14×10¹
CEC24	2.98×10³	2.74×10³	3.27×10³	3.43×10³	3.73×10³	2.52×10³	4.81×10¹	6.83×10²	1.14×10²	1.35×10¹	1.75×10²	4.44×10¹
CEC27	3.25×10³	3.21×10³	3.45×10³	3.72×10³	4.55×10³	3.21×10³	2.09×10¹	7.02×10²	1.37×10²	2.25×10²	7.31×10²	1.64×10¹

下载: 导出CSV

参考文献(29)

[1]	KHISHE M, MOSAVI M R. Chimp optimization algorithm[J]. Expert Systems with Applications, 2020, 149: 113338. doi: 10.1016/j.eswa.2020.113338
[2]	ALSATTAR H A, ZAIDAN A A, ZAIDAN B B. Novel meta-heuristic bald eagle search optimisation algorithm[J]. Artificial Intelligence Review, 2020, 53(3): 2237-2264. doi: 10.1007/s10462-019-09732-5
[3]	MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163-191. doi: 10.1016/j.advengsoft.2017.07.002
[4]	SALGOTRA R, SINGH U, SINGH G, et al. A self-adaptive hybridized differential evolution naked mole-rat algorithm for engineering optimization problems[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 383: 113916. doi: 10.1016/j.cma.2021.113916
[5]	BRAIK M S. Chameleon swarm algorithm: a bio-inspired optimizer for solving engineering design problems[J]. Expert Systems with Applications, 2021, 174: 114685. doi: 10.1016/j.eswa.2021.114685
[6]	ZERVOUDAKIS K, TSAFARAKIS S. A mayfly optimization algorithm[J]. Computers & Industrial Engineering, 2020, 145: 106559.
[7]	KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the ICNN'95−International Conference on Neural Networks. Piscataway: IEEE Press, 1995: 1942-1948.
[8]	GOLDBERG D. Genetic algorithms in search, optimization and machine learning[M]. Boston: Addison-Wesley Longman Publishing Co. , Inc. , 1989.
[9]	YANG X S. Nature-inspired metaheuristic algorithms[M]. United Kingdom: Luniver Press, 2010: 79-90.
[10]	HOU S, YU J Q, SU Y C, et al. Flow distribution optimization of parallel pumps based on improved mayfly algorithm[J]. Journal of Intelligent & Fuzzy Systems, 2023, 44(2): 2065-2083.
[11]	FARKI A, SALEKSHAHREZAEE Z, TOFIGH A M, et al. COVID-19 diagnosis using capsule network and fuzzy C-means and mayfly optimization algorithm[J]. BioMed Research International, 2021, 2021: 2295920. doi: 10.1155/2021/2295920
[12]	ZHANG S J, HOU T T, QU Q, et al. An improved mayfly method to solve distributed flexible job shop scheduling problem under dual resource constraints[J]. Sustainability, 2022, 14(19): 12120. doi: 10.3390/su141912120
[13]	XIAO Y Q, WU Y J. Robust visual tracking based on modified mayfly optimization algorithm[J]. Image and Vision Computing, 2023, 135: 104691. doi: 10.1016/j.imavis.2023.104691
[14]	GUO L, XU C, YU T H, et al. An improved mayfly optimization algorithm based on Median position and its application in the optimization of PID parameters of hydro-turbine governor[J]. IEEE Access, 2022, 10: 36335-36349. doi: 10.1109/ACCESS.2022.3160714
[15]	席万强, 常保帅, 林思伟, 等. 多策略改进蜉蝣算法的无人机航迹规划[J]. 电光与控制, 2023, 30(11): 80-84. XI W Q, CHANG B S, LIN S W, et al. A multi-strategy improved mayfly algorithm for UAV path planning[J]. Electronics Optics & Control, 2023, 30(11): 80-84(in Chinese).
[16]	李林丰, 刘卫东, 李乐. 基于改进蜉蝣算法的水下磁场测量误差补偿[J]. 西北工业大学学报, 2022, 40(5): 1004-1011. doi: 10.1051/jnwpu/20224051004 LI L F, LIU W D, LI L. Underwater magnetic field measurement error compensation based on improved mayfly algorithm[J]. Journal of Northwestern Polytechnical University, 2022, 40(5): 1004-1011(in Chinese). doi: 10.1051/jnwpu/20224051004
[17]	毛清华, 王迎港. 融合改进Logistics混沌和正弦余弦算子的自适应t分布海鸥算法[J]. 小型微型计算机系统, 2022, 43(11): 2271-2277. MAO Q H, WANG Y G. Adaptive t-distribution seagull optimization algorithm combining improved logistics chaos and sine-cosine operator[J]. Journal of Chinese Computer Systems, 2022, 43(11): 2271-2277(in Chinese).
[18]	宁杰琼, 何庆. 混合策略改进的蝴蝶优化算法[J]. 计算机应用研究, 2021, 38(6): 1718-1723. NING J Q, HE Q. Mixed strategy to improve butterfly optimization algorithm[J]. Application Research of Computers, 2021, 38(6): 1718-1723(in Chinese).
[19]	邬贵昌, 韦文山, 李尚平, 等. 基于混沌的多策略优化麻雀算法及应用[J]. 微电子学与计算机, 2022, 39(12): 21-30. WU G C, WEI W S, LI S P, et al. Multi-strategy optimization sparrow search algorithm based on chaos and its application[J]. Microelectronics & Computer, 2022, 39(12): 21-30(in Chinese).
[20]	张伟康, 刘升, 任春慧. 混合策略改进的麻雀搜索算法[J]. 计算机工程与应用, 2021, 57(24): 74-82. ZHANG W K, LIU S, REN C H. Mixed strategy improved sparrow search algorithm[J]. Computer Engineering and Applications, 2021, 57(24): 74-82(in Chinese).
[21]	张超. 基于t-分布精英保留机制的花朵授粉算法[J]. 安徽理工大学学报(自然科学版), 2018, 38(3): 50-58. ZHANG C. Flower pollination algorithm based on t-distribution elitist retention mechanism[J]. Journal of Anhui University of Science and Technology (Natural Science), 2018, 38(3): 50-58(in Chinese).
[22]	毛清华, 赵冰, 王迎港. 融合T-分布小波变异的混沌鲸鱼优化算法[J]. 小型微型计算机系统, 2024, 45(10): 2362-2369. MAO Q H, ZHAO B, WANG Y G. Chaotic whale optimization algorithm with T-distributed wavelet variation[J]. Journal of Chinese Computer Systems, 2024, 45(10): 2362-2369(in Chinese).
[23]	杜永兆, 范宇凌, 柳培忠, 等. 多种群协方差学习差分进化算法[J]. 电子与信息学报, 2019, 41(6): 1488-1495. DU Y Z, FAN Y L, LIU P Z, et al. Multi-populations covariance learning differential evolution algorithm[J]. Journal of Electronics & Information Technology, 2019, 41(6): 1488-1495(in Chinese).
[24]	刘小龙, 许岩, 徐维军. 基于统计引导和多项式差分学习的樽海鞘优化算法[J]. 运筹与管理, 2021, 30(1): 43-49. LIU X L, XU Y, XU W J. Salp swarm algorithm based on statistical guidance and polynomial difference learning[J]. Operations Research and Management Science, 2021, 30(1): 43-49(in Chinese).
[25]	毛清华, 王迎港, 牛晓辉. 基于反吸引速度更新机制的改进蜉蝣算法[J]. 北京航空航天大学学报, 2024, 50(6): 1770-1783. MAO Q H, WANG Y G, NIU X H. Improved mayfly optimization algorithm based on anti-attraction velocity update mechanism[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(6): 1770-1783(in Chinese).
[26]	王义, 张达敏, 邹诚诚. 增强全局搜索和自适应蜉蝣算法[J]. 哈尔滨工业大学学报, 2022, 54(11): 137-150. WANG Y, ZHANG D M, ZOU C C. Enhance global search and adaptive mayfly algorithm[J]. Journal of Harbin Institute of Technology, 2022, 54(11): 137-150(in Chinese).
[27]	蒋宇飞, 许贤泽, 徐逢秋, 等. 多策略融合改进的自适应蜉蝣算法[J]. 北京航空航天大学学报, 2024, 50(4): 1416-1426. JIANG Y F, XU X Z, XU F Q, et al. Multi-strategy fusion improved adaptive mayfly algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(4): 1416-1426(in Chinese).
[28]	肖子雅, 刘升. 精英反向黄金正弦鲸鱼算法及其工程优化研究[J]. 电子学报, 2019, 47(10): 2177-2186. XIAO Z Y, LIU S. Study on elite opposition-based golden-sine whale optimization algorithm and its application of project optimization[J]. Acta Electronica Sinica, 2019, 47(10): 2177-2186(in Chinese).
[29]	NADIMI-SHAHRAKI M H, TAGHIAN S, MIRJALILI S. An improved grey wolf optimizer for solving engineering problems[J]. Expert Systems with Applications, 2021, 166: 113917. doi: 10.1016/j.eswa.2020.113917