基于拦截捕获区的“多对多”能量最优目标分配方法

李昊键; 黎克波; 梁彦刚

doi:10.13700/j.bh.1001-5965.2024.0330

基于拦截捕获区的“多对多”能量最优目标分配方法

doi: 10.13700/j.bh.1001-5965.2024.0330

李昊键^{1, 2},
黎克波^{1, 2, ,},
梁彦刚^{1, 2}

1.
国防科技大学空天科学学院，长沙 410072
2.
太空系统运行与控制全国重点实验室，长沙 410072

基金项目:

国家自然科学基金(12472359,U2441205,62103435)

详细信息

通讯作者:
E-mail：likeboreal@nudt.edu.cn

中图分类号: V448.2；TJ765.3
计量
- 文章访问数: 108
- HTML全文浏览量: 32
- PDF下载量: 5
- 被引次数: 0
出版历程
- 收稿日期: 2024-05-17
- 录用日期: 2024-08-17
- 网络出版日期: 2025-04-02
- 整期出版日期: 2026-02-28

Multi-to-multi energy optimal task allocation method based on interception capture region

LI Haojian^{1, 2},
LI Kebo^{1, 2
, ,},
LIANG Yangang^{1, 2}

1.
College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410072，China
2.
State Key Laboratory of Space System Operation and Control，Changsha 410072，China

Funds:

National Natural Science Foundation of China (12472359,U2441205,62103435)

More Information

Corresponding author: E-mail：likeboreal@nudt.edu.cn

摘要

摘要:
针对多拦截器与多目标交战(MME)场景的任务分配问题，从制导的角度入手，提出基于拦截捕获区的“多对多”能量最优目标分配方法。分析三维现实真比例导引(3D-RTPN)拦截任意机动目标的捕获区与最优制导能量消耗；以多拦截器成功拦截机动目标与整体能量消耗最低为优化目标，构建目标分配代价矩阵；基于适应性匈牙利算法(AHA)实现多拦截器的多目标分配(MMA)。通过数值仿真算例，验证了所提方法的有效性。
- 多拦截器多目标交战 /
- 拦截捕获区 /
- 三维真比例导引 /
- 适应性匈牙利算法 /
- 多拦截器多目标分配
Abstract:
Aiming at the assignment problem of multimissile and multitarget engagement (MME) scenario, this paper proposes a multi-to-multi energy optimal task allocation method based on interception capture region from the perspective of guidance. The characteristics of the capture region and optimal energy cost in the scenario of three-dimensional realistic true proportional navigation (3D-RTPN) intercepting arbitrary maneuvering targets are analyzed. The weight matrix is then built with the intention of achieving both the lowest total energy consumption and successful interception. In order to achieve multimissile and multitarget assignment (MMA), the adaptable Hungarian algorithm (AHA) is used. Numerical simulation is used to confirm the MMA strategy's efficacy. The effectiveness of the proposed method is verified by numerical simulation.

HTML全文

图 1 RTPN三维捕获区

Figure 1. Three-dimensional capture region of RTPN

下载: 全尺寸图片幻灯片

图 2 RTPN二维捕获区

Figure 2. Two-dimensional capture region of RTPN

下载: 全尺寸图片幻灯片

图 3 拦截仿真结果

Figure 3. Simulation results of interception

下载: 全尺寸图片幻灯片

表 1 仿真主要参数

Table 1. Main parameters of simulation

参数	数值
弹头释放位置r_mc/km	[10, 10, 10]^T
子拦截器1位矢r_m1/km	r_mc+[1, 0, 0]^T
子拦截器2位矢r_m2/km	r_mc+[0, 1, 0]^T
子拦截器3位矢r_m3/km	r_mc+[0, 0, 1]^T
子拦截器4位矢r_m4/km	r_mc+[−1, 0, 0]^T
子拦截器5位矢r_m5/km	r_mc+[0, −1, 0]^T
子拦截器6位矢r_m6/km	r_mc+[0, 0, −1]^T
目标1初始时刻位矢r_t1/km	[60, 30, 60]^T
目标2初始时刻位矢r_t2/km	[50, 32, 62]^T
目标3初始时刻位矢r_t3/km	[62, 28, 50]^T
弹头释放时刻速度大小V_m/(m·s⁻¹)	1800
目标1速度大小V_t1/(m·s⁻¹)	2 000
目标2速度大小V_t2/(m·s⁻¹)	2 000
目标3速度大小V_t3/(m·s⁻¹)	2 000
弹头释放时刻速度倾角θ_mc/(°)	45
目标1初始时刻速度倾角θ_t1/(°)	0
目标2初始时刻速度倾角θ_t2/(°)	0
目标3初始时刻速度倾角θ_t3/(°)	0
弹头释放时刻速度方位角ψ_mc/(°)	−45
目标1初始时刻速度方位角ψ_t1/(°)	135
目标2初始时刻速度方位角ψ_t2/(°)	130
目标3初始时刻速度方位角ψ_t3/(°)	140
弹头释放时刻速度矢量v_mc/(m·s⁻¹)	V_m·[cosθ_mccosψ_mc, sinθ_mc, −cosθ_mcsinψ_mc]
子拦截器1速度矢量v_m1/(m·s⁻¹)	v_mc+[100, 0, 0]^T
子拦截器2速度矢量v_m2/(m·s⁻¹)	v_mc+[0, 100, 0]^T
子拦截器3速度矢量v_m3/(m·s⁻¹)	v_mc+[0, 0, 100]^T
子拦截器4速度矢量v_m4/(m·s⁻¹)	v_mc+[−100, 0, 0]^T
子拦截器5速度矢量v_m5/(m·s⁻¹)	v_mc+[0, −100, 0]^T
子拦截器6速度矢量v_m6/(m·s⁻¹)	v_mc+[0, 0, −100]^T

下载: 导出CSV

表 2 不同算法分配结果

Table 2. Allocation results of different algorithms

算法	目标序号
算法	拦截器1	拦截器2	拦截器3	拦截器4	拦截器5	拦截器6
AHA	3	1	2	2	1	3
GA+SQP （无整数约束）	3	1	2	2	1	3
GA（整数约束）	2	1	1	3	2	3

下载: 导出CSV

表 3 不同算法耗时与寻优结果

Table 3. Time consumption and optimization results of different algorithms

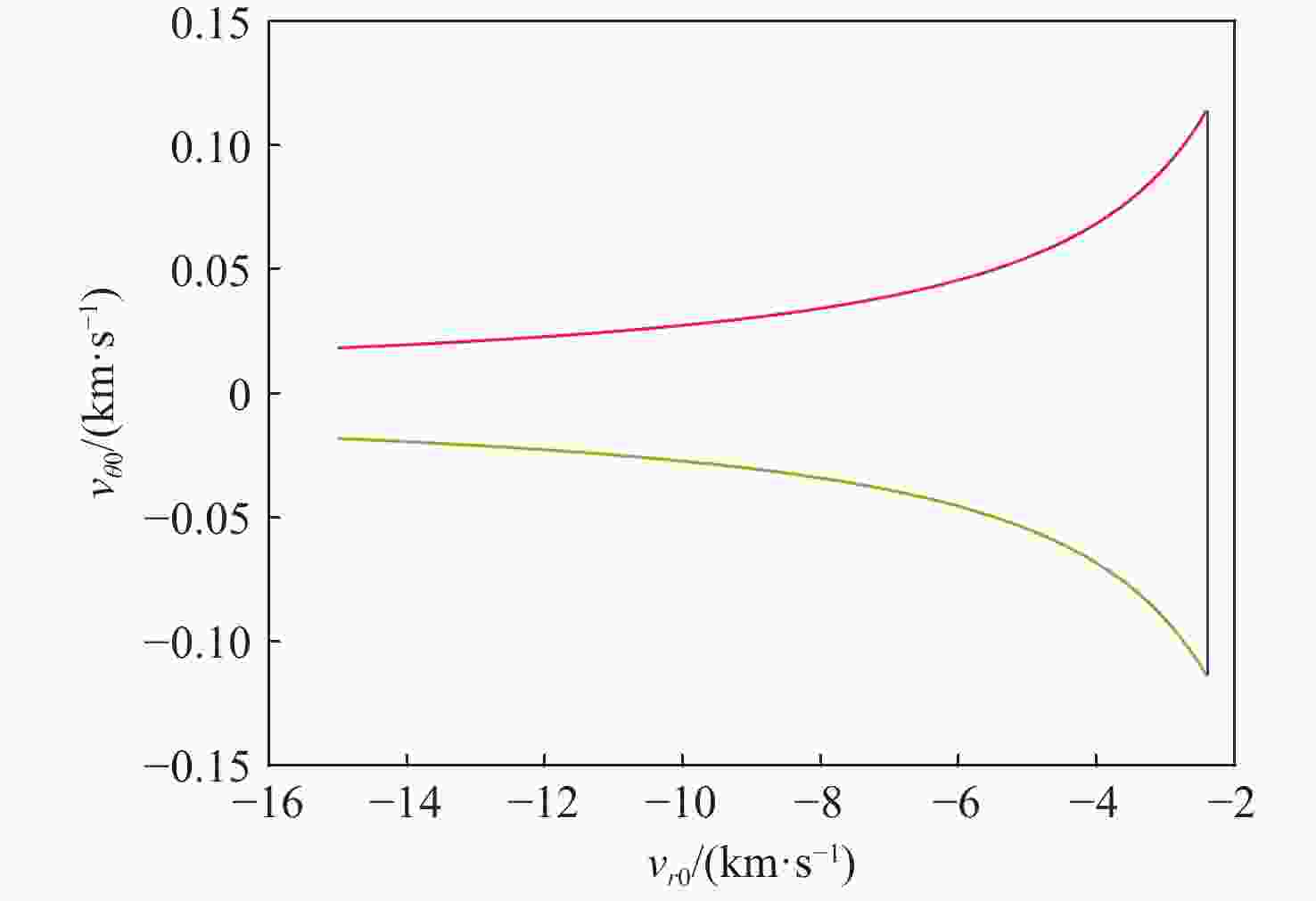
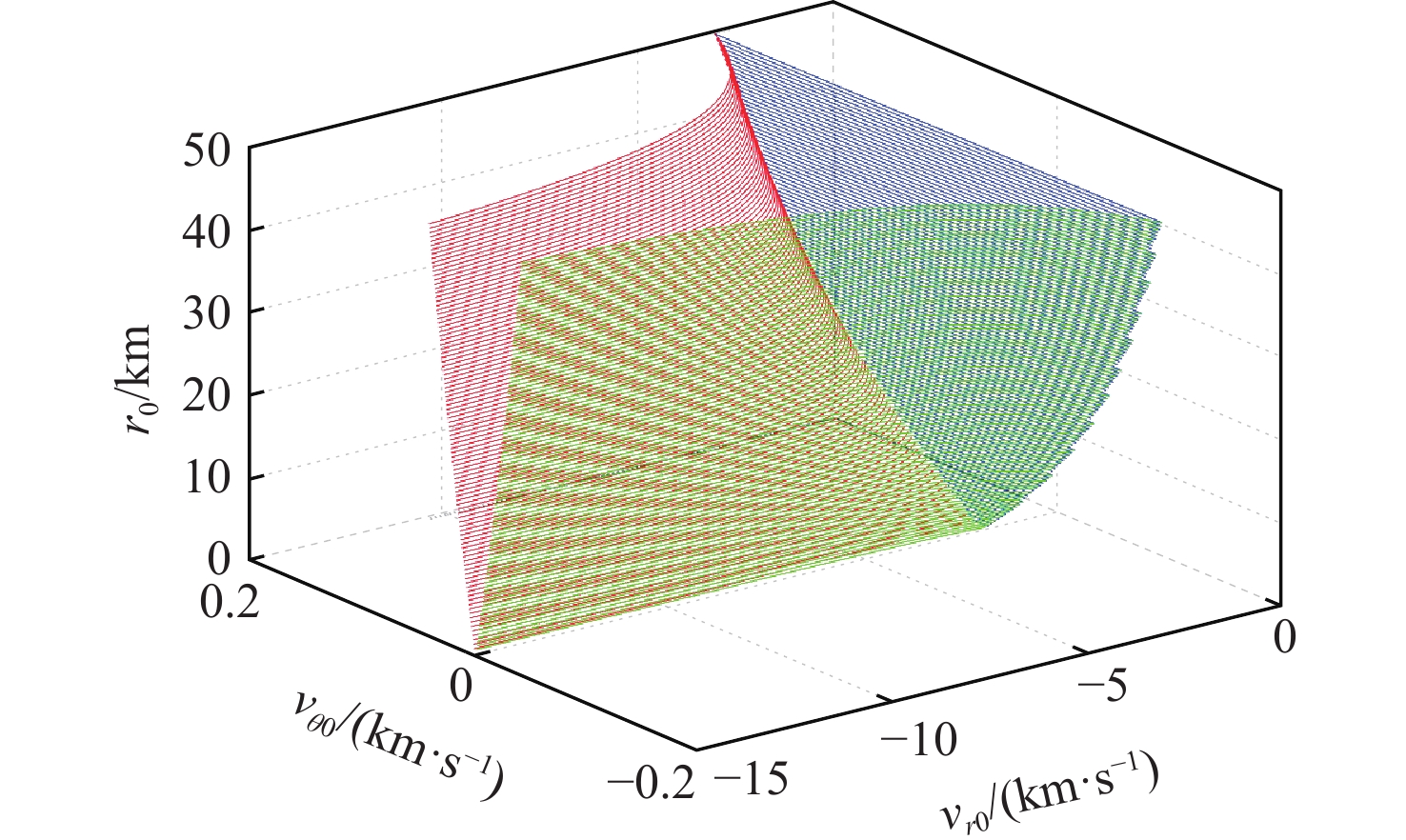
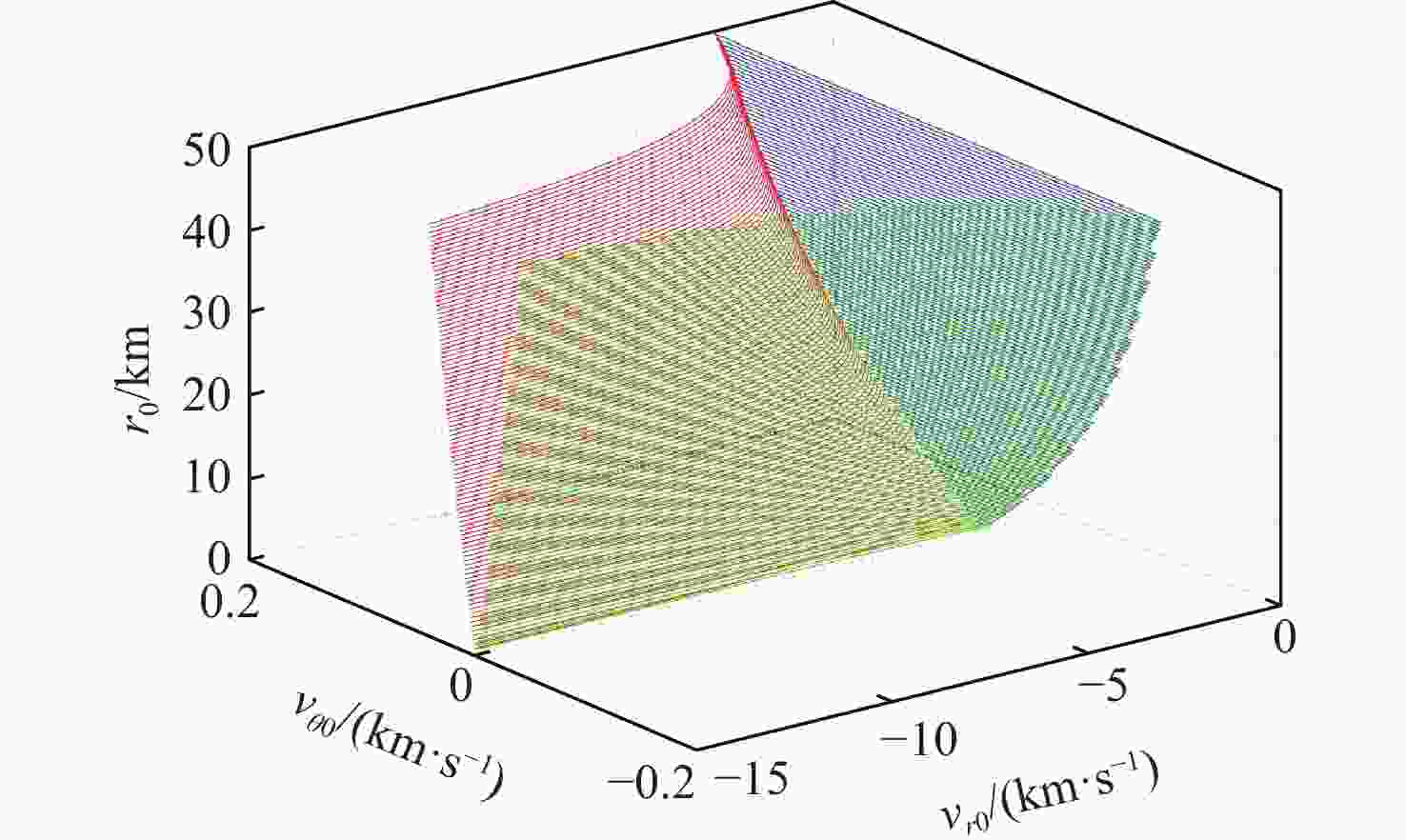
算法	求解耗时/s	代价矩阵+ 算法求解耗时/s	速度增量寻优结果/（m·s⁻¹）
AHA	0.0005	0.0077	9465.9
GA+SQP （无整数约束）	9.3168	9.3152	9465.9
GA（整数约束）	64.4299	64.4328	10150.9

下载: 导出CSV

参考文献(17)

[1]	谢愈, 刘鲁华, 汤国建, 等. 多拦截器总体拦截方案设计与分析[J]. 北京航空航天大学学报, 2012, 38(3): 303-308. XIE Y, LIU L H, TANG G J, et al. Design and analysis of interception project for multiple kill vehicle interceptor[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(3): 303-308(in Chinese).
[2]	CHEN B, YAN B, WANG Y M. Research on multiple kill vehicles firepower distribution strategy based on adjust genetic algorithm[C]//Proceedings of the 25th Chinese Control and Decision Conference. Piscataway: IEEE Press, 2013: 3582-3586.
[3]	YANG B Q, LI X L, MA J. Target assignment based on hybrid model predictive control[J]. Applied Mechanics and Materials, 2014, 556-562: 3622-3626.
[4]	顾佼佼, 赵建军, 颜骥, 等. 基于MODPSO-GSA的协同空战武器目标分配[J]. 北京航空航天大学学报, 2015, 41(2): 252-258. GU J J, ZHAO J J, YAN J, et al. Cooperative weapon-target assignment based on multi-objective discrete particle swarm optimization-gravitational search algorithm in air combat[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2): 252-258(in Chinese).
[5]	MERKULOV V I, PLYASHECHNIK A S. Simplified target assignment problem for group engagement of aircraft[J]. Automation and Remote Control, 2019, 80(3): 490-501. doi: 10.1134/S0005117919030081
[6]	KIM J, LEE W C, CHO D H, et al. Decentralized weapon target assignment against high-speed enemy missiles[C]//Proceedings of the AIAA Scitech 2020 Forum. Reston: AIAA, 2020.
[7]	张进, 郭浩, 陈统. 基于可适应匈牙利算法的武器-目标分配问题[J]. 兵工学报, 2021, 42(6): 1339-1344. ZHANG J, GUO H, CHEN T. Weapon-target assignment based on adaptable Hungarian algorithm[J]. Acta Armamentarii, 2021, 42(6): 1339-1344(in Chinese).
[8]	GUO J G, HU G J, GUO Z Y, et al. Evaluation model, intelligent assignment, and cooperative interception in multimissile and multitarget engagement[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 3104-3115. doi: 10.1109/TAES.2022.3144111
[9]	GENG Z, HUANG Y Y, ZHANG H, et al. Improved sparrow search algorithm applied to multi-stage weapon target assignment[C]//Proceedings of the International Conference on Cyber-Physical Social Intelligence. Piscataway: IEEE Press, 2022: 98-103.
[10]	邹子缘, 陈琪锋. 基于决策树搜索的空间飞行器集群对抗目标分配方法[J]. 航空学报, 2022, 43(S1): 726910. ZOU Z Y, CHEN Q F. Target assignment method of spacecraft cluster confrontation based on decision tree search[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(S1): 726910(in Chinese).
[11]	高树一, 林德福, 郑多, 等. 针对集群攻击的飞行器智能协同拦截策略[J]. 航空学报, 2023, 44(18): 328301. GAO S Y, LIN D F, ZHENG D, et al. Intelligent cooperative interception strategy of aircraft against cluster attack[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(18): 328301(in Chinese).
[12]	苏山, 马泽远, 张立, 等. 改进粒子群优化多拦截器目标分配方法研究[J]. 弹箭与制导学报, 2024, 44(1): 41-48. SU S, MA Z Y, ZHANG L, et al. Research on multi-interceptor target assignment method using improved particle swarm optimization[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2024, 44(1): 41-48(in Chinese).
[13]	LI K B, ZHANG T T, CHEN L. Ideal proportional navigation for exoatmospheric interception[J]. Chinese Journal of Aeronautics, 2013, 26(4): 976-985. doi: 10.1016/j.cja.2013.06.007
[14]	LI K B, SU W S, CHEN L. Performance analysis of three-dimensional differential geometric guidance law against low-speed maneuvering targets[J]. Astrodynamics, 2018, 2(3): 233-247. doi: 10.1007/s42064-018-0023-z
[15]	白志会, 黎克波, 苏文山, 等. 现实真比例导引拦截任意机动目标捕获区域[J]. 航空学报, 2020, 41(8): 323947. BAI Z H, LI K B, SU W S, et al. Capture region of RTPN guidance law against arbitrarily maneuvering targets[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(8): 323947(in Chinese).
[16]	LI K B, BAI Z H, HYO-SANG S, et al. Capturability of 3D RTPN guidance law against true-arbitrarily maneuvering target with maneuverability limitation[J]. Chinese Journal of Aeronautics, 2022, 35(7): 75-90. doi: 10.1016/j.cja.2021.10.004
[17]	YANG C D, YANG C C. Analytical solution of three-dimensional realistic true proportional navigation[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(3): 569-577. doi: 10.2514/3.21659