Prescribed-time convergent cooperative guidance method with impact time and line-of-sight angle constraints
-
摘要:
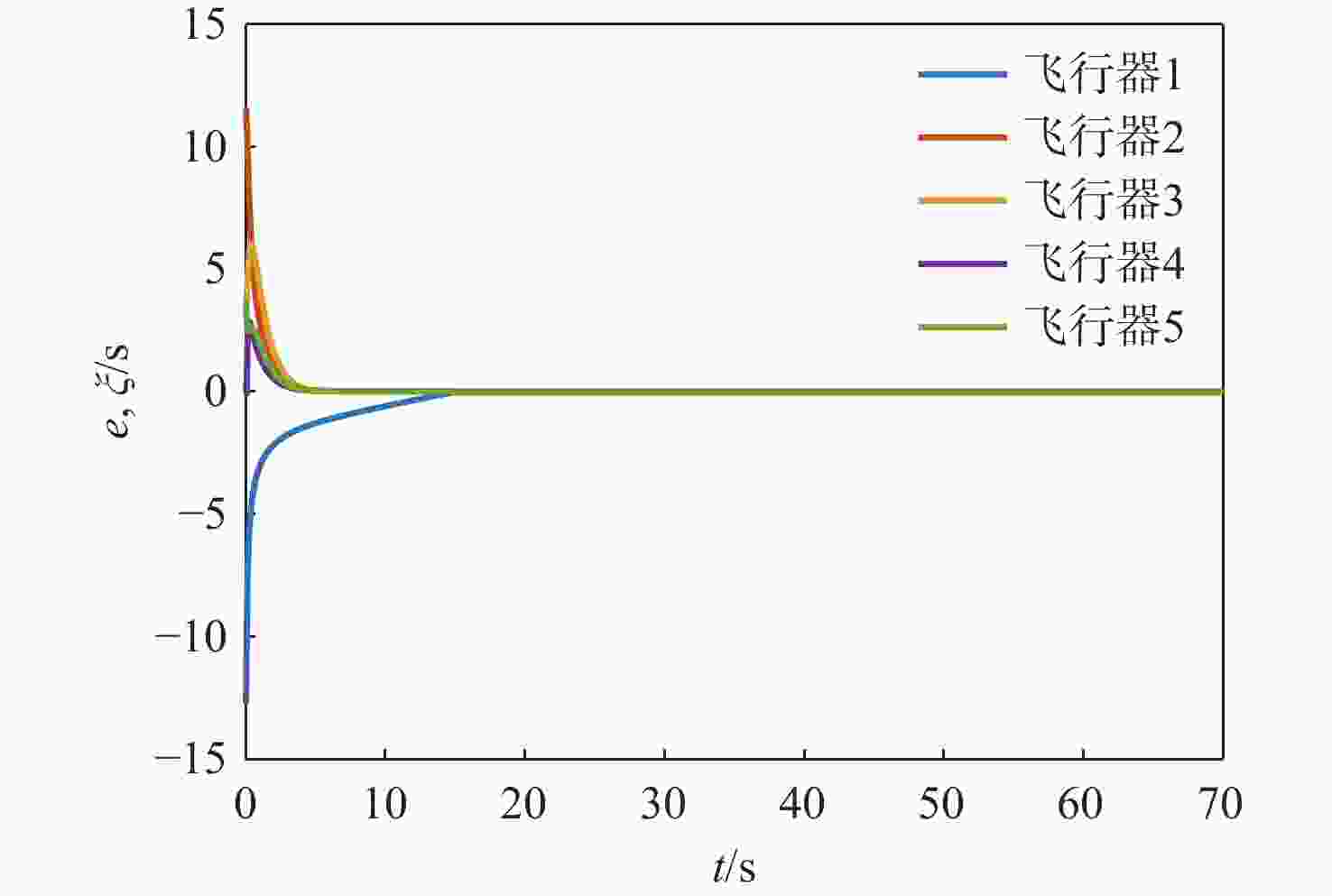
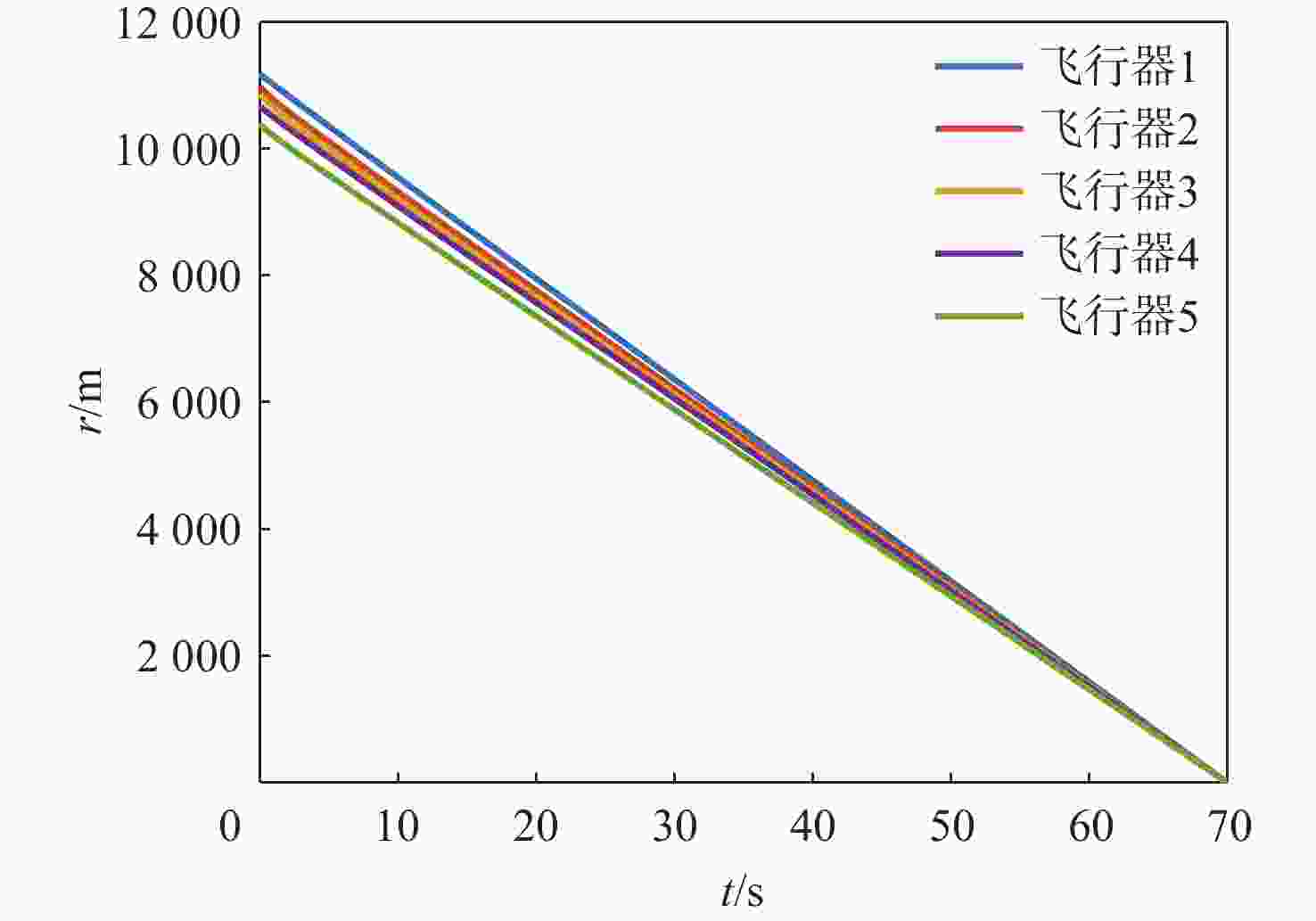
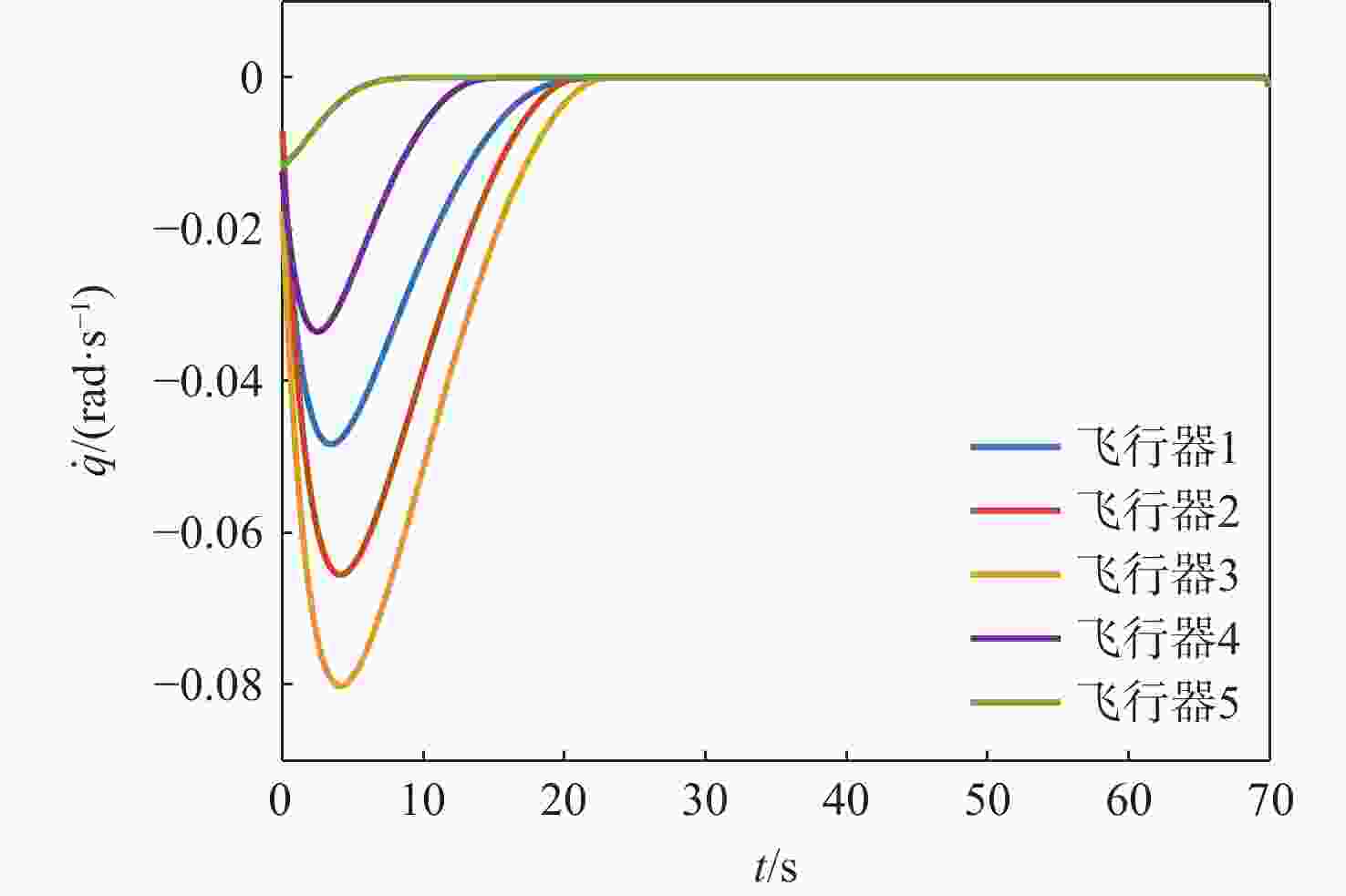
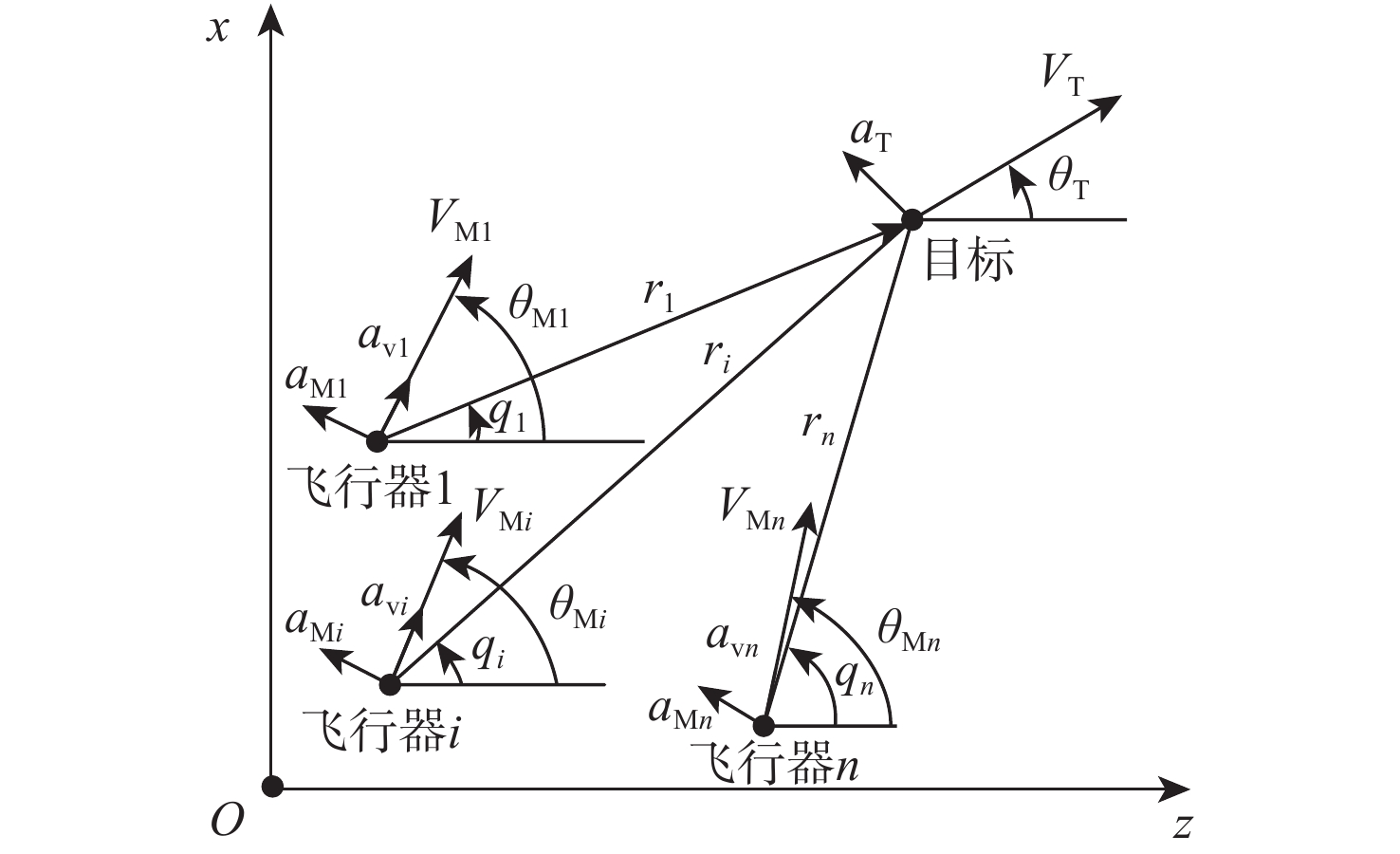
基于预定时间收敛一致性理论,设计多飞行器区域封控约束协同拦截制导律。视线(LOS)方向设计预定时间收敛协同制导律,使多个飞行器命中时间误差和命中时间一致性误差收敛到零,命中时间趋于一致,满足指定时间同时命中要求;视线法向结合滑模控制方法设计预定时间收敛滑模面和视线角约束制导律,使各飞行器视线角误差、视线角速率收敛到零,实现多个飞行器按各自指定视线角命中目标,满足期望视线角度要求。视线方向和视线法向的设计使预定时间收敛协同制导律能够同时满足攻击时间和视线角度的双重约束。理论分析表明,所设计的制导方法可保证多飞行器以期望视线角度同时命中目标。仿真结果验证了所提方法的正确性和有效性。
Abstract:Based on the theory of prescribed-time convergence consensus, a cooperative interception guidance law for multiple flight vehicles under regional confinement constraints is designed. In the line-of-sight (LOS) direction, a prescribed-time cooperative guidance law is designed to ensure that the impact time errors and the consensus errors of impact time converge to zero, thereby causing the impact times to tend toward consistency and satisfying the requirement of simultaneous interception at a designated time. In the vertical direction of the LOS, by integrating sliding mode control, a prescribed-time convergent sliding mode surface and a guidance law with LOS angle constraints are designed to drive the LOS angle errors and LOS angular rates of each flight vehicle to zero. This enables multiple flight vehicles to intercept the target at their respective specified LOS angles, thereby meeting the desired LOS angle requirements. The designs along the LOS direction and vertical to the LOS direction enable the prescribed-time convergence cooperative guidance law to simultaneously satisfy the dual constraints of impact time and LOS angle. Theoretical analysis demonstrates that the proposed guidance method ensures multiple flight vehicles intercept the target simultaneously at the desired LOS angles. Simulation results verify the correctness and effectiveness of the proposed method.
-
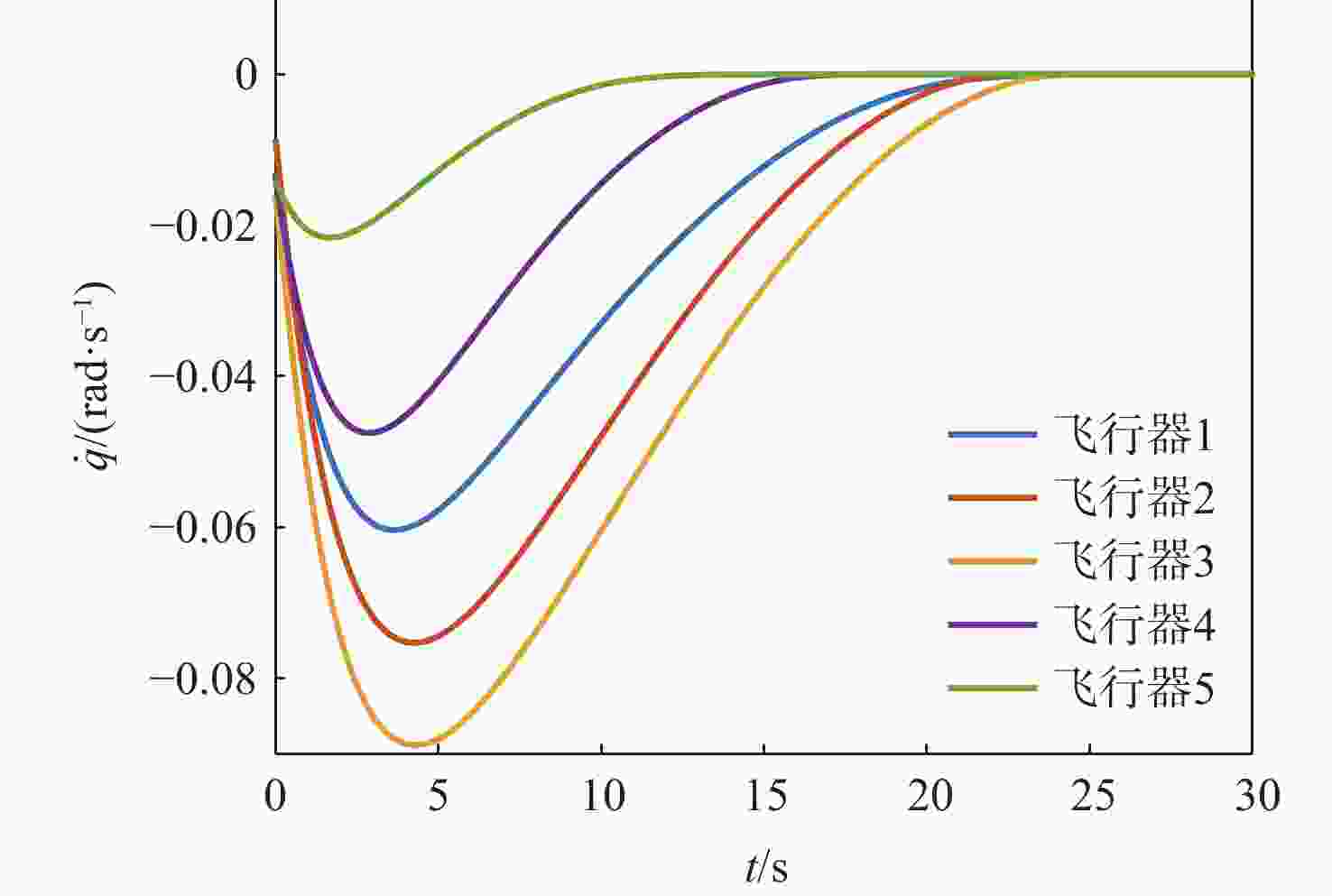
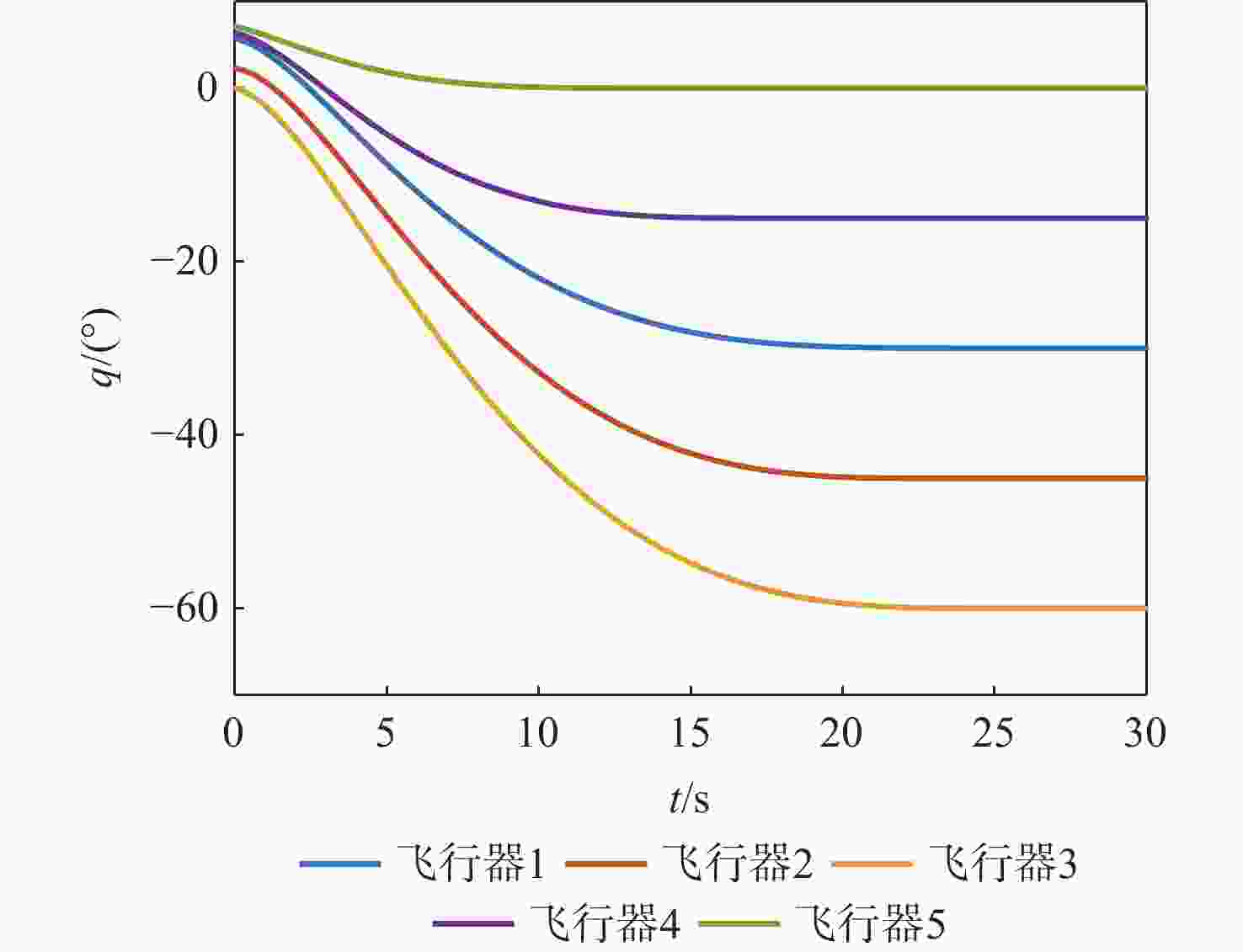
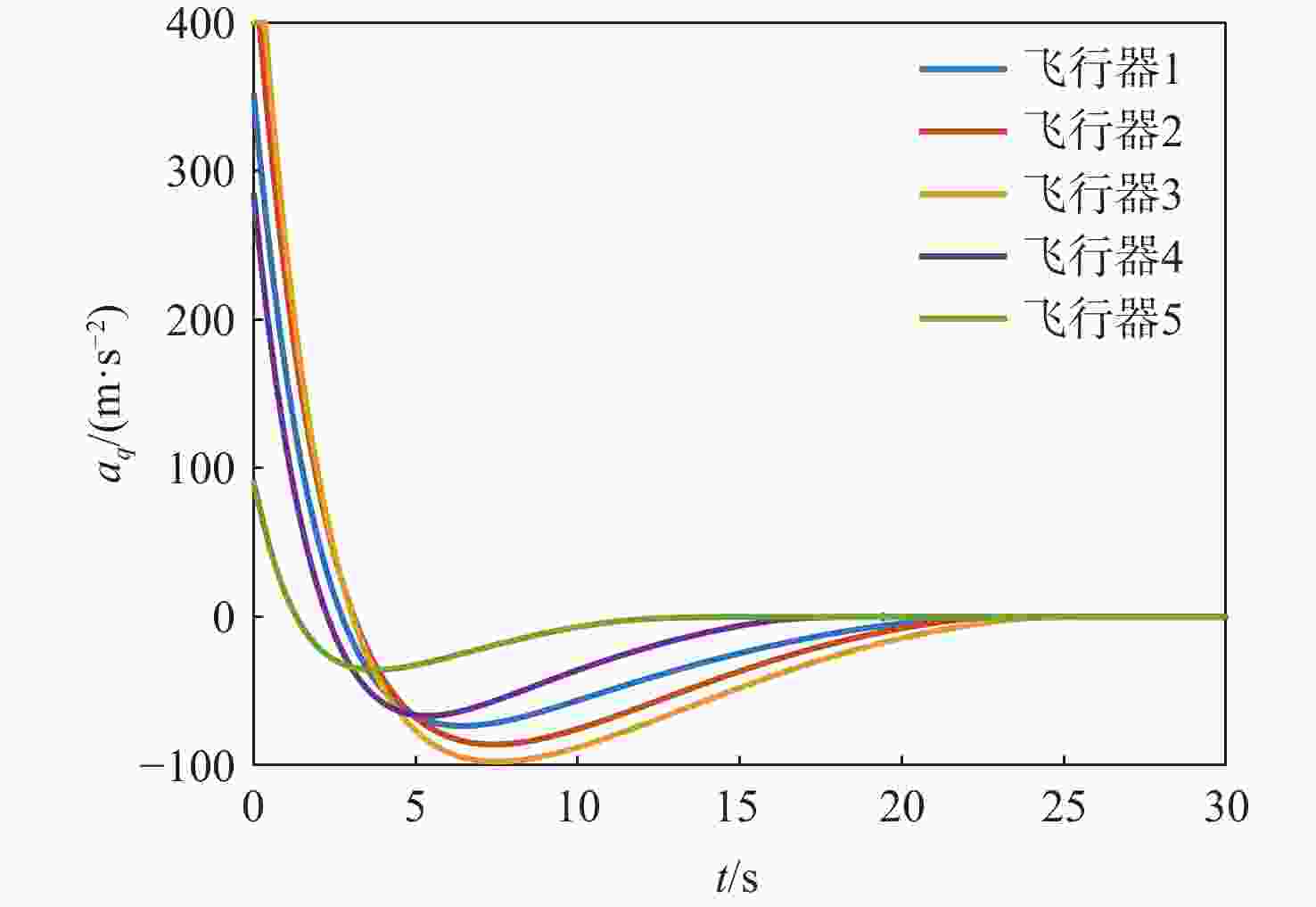
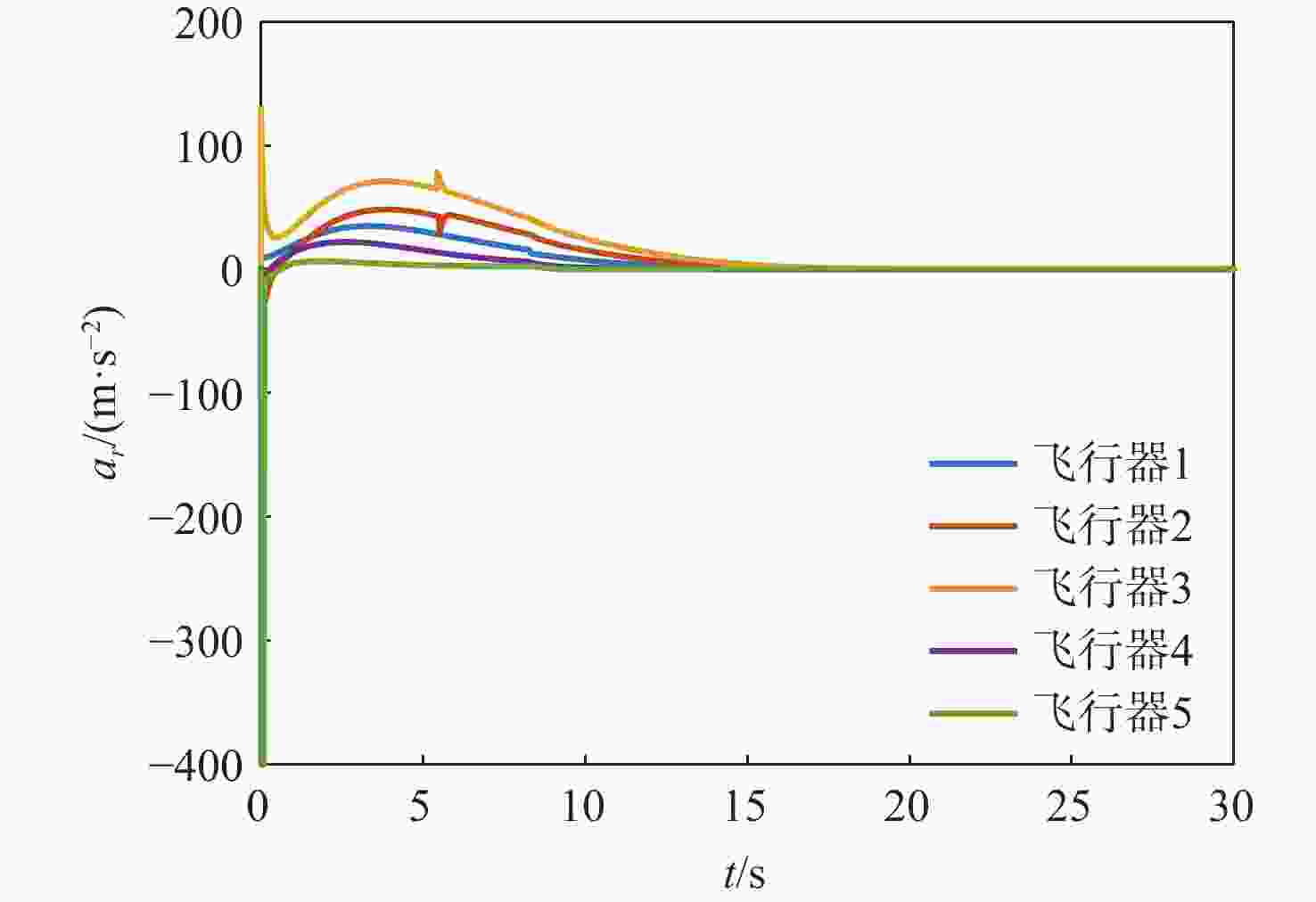
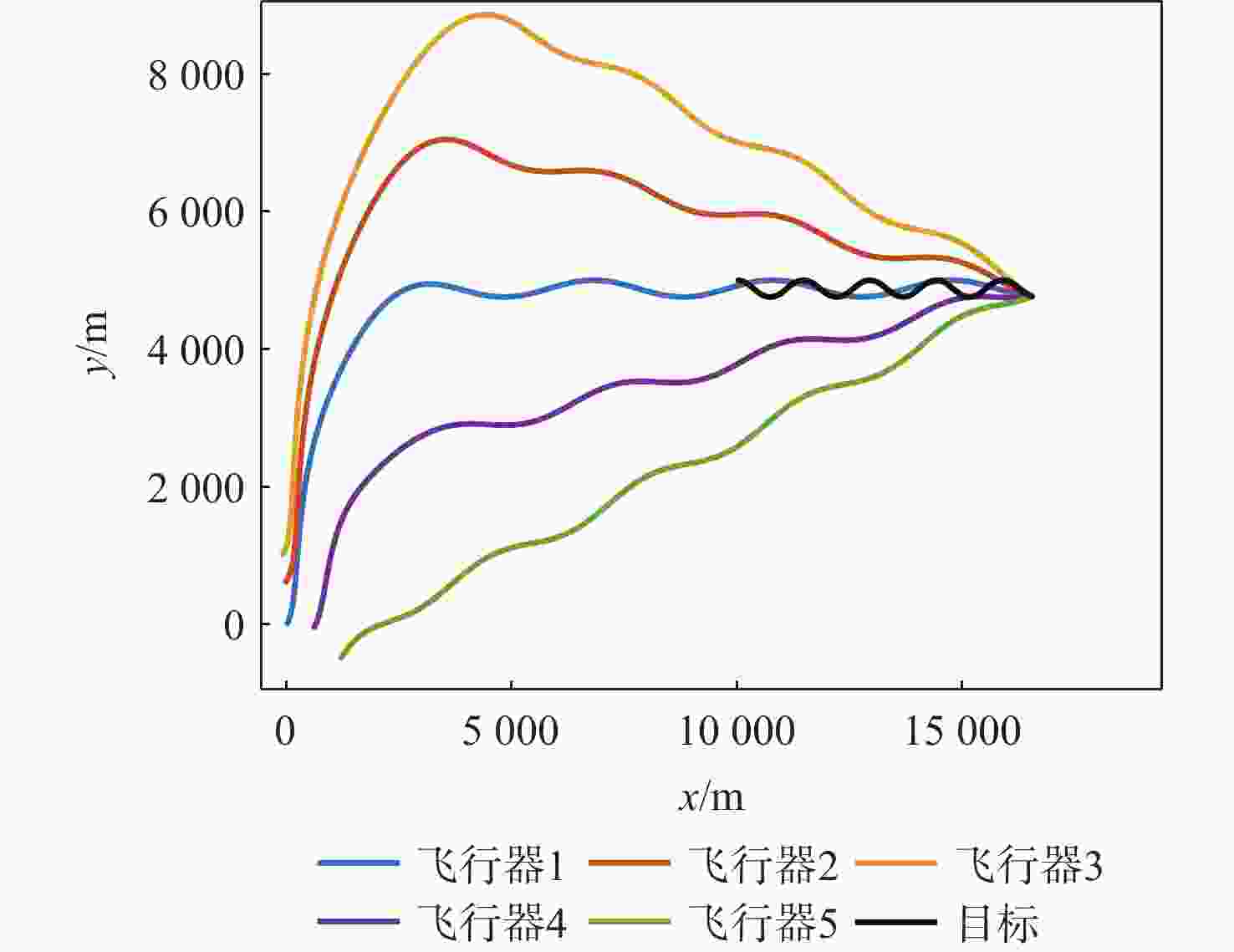
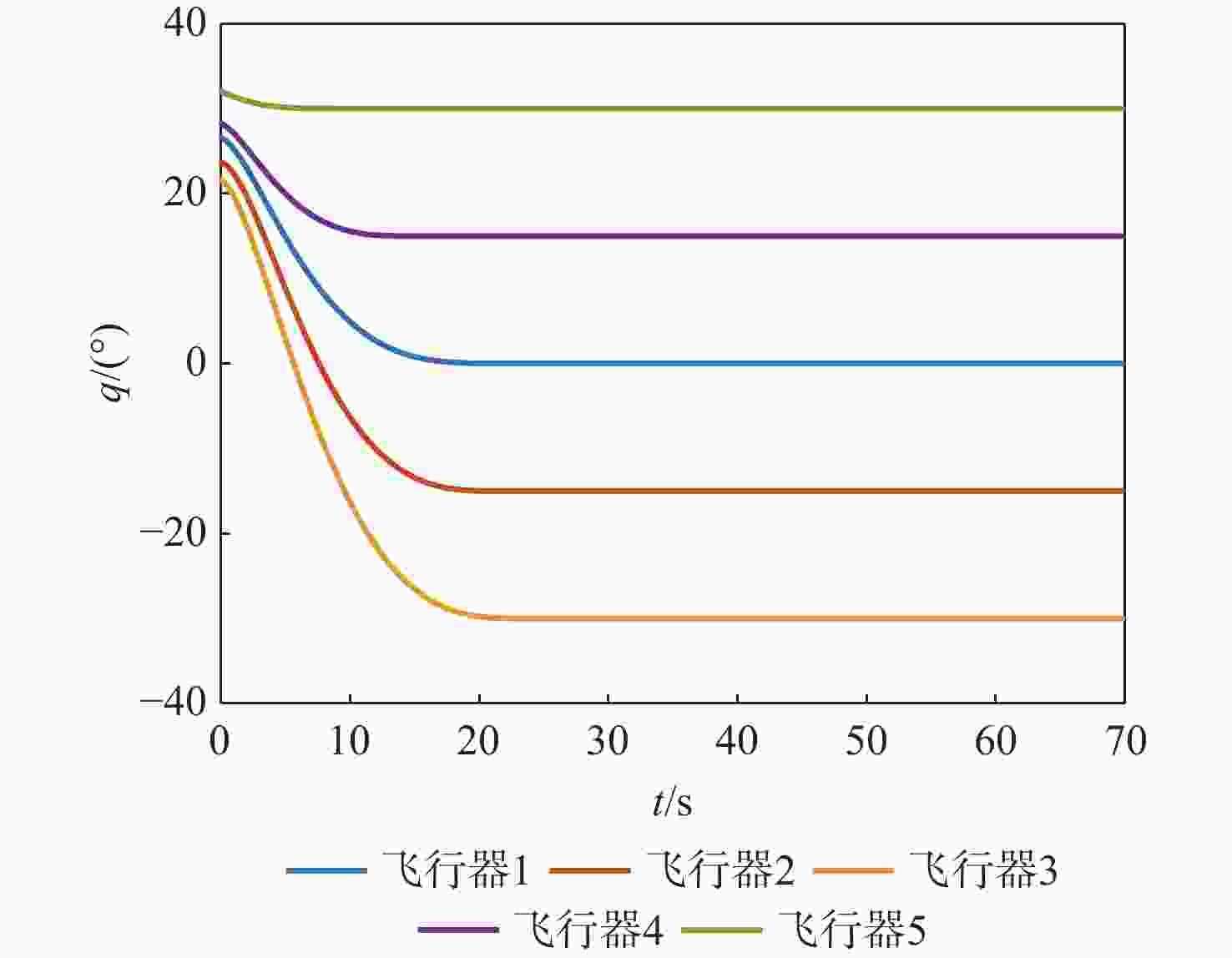
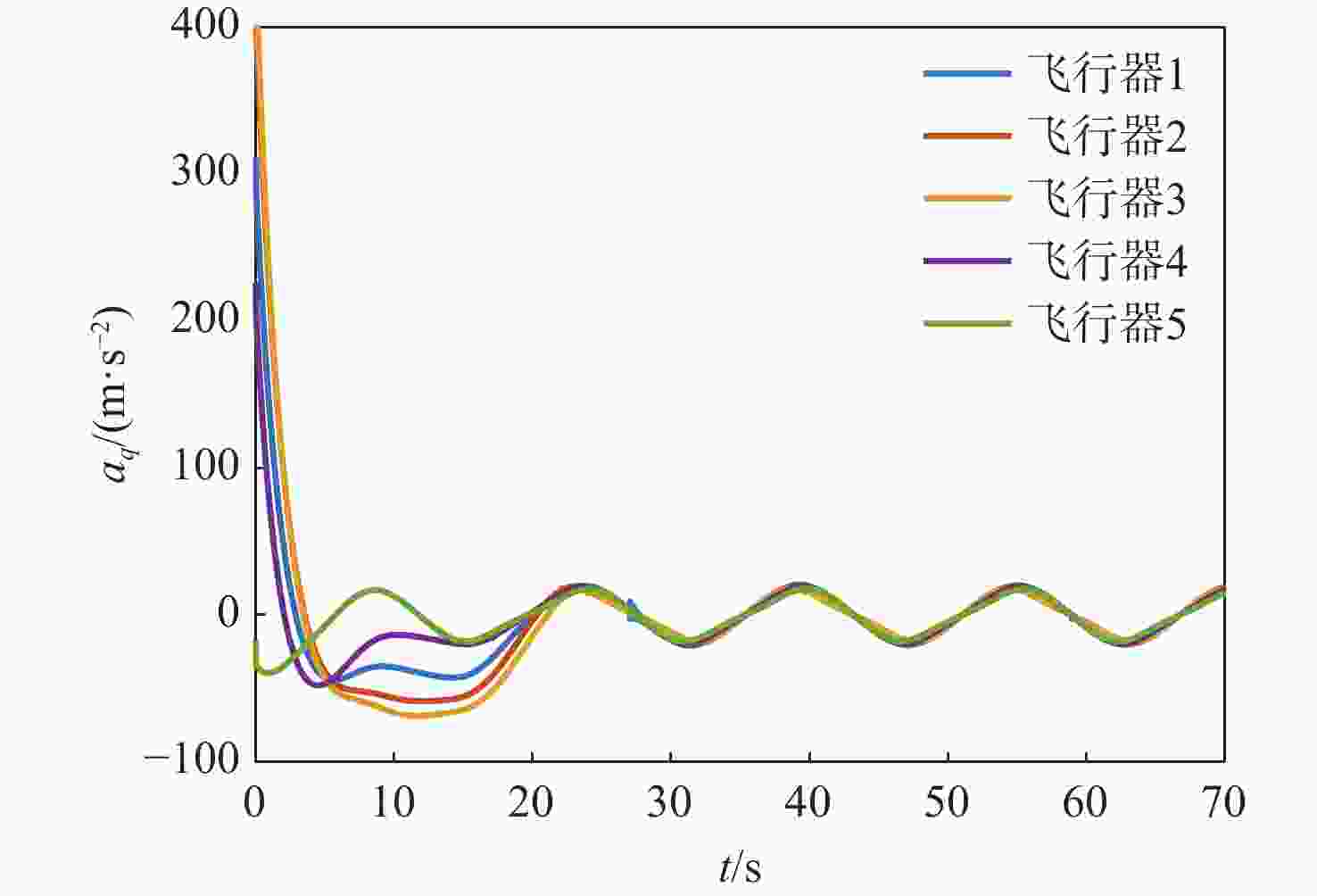
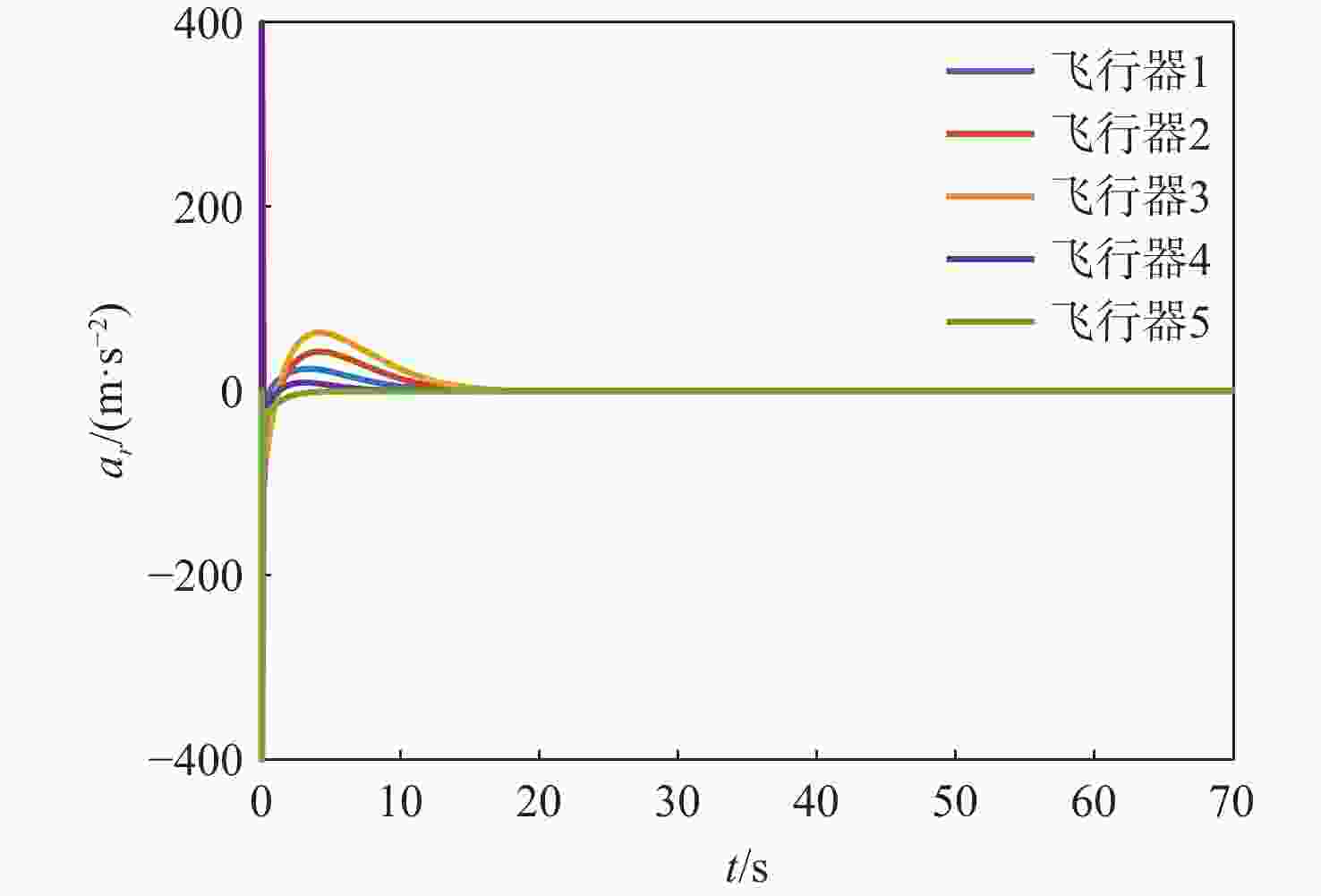
表 1 场景1飞行器和目标初始参数
Table 1. The initial parameters of vehicle and target in scene 1
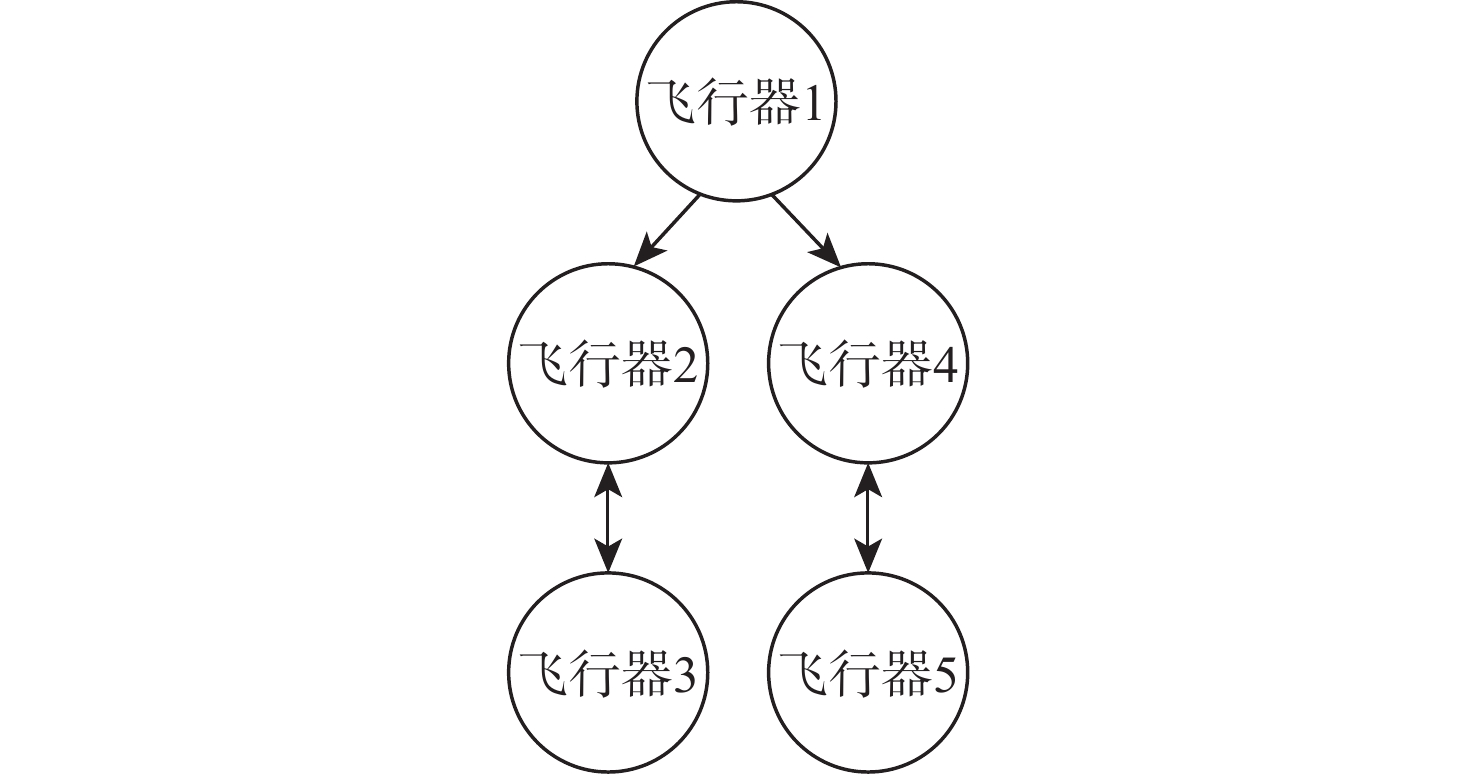
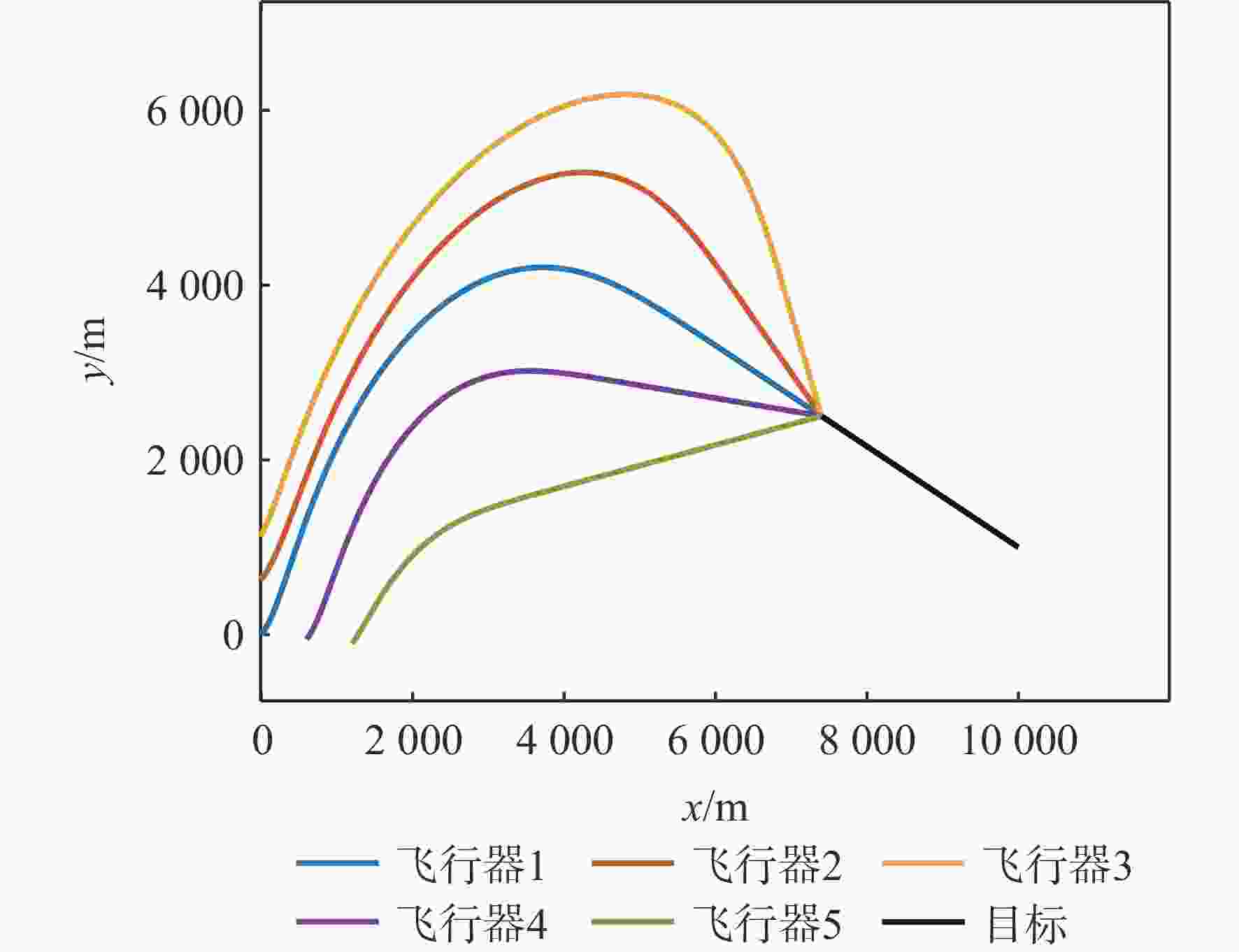
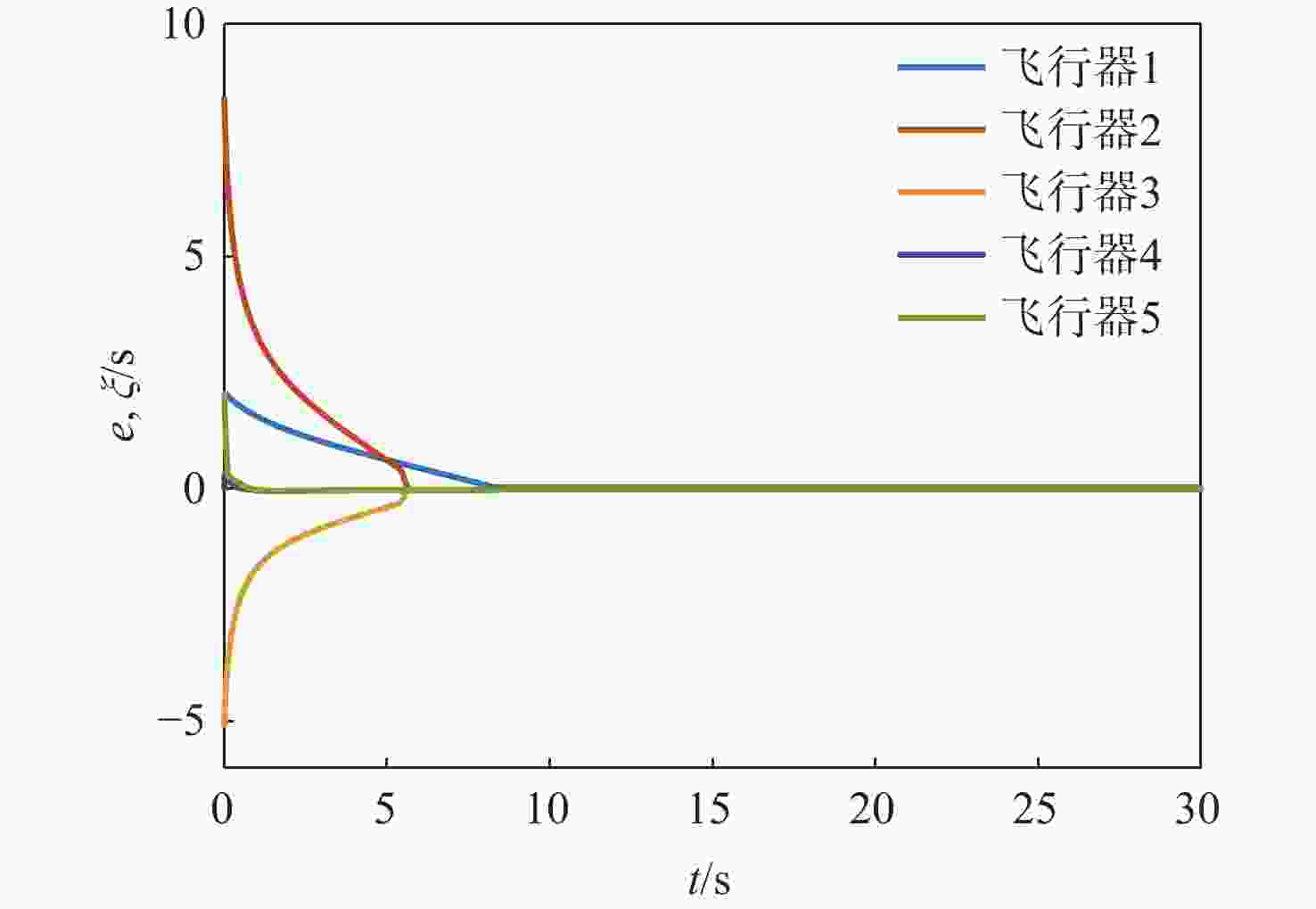
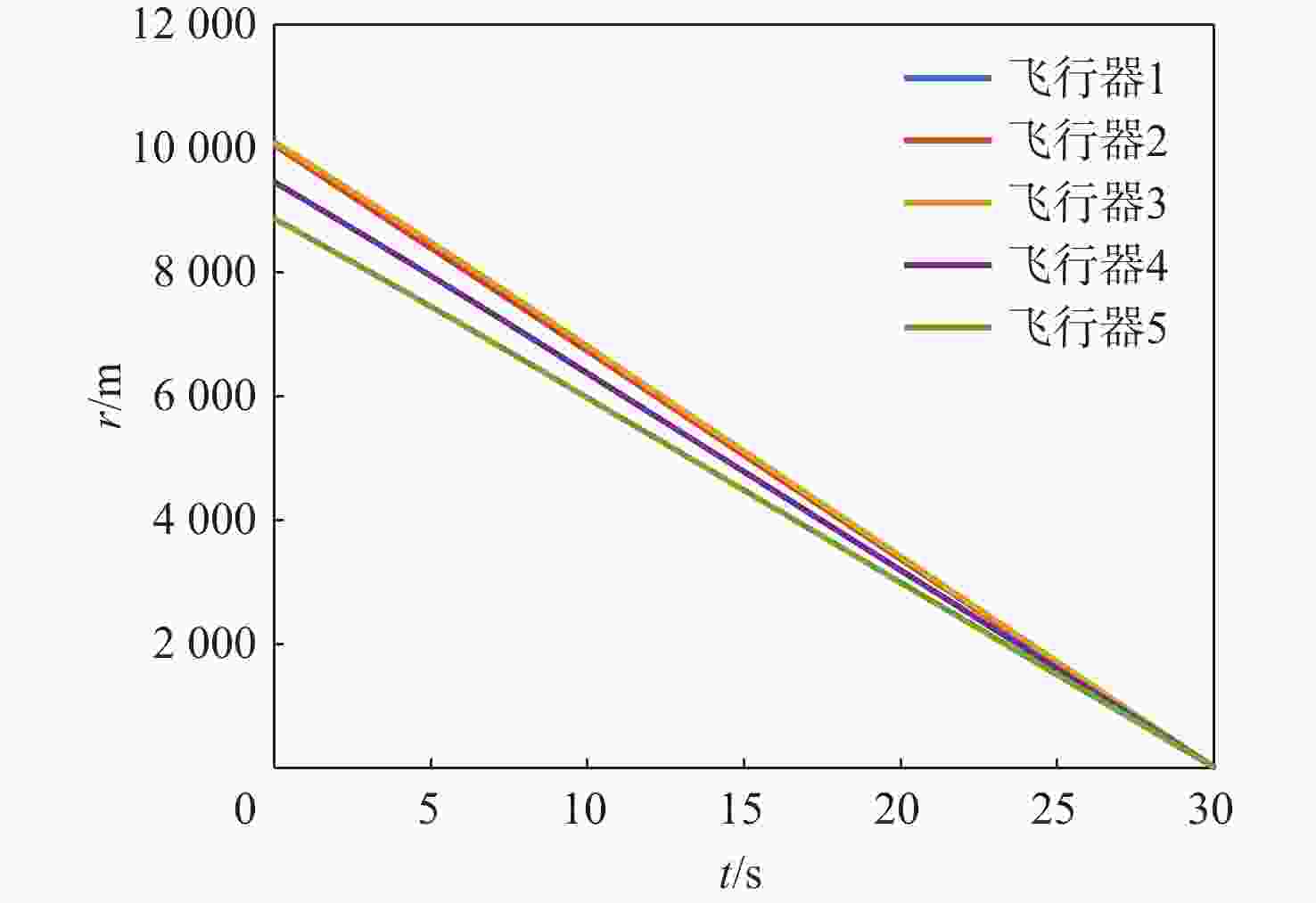
飞行器/目标 位置/m 弹道倾角/(°) 速度/(m·s−1) 飞行器1 (0, 0) 45 300 飞行器2 (−50, 600) 30 300 飞行器3 (−100, 1000 )45 300 飞行器4 (600, −50) 45 300 飞行器5 ( 1200 , −100)45 300 目标 ( 10000 ,1000 )150 100 表 2 场景2飞行器和目标初始参数
Table 2. The initial parameters of vehicle and target in scene 2
飞行器/目标 位置/m 弹道倾角/(°) 速度/(m·s−1) 飞行器1 (0, 0) 45 300 飞行器2 (−50, 600) 30 350 飞行器3 (−100, 1000 )45 400 飞行器4 (600, −50) 45 300 飞行器5 ( 1200 , −500)30 300 目标 ( 10000 ,5000 )0 100 -
[1] 周敏, 王一鸣, 郭建国, 等. 多弹协同末制导方法综述[J]. 航空兵器, 2023, 30(4): 17-25.ZHOU M, WANG Y M, GUO J G, et al. A survey of multi-missile cooperative terminal guidance[J]. Aero Weaponry, 2023, 30(4): 17-25(in Chinese). [2] 赵世钰, 周锐. 基于协调变量的多导弹协同制导[J]. 航空学报, 2008, 29(6): 1605-1611. doi: 10.3321/j.issn:1000-6893.2008.06.031ZHAO S Y, ZHOU R. Multi-missile cooperative guidance using coordination variables[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1605-1611(in Chinese). doi: 10.3321/j.issn:1000-6893.2008.06.031 [3] 张友安, 马国欣, 王兴平. 多导弹时间协同制导: 一种领弹-被领弹策略[J]. 航空学报, 2009, 30(6): 1109-1118.ZHANG Y A, MA G X, WANG X P. Time-cooperative guidance for multi-missiles: a leader-follower strategy[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(6): 1109-1118(in Chinese). [4] LI G F, WANG X Z, ZUO Z Y, et al. Fault-tolerant formation control for leader-follower flight vehicles under malicious attacks[EB/OL]. (2024-04-22)[2024-06-01]. https://ieeexplore.ieee.org/document/10506534. [5] LI G F, ZUO Z Y. Robust leader-follower cooperative guidance under false-data injection attacks[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(4): 4511-4524. doi: 10.1109/TAES.2023.3242637 [6] JEON I S, LEE J I, TAHK M J. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266. doi: 10.1109/TCST.2005.863655 [7] JEON I S, LEE J I, TAHK M J. Homing guidance law for cooperative attack of multiple missiles[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 275-280. doi: 10.2514/1.40136 [8] 李国飞, 李博皓, 吴云洁, 等. 多群组飞行器攻击时间控制协同制导方法[J]. 宇航学报, 2023, 44(1): 110-118.LI G F, LI B H, WU Y J, et al. Cooperative guidance law with impact time control for clusters of flight vehicles[J]. Journal of Astronautics, 2023, 44(1): 110-118(in Chinese). [9] 李国飞, 朱国梁, 吕金虎, 等. 主-从多飞行器三维分布式协同制导方法[J]. 航空学报, 2021, 42(11): 524926.LI G F, ZHU G L, LYU J H, et al. Three-dimensional distributed cooperative guidance law for multiple leader-follower flight vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(11): 524926(in Chinese). [10] LI G F, LV J H, ZHU G L, et al. Distributed observer-based cooperative guidance with appointed impact time and collision avoidance[J]. Journal of the Franklin Institute, 2021, 358(14): 6976-6993. doi: 10.1016/j.jfranklin.2021.06.030 [11] KIM M, JUNG B, HAN B, et al. Lyapunov-based impact time control guidance laws against stationary targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 1111-1122. doi: 10.1109/TAES.2014.130717 [12] PARK B G, KIM T H, TAHK M J. Optimal impact angle control guidance law considering the seeker’s field-of-view limits[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2013, 227(8): 1347-1364. doi: 10.1177/0954410012452367 [13] 周慧波. 基于有限时间和滑模理论的导引律及多导弹协同制导研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.ZHOU H B. Study on guidance law and cooperative guidance for multi-missiles based on finite-time and sliding mode theory[D]. Harbin: Harbin Institute of Technology, 2015(in Chinese). [14] ZHAO J L, ZHOU J. Fixed-time second order sliding mode guidance law for interceptors with impact angle constraints[C]//Proceedings of the 2019 IEEE 3rd Advanced Information Management, Communicates, Electronic and Automation Control Conference. Piscataway: IEEE Press, 2020: 1010-1014. [15] ZHANG M J, MA J J. Adaptive fixed-time cooperative intercept guidance law with line-of-sight angle constraint[C]//Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation. Piscataway: IEEE Press, 2019: 1992-1998. [16] LI G F, WU Y J. Adaptive cooperative guidance with seeker-less followers: a position coordination-based framework[J]. ISA Transactions, 2023, 143: 168-176. doi: 10.1016/j.isatra.2023.09.024 [17] KUMAR S R, RAO S, GHOSE D. Non-singular terminal sliding mode guidance and control with terminal angle constraints for non-maneuvering targets[C]//Proceedings of the 2012 12th International Workshop on Variable Structure Systems. Piscataway: IEEE Press, 2012: 291-296. [18] 景亮. 多拦截弹时间收敛协同制导律研究[D]. 哈尔滨: 哈尔滨工业大学, 2021.JING L. Reserch on time convergence cooperative guidence law for mutiple interceptor[D]. Harbin: Harbin Institute of Technology, 2021(in Chinese). [19] 田野, 蔡远利, 邓逸凡. 一种带时间协同和角度约束的多导弹三维协同制导律[J]. 控制理论与应用, 2022, 39(5): 788-798. doi: 10.7641/CTA.2021.10245TIAN Y, CAI Y L, DENG Y F. A 3D cooperative guidance law for multiple missiles with line-of-sight angle constraint[J]. Control Theory & Applications, 2022, 39(5): 788-798(in Chinese). doi: 10.7641/CTA.2021.10245 [20] CHEN Z Y, YU J L, DONG X W, et al. Three-dimensional cooperative guidance strategy and guidance law for intercepting highly maneuvering target[J]. Chinese Journal of Aeronautics, 2021, 34(5): 485-495. doi: 10.1016/j.cja.2020.12.014 [21] 王鹏, 赵石磊, 陈万春. 基于可达区在线预测的GPI中制导协同拦截策略[J]. 北京航空航天大学学报, 2024, 50(11): 3463-3476. doi: 10.13700/j.bh.1001-5965.2022.0856WANG P, ZHAO S L, CHEN W C. Cooperative interception strategy for midcourse guidance of GPI based on online prediction of reachable area[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(11): 3463-3476(in Chinese). doi: 10.13700/j.bh.1001-5965.2022.0856 [22] 于江龙, 董希旺, 李清东, 等. 拦截机动目标的分布式协同围捕制导方法[J]. 航空学报, 2022, 43(9): 325817.YU J L, DONG X W, LI Q D, et al. Distributed cooperative encirclement hunting guidance method for intercepting maneuvering target[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(9): 325817(in Chinese). [23] ZHANG L, WEI C Z, JING L, et al. Fixed-time sliding mode attitude tracking control for a submarine-launched missile with multiple disturbances[J]. Nonlinear Dynamics, 2018, 93(4): 2543-2563. doi: 10.1007/s11071-018-4341-8 [24] LIN Q, ZHOU Y J, JIANG G P, et al. Prescribed-time containment control based on distributed observer for multi-agent systems[J]. Neurocomputing, 2021, 431: 69-77. doi: 10.1016/j.neucom.2020.12.030 [25] 池海红, 丁栖航, 张国良. 预定时间多导弹三维协同制导律[J]. 宇航学报, 2023, 44(8): 1238-1250. doi: 10.3873/j.issn.1000-1328.2023.08.012CHI H H, DING X H, ZHANG G L. Three-dimensional cooperative guidance law for multiple missiles with predefined-time convergence[J]. Journal of Astronautics, 2023, 44(8): 1238-1250(in Chinese). doi: 10.3873/j.issn.1000-1328.2023.08.012 [26] SÁNCHEZ-TORRES J D, SANCHEZ E N, LOUKIANOV A G. Predefined-time stability of dynamical systems with sliding modes[C]//Proceedings of the 2015 American Control Conference. Piscataway: IEEE Press, 2015: 5842-5846. -






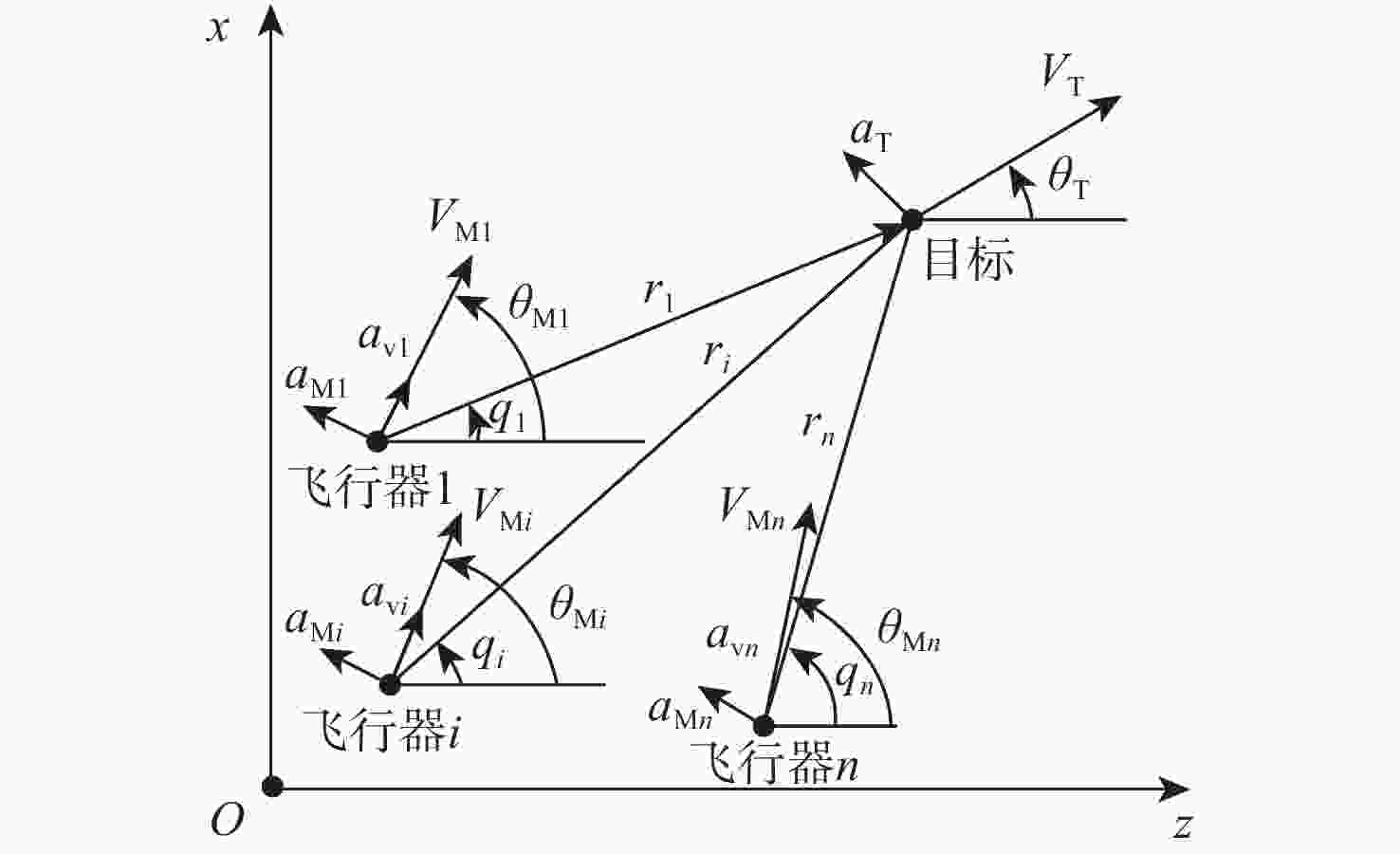
 下载:
下载: