一种基于指数积公式的空间机械臂自标定方法

王业聪; 危清清; 胡成威; 丁希仑

doi:10.13700/j.bh.1001-5965.2018.0071

一种基于指数积公式的空间机械臂自标定方法

doi: 10.13700/j.bh.1001-5965.2018.0071

1.
北京航空航天大学机械工程及自动化学院, 北京 100083
2.
北京空间飞行器总体设计部空间智能机器人系统技术与应用北京重点实验室, 北京 100094

基金项目:

国家重点研发计划 2017YFB1300400

国家自然科学基金 91748201

详细信息

作者简介:
王业聪男，博士研究生。主要研究方向：拟人双臂机器人技术

丁希仑男，博士，教授，博士生导师。主要研究方向：空间机器人、仿生机器人、变胞机构

通讯作者:
丁希仑, E-mail:xlding@buaa.edu.cn

中图分类号: TP242
计量
- 文章访问数: 1004
- HTML全文浏览量: 142
- PDF下载量: 459
- 被引次数: 0
出版历程
- 收稿日期: 2018-01-30
- 录用日期: 2018-04-27
- 网络出版日期: 2018-11-20

A self-calibration method for space manipulators based on POE formula

1.
School of Mechanical Engineering & Automation, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
2.
Beijing Key Laboratory of Intelligent Space Robotic Systems Technology and Applications, Beijing Institute of Spacecraft System Engineering, Beijing 100094, China

Funds:

National Key R & D Program of China 2017YFB1300400

National Natural Science Foundation of China 91748201

More Information

Corresponding author: DING Xilun, E-mail:xlding@buaa.edu.cn

摘要

摘要:
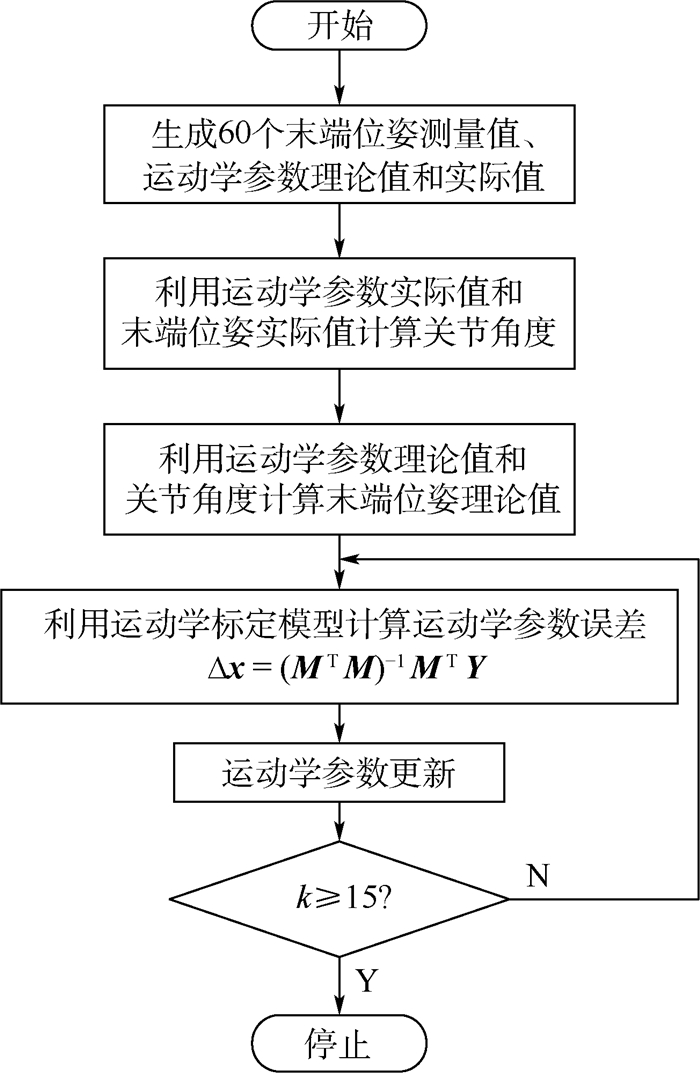
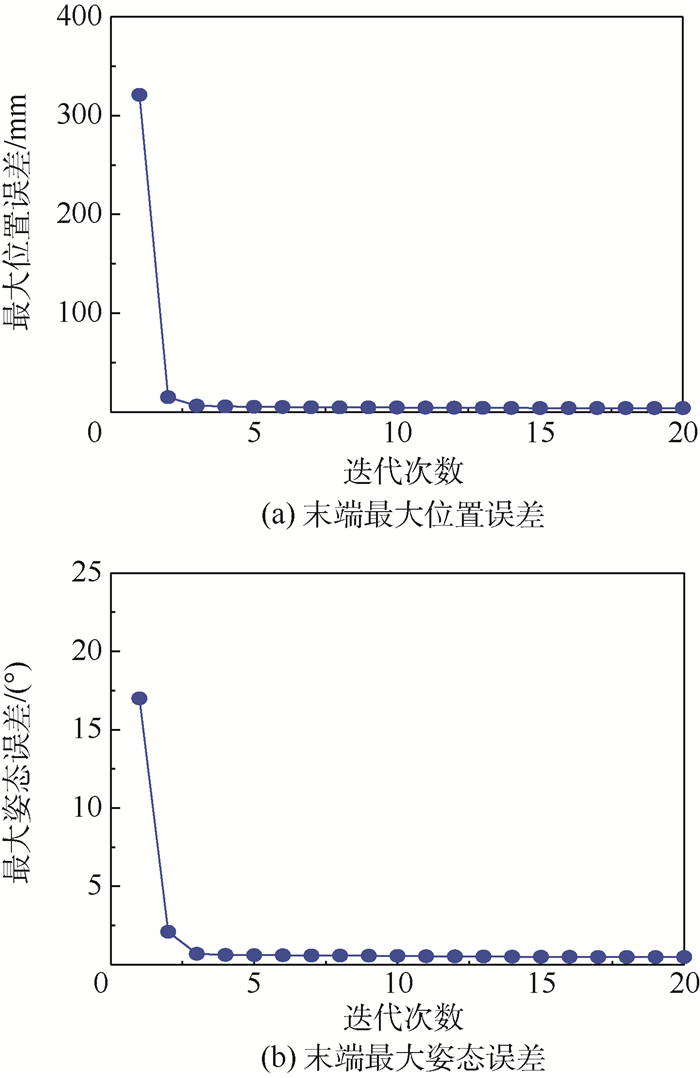
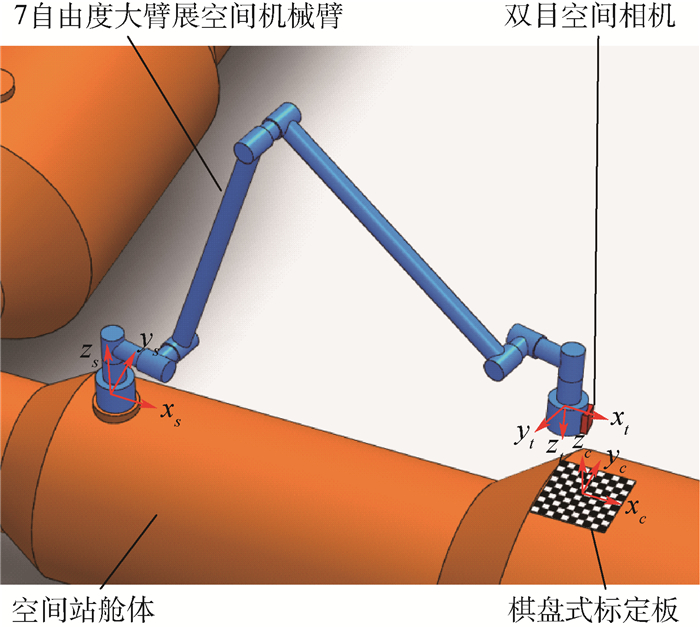
为了克服发射过程和在轨极端温度环境对空间机械臂末端位姿精度的影响，提出了一种基于指数积（POE）公式的空间机械臂运动学在轨自标定方法。该方法使用空间机械臂末端双目空间相机和棋盘式标定板测量空间机械臂末端位姿实际值。根据关节旋量理论值和实际值之间的伴随变换关系建立了空间机械臂实际运动学模型，对运动学模型取微分建立了线性化的运动学误差模型，给出了基于最小二乘法的运动学标定模型。进行了7自由度空间机械臂运动学自标定仿真，仿真结果表明运动学标定过程能快速收敛到稳定值，标定后空间机械臂末端位姿精度有明显提高。
- 空间机械臂 /
- 标定 /
- 指数积(POE) /
- 伴随变换 /
- 空间相机 /
- 标定板
Abstract:
To overcome the influence of launching process and on-orbit extreme temperature environment on the tool pose accuracy of a space manipulator, a space manipulator kinematics on-orbit self-calibration method based on product of exponentials (POE) formula was presented. Using the binocular space camera fixed on the end-effector and a checkerboard calibration plate, the actual tool pose of the space manipulator was measured. According to the adjoint transformation between the theoretical value and actual value of joint twists, the actual kinematics model of the space manipulator was established. The linearized kinematics error model of the space manipulator was obtained by differentiating the kinematics model. A least-squares kinematics calibration model for the space manipulator was given. Kinematics self-calibration simulation of a seven-degree-of-freedom space manipulator was carried out. The simulation results show that the kinematics calibration process can converge to a stable value quickly and there is a significant improvement on the tool pose accuracy of the space manipulator after kinematics calibration.
- space manipulator /
- calibration /
- product of exponentials (POE) /
- adjoint transformation /
- space camera /
- calibration plate

HTML全文

图 1 空间机械臂运动学自标定系统

Figure 1. Kinematics self-calibration system for space manipulator

下载: 全尺寸图片幻灯片

图 2 7自由度空间机械臂

Figure 2. A 7-DOF space manipulator

下载: 全尺寸图片幻灯片

图 3 空间机械臂运动学自标定仿真流程

Figure 3. Kinematics self-calibration simulation process for the space manipulator

下载: 全尺寸图片幻灯片

图 4 迭代过程中末端位姿误差

Figure 4. Pose errors of the end-effector during iterative procedure

下载: 全尺寸图片幻灯片

图 5 末端位姿误差

Figure 5. Pose errors of the end-effector

下载: 全尺寸图片幻灯片

表 1 空间机械臂运动学参数理论值和实际值

Table 1. Theoretical values and actual values of kinematics parameters of the space manipulator

参数	理论值	实际值(预设值)
ξ₁	[0 0 1 0 0 0]^T	[0.005 3 -0.005 2 1.000 0 0.100 5 -0.099 5 -0.001 0]^T
ξ₂	[1 0 0 0 1 500 0]^T	[1.000 0 0.007 0 -0.006 9 -10.401 3 1 500.128 8 10.237 0]^T
ξ₃	[0 0 1 0 -1 000 0]^T	[0.008 8 -0.008 7 0.999 9 8.851 8 -1 000.122 7 -8.729 7]^T
ξ₄	[0 0 1 0 -5 000 0]^T	[0.010 6 -0.010 4 0.999 9 52.616 0 -5 000.248 9 -52.372 8]^T
ξ₅	[0 0 1 0 -9 000 0]^T	[0.012 4 -0.012 1 0.999 9 110.220 7 -9 000.253 1 -109.983 9]^T
ξ₆	[1 0 0 0 4 500 0]^T	[0.999 8 0.015 7 -0.015 7 -69.617 5 4 500.653 5 69.001 3]^T
ξ₇	[0 0 1 0 -10 000 0]^T	[0.017 8 -0.017 1 0.099 7 173.282 4 -9 998.774 8 -174.560 3]^T
ξ_st	[0 0 0 10 000 0 6 000]^T	[0.114 4 0.129 3 0.114 4 9 603.673 9 -199.070 3 6 652.637 1]^T

下载: 导出CSV

参考文献(21)

[1]	BAI Y, WANG D L. Improve the robot calibration accuracy using a dynamic online fuzzy error mapping system[J]. IEEE Transactionson Systems, Man and Cybernetics, 2004, 34(2):1155-1160. doi: 10.1109/TSMCB.2003.821453
[2]	CHEN G, LI T, CHU M, et al. Review on kinematics calibration technology of serial robots[J].International Journal of Precision Engineering and Manufacturing, 2014, 15(8):1759-1774. doi: 10.1007/s12541-014-0528-1
[3]	ROTH Z S, MOORING B W, RAVANI B.An overview of robot calibration[J].IEEE Journal of Robotics and Automation, 1987, 3(5):377-385. doi: 10.1109/JRA.1987.1087124
[4]	SCHROER K, ALBRIGHT S L, GRETHLEIN M.Complete, minimal and model-continuous kinematic models for robot calibration[J].Robotics and Computer-integrated Manufacturing, 1997, 13(1):73-85. doi: 10.1016/S0736-5845(96)00025-7
[5]	HAYATI S.Robot arm geometric link parameter estimation[C]//22nd IEEE Conference on Decision and Control.Piscataway, NJ: IEEE Press, 1983, 22: 1477-1483.
[6]	STONE H W.Kinematic modeling, identification, and control of robotic manipulators[M].New York:Kluwer Academic Publisher, 1987.
[7]	ZHUANG H Q, ROTH Z S, HAMANO F.A complete and parametrically continuous kinematic model for robot manipulators[J].IEEE Transactions on Robotics & Automation, 1992, 8(4):451-463.
[8]	ZHUANG H Q, WANG L K, ROTH Z S.Error-model-based robot calibration using a modified CPC model[J].Robotics and Computer-Integrated Manufacturing, 1993, 10(4):287-299. doi: 10.1016/0736-5845(93)90042-I
[9]	CHEN I M, YANG G L.Kinematic calibration of modular reconfigurable robots using product-of-exponentials formula[J].Journal of Robotic Systems, 1997, 14(11):807-821. doi: 10.1002/(ISSN)1097-4563
[10]	HE R B, ZHAO Y J, YANG S N, et al.Kinematic-parameter identification for serial-robot calibration based on POE formula[J].IEEE Transactions on Robotics, 2010, 26(3):411-423. doi: 10.1109/TRO.2010.2047529
[11]	HE R B, LI X W, SHI T L, et al.A kinematic calibration method based on the product of exponentials formula for serial robot using position measurements[J].Robotica, 2015, 33(6):1295-1313. doi: 10.1017/S026357471400071X
[12]	CHEN G L, WANG H, LIN Z Q.Determination of the identifiable parameters in robot calibration based on the POE formula[J].IEEE Transactions on Robotics, 2014, 30(5):1066-1077. doi: 10.1109/TRO.2014.2319560
[13]	ANGULO V R D, TORRAS C.Self-calibration of a space robot[J].IEEE Transactions on Neural Networks, 1997, 8(4):951-963. doi: 10.1109/72.595895
[14]	LIANG P, CHANG Y L, HACKWOOD S.Adaptive self-calibration of vision-based robot systems[J].IEEE Transactions on Systems Man & Cybernetics, 1989, 19(4):811-824.
[15]	GONG C, YUAN J, NI J.Nongeometric error identification and compensation for robotic system by inverse calibration[J].International Journal of Machine Tools & Manufacture, 2000, 40(14):2119-2137.
[16]	LIU Y, LIU H, NI F L, et al.New self-calibration approach to space robots based on hand-eye vision[J].Journal of Central South University of Technology, 2011, 18(4):1087-1096. doi: 10.1007/s11771-011-0808-1
[17]	DU G L, ZHANG P.Online robot calibration based on vision measurement[J].Robotics and Computer-integrated Manufacturing, 2013, 29(6):484-492. doi: 10.1016/j.rcim.2013.05.003
[18]	ZHANG X C, SONG Y T, YANG Y, et al.Stereo vision based autonomous robot calibration[J].Robotics and Autonomous Systems, 2017, 93:43-51. doi: 10.1016/j.robot.2017.04.001
[19]	高文斌, 王洪光, 姜勇.一种基于指数积的串联机器人标定方法[J].机器人, 2013, 35(2):156-161. GAO W B, WANG H G, JIANG Y.A calibration method for serial robots based on POE formula[J].Robot, 2013, 35(2):156-161(in Chinese).
[20]	LOU Y J, CHEN T N, WU Y Q, et al.Improved and modified geometric formulation of POE based kinematic calibration of serial robots[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway, NJ: IEEE Press, 2009: 5261-5266.
[21]	PARK F C, OKAMURA K.Kinematic calibration and the product of exponentials formula[M].Cambridge:MIT Press, 1994:119-128.