现代体系作战中，潜艇的侦察距离短、作战隐蔽，常常需要反潜机或其他水面舰艇配合作战。无人机因其具有隐蔽性强、飞行灵活、小巧轻便等特点而被广泛应用在海战搜索侦察、对海对空作战上。因此，无人机配合潜艇在作战中执行各类任务是一种很好的方案，也推动了潜射无人机的发展。潜射无人机通过导弹发射管等自主弹射装置，用气动或火箭助推的方式弹射出海面。在到达指定高度后，潜射无人机迅速展开机翼进行稳定飞行，完成侦察攻击等作战任务。

现有的潜射无人机正朝着小型化、用途和智能化方向发展。其中，纵列式旋翼无人机具备了纵列式直升机易于收放、重心变化范围大、机身利用率高、载荷大、悬停效率高、悬停功率低、运输能力强等特点，能够实现定点空投、慢速飞行拖曳电子反潜设备等功能，但其弹射后的控制与一般纵列式直升机一样，具有非线性、强耦合、容易不稳定等特征。

现有的纵列式旋翼无人机姿态控制的设计方法包括经典控制方法和现代控制方法^[1]。采用智能控制方法进行的姿态控制设计目前还在初步研究阶段。

经典控制方法中的PID控制律目前仍是大多数纵列式旋翼无人机工程中采用的姿态控制方法。现有的姿态控制技术均是采用内外环分层设计思想^[2]。针对PID控制律非线性系统存在强耦合时无法解耦控制等主要缺点，可以通过对无人直升机的各个姿态通道进行解耦设计，再对解耦的姿态通道进行PID控制。

现代控制理论应用到纵列式旋翼无人机姿态控制的主要方法有H_∞鲁棒控制方法、LQR最优控制方法等。其中，H_∞回路成形方法已经在纵列式直升机上成熟运用^[3-4]。LQR控制方法则是基于小扰动原理，计算出无人机在不同飞行工作点下的线性化模型，对每个飞行工作点单独设计合适的LQR控制律，进而完成全飞行包络线下的LQR姿态控制设计^[5]。

此外一些传统的非线性控制方法，如动态逆的控制方法、基于反步式设计方法的控制器设计、非线性结构解耦算法和基于双闭环结构的增稳控制律设计等，在姿态控制设计上表现的效果也不错^[6-7]。

基于智能控制方法的姿态控制技术目前已经成为一个研究热点，可以通过长短期记忆学习(LSTM)网络和模糊PID控制等方法增加模型精度和鲁棒性^[8]，但其算法的实时性还达不到实际工程要求。

考虑到潜射系统应用场景特点，本文采用L1自适应控制方法对纵列式潜射无人机进行姿态控制，经过适当设计可保证控制系统的稳定性^[9]，同时能有效解决参数不确定性和气动干扰问题。

1.   数学模型建立

本文潜射选用的旋翼无人机为纵列式布局，纵列式旋翼无人机的潜射过程控制主要有2个阶段：助推段和旋翼展开阶段。在助推段，无人机升至指定高度后，利用助推火箭发动机将自身的俯仰角姿态调整到一定角度。随后旋翼无人机接入飞控动力系统，控制旋翼展开来控制自身姿态至平飞状态，如图 1所示。

图  1  旋翼无人机潜射过程

Figure  1.  Block diagram of underwater-launched process of rotor UAV

下载: 全尺寸图片 幻灯片

1.1   助推段模型

助推段发射方案可以采用气动弹射和火箭助推。气动弹射方法原理简单，研究成熟，但单独使用气动弹射无法满足无人机质量和弹射结构尺寸限制。如果加入助推火箭，经计算，气动弹射装置对整个发射过程的作用并不显著。对于火箭助推发射的方案，火箭发动机尾焰会对电子设备造成烧蚀，隔热层材料会增大生产成本和发射筒质量，但可通过同心筒的特殊设计进行尾焰导流。参考已有的大型导弹发射系统，火箭发动机的尾焰回流不会对无人机产生烧蚀。本文采用直接使用火箭助推的方案进行发射。

折叠状态的纵列式旋翼无人机与火箭助推装置的组合体在助推段主要受重力和推力作用，为简化模型可将助推段的气动力忽略。

1.2   旋翼无人机气动力模型

为简化气动力模型，忽略纵列式旋翼无人机前、后旋翼转动间的气动干扰影响和旋翼气流的压缩性影响。

以前旋翼为例，其所受升力计算式如下^[10]：

式中: T_f、Y_f和H_f分别为前旋翼所受的升力、横侧向力和阻力；T_CF、Y_CF和H_CF分别为前旋翼升力系数、横侧向力系数和阻力系数；α_∞为旋翼桨叶升力线斜率；σ为旋翼实度系数；ρ为空气密度；R_B为旋翼半径；Ω为旋翼转速。

前旋翼所受的气动力矩计算式如下^[11]：

式中: Q_f、M_HF和L_HF分别为前旋翼所受的扭矩、横侧向桨毂力矩和纵向桨毂力矩；b_s为旋翼的桨叶数；e_s为旋翼挥舞铰的偏置距离；M_W为桨叶对挥舞铰的转动惯量；a_f和b_f分别为前旋翼的纵向挥舞角和横侧向挥舞角；Q_CF为扭矩系数。其中，下角标为r或R的参数均与后旋翼有关，下角标为f或F的参数均与前旋翼有关。

后旋翼的气动力和气动力矩模型与前旋翼类似，因此不再赘述。

机身的气动力与机身处的动压、迎角和侧滑角相关，而机身动压、迎角和侧滑角主要受旋翼对机身的下洗和侧洗影响^[11]。

机身处动压Q_fus的计算式如下：

式中：u、v、w分别为无人机在机体坐标系x、y、z轴上的速度分量；W_FUS为无人机前、后旋翼叠加后的等效下洗气流速度。

纵列式旋翼无人机机身在机体坐标系x、y、z轴上所受的阻力D_x、D_y、D_z计算式如下：

式中：V_∞表示无穷远端空气流动速度；S_x、S_y、S_z分别为机身处在机体坐标系x、y、z轴上的等效阻力平板面积。

机身横侧向力Y_fus和升力T_fus计算如下：

式中：C_Yβ为机身横侧向力气动系数；C_Tα为机身升力气动系数；α_fus和β_fus分别为机身处的迎角和侧滑角。

1.3   旋翼无人机动力学模型

引入旋翼纵向与横侧向挥舞角方程对旋翼/稳定杆动力系统模型的表示如下^[12]：

式中：τ_f为自动倾斜器动作响应的时间常数；a、b分别为前旋翼的纵、横侧向挥舞角；C_au、C_bv分别为纵向、横侧向线速度对挥舞角的交叉导数；A_uals、A_ubls、B_uals、B_ubls为电机到旋翼的机械传递参数；u_a、u_b分别为纵、横侧向周期变矩输入。

在来流角较小的情况下，前旋翼拉力近似等于旋翼气动升力T_f。旋翼的纵、横侧向倾角一般均小于10°。因此，前旋翼拉力在机体坐标系x、y、z轴下的分量X_mf、Y_mf、Z_mf可近似计算如下^[13]：

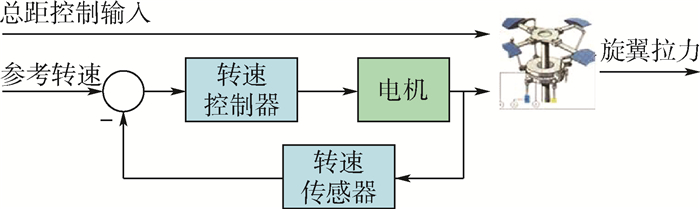
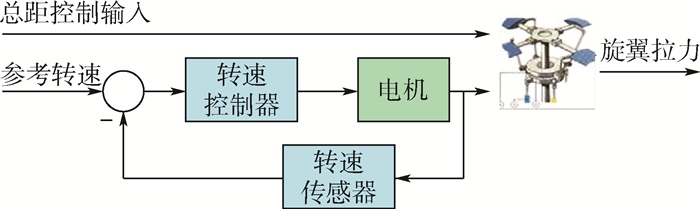
控制总距的电机与转速控制器形成闭环回路，其闭环系统结构如图 2所示。

图  2  动力闭环系统结构

Figure  2.  Structure diagram of dynamic closed-loop system

下载: 全尺寸图片 幻灯片

总距控制输入与旋翼拉力之间近似满足一阶关系：

式中：K_c为减速器等装置的机械传递系数；K_τc为总距控制系统的时间常数；u_c为总距输入量。

无人机旋翼处的迎角和侧滑角一般为小角度，所以旋翼所受的气动合力在机体坐标系x轴下的分量近似为H_f+H_r，在机体坐标系y轴下的分量近似为Y_f+Y_r；旋翼所受的气动合力矩在机体坐标系x、y、z轴下的分量分别近似为L_HF+L_HR、M_HF+M_HR、Q_f+Q_r。

前、后旋翼气动力在机体坐标系x、y、z轴上分解的合力矩L_p、M_p、N_p计算如下：

式中：h_f、h_r分别为前、后旋翼桨毂中心到无人机重心在垂向上的距离；l_f、l_r分别为前、后旋翼桨毂中心到无人机横侧向上的距离。

通过旋翼无人机的滚转和俯仰姿态角可以计算出无人机的重力在机体坐标系上的3个分量：

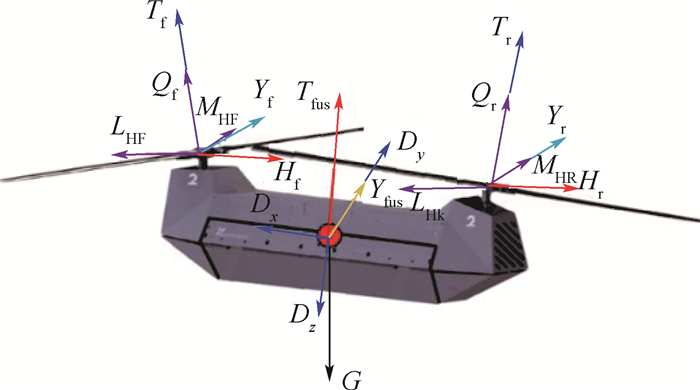
式中：m为无人机质量；g为重力加速度；θ为俯仰角大小；ϕ为滚转角大小。对旋翼无人机进行受力分析可知，合力是由前后旋翼气动力、机身气动力和重力组成。合力矩是由旋翼气动力对重心产生的力矩、旋翼扭矩与桨毂力矩和机身气动力矩组成的。具体受力分析如图 3所示。

图  3  纵列式旋翼无人机受力分析

Figure  3.  Force analysis diagram of tandem rotor UAV

下载: 全尺寸图片 幻灯片

旋翼无人机所受合力在机体坐标系x、y、z轴的分量为

所受合力矩在机体坐标系x、y、z轴的分量为

根据牛顿第二定律和动量矩定理可得到旋翼无人机的六自由度刚体力学模型：

式中：I_xx、I_yy、I_zz分别为无人机绕机体坐标系x、y、z轴的惯性张量；p、q、r分别为无人机绕机体坐标系x、y、z轴的角速度。

为方便姿态解算，现采用zyx欧拉角来描述姿态转动，因此旋翼无人机的运动学方程组为

式中：ψ为旋翼无人机的偏航角。

将合力表达式(11)代入到平动方程式(13)，合力矩表达式(12)代入到转动方程式(14)，结合运动学方程(15)，就可以得到纵列式旋翼无人机的全量非线性系统：

式中：u为无人机控制输入量，即纵向变距控制输入量、总距控制输入量、横侧向变距控制输入量和偏航量；X为无人机的飞行状态变量。

在不同飞行状态工作点下，根据小扰动原理，可将无人机非线性模型进行线性化，并将横侧向、纵向运动分离，从而方便设计无人机旋翼展开的姿态控制律。

2.   潜射过程控制系统设计

2.1   发射窗口设计

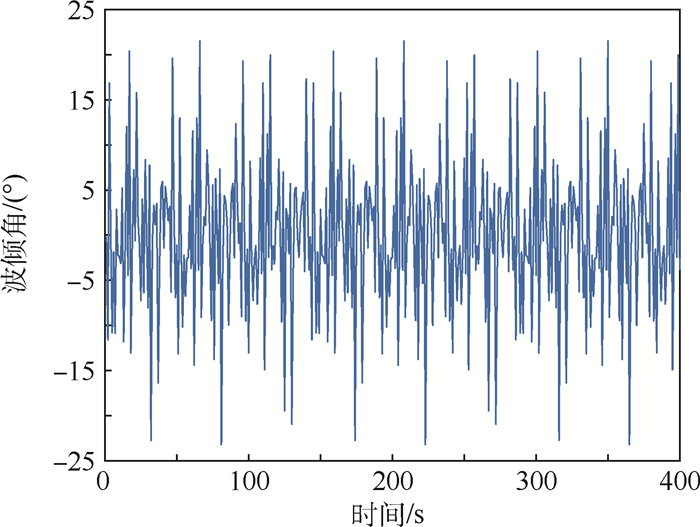
海浪的运动因受到海风、洋流、潮汐等多种因素的影响，通常表现为随机的、不规则的运动状态。因此，旋翼无人机发射筒漂浮在海面上时，会受到海浪运动的影响。为了保证安全发射，有必要在短时间内预测波浪的运动，从而选择合适的时间弹射。相关研究表明，发射筒在海面上的姿态通常取决于波浪倾角，因此对发射筒运动姿态的研究已经转化为对波浪倾角的研究。由于无法获得实时观测的海浪波倾角数据，需要先建立一个随机海浪模型，通过仿真获得波倾角数据^[14]。

通过分析大量实验观测到的数据可知，成熟海浪是一个随机过程。通过随机海浪理论得知，多个随机独立变量可以构成对海浪的模拟。本文将海浪波假定为长峰波，即波仅在主风方向上，波线无限长，波峰相互平行，海面上某一点的海面波动η(x, t)可以用多个随机初始相角的余弦波叠加实现，即

式中：ζ_ai为第i个余弦波的振幅大小；x为波点位置；t为时间；k_i为第i个余弦波的波数，是一个在(0, 2π)范围内的随机变量；ω_i为第i个余弦波的频率；ε_i为第i个余弦波的初相位。

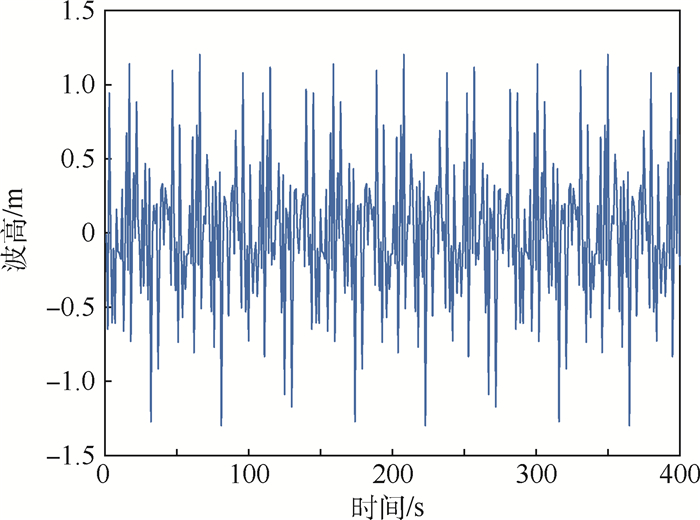
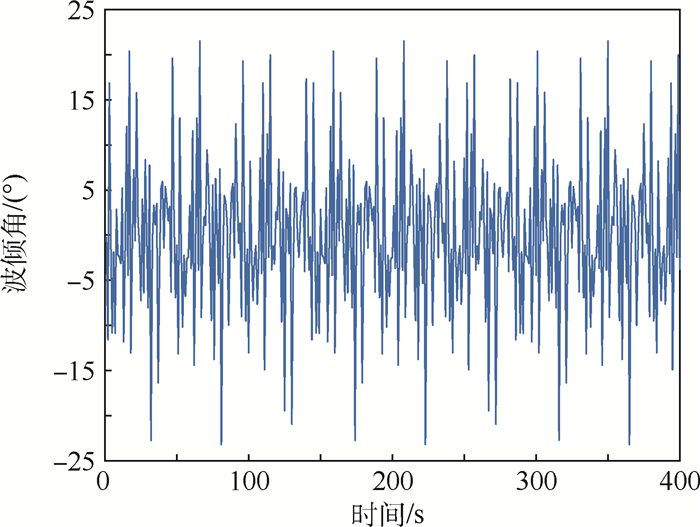
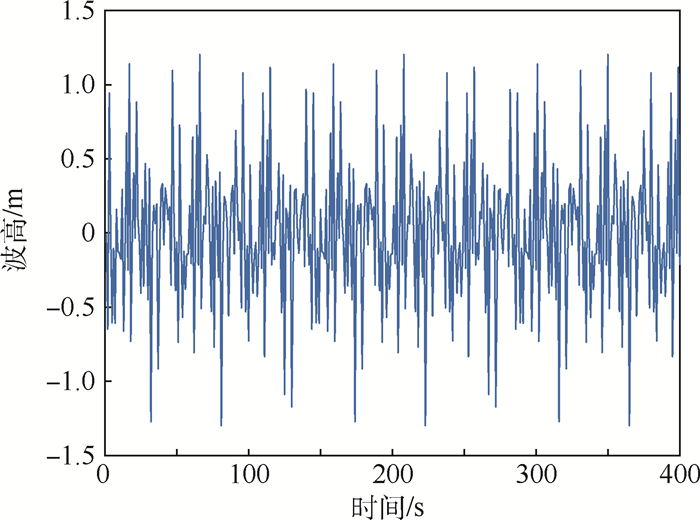
本文假设模拟的波浪谱为皮尔逊-莫斯科维茨谱。根据已有的海况数据，在三级海况下，有义波高在0.5~1.25 m。波浪谱是一个窄带谱，其能量主要集中的频带区间为0.5~3 rad/s。仿真得到的随机海浪的波高和波倾角数据如图 4和图 5所示。

图  4  波高

Figure  4.  Height of wave

下载: 全尺寸图片 幻灯片

图  5  波倾角

Figure  5.  Slope of wave

下载: 全尺寸图片 幻灯片

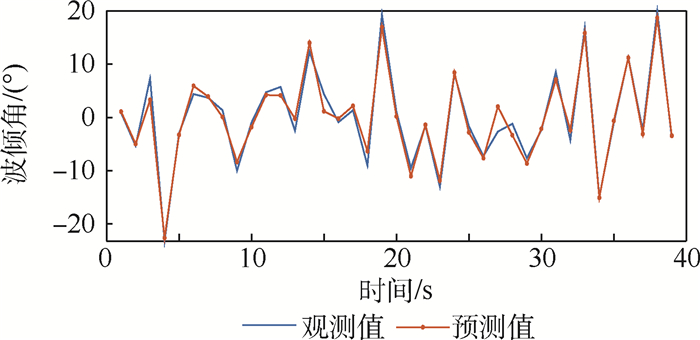
本文通过建立LSTM网络模型对波倾角进行预测，将仿真得到的波倾角数据按照顺序划分训练集和测试集，前90%作为训练集，剩余的作为测试集，由此可得到该神经网络模型预测的准确性ε，如图 6所示。

图  6  长短期记忆学习网络

Figure  6.  Long short-term memory learning network

下载: 全尺寸图片 幻灯片

在进行预测时，采用已有的波倾角数据作为输入，每次预测只对下一个时间点的波倾角值进行预测，然后将下一时间点测得的实际波倾角作为新的输入更新网络，就可以得到接下来一段时间内的波倾角数据，如图 7所示。

图  7  波倾角预测结果

Figure  7.  Prediction results of slope of wave

下载: 全尺寸图片 幻灯片

2.2   姿态控制律设计

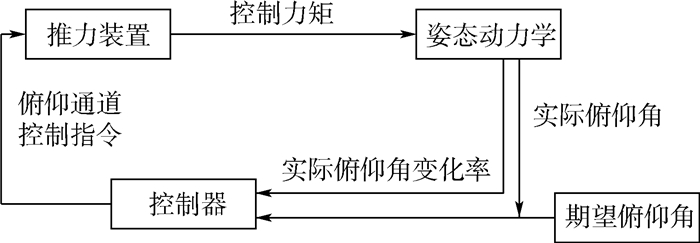
为减少发射装置的复杂度，在助推段的姿态控制上可以仅对俯仰进行控制，并选择合适的发射时机，尽可能减小初始的偏航角和偏航角速度，如图 8所示。

图  8  俯仰通道控制原理图

Figure  8.  Schematic diagram of pitch channel control

下载: 全尺寸图片 幻灯片

本文的设计重点在于潜射无人机在旋翼展开时的姿态环控制，而不是旋翼展开的执行机构装置，因此假设旋翼展开产生的冲击载荷对无人机姿态控制的影响较小，可忽略不计。

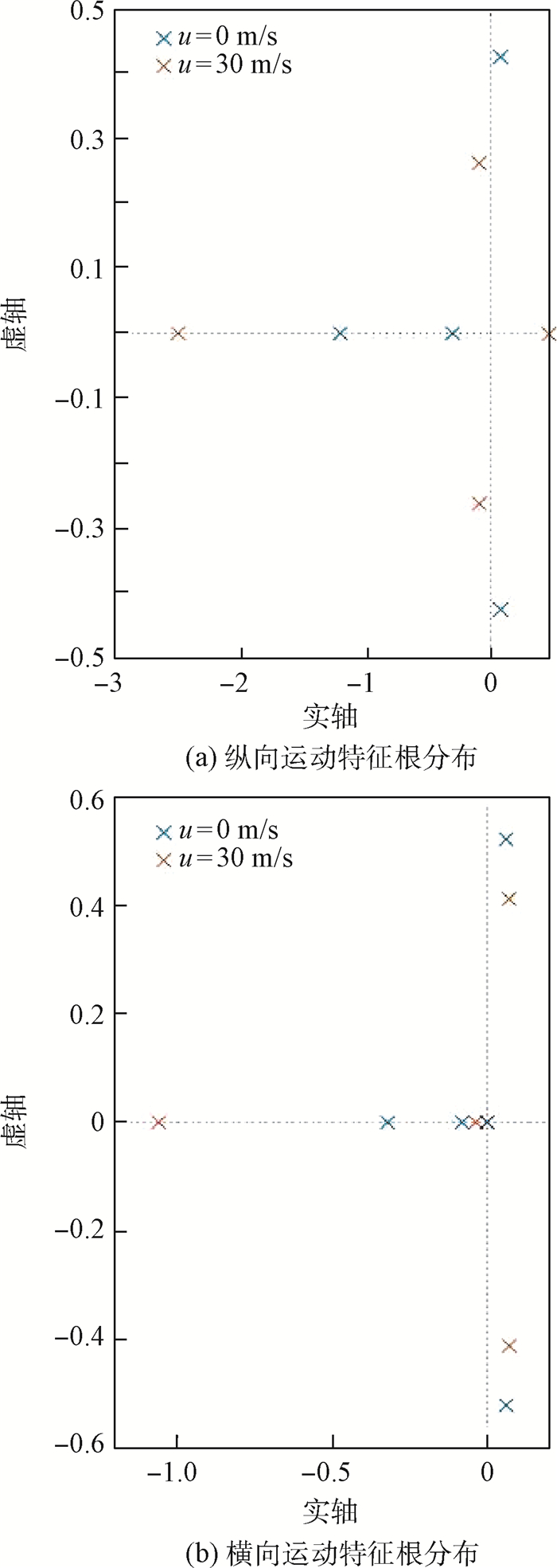
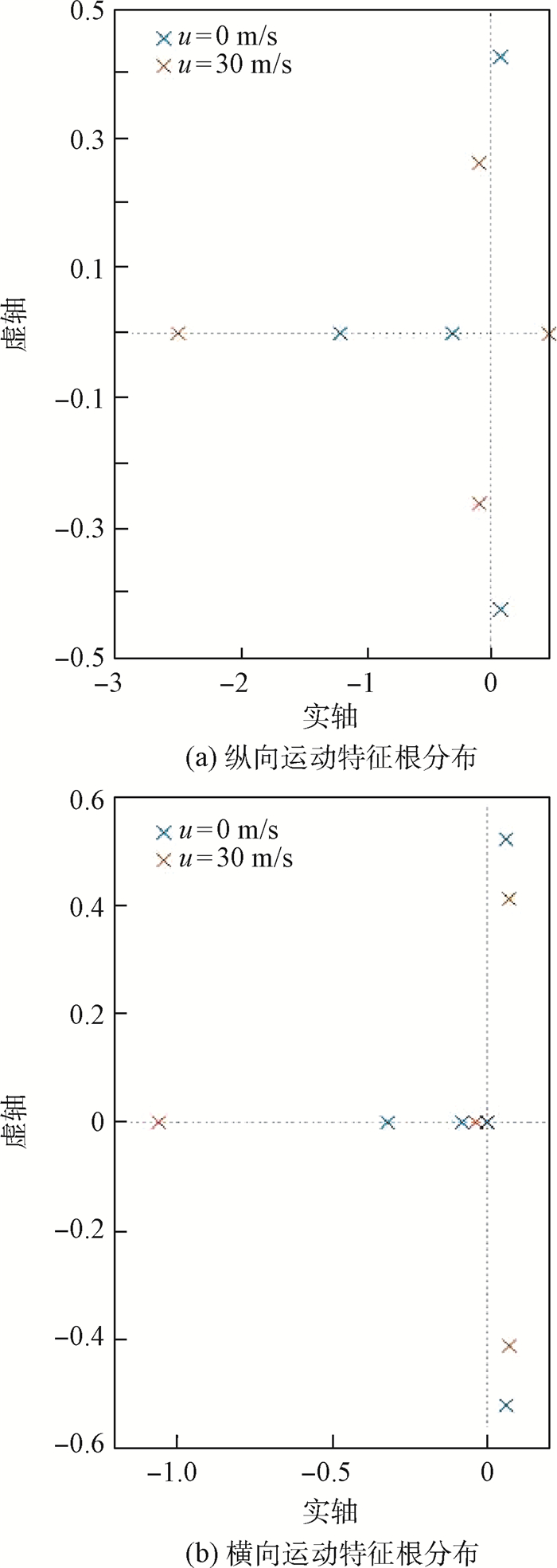
分析线性化后的模型，可计算出纵列式旋翼无人机的纵、横侧向运动的特征根，具体分布如图 9所示。可以看出，纵列式旋翼无人机是一个静不稳定系统，因此无人机的姿态控制需要进行增稳设计。为此，本文选用L1自适应控制方法来设计无人机旋翼展开时的姿态控制律。

图  9  旋翼无人机纵、横侧向分离运动的特征根

Figure  9.  Horizontal and vertical separation motion characteristic roots of rotor UAV

下载: 全尺寸图片 幻灯片

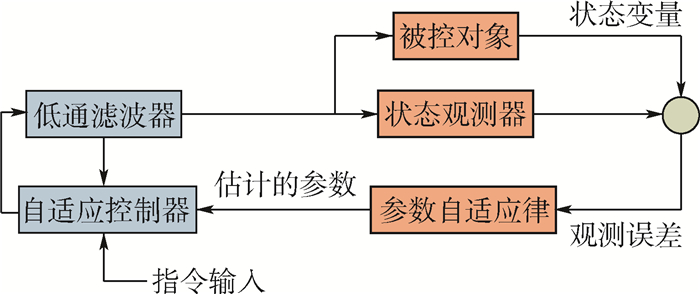
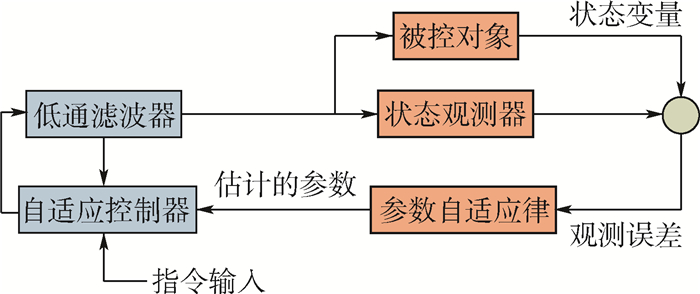
L1自适应控制器整体结构由全阶状态观测器、参数自适应律、自适应控制器和低通滤波器构成，具体结构如图 10所示。

图  10  L1自适应控制结构示意图

Figure  10.  Schematic diagram of L1 adaptive control structure

下载: 全尺寸图片 幻灯片

L1自适应控制器的低通滤波器的作用是滤除控制输入信号中的高频信号，其带宽的设计直接影响着控制系统的幅值裕度和相角裕度，从而影响着控制系统的鲁棒性^[15]。

将带有不确定性参数的旋翼无人机非线性状态方程式进行线性化，并分离出如下纵向运动方程：

式中：x_h(t)为可测量的纵向运动状态；A_h、b_h和c_h^T分别为纵向运动状态矩阵、输入矩阵和输出矩阵；u_h(t)和y_h(t)分别为纵向运动系统的控制输入和输出；ω_h为与输入量有关的不确定性参数；θ_h^T(t)x_h(t)代表与状态变量有关的不确定性部分；σ_h(t)代表与状态变量无关的不确定性部分。结合纵向运动建模情况可知，参数ω_h、θ_h与纵列式潜射无人机的质量、转动惯量和气动参数相关，σ_h与外界阵风干扰相关。

假设模型不确定性参数满足如下条件。

1) 参数θ_h(t)和σ_h(t)满足：

式中：Θ为已知凸集；Δ₀∈R⁺。

2) 参数θ_h(t)和σ_h(t)连续可微且一致有界：

3) 输入加权参数中ω_h的任意分量ω∈R满足：

对于本文设计的纵列式旋翼无人机潜射控制系统，以上假设均可以满足。

在设计L1自适应控制器前，本文先采用LQR控制方法设计状态反馈增益阵，使得姿态控制具有增稳效果。LQR的设计方法是先拟定一个与状态变量和控制输入相关的指标函数：

指标函数中的Q阵和R阵分别实现了对状态变量和控制输入的加权，Q阵和R阵均为对角半正定矩阵。LQR最优控制是通过预先根据实际模型情况选定Q阵和R阵，找出一个合适的反馈增益阵K_m，使反馈控制输入u=-K_mx，使指标函数J达到最优。

由最优控制理论可知，LQR中的反馈增益阵K_m的解为

式中：P_m阵通过求解如下黎卡提方程得到：

现记状态反馈后的状态矩阵为

全阶状态观测器形式如下：

式(23)与式(18)不同的是：模型中的不确定参数ω_h、θ_h、σ_h均为参数自适应律计算出的估计值、、，观测器据此计算状态变量的估计值。估计的状态变量与真实状态变量的偏差将用于参数自适应律的计算。

待估计参数的自适应律计算公式如下：

式中：Γ为自适应增益；Proj(·)为投影算子，保证了估计值参数的有界性。

P=P^T为如下李雅普诺夫方程：

对于任意Q=Q^T的解。

L1自适应控制器输入的具体形式如下：

式中：k为自适应反馈增益；D(s)为低通滤波器；r(s)为指令输入r(t)的拉普拉斯变换；为的拉普拉斯变换；设计指令输入的增益k_g，可使得系统输出能稳定地跟踪指令输入信号。

状态观测器输出的传递函数表达为

式中：c为系统输出矩阵。当时间趋于无穷，输出值可达到：

为使得，则可以求解出：

因此，可以求解出增益k_g=-1/(c^TA_m^-1b)。

设计的低通滤波器形式为

低通滤波器C(s)的设计需保证C(0)=1，这里选取D(s)=1/s进行简化设计。

k为自适应反馈增益，其值直接影响着低通滤波器带宽。为保证闭环系统的渐进稳定性，k的设计必须满足闭环系统L1小增益定理。现定义：

则根据闭环系统L1小增益定理，设计的增益k需满足：

3.   潜射过程控制仿真

3.1   火箭助推姿态控制仿真

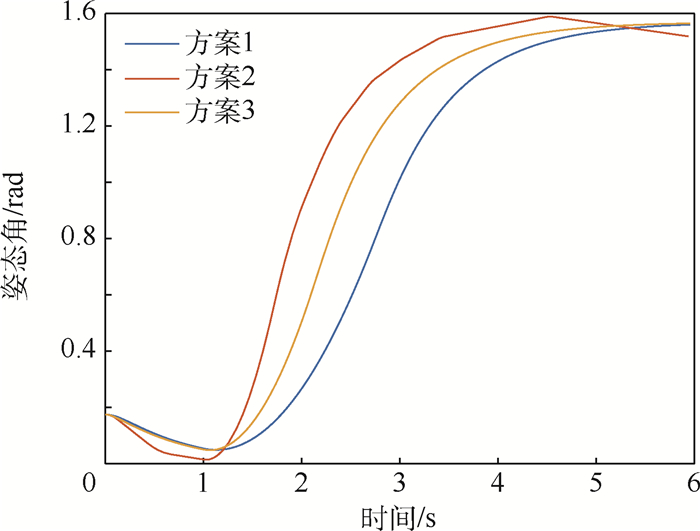
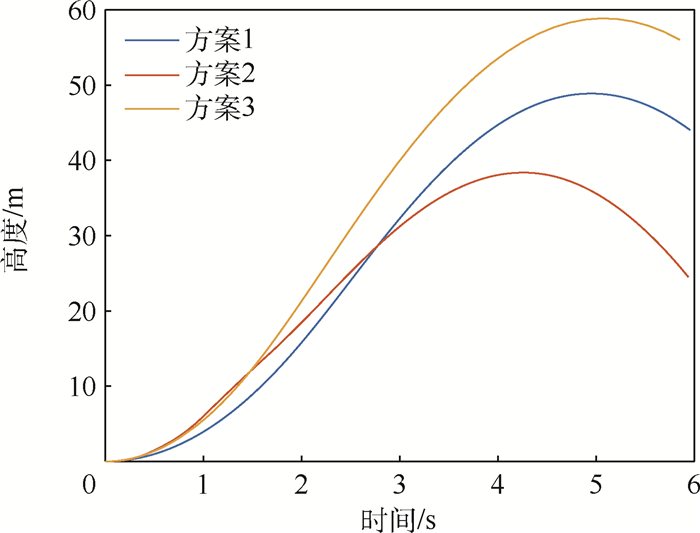
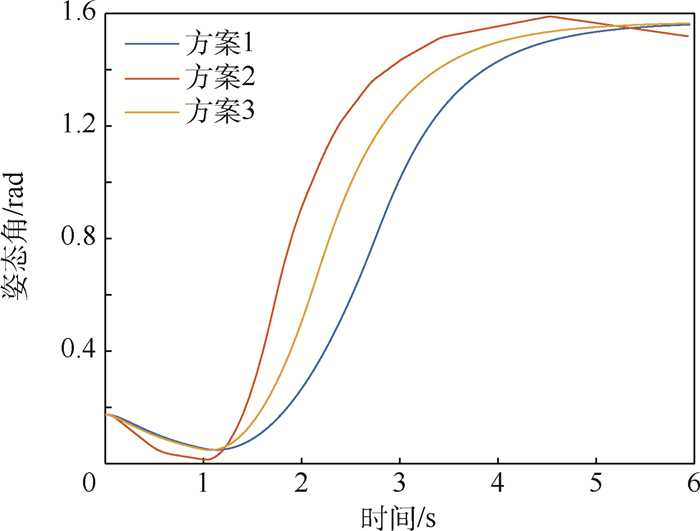
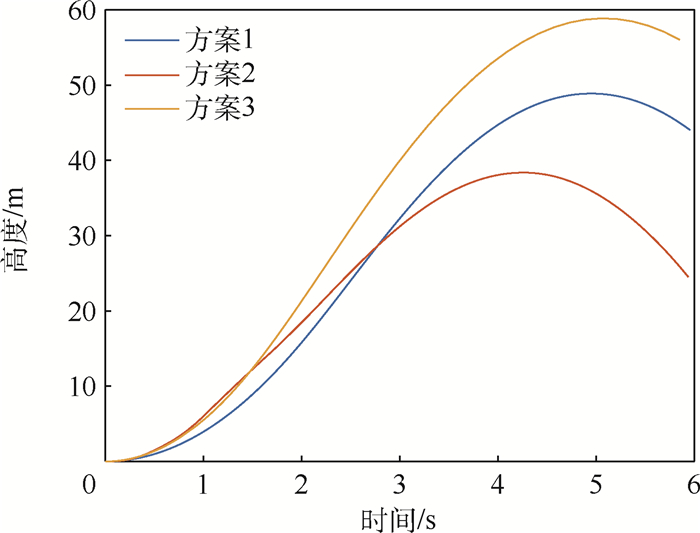
在助推段无人机是从筒内发射，能够选取的发射方案有限。现在控制总推力一定的情况下，对连续差分推力控制(方案1)、脉冲推力差分控制(方案2)和推力矢量姿态控制(方案3)进行了建模仿真，仿真结果如图 11和图 12所示。

图  11  姿态角变化曲线比较

Figure  11.  Comparison of attitude angle change curves

下载: 全尺寸图片 幻灯片

图  12  高度变化曲线比较

Figure  12.  Comparison of height change curves

下载: 全尺寸图片 幻灯片

通过对比3个方案的姿态角曲线和飞行高度曲线可以得到，推力矢量姿态控制方案的姿态角控制的快速性和稳定性更优，并且可以满足具体的设计要求，最终选定采用推力矢量姿态控制的方案。

由于发射空间有限，本文采用了二维平面的燃烧舵式推力矢量控制技术，通过预测波倾角对弹射时机进行选择，从而尽可能减小初始状态的偏航角和偏航角速度，确保在助推段的短时间内偏航姿态保持在旋翼可安全展开的范围内。

3.2   旋翼展开姿态控制仿真

在前飞速度为30 m/s情况下，纵列式旋翼无人机线性化后的纵向运动状态方程如下：

式中：x_h=[u w q θ]^T为无人机纵向运动的状态变量；u_h=[u_b u_c]^T为控制输入变量。

用LQR控制方法设计出的状态反馈增益阵为

考虑到纵向实际飞行状态、纵列式旋翼无人机系统特性与外界环境干扰情况，选取的纵向模型各项不确定参数变化范围为

由此可知，，选取自适应增益Γ=10 000。经粗略计算发现当选取k>80时，满足式(31)中的稳定条件。因此，选取增益k=100。

为验证纵向俯仰姿态L1自适应控制器的跟踪性能，现给定10°的俯仰角阶跃指令信号进行仿真。将模型中未知参数重新设定如下：

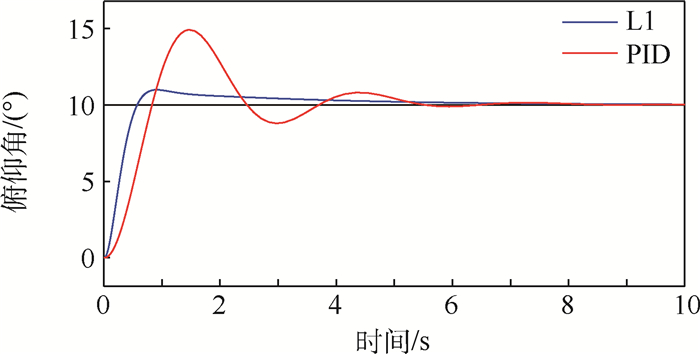
将L1自适应控制下的俯仰角输出与固定参数的PID控制进行对比，仿真结果如图 13所示。对比图 13中L1自适应控制器和PID控制器的输出响应可知，固定参数的PID控制器在系统受扰后动态特性变差。而L1自适应控制器下的输出超调量约5%，响应上升时间约0.4 s，稳定时间约5 s，在抗干扰性和对气动参数不确定变化的鲁棒性上表现得更好。

图  13  俯仰通道输出响应

Figure  13.  Output response of pitch channel

下载: 全尺寸图片 幻灯片

在前飞速度为30 m/s情况下，纵列式旋翼无人机线性化后的横侧向运动状态方程如下：

式中：x_l=[p ϕ r v]^T为无人机横侧向运动的状态变量；u_l=[u_a u_r]^T为控制输入变量，u_r为旋翼无人机偏航控制输入量。

用LQR控制方法设计出的状态反馈增益阵为

考虑到横侧向实际飞行状态、纵列式旋翼无人机系统特性与外界环境干扰情况，选取的横侧向模型各项不确定参数变化范围为

由此可知，，选取自适应增益Γ=10 000，经粗略计算发现当选取k>120时，满足式(31)中的条件。因此选取增益k=150。

为验证横侧向俯仰姿态L1自适应控制器的稳定性能，现假定无人机在初始时刻受到10°的滚转角扰动和1(°)/s的偏航角速率扰动。将模型中的未知参数重新设定如下：

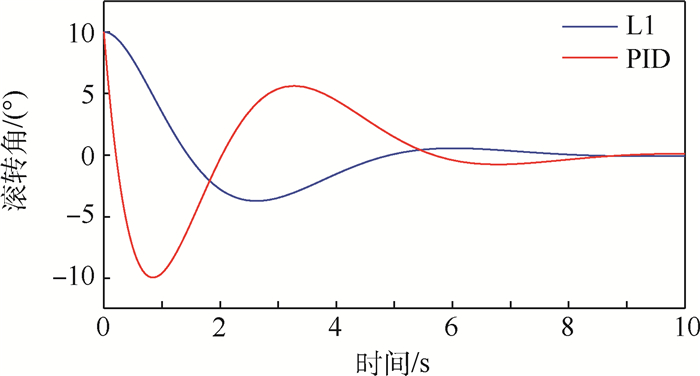
将L1自适应控制下的滚转角输出与固定参数的PID控制进行对比，仿真结果如图 14所示。对比图 14中L1自适应控制器和PID控制器的输出响应可知，L1自适应控制器在气动参数变化和环境干扰的情况下，仍能在8 s内较好地快速控制滚转角至稳定状态，动态过程最大振幅不超过3°；而PID控制器的输出产生了-10°的振荡，飞行姿态的控制效果变差。

图  14  滚转通道输出响应

Figure  14.  Output response of roll channel

下载: 全尺寸图片 幻灯片

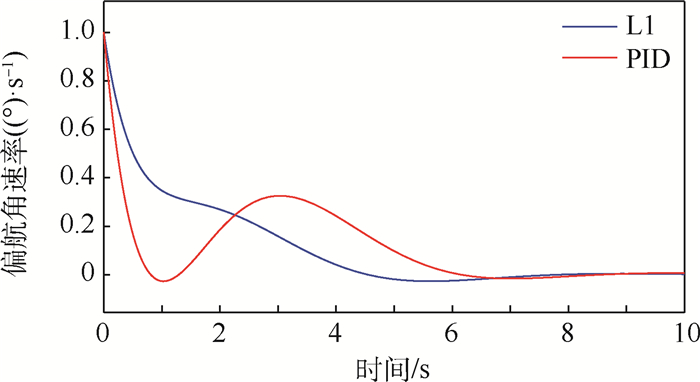
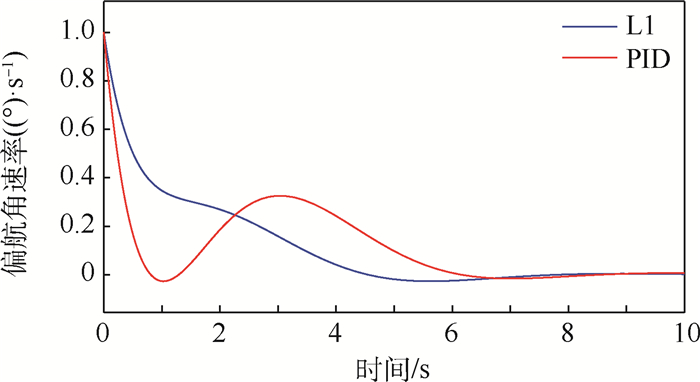
将L1自适应控制下的偏航角输出与固定参数的PID控制进行对比，仿真结果如图 15所示。对比图 15中L1自适应控制器和PID控制器的输出响应可知，在气动参数变化和环境干扰的情况下，PID控制器的输出动态特性较差，过渡过程中的振荡振幅约0.3(°)/s。L1自适应控制器控制偏航角速率收敛的过程有较小的波动，但无振荡情况，偏航通道在7 s后稳定收敛至0。

图  15  偏航通道输出响应

Figure  15.  Output response of yaw channel

下载: 全尺寸图片 幻灯片

综合以上仿真结果可知，L1自适应姿态控制器相比PID基本姿态控制器，其控制品质较好，动态响应特性得到改善，在对气动参数变化的鲁棒性和对环境的抗干扰性方面表现得更好。

3.3   潜射过程总体仿真

旋翼无人机潜射过程中仿真条件设定如下：

1) 在t=0 s时刻，旋翼无人机弹射出筒，同时火箭点火，助推无人机垂直升空。

2) 在t=3 s时刻，助推火箭脱落，旋翼展开。

3) 无人机最终调整自身俯仰姿态至-5°，以实现稳定前飞状态。

4) 仿真总时长为10 s，仿真步长设定为0.01 s。

5) 旋翼无人机模型中的不确定性参数与3.2节相同。

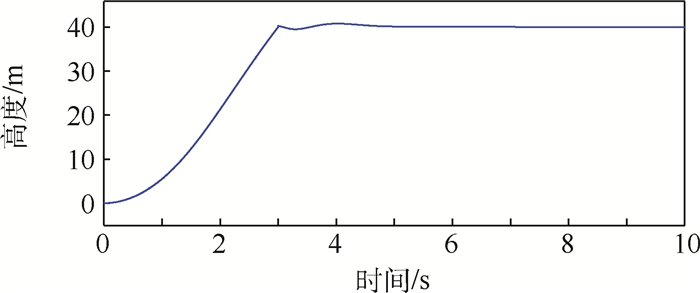
在MATLAB软件中搭建Simulink框架仿真上述整个潜射过程，旋翼无人机高度变化如图 16所示。

图  16  旋翼无人机潜射过程高度变化

Figure  16.  Height of rotor UAV during underwater- launched process

下载: 全尺寸图片 幻灯片

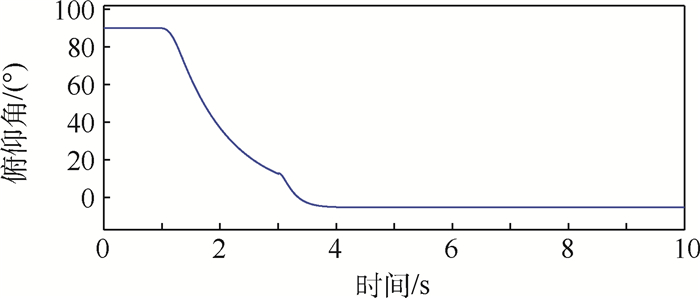
从图 16结果中可知，旋翼无人机潜射升空的加速度约为8.9 m/s²，在t=3 s时刻，火箭脱落，旋翼无人机的高度下降约1 m后在1 s内又控制稳定在40 m。此结果验证了旋翼展开的响应快速性。

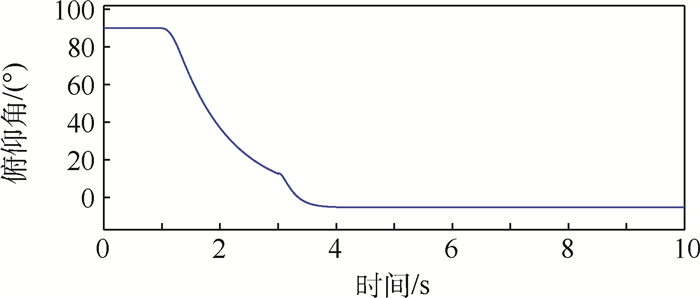
旋翼无人机的俯仰角变化如图 17所示。

图  17  旋翼无人机潜射过程俯仰角变化

Figure  17.  Pitch angle of rotor UAV during underwater- launched process

下载: 全尺寸图片 幻灯片

观察图 17结果可知，助推火箭的矢量控制发动机在1 s后开始控制箭体和无人机的俯仰角姿态，在t=3 s时火箭姿态发动机能将无人机的俯仰姿态调整至12.6°，之后火箭脱落，无人机旋翼展开，通过已设计的L1姿态控制器将自身俯仰姿态在1 s内控制到-5°，实现了无人机的稳定前飞。

潜射过程总体仿真的结果表明，助推火箭能够通过矢量姿态发动机在2 s内快速控制旋翼无人机在发射过程中的俯仰姿态。旋翼无人机在助推火箭脱落后，旋翼能够快速展开，动力系统能够在1 s内将无人机保持在指定高度。设计的旋翼展开姿态控制器对气动参数的不确定变化具有鲁棒性，其动态响应时间小于1 s，能够实现无人机在潜射场景中的姿态稳定飞行。

4.   结论

本文提出了一种针对纵列式布局小型旋翼无人机的潜射控制系统方案，使得旋翼无人机能够在潜射过程中快速准确地调整发射时间和自身姿态，从而实现姿态稳定飞行。

具体工作如下：

1) 预测海浪模型能够完成无人机发射时间窗口的优化。

2) 设计出的潜射助推方案和火箭助推的姿态控制律能够确保无人机稳定的上升至指定高度。

3) 设计出的L1自适应姿态控制器能够保证无人机在旋翼展开时快速调整自身俯仰姿态，且对气动参数的变化具有一定的鲁棒性。

本文完成了纵列式布局旋翼无人机的潜射控制系统仿真验证，仿真结果表明，设计的无人机潜射控制系统能够在10 s内将无人机成功助推至一定高度，实现无人机的姿态稳定飞行，确保无人机能够正常执行反潜等任务。