-
摘要:
针对无人机（UAV）的航迹规划问题，提出了一种基于混沌多精英鲸鱼优化算法（CML-WOA）的航迹规划方法。首先，在已知飞行环境下，建立3D飞行空间模型和航迹代价模型。通过引入罚函数，将有约束3D航迹规划问题转化为无约束多维函数优化问题，利用CML-WOA求解模型来获得最优航迹。其次，为克服WOA易陷入局部最优的缺陷，引入立方映射混沌算子改善初始种群，增强种群多样性，并通过自适应框架融入正余弦算法（SCA），利用多精英搜索策略有效地提高了算法开发能力和探索能力。最后，使用贪婪策略保证了收敛效率。通过20个基准函数测试和航迹规划仿真实验对提出的改进WOA进行验证。结果表明：所提算法相对其他算法，寻优性能明显提升，具有较强局部最优规避能力和更高的收敛精度与收敛速度；能够稳定快速地规划出代价最少、满足约束的安全可行的飞行航迹。
-
关键词:
- 航迹规划 /
- 鲸鱼优化算法(WOA) /
- 混沌算子 /
- 多精英搜索 /
- 正余弦算法(SCA) /
- 全局优化
Abstract:Aimed at the path planning problem of Unmanned Aerial Vehicle (UAV), a path planning method based on a Chaotic Multi-Leader Whale Optimization Algorithm (CML-WOA) is proposed. In the known flight environment, 3D model of flight area and a flight path cost model are established. By introducing penalty functions, the constrained 3D path planning problem is transformed into an unconstrained multi-dimensional function optimization problem, which is solved using CML-WOA to obtain the optimal flight path. To overcome the defect that the WOA is easy to fall into local optimum, this paper introduces the cubic mapping chaos operator to improve the initial population and enhance the population diversity. And the Sine Cosine Algorithm (SCA) is integrated through an adaptive framework. A multi-leader search strategy is used to effectively improve the algorithm exploitation and exploration capability. Finally, a greedy strategy is used to ensure the convergence efficiency. The proposed improved CML-WOA is tested and validated by 20 benchmark functions test and path planning simulation experiments. The results show that the algorithm has significantly improved performance compared to other algorithms, with strong local optimal avoidance capability, higher convergence accuracy and convergence speed. Also, it is able to provide stable and fast planning of safe and feasible flight path with minimum cost and satisfying constraints.
-
图 8 8种算法在9个基准测试函数上的收敛箱式图
Figure 8. Convergence box diagram of eight algorithms on nine benchmark test functions
表 1 测试函数
Table 1. Test functions
函数分类 测试函数 维度 范围 最优值 单峰
测试
函数
30 [-100, 100] 0 30 [-10, 10] 0 30 [-100, 100] 0 30 [-100, 100] 0 30 [-30, 30] 0 30 [-100, 100] 0 30 [-1.28, 1.28] 0 多峰
测试
函数
30 [-5.12, 5.12] 0 30 [-32, 32] 0 30 [-600, 600] 0 30 [-50, 50] 0 30 [-50, 50] 0 固定
维度
测试
函数
2 [-65, 65] 0.998 4 [-5, 5] 0.000 3 2 [-5, 5] -1.031 6 2 [-2, 2] 3 3 [1, 3] -3.86 6 [0, 1] -3.32 4 [0, 10] -10.153 2 4 [0, 10] -10.536 3 
下载: 导出CSV
表 2 F1~F7算法测试结果比较
Table 2. Results comparison among test functions F1-F7 of algorithms
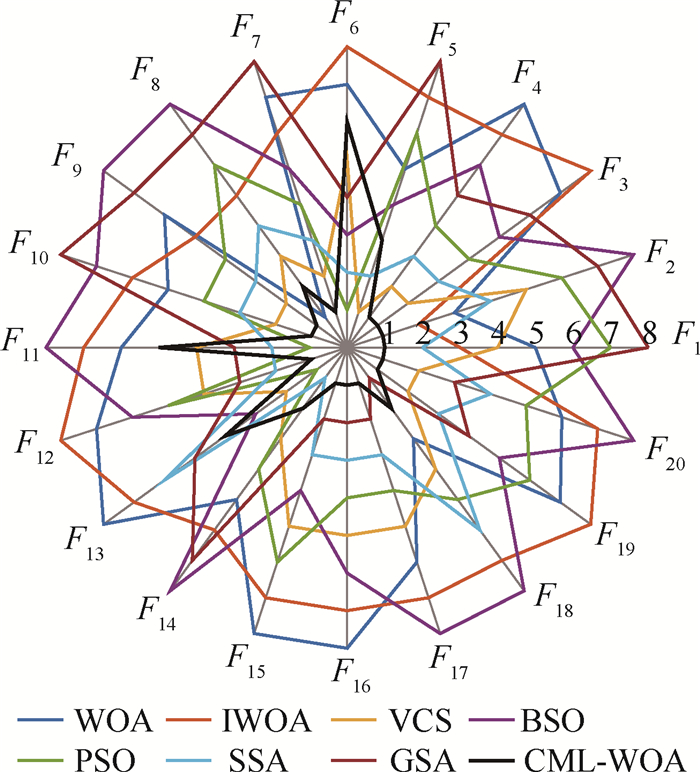
测试函数 统计值 WOA IWOA VCS BSO PSO SSA GSA CML-WOA F1 最优值 4.01×10-116 1.30×10-118 7.21×10-121 1.65×10-53 2.73×10-26 0 2.57×10-19 0 平均值 2.56×10-99 2.19×10-106 2.93×10-106 1.11×10-25 1.60×10-39 9.94×10-100 1.31×10-18 0 标准差 1.37×10-98 8.11×10-106 1.37×10-105 5.19×10-25 3.17×10-39 5.32×10-99 6.82×10-19 0 耗时/s 0.788 1 0.779 3 3.336 5 3.837 1 2.662 3 4.377 1 8.332 5 3.013 5 F2 最优值 1.38×10-72 1.25×10-76 3.22×10-59 8.71×10-11 2.07×10-22 2.50×10-76 1.16×10-9 5.90×10-294 平均值 5.92×10-65 1.50×10-69 1.02×10-52 7.58×10-3 2.86×10-21 6.25×10-53 2.36×10-9 2.60×10-160 标准差 1.84×10-64 8.38×10-69 5.12×10-52 1.17×10-2 3.43×10-21 3.40×10-52 7.60×10-10 0 耗时/s 1.063 2 1.061 5 3.645 4 4.700 3 2.868 0 4.773 7 8.296 9 3.305 5 F3 最优值 1.04×10-44 4.01×10-28 4.42×10-111 7.70×10-54 3.98×10-33 0 3.02×10-19 0 平均值 2.22×10-4 1.33×10-4 8.68×10-97 2.98×10-8 2.47×10-30 2.99×10-58 1.76×10-18 3.55×10-297 标准差 8.10×10-4 5.71×10-4 3.67×10-96 1.63×10-7 3.92×10-30 9.64×10-58 1.31×10-18 0 耗时/s 1.898 1 1.980 2 4.532 4 7.302 0 3.707 5 6.210 0 9.224 7 4.354 4 F4 最优值 6.60×10-2 5.77×10-8 1.09×10-57 8.95×10-16 3.07×10-20 3.24×10-242 3.81×10-10 0 平均值 2.13×101 8.78 1.10×10-51 3.54×10-2 8.17×10-19 1.75×10-43 8.45×10-10 0 标准差 1.31×101 9.07 5.31×10-51 1.44×10-1 6.12×10-19 6.69×10-43 2.59×10-10 0 耗时/s 0.784 8 0.772 6 3.434 0 3.774 7 2.624 0 4.318 3 8.101 3 3.204 7 F5 最优值 9.96×10-1 9.76×10-1 1.94×10-13 0 4.58×10-5 1.70×10-11 1.01 9.53×10-4 平均值 2.04×101 5.49×101 8.86×10-9 1.91 2.22 1.51×10-5 7.43 2.93×10-1 标准差 9.19×101 2.78×102 2.74×10-8 2.02 4.91 3.90×10-5 3.21×101 1.02 耗时/s 1.176 1 1.170 9 3.809 7 5.174 9 2.982 4 4.910 2 8.335 2 5.534 0 F6 最优值 2.26×10-3 4.5×10-3 3.89×10-25 0 0 0 4.50×1019 1.84×10-32 平均值 3.38×10-3 1.16×10-1 4.18×10-16 8.32×10-21 0 0 1.15×10-18 8.60×10-3 标准差 4.00×10-2 1.14×10-1 2.13×10-15 4.42×10-20 0 0 6.32×10-19 1.89×10-2 耗时/s 0.794 4 0.776 5 3.312 0 3.932 3 2.619 2 4.354 3 8.082 8 3.476 1 F7 最优值 5.12×10-5 1.09×10-5 1.19×10-5 1.98×10-4 9.60×10-5 3.50×10-5 3.62×10-4 4.63×10-6 平均值 2.42×10-3 2.04×10-3 3.42×10-4 1.27×10-3 7.21×10-4 6.46×10-4 5.38×10-3 2.47×10-4 标准差 2.82×10-3 3.27×10-3 2.69×10-4 1.11×10-3 5.28×10-4 3.57×10-4 3.44×10-3 1.93×10-4 耗时/s 1.130 0 1.180 0 3.691 2 4.844 1 2.927 3 4.906 7 8.551 8 3.478 1
下载: 导出CSV
表 3 F8~F12算法测试结果比较
Table 3. Results comparison among test functions F8-F12 of algorithms
测试函数 统计值 WOA IWOA VCS BSO PSO SSA GSA CML-WOA F8 最优值 0 0 0 0 0 0 0 0 平均值 0 2.36×10-16 0 5.67 4.64×10-1 0 2.08 0 标准差 0 1.29×10-15 0 4.34 5.04×10-1 0 1.59 0 耗时/s 0.824 4 0.812 5 3.379 4 4.112 4 2.686 8 4.472 2 7.798 9 3.097 1 F9 最优值 8.88×10-16 8.88×10-16 8.88×10-16 4.44×10-15 8.88×10-16 8.88×10-16 1.09×10-9 8.88×10-16 平均值 3.84×10-15 3.37×10-15 8.88×10-16 6.80×10-1 3.01×10-15 8.88×10-16 2.29×10-9 8.88×10-16 标准差 2.30×10-15 2.31×10-15 0 8.56×10-1 1.77×10-15 8.88×10-16 6.82×10-10 0 耗时/s 1.139 8 1.118 9 3.660 8 5.039 3 2.990 2 4.954 5 8.690 0 3.366 7 F10 最优值 0 0 0 2.71×10-2 0 0 9.36×10-2 0 平均值 4.13×10-2 4.47×10-2 0 1.75×10-1 3.88×10-2 0 9.05×10-1 0 标准差 9.08×10-2 1.12×10-1 0 1.03×10-1 2.67×10-2 0 6.32×10-1 0 耗时/s 1.396 5 1.374 9 4.066 0 5.773 5 3.227 2 5.491 3 8.750 0 3.699 0 F11 最优值 2.41×10-3 5.57×10-3 1.61×10-24 9.42×10-32 9.42×10-32 9.42×10-32 1.07×10-20 9.42×10-32 平均值 1.61×10-1 2.27×10-1 4.91×10-18 2.44×10-1 9.42×10-32 9.42×10-32 5.29×10-20 4.25×10-5 标准差 3.86×10-1 4.19×10-1 2.14×10-17 1.02 3.34×10-47 3.53×10-34 3.56×10-20 2.97×10-4 耗时/s 3.155 6 3.140 2 5.822 1 10.999 5 4.959 2 8.483 5 10.533 0 6.326 9 F12 最优值 3.35×10-3 2.29×10-2 3.02×10-23 1.34×10-32 3.44×10-32 1.34×10-32 2.74×10-20 1.34×10-32 平均值 9.82×10-2 1.71×10-1 1.48×10-17 3.84×10-3 2.21×10-3 1.38×10-32 1.57×10-19 1.34×10-32 标准差 6.99×10-2 1.11×10-1 4.88×10-17 1.04×10-2 4.20×10-3 1.25×10-33 1.05×10-19 5.56×10-48 耗时/s 3.149 3 3.145 4 5.768 7 11.117 3 4.993 7 8.603 5 10.547 6 6.234 5
下载: 导出CSV
表 4 F13~F20算法测试结果比较
Table 4. Results comparison among test functions F13-F20 of algorithms
测试函数 统计值 WOA IWOA VCS BSO PSO SSA GSA CML-WOA F13 最优值 9.98×10-1 9.98×10-1 9.98×10-1 9.98×10-1 9.98×10-1 9.98×10-1 9.98×10-1 9.98×10-1 平均值 5.89 5.09 1.42 3.35 9.98×10-1 5.22 5.2 6.01 标准差 4.93 3.95 2.13 3.45 5.82×10-17 5.49 3.79 5.12 耗时/s 15.793 1 15.603 5 19.221 3 48.949 5 17.548 9 30.023 6 22.608 2 16.261 7 F14 最优值 3.49×10-4 4.58×10-4 3.07×10-4 3.07×10-4 3.07×10-4 3.07×10-4 1.88×10-3 3.11×10-4 平均值 3.59×10-3 5.08×10-3 5.65×10-4 7.71×10-3 5.95×10-4 3.37×10-4 5.51×10-3 4.08×10-4 标准差 4.70×10-3 3.07×10-4 3.45×10-4 1.92×10-2 3.88×10-4 8.26×10-5 3.97×10-3 3.31×10-4 耗时/s 0.974 8 0.953 1 3.491 5 4.506 8 2.796 9 4.593 2 8.054 0 3.124 3 F15 最优值 -1.03 -1.03 -1.03 -1.03 -1.03 -1.03 -1.03 -1.03 平均值 -1.03 -1.03 -1.03 -1.03 -1.03 -1.03 -1.03 -1.03 标准差 3.70×10-9 7.35×10-10 6.04×10-16 5.92×10-16 6.45×10-16 5.04×10-16 4.72×10-16 3.06×10-16 耗时/s 0.651 0 0.573 5 3.118 7 3.270 6 2.408 0 4.057 0 6.912 4 3.552 3 F16 最优值 3.00 3.00 3.00 3.00 3.00 3.00 3.00 3.00 平均值 1.21×101 1.28×101 3.00 3.00 3.00 3.00 3.00 3.00 标准差 1.93×101 1.77×101 1.716×10-15 2.28×10-15 1.56×10-15 1.37×10-15 3.94×10-15 1.06×10-15 耗时/s 0.443 3 0.428 9 2.929 4 2.821 0 2.297 8 3.679 1 6.846 8 2.344 8 F17 最优值 -3.86 -3.86 -3.86 -3.71 -3.86 -3.86 -3.86 -3.86 平均值 -3.75 -3.76 -3.86 -3.18 -3.86 -3.86 -3.86 -3.86 标准差 1.02×10-1 1.54×10-1 2.69×10-15 4.20×10-1 2.68×10-15 2.32×10-15 2.31×10-15 2.17×10-15 耗时/s 1.716 9 1.714 9 4.247 6 6.941 1 3.571 1 6.145 1 8.411 6 3.473 2 F18 最优值 -3.27 -3.14 -3.32 -2.73 -3.32 -3.32 -3.32 -3.32 平均值 -3.01 -2.70 -3.29 -1.35 -3.27 -3.27 -3.31 -3.30 标准差 1.77×10-1 4.83×10-1 5.34×10-2 7.33×10-1 5.83×10-2 5.92×10-2 2.22×10-2 5.79×10-2 耗时/s 1.773 1 1.170 8 4.322 7 6.934 4 3.630 3 6.176 7 9.296 6 4.463 4 F19 最优值 -9.81 -10.12 -10.15 -1.72 -10.15 -10.15 -10.15 -10.15 平均值 -5.86 -4.71 -10.15 -6.8×10-1 -5.97 -8.18 -6.94 -10.15 标准差 2.30 2.42 6.56×10-15 3.38×10-1 3.55 2.49 3.72 6.35×10-15 耗时/s 3.210 0 3.190 9 5.737 1 11.526 2 5.126 5 8.617 4 10.264 8 5.079 3 F20 最优值 -10.11 -10.42 -10.53 -4.57 -10.53 -10.53 -10.53 -10.53 平均值 -4.17 -3.68 -10.53 -1.00 -7.79 -8.88 -9.68 -10.53 标准差 2.37 2.19 2.91×10-15 8.32×10-1 3.71 2.65 2.34 2.51×10-15 耗时/s 6.000 4 6.001 4 8.826 4 19.921 0 7.758 9 13.714 2 12.980 1 12.753 2
下载: 导出CSV
表 5 算法性能排序结果
Table 5. Results of sort of algorithm performance
算法 平均排序 算法 平均排序 WOA 5.9 PSO 4.35 IWOA 6.4 SSA 3.1 VCS 3.2 GSA 5 BSO 6.2 CML-WOA 1.85
下载: 导出CSV
表 6 Wilcoxon统计检验结果
Table 6. Results of statistical tests of Wilcoxon
算法 WOA IWOA VCS BSO PSO SSA GSA F1 - - - - - - - F2 - - - - - - - F3 - - - - - - - F4 - - - - - - - F5 - - + - = = - F6 - - = + + + = F7 - - - - - - - F8 = = = - - - - F9 - - = - = - - F10 = = - - - = - F11 - - - - + + - F12 - - - = = - = F13 = = = = + = = F14 - - = = = = - F15 - - - = - - - F16 - - - - - - - F17 - - = - = - - F18 = = + = + + + F19 - - = - - - - F20 - - = - - - - (-/=/+) 16/4/0 16/4/0 10/8/2 14/5/1 11/5/4 13/4/3 16/3/1 注：表中“+”表示该算法性能明显优于CML-WOA；“=”表明该算法性能与CML-WOA无明显差别；“-”表示该算法性能明显劣于CML-WOA。
下载: 导出CSV
表 7 威胁源参数
Table 7. Parameters of threat source
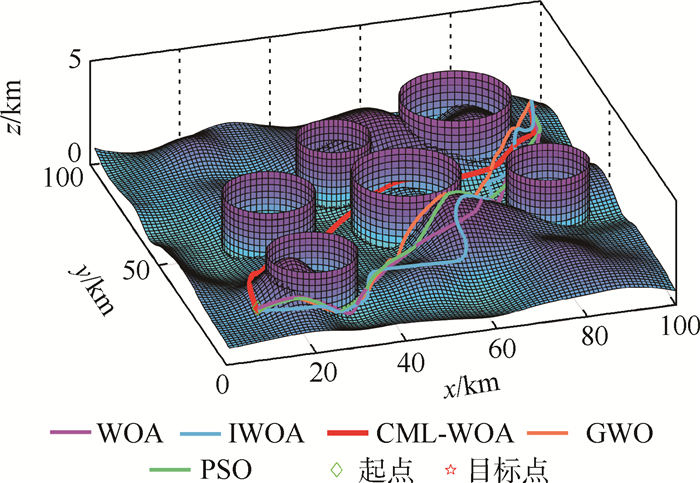
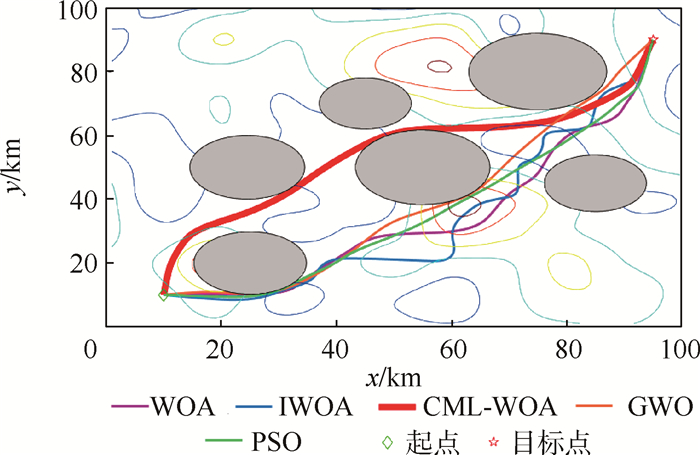
威胁源 威胁类型 位置/km 作用半径/km 高度/km Threat 1 探测雷达 (25，20) 9.8 2.8 Threat 2 地空导弹 (55，50) 11.7 2.9 Threat 3 防空高炮 (85，45) 8.9 3.0 Threat 4 地空导弹 (45，70) 8.0 3.0 Threat 5 探测雷达 (24.5，50) 10.0 2.8 Threat 6 防空高炮 (75，80) 12.0 3.1
下载: 导出CSV
表 8 20维下的规划代价值
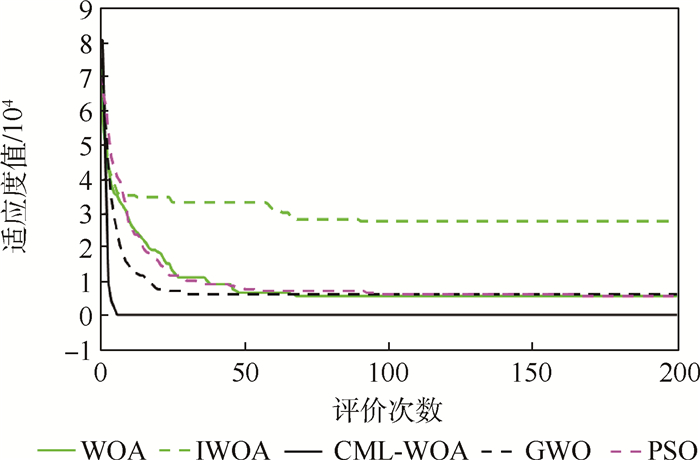
Table 8. Planning cost in 20 dimensions
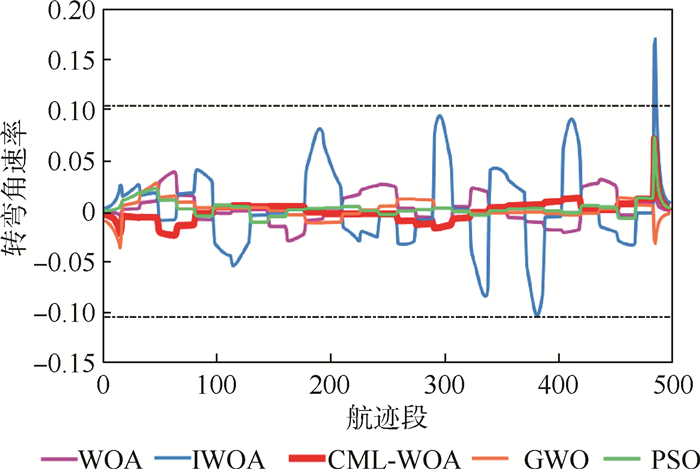
航迹节点数 结果 WOA IWOA PSO GWO CML-WOA 20 平均适应值 2.31×104 2.22×104 2.00×104 2.01×104 8.32×101 标准差 8.84×103 7.35×103 6.35×103 8.21×103 2.92 最大适应值 5.29×104 5.16×104 5.58×104 6.08×104 86.237 8 最小适应值 80.709 8 79.061 2 76.668 6 75.486 7 73.773 7 成功率 0.65 0.60 0.55 0.60 1.00 耗时/s 10.477 7 11.153 1 10.606 1 11.082 9 13.256 1
下载: 导出CSV
-
[1] 胡中华, 赵敏, 姚敏, 等. 无人机航迹规划技术研究及发展趋势[J]. 航空电子技术, 2009, 40(2): 24-29. doi: 10.3969/j.issn.1006-141X.2009.02.006HU Z H, ZHAO M, YAO M, et al. Research and development trend of path planning for unmanned air vehicle[J]. Avionics Technology, 2009, 40(2): 24-29(in Chinese). doi: 10.3969/j.issn.1006-141X.2009.02.006 [2] 符小卫, 高晓光. 一种无人机路径规划算法研究[J]. 系统仿真学报, 2004, 16(1): 20-21. doi: 10.3969/j.issn.1004-731X.2004.01.007FU X W, GAO X G. Study on a kind of path planning algorithm for UAV[J]. Acta Simulata Systematica Sinica, 2004, 16(1): 20-21(in Chinese). doi: 10.3969/j.issn.1004-731X.2004.01.007 [3] 谌海云, 陈华胄, 刘强. 基于改进人工势场法的多无人机三维编队路径规划[J]. 系统仿真学报, 2020, 32(3): 414-420. https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ202003009.htmCHEN H Y, CHEN H Z, LIU Q. Multi-UAV 3D formation path planning based on improved artificial potential field[J]. Journal of System Simulation, 2020, 32(3): 414-420(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ202003009.htm [4] 单文昭, 崔乃刚, 黄蓓, 等. 基于PSO-HJ算法的多无人机协同航迹规划方法[J]. 中国惯性技术学报, 2020, 28(1): 122-128. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGXJ202001019.htmSHAN W Z, CUI N G, HUANG B, et al. Multiple UAV cooperative path planning based on PSO-HJ method[J]. Journal of Chinese Inertial Technology, 2020, 28(1): 122-128(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGXJ202001019.htm [5] 李文广, 胡永江, 庞强伟, 等. 基于改进遗传算法的多无人机协同侦察航迹规划[J]. 中国惯性技术学报, 2020, 28(2): 248-255. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGXJ202002018.htmLI W G, HU Y J, PANG Q W, et al. Track planning of multi-UAV cooperative reconnaissance based on improved genetic algorithm[J]. Journal of Chinese Inertial Technology, 2020, 28(2): 248-255(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGXJ202002018.htm [6] YU X B, LI C L, ZHOU J F. A constrained differential evolution algorithm to solve UAV path planning in disaster scenarios[J]. Knowledge-Based Systems, 2020, 204: 106209. doi: 10.1016/j.knosys.2020.106209 [7] WANG X F, ZHAO H, HAN T, et al. A grey wolf optimizer using Gaussian estimation of distribution and its application in the multi-UAV multi-target urban tracking problem[J]. Applied Soft Computing, 2019, 78: 240-260. doi: 10.1016/j.asoc.2019.02.037 [8] 钱洲元, 雷明. 面向无人机航迹规划的自适应乌贼算法[J]. 哈尔滨工业大学学报, 2019, 51(10): 37-46. doi: 10.11918/j.issn.0367-6234.201805004QIAN Z Y, LEI M. Adaptive cuttlefish algorithm for UAV path planning[J]. Journal of Harbin Institute of Technology, 2019, 51(10): 37-46(in Chinese). doi: 10.11918/j.issn.0367-6234.201805004 [9] 魏江, 王建军, 王健, 等. 基于改进蚁群算法的三维航迹规划[J]. 计算机工程与应用, 2020, 56(17): 217-223. https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG202017032.htmWEI J, WANG J J, WANG J, et al. 3D path planning based on improved ant colony algorithm[J]. Computer Engineering and Applications, 2020, 56(17): 217-223(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG202017032.htm [10] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. doi: 10.1016/j.advengsoft.2016.01.008 [11] 崔东文. 鲸鱼优化算法在水库优化调度中的应用[J]. 水利水电科技进展, 2017, 37(3): 72-76. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD201703012.htmCUI D W. Application of whale optimization algorithm in reservoir optimal operation[J]. Advances in Science and Technology of Water Resources, 2017, 37(3): 72-76(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD201703012.htm [12] BHASKAR N, KUMAR P M. Optimal processing of nearest-neighbor user queries in crowdsourcing based on the whale optimization algorithm[J]. Soft Computing, 2020, 24(17): 13037-13050. doi: 10.1007/s00500-020-04722-0 [13] AGRAWAL R K, KAUR B, SHARMA S. Quantum based whale optimization algorithm for wrapper feature selection[J]. Applied Soft Computing, 2020, 89: 106092. doi: 10.1016/j.asoc.2020.106092 [14] MOHANAKRISHNAN U, RAMAKRISHNAN B. MCTRP: An energy efficient tree routing protocol for vehicular ad hoc network using genetic whale optimization algorithm[J]. Wireless Personal Communications, 2020, 110(1): 185-206. doi: 10.1007/s11277-019-06720-4 [15] LONG W, WU T B, JIAO J J, et al. Refraction-learning-based whale optimization algorithm for high-dimensional problems and parameter estimation of PV model[J]. Engineering Applications of Artificial Intelligence, 2020, 89: 103457. doi: 10.1016/j.engappai.2019.103457 [16] PHAM Q V, MIRJALILI S, KUMAR N, et al. Whale optimization algorithm with applications to resource allocation in wireless networks[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 4285-4297. doi: 10.1109/TVT.2020.2973294 [17] ZHANG H P, WANG H L, LI N, et al. Time-optimal memetic whale optimization algorithm for hypersonic vehicle reentry trajectory optimization with no-fly zones[J]. Neural Computing and Applications, 2020, 32(7): 2735-2749. doi: 10.1007/s00521-018-3764-y [18] 吴坤, 谭劭昌. 基于改进鲸鱼优化算法的无人机航路规划[J]. 航空学报, 2020, 41(S2): 724286. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB2020S2012.htmWU K, TAN S C. Path planning of UAVs based on improved whale optimization algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(S2): 724286(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB2020S2012.htm [19] ABDEL-BASSET M, CHANG V, MOHAMED R. HSMA_WOA: A hybrid novel slime mould algorithm with whale optimization algorithm for tackling the image segmentation problem of chest X-ray images[J]. Applied Soft Computing, 2020, 95: 106642. doi: 10.1016/j.asoc.2020.106642 [20] 覃溪, 龙文. 基于随机差分变异的改进鲸鱼优化算法[J]. 中国科技论文, 2018, 13(8): 937-942. doi: 10.3969/j.issn.2095-2783.2018.08.016QIN X, LONG W. An improved whale optimization algorithm based on stochastic differential mutation[J]. China Sciencepaper, 2018, 13(8): 937-942(in Chinese). doi: 10.3969/j.issn.2095-2783.2018.08.016 [21] 孔芝, 杨青峰, 赵杰, 等. 基于自适应调整权重和搜索策略的鲸鱼优化算法[J]. 东北大学学报(自然科学版), 2020, 41(1): 35-43. https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX202001007.htmKONG Z, YANG Q F, ZHAO J, et al. Adaptive adjustment of weights and search strategies-based whale optimization algorithm[J]. Journal of Northeastern University (Natural Science), 2020, 41(1): 35-43(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX202001007.htm [22] MIRJALILI S. SCA: A sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120-133. http://www.sciencedirect.com/science/article/pii/S0950705115005043 [23] LIU Z Z, WANG Y, YANG S X, et al. An adaptive framework to tune the coordinate systems in nature-inspired optimization algorithms[J]. IEEE Transactions on Cybernetics, 2019, 49(4): 1403-1416. http://ieeexplore.ieee.org/document/8314547/ [24] 郑昌文. 飞行器航迹规划方法研究[D]. 武汉: 华中科技大学, 2003: 99-102.ZHENG C W. Research on route planning for air vehicles[D]. Wuhan: Huazhong University of Science and Technology, 2003: 99-102(in Chinese). [25] POLI R, KENNEDY J, BLACKWELL T. Particle swarm optimization[J]. Swarm Intelligence, 2007, 1(1): 33-57. http://www.cell.com/servlet/linkout?suffix=e_1_5_1_2_25_2&dbid=16&doi=10.1016/j.tibtech.2008.09.005&key=10.1007%2Fs11721-007-0002-0&cf= [26] WANG T T, YANG L, LIU Q. Beetle swarm optimization algorithm: theory and application[EB/OL]. (2018-08-01)[2020-10-14]. https://arxiv.org/abs/1808.00206. [27] XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. doi: 10.1080/21642583.2019.1708830 [28] LI M D, ZHAO H, WENG X W, et al. A novel nature-inspired algorithm for optimization: Virus colony search[J]. Advances in Engineering Software, 2016, 92: 65-88. http://www.sciencedirect.com/science/article/pii/s0965997815001702 [29] RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA: A gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232-2248. -
下载:
点击查看大图
图(14) / 表(8)
计量
- 文章访问数: 680
- HTML全文浏览量: 95
- PDF下载量: 235
- 被引次数: 0
