Topology optimization for periodic thermal conductive material using SIMP method
-
摘要: 为了实现基于宏观热传导条件的周期性材料微结构设计,建立了基于固体各向同性材料惩罚法的周期性结构拓扑优化模型.模型以体积比为约束,散热弱度最小为优化目标.为了满足周期性约束,将设计域划分为若干相同子区域,并重新分配散热弱度.基于偏微分方程的图像处理方式可以有效地消除棋盘格和网格依赖性现象.讨论并分析了不同子区域个数及不同载荷工况对拓扑优化构型的影响.数值实验结果表明:周期性结构的建模方式可以实现基于宏观稳态热传导条件的周期性材料微结构设计.子区域个数不同时,优化得到不同的微结构构型,这反映了尺寸效应对材料设计的影响.当子区域个数不断增加时,优化结果逐渐趋向收敛于均匀化方法对应的极限值.Abstract: In order to obtain periodic material microstructure under macroscopic thermal conduction condition, the optimal topological model of periodic structure was built by solid isotropic material with penalization (SIMP) method. The volume fraction was referred as constraint and minimized thermal compliance was taken as optimization objective in this model. To satisfy the periodic constraint, the designable domain was divided into a certain number of identical unit cells and the thermal compliance was reallocated. The filtered variable implicitly as a solution of a partial differential equation (PDE) was applied to eliminate the checkerboard patterns and mesh-dependence problems efficiently. The optimal topological configurations were analyzed and compared with different numbers of unit cells and different load cases. The numerical results indicate that proposed periodic model is valid in design of periodic material microstructure with macroscopic steady state thermal conduction condition. Microstructure configurations are different when number of unit cells changes and it reflects the influences of size effect to periodic material design. With an increasing number of unit cells, the optimal results gradually converge to the results using homogenization method.
-
由于制造装配简单、易于模块化、成本低等优点，周期性结构在结构设计中受到了越来越多的关注[1]，因此研究其优化设计方法具有重要的理论和工程意义。文献[2-3]分别应用双向渐进结构优化 (BESO) 法和密度法研究了周期性结构拓扑优化方法并获得了较好的结果。文献[4-5]对周期性结构拓扑优化方法进行了分析讨论。文献[6]将周期性结构拓扑优化方法和材料设计方法进行了比较。已有的周期性结构拓扑优化方法通常忽略不确定因素的影响，从而可能导致优化得到的结构稳定性和可靠性较差[7]。相反，考虑不确定条件的结构稳健拓扑优化往往能获得更加稳定的结构[8-9]。
结构稳健拓扑优化已引起了广大学者的重视。文献[10]研究了随机不确定载荷和材料性能下的结构鲁棒拓扑优化。文献[11]对随机载荷下的桁架结构进行优化研究，通过等效成一个凸的极小-极大问题来求解该问题。文献[12]给出了载荷大小不确定条件下的结构柔度均值和方差的解析计算公式，并基于水平集方法实现了结构的稳健拓扑优化。文献[13]采用椭球模型对桁架结构进行了非概率稳健性优化。文献[14-15]提出了任意载荷不确定条件下的结构柔度均值和方差的数值计算方法，并基于密度法实现了结构的稳健拓扑优化。文献[16-17]分别研究了多工况条件下考虑载荷不确定性的结构稳健拓扑优化设计方法。
本文将研究载荷不确定性条件下的周期性结构稳健拓扑优化设计方法，其目标为最小化结构柔度均值和标准差的加权和，约束条件为体积和周期性。由于其简单高效且可以得到设计清晰的结构，本文将采用软删双向渐进结构优化 (Soft-kill BESO) 法[18-20]对周期性结构进行稳健性拓扑优化设计。
本文的主要架构如下：首先，建立周期性结构稳健拓扑优化模型；然后，推导了目标函数以及敏度数计算方法；最后，通过算例说明本方法的有效性以及优化结果的稳健性。
1. 周期性结构
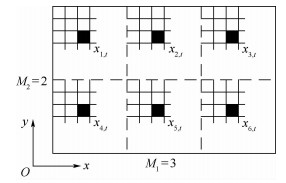
周期性结构是指整体结构由相同形式的子结构组成，即不同子结构相同位置上的单元保持一致元态的结构。以平面周期性结构的设计为例，为了在优化过程中考虑结构的周期性，需将设计区域分割成相同的子域。
如图 1所示，整个区域被分割成M=M1×M2个子域，M1和M2分别表示沿坐标轴x和y方向上的子域数，xs, t为二元态设计变量，本文表示单元 (s, t) 的密度，s和t分别为子域在整体结构中的位置以及该单元在子域中的位置，当该单元为实体单元时其值为1，否则为空单元时取xmin，其中xmin>0是为了避免优化求解过程中结构刚度阵奇异而赋予空单元的一个很小的正实数。
2. 材料插值技术
本文采用的Soft-kill BESO法进行结构拓扑优化设计。该方法在优化过程中将低效能材料单元赋予一个很小的数值，而不是直接删除。以下分析均以第s个子域为例进行表述。应用材料插值技术，每个单元的弹性模量为
(1) 式中：E0为固体单元的弹性模量；p为惩罚因子。由于xs, t为二元态元素，可得
(2) 3. 不确定载荷的周期性结构稳健拓扑优化模型
考虑周期性的结构稳健拓扑优化设计模型可以表示为
(3a) 
(3b) 
(3c) 
(3d) 
(3e) 
(3f) 式中：t=1, 2, …, N；s=1, 2, …, M；J为目标函数；μ(c) 与σ(c) 分别为结构柔度c的均值和标准差；正数α和β为权重系数，且α+β=1；K为结构刚度矩阵；f和u分别为作用力和位移向量；ω∈Θ表示载荷具有不确定性；Vs为第s个子域的总体积；vs, t为第s个子域的第t个单元的体积；V*为最终目标体积；N为每个子域的单元数; M为结构中子域的个数。
对于Soft-kill BESO法，二元态设计变量xs, t为单元的密度，当单元存在时为1，删除时为xmin。约束方程 (3e) 要求每个子域相同位置的单元状态相同，确保了结构设计结果具有周期性。
4. 结构柔度均值和方差的计算[14-15]
对于任一不确定载荷，假设其大小hi和作用方向概率分布均已知。设f2i-1和f2i分别为该载荷的作用点沿x方向和沿y方向施加单位载荷时的结构整体载荷向量，且此时结构整体位移向量为u2i-1和u2i，则对于任意的n个不确定载荷
(4) 式中：ξi定义为
(5) 
(6) 其中：θi为该载荷作用方向与x方向的夹角。
相应的结构位移为
(7) 设m=2n，引入ξi的二阶和四阶中心距分别为
(8) 
(9) 则结构柔度的均值和方差分别为
(10) 
(11) 式中：
5. 敏度数计算、过滤及周期性处理
5.1 敏度数的计算
单元敏度数在Soft-kill BESO法迭代过程中具有很重要的作用，每次迭代过程中根据单元敏度数的大小决定该单元是否删除或者添加。本文的优化目标是结构柔度均值和标准差的加权和，其对密度xs, t的导数为
(12) 式中：
(13) 式中：ks, t0为固体时单元 (s, t) 的刚度阵；ui(s, t)和uj(s, t)分别为载荷fi和fj作用下单元 (s, t) 的位移向量。则单元 (s, t) 的敏度数为
(14) 5.2敏度数过滤及周期性处理
为了克服拓扑优化中常存在的棋盘格、网格依赖性等现象，本文将用敏度过滤法对敏度数进行过滤。首先定义节点敏度数，其本身没有任何物理意义，只是节点相邻单元敏度数的平均值，其表达式为
(15) 式中：Nk为与节点k相连的单元数；Vs, q为与节点k相连的单元q的体积。采用文献[2]中的过滤方法，可以得到过滤后的敏度数公式为
(16) 式中：Mr为过滤区域内包含的节点个数; w(rtk) 线性的权重因子，其定义为
(17) 其中：rmin为指定的过滤半径，指定了节点的过滤区域；rtk为单元t的中心点到节点k的距离。
为了使收敛过程更加稳定，对敏度数进行更新。将敏度数的历史信息和当前迭代信息进行平均是一个比较有效的方法，即
(18) 式中：ite代表当前迭代次数。
为了满足周期性要求，要求每个子域对应位置单元的敏度数一样大，单元删除与添加保持一致。任何子域中单元t的敏度数可以规划为所有子域单元相应第t单元柔度变化的平均值，即
(19) 6. Soft-kill BESO法
Soft-kill BESO法主要根据单元敏度数信息对设计区域的单元进行删除或者添加。在每次单元删除或添加的迭代过程中，首先定义目标体积为
(20) 式中：ER为体积进化率，当体积达到约束值时就不再变化，随后的迭代过程的目标值即为约束值，即
(21) 根据敏度数的大小及每次迭代的目标体积Vite，根据二分法依次移除或者添加相应的单元，具体方法见文献[20]。
7. 本文方法流程
综合上述各部分的分析，可以给出载荷不确定下周期性结构稳健拓扑优化的具体过程如下：
1) 创建分析模型，施加约束边界和载荷条件。
2) 将设计区域划分为有限个周期单元，并初始化。
3) 进行有限元分析，并根据式 (14) 获得敏度数。
4) 通过式 (16) 和式 (18) 对敏度数进行过滤更新。
5) 通过式 (19) 实现周期性约束。
6) 利用第6节算法进行设计变量的更新。
7) 重复3)~6) 直到满足不等式 (22)。
(22) 式中：τmax为允许的收敛误差；NN为考虑的迭代次数。
8. 数值算例
针对本文算例，载荷大小不确定性对结构优化影响较小，因此，在算例分析时只考虑载荷方向不确定情况。本节以2个算例来说明本文方法有效性，并对载荷不确定性对周期性结构优化结果的影响进行分析总结。采用单位双线性正方形平面应力单元离散结构。材料特性为：弹性模量E=1 Pa，泊松比μ=0.3。优化过程中xmin=10-3，惩罚因子p=3，优化结束的准则为τ≤τmax=0.001。
8.1 双侧固定梁结构问题
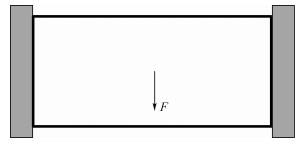
双侧固定梁结构如图 2所示，设计域为80 m×40 m的长方形，左、右两侧均固定。中间施加一集中力F，大小为10 N，其作用方向与水平方向夹角服从均匀分布，区间为[-π/2-π/6, -π/2+π/6]。材料的许用体积为设计域的50%。
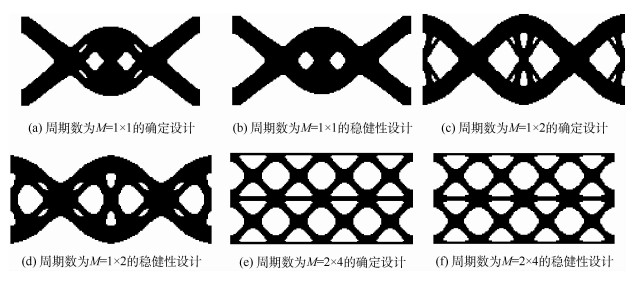
将整个设计区域离散为12 800(160×80) 个单元，并将均值和方差的权重系数α、β设置为0.5。对周期数为M=1×1、M=1×2、M=2×4的确定载荷情况、载荷方向不确定情况进行优化，优化结果如图 3和表 1所示。
图 3 双侧固定梁拓扑优化得到的构型Figure 3. Layouts obtained from topology optimization of bilateral clamped beam表 1 双侧固定梁拓扑优化结果Table 1. Topology optimization result of bilateral clamped beamJ 周期数 稳健性优化 确定性优化 均值 标准差 目标函数 均值 标准差 目标函数 M=1×1 525.62 11.98 268.80 529.72 7.84 268.78 M=1×2 601.58 1.78 301.68 615.17 17.70 316.44 M=2×4 862.01 35.40 448.71 884.58 33.04 458.81 由图 3可知，优化结果边界清晰、周期性明显，说明本文方法是有效的。相对于确定优化，稳健性优化结构的材料更加集中于水平传力路线上，这样的最优结果增加了结构的水平承载能力。总之，在载荷存在方向不确定的情况下，稳健性优化得到的结构更加稳定，抵抗不确定性的能力更强。
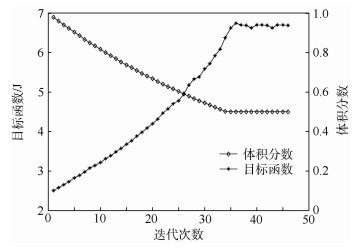
图 4给出了周期数M=2×4的稳健性优化的收敛历史曲线。拓扑优化从满设计开始，去除率为2%，过滤半径取3。每次迭代去除2%的材料直到体积约束50%满足为止，然后体积保持常数，进行单元优化分布直到收敛条件满足为止。由图 4可知，体积分数和目标函数逐渐收敛且收敛过程迅速平稳，再次说明用该方法的有效性和稳定性。
图 4 双侧固定梁拓扑优化迭代历史Figure 4. Iteration history of topology optimization of bilateral clamped beam8.2 米歇尔结构问题
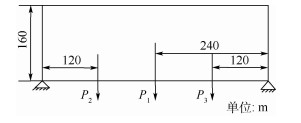
如图 5所示，初始结构为480 m×160 m的矩形区域，两底端角点均简支，结构下端中心及距两侧各四分之一处分别作用一个竖直向下的不确定载荷P1、P2和P3。大小均为1 N，其作用方向均符合正态分布，方向的均值为θ=-π/2，标准差均为σ=π/6。材料的许用体积为设计域的40%。
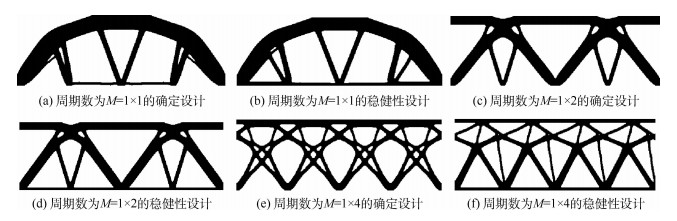
将整个设计区域离散为76 800(480×160) 单元，将均值和方差的权重系数α、β设置为0.5。对周期数为M=1×1, M=1×2, M=1×4的确定载荷情况、载荷方向不确定情况进行优化，优化结果如图 6所示。
图 6 米歇尔结构拓扑优化得到的构型Figure 6. Layouts obtained from topology optimization of Michelle structure由图 6可知，优化结果边界清晰、周期性明显，说明本文方法是有效的。考虑载荷方向不确定性时与确定性时获得的结构构型相比变化明显：结构底端出现连接端点及载荷作用点的横杆，使得水平方向承载能力加强了，进而增加了结构整体的稳健性。
稳健优化结果和确定优化结果在载荷不确定下的目标值如表 2所示，可知确定性载荷条件下得到的结构在考虑载荷不确定性时的柔度均值、标准差和目标函数值均高于稳健优化得到的结果。因此，稳健优化的结构更加坚固和稳定，这证明了本文方法的有效性。
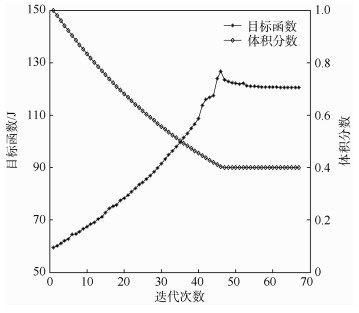
表 2 米歇尔结构拓扑优化结果Table 2. Topology optimization result of Michelle structureJ 周期数 稳健性优化 确定性优化 均值 标准差 目标函数 均值 标准差 目标函数 M=1×1 92.43 10.46 51.45 141.66 67.41 104.54 M=1×2 120.52 14.87 67.70 359.52 235.67 297.60 M=1×4 139.89 20.44 80.17 265.13 132.34 198.74 图 7给出了周期数为M=1×2稳健性优化的收敛历史曲线。拓扑优化从满设计开始，去除率为2%，过滤半径取4。每次迭代去除2%的材料直到体积约束40%满足为止，然后体积保持常数，进行单元优化分布直到收敛条件满足为止。由图可知，体积分数和目标函数逐渐收敛且收敛过程迅速平稳，说明该方法在本例中的应用是有效和稳定的。
9. 结论
本文研究了周期性约束下结构的稳健拓扑优化方法，针对线弹性体结构，基于概率方法提出了周期性结构稳健拓扑优化模型和求解方法。本文的主要贡献及结论：
1) 提出了弹性结构的周期性稳健拓扑优化模型。
2) 推导了周期性约束及载荷不确定条件下单元敏度数计算方法。
3) 应用数值算例验证了算法的稳定性和有效性。
4) 对不同约束条件下的算例研究表明：针对周期性结构，稳健性优化设计比确定性优化设计得到的结果更加稳定。
-
[1] Sigmund O.Materials with prescribed constitutive parameters-an inverse homogenization problem[J].International Journal of Solids and Structures, 1994, 31(17):2313-2329. [2] Sigmund O, Torquato S.Design of materials with extreme thermal expansion using a three-phase topology optimization method[J].Journal of the Mechanics and Physics of Solids, 1997, 45(6):1037-1067. [3] Zhang W H, Wang F W, Dai G M, et al.Topology optimal design of material microstructures using strain energy-based method[J].Chinese Journal of Aeronautics, 2007, 20(4):321-328. [4] 张卫红, 孙士平.多孔材料/结构尺度关联的一体化拓扑优化技术[J].力学学报, 2006, 38(4):522-529. Zhang W H, Sun S P.Integrated design of porous materials and structures with scale-coupled effect[J].Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(4):522-529(in Chinese). [5] Hunag X, Xie Y M.Optimal design of periodic structures using evolutionary topology optimization[J].Structural Multidisciplinary Optimization, 2008, 36(6):597-606. [6] Zuo Z Z, Xie Y M, Huang X D.Optimal topological design of periodic structures for natural frequencies[J].Journal of Structural Engineering, 2011, 137(10):1229-1240. [7] Xie Y M, Zuo Z H, Huang X D, et al.Convergence of topological patterns of optimal periodic structures under multiple scales[J].Structural Optimization, 2012, 46(1):41-50. [8] Yan J, Cheng G D, Liu L.A uniform optimum material based model for concurrent optimization of thermoelastic structures and materials[J].International Journal for Simulation and Multidisciplinary Design Optimization, 2008, 2(4):259-266. [9] Liu L, Yan J, Cheng G D.Optimum structure with homogeneous optimum truss-like material[J].Computers and Structures, 2008, 86(13-14):1417-1425. [10] Niu B, Yan J, Cheng G D.Optimum structure with homogeneous optimum cellular material for maximum fundamental frequency[J].Structural and Multidisciplinary Optimization, 2009, 39(2):115-132. [11] 刘远东, 尹益辉, 郭中泽.静动态力学条件下多孔金属的材料/结构多级优化设计研究[J].中国科学:技术科学, 2012, 42(10):1172-1178. Liu Y D, Yin Y H, Guo Z Z.Static and dynamic design based on hierarchical optimization for materials and structure of porous metals[J].Scientia Sinica:Technologica, 2012, 42(10):1172-1178(in Chinese). [12] Li Q, Steven G P, Querin O M, et al.Shape and topology design for heat conduction by evolutionary structural optimization[J].International Journal of Heat and Mass Transfer, 1999, 42(17):3361-3371. [13] Li Q, Steven G P, Xie Y M, et al.Evolutionary topology optimization for temperature reduction of heat conducting fields[J].International Journal of Heat and Mass Transfer, 2004, 47(23):5071-5083. [14] Bendsoe M P, Sigmund O.Topology optimization-theory, methods and applications[M].Berlin:Springer, 2003:270-272. [15] 左孔天, 陈立平, 张云清, 等.用拓扑优化方法进行热传导散热体的结构优化设计[J].机械工程学报, 2005, 41(4):13-21. Zuo K T, Chen L P, Zhang Y Q, et al.Structual optimal design of heat conductive body with topology optimization method[J].Chinese Journal of Mechanical Engineering, 2005, 41(4):13-21(in Chinese). [16] 龙凯, 左正兴.稳态热传导下的连续体结构拓扑优化[J].中国机械工程, 2007, 18(24):2939-2943. Long K, Zuo Z X.Topological optimization of continuum structure for heat conduction[J].China Mechanical Engineering, 2007, 18(24):2939-2943(in Chinese). [17] 龙凯, 左正兴.多工况稳态热传导下的连续体拓扑优化[J].中国机械工程, 2007, 18(16):1925-1929. Long K, Zuo Z X.Topological optimization of continuum structure for heat conduction under multiple loading[J].China Mechanical Engineering, 2007, 18(16):1925-1929(in Chinese). [18] 刘书田, 贺丹.渐进密度AESO方法及其在热传导结构拓扑优化中的应用[J].计算力学学报, 2009, 26(2):151-156. Liu S T, He D.Progressive AESO algorithm and application in topology optimization of heat conduction structures[J].Chinese Journal of Computational Mechanics, 2009, 26(2):151-156(in Chinese). [19] Gao T, Zhang W H, Zhu J H, et al.Topology optimization of heat conduction problem involving design-dependent heat load effect[J].Finite Elements in Analysis and Design, 2008, 44(14):805-813. [20] 张晖, 刘书田, 张雄.拓扑相关热载荷作用下稳态热传导结构拓扑优化[J].中国机械工程, 2009, 20(11):1339-1343. Zhang H, Liu S T, Zhang X.Topology optimization of steady-state heat conduction problems with design-dependent heat loads[J].China Mechanical Engineering, 2009, 20(11):1339-1343(in Chinese). [21] Bendsoe M P.Optimization of structural topology, shape and material[M].Berlin:Spriner, 1995:83. [22] Sigmund O, Petersson J.Numerical instabilities in topology optimization:A survey on procedures dealing with checkerboards, mesh-dependencies and local minima[J].Structural and Multidisciplinary Optimization, 1998, 16(1):68-75. [23] Sigmund O, Maute K.Sensitivity filtering from a continuum mechanics perspective[J].Structural and Multidisciplinary Optimization, 2012, 46(4):471-475. [24] Lazarov B S, Sigmund O.Filters in topology optimization based on Helmholtz-type differential equations[J].International Journal for Numerical Methods in Engineering, 2011, 86(6):765-781. [25] 焦洪宇, 周奇才, 李文军, 等.基于变密度法的周期性拓扑优化[J].机械工程学报, 2013, 49(13):66-72. Jiao H Y, Zhou Q C, Li W J, et al.Periodic topology optimization using variable density method[J].Journal of Mechanical Engineering, 2013, 49(13):66-72(in Chinese). [26] Andreassen E, Clausen A, Schevenels M, et al.Efficient topology optimization in MATLAB using 88 lines of code[J].Structural and Multidisciplinary Optimization, 2011, 43(1):1-16. [27] Sigmund O, Maute K.Topology optimization approaches[J].Structural and Multidisciplinary Optimization, 2013, 48(6):1030-1055. -
下载:
点击查看大图
计量
- 文章访问数: 1134
- HTML全文浏览量: 87
- PDF下载量: 650
- 被引次数: 0
下载:
