Trajectory optimization method of aircraft endurance flight based upon control surface trimming
-
摘要: 舵面偏转除了能够提供保证飞机稳定飞行的配平力矩,还将改变飞机的升阻比,从而影响其续航性能。在基于飞机质点假设的传统航迹优化方法的基础上,研究了飞机的升阻特性对其续航性能的影响:在上升段、巡航段及下降段前期增大升阻比,在下降段后期减小升阻比,有利于提高飞机的续航性能;提出了基于舵面配平的续航飞行航迹优化方法,以获得更接近于发挥飞机实际潜力的最优航迹与最大航程。对于多操纵面布局飞机,通过该方法能够确定其最优舵面组合配平规律。算例飞机的优化结果表明:相比单一舵面配平,最优舵面组合配平能够使算例飞机的总航程最大提高7.5%。Abstract: Besides providing balancing moment for stable flight, control surface deflection will change the lift-drag ratio of the airplane, which affects the endurance performance of the airplane. Based on the traditional flight trajectory optimization which assumes that the airplane is a particle, the effects of lift-drag characteristic on aircraft endurance performance are analyzed. Increasing lift-drag ratio at climb segment, cruise segment and earlier descent segment, and decreasing lift-drag ratio at later descent segment will improve the endurance performance of the airplane. In order to obtain the optimum flight trajectory and range closer to the actual potential of airplane, a trajectory optimization method of aircraft endurance flight based upon control surface trimming is proposed. Through this method, the optimum combined trimming mode of control surfaces can be obtained for multi-control surface airplane. The optimization result of a type of aircraft indicates that, compared to single trimming modes of control surface, the optimum combined trimming mode increases the total range by 7.5% at most for the example airplane.
-
翼伞不同于常规降落伞,是一种利用前缘切口进入的冲压滞止空气来保持设计翼型的柔性翼,可以产生升力滑翔飞行,应用很广泛。翼伞系统主要由伞衣和伞绳组成,伞衣和伞绳都由柔性材料制成,在飞行时翼伞结构会发生比较大的变形,偏离预先的设计图纸。
由于试验手段和试验经费的限制,使得数值模拟成为分析翼伞流固耦合问题的主要手段。Kalro等[1]根据空投试验给定伞衣的外形变化,并分析了开伞阶段的运动过程。Kalro和Tezduyar[2]使用流体有限元和结构有限元并行耦合算法计算了翼伞的稳态飞行时的外形。Ibos等[3]开发了SINPA软件计算了翼伞的流固耦合问题并与试验对比。Fogell等[4]分析了无限长翼伞一个气室的弱流固耦合问题。Altmann[5]使用势流理论和索有限元法分析了翼伞的流固耦合问题。国内目前对翼伞结构变形的研究较少,朱旭和曹义华[6-7]研究了刚性翼伞平面形状和一些设计参数对气动性能的影响。陆伟伟等[8]预先给定伞衣的鼓包变形情况,并计算了翼伞的气动性能。张春和曹义华[9]在刚性肋片的假设下使用壳单元计算了伞衣的变形。
本文在使用计算流体力学(CFD)方法计算三维翼伞定常气动特性的基础上,分析了前缘切口和翼肋开孔对压强分布的影响;在建立翼伞系统的结构有限元模型时不满足于刚性假设和壳单元,基于翼伞柔性结构的特点并考虑伞绳对结构变形的影响,分别使用不能承受弯矩的膜单元和只能单向受拉的索单元模拟伞衣和伞绳,建立了翼伞结构的索膜有限元模型,结合CFD方法计算了翼伞结构的变形和应力分布,得到的相关结论为工程设计提供了一定的参考。
1. 气动载荷计算
1.1 网格划分
本文分析的翼伞为经过飞行试验的矩形翼伞,几何参数为:展长为2.4 m,弦长为0.8 m,伞衣的前缘从正面看设计为圆弧形状,半径为1.6 m,展向划分为15个气室。在每个翼肋的下方弦向分布着4个伞绳连接点,如图 1所示。由于伞绳很细,阻力较小,翼伞系统的载荷主要是伞衣受到的压强载荷,在CFD计算时不考虑伞绳的影响,主要分析伞衣的气动特性和表面压强分布,同时不考虑伞衣透气性的影响。
内腔和外部流场划分为非结构网格,入口边界距离翼伞5倍弦长,其余边界距离翼伞10倍弦长。在距离翼伞比较近的区域进行了网格加密,并在壁面附近划分了边界层网格,网格数目为300万,伞衣周围的网格弦向剖面如图 2所示。
模拟海平面处5°攻角速度10 m/s翼伞稳态飞行的气动特性,入口为速度入口,出口为自由出口,其他外部边界为自由边界条件,翼伞上下翼面和翼肋为壁面边界,内腔和外部流场通过interface交换数据;为了考虑翼肋上开孔的影响,将内腔用翼肋划分为15份气室,相邻气室在翼肋开孔处用interface交换数据;湍流模型采用k-ω二方程模型。
1.2 计算结果
翼伞中部气室弦向剖面的压力分布云图如图 3所示。可以看出,驻点位于切口的上半部分,内腔保持为驻点滞止压力维持伞衣的成形。气体从驻点沿切口往下流动越过一个钝角才能到达下翼面,因此在下翼面前部产生一个小的流动分离区导致下翼面的低压区[10]。该区域虽然会影响翼伞的升力系数,但是对前缘的成形应有着积极作用。
边缘气室内腔速度矢量如图 4所示。可以看出,在每个气室的内腔,除了文献[11]中弦向的漩涡外,还有着展向的漩涡。同时中部气室的内腔气体通过翼肋开孔向边缘气室流动,以此来改善翼尖气室的充气状况,减小翼尖塌陷现象发生的可能性。
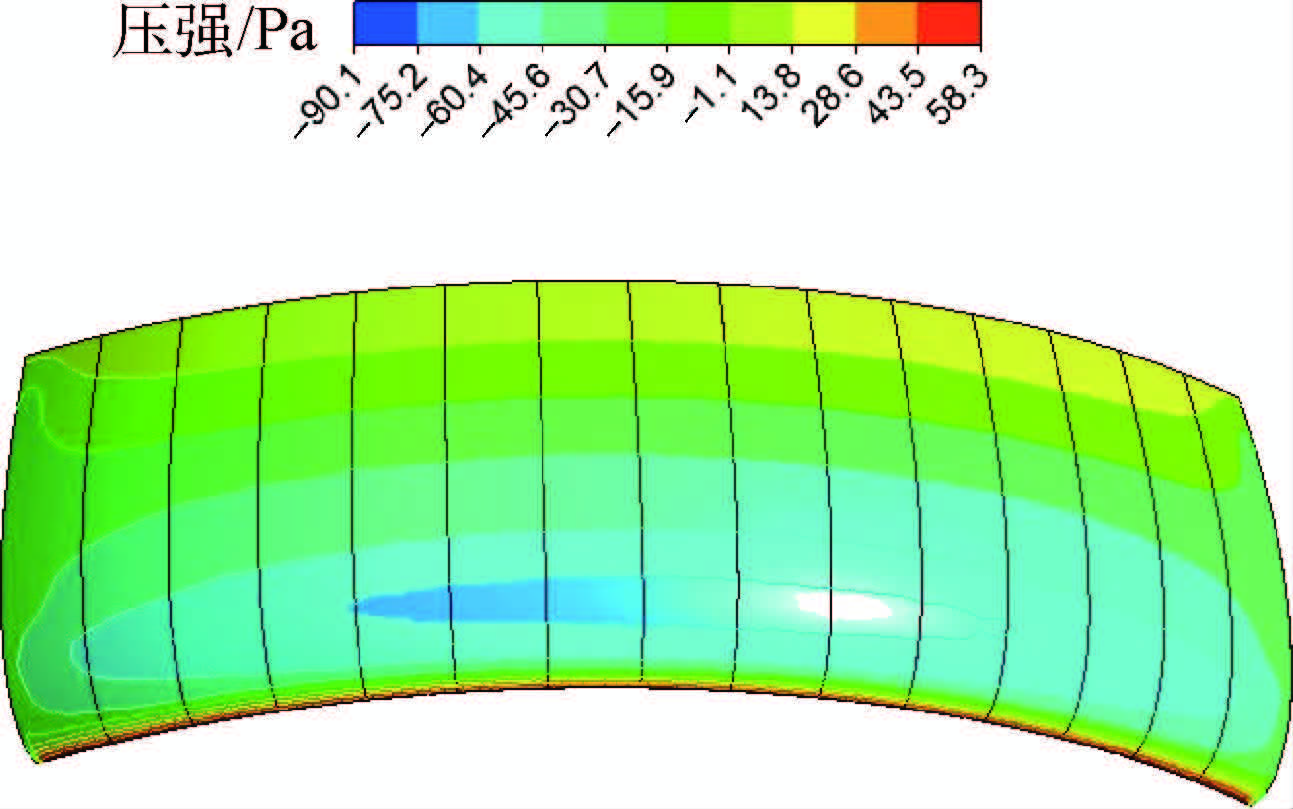
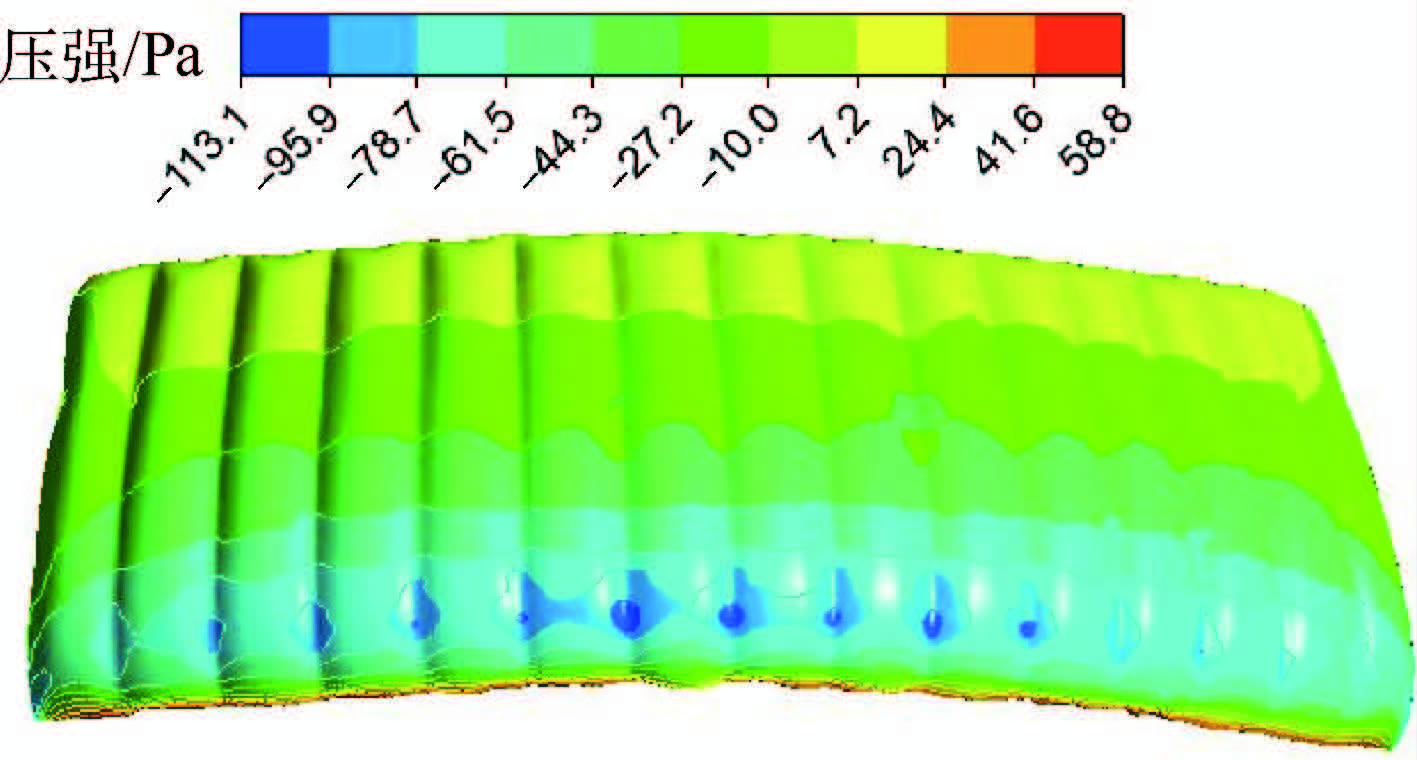
图 5为翼伞外表面压力分布云图。可以看出,由于伞衣弧形和翼尖涡等因素的影响,上翼面负压区主要分布在中部气室,该区域受到的载荷最大。把得到的表面压力分布和内腔压力分布施加在翼伞结构上,计算结构的变形。
2. 翼伞的索膜有限元模型
有限元法是当今结构分析中应用最广泛的数值方法。翼伞一般由柔性织物材料制成,抗弯刚度很小,是通过形状变化来承受载荷的[12],变形具有大往移小应变的特点,属于有限元法中的几何非线性问题。使用U.L.格式分析几何非线性问题的增量形式矩阵方程如下[13]:

(1) 式中:u为节点位移增量向量;ttKL为切线刚度矩阵;ttKNL 为初应力矩阵;t+ΔtQ为节点外载荷向量;ttF为Kirchhoff应力张量等效载荷向量。所有这些矩阵或向量元素都是对应于t时刻位形并参考t时刻位形确定的。
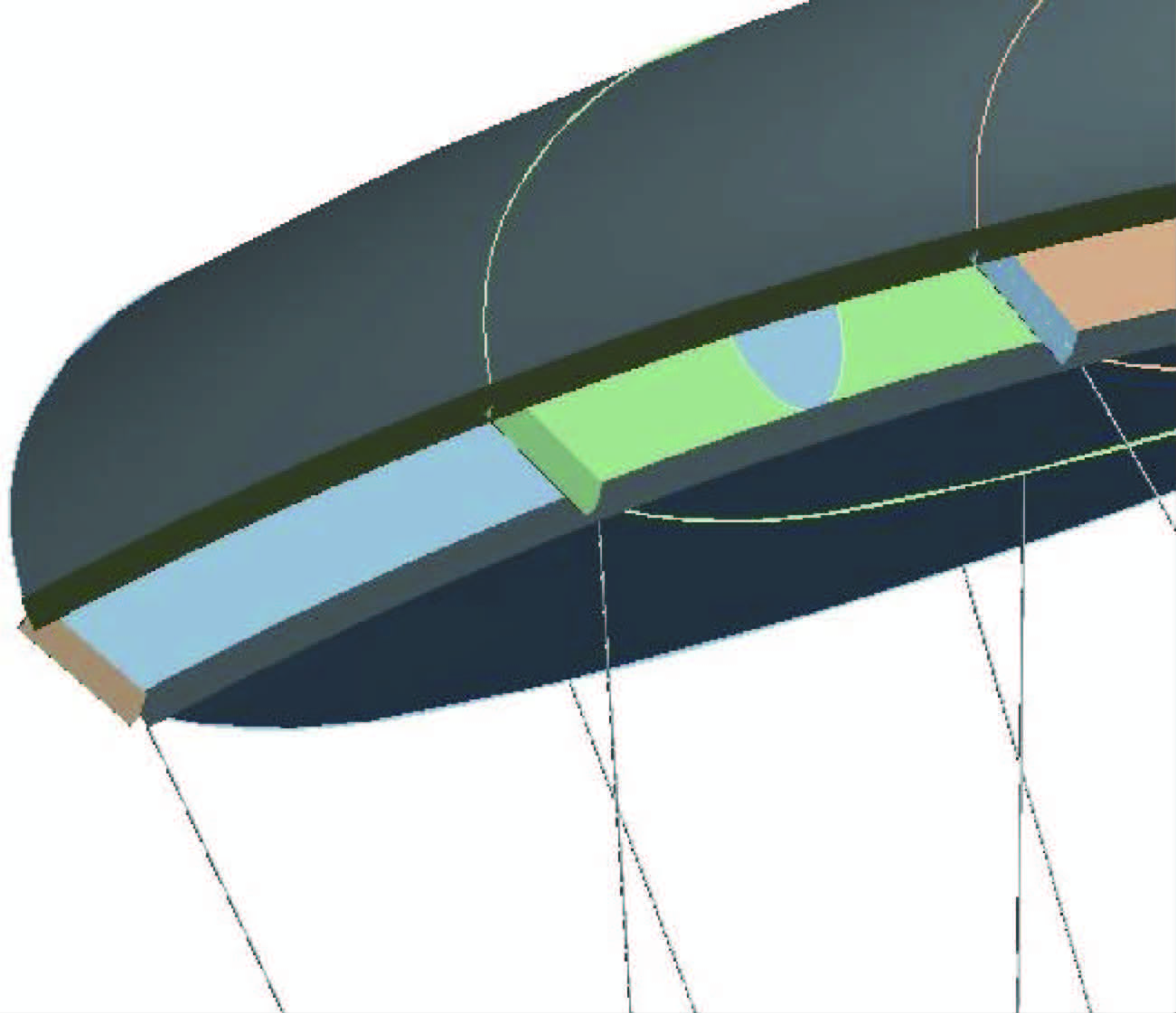
相比于壳单元,用不能承受弯矩的膜单元来模拟伞衣更符合伞衣的结构特点;同时用不能承受弯矩只能单向受拉的索单元来模拟伞绳的作用。在建模的过程中,为了保证伞衣开口的正确成形和准确模拟翼伞真实结构,在上下翼面前端和翼肋切口处加上宽度为1 cm的加强带,如图 6所示。加强带也使用索单元来模拟。
由于膜单元的法向应力为0,导致膜单元刚度矩阵含有零对角元素,而总体刚度矩阵是单元刚度矩阵的集成,当相邻膜单元处于同一平面或接近同一平面时,总体刚度矩阵中与平面法向方向相对应的主对角元素会出现小主元的情况,导致计算发散。对应的物理意义是:平面膜材无法承受法向载荷,只有具有一定曲率的膜材才能承受法向载荷。设计图纸为变形前的外形,膜材曲率不够,只施加垂直于表面的压强载荷会导致计算发散。为了解决第1个载荷子步结构计算发散的问题,在伞衣上通过温度载荷施加预应力。

(2) 式中:ε为初始预应变;α为热膨胀系数;T为施加温度;T0为参考温度。由于预应力、预应变的存在,膜材具有了一定的刚度可以进行第1个载荷子步的计算,在每个载荷子步逐渐使得温度载荷趋向于T0,最后1个载荷子步的计算完全消除了预应力,这样预应力就不会影响得到的最终变形结果。
翼伞结构网格划分如图 7所示。伞衣划分为三角形膜单元,单元数目为11万,节点数目为6万;由于伞绳各段的长度不长,伞绳和加强带划分为两节点直线索单元[14],单元数目为819,节点数目为1 610。固定2个伞绳汇交点,同时为了避免翼伞向两侧倾倒的刚体运动,在翼伞中部施加了展向的对称边界条件。
3. 计算结果及分析
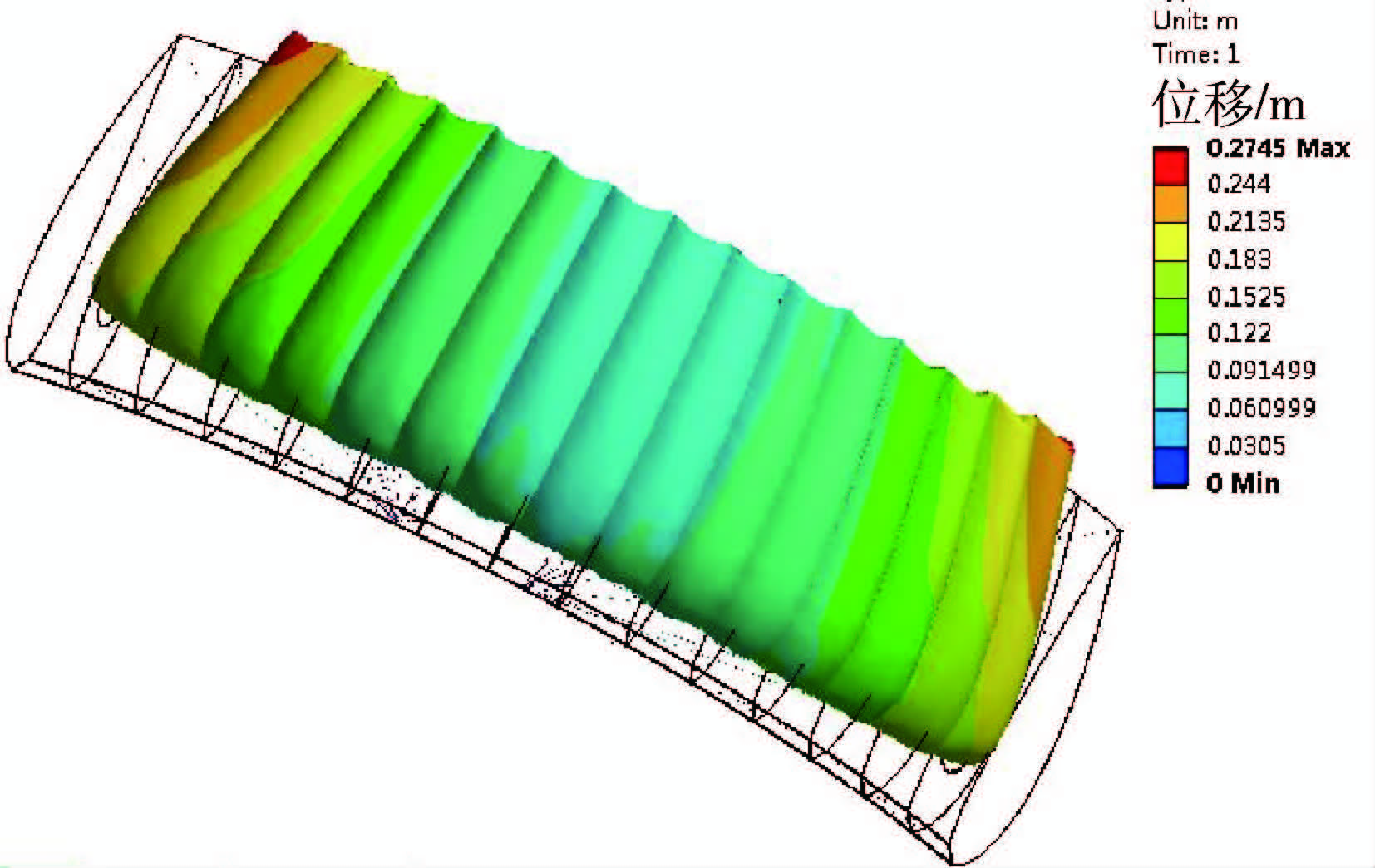
5°攻角下CFD计算的伞衣内表面和外表面压力分布通过插值映射传递到伞衣结构上,为了避免计算发散,该载荷以随着子步时间线性增加的方式施加在伞衣上。伞衣材料为MIL-C-7020Ⅲ[15](美国海空军航空兵C-9伞即采用该材料),弹性模量为430 MPa,泊松比为0.14,伞衣厚度为1 mm;伞绳材料为Kevlar29,弹性模量为97 GPa,直径为1 mm;加强带为芳纶织带,弹性模量为400 GPa,厚度为2 mm。计算得到的位移分布云图如图 8所示。由于翼伞结构存在着大位移,以下显示的所有变形结果均为真实比例,没有进行过放大处理。
从图 8可以看出,由于伞衣充气形成“鼓包”,变形以后展向长度缩小了2个气室的宽度0.32 m,实际飞行展长相对设计展长而言减小了13%。同时,由于飞行时受到压差阻力的作用,整个伞衣从理想设计位置向后移动,翼尖部分的向后位移更大,伞衣外形不再保持为矩形,而是向后弯曲形成一个附加的约为2°的后掠角。相对理想设计位置最大的位移发生在翼尖后缘0.27 m处,发生这么大的位移是由伞衣的受力特性和伞绳的约束特性共同决定的。当气室充气时,气室间上下翼面必须弯曲形成足够的曲率来承受载荷,每个气室宽度都会减小;伞绳为柔性结构只能约束伞绳汇交点和翼肋连接点的相对距离,导致翼肋在以汇交点为圆心、伞绳长度为半径的圆弧上的大范围移动,类似于手风琴的收缩造成了与理想设计外形的较大差别。
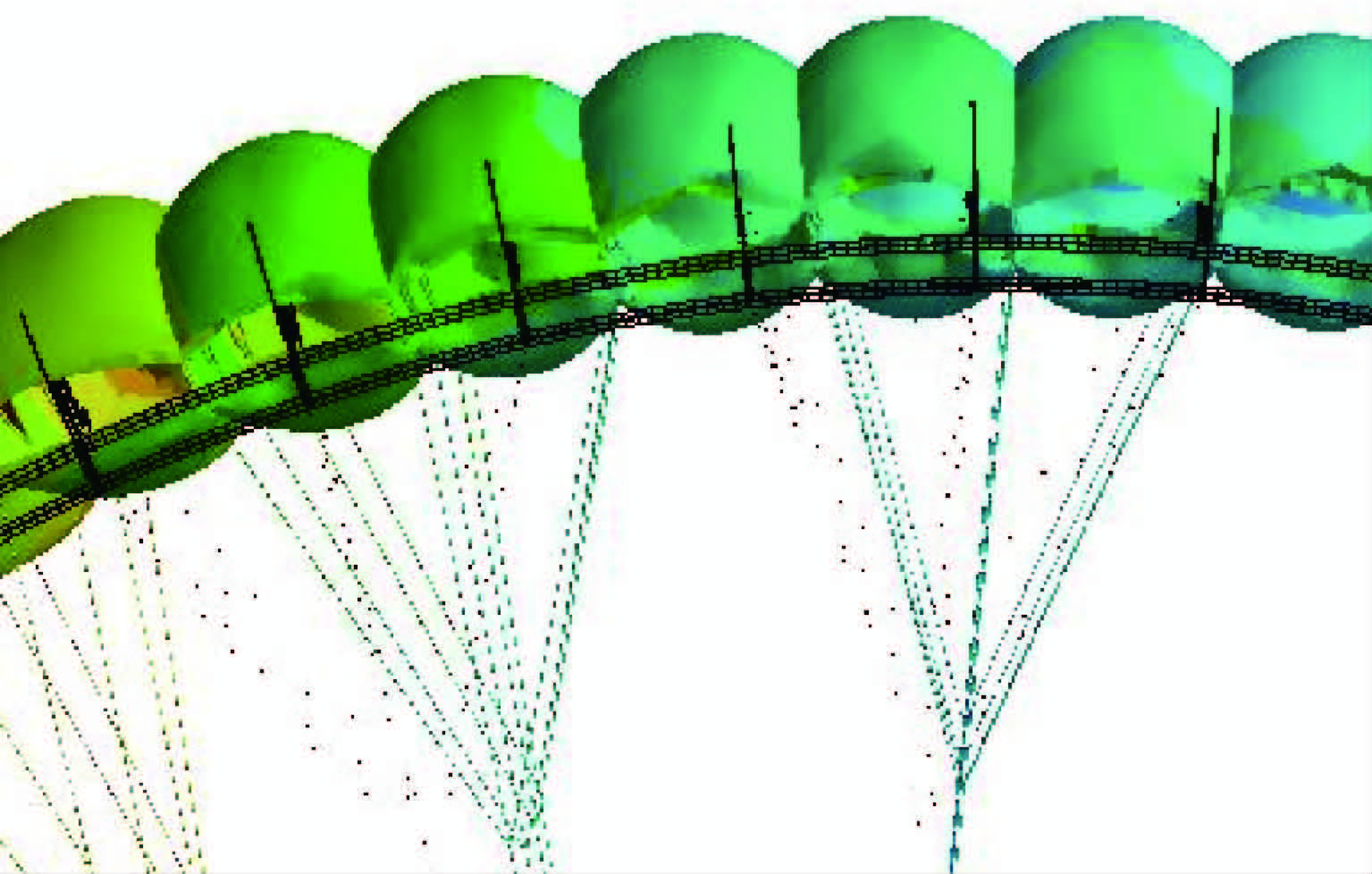
图 9为翼伞变形的正视图。可以看出,发生了前述的伞衣和伞绳的展向移动,同时前缘有比较小的向上移动,形成一个约为1.4°的附加攻角,这是因为伞衣受到的气动载荷主要作用在前端,在柔性伞绳的约束下,伞衣整体发生了俯仰方向的转动。开口上方有一些褶皱的现象,这是距驻点比较近、内外压差很小引起的,有引起开口闭合气室坍缩的危险,所以在这里加上了加强带。上下翼面的“鼓包”清晰可见,设计时该翼伞的翼型选择为Clark-Y18,最大厚度为18%,形成“鼓包”以后最大厚度增大为26%左右。图 10为飞行中的该翼伞“鼓包”变形图,与仿真结果比较类似,具有一定的参考意义。
变形后的伞衣外表面压力分布云图如图 11所示。与图 5对比可以看出,在各个气室相交的凹陷处出现了低压极值,气室凸出部位的吸力减小,前缘的压力分布变得不均匀,这应该是由“鼓包”引起的展向流动分离引起的。变形前仿真得到的伞衣升力系数为0.36,阻力系数为0.05,升阻比为7.2,变形后得到的升力系数为0.30,阻力系数为0.055,升阻比为5.5。
翼肋上的等效应力云图如图 12所示。可以看出,开孔附近和伞绳连接处的应力较大,最大应力为377 419 Pa,这是因为上翼面的载荷通过翼肋传递到伞绳,以及应力集中效应,为了防止被撕裂,在这些区域应采用加强措施。由于翼肋的法向载荷很小,翼肋并没有发生比较大的变形,只是发生了空间的位移。
4. 结 论
本文对稳态飞行情况下的矩形翼伞气动变形进行了三维数值模拟,主要得到了以下结论:
1) 开口会引起流动分离,下翼面前缘附近产生一个低压区,冲压空气通过翼肋开孔向边缘气室流动,以此来改善翼尖气室的充气状况。
2) 由于柔性伞绳的约束特性,气动力作用下翼伞会相对于理想设计位置发生较大的位移,伞衣充气变形后该翼伞的展长相对于设计值减少了13%,同时附加了2°的后掠角和1.4°的攻角。
3) “鼓包”使得气室中部的最大厚度增大了8%,伞衣充气变形后升阻比下降。气室开口上方有一些褶皱的现象,为了防止气室坍缩需要加上加强带辅助成形。
4) 翼肋没有发生比较大的变形,只是有空间的整体位移,开孔附近和伞绳连接处的应力较大,需合理布置加强结构以满足强度要求。
-
[1] HUANG G Q,LU Y P,NAN Y.A survey of numerical algorithms for trajectory optimization of flight vehicles[J].Science China Technological Sciences,2012,55(9):2538-2560. [2] RIVAS D,FRANCO A,VALENZUELA A.Optimization of unpowered descents for commercial aircraft:AIAA-2011-7019[R].Reston:AIAA,2011. [3] CHERN J S,LIU Y C,CHEN C S.Investigation of maximum range cruise flight for B787:AIAA-2010-7809[R].Reston:AIAA,2010. [4] SHAPIRA I,BEN-ASHER J.Range maximization for emergency landing after engine cutoff[J].Journal of Aircraft,2005,42(5):1296-1306. [5] LI X,NAIR P B,ZHANG Z G.Aircraft robust trajectory optimization using nonintrusive polynomial chaos[J].Journal of Aircraft,2014,51(5):1592-1603. [6] NG H K,SRIDHAR B,GRABBE S.Optimizing aircraft trajectories with multiple cruise altitudes in the presence of winds[J].Journal of Aerospace Information Systems,2014,11(1):35-47. [7] 陈晓,王新民,周健.无人飞行器纵向剖面轨迹优化[J].控制理论与应用,2013,30(1):31-36. CHEN X,WANG X M,ZHOU J.Optimization of vertical profile trajectory for unmanned aerial vehicle[J].Control Theory & Applications,2013,30(1):31-36(in Chinese). [8] FLANZER T C,BOWER G C,KROO I M.Robust trajectory optimization for dynamic soaring:AIAA-2012-4603[R].Reston:AIAA,2012. [9] MUELLER R.Multi-objective optimization of an aircraft trajectory between cities using an inverse model approach:AIAA-2012-4489[R].Reston:AIAA,2012. [10] VALENZUELA A,RIVAS D,FRANCO A.Cruise optimization using trajectory patterns:AIAA-2010-9140[R].Reston:AIAA,2010. [11] SACHS G,LENZ J,HOLZAPFEL F.Trajectory optimization for maximizing the range of powered sailplanes with retractable propeller:AIAA-2009-5626[R].Reston:AIAA,2009. [12] 方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005:26-30,34,43. FANG Z P,CHEN W C,ZHANG S G.Aircraft flight dynamics[M].Beijing:Beihang University Press,2005:26-30,34,43(in Chinese). [13] WANG G,HU Y,WU C,et al.Improving performance of flying wing UAV with propeller thrust involved trimming the pitching moment:AIAA-2013-4421[R].Reston:AIAA,2013. [14] 周堃,王立新.大型军用运输机的飞行航迹优化[J].北京航空航天大学学报,2010,36(6):654-658. ZHOU K,WANG L X.Vertical flight trajectory optmization of heavy military airlift aircraft[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(6):654-658(in Chinese). [15] WU S F,GUO S F.Optimum flight trajectory guidance based on total energy control of aircraft[J].Journal of Guidance,Control and Dynamics,1994,17(2):291-296. [16] CAVCAR A.Climb performance of piston-propeller airplane with cambered wing and variable propeller efficiency[J].Journal of Aircraft,2011,48(5):1701-1707. -

 点击查看大图
点击查看大图
计量
- 文章访问数: 1050
- HTML全文浏览量: 108
- PDF下载量: 493
- 被引次数: 0







 下载:
下载:












 下载:
下载: