Gap filling method for space environment data based on singular spectrum analysis
-
摘要: 空间环境数据具有典型的非线性、非平稳特征,并经常包含有缺失数据,给预报模型的建立、预测以及物理过程的分析带来了一定的困难。为了实现对缺失数据的插补,基于奇异谱分析(SSA)迭代插补的思想,设计了一种能够适用于不同缺失数据分布的插补方案。该方案提取出原始时间序列中缺失数据分布数组,利用缺失数据分布数组生成交叉验证所用的测试数据集,并利用离散粒子群优化算法寻找SSA的2个关键性参数,即嵌入窗口长度和主成分个数。通过不同太阳活动年份实际观测的太阳风参数、地磁指数等实例验证了算法的有效性。
-
关键词:
- 奇异谱分析(SSA) /
- 离散粒子群优化算法 /
- 数据插补 /
- 空间环境 /
- 时间序列
Abstract: The space environment data is known to be nonlinear and non-stationary and often contains missing values, which brings great challenge to the model-building procedures, predictions and posterior analysis. To fill the data gaps, a new gap filling method based on the iterative singular spectrum analysis (SSA) algorithm was put forward. The new method considered the distribution of missing values by extracting a distribution array first and used the array to generate the test data set. The discrete particle swarm optimization algorithm was adapted to obtain the two key parameters of SSA, i.e. the embedded window size and the number of principal components. Taking the solar wind parameters and geomagnetic indices of different solar activity years as examples, the test results demonstrate that the filling method is effective. -
近年来,弹道导弹攻防技术得到了很大的发展,传统的利用目标雷达散射截面积(RCS)、结构和形状等信息进行识别的技术已不能满足要求,需要采用不依赖于目标形状和电磁特性的方法进行目标识别[1]。自美国海军实验室的Chen教授将微动拓展到雷达领域以来[2],利用微动特征进行目标识别的方法越来越受到国内外学者们的关注[3]。另外,随着战场环境的日趋复杂,单部雷达也暴露出对目标姿态敏感、由于遮挡效应不能获取目标完整的微动信息、部分进动参数无法解耦等缺点。组网雷达能够获得不同视角下目标的微动信息,能够克服单部雷达存在的上述缺点。同时针对传统组网雷达进行目标参数特征提取时,仅仅利用其多视角信息而并没有充分利用所有信息这一不足,本文在利用组网雷达多视角信息进行参数提取的基础上,还对提取的参数进行了融合处理,合理利用了组网雷达信息,提高了参数估计的精度。
窄带雷达因其距离分辨率有限,在刻画目标尺寸、结构等细节上存在不足,所以一般用于空间目标的粗分辨。宽带雷达距离分辨率高,在对目标进行观测时,可将目标等效为一些强的散射点[4],通过对这些孤立散射点的分析来提取目标参数并进行成像。文献[5]利用单部雷达对进动目标参数进行了提取,但由于单一视角的局限性,在对参数进行提取过程中,对锥体目标底面半径进行了近似,同时对部分模糊参数进行了优化,过程较为复杂。文献[6]对雷达参数与目标参数之间关系进行了分析,得出了要对参数进行解耦至少需要2个不同视角的观测信息。同时分析了在一定范围内,2个雷达视角之间差距越大,参数估计的越精确。文献[7]利用广义Hough变换、参数拟合等方法从多视角距离像中提取出目标参数,但是广义Hough变换解算复杂,同时在推导过程中忽略了底面半径对参数的影响。
为充分利用组网雷达信息,本文在利用宽带多视角信息进行参数求解的基础上,提出了一种根据雷达性能指标进行融合的新算法。首先,通过距离像分析和Hough变换实现了锥顶散射点关联和参数提取。然后,以进动角为例,通过文献[8]分析得出的融合权系数与雷达性能之间的关系对进动角进行了融合,同时根据融合后的参数重构了目标的空间位置。最后,在不同信噪比条件下,通过定义一个整体参数误差公式,利用不同融合方法对整体参数误差进行了仿真,结果表明本文融合算法得到的精度较好,验证了算法的适用性。
1. 进动锥体目标距离像分析
1.1 锥体进动建模
进动锥体目标模型如图 1所示,锥体对称轴与锥旋轴的交于O点,锥体底面半径为r,锥顶与O点的距离为h1,底面中心与O点的距离为h2,半锥角为ε,进动角为θ,进动角速度为ω。雷达视线与锥体对称轴的夹角(观测角)为β,与进动轴的夹角为α。由文献[9]可知,雷达观测到的散射点数量与雷达视角相关。当满足β∈(0, ε)∪(π/2, π-ε)时,锥体目标上可观测到A、B、C3个强散射点。由于ε较小[9],因此本文主要对β∈(π/2, π-ε)进行锥体进动分析。
由文献[6]可知,雷达视线角β(t)满足式(1),其中φ0为初相。

(1) 假设平动分量已补偿,设初始时刻雷达距O点的距离为R0且满足远场条件。散射点A、B、C到雷达视线的径向距离变化表达式为

(2) 分析式(2) 可知,散射点A满足正弦变化,散射点B、C由于进动,径向距离变化存在着非正弦变化的分量rsin β(t)。同时由式(1) 可知,进动角θ与雷达视角α存在耦合,仅依靠单一视角不易获取参数。所以本文考虑利用组网雷达多视角的优点,从满足正弦变化的散射点A进行参数提取。
1.2 散射点关联
组网雷达中每部雷达由于观测视角不同,得到的距离像也不同。利用组网雷达多视角信息,首先要确定各雷达站距离像中属于同一散射点的峰值位置,即距离像匹配。由式(2) 可知,A、B、C 3个散射点的径向距离变化之和满足正弦变化,与A点有相同的频率ω和初相φ0。

(3) 在一个周期内,利用相同时间间隔对3个散射点径向距离和进行采样,通过最小二乘拟合,可估计出频率ω和初相φ0。此时,可采用二参数Hough变换提取距离像中散射点A的振幅和中值参数,由此便可利用组网雷达散射点A的信息。
2. 参数求解
2.1 进动角θ、结构参数h1和雷达视角αi的求解
由式(1) 和式(2) 可得,第i部雷达观测得到的散射点A的振幅lAi和中值lCi表达式为

(4) 为解决进动角θ与雷达视角αi之间的耦合,对式(4) 进行变形,可得

(5) 式(5) 有2个未知参数h1和θ,可通过第i部和第j部雷达联立2个方程组进行求解。

(6) 
(7) 
(8) 2.2 结构参数h2、r的求解
联立式(3) 和式(7) 即可求出结构参数h2。当cos(ωt+φ0)=0时,由式(2) 得

(9) 在提取出散射点A信息时条件下,利用“clean”算法[10]减去雷达回波中散射点A的分量,再运用峰值法提取散射点B、C某个时间上的距离值,求出|RB-RC|的值,此时联立式(6)、式(8) 和式(9) 可求出r的值。
3. 进动角自适应融合
3.1 进动角加权系数矩阵求解
在第2节参数求解的公式中,可以看出进动角与雷达视角和结构参数均有关系,一定程度上进动角的估计精度影响着雷达视角和结构参数的估计精度。同时可知利用2部不同视角的雷达即可求出进动角等参数,现以组网雷达中任意2部雷达作为参数求解单元,则n个单元求得的矩阵


(10) 式中:θ=(θ, θ, …, θ)T,θ为进动角真实值; V=(v1, v2, …, vn)T,vk为第k个单元求出进动角产生的误差,满足(0, σk2)的高斯分布且进动角误差之间相互独立(k=1, 2, …, n), σk2为第k个单元求出的进动角误差方差。令进动角估计值







(11) 式中:



(12) 3.2 进动角误差方差分析
由式(12) 和式(6) 可知,加权系数与进动角误差的方差有关,而进动角与散射点A距离像的振幅lA和中值lC有关。
以第k求解单元中雷达1与雷达2为例进行分析,提取散射点A距离像的中值与振幅。为简化分析,令x1=lA1,x2=lC1,x3=lA2,x4=lC2,θk=f(x), x=(x1, x2, x3, x4)。现对θk进行全微分,得

(13) 根据误差的传递性,θk的估计方差为

(14) 由式(10) 可知

在相同观测时间内,同部雷达同一散射点距离像幅值与中值的微分是一致的,仅与雷达分辨力相关,所以dxi满足dx1=dx2、dx3=dx4。在多数情况下锥体目标散射点之间是稀疏的,散射点B、C对散射点A的影响可以忽略。在雷达达到其理想分辨力的情况下,由文献[8]可以得到D(dxi)满足:

(15) 式中:SNR为散射点A在距离像上的峰值信噪比;δr为距离分辨率,即为c/(2B)。c为光速,Br为雷达带宽。综上分析加权系数矩阵满足的表达式为

(16) 
(17) 式中:δr1和δr2为第1、2部雷达分辨率;SNR1和SNR2为第1、2部雷达信噪比。
由此可看出,进动角权系数矩阵与雷达带宽和回波信噪比有关,而这2个因素也正是判断雷达性能指标的依据之一。当雷达带宽确定时,可通过提高回波的信噪比来提高提取数据的精度。而文献[11]仅仅指出加权因子与雷达性能有关,却并没有具体指出与雷达性能的关系。
3.3 融合求解
经过上述推导,进动角θ可通过每个求解单元求出的进动角通过加权系数矩阵进行融合来提高估计精度,表达式如下:

(18) 对于结构参数,可以运用同样的方法进行融合处理,在此不具体阐述。雷达视角αi仅与雷达和目标之间的空间位置有关,无法进行融合,可利用融合后的结构参数θ和h1对αi进行求解来提高αi的估计精度。
4. 锥体目标三维空间位置重构
4.1 组网雷达模型
图 2为组网雷达观测锥体目标示意图,假设目标平动已补偿,N部雷达均可达到时间上和空间上的同步要求。以O为原点建立参考坐标系O-XYZ,其中OZ为锥旋轴,初始时刻锥体对称轴与Z轴所在平面为YOZ面,XYZ满足右手坐标系,同时建立全局坐标系O0-X0Y0Z0。参考坐标系与全局坐标系之间的坐标转换可参考文献[12]。设雷达网中有N部雷达,Ri表示第i部雷达,ni表示Ri雷达的视线,其中i=1, 2, …, N。设雷达Ri在O0-X0Y0Z0全局坐标系中的俯仰角和方位角为(γi, χi),则雷达视线方向矢量为ni=[cos γi cos χi, cos γi sin χi, sin γi]。
4.2 三维矢量求解
文献[13]中指出三维微动特征为旋转矢量ω及旋转轴的单位矢量e。在结构参数已知的条件下,可利用旋转矢量ω和旋转轴的单位矢量e对锥体目标进行空间位置重构。由图 2可知,


在全局坐标系下,令



(19) 式中:RA1和RA2为同一时刻获得的散射点径向距离值。不同时刻获得的RAi不同,求解得到的锥顶坐标也不同。在一个进动周期内,在等间隔时间对锥顶坐标进行求取,可重构出锥顶在空间中位置。
令旋转轴矢量e=(ex, ey, ez)T,根据全局坐标系下雷达视线方向矢量ni、参考坐标系下雷达视角αi和进动角θ,在一个求解单元中,可联立如下方程组:

(20) 利用式(19) 和式(20) 解出的旋转矢量ω和旋转轴的单位矢量e即可重构出锥体顶点的空间位置。锥体底面2个散射点由于具有滑动性,不同的雷达视角观测得到的位置不同,不易进行重构。在结构参数已知的条件下,通过锥顶的空间位置,即可确定出锥体目标的位置。
综上,基于自适应融合的弹道目标空间位置重构具体步骤如下:
步骤1 建立锥体进动模型,由几何关系求出散射点径向距离表达式。通过分析3个散射点径向距离和与锥顶散射点径向距离的关系实现锥顶散射点匹配关联。
步骤2 利用Hough变换提取出锥顶散射点的中值与幅值,联立2部雷达解出进动角、雷达视角和结构参数。
步骤3 以进动角误差方差最小来求解最佳权系数矩阵,再根据系数矩阵求出融合后进动角的估计值。对于结构参数上述融合算法进行了处理。
步骤4 建立组网雷达模型,在利用融合的估计值求出锥顶坐标和锥旋轴矢量的基础上,实现了锥体目标空间位置的重构。
5. 仿真分析
5.1 仿真结果
雷达参数设置:组网雷达系统中有3部雷达,均发射线性调频信号,载频分别为:10、20、20 GHz,信号带宽分别为2、3、3 GHz,现有的国内公开报道的高分辨雷达的带宽可以达到3.2 GHz[14],所以本文的参数设置具有合理性。现对3部雷达进行编号分别为1、2、3。3部雷达雷达观测时间均为2 s,脉宽均为50 μs,重复频率为500 Hz,在全局坐标系下的俯仰角和方位角分别为(π/8, π/4) rad、(π/6, π/8) rad、(π/8, π/4) rad,回波信噪比分别为10、8、10 dB。目标参数设置:目标为旋转对称锥体,h=2.5 m,h1=2 m,h2=0.5 m,r=0.5 m,θ=10°,锥旋角速度为ω=4 π rad/s,锥旋轴在全局坐标系下的视角为(π/2, π/4) rad, φ0=-45°。根据设置的雷达视角和锥旋轴视角参数,由式(20) 可解出3部雷达在参考坐标下的理论值分别为α1=145.34°、α2=167.53°和α3=177.04°,满足锥体目标3个散射点可见的条件。
组网雷达中的3部雷达,以雷达1和雷达2为求解单元1,雷达1和雷达3为求解单元2,雷达2和雷达3为求解单元3。图 3为单元1中的2部雷达得到的时间距离像。图 4(a)为雷达2散射点距离和序列。由1.2节分析可知,通过距离和序列可求出锥旋角速度ω和初相φ0。利用已知的锥旋频率ω和初相φ0对雷达2散射点进行二参数Hough变换,如图 4(b),可提取出散射点A的中值和幅值。运用上述方法均可提取得到3部雷达散射点A的中值和幅值。
表 1为3个求解单元得到的进动角、锥体顶点坐标(t=0.25 s)和锥旋轴矢量。在一个锥旋周期内(t=0~0.5 s),以0.025 s为一个时间步长,确定出相应时刻RA的值,通过式(19) 可求出对应的锥顶坐标。求锥顶坐标时利用到了散射点A的距离值,可按照进动角的融合法则进行融合。对旋转轴矢量的融合是将3个单元求出的结果取平均。表 2为提取出的相关参数。
表 1 求解单元估计结果Table 1. Estimation results of solving unit参数 理论值 单元1 单元2 单元3 3个单元参数融合 估计值 误差/% 估计值 误差/% 估计值 误差/% 参数融合 误差/% θ 10° 10.332° 3.32 10.317° 3.17 9.774° 2.26 10.184° 1.84 xA -0.275 -0.282 2.54 -0.268 2.54 -0.271 1.45 0.272 1.10 yA 1.286 1.318 2.49 1.307 1.63 1.305 1.48 1.310 1.87 zA 1.262 1.292 2.38 1.288 2.06 1.284 1.74 1.286 1.90 ex 0 0.000 1 0.01 0.000 1 0.01 0.000 1 0.01 0.000 1 0.01 ey 0.707 0.724 2.40 0.720 2.16 0.721 1.98 0.722 2.18 ez 0.707 0.723 2.26 0.720 1.84 0.719 1.70 0.721 1.98 表 2 参数估计结果Table 2. Estimation results of parameters参数 理论值 雷达1 雷达2 雷达3 3部雷达参数融合 估计值 误差/% 估计值 误差/% 估计值 误差/% 参数融合 误差/% h1 2 m 2.053 m 2.65 1.968 m 1.60 1.972 m 1.40 1.977 m 1.25 h2 0.5 m 0.514 m 2.80 0.512 m 2.40 0.507 m 1.40 0.511 m 1.80 r 0.5 m 0.492 m 1.60 0.507 m 1.40 0.507 m 1.40 0.506 m 1.20 α1 145° 146.58° 1.09 α2 167° 165.74° 0.75 α2 177° 176.15° 0.48 由表 1和表 2的数据可看出,融合后的参数整体上比未融合的数据误差小。利用融合后的参数和在一个锥旋周期求出的锥顶坐标(t=0.025 s为步长)对锥顶散射点进行了空间位置重构,如图 5所示。由图可看出重构后的轨迹与理论值几乎重合,从而验证了重构方法的准确性和数据融合算法的精确性。
5.2 算法性能分析
为了有效地分析参数的整体估计性能,定义一个整体参数误差来分析不同数量单元融合后整体数据的误差大小。由于参数的类型不同对目标姿态和微动特性影响程度也不同,现对所有估计出的参数按照影响大小设定不同的权值。定义参数误差矩阵


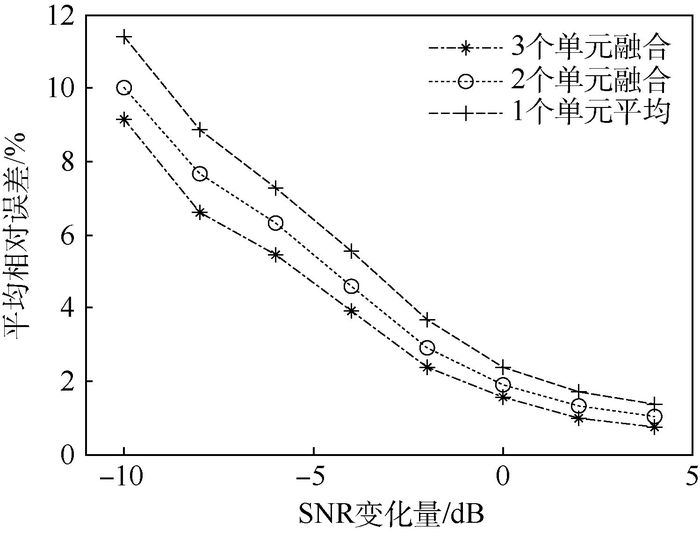
(21) 以5.1节中雷达参数的设置进行分析,设组网中有3部雷达,按照每2部雷达作为一个求解单元,一共有3种求解单元。图 6为不同求解单元数在不同信噪比条件下得到的平均误差示意图。横坐标表示的是在原来雷达回波信噪比的基础上进行提高信噪比和降低信噪比。为了验证本文算法的适用性,减少由于雷达参数不同而引入的系统误差。其中1个单元的结果是由单元1、2、3的结果平均得到的。2个单元的结果是单元1与单元2融合得到的。3个单元的结果是单元1、2、3平均得到的。
6. 结论
本文通过对进动目标距离像进行分析实现了参数求解,并以各个单元(雷达)所求参数误差方差最小为准则对参数进行了融合求解。通过理论分析和仿真实验,表明:
1) 进动角和结构参数误差的大小与雷达性能是相关的。可通过组网雷达的不同性能进行融合处理,降低参数误差。
2) 锥顶坐标和锥旋矢量可以实现锥体目标空间位置的重构,利用融合的参数重构出的目标位置与理论位置接近。
3) 所有单元求出参数进行融合估计与直接将所有参数进行平均估计相比,参数整体误差要小。
4) 进动目标空间位置重构可以为目标识别和目标二维成像提供一定参考。
5) 本文方法不仅可以运用在微动层面,在利用组网进行参数优化求解上均有一定的参考意义。
由于本文未考虑遮挡效应,后期将对不同雷达获取的不同散射点数量进行分析和参数提取。
-
[1] BROOMHEAD D S, KING G P.Extracting qualitative dynamics from experimental data[J].Physica D,1986,20(2-3):217- 236. [2] GHIL M, ALLEN R M,DETTINGER M D,et al.Advanced spectral methods for climatic time series[J].Reviews of Geophysics,2002:40(1):3.1-3.41. [3] ZHIGLJAVSKY A. Singular spectrum analysis for time series: Introduction to this special issue[J].Statistics and Its Interface,2010,3(3):255-258. [4] SCHOELLHAMER D H. Singular spectrum analysis for time series with missing data[J].Geophysical Research Letters,2001,28(16):3187-3190. [5] SHEN Y, PENG F,LI B.Improved singular spectrum analysis for time series with missing data[J].Nonlinear Processes in Geophysics,2014,1(2):1947-1966. [6] GOLYANDINA N, OSIPOV E.The “Caterpillar”-SSA method for analysis of time series with missing values[J].Journal of Statistical Planning and Inference,2007,137(8):2642-2653. [7] KONDRASHOV D, GHIL M.Spatio-temporal filling of missing points in geophysical data sets[J].Nonlinear Processes in Geophysics,2006,13(2):151-159. [8] BECKERS J M, RIXEN M.EOF calculations and data filling from incomplete oceanographic datasets[J].Journal of Atmospheric and Oceanic Technology,2003,20(12):1839-1856. [9] KONDRASHOV D, SHPRITS Y,GHIL M.Gap filling of solar wind data by singular spectrum analysis[J].Geophysical Research Letters,2010,37(15):1-6. [10] KONDRASHOV D, DENTON R,SHPRITS Y Y,et al.Reconstruction of gaps in the past history of solar wind parameters[J].Geophysical Research Letters,2014,41(8):2702-2707. [11] WANG H Z, ZHANG R,LI W.Improved interpolation method based on singular spectrum analysis iteration and its application in missing data recovery[J].Applied Mathematics and Mechanics,2008,29(10):1227-1236. [12] LIU W,JIN W D, WANG H Z,et al.An optimized atmospheric missed data recovery algorithm based on singular spectrum iteration[C]//Proceedings of IEEE Conference on Cybernetics and Intelligent.Piscataway,NJ:IEEE Press,2008:1129-1132. [13] GOLYANDINA N, NEKRUTKIN V,ZHIGLJAVSKY A.Analysis of structure of time series: SSA and related techniques[M].Boca Raton:The Chemical Rubber Company Press,2001:30-73. [14] CHENG D. Time series decomposition using singular spectrum analysis[D].Tennessee:East Tennessee State University,2014:12-14. [15] CLAESSEN D, GROTH A.A beginner's guide to SSA[EB/OL].Paris:Ecole Normale Supérieure,2010[2015-05-10]. [16] WANG R, MA H,LIU G,et al.Selection of window length for singular spectrum analysis[J].Journal of the Franklin Institute,2015,352(2):1541-1560. [17] GOLYANDINA N. On the choice of parameters in singular spectrum analysis and related subspace-based methods[J].Statistics and Its Interface,2010,3(3):259-279. [18] MAHMOUDVAND R, ZOKAEI M.On the singular values of the Hankel matrix with application in singular spectrum analysis[J].Chilean Journal of Statistics,2012,3(1):43-56. [19] VALLE Y, VENAYAGAMOORTHY G K,MOHAGHEGHI S,et al.Particle swarm optimization:Basic concepts,variants and applications in power systems[J].IEEE Transactions on Evolutionary Computation,2008,12(2):171-195. [20] KENNEDY J, EBERHART R C.Particle swarm optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks.Piscataway,NJ:IEEE Press,1995:1942-1948. [21] CHOWDHURY S, TONG W,MESSAC A,et al.A mixed-discrete particle swarm optimization algorithm with explicit diversity-preservation[J].Structural and Multidisciplinary Optimization,2013,47(3):367-388. [22] BOUBAKER S, DJEMAI M,MANANANNI N,et al.Active modes and switching instants identification for linear switched systems based on discrete particle swarm optimization[J].Applied Soft Computing,2014,14:482-488. [23] 郭文忠,陈国龙. 离散粒子群优化算法及其应用[M].北京:清华大学出版社,2012:13-16. GUO W Z,CHEN G L.Discrete particle swarm optimization algorithm and its application[M].Beijing:Tsinghua University Press,2012:13-16(in Chinese). [24] KOROBEYNIKOV A. Computationk- and space-efficient implementation of SSA[J].Statistics and Its Interface,2010,3(3): 357-368. 期刊类型引用(4)
1. 赵锋,徐志明,刘蕾,艾小锋. 弹道目标特征提取研究现状与展望. 信息对抗技术. 2022(03): 15-32 .  百度学术
百度学术2. 徐志明,艾小锋,刘晓斌,吴其华,赵锋. 基于散射中心滑动特性的双基地雷达锥体目标微动特征提取方法. 电子学报. 2021(03): 461-469 .  百度学术
百度学术3. 王红敏,宁生科,董涛. 基于红外触发技术的外弹道目标微动参数估计研究. 兵器装备工程学报. 2021(07): 92-97 .  百度学术
百度学术4. 陈尔康,高长生,荆武兴. 空间目标的轨迹和姿态数据生成. 西北工业大学学报. 2019(02): 378-385 .  百度学术
百度学术其他类型引用(1)
-

 点击查看大图
点击查看大图
计量
- 文章访问数: 949
- HTML全文浏览量: 102
- PDF下载量: 952
- 被引次数: 5







 下载:
下载:





 百度学术
百度学术
 下载:
下载: