-
摘要:
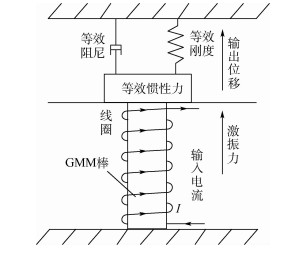
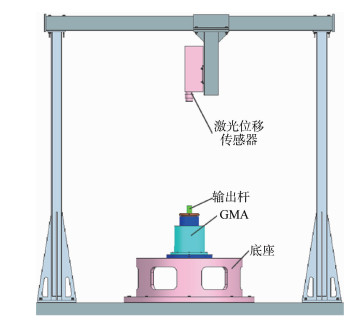
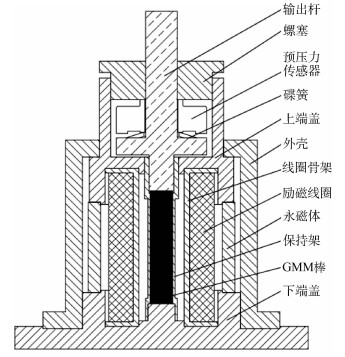
超磁致伸缩作动器（GMA）输入输出之间存在着磁滞非线性关系，当研究其中高频输出特性时，为了降低材料自身迟滞非线性特性的影响，往往选用零点与饱和状态之间线性度较好的不饱和小回线，因此很有必要开展动态不饱和小回线数学模型的研究。首先在综合研究磁致伸缩材料（GMM）和GMA结构动力学特性的基础上结合安培环路定理提出以励磁电流为输入、应变为输出的动态Jiles-Atherton（J-A）模型，然后在引入磁滞回线特性变量的基础上得出J-A模型关键模型参数对其特性的影响规律，根据不饱和小回线仿真与实验波形的偏离特性提出模型参数的修正方法得到不饱和小回线动态J-A模型。最后，在不同频率和不同饱和幅值下通过实验验证该数学模型的正确性。
-
关键词:
- 超磁致伸缩作动器(GMA) /
- 动态 /
- Jiles-Atherton (J-A)模型 /
- 小磁滞回线 /
- 参数修正
Abstract:Hysteresis nonlinear relationship between input and output exists in giant magnetostrictive actuator (GMA). In order to lower hysteresis nonlinearity of material, minor hysteresis loops are often applied when the high frequency characteristics are studied. Therefore, it is very important to research the mathematic model of minor hysteresis loops. First, the dynamic hysteresis model is established combining Ampere circuital theorem with giant magnetostrictive material (GMM) and structural dynamic characteristic of GMA, which regards exciting current as input variable and strain as output variable. Then, the laws between model parameters and hysteresis loop characteristic are achieved by simulation and minor hysteresis loop dynamic Jiles-Atherton (J-A) model is proposed through modifying the model parameters according to the error characteristic between simulation and experiment waveform. Finally, the mathematic model is proved at different frequencies and exciting currents by experiment.
-
图 4 J-A模型参数对磁滞回线特性影响
Figure 4. Influence of J-A model parameters on hysteresis loop properties
图 7 J-A模型修正前后和实验对比
Figure 7. Comparison between J-A model before and after modification and experiment loop
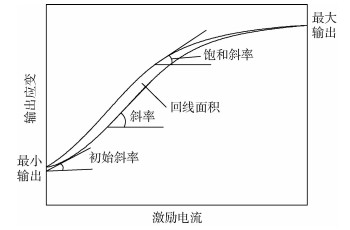
表 1 J-A模型参数对磁滞回线特征参数的影响规律
Table 1. Influencing laws of J-A model parameters on hysteresis loop characteristic parameters
参数 初始斜率 斜率 饱和斜率 最大输出 最小输出 回线面积 a↑ ↓ ↓ ↓ ↓ ↓ - α↑ ↑ ↑ - ↑ ↑ ↓ c↑ ↑ ↑ - - ↓ ↓ k↑ ↑ - ↓ - ↑ - 注：↑表示该变量增大；↓表示该变量减小；-表示该变量保持基本不变的状态。 
下载: 导出CSV
表 2 J-A模型修正前后和实验磁滞回线特征参数
Table 2. Characteristic parameters of J-A model before and after modification and experiment hysteresis loop
参数 数值 实验 模型修正前 模型修正后 初始斜率/(10-4A-1) 2.08 1.00 2.00 斜率/(10-4A-1) 3.4 2.8 3.4 饱和斜率/(10-4 A-1) 1.0 0.7 1.0 最大输出应变/10-4 5.2 4.7 5.2 最小输出应变/10-4 -5.54 -5.4 -5.5
下载: 导出CSV
-
[1] GORAN E.Handbook of giant magnetostrictive materials[M].Sa Diego:Academic Press, 2000:1-13. [2] OHMATA K, ZAIKE M, KOH T.Three-link arm type vibration control device using magnetostrictive actuators[J].Journal of Alloys and Compounds, 1997, 258(1):74-78. https://www.researchgate.net/publication/248171953_A_three-link_arm_type_vibration_control_device_using_magnetostrictive_actuators [3] TALEBIA S, HOJJA Y, GHODSI M.A combined Preisach-hyperbolic tangent model for magnetic hysteresis of Terfenol-D[J].Journal of Magnetism and Magnetic Materials, 2015, 396:38-47. doi: 10.1016/j.jmmm.2015.08.006 [4] 孙英.超磁致伸缩致动器的神经网络控制与动态模型及实验研究[D].天津:河北工业大学, 2007:26-45. http://cdmd.cnki.com.cn/Article/CDMD-10080-2008156848.htmSUN Y.Neural network control and dynamic model as well as experiment for giant magnetostrictive actuator[D].Tianjin:Hebei University of Technology, 2007:26-45(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10080-2008156848.htm [5] SABLIK M J, JILES D C.Coupled magnetoelastic theory of magnetic and magnetostrictive hysteresis[J].IEEE Transactions on Magnetics, 1993, 29(3):2113-2123. https://www.researchgate.net/publication/3097103_Coupled_magnetoelastic_theory_of_magnetic_and_magnetostrictive_hysteresis [6] 田春.超磁致伸缩执行器的本征非线性研究及其补偿控制[D].上海:上海交通大学, 2007:18-32. http://cdmd.cnki.com.cn/Article/CDMD-10497-2008110000.htmTIAN C.Research and compensation control on constitutive nonlinear of giant magnetostrictive actuators[J].Shanghai:Shanghai Jiao Tong University, 2007:18-32(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10497-2008110000.htm [7] DU R, ROBERTSON P.Dynamic Jiles-Atherton model for determining the magnetic power loss at high frequency in permanent magnet machines[J].IEEE Transactions on Magnetics, 2014, 51(6):1-10. https://www.researchgate.net/publication/273161866_Dynamic_Jiles-Atherton_Model_for_Determining_the_Magnetic_Power_Loss_at_High_Frequency_in_Permanent_Magnet_Machines [8] JILES D C, THOELKE J B.Theory of ferromagnetic hysteresis:Determination of model parameters from experimental hysteresis loops[J].IEEE Transactions on Magnetics, 1989, 25(5):3928-3930. doi: 10.1109/20.42480 [9] LADJIMI O, SIXDENIER F, MORAL L.Temperature dependent extension of the Jiles-Atherton model:Study of the variation of microstructural hysteresis parameters[J].IEEE Transactions on Magnetics, 2012, 48(10):2567-2572. doi: 10.1109/TMAG.2012.2201735 [10] NOUICER A, NOUICER E, FELIACH M.A neural network for incorporating the thermal effect on the magnetic hysteresis of the 3F3 material using the Jiles-Atherton model[J].Journal of Magnetism and Magnetic Materials, 2015, 373:240-243. doi: 10.1016/j.jmmm.2014.03.051 [11] IZYDORCZYK J.A new algorithm for extraction of parameters of Jiles and Atherton hysteresis model[J].IEEE Transactions on Magnetics, 2006, 42(10):3132-3134. doi: 10.1109/TMAG.2006.880094 [12] HAMIMID M, MIMOUNE S, FELIACHI M.Minor hysteresis loops model based on exponential parameters scaling of the modified Jiles-Atherton model[J].Physica B:Condensed Matter, 2012, 407(13):2438-2441. doi: 10.1016/j.physb.2012.03.042 [13] CHWASTEK K.Modelling offset minor hysteresis loops with the modified Jiles-Atherton description[J].Journal of Physics D-Applied Physics, 2009, 42(16):1-5. https://www.researchgate.net/publication/236645737_Modelling_offset_minor_hysteresis_loops_with_the_modified_Jiles-Atherton_description [14] 李超, 徐启峰.J-A模型误差修正和温度特性仿真[J].电工技术学报, 2014, 29(9):232-238. http://www.cnki.com.cn/Article/CJFDTOTAL-DGJS201409033.htmLI C, XU Q F.Error modification and temperature simulation of J-A model[J].Transactions of China Electrotechnical Society, 2014, 29(9):232-238(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-DGJS201409033.htm [15] JILES D C, ATHERTON D L.Theory of ferromagnetic hysteresis[J].Journal of Applied Physics, 1984, 55(6):2115-2120. doi: 10.1063/1.333582 [16] JILES D C.Frequency dependence of hysteresis curves inconducting magnetic materials[J].Journal of Applied Physics, 1994, 76(10):5849-5855. doi: 10.1063/1.358399 [17] BERTOTTI G.Physical interpretation of eddy current losses in ferromagnetic materials[J].Journal of Applied Physics, 1985, 57(6):2110-2126. doi: 10.1063/1.334404 [18] ZHENG X J, LIU X E.A nonlinear constitutive model for Terfenol-D rods[J].Journal of Applied Physics, 2005, 97(5):1-8. http://www.oalib.com/references/16422151 [19] STORN R, PRICE K.Differential evolution-a simple and efficient heuristic for global optimization over continuous space[J].Journal of Global Optimization, 1997, 11(4):341-359. doi: 10.1023/A:1008202821328 [20] 贾振元, 王晓煜, 王福吉.超磁致伸缩执行器的动力学参数及磁滞模型参数的辨识方法[J].机械工程学报, 2007, 43(10):9-13. doi: 10.3901/JME.2007.10.009JIA Z Y, WANG X Y, WANG F J.Identification method of giant magnetostrictive actuator dynamics and model parameters[J].Chinese Journal of Mechanical Engineering, 2007, 43(10):9-13(in Chinese). doi: 10.3901/JME.2007.10.009 -
下载:
点击查看大图
计量
- 文章访问数: 971
- HTML全文浏览量: 68
- PDF下载量: 643
- 被引次数: 0
